Harmonics.

What are they and how do they behave?

Let us look at a simple instrument with a single string. (Fig. 1)

Assuming that the string is taut it will emit a sound when plucked. The frequency of the sound depends on the distance between A and B, the diameter and composition of the string and the amount of tension on the string.
Let us assume we have tuned the string to A = 440, we hear the note A or, in musical notation:

But is that all we hear? In this arrangement it is not. You see the note A = 440 is generated by a movement between the nodes (or endpoints in this case) that looks like this: (Fig 2)

But that is not all that it does.

Parts of the string or better, equal subdivisions of the string take on a life of their own and resonate together with the fundamental note. These notes produced by those sections are known as overtones or harmonics

The laws governing harmonics are unbelievably precise. If for instance we have a string tuned to A = 440 and we halve it, both halves will sound at the frequency of 880 which is A one octave higher.

Assuming the tuning of 440 is precise, the halving of the string accurate and the string is of equal diameter and composition over the entire length, the resultant harmonic is precisely 880, not anywhere between 880.1111 and 879.9999. It is important to remember this.

So let us have a look at a few harmonics of a string.

Remember that the sections involved are always precise subdivisions of the entire length.

The harmonics reach quickly frequencies that pass into the inaudible and beyond. They are believed to extend into infinity.

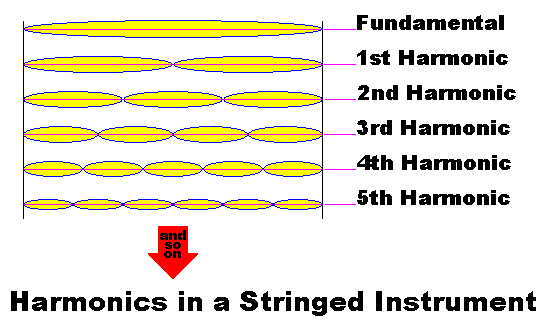
The amplitude (volume) of the harmonics is always smaller than the amplitude of the fundamental.

Now, all this happens as it is stated here only in a pure system. Using a drawn wire for instance we have a fairly pure resonator as in a drawn wire the molecules have been aligned in the direction of the wire in the drawing process and the thickness is even. If you were to use a rubber band for instance the results would be quite different.

Because of variation in thickness and composition along the length of a rubber band the subdivisions produce a variety of harmonics that differ from each other, thus cancelling each other out or creating beat frequencies.

That is why you cannot create with a stretched rubber band the same quality of sound as with a stretched wire, even though the fundamental note of both is precisely the same.