GYRO DROP EXPERIMENT
Performed by Kenneth Gerber, M.D., Richard F. Merritt
Analysis by Edward Delvers
 

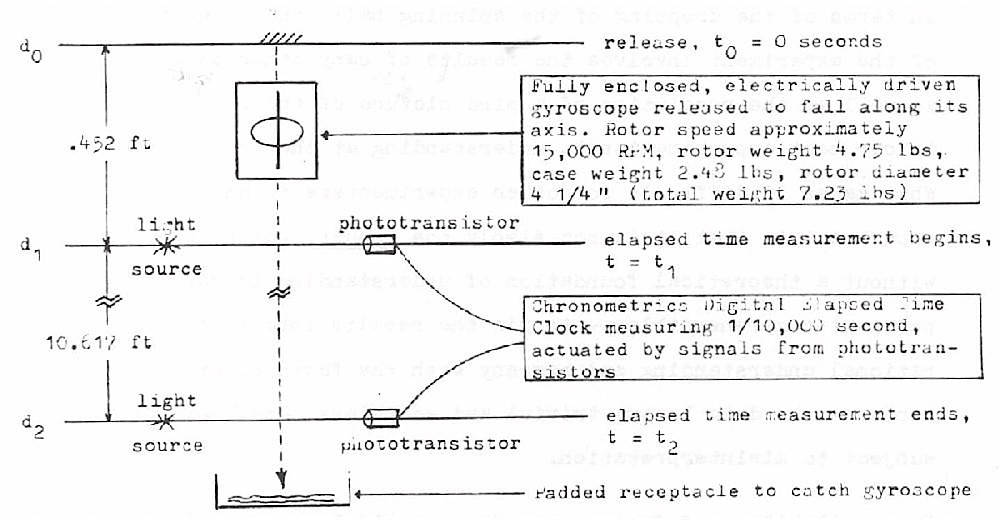
In this experiment a fully enclosed, electrically driven gyroscope is released to fall freely under the influence of gravity. The elapsed time taken to fall a measured distance of 10.617 feet was measured, with the rotor stopped and also with the rotor spinning at approximately 15,000 RPM.

Data was gathered on a Chronometrics Digital Elapsed Dime Clock measuring 1/10,000 second, actuated by two phototransistor sensors placed in the paths of two light beams which were consecutively interrupted by the edge of the casing of the falling gyroscope.

The gyroscope, of total weight 7.23 lbs (rotor weight 4.75 lbs, case weight 2.48 lbs) was released to fall along its axis. Electrical leads supplying power to the 41/4" diameter rotor were disconnected just prior to release.

 

 

EXPERIMENTAL SET-UP

 

SUMMARY OF EXPERIMENTAL RESULTS

 

*Note: Value for gravitational acceleration at sea level, 390 Latitude (Washington, D.C.) based on the formula of the U. S. Coast and Geodetic Survey.
The data for the non-rotating gyroscope is normalized to this value, and the data for the rotating gyroscope is compared to it.

 

 

FICTITIOUS FORCE INCREMENT
 

A hypothetical, fictitious force increment which would have to be applied to the non-rotating gyroscope to impart the increased acceleration noticed in its rotating mode, was calculated for comparison purposes.

Force increment: F = (FR - FNR ) = .024 lbs. = .38 oz.
 
DATA

 

 

STATISTICAL ANALYSIS

 

Value for Student's "t" Test:

t = 2.3980

p = .0275355685 (18 degrees of freedom)

 On the basis of the Standard Deviations of the data from this experiment, one can say with a 97% level of confidence that a fully encased, spinning gyroscope drops faster than the identical gyroscope non-spinning, when released to fall along its axis.

 

 

APPENDIX
 

The following are calculations performed on the measured data to arrive at the values given in the Summary of Experimental Results (above).

a) Calculation to find velocity v1 at beginning of elapsed time measurement for the Non-Rotating gyroscope, using the equation

d = vi t + 1/2 at2 , with
d = (d2 - d1 ) = 10.617 feet (measured); t = (t2 - t1 ) = 0.66203 seconds (ms'd)

a = 32.1549 ft/sec (normalized value); vi = unknown, velocity v1 at time t1.

Substituting values: vi = 5.393 feet/second

 

 b) Calculation to find the distance between release position and beginning of elapsed time measurement segment for the Non-Rotating gyroscope.
vf 2 = vi 2 + 2ad , with

vf = 5.593 ft/sec (from (a) above); vi = 0 ft/sec (initial velocity);

a = 32.1549 ft/sec (normalized value); d = (d1 - d0 ) = unknown.

Solving the equation: d = (d1 - d0 ) = 0.4522 feet

 

c) Calculation to find time already spent falling when the elapsed time measurement begins for the Non-Rotating condition of the gyroscope

vf = vi + at, with

vf =v1 at t1 = 5.393 ft/sec (from (a) above); vi = 0 ft/sec;

a = 32.1549 ft/sec2 (normalized value); t = (t1 - t0 ) = unknown.

Solving the equation: t = (t1 - t0) = 0.1677 seconds

 

d) Calculation to find total time taken to fall total distance for the Non-Rotating condition of the gyroscope.

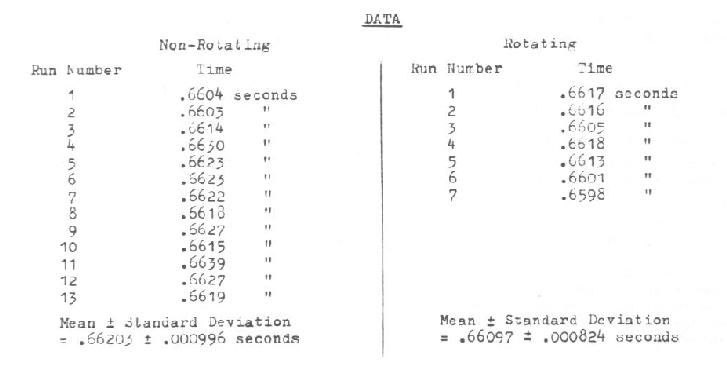
t total NR = (t2 - t1) NR + (t1 - t0) NR = 0.66203 + 0.1677 = 0.82973 seconds

d total NR = (d2 - d1) NR + (d1 - d0) NR = 10.617 + 0.4522 = 11.0692 feet

 

e) Calculation to find time already spent falling by the Rotating gyroscope when elapsed time measurement begins. This assumes the acceleration of the Rotating gyroscope is constant. It is found by comparing the ratio or the initial time interval to measured elapsed time interval for the Non-Rotating gyroscope, to that of the Rotating gyroscope.

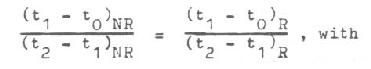
(t1 - t0) NR = 0.1677 sec. (calculated); (t2 - t1) NR = 0.66203 sec. (measured);
(t1 - t0) R = unknown; (t2 - t1) R = 0.66097 sec. (measured).
Solving the equation: (t1 - t0) R = 0.1674 seconds

 

f) Calculation to find acceleration (aR) of the Rotating gyroscope using total time and total distance values, using the equation

d = v i t + 1/2at2 , with

d = 11.069 ft (from (d) above); vi = 0 ft/sec; a = aR = unknown;
t = ttotalR = (t2 - t1 ) R + (t1 - t0) R = 0.66097 + 0.1674 = 0.82857 seconds.
Solving the equation: a = a R = 32.2619 feet/second2.

 

g) Change in Acceleration:

a = aR - a NR = 32.2619 ft/sec2 - 32.1549 ft/sec2 = 0.1070 ft/sec2

Percentage change in acceleration: a/ aNR = 0.00333 = 0.333 %

 

h) Fictitious Force Increment: Calculation to find a hypothetical, fictitious force increment which would have to be applied to the Non-Rotating gyroscope to cause the increased acceleration observed for the Rotating gyroscope. The mass (m) of the gyroscope is assumed not to have changed, for the purposes of this calculation. Using the equation: F = ma

a ratio is set up:

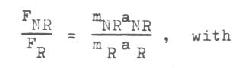
F NR = 7.23 lbs. (measured gyro and case weight); FR = unknown;

a NR = 32.1549 ft/sec2 (normalized value); aR = 32.2619 ft/sec2 (from (f) above). Solving the equation: F = 7.254 lbs.

The fictitious force increment is: F = FR - F NR = 7.254 - 7.23 = 0.024 lbs.;

or converted to ounces: 0.024 lbs. x 16 oz/lb = 0.38 ounces.

 

REFERENCES
 

(1) "The Effect of Gravity on Rotating Objects," Edward C. Delvers and Bruce E. DePalma, 18 March 1974, Simularity Institute reprint.

(2) "Is God Supernatural," Robert L. Dione, Bantam Books, NY, 1976 553-02723-150

(3) "Gyro Drop Experiment," by Kenneth Gerber, M.D., U.S. Department of Health, Education and Welfare; Public Health Service; National Institutes

of Health; National Heart, Lung and Blood Institute; Bethesda, MD 20014, Richard F. Merritt, and Edward Delvers, 1977

(4) "The Cause of Gravitation," A. Bernard Rendle, Modal Research, 51 Dorking Road, Gt. Bookham, Surrey, England, 1971

(5) Unpublished "Elastic Collision Experiment Data," Simularity Institute report.

Back to the Homepage