Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
Wormhole Theory
Return to Modern Relativity
12.1 Metric Engineering
NASA inertia manipulation plans - http://www.lerc.nasa.gov/WWW/bpp/TM-107289.htm
If we limit our physics to special relativity, accomplishing interstellar flight is virtually a technological impossibility. Distances between the stars are too large. As far away as most of the interesting stars are, even if one could accelerate a ship with a high enough acceleration to make a round trip within a crews life time the huge accelerations would crush the crew against the hull of the ship. Even if this crushing problem were overcome, the speed c becomes a cosmic speed limit so the round trip winds up returning the crew generations after they left according to the time of the earth. Also, the fuel requirements to produce such accelerations are impossibly high. All these problems can potentially be done away through a new field of research called metric engineering. The metric tensor is responsible for how all things in the universe tend to age and move. The form that it can take is also determined by what matter is in the space according to Einstein's field equations. It is possible to artificially engineer different metrics by choosing particular arrangements of matter. It is possible that we will be able to engineer a metric that will change the remote coordinate speed of light around starships thus removing the speed c limitation, or to engineer a metric that manipulates inertia itself making a state of acceleration the natural state of the ship instead of a state of constant velocity. This would eliminate fuel requirements altogether as well as eliminate the problems of the crew becoming crushed from the acceleration of the ship.
Here's a simple example of metric engineering
The vacuum of space is actually filled with fields and because of their existence also virtual particles. This means that the vacuum has a nonzero energy density even though vacuum is usually taken to be the zero point for energy density. Now consider if we might polarize the vacuum so that some of the energy from one spot is moved to another spot. Now we have one spot that has a positive energy density relative to the zero point and another spot with a negative energy density relative to the zero point. This second spot is called a hole. Now the positive
143
144 Chapter 12 The New Frontiers
energy density will have the properties of a mass. It will attract all things toward itself, including the hole. On the other hand, the hole would have the properties of a negative mass. It would repel all things from it including the positive mass. As a result the positive mass accelerates in the direction away from the hole and the hole is drawn by the positive mass to chase it. The natural state of this system is a state of acceleration instead of a state of constant velocity. The cabin of a ship could be placed between the positive mass and the hole and it would be drawn to accelerate along with the system. The crew would be drawn to accelerate away at the same rate as the cabin and so they would not be crushed against the walls of the ship.
Exercises
Problem 12.1.1
Consider a positive mass M at r1 and a negative mass -M at r2. Find the acceleration of the system and show that total momentum and energy are conserved.
______________________________________________________________________________
12.2 Wormholes
There are more than one type of wormhole First we'll look at the type associated with Schwarzschild black holes. We'll second look at those associated with Kerr-Newman black holes. Third we will look at the Morris-Thorne wormhole. Finally we will consider a fourth type of wormhole geometry.
The Schwarzschild spacetime's interval expressed in a remote observer's spherical coordinate system takes the form of Eqn.10.1.1
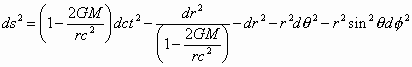
This has a coordinate singularity where the dr2/(1 - 2GM/rc2) term becomes infinite at
r = 2GM/c2. This infinity problem can be removed by a transformation to a different choice of spacetime coordinates. There are various transformations that do this, but a particular choice of transformation called the Kruskal-Szekeres transformation revealed something previously unknown about the black hole spacetime geometry . For our external region of space the Kruskal-Szekeres coordinate transformation is
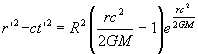
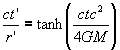
(12.2.1)
12.2 Wormholes 145
R is a constant.
The transformation above is only valid down to the event horizon. Beyond this an extension must be done in which the transformation becomes
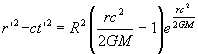
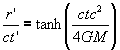
(12.2.2)
With this transformation the equation for the invariant interval becomes
![]()
(12.2.3)
Note that if we choose R = 4GM/e1/2c2 then for r' » r » 2GM/c2 the interval becomes that of special relativity with the exception that it's in spherical coordinates. Thus this could serve as a transformation to a frame local to the event horizon. However, we must transform to a frame where the affine connections also vanish there to have a local free fall frame.
Now if we consider working out the inverse transformations to these we must note that the squared r' and ct' each have two roots. This leads us to realize that the Schwarzschild spacetime actually has two, not one external regions and two, not one, internal regions, each corresponding to our choice of sign. The inverse transformation for our external region is

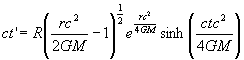
(12.2.4)
146 Chapter 12 The New Frontiers
The internal region referred to as the black hole internal region has the inverse transformation given by
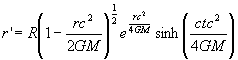
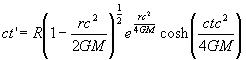
(12.2.5)
The second internal region corresponding to the other choice of sign has the inverse transformation given by
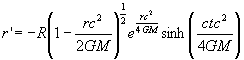
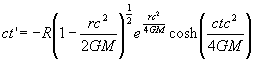
(12.2.6)
This region has become termed the white hole interior region.
The second external region has the inverse transformation given by
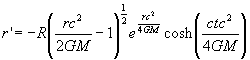
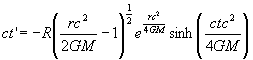
(12.2.7)
12.2 Wormholes 147
The spacelike hypersurfaces extending through from one external region to another are called wormholes.
At this point the question arises, whether it is possible for objects or information to transverse the wormholes from one external region to the other. There are two potential problems with this being argued to date. First off, is the question of wormhole stability. Second, and really the only relevant problem is that in this spacetime there are no time-like or light-like geodesics connecting the two external regions. The argument over wormhole stability goes as follows. A hypersurface that is apparently space-like in the Schwarzschild (r,ct) coordinates is never space-like for the internal regions in the Kruskal-Szekeres (r',ct') coordinates. As a result any wormhole "static" in the (r,ct) system is always dynamic for the interior regions in the (r',ct') system. This leads to a short life-span of the connection between any two external regions according to the (r',ct') frame. The life-time of the wormholes are argued to be to short lived for information to be communicated between the two external regions.
The real problem with transversing a wormhole is that none of the geodesics connecting these two external regions are time-like or light like. For information to cross from one external region to the other, it would have to follow a space-like path during at least part of the journey. In other words, in order for information to cross from one side of a wormhole to the other without winding up hitting the physical singularities it would have to travel faster than light in a way not allowed even by general relativity. If information could do this, then the first problem of stability wouldn't be a problem at all as the information could travel through the wormhole arbitrarily fast and make it through before the wormhole connection was broken. This is why the second problem is the real problem with transversing this type of wormhole.
148 Chapter 12 The New Frontiers
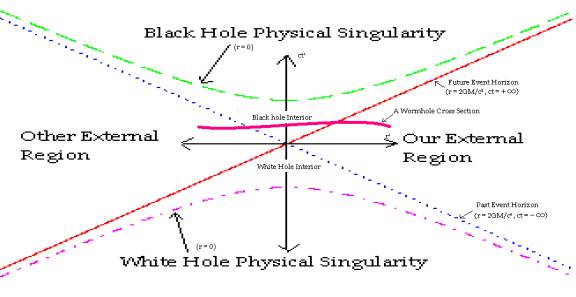
(Figure 12.2.1)
Another way to conceptualize a wormhole topology goes as follows.
The Schwarzschild spacetime's interval expressed in a remote observer's spherical coordinate system takes the form
ds2 = (1 - r0/r)dct2 - dr2/(1 - r0/r) - r2(dq2 + sin2qdf2)
Consider a hypersurface given by ct = constant resulting in
ds2 = - dr2/(1 - r0/r) - r2(dq2 + sin2qdf2)
One does so by imagining an extra-dimensional flat space in which this surface is imbedded.
ds2 = - dw2 - dr2 - r2(dq2 + sin2qdf2) = - dr2/(1 - r0/r) - r2(dq2 + sin2qdf2)
This results in
dw = ± (r/r0 - 1)-1/2dr
The anti-derivative of which gives
w2 = 4r0(r - r0)
Sweeping this around the w axis to include all q results in a paraboloid surface

We usually pick the upper half of the surface to represent our external region. The lower half is used to represent the other external region previously discussed.
Such a wormhole surface is also sometimes called an Einstein-Rosen bridge.
Next we will consider the Kerr-Newman black holes(charged-rotating black holes) that have geodesic paths between certain external regions that are likely to be transversable, at least going one way.
12.2 Wormholes 149
The next is a conformal diagram for the maximal extension for a Kerr-Newman space-time(a charged rotating Black Hole).
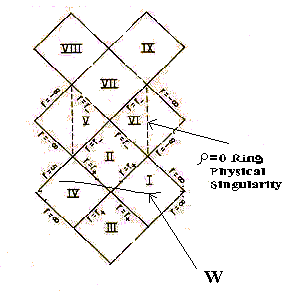
(Figure 12.2.2)
The curve W is a spacelike hypersurface connecting two different external regions and the question of the stability of a connection allowing this path to form is as valid for this spacetime as it was for the Schwartzschild wormholes. Even if the different regions do reach a stable connected state we still have a problem trying to transverse a path between region I and region IV. That problem is that no timelike paths connect the regions. However, There is a time-like geodesic from region I to region VIII or IX. These paths are likely to be transversable. Since these are timelike geodesic paths and not a spacelike hypersurface, they are not called wormholes, but I see no problem with qualifying the word and calling such a geodesic path a timelike wormhole. This is a different aspect of the black hole geometry and so the problem of wormhole stability really does not apply. One might argue that region VIII or IX is nothing more than a mathematical repeat of region I. If this is the case, then the path is a closed timelike loop and a probe dropped into the hole would fall back out to the same point in space and time from which it started. This presents a grandfather time paradox. With a little boost along, or at the beginning of the path, the probe comes out to arrive at the same point in space from where it was thrown in even before the time it was released! However if region VIII and IX do turn out to be other universes or if the event horizon between region VII and VIII or IX corresponds the outer horizon at the birth of what appears to be another hole far removed from the one entered, then such a causality paradox can be avoided. If it is the case that this is indeed an exit into another universe or location, then we should also note that the trip is likely to be one way only. One can only travel "up" along the diagram. This is probably where the TV series Stargate SGI came up
150 Chapter 12 The New Frontiers
with the concept of outgoing wormholes Vs incoming wormholes. Each stargate can only dial out and once you've dialed out, as long as that wormhole stays open, no one can come through from their end to yours.
We next turn to the Morris-Thorne wormhole. The Morris-Thorne Wormhole can be expressed by the following interval.
![]()
(12.2.8)
w is allowed to run from - ¥ to + ¥ . r is a function of w that reaches some minimal value above zero at some finite value of w. In the limit that w ® ± ¥ , r = |w| . F (w) is just a gravitational potential allowed by the spacetime geometry. One falling along the -w direction falls "inward" toward the hole with decreasing r until reaching the minimal value of r. This minimal value is the radius of the wormhole throat. Continuing along the -w direction, one finds himself falling "outward" again away from the hole again with increasing r. This type of wormhole has great advantages over the spacelike wormholes associated with black holes previously discussed. For instance, there is no event horizon associated with this wormhole. The coordinate speed of light is nowhere zero. Because of this, remote observers can observe travelers cross from one external region to the other. Also, with this kind of wormhole timelike geodesics connect the different external regions. So one needn't travel at locally faster than c speeds to transverse the wormhole.
The stress energy tensor required for this exact spacetime is
T00 = (c4/8pG)[1 - (dr/dw)2 -2rd2r/dw2]e-2F/c2/r2
T ww = -(c4/8pG)[1 - (dr/dw)2 -2r(dr/dw)(dF/dw)/c2]/r2
Tqq = (c4/8pG)[d2r/dw2 + (dr/dw)(dF/dw)/c2 + r(d2F/dw2)/c2 + r(dF/dw)2/c4]/r3
Tff = (c4/8pG)[d2r/dw2 + (dr/dw)(dF/dw)/c2 + r(d2F/dw2)/c2 + r(dF/dw)2/c4]/r3sin2q
All other Tmn = 0
(12.2.9)
If anyone discovers how to construct this stress energy tensor with obtainable matter and fields, then this kind of wormhole can be artificially constructed.
Finally lets consider another method of wormhole engineering. Similar to the second method to conceive of a Schwarzschild wormhole, consider starting out with the hyperspace in which our universe is imbedded expressed in cylindrical coordinates
ds2 = dct2 - dw2 - dr2 - r2(dq2 + sin2qdf2)
We can choose the behavior of w to be w(z,r) = a/Z where a is a function of r and Z is a function of z. The finction a(r) will have boundary conditions of a = 0 for r > R and da/dr = d2a/dr2 = 0 at r = 0. The interval according to an observer for our universe becomes
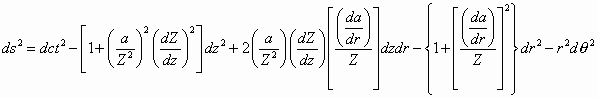
To imagine the wormhole geometry, consider the following behavior of w(z,0). (Figure 12.2.4)
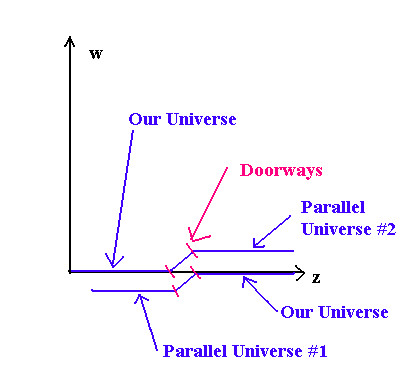
The "Doorways" are matter regions controlling the behavior of Z(z) and a(r). To see how this kind of wormhole can shorten the trip between two doors into our universe consider the next spacetime geometry. (Figure 12.2.5)

By manipulating L in the above graph, the path through hyperspace through the wormhole between the two gates into our universe can be made shorter than the path between them that exists in our universe (at w = 0). This path through the wormhole can then be transversed faster than light can travel the distance by the shortest path in our universe at w = 0.
Consider the following choice of behavior for a(r).

The sparse matter region does not change the slope of a(r). The matter at R1, and R2 does. As such we should be able to form a wormhole with a similar behavior for a(r) merely by producing a stress energy tensor containing the nonzero terms of the stress-energy tensor that depend on d2a/dr2. For the above graph, these are delta functions in the stress-energy tensor at R1 and R2.
12.2 Wormholes 151
Exercises
Problem 12.2.1
How would the Meisner-Thorne wormhole appear from an outside observer?
Problem 12.2.2
Describe how figure 12.2.2 relates to Eqn.11.1.20.
Problem 12.2.3
What is the coordinate speed of light described by Eqn.12.2.3? Draw a path from one external region to another on figure 12.2.2 that does not violate this speed limit and does not intersect a physical singularity.
Problem 12.2.4
Use the same method as leading to the paraboloid wormhole geometry above, and use the weak field solution in problem 9.2.5 to graph a spacelike hypersurface for the interior of a uniformly dense sphere of matter. Include the exterior paraboloid solution to get a picture for the entire surface.
______________________________________________________________________________
12.3 Time travel
In this section we investigate the possibility of time travel (the sci-fi sense of the term) within the realm of general relativity. We already know that in special relativity faster than c information transfer would lead to this kind of time travel. It is because of this that it is often said that special relativity implies information can not be transferred faster than c. Since this page is about general relativity we are not concerned with this method of time travel. First we will look at a possible form of time travel associated with black holes. Second we will look at the possibility of a the Morris-Thorne-Yurtsever wormhole time machine. Finally, we will look at the possibility where metric engineering is used to construct a "Seven Days" like time machine and discuss the physical problems with this kind of time machine.
Refer to figure 12.2.2. As has been shown in section 11.1, an object dropped radialy along the polar axis into the hole gets thrown back out in a finite proper time. On the above graph this motion is described by a path that that is a vertical line going from region I through region II then VI then VII and back out into region IX. Region I is the external region representing our universe outside of the hole. As discussed in section 12.2, Region IX may be another universe all together or the path may actually come out an opening into our same universe from a far removed hole. However, Region IX may also just be a mathematical repeat representative of the same universe from which the object entered. If this is the case, then since the probe falls back out to the same remote observer coordinate from which it is dropped we find that a closed time-like loop is formed. The probe returns to the same point in space and time from which it is dropped according to the remote observer coordinates. With a boost along the path it can even return to the point in space from which it was dropped at a time before it started its journey.
Using the definitions of g and Lz eqn 11.1.38 and eqn 11.1.39 for motion in a Kerr-Newman spacetime (the spacetime for a charged rotating black hole), it is easy to work out the time travel equation. This is

(12.3.1)
In this idealized space-time one can actually travel as far back in time as one desires. In a realistic space-time in which the hole has a beginning where it is formed under the gravitation of a rotating star, one can only travel as far back in time as the hole existed. Thus, if metric engineering is used to construct this type of time machine, a time traveler can not travel to a time prior to the time machines creation. However, one might travel far out into the galaxy and find a
152 Chapter 12 The New Frontiers
very old black hole to use for travel as far back as it existed.
This type of time travel does lead to grandfather paradoxes and as a result physicists have felt compelled to create new objections to the possibility. As we've discussed region IX may be representative of another universe altogether in which case there is no grandfather paradox, but other objections have been offered. Some have suggested that in such cases where general relativity seems to allow this kind of time travel, the universe might be ordered in such a way that there will actually be some quantum mechanics effects that arise to negate the possibility. One type of grandfather paradox that superficially seems to be implied by the realization of the possibility is that there is a point in between the outer and inner event horizon where the in falling object seems to collide with its future self. Fortunately, when we study the graph we see that this needn't occur because this "single point" actually exists in two separate locations in the maximal extension. One is in region II and the other is in region VII.
One possible way out of the logic grandfather paradox that still allows for this sci-fi type of time travel is as follows. Region I and region IX do look graphically like separate universes. If they are not altogether separate universes or separate external regions, they may still be separate phases of the same universe. In quantum mechanics, the state of a system is described by a wave function. Where continuum states are concerned, the wave function is comprised of an infinite number of phase waves. These are often called Eigenstates, but more often so when considering discrete states. Though quantum mechanics works as far as making experimental and observational predictions is concerned, there are various different ways of interpreting quantum mechanics. One of these is the many worlds interpretations. In this interpretation each phase state corresponds to an actual reality and when a determination is made as to which state is actually measured, these different phases of reality split apart leaving us with many worlds. If region IX is actually a different phase of the same universe, then we can get around the logic grandfather paradox in the following way. At some point in a remote observer's time there is the possibility of an arrival of a time traveler from the future who intends to kill his grandfather before his father is conceived. This point is where the phases split. In one phase, no time traveler arrives and so in this phase the time traveler is born. This time traveler leaves this phase of the universe for the original point in time, only in the other phase of the universe. In that phase of the universe, the time traveler kills his grandfather before his father is conceived and so in that phase of the universe there is no time traveler born to kill his grandfather in this phase of the universe. In this way the grandfather paradox is not disastrous or a threat in any way. Instead, the different phases are not only not a danger to each other, but they each seem to be responsible for the form the other takes.
Next consider a Morris-Thorne-Yurtserver type wormhole time machine. Due to a quantum mechanics uncertainty principle, there are large energy fluctuations in the vacuum at very small scales. These fluctuations are large enough to produce micro-wormholes. If one could locate such a wormhole and feed it what energy it needs to enlarge it to our macro world's scales then one may use it as a quick portal shortcut from one end to the other. It could be used to travel or communicate effectively "instantaneously" from one end to the other. Note-the simultaneity is according to an observers frame for which the observer is still with respect to one entrance of the wormhole. The wormhole time machine assumes the possibility that both ends open into the same universe. Consider the possibility that one end of the wormhole remains on earth while the other entrance moves away carried inside a ship moving off at a constant rate. If an observer on earth watches the clock on the ship by looking through a telescope at it instead of through the wormhole, ordinary time dilation will be observed to take place. Likewise, if the ship observer watches the earth's clocks through a telescope instead of through the hole ordinary dime dilation is observed in the traditional twin paradox fashion. For simplicity, lets say the clocks were synchronized at the instant the ship and earth were together. Now if a signal is sent through the wormhole from the earth to the ship then it arrives virtually instantaneously according to the earth's externally inertial frame. Due to the time dilation the signal will arrive according to the ship's clock some time readout earlier than the earth's clocks read. Lets say that the ship immediately returns the signal through the wormhole. A symmetry is then assumed in which the return signal will also be received back at earth virtually instantaneously according to the "ship frame". This assumption may be unphysical and may be what invalidates the scenario which we will come back to. If the assumption is not unphysical, then because the ship observed the earth clocks to run slow due to time dilation the return signal will be received at an Earth clock time readout even before this. In that case, the signal will arrive back at earth at a time before it was sent from earth. Now we return to the symmetry assumption that was made. Consider the possibility that such a wormhole only formed so that each end is initially stationary with respect to the other. To set up the time travel paradox we have to accelerate one end of the wormhole. This sets up an intrinsic asymmetry between the history of each wormhole entrance. As a result if communication is instantaneous from entrance A to entrance B according to an observer at rest at entrance A, then the asymmetry in the history of the two entrances may produce an asymmetry in the result for a signal traveling from B to A. In that case communication from B to A through the wormhole may not be instantaneous according to an observer at rest with respect to B at all. Simultaneity may become direction dependent. For example, looking through the wormhole from A at B, the earth frame may observe the same ship clock readout as observing it without looking through the wormhole. Whereas looking through the wormhole from B at A, the ship observer may observe a time on earth's clock advanced of the time observed looking along another path. Again, the asymmetry would be due to the acceleration of one entrance of the wormhole from an initially static state. This situation would prevent a grandfather paradox.
The final type of time machine time travel we will discuss makes use of metric engineering to manufacture a desired spacetime geometry. This is something along the lines of a Jules Verne type of time machine. Consider the following metric
ds2 = [T(ct)]2dct2 - dr2 - r2(dq2 + sin2qdf2)
(12.3.2)
12.3 Time Travel 153
This as it stands is a vacuum field solution with a zero Riemann tensor. T(ct) appears because it corresponds to a frame in which we chose to vary how our clocks run mechanically. Because of this, if we choose T(ct) = 1 to correspond to o forward running clock, then T(ct) = -1 corresponds to a clock running backward. So far there is no sci-fi like time travel associated with this metric. Next we will make a modification to the metric as follows.
ds2 = {1 - [1 - A(ct)]f(r)}2dct2 - dr2 - r2(dq2 + sin2qdf2)
(12.3.3a)
If we have df/dr = d2f/dr2 = 0 at r = 0 and at r = ¥, and f = 0 at r = 0, and f = 1 at r = ¥, then this metric will be a vacuum field solution with a zero Riemann tensor at these locations. The interesting aspect of this metric is that if A < 0 then an observer at the origin will observe that forward running clocks at r = ¥ will actually run backwards. Unfortunately there is one severe physical problem with this kind of time machine metric. The stress energy tensor diverges on the event horizon ( where we have (1 - A)f(r) = 1 ) where there is a singularity in the contravariant metric tensor.
While A is a constant, we can more simply express the above interval with the form
ds2 = [T(r)]2dct2 - dr2 - r2(dq2 + sin2qdf2)
(12.3.3b)
The exact solution for the Einstein tensor is
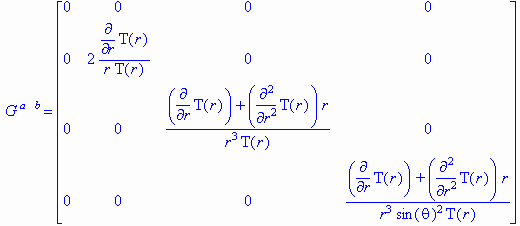
(12.3.4)
And the stress-energy tensor's solution is given by Einstein's field equations
Tmn = (c4/8pG)Gmn
The terms diverge because T(r) is in the denominator and T(r) must go to zero at the event horizon. Our next step then is to modify the metric so as to eliminate this divergence problem
154 Chapter 12 The New Frontiers
and keep the time travel. So we modify the metric to take the following form.

(12.3.5)
Where [G(r)]2 goes to +1 a finite distance from the event horizon ( the event horizon is where T(r) = 0 ).
We choose a G(r) and a T(r) so that around the event horizon the Tctct term is identically zero and so that G(r) does not vanish there. In that case the stress energy tensor will finite everywhere. For example, lets say that around the event horizon at r = R, T(r) is given by
T(r) = -k(r - R)3
We also make a particular choice for G(r).
G(r) = (2r + R)/(r - R)
The solution for the Einstein tensor right around the event horizon is then

This is not only not infinite at the event horizon, but it vanishes there and it is a tensor, so it vanishes there in every frame. This means the problem of the event horizon divergence has been eliminated.
There is one more major physical problem. In some frames T00 is less than zero. In other words they find a negative energy density. This is what is called a weak energy condition(WEC) violation. We could eliminate the WEC violation by adding a T00 mass term but it has not been determined if this would nullify the time travel characteristics of the resulting spacetime. If it should turn out that such a term can not be added while keeping the same time travel characteristics then some sort of exotic matter would be required.
12.3 Time Travel 155
Exercises
Problem 12.3.1
Have a computer work out the Einstein tensor and there from the stress-energy tensor for 12.3.5. GRTensorII is a free downloadable tensor calculus package that is good for this kind of work.
Problem 12.3.2
Describe how Eqn. 11.1.20 relates to figure 12.2.2.
Problem 12.3.3
Draw lines of constant remote observer coordinate time extending to all regions on figure 12.2.1
_____________________________________________________________________________
12.4 Manipulation of Inertia Through Metric Patching
See the Paper at LANL archive http://xxx.lanl.gov/abs/gr-qc/0106003/
Abstract. This paper will present the exact solution for the stress-energy tensor of a spherical matter shell of finite thickness that will patch together different metrics at the boundaries of the shell. The choice of vacuum field solutions for the shell exterior and hollow interior that we make will allow us to manipulate the inertial state of an object within the shell. The choice will cause it to be in a state of acceleration with the shell relative to an external observer for an indefinite time. The stress-energy tensor's solution results in zero energy requirements, and only finite stress requirements, and we show how any WEC violation can be avoided.
This section will be a brief summary of the paper mentioned above.
Consider what would happen should we have the case of a piecewise invariant interval as follows.
For r < R
ds2 = dct2 - dr2 - r2(d
q2 + sin2qdf2)(12.4.1)
For R < r < R + D (The shell's matter region)
ds2 = (1 +
afcosq/c2)2dct2 - dr2 - r2(dq2 + sin2qdf2)(12.4.2)
156 Chapter 12 The New Frontiers
For r > R + D
ds2 = (1 +
arcosq/c2)2dct2 - dr2 - r2(dq2 + sin2qdf2)(12.4.3)
A space ship placed in the region r < R needn't keep running its engines to keep from accelerating with the stars because there is no gravitational force in this region according to this coordinate frame. From the perspective of an external observer, the form of the metric is different. From an external observers perspective, the matter region produces a gravitational field which causes the ship to accelerate itself away following geodesic motion with a proper acceleration a indefinitely.
The matter region requires certain stress terms in accordance with Einstein's field equations given by
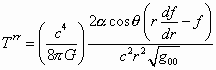
(12.4.4)

(12.4.5)
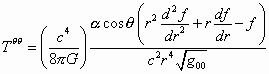

(12.4.6)
(12.4.7)
12.4 Manipulation of Inertia Through Metric Patching 157
All other Tmn = 0
.
T00 is zero. Since T00 has the interpretation of ship frame energy density and so there is zero ship frame energy requirement. The matter shell that could physically be constructed will have mass, but this is a requirement of materials, not of the inertia manipulation characteristics of the spacetime.
Taken as it, is has negative energy density. TmnUmUn is less than zero for some time-like vectors, but there is a way around the WEC violation. Consider the weak field approximation
ds2 = (1 + 2f/c2)dct2 - ds 2
(12.4.8)
The exact gravitational potential for the above spacetime is f = a fcosq . The addition of enough spherically symmetric mass into the T00 term will eliminate any WEC violation altogether, while in the weak field approximation it will merely add a term to the potential that is a function of r.
f
new = afcosq +V(r)(12.4.9)
This potential still has the inertia manipulating characteristics of the old potential, but has the addition of a central attraction.
The crew of such a ship would not be crushed against the hull of the ship for any amount of acceleration, but would instead accelerate with the ship in a weightless state of free fall. All fuel requirements would also then be eliminated.
Consider the spacetime interval given by
ds2 = [1 + y/c2]2[1 + 2F/c2]dct2 - dr2/[1 - 2r(dF/dr)/c2] - r2dq2 - r2sin2qdf2
12.4.10
where y is a function of z and F is a function of r.
y
and F correspond to Newtonian gravitational potentials.In the case that y = arcosq and F = - GM/r, where a is a function of time, the interval is a vacuum field solution to first order in the potentials. If either a or M is zero as well, it exactly reduces to a vacuum field solution.
One can use this spacetime as a means of gravitational self propulsion in the following way. Let y and F vary in the matter shell according toy = afcosq and Ñ 2 F = 4pGr. In the hollow interior, y = 0 and F = constant. The hollow interior will be the a vacuum field solution with a zero Riemann tensor and to first order in the potentials, the stress energy tensor of the shell will be
T00 = rc2/g00
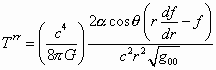
12.4.11

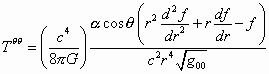

all other Tmn = 0.
This means that if this stress-energy is physically produced, to first order in the potentials it will have the desired spacetime interval above as its solution. a will be the proper acceleration of the ship and the crew will accelerate with the ship in a weightless state of free fall. Given a large enough r for a given a , this stress-energy does not violate the weak energy condition.
Neglecting the df/dr and f terms in examining the source for the behavior of d2f/dr2 it turns out that one can physically produce those terms with a simple pressure dipole approximated by
pressure = ± (c4/8pG)(a/c2)d2f/dr2
12.4.12
The + sign is taken for the half of the shell in the direction of the acceleration and the minus sign is taken for the other half of the shell.
Exercises
Problem 12.4.1
Consider a constant proper acceleration. Invert Eqn. 3.3.9 and apply the result with approximation for a small distance and weak field to Eqn 12.4.9 to show that the external observer does reckon that there is a gravitational field there.
___________________________________________________________________________________________
158 Chapter 12 The New Frontiers
12.5 Relativistic Unification Theories
In doing pre-relativistic physics we often think of the electric and magnetic "fields" as two separate vector fields. We express the electric and magnetic field vectors as two separate three-component vectors.
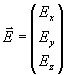
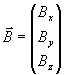
(12.5.1)
It turns out that these pseudo-vectors taken separately do not transform like the vectors of relativity. By themselves, they do not transform like tensors. It turns out that these are actually incomplete components of the actual field vector known as the electromagnetic field tensor. In local Cartesian coordinates the electromagnetic field tensor is Eqn. 6.3.11

In finding this electromagnetic field tensor it was discovered that the electric and magnetic "fields" were actually incomplete components of a single unified electromagnetic field. As gravitation and other fields have similar characteristics it is thought that all of the fields that we think of as separate are actually all just different aspects of a single potential or unified field. It is commonly known that after the core development of general relativity Einstein continued to work on a unification theory for unification of the gravitational and electromagnetic "fields". What is not commonly known is that he did have success in developing the basis for such a unification theory. However, most modern attempts at finding a good unified field theory are rooted in Kaluza-Klein unification or in quantization unification because people have been able to produce results more descriptive of a wider range of particle fields characteristic of the observed nature of the universe.
In relativity, the metric tensor plays the role of a gravitational potential. Outside of Einstein's unification the metric tensor is completely symmetric. We note that the electromagnetic field tensor is completely anti-symmetric. In Einstein's unification theory, the metric tensor can be written as a sum of a symmetric and an anti-symmetric part, but Eqn.4.4.3 glnglr = dnr will remain valid. This also leads to an affine connection that can be written as a sum of a symmetric and an anti-symmetric part.
12.5 Relativistic Unification Theories 159
Einstein then defined a tensor density
![]()
(12.5.2)
detg = the determinant of the metric tensor.
This tensor density then also can be written as the sum of a symmetric sDmn and an anti-symmetric aDmn part.
The Lagranginan density for his theory is DmnRmn and his field equations are
Rmn = 0
(the free-space gravitational field eq)
and
Dmn,r + GmlrDln + GnrlDml - GlrlDmn + (2/3)glnglrGabaDmb = 0
(12.5.3)
The latter implies
a
Dmn,n = 0(12.5.4)
This generates Maxwell's curl equations when we make the relations
Ei = E0aDjk
Bi = (E0/c)aDi0
(12.5.5)
E0 is a parameter with units of electric field.
Making this final relation we see that the gravitational and electric and magnetic "fields" all come from the same unified source(the metric tensor). The metric tensor gives rise to the affine connections that we interpret as a gravitational field and it also gives rise to the components of the density tensor that we interpret as electric and magnetic fields. In fact E0aDmn is the dual tensor Eqn. 7.1.4 of the electromagnetic field tensor above.
Kaluza-Klein theories take a different approach to unification of the fields then Einstein's approach to unification. These introduce extra dimensions to the spacetime and the electromagnetic potential is related to the elements of the metric tensor corresponding to the extra dimensions. String theories were born from this train of thought. Here we will present the
160 Chapter 12 The New Frontiers
basis of the actual Kaluza-Klein theory. First we introduce the five dimensional metric tensor.
We distinguish it from the ordinary four dimensional metric tensor by putting a bar underneath.
![]()
Though the indices include a fifth dimension for m = 4, the metric and all equations are written only as functions of the four dimensions whish we can normally observe. For m ,n = 0,1,2,3 the ordinary metric tensor is related to the five dimensional metric tensor by
![]()
(12.5.6)
Here, one element is taken to be a given,
![]()
(12.5.7)
The electromagnetic field tensor is then written in terms of an electromagnetic potential.
![]()
(m ,n = 0,1,2,3)
(12.5.8)
And the electromagnetic potential is related to the five dimensional metric tensor.
![]()
(12.5.9)
V0 is merely included here as a parameter of the theory with units of voltage.
12.5 Relativistic Unification Theories 161
The Lagrangian density for this theory is.
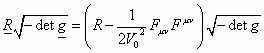
This results in the Einstein field equations for electromagnetism "alone" and an otherwise vacuum region becoming
![]()
(12.5.10)
From this,![]() . But this is
related to the electromagnetic field tensor by .
. But this is
related to the electromagnetic field tensor by .![]() Which results in
Which results in ![]() . This is
comparable to the section on Maxwell's equations Eqn. 7.1.5 for Jm
= 0.
. This is
comparable to the section on Maxwell's equations Eqn. 7.1.5 for Jm
= 0.
Exercises
Problem 12.5.1
Considering Kaluza-Klein theory, explain how in accordance with parallel transport, Eqn. 12.5.8 and expression of the metric components in terms of the ordinary dimensional coordinates only demands rotational invariance about the extra-dimensional axis.
Problem 12.5.2
In Kaluza-Klein theory the metric tensor is the potential for other fields in nature besides the gravitational field. How is the relation between the electromagnetic field and the metric tensor different in Einstein's unification theory?
Problem 12.5.3
Find the expressions for E0 and V0 in terms of known physical constants.
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru
Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)
New World Order(Macro Philosophy) /Astronomy
Zamanda yolculukla ilgili sayfalar: Hazırlayan Çetin BAL; Time Travel Page
| Sayfalar: | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. |