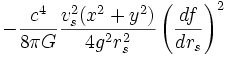Mathematics of the Alcubierre drive

Using the 3+1 formalism of general relativity, the spacetime is described by a foliation of space-like hypersurfaces of constant coordinate time t. The general form of the Alcubierre metric is:

where α is the lapse function that gives the interval of proper time between nearby hypersurfaces, βⁱ is the shift vector that relates the spatial coordinate systems on different hypersurfaces and γ_ij is a positive definite metric on each of the hypersurfaces. The particular form that Alcubierre studied (1994) is defined by:

 

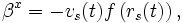
β^y = β^z = 0

γ_ij = δ_ij

where

and

with R > 0 and σ > 0 arbitrary parameters. With this particular form of the metric, it can be shown that the energy density measured by observers whose 4-velocity is normal to the hypersurfaces is given by

where g is the determinant of the metric tensor. Thus, as the energy density is negative, 'one needs exotic matter to travel faster than the speed of light' (Alcubierre, 1994). The existence of exotic matter is not theoretically ruled out and the Casimir effect lends support to the proposed existence of such matter; however, generating enough exotic matter and sustaining it to perform feats such as faster-than-light travel (and also to keep open the 'throat' of a wormhole) is thought to be impractical. Low (1999) has shown that within the context of general relativity, it is impossible to construct a warp drive in the absence of exotic matter. It is generally believed that a consistent theory of quantum gravity will resolve such issues once and for all.

Physics of the Alcubierre drive

For those familiar with the effects of special relativity, such as Lorentz contraction, mass increase and time dilation, the Alcubierre metric has some apparently peculiar aspects. Since a ship at the center of the moving volume of the metric is at rest with respect to locally flat space, there are no relativistic mass increase or time dilation effects. The on-board spaceship clock runs at the same speed as the clock of an external observer, and that observer will detect no increase in the mass of the moving ship, even when it travels at FTL speeds. Moreover, Alcubierre has shown that even when the ship is accelerating, it travels on a free-fall geodesic. In other words, a ship using the warp to accelerate and decelerate is always in free fall, and the crew would experience no accelerational g-forces. Enormous tidal forces would be present near the edges of the flat-space volume because of the large space curvature there, but by suitable specification of the metric, these would be made very small within the volume occupied by the ship.

The Alcubierre drive and science fiction

Note that faster-than-light travel is often used in science fiction to denote a wide variety of imaginary propulsion methods, most of which have nothing to do with the Alcubierre drive or any other physical theory. Star Trek fans claim that, in Star Trek, the Alcubierre theory has largely been accepted due to the similarity of the appropriate terms, in order to explain the apparent breaking of the laws of physics in most of the series. Dr. Alcubierre's paper on the physics of space warp was published in 1994, well after the physics of the warp drive were set down by Paramount Pictures, and similarities between the two are strictly coincidental in nature (in particular, "subspace" has little or nothing to do with the kind of gravitational and spatial distortions postulated by Dr. Alcubierre).

Although it precedes Alcubierre drive, the anime version of Captain Future featured a similar mechanism, called undulating mode.

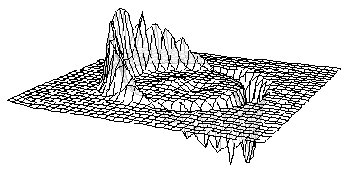
The Alcubierre metric defines the so-called warp drive spacetime introduced by Miguel Alcubierre in 1994. This is a Lorentzian manifold which, if interpreted in the context of general relativity, exhibits features reminiscent of the warp drive from Star Trek: a warp bubble appears in previously flat spacetime and moves off at effectively superluminal speed. Even more striking, inhabitants of the bubble feel no awkward inertial effects, and travelers making a round trip inside a warp bubble experience no time dilation of the kind known from the famous twin paradox from special relativity.

The Alcubierre metric may be written

 

where

 

and

Alcubierre chose a specific form for the function f, but other choices give a simpler spacetime exhibiting the desired "warp drive" effects more clearly and simply.

The original warp drive metric, and simple variants of it, happen to have the ADM form which is often used in discussing the initial value formulation of general relativity. This may explain the widespread misconception that this spacetime is a solution of the field equation of general relativity. Metrics in ADM form are adapted to a certain family of inertial observers, but these observers are not really physically distinguished from other such families.

Alcubierre interpreted his "warp bubble" in terms of a contraction of "space" ahead of the bubble and an expansion behind. But this interpretation might be misleading, since the contraction and expansion actually refers to the relative motion of nearby members of the family of ADM observers. Natario has suggested a significantly different kind of warp bubble metric which does not feature expansion.

All known warp drive spacetimes violate various energy conditions. It is true that certain experimentally verified quantum phenomena, such as the Casimir effect, when approximated in the context of relativistic classical field theories, lead to stress-energy tensors which also violate the energy conditions. This initially led some to hope that Alcubierre type warp drives could perhaps be physically realized by clever engineering taking advantage of such quantum effects. Unfortunately, it turns out that a rather general class of warp drive spacetimes also violates certain quantum inequalities, and such violations are much harder to dismiss. The energy conditions in general relativity were never more than rough rules of thumb, but the quantum inequalities are generalizations of the uncertainty principle and seem to stand on solid ground in quantum field theory. Another problem with a large class of warp drive spacetimes is that even if the violations of the quantum inequalities were acceptable, the energy requirements may be absurdly gigantic, e.g. the mass-energy content of a star might be required to transport a small spaceship across the Milky Way galaxy. Counterarguments to these apparent problems have been offered, but not everyone is convinced they can be overcome. (If they could be, it has been suggested that an intense flux of blue shifted starlight would fry any inhabitants of the bubble.)

Perhaps the most troubling objection of all is that if warp drives were genuinely possible, we would expect to see, even in toy models such as the Alcubierre warp drive, some indication of mass-energy being gathered up, transported, concentrated, reorganized and used to create and operate the warp bubble. But by their very nature, current warp drive metrics seem to have a very different character: the bubble appears (and may eventually disappear) "spontaneously". We can observe a kind of "circulation" of energy-momentum around the bubble, but nothing which suggests a phenomenon which can be created or controlled by physical means.

At present it seems fair to say that the consensus among physicists is that warp drive spacetimes of type considered here are probably impossible to realize. Some general counteraguments have been offered to the construction of any warp drive (not just ones of the Alcubierre or Natario forms). Nevertheless, a few physicists continue to hold out hope that some kind of warp drive might after all be physically possible, at least in principle.

• References

• Alcubierre, Miguel (1994). The Warp Drive: Hyper-Fast Travel Within General Relativity, Class. Quantum Grav., 11: L73-L77. eprint
• Low, Robert (1999). Speed Limits in General Relativity, Class. Quantum Grav., 16: 543-549. eprint
• Berry, Adrian (1999). The Giant Leap: Mankind Heads for the Stars, Headline. ISBN 0-747-27565-3. Apparently a popular book by a science writer, on space travel in general.
• Lobo, Francisco S. N.; & Visser, Matt (2004). Fundamental limitations on 'warp drive' spacetimes. Class. Quant. Grav. 21: 5871-5892. See also the eprint. arXiv. URL accessed on June 23, 2005.
• Natario, Jose (2002). Warp drive with zero expansion. Class. Quant. Grav. 19: 1157-1166. See also the eprint. arXiv. URL accessed on June 23, 2005.
• Broeck, Chris Van Den (1999). A `warp drive' with more reasonable total energy requirements. Class. Quant. Grav. 16: 3973-3979. See also the eprint. arXiv. URL accessed on June 23, 2005.
• Low, Robert J. (1999). Speed Limits in General Relativity. Class. Quant. Grav. 16: 543-549. See also the eprint version. arXiv. URL accessed on June 30, 2005.
• Hiscock, William A. (1997). Quantum effects in the Alcubierre warp drive spacetime. Class. Quant. Grav. 14: L183-L188. See also the eprint. arXiv. URL accessed on June 23, 2005.
• Pfenning, Michael J.; Ford, L. H. (1997). The unphysical nature of 'Warp Drive'. Class. Quant. Grav. 14: 1743-1751. See also the eprint. arXiv. URL accessed on June 23, 2005.
• Alcubierre, Miguel (1994). The warp drive: hyper-fast travel within general relativity. Class. Quant. Grav. 11: L73-L77. See also the eprint version. arXiv. URL accessed on June 23, 2005.

  Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

  The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

  Ana Sayfa /index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

  Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

  Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

  New World Order(Macro Philosophy) /Astronomy