Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
A Warp Drive embedded in the Kerr Spacetime?
!!!Under Construction!!!
In the previous section <http://members.tripod.com/da_theoretical1/schwarp.html> the dynamics of a warp drive in Schwarzchild space were briefly outlined, it is the goal of this section to formalize the prior approach. In order to do so the Schwarzchild spacetime is replaced with the Kerr spacetime whereby it is hoped that warp drive spacetime can be explained through the local momentum tensors of the Kerr geometry. It is in this section that it is discussed how the momentum tensors in the Kerr spacetime can have an active role in producing a geometry akin to the warp drive symmetry.
Kerr Space and relation
to Schwarzchild Space
In the earlier section it was explored how a potential warp drive spacetime may behave within Schwarzchild space. To begin let us look at the Kerr Spacetime, when the Kerr Spactime is set so angular momentum is set to a=0 the result is the Schwarzchild space. Mathematically this space is defined with the following equation:
ds2=-
a2dt2+v2(df-wdt)+(r2/D)dr2+r2dq2If graphed the geometry of the Kerr geometry would somewhat resemble Figure 1 as seen below.

Figure 1
Generic representation of Kerr Spacetime in one dimension as viewed from the z
plane, also note the horizons and singularity are not drawn to scale. a:
represents the direction of angular momentum, A: outer horizon, B: inner horizon,
C: singularity, D: "wormhole throat."
If the Schwarzchlid geometry were graphed in the similar fashion one would have
only horizon, and the ring singularity would be replaced with a point
singularity. Now before we get a head of ourselves to much let us look at the
Schwarzchild Warp Drive as seen in the previous section:
ds2={1-(2GM)'A'(r's)[vsr' 1-f'(r's)]2}-{dr'2/1-(2GM/r)'}-r'2 2d
f'2-dz'2.For brevity we will now assume that this also the solution of the Kerr spacetime when a=0, and the egrosphere has minimal frame dragging so that it corresponds to a photon sphere of Schwarzchild black hole. From the last section we know if the Kerr spacetime is set with a=0 we may conclude that
0=R00-T00=(1/2)[T11+T22+T33]
However if R00-T00>0, for the proposed spacetime that would imply that it is given by a Kerr geometry. This is also reveals a problem with the Kerr spacetime the geodesics of photons no longer remain symmetric. However under ideal cases it is somewhat easy to calculate the stress-energy associated with angular momentum tensors by
a=GJ/Mc3
which would alter the noted energy density from the previous section of
T00=-[1/A2]2[vs2/4][sin
q2][dg(rs)/drs]2.The problem with this method is that it will only yield the total angular momentum of the system.
Dynamic Frame Dragging
Now for the interesting part the inner horizon of the Kerr Spacetime would have an inner egrosphere, which would act to frame drag the space located between the outer and inner horizons, resulting from the fact that inner horizon has a higher angular momentum via conservation laws. This is a simple supposition to make when one understand the properties of the Kerr spacetime and that of angular momentum (to aid in further exploration refer to figure 2 below through this discussion).
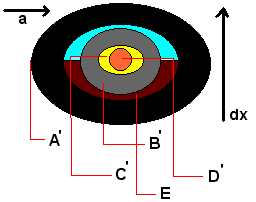
Figure 2
The Kerr Spacetime moving through space.
However, what becomes interesting is when one considers the Kerr Spacetime moving in the the x coordinate, as depicted with dx in figure 2. The region between the outer horizon (A') and inner horizon (B'), which is labeled as E, in region E the inner frame dragging egrosphere (not depicted), would be forced to fold on itself in the direction of travel. Thus the frame dragging effect begins to compress in front of the inner horizon, and from A' is forced to expand in the opposite direction, this is the property associated with the warp drive spacetime. From the graph it is seen that if a particle travels in region B' it is allowed to escape back into region E through the warp drive space, and from quantum theory has to potential to interact with the outer egrosphere again (possibly generating a new kind of quantum pressure), but this is speculation. One potential problem as seen from figure 2 is that there appears to exist a double coordinate transformation when one the compares Kerr metric with the Schwarzchild Warp Drive. The first being r(vs2*1-f(rs))1/2-->r' and the second coordinate transformation corresponding to x(vh21-f(x))1/2-->x', before I go into that problem I would like to discuss how the Kerr spacetime effect to geodesics such that light traveling to or from a Kerr horizon is manipulated by a lapse function. As light enters the horizon the light becomes ever more blue shifted, while a light beam attempting to leave becomes ever more red shifted the magnitude of this lapse function is given by:
a=(r/S)(D)1/2.
This may be of importance later as there has been a
warp drive spacetime proposed with an arbitrarily large lapse function <http://members.tripod.com/da_theoretical1/lwh/ESAAwarp.html>. However, back to the Kerr warp drive, we will first write such a coordinate transformation in the Schwarzchild geometry since it is identical to the Kerr geometry when a=0. We now attribute the coordinate transformation in the x direction so that we may have the following metricg_00={1-(2GM)'A'(r's)[vsr'*1-f'(r's)]2}
g_11={[v2*1-f(x)]2 dr'2/1-(2GM/r)'}
g_22=g_33=-1.
so one has a solution which corresponds to:
ds2={1-(2GM)'A'(r's)[vsr' 1-f'(r's)]2}dt2-{[v2 1-f(x)]2 dr'2/1-(2GM/r)'}-r'2 d
f'2-dz'2.In comparison to the Kerr metric one can make a generic substitution of order
ds^2=-{A'(
r')+v2(df-w*1-f'(r')dt)}dt2+([v^2*1-f(x)]2r2/D)dr2+r2dq^2.With this solution figure 2 becomes rather obvious. What is more interesting is that when the line element (v*1-f(x))2 is removed from the right hand one has, d*1-f/dx which is identical to the original Kerr solution. Thus the coordinate transformation takes on the role of a lapse function of the inner horizon, roughly corresponding to:
a=kgM(r/S)(D)1/2/2pD.
Therefore indicating the compression of the of the inner ergosphere in the direction of travel of the horizon as function of the inner an outer angular velocities, corresponding to the before mention double coordinate transformation.
The energy density for this consideration can now be calculated from
T00=-[1/A2+
v]2[w/4][sinq2][d*1-f(r)/dr]2.for the momentum tensors we have:
T11=[1/a][
D/(vh2*1-f(x))2r2] [dg(r)/dr]2*T00T22=[1/a]*T00
T33=[1/a]*T00.
In order to calculated divergence in the separate moment tensors one can use partial differention, denoted by dq in the following example dq*T11/dq*T22=f({1/T22},T33). It is also plain to see here that R00-T00>0, which shows qed that such a space is indeed non Schwarzchild in nature. Although this spacetime in non Schwarzchild it still remains symmetrical with a=0, e.g. one can reduce the proposed Kerr spacetime by considering a function of order 1-f(x,r). This construction would be far more realistic if some arbitrary coordinate k rotated into k', however this was meant to construct a proof of concept and not to create more of a mess!
Gravitational Waves
The proposition rest on the assertion that the overlapping frame dragging creating a compressed gravitational wave...
note: page is currently under construction analysis are not final, the calculations have not been checked, and until more work is done, should only be considered as a proposition....
back to Warp Drive Physics Homepage <http://members.tripod.com/da_theoretical1/wdphysics.html>
©2001: Edward Halerewicz, Jr.
H
içbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru