Time Travel Research Center © 2005 Cetin BAL - GSM:+90  05366063183 - Turkey / Denizli 

 

 
To the Stars: The Reality of Warpdrive Physics- Sun Feb 1 21:38:10 2004 GMT

bludot  writes:

Introduction

I'm sure many people have wondered about the feasibility of travelling to other stars. In this article I hope to give a semi-quantitive overview of some of the current research in to warp drives and hopefully inspire some of you to take a further interest in what I consider be quite an interesting topic.

I will not give a full definition of a warp drive right now since we haven't done the necessary mathematics. However, a qualitive description of the properties that we require of a warp drive is useful since we then have something to aim for. So, what properties are we looking for? Ideally we would like a way by which a human could travel interstellar distances and return within a single lifetime of both those on board the ship and those that remain on the Earth.

A Short Introduction to General Relativity

General Relativity was the theory proposed by Einstein in 1915 that incorporated gravity into his special theory of relativity. I won't go into the details of how he did this or explain why Newton's theory of gravity was incompatible with SR here, but I will use some results from General Relativity and they will be explained when they are called upon.
 

Length

Of central importance to our discussion is the concept of length and it's more generalised counterpart, an interval (you can think of the interval as a length that includes time). The reason for it's importance originates from the fact that it is a physically invariant quantity, hence all observers will measure the same interval between events. This sort of invariance is most easily visualised in terms of the result of some experiment; for instance the outcome of measuring the length of a rod in normal everyday space is not dependent on the nature of the coordinate system we impose on space. The length of the rod is a physical reality distinct from any arbitrary choice we may make. We say length is invariant under rotations in 3D space. At least in Euclidean (flat) space ;)

Newtonian Length

We have briefly referred to our natural concept of length previously, we now will discuss it in more detail. In Newtonian mechanics the concept of an interval does not really exist. Newtonian mechanics makes a distinction between spatial and temporal separation, i.e. separation in space and separation in time of events. The spatial separation of two events we call length and the temporal we call time. Furthermore, we have a formula for calculating length, the well known Pythagoras' Theorem, which if we are using a Cartesian coordinate system, has the form:

\begin{displaymath}ds^2 = dx^2 + dy^2 + dz^2\end{displaymath}

However, let us change to a cylindrical coordinate system, the formula for length then becomes,
 

\begin{displaymath}ds^2 = dr^2 + r^2d\theta^2 + dz^2 \end{displaymath}

Or if we change to spherical coordinates the formula for length becomes,
 

\begin{displaymath}ds^2 = dr^2 + r^2 \sin^2(\theta) d\theta^2 + r^2d\phi^2\end{displaymath}

So it is clear that the formula for length is certainly dependent on the coordinate system we choose. We could write this more generally as,

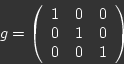\begin{displaymath}ds^2 = \sum_{ij} g_{ij} dx^i dx^j\end{displaymath}

where $g_{ij}$ represents the coefficient of a term in the formula for $ds^2$. We can express $g_{ij}$ in the form of a matrix, so for the case of Cartesian coordinates,
 

\begin{displaymath} (1)

This is actually a mathematical object known as the metric tensor, and encodes how length is calculated. Now that we have developed a slightly more sophisticated understanding of length, we will move on to Special relativity and how the definition of length changes to accommodate this theory.

Length and Intervals in Special Relativity

In the transition from Newtonian mechanics to Special Relativity we obtain new formulas relating measurements made by two observers moving relative to one another. It can then be shown that the former concepts of length and time no longer remain invariant, i.e. they appear different to different observers. However, what is found to be invariant is the quantity,

\begin{displaymath}ds^2 = dx^2 + dy^2 + dz^2 - c^2dt^2\end{displaymath}

This is our first meeting with a generalised form of length, in that it combines all coordinates, including time. In SR this is known as the invariant. A distinction is no longer made between space and time separation. You may be curious how this relates to Newtonian mechanics. Well let us consider what occurs when the spatial components $dx$, $dy$, and $dz$ are a lot smaller than $cdt$. Then the interval reduces to, $ds^2 = dx^2 + dy^2 + dz^2 - c^2dt^2 \approx -c^2dt^2$ and hence $dt = dt'$ and $dx^2 + dy^2 + dz^2 = dx'^2 + dy'^2 + dz'^2$. We can write the interval of special relativity in terms of the metric tensor $g$, as we did previously with Newtonian mechanics. We then have again $ds^2 = g_{ij} dx^i dx^j$ where $g$ is,

\begin{displaymath} (2)

This is the metric of SR. Since length ( $dx^2 + dy^2 + dz^2$) and time $dt$, no longer remain invariant as measured by observers but $ds^2 = dx^2 + dy^2 + dz^2 - c^2dt^2$ does, SR suggests that the invariant is what should be considered to be the true 'length'. Note that we have adopted the common convention of defining the speed of light as $1$, so $c = 1$.

Curvature

The concept of curvature is crucial to the General Theory of Relativity, unfortunately a full mathematical treatment would be too lengthy to undertake here and so again I will give a semi-quantitive outline. Consider the metric of 3D Euclidean space given in (1). We have already seen that the components of the metric are dependent on the choice of coordinate system, however there is a crucial point that must be made: we can return to the original metric via the inverse coordinate transform. This may seem an obvious point, but lets consider it more carefully. It means that there exists a transform that will take a metric which varies with position and at each point in space return it to,

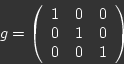
\begin{displaymath}

But this begs the question: if we invented a metric whose components were an arbitrary function of position could we still use a coordinate transform to return it everywhere to (1)? The obvious answer is "no". So what is the physical significance of this? Well, what it means physically to return to (1) everywhere is that we can construct a Cartesian coordinate system over the entire space. This can be easily visualised if we consider the 2D geometry of a piece of paper. Firstly it is quite clear that we can construct a global Cartesian system for a piece of paper:

\includegraphics[width=15cm]{/home/sickall/doc/visual/warpdrive2.eps}

However, let us now roll this paper into a cylinder. We have looked at cylindrical coordinates previously when we said in 3D space it had the metric:

\begin{displaymath}ds^2 = dr^2 + r^2d\theta^2 + dz^2 \end{displaymath}

However, since we are now confined to a surface of a cylinder $dr = 0$ so the metric becomes,

\begin{displaymath}ds^2 = r^2d\theta^2 + dz^2 \end{displaymath}

where $r$ is a constant. However if we now make a change of coordinates: $x' = r\theta$, $z' = z$, we can see that the metric reduces to the Cartesian form $ds^2 = {dx'}^2 + {dz'}^2$. This shows that if we were beings confined to live on a surface of a cylinder we could still impose a Cartesian coordinates system over the entire cylinder, like this:

\includegraphics[width=5cm, height=7cm]{/home/sickall/doc/visual/cylinder.eps}

A consequence of this, is that all of the familiar rules of geometry hold true e.g. parallel lines never meet, the sum of the internal angles of a triangle is 180 etc..

Let us now attempt to do something similar with a sphere.

\includegraphics[width=7cm, height=7cm]{/home/sickall/doc/visual/sphere.eps}

From the picture we can see that if we try to impose a Cartesian system over the entire surface we run into problems. What would be parallel lines meet at the poles and other terrible things. What this demonstrates is that if we were beings confined to live on a sphere we would not be able to construct a Cartesian coordinate system over the entire surface. In terms of the metric it means there doesn't exist a coordinate transform that takes us from $ds^2 = r^2 \sin^2(\theta) d\theta^2 + r^2d\phi^2$ to $ds^2 = dx^2 + dy^2$ everywhere.

The qualification of 'everywhere' is important. Although we can not cover the entire surface of a sphere with a Cartesian coordinate system we can make one that works locally. What I mean by this is that if we take some point $P$ on the surface, say for instance the point on which you are standing right now, we can draw a Cartesian coordinate system on the floor and it will work. However the bigger the area we try to cover the less like a Cartesian coordinate system it will be. In terms of the metric this means there exists a transformation that will make the metric equal to

\begin{displaymath}g = \left( \begin{array}{ccc}

at $P$ and even the first order derivatives of $g$ at $P$ zero. However, what is found is that for a sphere the second order derivatives are non-zero. The only time when higher order derivatives are zero is for a piece of paper. These second order terms define the curvature. They tells us how much 'parallel' lines converge or by how much the sum of angles in a triangle exceeds 180.

What we have just done above can be directly transferred to General Relativity. In General Relativity flat space is characterised by the metric of SR,

\begin{displaymath} (3)

If space were flat everywhere, we could construct a global SR coordinate system (a global inertial frame). However, when gravity is present this is not possible, particles on straight paths curve when acted on by gravity. Einstein concluded that this must be because gravity affects the metric of space time i.e. gravity is curvature of space time. He hypothesised that the curvature was affected by mass and energy through the equation:

\begin{displaymath}G(g) = 8\pi T\end{displaymath}

$G$ is the Einstein Gravity tensor and is basically a second order differential operator that acts on $g$ and $T$ is called the stress-energy tensors whose components correspond to the energy and momentum density at points in space.

Bringing it Together

So distilled to its most fundamental parts General Relativity says that gravity is just curvature of space-time which manifests itself as non-zero second order differentials of the metric. For a given distribution of mass T, we can find the metric using the equation $G(g) = 8\pi T$ . Finally, all particles travel on straight lines through space-time but since space-time is curved they follow curved paths as seen by us.

The 3+1 Formalism

We are now nearly in a position to tackle the warpdrive metric however we need to cover one last thing: the 3+1 formalism. This is a way of formulating General Relativity in which space-time is separated back into space (3 dimensions) and (+) time (1 dimension), much like Newtonian theory. This was first done so that problems in GR could be modelled on computer, in which it is natural to parametrise the problem in terms of time and view a systems evolution in space. This separation can be done by considering space at a time $t$ and then again at $t+dt$. Since space is 3 dimensional this will consist of slices of 3 dimensional surfaces (hyper-surfaces) imbedded in a 4-dimensional space. What we are doing is shown in this diagram:
 

\includegraphics[width=15cm]{/home/sickall/doc/visual/warpdrive1.eps}


As can be seen for each $dt$ that passes we move from one hypersurface to the next. What we need is a way of finding what the coordinate system on the next hypersurface is given the present one (or how we get from one to another). Firstly, we must specify how far apart the surfaces are in time. Remember that our label $t$ is only a parameter and does not correspond to actual time elapsed i.e. the proper time. Let us define a constant $\alpha$ that relates our parameter $t$ to the actual time passed $\tau$. We then have $\alpha dt = d\tau$. The constant $\alpha$ is called the lapse function and it's value can vary with position. Furthermore we must specify how much our coordinate system shifts along through space. We do this using the shift vector $\beta^i$, which tells us what direction and how much we move the coordinate system between hypersurfaces. This means the coordinates on the new hypersurface is given by ${x'}^i = x^i + \beta^i dt$. So we can see that if one were to remain at rest relative to the coordinate system then in a time $\alpha dt$, we would move, according to the diagram,

\begin{displaymath} (4)

Where we have defined the 3D metric $\gamma$ so that we can calculate the amount our coordinate system shifts by. The key thing to recognise here is that $\beta$ is telling us how much our coordinate system shifts through space between hypersurfaces and $\alpha$ is saying how much time passes. Additionally by just specifying $\alpha$, $\beta$ and the metric $\gamma$ we have obtained a full metric (4) for space-time.

The Aculbierre Warp Drive

By using the 3+1 formalism Alcubierre constructed a metric that had very interesting properties. These properties were the ones that we set out at the beginning as being what was required for realistic interstellar travel.
 

The Metric

The metric that Aculbierre proposed was this; take an arbitrary metric written in terms of the shift and lapse, (4), and set the lapse, shift and the 3D metric $\gamma$ as the following:

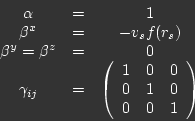\begin{displaymath} (5)

Lets have a look at what this all means. The lapse function $\alpha = 1$ everywhere, so the parameter $t$ we use to label successive hypersurface is the time elapsed between them. Furthermore the metric of the 3D space in each hypersurface is just

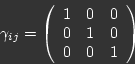
\begin{displaymath}\gamma_{ij} =

but this is just the metric of everyday life, the very familiar Pythagorean theorem of 3D. So 3D space is flat on each hypersurface. Finally we come to the shift function, which is where the heart of the warp drive lies. In the above expressions we gave the shift as,

\begin{displaymath}\beta^x = -v_sf(r_s)\end{displaymath}
\begin{displaymath}\beta^y = \beta^z = 0\end{displaymath}

So we see that there is no shift in the $y$ and $z$ directions. But something is happening in the $x$. In the Alcubierre paper,

\begin{displaymath}r_s = \sqrt{(x-x_s)^2 + y^2 + z^2}\end{displaymath}

where, $x_s$ is the position of the ship in the $x$ direction. So $r_s$ just gives us the distance from the ship of a point at $P(x,y,z)$. The speed of the ship is defined by $v_s$. Now lets look at the function $f(r_s)$. Since it is a function of $r_s$ we can see that it is cylindrically symmetric about the ship. In the paper it is defined by some horrible expression, however the only real property it needs is that it looks like a top-hat. This means, $f(r) = 1$ if $r < a$ and zero otherwise. This defines our warp bubble. Lets first look at the case when $r > a$. Since

\begin{displaymath}\beta^x = -v_sf(r_s)\end{displaymath}

we see that the shift in the x direction is also zero. So if you were a person at a distance $r > a$ from the ship (which is at $r = 0$) then as time progressed nothing would happen; there would be no movement. However lets look what happens when $r < a$. We now have,

\begin{displaymath}\beta^x = -v_s\end{displaymath}

So all our coordinates which are less than a distance $a$ from the ship shift backwards by an amount $-v_s dt$! This may seem odd at first since we want our ship to move forwards. But consider this diagram:

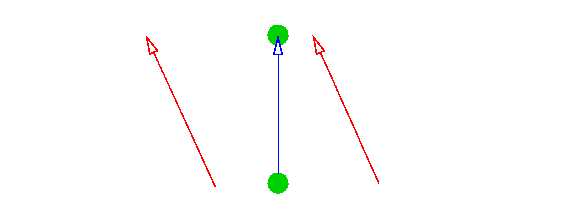
We can see that by shifting the coordinates backwards we have effectively moved everything inside the warp-bubble forwards relative to the coordinate system by $v_sdt$. So if Earth were at $x = 0$ and some other star was at $x = 100$ then we could arbitrarily choose $v_s = 1$. Then for each $dt$ that passed we would shift the coordinate system relative to anything in the warp bubble backwards by $1$, until the warp bubble had shifted the coordinate system back $100$ times and we were now at $x = 100$. That is really all there is to the Alcubierre warp drive, you just need to stick a ship inside such a bubble and choose a value for $v_s$ and your off.

The Properties

There a number of properties of the warpdrive that warrant further analysis.
 

Arbitrariness of $v_s$

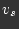
Some of you may be worried about the fact we are permitted to choose any value we like for $v_s$. Since in special relativity if we assign a velocity greater than $c$ then we run into all sorts of paradoxes. However, one must remember that these paradoxes are a consequence of the fact that due to the metric of SR if we travel faster than $c$ we will causally connect spacelike separated events. This will obviously lead to contradictions since by definition spacelike separated events are not causally connected. So the real concern we should have is; how high can we make $v_s$ before the warpdrive starts moving on a spacelike, rather than timelike, path? To answer this question we must consider the warpdrive metric, which if we simplify our last expression, is,

\begin{displaymath}ds^2 = -dt^2 + (dx-vf(r_s)dt)^2 + dy^2 + dz^2\end{displaymath}

For people far from the warp field, in flat space, $f(r) = 0$ and so,

\begin{displaymath}ds^2 = -dt^2 + dx^2 + dy^2 + dz^2\end{displaymath}

which is just the metric of Special Relativity. We can see that for non-moving observers, $dx=dy=dz=0$ and so $-dt^2 = ds^2$ i.e. the interval between two events at the same place in space is just equal to the time between them. Now let us consider what happens if we are travelling on the warp ship, for which $dx = v_s dt, dy = dz = 0$ and $f = 1$. Then we have

\begin{displaymath}ds^2 = -dt^2 + (v_sdt-v_sdt)^2 = ds^2\end{displaymath}

So we see again that $-dt^2 = ds^2$. This is amazing in that not only is the ship travelling on a timelike curve $ds^2 < 0$ but the time on board the ship in equal to the time of observers in flat space. We have avoided the time dilation of Special Relativity! Furthermore, the $ds^2$ has no dependence on $v_s$, so we are free to make $v_s$ as large as we like!

Energy Requirement

Recall that the curvature of space-time and the energy density present was given by the equation,

\begin{displaymath}G = 8\pi T \end{displaymath}

We can use this equation, by using $g$ for the warpdrive to calculate $G$, to work out how much energy we need to construct the warpdrive. In doing so it can be shown that the energy density is given by,

\begin{displaymath}T^{00} = -{1 \over {8\pi}} {{v_s}^2\rho^2 \over {4{r_s}^2}} {{df}\over {dr_c}}\end{displaymath}

As we can see, this is negative everywhere, and tends to infinity in the wall of the warp bubble as $f$ approaches the top-hat type function. It has been calculated that it would require a negative energy greater than the mass of the universe to construct this bubble. This is a big problem. I would like to emphasise the fact that this is negative energy. Think about what that means; this would correspond to a negative mass. Now, such a thing is forbidden by classical theories of physics, and so would have been a reason to reject the warpdrive space-time immediately as implausible. However, quantum theory comes to the rescue as it does allow for negative energy densities. Whether the amount of negative energy that can be generated by quantum field theories is limited by some uncertainty principle is still being researched. So our warp-drive proposal certainly isn't dead yet. Furthermore, subsequent papers on warp-drives have managed to reduce the total energy requirement to merely a few stars rather than the known universe.

 

Other Things like Expansion

If one calculates the expansion of space-time in the Alcubierre metric it is found that space is expanding behinds the craft and contracted in front. This has led to the more heuristic explanation of the warpdrive as pushing things behind it away and pulling things in front towards it. This is slightly inaccurate as you can construct warp-drive spacetimes that have zero expansion of space-time, but it is still a nice picture to have.
 

Problems

I have already mentioned one very major problem with the warp-drive; it needs totally unreasonable amounts of negative energy. One can by some clever tricks reduce the total energy requirement to an amount that one could imagine an arbitrarily advanced civilisation could utilise and then appeal to quantum mechanics to provide us with the negative. However, in addition to this there are a number of other problems that have been identified. One of these is that part of the warp bubble becomes causally disconnected from the ship once light speed is surpassed. This means that once you jump to light-speed you would have no way of controlling the warp bubble, i.e. you wouldn't be able to turn it off. Even more problematic is the possibility is that some of the material in warp field must move in space-like way. If this was the case it would totally rule out the warpdrive, since as we said nothing can move on spacelike curves. However, many of these problems have been at least partially solved in more recent papers, and so the warpdrive is still far from ruled out.

Conclusions

Well, that is the end of my talk. I hope you have enjoyed it, it was certainly fun learning about this myself and hopefully I have given you all a better understanding of at least one fascinating area of general relativity. Thank you.

by bludot
 

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

Ana Sayfa /index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy)  /Astronomy