De Broglie Dalgaboyu

Elektromanyetik ışımanın kendine has bir doğası olduğunu görmüştük. Dalga özelliklerinin yanı sıra sanki bir parçacıkmış gibi davranıyorlardı. Hayatımızda daha önce hiç görmemiş olduğumuz bir olgu! Bütün bunları söyledikten sonra herhalde size, düşününce akla mantığa sığmayacak, başka bir olgu söylesem yadırgamazsınız: Hareket eden bir kütle bazı yönleriyle, sanki bir dalgaymış gibi davranır. Bir elektron, hatta herşey dalgalar gibi davranır! Burada şunu söylemek isteriz ki bahis konusu olan dalgalar bu sefer elektromanyetik dalga değildir. Bu tamamen farklı bir olaydır; madde dalgaları, olasılık dalgaları.

Amerikan bilim adamı Richard Feynman tarafından bu dalga-parçacık ikilemine güzel bir yaklaşım yapılmıştır: Hiçbir parçacık bir A noktasından bir B noktasına tek bir düz yoldan gitmez, ama parçacığın A'dan B'ye aynı anda olası her yoldan gittiği var sayılır. Yani bu demek olurki parçacığın hiçbir kesin geçmişi yoktur. Bu düşünce tarzının adı GEÇMİŞLER TOPLAMI'dır. Bunu akılda canlandırmak çok zordur, çünkü hayatımızda daha önce buna benzer hiçbirşey görmedik.

Elektromanyetik dalgalarda da olduğu gibi hem parçacık hem de dalga özelliği aynı anda gözlenemez. 1924 yılında, maddenin bu özelliğini farkeden ilk kişi bir Fransız, Louis Victor De Broigle idi.

Bir ışık fotonunun momentumunu p=h/l denklemi ile belirtmiştik. Burada 'p' momentum, 'h' Planck sabiti ve 'l' ise dalgaboyudur. Bu formül madde dalgaları için de geçerlidir. (Madde dalgaları genellikle De Broglie dalgaları diyemomentum <2yy.htm> isimlendirilir). Relativistik etkileri ihmal edersek, bir parçacığın 'unu m.V olarak gösterebiliriz. Burada 'm' cismin kütlesi ve 'V' ise hızıdır. Kırmızıyla yazılmış formülde içler dışlar çarpımı yaparsak aşağıdaki formülü elde ederiz:

l metre cinsinden, h joule cinsinden ve p ise kgm/s cinsindendir.

Buradan, bir yargıya varabiliriz:

Işık Dalgaları Foton Olduğu gibi Madde Dalgaları da Parçacıktır!

Dalga Gibi Davranan Elektronlar

Bir elektron küçük bir parçacık ve yaklaşık olarak (me) = 9,11.10-31 kg 'lık bir kütleye sahip. De Broglie'nin hipotezinden de bildiğimiz gibi, elektronlar dalga özelliği göstermelidir. O zaman 192 x 10-19 Joule enerjiye sahip olan bir elektronun dalgaboyonu hesaplayalım (Burada bahis konusu olan enerji kinetik enerjidir <3xx.htm> ve verilmiş değer bir elektron için normal bir enerjidir). Momentumu bulmak için kinetik enerjiyi kullanacağımız bir formül düzenleyelim: (Relativistik olmayan hesaplamalar yapacağız)

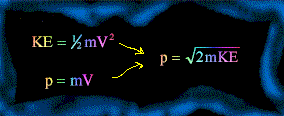
Bilinmeyenleri denklemde yerine koyalım ve elektronun momentumunu hesaplayalım:

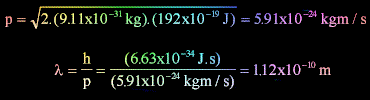
Daha önce de açıkladığımız gibi, deneysel verilere dayanarak, ışığın girişim ve kırınım gösterdiğini söylemiştik. Birer parçacık olan elektronlar da girişim ve kırınım özelliği gösteriyor dersek, sakın şaşırmayın. Bir parçacık nasıl böyle işler yapar? Ne, nnnnne, ne yani, ne? Ne oluyor? Doğanın bu yüzünü, makroskopik dünyada, daha önce hiç görmedik ve bu sebepten dolayı pek mantıklı gelmiyor olabilir.

Bir Merminin Dalgaları

Eğer kainattaki her maddenin bir dalga karakteri varsa, biz bunu neden farkedemiyoruz?

Düşünün ki 0.0001 kg kütlesi olan bir mermimiz var ve 200 m/s gibi bir hızla yoluna devam ediyor. Merminin dalgaboyunu hesap edelim:

l = h / p

Elimizdeki verileri formüle yerleştirirsek, merminin dalgaboyunu 3.3 x 10-32 m olarak buluruz. Galiba birşeyler gözlemek için bu dalgaboyu epey küçük.

Örneğin; bu mermi bir delikten geçerken, kırınım etkilerini görmek istiyorsak, merminin geçeceği deliğin ebadı; mermiye eşlik eden dalganın dalgaboyu (3.3 x 10-32 m) ile kıyaslanabilir olmalıdır. ile kıyaslanabilir olmalıdır yani 3.3 x 10-32 m ile kıyaslanabilir olmalıdır. Acaba bir merminin bu büyüklükteki bir delikten geçmesi olası mıdır?

Bir önceki sayfa

Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.

Ana Sayfa /i ndex /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy) / Astronomy