Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 -Turkey/Denizli
Black Holes, Singularities & Wormholes
Contents
Black Holes
Singularities
Wormholes
Black Hole
A massive astrophysical object that is theorized to be
created from the collapse of a neutron star. The
gravitational forces are so strong in a black hole that they
overcome neutron degeneracy pressure and, roughly speaking,
collapse to a point (known as a singularity). Even light
cannot escape the gravitational pull of a black hole within
the black hole's so-called Schwarzschild radius.
Uncharged, zero angular momentum black holes are called
Schwarzschild black holes. Uncharged nonzero angular
momentum black holes are called Kerr black holes.
Nonspinning charged black holes are called Reissner-Nordström
black holes. Charged, spinning black holes are called Kerr-Newman
black holes. The black hole no hair theorem shows that mass,
charge, and angular momentum are the only properties which a
black hole can possess.
Features of a Black
Hole

A black hole forms when an object collapses to a small size
(perhaps to a singularity) and the escape velocity in its
neighborhood is so great that light cannot escape. The
boundary of this region is called the event horizon because
any event that occurs inside is invisible to outside
observers. The radius of the region is RS,
the Schwarzschild radius.
Strange Stuff Explained: Black Holes

A massive star starts to collapse when it exhausts its
nuclear fuel and can no longer counteract the inward pull of
gravity.

The crushing weight of the stars overlying layers implodes
the core, and the star digs deeper into the fabric of space-time.

Although the star remains barely visible, its light now has
a difficult time climbing out of the enormous gravity of the
still-collapsing core.

The star passes through its event horizon and disappears
from our universe, forming a singularity of infinite density.
Pile enough matter into a small enough volume and its
gravitational pull will grow so strong that nothing can
escape from it. That includes light, which travels at the
absolute cosmic speed limit of 186,000 miles per second. In
a stroke of descriptive genius, physicist John Wheeler named
these objects black holes. The radius of a black hole is
called the event horizon because it marks the edge beyond
which light cannot escape, so any event taking place inside
the event horizon can never be glimpsed from outsidein
effect, the inside of the black hole is cut off from our
universe. It has even been speculated that black holes could
be pathways into other universes. Gravity is so strong at
the center of a black hole, that even Einsteins
gravitational laws must break down. The theory that governs
the incredibly dense matter and strong gravitational fields
at the center of a black hole is not yet known.
How Black Holes Might Appear in Nature
- Micro-Black Holes
- Formation:
Possibly formed in small regions of high density during
the first few seconds of the Big Bang.
- Unusual Features:
Micro-black holes aren't so black! Quantum mechanics and
thermodynamics tell us that they should radiate all
forms of energy due to the strongly varying
gravitational fields just outside their event horizon.
These black holes slowly radiate themselves away,
finally disappearing in a flash of high-energy radiation.
- Size: If a
micro-black hole is created with a mass of greater than
10^17 grams, it would still be around today. This mass
corresponds to about a cubic kilometer of water. In
terms of size, it would be smaller than an electron!
- Observations: Once believed to be a possible source of gamma-ray bursts, there is no current observational evidence for their existence.
- Formation:
Possibly formed in small regions of high density during
the first few seconds of the Big Bang.
- Stellar-Mass Black
Holes
- Formation:
When a star with a mass of greater than 10 times the
mass of the Sun explodes in a supernova, the central
core left behind will collapse into a black hole.
- Unusual Features:
When this type of black hole is part of a binary system,
matter can sometimes stream from the other star into a
disk surrounding the black hole. This is called an
accretion disk.
- Size: These
black holes would range from about 5 to 100 times the
mass of the Sun, giving them diameters of 20 to 400
miles.
- Observations: At present, there are over 25 objects astronomers suspect may be black holes near or in our own galaxy.
A partial list: Cygnus X-1, A0620-00, V404 Cygni, LMC X-1, LMC X-3.
What does an X-Ray binary star look like?
Where is Cygnus X-1? - Formation:
When a star with a mass of greater than 10 times the
mass of the Sun explodes in a supernova, the central
core left behind will collapse into a black hole.
- Super-Massive Black
Holes
- Formation:
Formed via accretion from smaller bodies in the centers
of many galaxies.
- Unusual Features:
On this scale, some of the infalling matter may become
redirected into jets and ejected over the poles of the
black holes. This phenomenon may explain the radio jets
observed from the centers of some galaxies.
- Size: HUGE!
One million to one billion times the mass of the Sun.
They would be about the size of our solar system.
- Observations:
Active Galactic Nuclei (AGN), Seyfert Galaxies, Quasars.
HST's View fo the Jet in Galaxy M87
HST's view of the accretion Disk in Galaxy NGC 4261
- Formation:
Formed via accretion from smaller bodies in the centers
of many galaxies.
The Black Hole Next
Door
Some theorists believe black holes are part of every day
life and are even formed by nature right here on Earth. In
Science News Online you can find the article The Black Hole
Next Door by Peter Weiss about micro black holes. It also
explains why the CERN Large Hadron Collider (which will be
online in the spring or summer 2007) is important for
current theories about multiple dimensions.
Final Proof Provided for Milky Ways Central Black Hole
"We could not believe our eyes."
-- Astronomer Thomas Ott on the surprising discovery of a
star swinging around the very heart of the Milky Way.
Surprising observations of a star swiftly orbiting the
cloudy heart of the Milky Way Galaxy have verified with near
certainty the existence of a central black hole, a
theoretical object that still eludes direct detection.
Astronomers watched the star for a decade, tracking two-thirds
of its path around the galactic center. No object has ever
before been seen so close to the center of any galaxy, nor
has any other object previously been observed making more
than a small fraction of its orbital trek around a galaxy.
"Our work proves that there is indeed a supermassive black
hole in our own galaxy," said Rainer Schoedel, a PhD student
at the Max-Planck Institute for Extraterrestrial Physics (MPE)
in Germany.
An international team of astronomers photographed the star
as it zoomed around the galactic center at speeds ultimately
exceeding 11 million mph (5,000 kilometers per second).
Early this year, the star flitted precariously close to the
black hole, coming within 17 light-hours, or just three
times the distance from the Sun to Pluto.
The observations rule out nearly all other possible
explanations for the tremendous amount of matter -- equal to
some 2.6 million suns -- packed into a tight spot at the
center of our galaxy.
"If one accepts the universal validity of the laws of
physics," Schoedel told SPACE.com, "it is extremely hard to
avoid the conclusion that the supermassive black hole in the
Milky Way does indeed exist."
Chandra Catches Milky Way Monster Snacking
Einstein's Relativity Theory predicted Black Holes. Black
holes are formed by the gravitational collapse of solar
masses. Astronomical observations suggest a super-massive
black hole containing millions to billions of solar masses
in the center of most galaxies. As it turns out our Milky
Way is no exception.
Also see Animations & Video and The Chandra Spacecraft.
New Twists on the Milky Way's Big Black Hole
The supermassive black hole at the center of our Milky Way
Galaxy is heftier than thought and rotates at an amazing
clip, new research shows.
For years scientists said the black hole contained about 2.6
million times the mass of the Sun. They now believe the
figure is somewhere between 3.2 million and 4 million solar
masses.
And a new study suggests all that mass, confined to an area
about 10 times smaller than Earth's orbit around the Sun,
spins around about once every 11 minutes. The Sun, for
comparison, takes about a month to make a revolution on its
axis. Earth spins once every 24 hours.
Black holes can't be seen or measured directly, because
light passing near them gets trapped. So astronomers measure
a black hole's mass by observing the orbital speed of nearby
stars.
The new mass estimate was made by two separate groups, one
at the University of California, Berkeley, and another at
the University of California, Los Angeles, UC Berkeley
physicist Reinhard Genzel told SPACE.com.
Astronomers Watch a Black Hole Eat a Meal
Astronomers from the Institute of Astronomy (IoA) in
Cambridge, England have watched a bundle of matter at the
heart of a galaxy 100 million light-years away as it orbited
a supermassive black hole four times on its way to being
destroyed. The material was approximately the same distance
as our Earth is from the Sun, but instead of taking a year,
it only took a quarter of a day, because of the massive
gravity of the black hole. By tracking the matter's doomed
orbit, astronomers were then able to calculate the mass of
the black hole: between 10 and 50 million solar masses.
Static, Uncharged - Schwarzschild Black Holes.
The first kind of black holes hypothesized, and hence, the "simplest".
In 1916, Karl Schwarzschild hypothesized the existence of
black holes from Einstein's theory of relativity. However,
Schwarzschild only considered mass as a factor.
The Schwarzschild black hole non-moving, and does not have
any charge. Put simply, it is brought about by the collapse
of a stationary star. Light bends around the edge of the
black hole, an observation that involves the theory of a
photon sphere. A photon sphere occurs at a distance of 1.5
times the Schwarzschild radius. At this distance, light rays
orbit unstably around the black hole. Photons orbit in a
sphere around the gravity pull (assuming that the pull is
equal in all directions).
Moving closer into the cosmic phenomena, we eventually reach
the mathematical construct: an event horizon. It marks the
distance where the gravity pull of the black hole is so
strong that even light cannot escape it, and occurs at the
Schwarzschild radius.
When an object is compressed below its Schwarzschild radius
(RS), it becomes a black hole.
Static, Charged - Reissner-Nordström Black
Holes
Unlike the simpler Schwarzschild black hole, the Reissner-Nordström
black hole contains charge. It has more than one event
horizon. A second, inner horizon forms just above the
singularity. It is termed the Cauchy horizon. Electrons
appear to "hover" around this second horizon. In other words,
a charged black hole has two radii where time seems to stop.
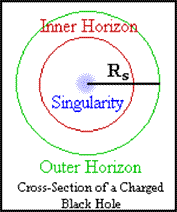
The more charge the black hole has, the smaller the outer
event horizon is, and the larger the inner event horizon. If
enough charge is amassed to equal the mass of a black hole,
then both the outer and the inner horizon would merge.
However, this would be near impossible as the minimum mass
that a black hole is calculated to have is 10^30 times the
speed of light. If charge becomes greater than the mass of
the black hole, then both horizons would vanish, revealing
the singularity ("naked singularity"). When this happens, we
may actually be free to move around the singularity and
resist being sucked into it without having to go faster than
the speed of light. However, in order for this to occur, we
have to generate charge equal to or more than the value of
at least 3 solar masses, or 6 x 10^30. This would be near
impossible to do.
Kerr Black Holes
The Schwarzschild reference frame is static outside the
Black Hole, so even though space is curved, and time is
slowed down close to the Black Hole, it is much like the
absolute space of Newton. But we will need a generalized
reference frame in the case of rotating Black Holes. Roy
Kerr generalized the Schwarzschild geometry to include
rotating stars, and especially rotating Black Holes. Most
stars are rotating, so it is natural to expect newly formed
Black Holes to process significant rotation too.
Features of a Kerr Black Hole
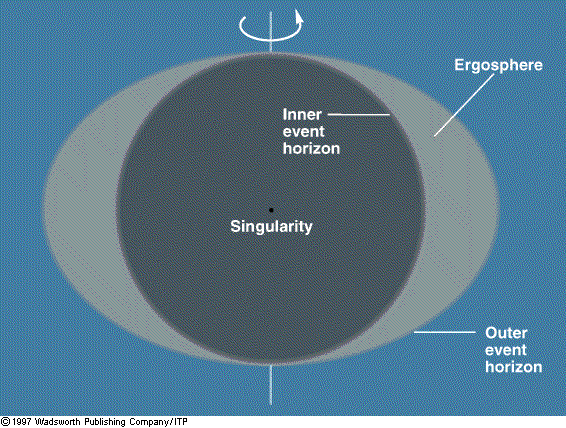
The Kerr black hole consists of a rotating mass at the
center, surrounded by two event horizons. The outer event
horizon marks the boundary within which an observer cannot
resist being dragged around the black hole with space-time.
The inner event horizon marks the boundary from within which
an observer cannot escape. The volume between the event
horizons is known as the ergosphere.
What is a Kerr black hole?
The usual idealised "static" black hole is stationary,
unaccelerated, at an arbitarily-large distance from the
observer, is perfectly spherical, and has a point-singularity
at its centre.
When one of these idealised black holes rotates, it gets an
extra property. It's no longer spherically symmetrical , the
receding and approaching edges have different pulling
strengths and spectral shifts, and the central singularity
is no longer supposed to be a dimensionless point.

The equatorial bulge in the
event horizon can be deduced in several ways
- ... as a sort of
centrifugal forces effect. Since it's possible to
model the (distantly-observed) hole as having all its mass
existing as an infinitely-thin film at the event horizon
itself (i.e. where the mass is "seen" to be), you'd expect
this virtual film to have a conventional-looking
equatorial bulge, through centrifugal forces.
- ... as a sort of mass-dilation
effect. Viewed from the background frame, the "moving
film" of matter ought to appear mass-dilated, and
therefore ought to have a greater gravitational effect,
producing an increase in the extent of the event horizon.
Since the background universe sees the bh equator to be
moving faster than the region near the bh poles, the
equator should appear more mass-dilated, and should have a
horizon that extends further.
- ... as a shift effect.
This tidy ellipsoidal shape isn't
necessarily what
people actually see - it's an idealised shape that's
designed to illustrate an aspect of the hole's
deduced geometry
independent of the observer's viewing angle. In fact, the
receding and approaching sides of the hole (viewed from
the equator) might appear to have different radii, because
it's easier for light to reach the observer from the
approaching (blueshifted) side than the receding (redshifted)
side (these shifts are superimposed on top of the normal
Schwarzchild redshift).
If we calculate these motion shifts using either the SR shift assumptions f'/f = (flat spacetime propagation shift) × root[1 - v²/c²] or the plain fixed-emitter shift law f'/f = (c-v)/c, and then treat them as "gravitational", then by multiplying the two opposing shifts together and rooting the result, we can get the same averaged dilation factor of f'/f=root(1 - v²/c²) in each case, and by applying the averaged value, we recreate the same sort of equatorially-dilated shape that we got in the other two arguments.
Of course, none of these "film" arguments work for a
rotating point, which immediately tells us that the
distribution of matter within a rotating black hole is
important, and that the usual method of treating the actual
extent of a body within the horizon as irrelevant (allowing
the use of a point-singularity) no longer works when the
hole is rotating (a rotating hole can't be said to contain a
point-singularity).
In the case of a rotating hole, the simplest state that we
can claim is equivalent to the rotating film of matter for a
distant observer is a ring-singularity.
Notes
- The idea of being able to treat a non-rotating black
hole as either a point-singularity or a hollow infinitely-thin
film is a consequence of the result that the actual mass-distribution
is a "null" property for a black hole, as long as it is
spherically symmetrical. If the mass fits into a
Schwarzchild sphere, the usual static model of a black
hole allows the hole's mass to be point-sized, golfball-sized,
or of any size up to the size of the event horizon.
It's usual to treat all the matter as being compacted to a dimensionless point, but sometimes it's useful to go to the other extreme and treat the matter as being at its "observed" position - as an infinitely-thin film at the event horizon (see Thorne's membrane paradigm).
- The idea of being able to treat all shifts as being
propagation effects is something that probably ought to be
part of GR - in the context of black holes, the time-dilation
effect comes out as a curved-space propagation effect due
the enhanced gravitation due to kinetic energy. However,
there's a slight "political" problem here, in that GR is
supposed to reduce to SR, and SR is usually interpreted as
having Lorentz shifts which are supposed to be non-gravitational
(because allowing the possibility of gravitational effects
upsets the usual SR derivations). A GR-centred physicist
might not have a problem with this approach of treating
all shift effects as being equivalent, a SR-centred one
probably would.
- The "bulginess" of a Kerr black hole is illustrated on p.293 of the Thorne book (fig 7.9). Thorne says that the effect of the spin on the horizon shape was discovered Larry Smarr in 1973.
Overview of Kerr Spacetime
Kerr spacetime is the unique explicitly defined model of the
gravitational field of a rotating star. The spacetime is
fully revealed only when the star collapses, leaving a black
hole -- otherwise the bulk of the star blocks exploration.
The qualitative character of Kerr spacetime depends on its
mass and its rate of rotation, the most interesting case
being when the rotation is slow. (If the rotation stops
completely, Kerr spacetime reduces to Schwarzschild
spacetime.)
The existence of black holes in our universe is generally
accepted -- by now it would be hard for astronomers to run
the universe without them. Everyone knows that no light can
escape from a black hole, but convincing evidence for their
existence is provided their effect on their visible
neighbors, as when an observable star behaves like one of a
binary pair but no companion is visible.
Suppose that, travelling our spacecraft, we approach an
isolated, slowly rotating black hole. It can then be
observed as a black disk against the stars of the background
sky. Explorers familiar with the Schwarzschild black holes
will refuse to cross its boundary horizon. First of all,
return trips through a horizon are never possible, and in
the Schwarzschild case, there is a more immediate objection:
after the passage, any material object will, in a fraction
of a second, be devoured by a singularity in spacetime.
If we dare to penetrate the horizon of this Kerr black hole
we will find ... another horizon. Behind this, the
singularity in spacetime now appears, not as a central focus,
but as a ring -- a circle of infinite gravitational forces.
Fortunately, this ring singularity is not quite as dangerous
as the Schwarzschild one -- it is possible to avoid it and
enter a new region of spacetime, by passing through either
of two "throats" bounded by the ring (see The Big Picture).
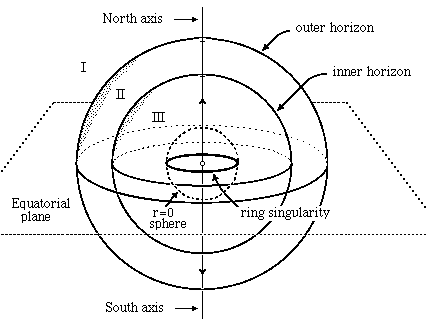
In the new region, escape from the ring singularity is easy
because the gravitational effect of the black hole is
reversed -- it now repels rather than attracts. As distance
increases, this negative gravity weakens, just as on the
positive side, until its effect becomes negligible.
A quick departure may be prudent, but will prevent discovery
of something strange: the ring singularity is the outer
equator of a spatial solid torus that is, quite simply, a
time machine. Travelling within it, one can reach
arbitrarily far back into the past of any entity inside the
double horizons. In principle you can arrange a bridge game,
with all four players being you yourself, at different ages.
But there is no way to meet Julius Caesar or your (predeparture)
childhood self since these lie on the other side of two
impassable horizons.
This rough description is reasonably accurate within its
limits, but its apparent completeness is deceptive. Kerr
spacetime is vaster -- and more symmetrical. Outside the
horizons, it turns out that the model described above lacks
a distant past, and, on the negative gravity side, a distant
future. Harder to imagine are the deficiencies of the
spacetime region between the two horizons. This region
definitely does not resemble the Newtonian 3-spacebetween
two bounding spheres, furnished with a clock to tell time.
In it, space and time are turbulently mixed. Pebbles dropped
experimentally there can simply vanish in finite time -- and
new objects can magically appear.
The complete model of Kerr spacetime built in Chapter 3 adds
two more horizons to each such interhorizon region (there
will be many regions) -- and shows that Kerr spacetime is
organized symmetrically around the spatial 2-spheres at
which these horizons intersect.
Kerr-Newman Black Hole
A rotating charged black hole. An exact, unique, and
complete solution to the Einstein field equations in the
exterior of such a black hole was found by Newman et al.
(1965), although its connection to black holes was not
realized until later (Shapiro and Teukolsky 1983, p. 338).
Rotating (Kerr) Black Holes, Charged and
Uncharged
Most stars spin on an axis. In 1963, Roy Kerr reasoned that
when rotating stars shrink, they would continue to rotate.
Kip Thorne calculated that most black holes would rotate at
a speed 99.8% of their mass. Unlike the static black holes,
rotating black holes are oblate and spheroidal. The lines of
constant distance here are ellipses, and lines of constant
angle are hyperbolas.
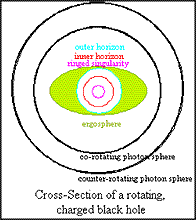
Unlike static black holes, rotating black holes have two
photon spheres. In a sense, this results in a more stable
orbit of photons. The collapsing star "drags" the space
around it into rotating with it, kind of like a whirlpool
drags the water around it into rotating. As in the diagram
above, there would be two different distances for photons.
The outer sphere would be composed of photons orbiting in
the opposite direction as the black hole. Photons in this
sphere travel slower than the photons in the inner sphere.
In a sense, since they are orbiting in the opposite
direction, they have to deal with more resistance, hence
they are "slowed down". Similarly, photons in the inner ring
travel faster since they are not going against the flow. It
is because the photon sphere in agreement with the rotation
can travel "faster" that it is on the inside. The closer one
gets to the event horizon, the faster one has to travel to
avoid falling into the singularity - hence the "slower"
moving photons travel on the outer sphere to lessen the
gravitational hold the black hole has.
The rotating black hole has an axis of rotation. This,
however, is not spherically symmetric. The structure depends
on the angle at which one approaches the black hole. If one
approaches from the equator, then one would see the cross-section
as in the diagram above, with two photon spheres. However,
if one approached at angles to the equator, then one would
only see a single photon sphere.
The position of the photon spheres also depend on the speed
at which the black hole rotates. The faster the black hole
rotates, the further apart the two photon spheres would be.
For that matter, a black hole with a speed equal to its mass
would have the greatest possible distance between the two
photon spheres. This is because of greater difference in the
speed between the photon spheres. As the speed of rotation
increases, the outer sphere of photons would slow down as it
meets greater resistance, even as the inner sphere would
travel "faster" as it is pushed along by the centripetal
forces.
Next, we move on to look at the ergosphere. The ergosphere
is unique to the rotating black hole. Unlike the event
horizon, the ergosphere is a region, and not a mathematical
distance. It is a solid ellipsoid (or a 3-dimensional
ellipse). The ergosphere billows out from the black hole
above the outer event horizon of a charged black hole
(a.k.a. Kerr-Newman), and above the event horizon of an
uncharged black hole (a.k.a. Kerr). This distance is known
as the static limit of a rotating black hole. At this
distance, it is no longer possible to stay still even if one
travels at the speed of light. One would inevitably be drawn
towards the singularity. The faster the rotation, the
further out it billows. When the ergosphere's radius is half
the Schwarzschild radius along the axis of rotation, it
experiences the greatest distance it can billow out. At this
point, even light rays are dragged along in the direction of
rotation. Strangely enough, it is postulated that one can
enter and leave as one likes since technically, you have not
hit the event horizon yet.
For a rotating black hole, the outer event horizon switches
time and space as we know it. The inner event horizon, in
turn, returns it to the way we know it. Singularity then
becomes a place rather than a time, and can technically be
avoided. When angular velocity increases, both the outer and
the inner event horizon move closer together.
In the diagram, you would have noticed that the singularity
here is drawn as a ring, and not a point, as it was for the
static black hole. In the case of a rotating black hole, the
gravity around the ringed singularity is repulsive. In other
words, it actually pushes one away, allowing you to actually
leave the black hole. The only way to approach the ring
singularity would be to come in from the equatorial plane.
Other trajectories would be repelled with greater strength,
proportional to the closer the angle is to the axis of
rotation.
In addition, there would be a third photon sphere about the
ring singularity. If light is parallel to the axis of
rotation, the gravity and the anti-gravity of the
singularity are balanced out. Light then traces out the path
of constant distance (which, in the case is an ellipsoid).
Technically, this might lead the light into another universe
through the singularity, and then back out again. At this
point within the black hole, we may see three types of light:
the light reflected from our universe behind us; the light
from other universes; and the light from the singularity.
Beyond the Event Horizon
Of all a black hole's bizarre characteristics, none seems
stranger than the fact that the solutions to Einstein's
equations tell us that these holes in space-time can serve
as bridges into other universes. As fans of science fiction
are well aware, a parallel universe is a universe entirely
separate from our own. Among the many speculations as to the
nature of these universes, is the idea that there could be
parallel versions of ourselves inhabiting these universes;
each living out a slightly different version of our lives.
This idea doesn't seem so irrational when viewed in relation
to the equally strange world of quantum mechanics [10]. It
is important to note, however, that the existence of these
other universes is, at present, a purely theoretical
construction.
Scientists often use a space-time diagram to demonstrate
graphically the
strange world of General Relativity (figure 5).
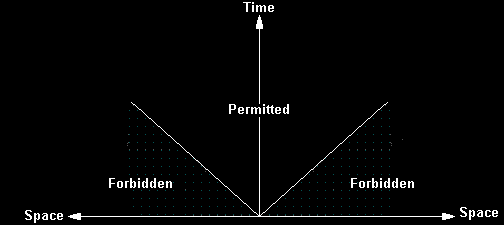
Figure 5: Space-time diagram [11].
The future is located at the top of the diagram. All motion
in space must travel within 45º of the vertical time line.
Paths that are inclined greater than 45º are space-like,
faster than light trips. Accordingly, the zone below the 45º
line is shaded gray and marked "forbidden". Professor Roger
Penrose of Oxford University has developed a special type of
space-time diagram that is very useful for representing the
solutions of black hole equations [12]. These diagrams
quickly show the black hole's connection with parallel
universes.
Figure 6 is a Penrose diagram of a simple Schwartzchild
black hole. Upon first glance, it appears far more complex
than the diagram in figure 5, yet it really isn't. Just as
before, all paths through space must be inclined at an angle
less than 45º from the vertical axis. The singularity of the
black hole, denoted by the row of shark's teeth at the top,
is at a 90º angle, hence it is space-like. The event
horizon's one way nature is shown by the sharp bend in it's
line. The path of a traveler into the hole is shown by the
curved line that passes through the event horizon. Two
things stand out as unusual about this diagram: First there
is an extra singularity in the past (at the bottom).
Secondly, there is the extra universe on the left.
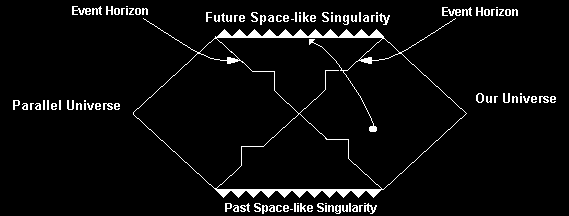
Figure 6: Penrose Diagram of Schwartzchild Black Hole [13].
The additional singularity, marked as past space-like
singularity on the diagram, is what is known as a white
hole. Very simply put, a white hole is the opposite of a
black hole. Instead of engulfing everything that comes near
it, the white hole repels matter. Notice the direction of
its event horizon. Some physicists maintain that the
singularity of a black hole opens into another universe (figure
7). The idea behind a white hole is that matter that falls
into a black hole in our universe is then belched out in
another. It is worth noting, however, that astronomers have
never observed a white hole, so their existence is doubted.
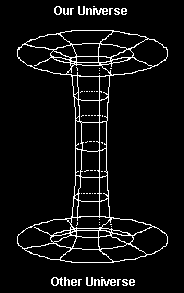
Figure 7: Black Hole Connected to Another Universe [15].
Figure 8 is a Penrose diagram of a Kerr black hole. It will
be remembered that the spinning black hole exhibits several
curious features, such as the ring singularity, the region
of negative space, and the region through which travels into
the past are possible. The ring singularity is denoted by
the rounded off sharks teeth to show that it is a bit more
forgiving than its non-rotating cousin. It should be obvious
that the singularity is vertical (time-like). This means
that one could escape from it with slower than light
velocities. The area marked negative closed time-like loop
is a region just inside the singularity. Very simply put,
this is a region in which the normal barriers between past
and future lose meaning. A traveler into this region could
visit any place in his past or future, were it not for the
one way nature of the event horizon. Just beyond the time-like
loop region, lies the area of negative space. Unfortunately,
this hole has not one, but two one way event horizons that
would prevent a traveler from ever re-entering our own
universe. However, as shown in the diagram, he would have
his choice of many other universes to visit. Figure 8 shows
four (three parallel universes, in addition to our own),
however, this diagram could be extended an infinite number
of times in both the past and future directions. Two
examples of a travelers path into the Kerr hole are shown in
the diagram. Path "A" takes the traveler into the ring
singularity, while path "B" shows his path into another
universe.
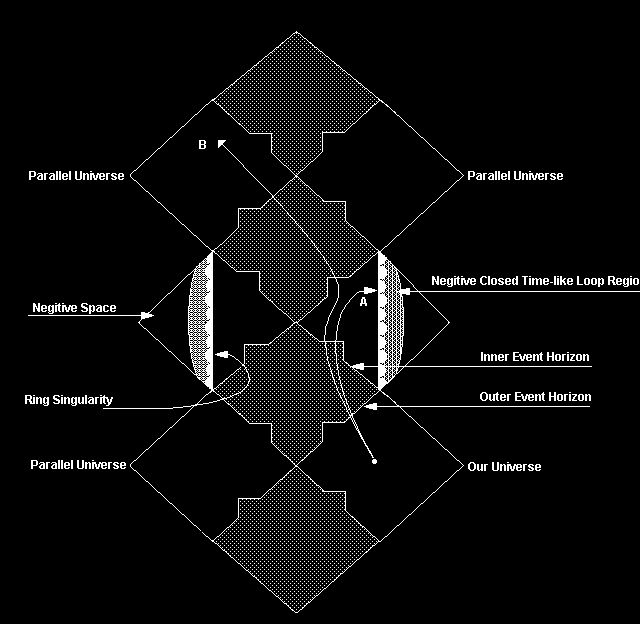
Figure 8: Penrose Diagram of a Kerr Black Hole.
More general in-depth information: Black Holes.
Developments in General Relativity: Black
Hole Singularity and Beyond
| Igor Novikov wrote: |
| At the 20-th Texas Symposium on
Relativistic Astrophysics there was a plenary talk
devoted to the recent developments in classical
Relativity. In that talk the problems of gravitational
collapse, collisions of black holes, and of black holes
as celestial bodies were discussed. But probably the
problems of the internal structure of black holes are a
real great challenge. In my talk I want to outline the
recent achievements in our understanding of the nature
of the singularity (and beyond!) inside a realistic
rotating black hole. This presentation also addresses
the following questions: Can we see what happens inside a black hole? Can a falling observer cross the singularity without being crushed? An answer to these questions is probably yes. |
Black Holes &
Thermodynamics
| Rong-Gen Cai, Li-Ming Cao and Da-Wei Pang wrote: |
| Recently Gibbons et al. in hep-th/0408217 defined a set of conserved quantities for Kerr-AdS black holes with the maximal number of rotation parameters in arbitrary dimension. This set of conserved quantities is defined with respect to a frame which is non-rotating at infinity. On the other hand, there is another set of conserved quantities for Kerr-AdS black holes, defined by Hawking et al. in hep-th/9811056, which is measured relative to a frame rotating at infinity. Gibbons et al. explicitly showed that the quantities defined by them satisfy the first law of black hole thermodynamics, while those quantities defined by Hawking et al. do not obey the first law. In this paper we discuss thermodynamics of dual CFTs to the Kerr-AdS black holes by mapping the bulk thermodynamic quantities to the boundary of the AdS space. We find that thermodynamic quantities of dual CFTs satisfy the first law of thermodynamics and Cardy-Verlinde formula only when these thermodynamic quantities result from the set of bulk quantities given by Hawking et al. We discuss the implication of our results. |
Singularity
A place where the known laws of physics no longer apply,
where, as Caltech physicist Kip Thorne (1940-) puts it,
gravity "unglues" space and time. Singularities may be
points, one-dimensional lines, or even two-dimensional
sheets. The general theory of relativity predicts that
singularities form inside black holes but are conceled from
the rest of the universe behind event horizons. A proper
formulation of quantum gravity may well avoid the infinities
associated with classical singularities.
Strange Stuff Explained: Singularity
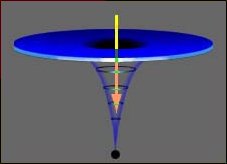
The destiny of all matter that falls into a black hole is to
get crushed to a point of zero volume and infinite densitya
singularity. General relativity also implies that our
expanding universe began from a singularity.
A singularity is a region of space-time in which
gravitational forces are so strong that even general
relativity, the well-proven gravitational theory of
Einstein, and the best theory we have for describing the
structure of the universe, breaks down there. A singularity
marks a point where the curvature of space-time is infinite,
or, in other words, it possesses zero volume and infinite
density. General relativity demands that singularities arise
under two circumstances. First, a singularity must form
during the creation of a black hole. When a very massive
star reaches the end of its life, its core, which was
previously held up by the pressure of the nuclear fusion
that was taking place, collapses and all the matter in the
core gets crushed out of existence at the singularity.
Second, general relativity shows that under certain
reasonable assumptions, an expanding universe like ours must
have begun as a singularity.
Wikipedia: Singularity
A (gravitational) singularity occurs when an astrophysical
model, typically based on general relativity, predicts a
point of infinite curvature. The term is closely related to
the mathematical meaning of "singularity": a gravitational
singularity occurs when the equations produce a mathematical
singularity.
The Big Bang cosmological model of the universe contains a
gravitational singularity at the start of time (t=0). At the
"Big Bang Singularity," the model predicts that the density
of the universe and the curvature of space-time are infinite.
However, the basic Big Bang model does not include quantum
effects, so its predictions are valid only shortly after the
projected singularity.
A singularity also exists within a black hole, where general
relativity predicts a region of infinite curvature. In a non-rotating
black hole, the singularity occurs at a single point in the
model coordinates, and is called a "point singularity". In a
rotating black hole, the singularity occurs on a ring, and
is called a "ring singularity". Rotating black holes are
sometimes referred to as Kerr black holes.
Until the early 1990s, it was widely believed that general
relativity hides every singularity behind an event horizon,
making naked singularities impossible. This is referred to
as the cosmic censorship principle. However, in 1991 Shapiro
and Teukolsky performed computer simulations of a rotating
plane of dust which indicated that general relativity allows
for naked singularities. What these objects would actually
look like is unknown. Nor is it known if singularities would
still arise if the simplifying assumptions used to make the
simulation tractable were removed.
Many physicists believe that gravitational singularities are
"unphysical", meaning that general relativity ultimately
ceases to be an accurate description of gravity somewhere in
the vincinity of what would otherwise be a singularity. It
is generally assumed that a theory of quantum gravity - a
theory that unifies general relativity with quantum
mechanics - will provide a better description of what
actually occurs where general relativity predicts a
singularity. However, no theory of quantum gravity has been
experimentally confirmed to date.
What exactly is a wormhole?
Wormholes are hypothetical entities that show up in
theoretical analyses of Einstein's theory of gravity
(general relativity). Nobody has yet seen a wormhole, nor
are we certain that they exist, but they seem to show up so
easily when we do calculations that many physicists suspect
that they might actually be out there in the real universe.
There are two main types of wormhole of interest to
physicists: Lorentzian wormholes (general relativity) and
Euclidean wormholes (particle physics).
Lorentzian wormholes are essentially short-cuts through
space and time. They are mainly studied by experts in
Einstein gravity, and if they exist in real life would be
more-or-less similar to the wormhole on Star Trek: Deep
Space 9. (But remember, the show is just entertainment, so
don't try to extract detailed physics from DS9; at best it
will give you a vague general idea of what is going on.)
The good news about Lorentzian wormholes is that, after
about ten years of hard work, we cannot prove that they do
not exist. The bad news is that they are very strange
objects: If they exist at all they need large amounts of
negative mass to hold them open and stop them from
collapsing. (Negative mass is not anti-matter, it's a region
where the energy of the universe is less than that of
ordinary vacuum - definitely weird stuff.) We can get small
amounts of negative energy in the laboratory (the Casimir
effect), but getting the large amounts needed to hold a
decent size Lorentzian wormhole open looks to be hopeless
with current technologies. (And there may be deep issues of
principle preventing us from collecting a lot of negative
energy in one place.)
If Lorentzian wormholes do exist, then it seems classically
to be relatively easy to turn them into time machines. This
embarrassing feature has led Stephen Hawking to promulgate
his Chronology Protection Conjecture. According to this
conjecture, quantum effects will conspire to effectively
prevent time travel even when it looks like classical
physics might allow time travel to occur.
Euclidean wormholes are even stranger: they live in "imaginary
time" and are intrinsically virtual quantum mechanical
processes. These Euclidean wormholes are of interest mainly
to the particle physicists (quantum field theorists). You
cannot give them a nice classical interpretation in terms of
a well-behaved classical gravitational field, and
unfortunately have to know a lot of quantum physics to
appreciate even their basic properties.
Strange Stuff Explained: Wormholes
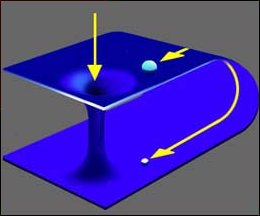
A beam of light traversing a path between two points in
curved space-time can take longer to complete the journey
than a hypothetical spaceship taking advantage of a
wormholes shortcut connection between the two distinct
regions of space-time.
Although they may seem more the stuff of science fiction
than science fact, physicists first dreamed up the idea of
wormholes. In 1935, Albert Einstein and Nathan Rosen
realized that general relativity allows the existence of bridges,
originally called Einstein-Rosen bridges but now known as
wormholes. These space-time tubes act as shortcuts
connecting distant regions of space-time. By journeying
through a wormhole, you could travel between the two regions
faster than a beam of light would be able to if it moved
through normal space-time. As with any mode of faster-than-light
travel, wormholes offer the possibility of time travel.
Until recently, theorists believed that wormholes could
exist for only an instant of time, and anyone trying to pass
through would run into a singularity. But more recent
calculations show that a truly advanced civilization might
be able to make wormholes work. By using something
physicists call exotic matter, which has a negative energy,
the civilization could prevent a wormhole from collapsing on
itself. The stuff of science fiction, to be sure. But
perhaps some day in the far future, it could also turn into
science fact.
Wikipedia: Wormhole
A wormhole, also known as an Einstein-Rosen Bridge, is a
hypothetical topological feature of spacetime that is
essentially a "shortcut" from one point in the universe to
another point in the universe, allowing travel between them
that is faster than it would take light to make the journey
through normal space. The name "wormhole" comes from an
analogy that was used to explain this; imagine that the
universe is the skin of an apple, and a worm is travelling
over its surface. The distance from one side of the apple to
the other is equal to half the apple's circumference if the
worm stays on the apple's surface, but if it instead burrows
a wormhole directly through the apple the distance it has to
travel is considerably less.
Theoretical basis
It is not known if wormholes are possible. A solution to the
equations of general relativity which would make wormholes
possible has not been discovered, without exotic matter, a
theoretical substance which has negative energy density.
However, neither wormhole-accommodating solutions to
relativity equations, nor the existence of exotic matter
have been disproven. Many physicists, including Stephen
Hawking (see Hawking's Chronology Projection Conjecture),
believe that due to the problems a wormhole would
theoretically create, including allowing time travel, that
something fundamental in the laws of physics would prohibit
them. However, this remains speculation, and the notion that
nature would censor inconvenient objects has already failed
in the case of the cosmic censorship principle.
Timeholes
A wormhole could potentially allow time travel. This could
be accomplished by accelerating one end of the wormhole
relative to the other, and then sometime later bringing it
back; relativistic time dilation would result in less time
having passed for the accelerated wormhole mouth compared to
the stationary one, meaning that anything which entered the
stationary wormhole mouth would exit the accelerated one at
a point in time prior to its entry. The path through such a
wormhole is called a closed timelike curve, and a wormhole
with this property is sometimes referred to as a "timehole."
It is thought that it may not be possible to convert a
wormhole into a time machine in this manner, however; some
mathematical models indicate that a feedback loop of virtual
particles would circulate through the timehole with ever-increasing
intensity, destroying it before any information could be
passed through it. This has been called into question by the
suggestion that radiation would disperse after traveling
through the wormhole, therefore preventing infinite
accumulation. The debate on this matter is described by Kip
S. Thorne in the book Black Holes and Time Warps [1], and
will likely require a theory of quantum gravity to resolve.
Wormholes in General Relativity
Reduced to its most basic elements, a Lorentzian wormhole is
a short-cut through space and time. The concept of a
Lorentzian wormhole is essentially synonymous with that of a
spacewarp -- a warping, beiding, or folding of space and
possibly time. ... While we do not have any direct
experimental evidence for the existence of such objects, it
is commonly believed that such objects might be formed in
regions of intense gravitational fields, where the highly
curved nature of the spacetime manifold might allow for the
existence of nontrivial topology.
Ideas along these lines have been floating around in the
physics literature for the past sixty years. The earliest
significant contribution I am aware of is the introduction,
in 1935, of the object now referred to as an Einstein-Rosen
bridge ... The field then lay fallow for twenty years until
the period 1955-1957 when Wheeler coined the term "wormhole"
and introduced his idea of "spacetime foam" ... A thirty
year interregnum followed, punctuated by isolated
contributions, until the major revival of interest following
the 1988 paper by Morris and Thorn ... The last six years
have been a considerable amount of activity, and the field
is now sufficiently mature to warrant an overall summary
being presented.
Lorentzian wormholes/spacewarp come in at least two
varieties:
1. Inter-universe wormholes (wormholes that connect "our"
universe with "another" universe).
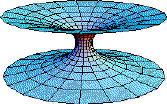
2. Intra-universe wormholes (wormholes that connect two
distant regions of our universe with each other).

Rotating traversable wormholes
| Edward Teo wrote: |
| The general form of a stationary, axially symmetric traversable wormhole is discussed. This provides an explicit class of rotating wormholes that generalize the static, spherically symmetric ones first considered by Morris and Thorne. In agreement with general analyses, it is verified that such a wormhole generically violates the null energy condition at the throat. However, for suitable model wormholes, there can be classes of geodesics falling through it which do not encounter any energy-condition-violating matter. The possible presence of an ergoregion surrounding the throat is also noted. |
Ringholes and closed timelike curves
| Pedro González-Díaz wrote: |
| It is shown that in a classical spacetime with multiply connected space slices having the topology of a torus, closed timelike curves are also formed. We call these spacetime ringholes. Two regions on the torus surface can be distinguished which are separated by angular horizons. On one of such regions (that which surrounds the maximum circumference of the torus) everything happens like in spherical wormholes, but the other region (the rest of the torus surface), while still possessing a chronology horizon and non-chronal region, behaves like a coverging, rather than diverging, lens and corresponds to an energy density which is always positive for large speeds at or near the throat. It is speculated that a ringhole could be converted into a time machine to perform time travels by an observer who would never encounter any matter that violates the classical averaged weak energy condition. Based on a calculation of vacuum fluctuations, it is also seen that the angular horizons can prevent the emergence of quantum instabilities near the throat. |
On a General Class of Wormhole Geometries
| A. DeBenedictis and A. Das wrote: |
| A general class of solutions is obtained which describe a spherically symmetric wormhole system. The presence of arbitrary functions allows one to describe infinitely many wormhole systems of this type. The source of the stress-energy supporting the structure consists of an anisotropic brown dwarf star which smoothly joins the vacuum and may possess an arbitrary cosmological constant. It is demonstrated how this set of solutions allows for a non-zero energy density and therefore allows positive stellar mass as well as how violations of energy conditions may be minimized. Unlike examples considered thus far, emphasis here is placed on construction by manipulating the matter field as opposed to the metric. This scheme is generally more physical than the purely geometric method. Finally, explicit examples are constructed including an example which demonstrates how multiple closed universes may be connected by such wormholes. The number of connected universes may be finite or infinite. |
Two Open Universes Connected by a Wormhole:
Exact Solutions
| Li-Xin Li wrote: |
| In this paper I present a spacetime of two open universes connected by a Lorentzian wormhole. The spacetime has the following features: (1) It can exactly solve the Einstein equations; (2) The weak energy condition is satisfied everywhere; (3) It has a topology of R² x Tg (g >= 2); (4) It has no event horizons. |
Wormholes and Time Travel? Not Likely
| Leonard Susskind wrote: |
| Wormholes have been advanced as both a method for circumventing the limitations of the speed of light as well as a means for building a time machine (to travel to the past). Thus it is argued that General Relativity may allow both of these possibilities. In this note I argue that traversable wormholes connecting otherwise causally disconnected regions, violate two of the most fundamental principles physics, namely local energy conservation and the energy-time uncertainty principle. |
Rebuttal to a Paper on Wormholes
| Leonard Susskind wrote: |
| In a recent paper on wormholes (gr-qc/0503097), the author of that paper demonstrated that he didn't know what he was talking about. In this paper I correct the author's naive erroneous misconceptions. |
| Leonard Susskind wrote: |
| None of this means that wormholes make sense. I share the prejudice of the author of [1] that they do not, and I hope to return to the problem. |
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru