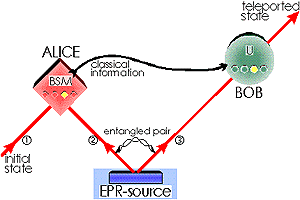
 |
||
ALICE now combines particles 1 and 2 and, by a
Bell-state measurement (BSM), projects them onto an entangled state,
e.g. onto Now, if the state of particle 1 is orthogonal to the state of particle 2, and if the state of particle 3 is orthogonal to the one of 2, then the state of particle 3 must be equal to the initial state of particle 1. However, ALICE could have obtained any of the other three Bell-states with the same probability. She tells BOB which result she obtained via a classical channel. Then BOB turns particle 3 with one of four unitary transformations (U) into an identical replica of particle 1. |
||
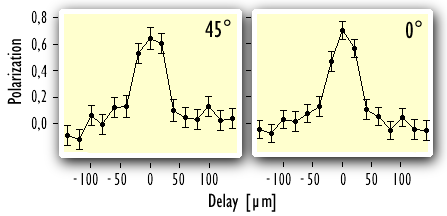
Polarization analysis of the teleported photon: The data shows the polarisation of the teleported photon as a function of the delay between the arrival of photon 1 and 2 at ALICE's beamsplitter (when translating the retroflecting UV-mirror). Only around zero delay interference occurs and allows registration of a Bell-state. The polarization of photon 3 is analyzed if detector p has indicated
that there is a photon to be teleported and if ALICE's Bell-state
analyzer has registered the state
The polarization, without any background subtraction, is 70%±3%. The results for the two non-orthogonal states (45° and 90°) proves teleportation of the quantum state of a single photon. You find more data plots and figures on our ftp-page. Zamanda yolculuk © 2005 Cetin BAL - GSM:+90 05366063183 -Turkey/Denizli |
 |
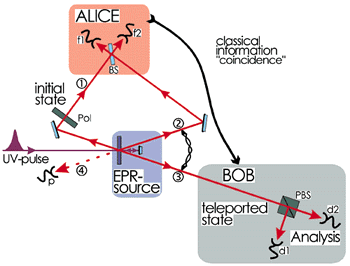A pulse of UV-light passing through a nonlinear crystal creates the
ancillary
entangled pair of photons 2 and 3. After retroflection during its second
passage through the crystal the UV-pulse creates another pair of photons.
One of these will be the teleported photon 1. It can be prepared to have any
polarization. Photon 4, deteced by detector p, serves as a trigger to
indicate that photon 1 is under way.
ALICE then looks for coincidences behind a beam splitter BS2
where photon 1 and the anciliaries are superposed. BOB, after receiving the
clasical information that ALICE obtained a coincidence count in detectors f1
and f2
identifying the Bell state
, knows that his
photon 3 is in the initial state of photon 1. This he can check using
polarization analysis with the polarizing beam splitter PBS and the
detectors d1 and d2.
Thus, photon 3 will turn out to have exactly the properties of photon 1 as defined by the polarizer.
|
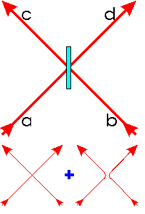
If one overlaps two particles at a beamsplitter,
interference effects determine the probabilities to find the two
particles incident one each from a and b either both in one of the two
outputs c and d or to find one in each output.
Only if two photons are in the state
they will leave the beamsplitter into different output arms. If one
puts detectors there, a click in each of them, i.e. a coincidence, means
the projection of the two photons onto the state
|
For the other three Bell states both photons will exit
together through one of the two output arms. Here polarisation analysis
can separate the state
 from the states
 . (This feature
of interferometric Bell-state analysis was used in the experiment
demonstrating
Quantum Dense Coding.)
The identification of all 4 Bell-states will be possible if one couples the two particles by some interaction. This should be soon possible for various systems (photons, atoms or trapped ions) which will also form the first 2-qubit quantum logic gates. |
|
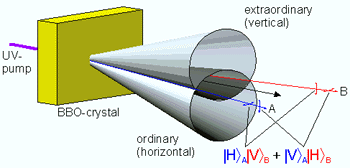
Inside a nonlinear crystal (BBO) an ultraviolet photon
(wavelength 490nm) may spontaneously split into two infrared photons (780
nm). The down-conversion photons (A and B) have orthogonal polarizations
(H or V). In the two beams along the intersections of the cones we observe
a polarization-entangled two-photon state.
For the experimental realisation of quantum teleportation it was necessary to use pulsed down-conversion. Only if the pulse width of the UV-light, and thus the time of generating photon pairs is shorter than the coherence time of the down-converted photons, interferometric Bell-state analysis can be performed. In the experiment the pulses from a mode-locked Ti:Saphire laser have been frequency doubled to give pulses of 200fs duration. The interfering light was observed after passage through IR-filters of 4nm bandwidth giving a coherence time of about 520fs. (A photograph of down-conversion light can be seen on our group home page.).
Alıntı: http://www.quantum.univie.ac.at/research/photonentangle/teleport/tpidea.htm
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /İndex /Roket bilimi / 
E-Mail /CetinBAL /Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri / UFO Technology