.
B is magnetic flux density, H is magnetic field strength, D is the displacement, E is electric field strength,
J is the electric current density, r is the electric volume charge density,
P is electric polarisation, M is magnetic Polarisation, Je are external current sources
Material properties are the permittivity e , the permeability m and the electrical conductivity g .

. Einstieg : ELEKTRODYNAMIK
========================
Teil 1: Maxwellsche Gleichungen
.
(ohne Relativitätstheorie + ohne Quantenmechanik)
in Basis-Form + universelle Erweiterungsmöglichkeiten
für
"klassische" elektromagnetische Felder

.

Durchflutungsgesetz: 1. Basis Maxwell-Gleichung (Felder) Ampere-Maxwell's Law (1) Induktionsgesetz: 2. Basis Maxwell-Gleichung (Felder) Faraday-Lorentz's Law (2) Elektrische Quelle: 3. Basis Maxwell-Gleichung (Quellen) electric Gauss' Law (3) Magnetische "Quelle": 4. Basis Maxwell-Gleichung (Quellen) magnetic Gauss' Law (4)

. Größen im Durchflutungsgesetz, Induktionsgesetz, elektrische und magnetische Divergenz:  Dielektrische Verschiebung D (->Maxwells "displacement"), elektrische Feldstärke E, magnetische Flußdichte B (->Induktion), magnetische Feldstärke H, elektrische Stomdichte J, elektrische Raumladungsdichte r . Die Ableitung von D ist die Verschiebungsstromdichte, die Ableitung von B entspricht magnetischen Flußdichteänderungen.

.   6 GRÜNDE (Auszug) für häufige Fehl-Interpretationen der Maxwell Gleichungen in diversen Publikationen / Lehrbüchern .

Nachstehende Ableitungen führen zu den erweiterten nichtrelativistischen, differentiellen Maxwellschen Gleichungen der klassischen Elektrodynamik unter Verwendung der elektromagnetischen klassischen Feldgrößen E, H, B, D. (Aus Webseite "relativistische Quantenelektrodynamik" wird jedoch ersichtlich, daß diese Feldgrößen nur abgeleitete Größen aus übergeordneten magnetischen Vektorpotentialen und neu formulierten elektromagnetischen Skalarpotentialen sind).

Hinweis für folgende Ableitungen: . B, D, ... = f ( Zeit t, Geschwindigkeit v )  evtl. zusätzlich auch abhängig von . Temperatur T(t) und/oder Volumenänderungen t (t) bei kompressiblen Medien etc.

(5a)

A ist ein VEKTOR B, D, ... oder ein SKALAR: j , m , e , g ... oder entsprechend ein TENSOR ...

mit kartesischen Einheitsvektoren ex, ey, ez

Der rechte Klammer-Ausdruck von Gl. (5a) komprimiert notiert, für z.B. Induktion B :

Vektor-Gradient :								(5b)
								(5c)

In kartesischen Koordinaten gilt für B ( analog für D, H, E)
Vektoranalytische Identitäten  div, rot, grad,  wobei rot H = curl H :

Der vektoranalytische Nabla-Operator für kartesische Koordinaten:

3-dim. Laplace-Operator (x,y,z) 4-dim. Laplace-Operator(x,y,z,t)

(6)

3 Verknüpfungsgleichungen: constitutive equations

D = e E + P

B = m H + M

J = g E + Je

(7)

. Zusätzliche Größen in den 3 Verknüpfungsgleichungen : elektrische Polarisation P, magnetische Polarisation M (->Magnetisierung), eingeprägte Stromdichte Je = f (externe Strom-/Spannungsquellen nichtelektrischen Ursprungs, z.B. Elektrolyten, thermoelektrische Spannungen etc.) Permeabilität m , Permittivität e , elektrische Leitfähigkeit g . Mit diesen Verknüpfungsgleichungen folgen in nichtrelativistischer Formulierung nach W. Stanek die 4 kompletten, auch v-abhängigen Maxwell Gleichungen =  . = f (Zeit t, Geschwindigkeit v , D , E , B , H , J , r , M , P , E , H , m , e , g ) . (Hinweis: In diesen erweiterten maxwell-gleichungen sind nicht explizit die Phänomene der Relativitätstheorie und die aus der Quantenmechanik bekannten "Welle-Teilchen"-Aspekte beinhaltet)

1.b) maxwell's equations (extended for moved bodies)
.
Attention: considering moving bodies the operators d / dt in the above shown maxwell's equations 1. - 4.
are both partial time derivatives and vector gradients as to electrodynamic field terms & velocity.
Using vector analysis maxwell's equations 1. - 4. were extended and re-formulated by W. Stanek as shown :
.

1. extended maxwell's equation (fields) Ampere-Maxwell's Law		(1a)
2. extended maxwell's equation (fields) Faraday-Lorentz'-Law		(2a)
3. extended maxwell's equation (sources) electric Gauss' Law		(3a)
4. extended maxwell's equation (sources) magnetic Gauss' Law		(4a)
using classic electrodynamic field terms for B, H, D, E etc work with area based vector analysis for field theory		( * )
using superior magnetic vectorpotential A & scalar potential PHIs work with line based vector analysis for field theory	grad (A.v) = (v Nabla) A + (A Nabla) v + v x curlA + A x curlv	( ** )
NOTE: Symmetric structure of Maxwell Equations	This shown re-formulation leads to a symmetric structure of Maxwell's equations (1a), (2a), (3a) and (4a). Similar to Dirac's suggestion to construct a set of symmetric Maxwell equations we automatically get both the electric charge density (Rho - Nabla.P) and(!) the magnetic charge density (-Nabla.M)

( * ) 1. EXAMPLE for evaluation with magnetic flux density Terms : Derivation of Faraday-Lorentz' Law
using equation ( * ) : Assuming special conditions/restrictions (-> in literature often not mentioned)
i.e. incompressible materials -> div v = 0, space independent constant movements -> (B grad) v = 0
and in magnetic fields directly from magnetic Gauss' law always -> div B = 0 the remaining term on the
right side in equation ( * ) yields -> rot ( B x v ) = - rot ( v x B ) = - curl ( v x B ). Inserting this result in
Faraday's Law eq. (2a) we can simply derive the extended 2. Maxwell's equation for moved bodies:

using equation ( ** ) assuming same condition mentioned above you also get eq. (2b) with Nabla x A = curl A = B
The first term on the right side of this equation (2b) was proved by Faraday, the second one by Lorentz.
NOTE: using this vector analytical formulation you get the Lorentz-Term E = v x B automatically !
The famous Lorentz law is therefore a (very important) vector IDENTITY ... but not really a separate physical LAW.
.
( * ) 2. EXAMPLE for evaluation with electric flux density Terms : Derivation of Ampere-Maxwell's Law
using equation ( * ) : Assuming special conditions/restrictions (-> in literature often not mentioned)
i.e. incompressible materials -> div v = 0, space independent constant movements -> (D grad) v = 0
and in electric fields directly from electric Gauss' law -> div D = r the remaining term on the
right side in equation ( * ) yields for the cross product -> rot ( D x v ) = - rot ( v x D ) = - curl ( v x D )
and in opposite to Faraday-Lorentz' Law in this Ampere-Maxwell's Law an additional term v div D = v r
Inserting these results in Ampere-Maxwell's Law (1a) we can derive
the extended 1. Maxwell's equation for moved bodies or particles:

The first term on the right side of this equation (1b) was proved by Ampere, the third term by Rowland,
the second term by Hertz (suggested and introduced by Maxwell), the fourth term by Roentgen.
NOTE: using this vector analytical formulation you get the "dualism" of Lorentz-Term H = - v x D automatically !
The Rowland and Roentgen terms are therefore (important) vector IDENTITIES ... but not really separate physical LAWS.
.
( * ) 3. EXAMPLE: Proof of extended 1. + 2. Maxwell's equations using famous HELMHOLTZ' formula
Helmholtz derived for any arbitrary vector flux X in physics (i.e. hydrodynamics) through a moved ( v )
and simultaneously deformable area element in his curl laws - as a subset of ( * ) - following formula :
.

.
Inserting this Helmholtz' formula ( *** ) in the Maxwell equations (1a) and (2a)
- prerequisiting both the same above mentioned conditions/restrictions and X = B alternatively X = D -
we immediately get the extended Maxwell's equations (1b) and (2b) in the 1. and 2. example !
NOTE: using ( *** ) the extended Maxwell's equations can be derived without any knowledge in vector analysis !
.
2. Maxwell's equations considering quantum field theory
.
2.a) Considering relativistic quantum mechanics PROCA has developed following
extended maxwell's equations in quantum field theory -> the so-called proca's equations
.

(8)

.
The difference between maxwell's equations in classic field theory and quantum field theory is shown in red boxes.
The additional "red box" terms consist of magnetic vectorpotential A, electric scalar potential PHI,
material properties in vacuum both permeability mue & permittivity eps. The magnetic flux density B is equal to rot A = curl A .
The special term k² = Kapa² = (m0 c / hbar)² is famous in quantum mechanics, because
Kapa is the Compton frequency devided by velocity c of light ... or Einstein's energy in view of quantum mechanics.
The mass in rest (no relativistic movements) is m0, the universal Planck's constant in quantum mechanics is hbar.
Note: These PROCA equations (8) can be also derived from unified equation Re + i Im = 0 in  section 3.
2.b) The well known relativistic Schrödinger equation, the so-called Klein-Gordon equation is:
 
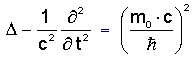
2.c) Extending this homogeneous Klein-Gordon wave equation ( f = 0 ) , applying a probability function
Y ("PSI") we get the non homogeneous Proca wave equations ( f not equal 0 )
.

General Proca wave equation

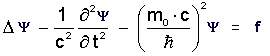(8a)

. Introducing magnetic Vectorpotential A and scalar Potential PHI we can derive following wave equations :
..

Proca wave equation = f ( A )		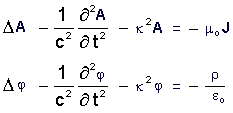(8b)
		(8c)
Proca wave equation = f ( PHI )

Using B = curl A and the constitutive relations
these equations (8a), (8b) or (8c) can be derived directly from equations (8)
... or can be also evaluated from unified equation Re + i Im = 0 in section 3

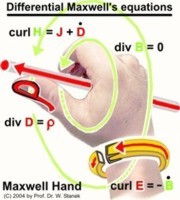
3. "Right Hand Rules as Memo Maps
for all central derivations from Maxwell's equations"

Central derivations from Maxwell's equations
with respect to all important phenomena inside electrodynamics are developed and visualized
as a new Mind Map with 10 memorable Memo Maps
based on variations of famous Maxwell's "Right Hand Rule".
.
Starting from differential equations we can formulate all central equations
governing electrodynamics and interdisciplinary physics.
These Memo Maps are valuable mnemonics for necessary derivations.
Using these 10 special pictures it's easy to bear all derivations in mind.
.
 
.
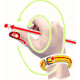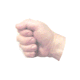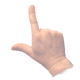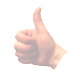
Variations of Maxwell's Hand as a MIND MAP with MEMO MAPS
(C) 2004 by Wolfram Stanek

.
4. Extended Maxwell's equations as a subset derived from only (=1)
unified equation Re + i Im = 0 in relativistic quantum electrodynamics
.
The idea for the following relativistic equation was an impuls - energy - quantum formulation on the basis of
Einstein's energy law, Newton's impuls law and Faraday's induction law considering relativistic and arbitrary
movements of an electron. In all derivations no conventional field terms D, E, B, H, J are explicitely used but only
the superior magnetic vector potential A & special formulation of an EXTENDED scalar potential PHIs. In the
following relativistic equation for quantum electrodynamics i.e. the maxwell's equations are embedded
"only" as a subset. In the case of maxwell's field theory as to real part the term 5)
equals to zero yielding the light field wave gauge A = PHIs / c ->
( for v << c & PHIs = PHI the so-called Lienard-Wiechert's potential A = v x PHI / c^2 ).
This real part gauge is also the condition for achieving the relativistic Schrödinger's equation
-> Klein-Gordon's equation equals to term 4). As to imaginary part of this equation
the Lorentz' gauge (including Coulomb's gauge with PHIs = const) is directly seen,
if term 6) = 0. With these gauges we can simply derive all maxwell's equations
in conventional field terms using also Maxwell's transformation B = curl A
and the known constitutive relations.
Prerequisite for all mentioned re-formulations is an experienced handling with operators in
vector analysis i.e. PHI (A) (line based fields) and quantum mechanics
representated i.e. by impuls operator p and energy Hamilton operator H :

unified theory operators

(10)

Additionally to Maxwell's equations (in rest and with moving bodies) also Lorentz-Einstein's relativistic
energy relations, Newton's impuls mechanics, Proca's equations, (relativistic) Schrödinger's equation
- > Klein-Gordon's equation, Bohm-Aharanov effects in quantum mechanics etc
are integrated in this one equation " Re + i Im = 0 " :
.
 
.
SOME INTERPRETATIONS:
.
1. Real part Re of this equation shows the DUALITY of classic waves (left side)
and quantum particles (right side).
2. Using the light field gauge term 5) = 0 and applying quantum flux (hbar / charge q)
to the imaginary part Im the re-formulated term 6)
yields the total electric field strength E = - d A / d t - grad ( PHIs ) ____________(9a)
with all influences (i.e. arbitrary translation, rotation, distortion movements) in classic electrodynamics:

By this simple re-formulation of the imaginary part Im we've automatically
changed the term 7) so that we also see the DUALITY of classic electric field strength E
and quantum flux based alternative formulation in quantum electrodynamics.
The 2. Maxwell equation = Faraday-Lorentz' law you get from (9) applying the operator "curl".
A good excercise for you: Where are the other Maxwell equations "hidden" in Re + i Im = 0 ?
.
3. Furthermore we have 6 possible gauges for electrodynamic field defined by
div A = ... (eq. Ib) as combination i.e. the simplest
gauges are Coulomb's gauge div A = constant and Lorentz' gauge div A = -[d(PHI)/dt] / c^2
The important 7th gauge (in literature often not mentioned) is the light field gauge term 5) = 0.
This light field gauge is a basis for classic electrodynamics.
But a further conclusion is, that PHOTONS (and GRAVITONS)
must have a rest mass m0 = 0, propagating with the velocity of light in vacuum.
4. From real part < Re > we see a surprising (but measured) phenomenon, that electrodynamics
can influence the mass of rigid bodies! The speed of rigid bodies v
is always less then speed of light c. From eq. (1a) we can conclude
that the gravitational masses of atoms in a material can be changed, especially reduced
or nullified or even inverted under special electrodynamic field conditions !
5. Using no classic field terms, i.e. E, H, D, B or mixed terms like in Proca's equations
the equation Re + i Im = 0 in quantum electrodynamics shows a
general result: magnetic vector potential A and scalar potential PHIs are superior,
classic field terms i.e. E, H, D, B are secondary because those are
simply to derive from primarily A and PHIs equations.
6. Term 6) = 0 in imaginary part < Im > in above shown equation Re + i Im = 0 implies not
only the Lorentz' gauge but also - choosing light field gauge term 5) = 0 -
the central basis for classical interdisciplinary physics.
.
Some examples for interdisciplinary evaluations of imaginary part < Im >
.
a) Directly from eq.(Ib) yields the special Lorentz gauge: div A = - { d (PHIs) / dt/ } / c^2 ___(11a)___
or from eq.(Ib) unified equations i.e. using naturics UNIT checks: div J = - d (RHO) / dt _______(11b)___
or directly from (1b) with J = v RHO

                       Zamanda yolculuk © 2005 Cetin BAL - GSM:+90  05366063183 -Turkey/Denizli 

.
It's clear, that you can get eq. (11b) directly from Ampère-Maxwell's law applying operator "div":
div curl H = 0 = div J + div [ d D /dt ] with electric Gauss' law div D = RHO:
Because of J = (current) FLOW and RHO = (electrical charge) DENSITY = charge q / m^3
(analogous quick derivation as for the basic equation in mechanics in the following lines)
eq. (11a) or (11b) can be written as an universal law:
.
div (FLOW DENSITY) = - d (specific DENSITY) / dt ___(11)_ _ => CONTINUITY law
.
FLOW DENSITY is based on electrodynamics, thermodynamics or hydrodynamics etc., too ...
Specific DENSITY means the equivalent medium (charge, mass etc.
Eq. (11) can be re-formulated i.e. with respect to mechanics

where RHOm = Mass Density in mechanics as formal equivalence with charge density in electrodynamics.
A separate quick development of new formulas can be related to naturics based UNIT checks, i.e.
directly from eq. (Ib) for electrodynamics leading to eq. (11c) governing mechanics:
RHO. A [As/m^3 Vs/m = Ws/m^3 s/m = Nm/m^3 s/m = kg/m^3 m/s] = RHOm. v __(11d)
RHO. PHIs / c^2 [As/m^3 V s^2/m^2 = Nm/m^3 s^2/m^2 =
kg m / s^2 m /m^3 s^2/m^2 = kg / m^3] = RHOm_(11e)_
Eq. (11d) and (11e) in eq. (1b) yields eq. (11c)
. .
b) additionally applying light field gauge: d (q A) / dt = - grad (q PHIs)___(12a)
because of q A = Impuls and q PHIs = (potential) energy eq. (12a) can be written as an universal law:
.
d (IMPULS) / dt = - grad (ENERGY) ___(12)__ => FORCE law__
.
eq. (12) or directly (11c) can be re-formulated i.e. with respect to mechanics:
d (m v ) / dt = m dv / dt + v dm / dt = - grad ( Wpot )___(12b)__
where m = Mass, v = speed of body, Wpot = m g h (i.e. and/or other force-"sources")
.
NOTE: Regarding (11b), (11c) and (12) we can formally switch between Newton's and Maxwell's relations
using Hamiltonian vector gradient formulation eq. (II), (III) shown above in unified equation Re + i Im = 0
... always thinking in analogies.
HINTS: Start from grad (A.v) = (v Nabla) A + (A Nabla) v + v x curlA + A x curlv _____(12c) = ( ** )
or simplify with A = v as needed i.e. for NAVIER-STOKES equations in hydrodynamics you directly get :

Using (12c), (12d) we can compare important features of Maxwell equations and Newton's law, too.
... it's a good excercise for you to test your capabilities in handling vector analytic operations!
.
NOTE: 1. Though the physicist Heinrich Hertz was convinced that Maxwell's equations are not
derivable from Newton's equations, you can prove it ... at least in a formal analogy
... useful for multiphysics applications in engineering.
2. But never forget thinking in analogies: In real mechanics nothing is identical
with electric charge in electrodynamics.
.
c) Integrating eq. (12) yields the well known universal energy law in general form:
.
Wtotal = Wkinetic + Wpotential = constant___(13)___ => ENERGY law
.
NOTE: Kinetic energy derived from relativistic Energy with Taylor approximation:
W (kinetic) = W (total) - W (restmass) = m c^2 - m0 c^2 = 0.5 m0 v^2 + ... tiny terms (x)
(x) can be neglected in non-relativistic applications
.
Further details: discussion about maxwell's equations combined with quantum mechanics
.
5. "Electrodynamics and its analogies in physics based on
extended Maxwell's equations for industrial applications in mechatronics"
.
by Wolfram Stanek et.al.

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

Ana Sayfa /İndex /Roket bilimi /  E-Mail /CetinBAL /Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /  UFO Technology 

Kuantum Teleportation / Kuantum Fiziği / Duyuru

New World Order(Macro Philosophy)/Astronomy