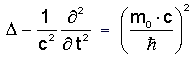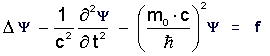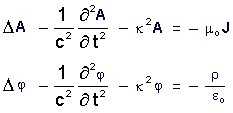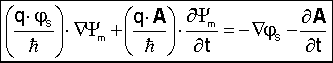1. "Klassische" Eich-Konventionen
Eine übergeordnete Eich-Konvention ist js = c A [ Term 5) = 0 in Gl. 1a)]
Mit v < c strukturgleich zum Lienard-Wiechert-Potential js = A c² / v
Aus Gleichung 1b), Term 6) = 0 - rechte Gleichungsseite - folgt jedoch durch
Multiplikation mit dem magnetischen Fluß-Quant Ym = hquer / q sofort auch die bekannte
Eichung für "klassische" Elektrodynamik --> Lorentz-Konvention : div A = - 1/c² djs/dt
Wenn das elektromagnetische Skalarpotential js = konstant bzw. Spezialfall js = 0,
dann ergibt sich analog die sogenannte Coulomb-Konvention : div A = 0

---

2. Verknüpfungsgleichungen + Elementar-Relationen + Lichtgeschwindigkeit
Durch Term 5) = 0, d.h. js = c A
(Größen - und "Einheiten"-Eich-Gleichung)
sind alle "Elemantar"-Relationen für elektromagnetischen Felder und elektrischen Strömungen
sofort angebbar (entsprechen den bekannten Verknüpfungsgleichungen ohne Polarisationen):
B=m H, D=e E, J=r c=g E
Formal analog sind deshalb mit js = c A und evtl.
Berücksichtigung der reziproken Zeit-Dimension [1/s] <--> d/dt
auch alle "Elementar"-Relationen für elektrotechnische Bauteile
wie Kondensatoren C, Spulen L, Widerstände R etc
durch Einheiten-Vergleich einfach im Kopf abzuleiten,
da diese nichts anderes als "konzentrierte" Feldelemente sind:
z.B.
Q(C) = C U , i(C) = C du/dt , u(L) = L di/dt , y(L) = L i , u(R) = R i ,
sowie Definition Lichtgeschwindigkeit c = |js|/ |A| aus Eichung js = c A
Äquivalente Formulierung der Lichtgeschwindigkeit c = 1 / Ö( mo eo )
aus diversen Ansätzen möglich: z.B. Ö[(ExH)/(DxB)] oder
quantentheoretisch: z.B. Ö{[- r/eo (hquer/m c)²] / [- J mo (hquer/m c)²]}
mit J = r c , sowie mo, eo im Vakuum ( E x H = Poynting-Vektor ).
Analog ergibt sich mit js = c A sofort der Wellenwiderstand :
Zo = c mo = 1 / (c×eo) = Ö(mo / eo) = E / H = 120 p [W],
mit mo = 4 p×10-7 [Vs/Am], c = 3×10 hoch 8 [m/s]
 

---

3. Relativistische Schrödinger-Gleichung + Proca-Wellengleichungen
3a) Relativistische zeitabhängige Schrödinger-Formulierung im feldfreien Raum bei Term 5) = 0 :
Gleichung Term 4) ist in Fachkreisen auch als sog. Klein-Gordon-Gleichung bekannt:
 
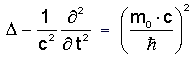
Hieraus Compton-Wellenlänge lc = 2p hquer/(m0 c) (aus rechter Gleichungsseite),
oder alternativ als Compton-Frequenz mit wc = c 2p/lc = (m0 c²)/hquer.
Diese alternative Frequenz-Formulierung der Compton-Wellenlänge ist jedoch nichts
anderes als die gequantelte Einstein-Energie des Teilchens mit Masse m0.
Aus zeitunabhänger Form (2. Term linke Seite obige Gleichung = 0) z.B. Yukawa-Kernkräfte
und Kernkraft-Reichweiten mit Austauschmasse PION (273-fache Masse von m0) etc.
Die Klein-Gordon-Gleichung gilt jedoch nur für Bosonen
(d.h. atomare Teilchen mit ganzzahligem Elektronen-Spin 0, 1, ...)
Diese Klein-Gordon-Gleichung kann auch als homogene Wellengleichung
mit f = 0 und angewandter Wahrscheinlichkeitsfunktion Y geschrieben werden:
.

.
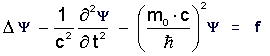
3b) Der Fall der inhomogenen relativistischen Wellengleichung führt mit
Abkürzung k = (m0 c / hquer) , Erregungsterme f ungleich 0
und komplettem Real-Teil Gl. (1a) auf die Proca-Wellengleichungen :
.

.
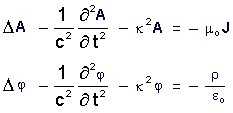
Dieselben inhomogenen Wellengleichungen für A und j leiten sich auch aus den
quantenmechanisch erweiterten Maxwell-Gleichungen nach Proca ab :
.

.
Vergleiche im Folgenden die klassischen Maxwell Gleichungen :
 
Von den klassischen Maxwell Gleichungen unterscheiden sich die
Proca-Gleichungen durch die rot eingerahmten Terme.

---

4. gesamte elektromagnetische Feldstärke E
Mit js = c A [ Term 5) = 0 in Gl. 1a)] und Multiplikation sowohl mit c als auch
magnetischem Fluß-Quant Ym = hquer / q folgt aus (1b) :
 

		1c) entspricht 1b)
------ E quantenorientiert ------	|--E "klassisch" --

Diese Umformung stellt die "dualen" elektromagnetischen Feldstärken
sowohl in der Quantenelektrodynamik (linke Gleichungsseite)
als auch in der "klassischen" Elektrodynamik (rechte Gleichungsseite)
in einer einzigen Gleichung dar.
gradYm ist die räumliche und dYm/dt die zeitliche Änderung der
magnetischen Fluß-Quanten. Räumliche Änderungen sind mit der
gequantelten Energie (q js / hquer) und zeitliche Änderungen mit
gequantelten Impulsen (q A / hquer) verknüpft.

Mit B = rot A liefert z.B. die rechte Seite von 1c)
direkt die gesamte "klassisch" elektrodynamische Feldstärke E :
E = - gradjs - dA/dt = - gradjel - dA/dt + v x rot A + ...
... + (evtl. Restglieder z.B: Spin-Terme, interdisziplinäre Potentiale etc)

---

5. Vier Maxwell Gleichungen (auch für bewegte Körper)
Die kompletten Maxwell Gleichungen für beliebig bewegte Körper
in differentieller Form als Basis der klassischen Elektrodynamik
(jedoch ohne relativistische und quantenmechanische Aspekte)
aus 1b) bzw. 1c) +5) +2) +3) mit Term 5) = 0 und Term 6) = 0 .
In abgeleiteten klassischen Feldgrößen wie elektrische Feldstärke E,
magnetische Feldstärke H, dielektrische Verschiebungsdichte D, magnetische
Flußdichte B , erregende Stromdichte J und elektrische Raumladungsdichte r
mit bekannten Verknüpfungsgleichungen (siehe Punkt 1) sofort ableitbar:

Hinweis: Im Fall ruhender Körper sind z.B. dD/dt oder dB/dt partielle Ableitungen,
im Fall bewegter Körper jedoch totale Ableitungen !
(=Summe aller nichtrelativistischen + nicht quantenorientierten Einflüsse + Wirkungen)
.
-------------------------------------------------------------------------------------------
Ableitungshinweise für Maxwell Gleichungen aus Modell-Gleichung (1) :
mit js = c A und Multiplikation sowohl mit c als auch
magnetischem Quanten-Fluß Ymag = hquer / q
folgt aus (1b) - rechte Gleichungsseite -
mit B = rot A die gesamte "klassisch" elektrodynamische Feldstärke E :
E = - gradjs - dA/dt = - gradjel - dA/dt + v x rot A + ...
... + (evtl. Restglieder z.B: Spin-Terme, interdisziplinäre Potentiale etc)
Vektoranalytische Rotation "rot" auf E angewendet liefert:
rot E = - rot gradjs - d (rotA) / dt , mit rot gradjs = 0 (immer !)
Daraus folgt für die Elektrodynamik direkt die 2. Maxwellsche Gleichung:
rot E = - dB/dt ( für ruhende Körper ) bzw.
weil dB/dt = dB/dt + (v grad) B und
(v grad) B = - rot (v x B) + v div B - B div v + ( B grad) v :
rot E = - dB/dt (auch für bewegte Körper)
Ableitungshinweise 1. Maxwellsche Gleichung vgl. nächsten Punkt 6.

---

6. Quanten-Kontinuums-Gleichung + klassische Kontinuitätsgleichung
Kontinuums-Gleichungen für
Quantenelektrodynamik + klassische Elektrodynamik : Gleichung 1b)
Kontinuumsgleichung Lorentz-Konvention: Term 5) = 0 + Term 6) = 0 ->
div A = - 1/c² djs/ dt bzw. div J = - dr/dt
In der klassischen Elektrodynamik ist J die "konventionelle" Stromdichte
(siehe ff Wahrscheinlichkeits-Stromdichte).
Hinweis mit Term 5) =0 : Wegen div D = r und div rot A = 0 (immer !)
ist in Gl. (1b) die 1. Maxwellsche Gleichung beinhaltet :
rot H = J + dD/dt
Da nach Planck-Einstein-de Broglie die Energie W = h f,
ist analog Produkt elektrischer und magnetischer Fluß gequantelt.

Die durch Term 7) bedingte alternative Formulierung über den magnetischen Fluß
ist jedoch übergeordnet einsetzbar, da mit ihr auch die Bohm - Aharanov - Versuche
(Elektronenstrahl-Interferenzen am Doppelspalt etc) besser erklärbar.
Quanten-Kontinuumsgleichung: Wegen quadratischer Glieder Gl. (1a)
ist Wahrscheinlichkeit |Y(r,t)|², daß Teilchen bei einer Ortsmessung im
Volumenelement am Ort r gefunden werden.
Divergenz der "Wahrscheinlichkeitsstromdichte" j(r,t) der Teilchen folgt aus Gl. (1b) :
div j(r,t) = - d|Y(r,t)|² / dt bzw. Teilchen-Geschwindigkeit am Ort r :
v(r,t) = j(r,t) / |Y(r,t)|² .
Geschwindigkeitsbeziehung entspricht der Führungsgleichung in der Bohmschen Quantenmechanik.

---

7. NICHT-relativistische Gleichungen Schrödinger, Bohm ...
Nichtrelativistische Gleichungen von Schrödinger, Bohm, Dirac, BCS, Ginzburg-Landau mit
Näherung linearer Faktoren 1/2 bei kinetischer Energie durch vereinfachende
Rücktransformation aus relativistischem Resultat erkennbar.
(vgl. Buch "Elektromagnetische Wandler und Sensoren", W.Cassing, W.Stanek u.a. )

---

8. relativistisch bewegtes Elektron + Einstein-Energie
Relativitätstheorie ist durch den relativistischen Modellgleichungs-Ansatz des Autors
automatisch beinhaltet: Der relativistische Energiesatz unter Berücksichtigung
aller elektromagnetischen Vektor- und Skalarpotential-Felder
ist im Maxwell Mindmap widergegeben. Spezialfall von A = 0 und js = 0 :
relativistische Energie W = Ö [(m0 c²)² + (c p)²],
wobei m0 die Ruhemasse des Elektrons und p = m v der relativistische Impuls ist.
Dies entspricht der Einsteinschen Masse-Energie-Äquivalenz bzw. m = m0 / Ö [ 1 - ( v / c )² ],
Der Wurzel-Ausdruck ist Basis für Lorentz-Längenkontraktion und Einstein-Zeitdilatation.

---

9. Einflüsse Gravitation mit Wahrscheinlichkeits-Funktion [ m r ]
Die Einflüsse der Gravitation durch Anwendung der Funktion (m r)
auf Gl. (1a) berücksichtigt (m = Masse, r = Radius) :
Dynamische (relativistische) Bewegungsgleichung nach Newton-Einstein.
Z.B. Weltall-Bedingung für "Weißen Zwerg" bzw. "Schwarzes Loch" :
"Ruhe-Energie des Elektrons bzw. Protons = mittlere Gravitations-Energie eines Teilchens".
Aus dieser Gleichung mit Gravitationskonstante ggrav direkt der Schwarzschild-Radius :
Rsch = ggrav * m0 / c²
Ein Stern mit doppelter Sonnen-Masse würde damit zu
schwarzem Loch mit nur 3 km Durchmesser komprimieren.
Gl. (1a) ist im Gravitationsfall mit bewegten Massen
die Basis für Gravitations-Wellen (mit Gravitonen)

---

10. Dyadische Erweiterung bei Temperatur+Volumenänderung
Sollen neben Zeit- und Geschwindigkeits-Einflüssen in obiger quantenelektrodynamischer
Modellgleichung zusätzlich noch Temperaturabhängigkeiten wie Materialerwärmung bzw.
Abkühlung (bis Supraleitungstemperaturen) bzw. elastische Materialverformungen wie
Elektrostriktion e = f(n) und Magnetostriktion m = f(n) berücksichtigt werden,
erweitern sich die Beziehungen für die übergeordneten elektromagnetischen Potentiale
um analog zum (v grad) A - Term aufgebaute dyadische Operator-Formulierungen:
Diese sind eine Funktion der von Permeabilität m und Permittivität e abhängigen
inneren Zustandsvariablen " Temperatur T " bzw. " spezifisches Volumen n "
(Procedere in Webseite Teil 1 : "komplette Maxwell-Gleichungen" skizziert).

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

 Ana Sayfa /İndex /Roket bilimi /  E-Mail /CetinBAL /Quantum Teleportation-2   

 Time Travel Technology /Ziyaretçi Defteri /  UFO Technology 

 Kuantum Teleportation / Kuantum Fiziği / Duyuru

  New World Order(Macro Philosophy)/Astronomy