in einer einzigen Modell-Gleichung : Re + i Im = 0 kompakt formuliert :
Diese Quantenfeldtheorie beinhaltet die Quantenelektrodynamik mit integrierter
Elektrodynamik + Relativitätstheorie + Quantenmechanik + Einflüsse Gravitation

Memory Power Fragen + infos zu mindmap maxwell-gleichungen (maxwell's equations)
+ quantenelektrodynamik (quantum electrodynamics)

MEMORY POWER FRAGE (1) an die Internet User, die an der zentralen Säule für
alle interdisziplinären physikalischen Phänomene interessiert sind:

1.

Können Sie NUR aus der HAND des obigen mindmaps alle 4 Maxwellsche Basis-Gleichungen in differentieller Form ableiten ?

Mnemotechnischer HINWEIS für die 1. Maxwellsche Gleichung rot H = J + d D / d t . Sie sehen plastisch Ihre "rot"ierende "H"and (= rot H, entspricht magnetischem Wirbelfeld mit Feldstärke H) um die Achse Ihres Daumens
( mit der Kontur eines Rho ), der auf einen Punkt . in Richtung der das Magnetfeld erzeugenden elektrischen Stromdichte J zeigt. Dies entspricht dem Spezialfall der bekannten "Rechtsschrauben-Regel" mit Richtungsangabe der Vektoren H und J. Bewegt sich zusätzlich rhythmisch Ihr Daumen ( = d D / d t), dann erinnern Sie sich auch noch an den Verschiebungsstrom. Ihr Daumennagel hat die Form des griechischen Buchstaben Rho und erinnert Sie deshalb an die Raumladungsdichte ...
Versuchen Sie nun mit Ihrer Bilder- und Wortschöpfungs-Kreativität die restlichen Maxwell Gleichungen aus der obigen HAND abzulesen, d.h. die 2. Maxwellsche Gleichung rot E = - d B / d t,
die 3. Maxwell Gleichung div D = Rho und die 4. Maxwell Gleichung div B = 0 mnemotechnisch
- für immer merk-fähig verknüpft - abzuleiten bzw. zu erfinden.
.

MEMORY POWER FRAGE (2)
auch an Internet User, die bisher noch keine Physik-Experten sind:

2.

Schritt 1 : Studieren Sie das obige Mindmap (Struktur + Bilder) maximal 2 Minuten, nachdem Sie folgende Zeilen gelesen haben. Setzen Sie beim Lesen beide Gehirnhälften ein: Linke Gehirnhälfte primär für Struktur, Numerieren, Sortieren, Ordnung, Wörter, Logik zuständig. Die rechte Gehirnhälfte primär für Bilder, Imagination -> Phantasie, Assoziationsfähigkeit und plastisches merk-fähiges Verknüpfen zuständig. Assoziieren Sie vor allem zu den einzelnen Skizzen die jeweiligen physikalischen Disziplinen :
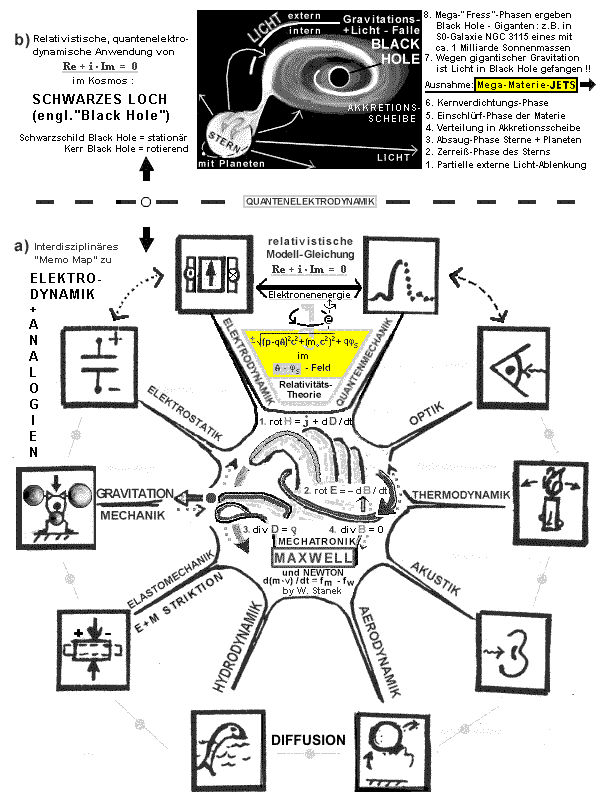
> z.B. Auge erinnert an Optik, Kerze mit bewegter Flamme an Thermodynamik, Ohr an Akustik, Luftballon an Aerodynamik, Fisch aus Wasser an Hydrodynamik, komprimierter Stab an Elastomechanik bzw. Elektrostriktion + Magnetostriktion, Hantel-Matador an Mechanik, Kondensator an Elektrostatik, Dauermagnet mit Magnetisierungspfeil im Innern einer Spule erinnert sowohl an Erregungsmöglichkeiten der Elektrodynamik wie Äquivalenz Dauermagnet + Spule (Dualität Dauermagnetfeld und elektr. Spulenfeld)
> Die Skizze mit durchgezogener + gepunkteter Kurve erinnert an Quantenmechanik bzw. and Dualität "Wellen und Teilchen (bzw. Intensitätsverteilungen)".
> Die durchgezogene Linie zwischen Elektrodynamik und Quantenmechanik soll mit der (erweiterten) Einstein-Energie-Formel und dem kreisenden Elektron daran erinnern, daß als zentraler "Schlüssel" zwischen beiden scheinbar getrennten Disziplinen die komplette relativistische Energie des Elektrons gesehen werden kann.
> Die strichlierte Linie zwischen Quantenmechanik und Optik erinnert daran, daß Licht sowohl als elektromagnetische Welle als auch als quantenmechanisches Teilchen interpretierbar ist (Dualität "Welle + Teilchen").
> Die punktierte Linie zwischen Elektrostatik und Elektrodynamik erinnert daran, daß die Elektrostatik in der Elektrodynamik beinhaltet ist und elektrische Ladungen ursächlich mit elektromagnetischen Felder zusammenhängen.
> Die durchgezogenen dünnen Linien mit dem dicken Punkt sollen daran erinnern, daß viele physikalische Disziplinen in bestimmten Anwendungsbereichen mit Grundlagen anderer im Mindmap angegebener Bereiche verschmolzen sind. Einige exemplarische Beispiele hierzu:
Ohne Grundlagen der Mechanik (Grundgleichung der Bewegung des Elektrons) ist die (erweiterte) Einsteinsche Energie-Beziehung für das Elektron nicht dirket abzuleiten. Selbst die Elektrostatik hängt mit der Mechanik zusammen (z.B. unterschiedliche mechanische Auslenkung aufgehängter gegensinnig polarisierter Plattenkondensatoren im Schwerefeld=Gravitation). Die Magnetohydrodynamik "lebt" vom gemeinsamen Eingriff der Elektrodynamik, Hydrodynamik und auch Thermodynamik. Das großtechnische Separieren elektrisch und magnetisch nichtleitender Materialien (z.B. Diamanten) mit Hilfe magnetisch leitender Flüssigkeiten kann nur bei paralleler Berücksichtigung von Elektrodynamik, Mechanik und Hydrodynamik verstanden werden (vgl. ferrohydrodynamische Bernoulli-Rosensweig-Beziehung). Diese interdisziplinäre Beispielsliste ist beliebig erweiterbar.
> Die moderne Mechatronik (= Kombination von nicht-elektrotechnischen Disziplinen - nicht nur Mechanik - und Elektrotechnik + Software) ist heute für innovative Systementwicklungen und Produktionsprozesse eine zentrale Ingenieurwissenschaft, die ohne Kenntnisse interdisziplinärer Prozesse und Zusammenhänge - wie eben skizziert - nicht optimal funktionieren kann. Einige aktuelle Beispiele aus der Automobilindustrie sollen diese Aussage unterstreichen: Intelligente Aktoren wie z.B. Aktive Tilger (engl. anti vibration systems) in Automobilen zur Geräuschbekämpfung und Vibrationsminimierung eingesetzt, können nur in paralleler Betrachtung von Elektrodynamik, Mechanik, Hydrodynamik und Akustik optimal ausgelegt werden. Die weltweite mechanische Kfz-Produktion (z.B. Fördern und Stapeln von Automobilblechen) funktioniert nur in paralleler Abstimmung von Elektrodynamik (hängendes Fördern und Abwerfen von z.B. Kotflügelblechen mit elektromagnetischen Schaltsystemen), Aerodynamik (Abwurfphase in Luft) und Mechanik (Anschlagphase in Stapelboxen). Die intelligenten Automobil-Sensoren funktionieren einsatzabhängig nur im Zusammenspiel von mechanischen mit im Prinzip allen möglichen physikalischen Disziplinen wie z.B. optischen, akustischen, kapazitiven, elektromagnetischen, quantenmechanischen SQUID-Meßprinzipien usw. Nicht nur für die Automobilindustrie ist diese interdisziplinäre Beispielsliste beliebig erweiterbar:
z.B. Computer-Technik: Harddisk-Drives (Kombination Spulen + Dauermagnet + Eisenkreise + Mechanik + elektronische software-gestützte Ansteuerung). Bei Quanten-Computern der Zukunft spielen fundierte Kenntnisse der Elektro-Quantenmechanik (Quantenelektrodynamik) eine entscheidende Rolle etc...

Kurz-INFO für Physik-Experten zu Quantenmechanik + Elektrodynamik = Quantenelektrodynamik

3.

Neu formulierte relativistische quantenelektrodynamische Gleichung

.

Modell-Ansatz: Die relativistische Einstein-Energie eines Elektrons im Feldraum wird mit Hilfe eines
übergeordneten elektromagnetischen Potentials F s = PHI s (by W. Stanek)
erweitert und die gesamte relativistische Elektronen-Energie in Vektorpotential-Formulierung
im Elektromagnetfeld A - PHI s mit Nabla-Operatoren,
Laplace-Operatoren und Naturkonstanten formuliert. Beliebig vorgegebene
Elektronen-Bewegungen der Geschwindigkeit v im A - Feld werden hierbei tensoriell als Vektorgradient
(Dyadenfeld) durch deformierbare Linienelement-"String"-Operatoren F (A) = PHI A
berücksichtigt. Unter Verwendung quantenmechanischer Impuls-Operatoren p und
Gesamt-Energie-Operatoren H ( = Hamilton-Operator)

kann auf der Basis nur des magnetischen Vektorpotentials A
und elektromagnetischen Skalarpotentials PHI s
eine quantenelektrodynamische Beziehung für eine kompakte Quantenfeldtheorie
abgeleitet werden, die relativistische Modellgleichungs-Invarianz aufweist und die
"Welle-Teilchen-Dualität" für Elektrodynamik + Quantenmechanik in einer einzigen
komplexen Gleichung mit Real- und Imaginär-Teil wiedergibt.
.
Anmerkung zu tensoriellem Linienelement-Operator F (A) = PHI A = ( v grad ) A
in der (Quanten-) Elektrodynamik:
In der Hydrodynamik wird dieser Operator als Spezialfall ( v grad ) v bei der Ableitung
der auf Geschwindigkeitsströmungen basierenden zentralen Navier-Stokes-Gleichung benutzt ...
... diese Gleichung ist übrigens - was allgemein nicht sehr bekannt ist -
strukturidentisch mit der kompletten elektrodynamischen Wirbelstrom-Gleichung !
(Fachbuch "Elektromagnetische Wandler und Sensoren", expert-Verlag 2002, by W. Stanek u.a.)
 

Schlußfolgerungen:
> Diese abgeleitete Beziehung zeigt relativistische Invarianz und gibt die "Welle-Teilchen-Dualität"
für Elektrodynamik + Quantenmechanik in einer einzigen komplexen Gleichung mit Real- und Imaginär-Teil wieder.
> Aus dieser abgeleiteten relativistischen quantenelektrodynamischen Gleichung lassen sich sofort die Compton-Frequenz im feldfreien Raum, bzw. als Spezialfall von Impuls-Energie-Quanten- Gleichgewichten die zentralen Resultate der klassischen (erweiterten) Maxwellschen Gleichungen ablesen.
> Für beliebige elektromagnetische Felder folgt aus dem Real-Teil eine neu formulierbare relativistische Universalfrequenz, wobei der erste Term auf der rechten Seite dem Quadrat des Quotienten Compton-Frequenz/Lichtgeschwindigkeit entspricht. In dieser unten angegebenen relativistischen quantenelektrodynamischen Gleichung sind die zentralen elektromagnetischen Energiedichten, Impulse und Kräfte, die Kontinuitätsgleichung, die Lichtgeschwindigkeit als Funktion elektromagnetischer Impuls- und Energie-Quanten sowie die bekannten Wellengleichungsformen und Drehimpulsvarianten beinhaltet.
> In dieser abgeleiteten Gleichung sind die relativistische zeitabhängige Schrödinger-Gleichung
im feldfreien Raum - die Klein-Gordon-Gleichung - für Bosonen, d.h. ganzzahliger Spin berücksichtigt.
> Im A - Phi s - Feldraum sind Aussagen analog zur Dirac-Gleichung für Fermionen (d.h. auch Elektronen mit halbzahligem Spin) für Eigen- und Wechselwirkungsfrequenzen möglich, jedoch im Gegensatz zur Dirac-Gleichung ohne gemixte A-, B-, E-Terme und nicht nur näherungsweise, sondern direkt auch für Elektron (da Ableitungsbasis). Die Proca-Gleichungen als erweiterte Klein-Gordon-Gleichungen sind direkt ableitbar.
> Aus Gl. (Ia) - Real-Teil - folgt im Vergleich von linker + rechter Seite, daß alle Impulse und Energien gequantelt sein müssen.
> Aus Gl. (Ib) - Imaginär-Teil - folgt im Vergleich von linker + rechter Seite, daß die beinhaltete Kontinuitätsgleichung sowohl für die klassische Elektrodynamik (ohne Plancksches Wirkungsquantum) als auch für die Quantenelektrodynamik (Quanten-Kontinuums-Gleichung) gültig ist.
Mit den quantenmechanischen Vertauschungsrelationen für die 3 Impuls-Orts-Unschärfen und 1 Energie-Zeit-Unschärfe (Heisenberg) sind aus dem Imaginär-Teil auch die halbzahligen Quantelungs-Phänomene des Elektrons erkennbar.
> Bei Anwendung einer Zustandsfunktion z.B. Stromdichte J auf Real- und Imaginär-Teil dieser komplexen quantenelektrodynamischen Gleichung sind auch die nichttemperaturabhängigen Grund-Phänomene der Supraleitung wie Meißner-Ochsenfeld-Effekt und die beiden Londonschen Supraleitungsgleichungen - bei Impuls-Energie-Quanten-Gleichgewichten direkt aus (Ia) bzw. (Ib) - zu gewinnen.
> Aus dem parallelen Vergleich von Real- und Imaginär-Teil dieser quantenelektrodynamischen Gleichung wird auch der nichtrelativistische Grundgedanke der Bohmschen Quantenmechanik (de Broglie-Bohm-Theorie) verständlich: Die Bohmsche Quantentheorie basiert auf der Ergänzung der nichtrelativistischen zeitabhängigen Schrödinger-Gleichung (Wellenfunktionen) durch quantenmechanische Wahrscheinlichkeitsverteilungen durch Bahnen der Teilchen, z.B. Ort-Zeit-Relation zwischen Stromdichte-Wahrscheinlichkeit div J(t) und zeitlich sich ändernde Raumladungsdichte-Wahrscheinlichkeit - als Quanten-Kontinuums-Gleichung in (1b) berücksichtigt. Die Bewegung der Teilchen wird nach Bohm durch die Form der Wellenfunktion bestimmt, die damit als eine Art "Führungswelle" (englisch "pilot wave") für diese Teilchen agiert. Mit Hilfe dieser Bohmschen Interpretation der Quantenmechanik kann der statistische Charakter der Vorhersagen der Quantenmechanik durch einen deterministischen Prozeß, d.h. die Bewegung eines Teilchens unter dem Einfluß seiner Wellenfunktion, erklärt werden. Einfach ausgedrückt braucht die Bohmsche nichtrelativistische Theorie zur Beschreibung eines Teilchens in einem äußeren Potentialfeld 2 Dinge: Die zeitabhängigen Wellenfunktionen und spezifischen Orte des Teilchens, wobei die Bewegung des Teilchens durch eine "Führungsgleichung" (englisch "guidance formula") in Form eines Geschwindigkeits-Operators erfaßt werden muß.
> Die parallele Betrachtung des physikalisch als Einheit zu sehenden Real- und Imaginär-Teils der neuformulierten Beziehungen (Ia+b) bis (III) läßt diese Bohmsche Interpretation der Quantenmechanik offensichtlich auch zu. Im Gegensatz bzw. als Ergänzung zur nichtrelativistischen Bohmschen Quantentheorie berücksichtigt die unten angegebene Modellgleichung durch (II) und (III) alle nur denkbaren Bewegungen eines Teilchens (Elektrons) im Potentialfeld und sie ist eine invariante relativistische Formulierung auf der Basis der erweiterten Einstein-Energie.
> Einflüsse der Gravitation (z.B. "Schwarze Löcher" und "Schwarzschild-Radius") vergleiche
Beispiele + Erläuterungen der Gl. (I)

.
Elektrodynamik + Relativitätstheorie + Quantenmechanik + Einflüsse Gravitation
in einer einzigen Quantenfeldtheorie - Gleichung Re + i Im = 0 zusammengefaßt :
 

diese Quantenfeldtheorie - Gleichung (I) mit zusätzlichen Informationen ?
.
A = magnetisches Vektorpotential, PHI s = elektromagnetisches Skalarpotential = PHI pot + PHI kin
PHI kin = v A - PHI rot = elektrokinetisches Skalarpotential =
= f ( Bahn+ Spin + Deformation + Translation )
PHI pot = v.a. elektrisches Potential + Massen-Potential, mo = Ruhe-Masse Elektron,
q = Elementarladung, c = Lichtgeschwindigkeit, v = (relativistische) Geschwindigkeit < c

---

MEMORY POWER FRAGE (3) an Physik-Experten zu
Quantenmechanik + Elektrodynamik = Quantenelektrodynamik

4.

Ableitung o.g. relativistischer quantenelektrodynamischer komplexer Gleichung

Versuchen Sie bitte, o.g. quantenelektrodynamische Modell-Gleichung (Ia+Ib) bis (III) selbst abzuleiten. (Ableitung setzt jedoch Kenntnisse der klassischen Elektrodynamik, Mechanik,
Vektor- bzw. Tensor-Analysis, Relativitätstheorie und Quantenmechanik voraus).

MEMORY POWER FRAGE (4) an Physik-Experten:
Können Maxwell-Gleichungen aus kompletter Newton-Gleichung abgeleitet werden ???

5.

Ableitung der Maxwell-Gleichungen für bewegte Körper aus kompletter Newton-Gleichung

Ein interessantes vektoranalytisches Rechen-"Experiment",
das im Gegensatz zur Meinung von Hertz funktioniert!
Versuchen Sie doch einmal, die Newton-Gleichung aus den
Maxwell-Gleichungen für bewegte Körper
mit Hilfe obiger MAXWELL MEMO HAND abzuleiten.
(Ableitung setzt jedoch Kenntnisse der klassischen Elektrodynamik, Mechanik,
und v.a. Vektor- bzw. Tensor-Analysis voraus).

Kurz-INFO für Physik-Experten zu "Verwandtschaft" Elelektrodynamik und Thermodynamik

6.

Ermittlung Elektrostriktion + Magnetostriktion aus a) Elektrodynamik und b) Thermodynamik

a) Sollen neben Zeit- und Geschwindigkeits-Einflüssen in obiger quantenelektrodynamischer Modellgleichung zusätzlich noch Temperaturabhängigkeiten wie Materialerwärmung / Abkühlung (bis Supraleitungstemperaturen) bzw. elastische Materialverformungen Tau wie Elektrostriktion e = f(Tau,...) & Magnetostriktion m = f(Mue,...) berücksichtigt werden, erweitern sich die Beziehungen für die übergeordneten elektromagnetischen Potentiale um analog zum (v grad) A - Term aufgebaute dyadische Operator-Formulierungen. Diese sind eine Funktion der von Permeabilität Mue und Permittivität Eps abhängigen inneren Zustandsvariablen " Temperatur T " bzw. "spezifisches Volumen" (Procedere-Prinzip in Webseite Teil 1 : "komplette Maxwell-Gleichungen" skizziert).
b) In o.g. Literatur wurden alternativ die Magnetostriktions-Kraftdichte f (magstrikt) = - grad p(Tau, H, Mue) und die Elektrostriktions-Kraftdichte f (elstrikt) = - grad p(Tau, E , Eps) über Entropie-Änderungen der Thermodynamik dS = dQ / T unter Einbindung der klassischen Feldgrößen E und H über den Druck-Gradienten grad p abgeleitet.
c) Dass dieser Weg in 5.c) auf der Basis thermodynamischer Potentiale auch zur Lösung führt ist schon aus folgendem Faktum zu "erahnen": Die elektrodynamische Wirbelstromgleichung läßt sich direkt aus den Maxwellschen Gleichungen oder auch aus obiger quantenelektrodynamischer Gleichung als Subset ableiten.
Diese partielle Differentialgleichung 2. Ordnung parabolischen Typs ist strukturidentisch mit der Wärmeleitungsgleichung der Thermodynamik (nach Fourier-Helmholtz)
... übrigens auch mit den Navier-Stokes-Gleichungen der Hydrodynamik bzw. Aerodynamik,
der Diffusionsgleichung in der Chemie (sog. Fick'sche Gleichungen) vgl. Diffusion im obigen
Maxwell Mind Map ... und im linear isotropen Fall auch mit der Elastomechanik ... usw