Zaman Yolculuğunu Araştırma Merkezi © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
Klasik Kuramın Sorunları
Klasik fıziğin, dünyamızı doğru ve tam olarak yansıtmadığını nasıl
bilebiliriz? Başlıca nedenler, gözlemsel kanıtlarla gösterilmiştir. Kuantum
kuramını fızikçiler bize kendi istekleriyle sunmadılar. Çoğunlukla kendi
istekleri dışında bir çok bakımdan, felsefe yönünden tatmin edici olmayan
bir yabancı dünyanın içine itildiler. Tüm görkemine karşın klasik dünyanın
da karmaşık sorunları vardır. Bu sorunların kaynağı, iki tür fiziksel
nesnenin birarada var olmak zorunda olmalarıdır: Her biri sonlu sayıda (altı
adet) değişkenle (üç konum ve üç momentum) tanımlanan parçacıklar; ve sonsuz
sayıda parametre gerektiren alanlar.
Bu ikili, fızik yönünden gerçek bir tutarlılığa sahip değildir.
Parçacıkların ve alanların dengede olmalarını (`tamamen oturmuş olmalarını')
gerektiren bir sistemde tüm enerji parçacıklardan alınıp alanlara verilir.
Bu, enerjinin `eş bölüşümü' denilen bir olayın sonucudur: denge durumunda,
enerji, sistemin tüm özgürlük derecelerinin arasına eşit miktarda yayılır.
Alanlar, sonsuz özgürlük derecelerine sahip oldukları için, zavallı
parçacıkların payına hiç bir şey düşmez!
Özellikle, klasik atomlar durgun olmadıkları için, parçacıkların tüm eylemi,
alanların dalga kiplerinin enerjisine dönüşür. Yeni Zelanda asıllı İngiliz
deneysel fizikçisi Ernest Rutherford 'un 1911'de sunduğu atomun `Güneş
sistemi' tasarımını anımsayınız. Gezegenlerin yerini elektronlar ve güneşin
yerini ise minik bir çekirdek alır. Bunları birarada tutan evrensel çekim
kuvveti değil elektromanyetik kuvvetlerdir. Bu tasarımda ortaya çıkan temel
ve görünüşte çözümsüz problem, çekirdeğin yörüngesinde hareket eden
elektronun, Maxwell denklemleri uyarınca, çekirdeğin üstüne doğru sarmal
hareketiyle ve saniyenin minik bir oranı içerisinde sonsuzluğa doğru giderek
artan yoğunlukta elektromanyetik dalgalar üretmesi gerektiğidir! Ancak,
böyle bir şey gözlenmemiştir. Aslında, gözlenen olayı yani atomların
kararlılığını, klasik kuramla açıklamak olası değildir. Atomlar, ancak
belirli frekanslarda elektromanyetik dalgalar (ışık), gözlemlendiği şekliyle
keskin spektral çizgileri yayabilirler.
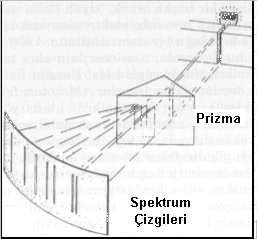
Üstelik bu frekanslar, klasik kuramda yeri olmayan `anlamsız' (çılgın)
kurallara2 bağlıdır.
Konumuzla ilgili bir başka örnek, `siyah cisim ışıması' olarak tanınan
olaydır. Belirli bir ısıda, elektromanyetik ışımanın parçacıklarla dengede
olduğu bir cisim düşünün. 1900 yılında Rayleigh ve Jeans , bu durumda, tüm
enerjinin alan tarafından sı- nırsız olarak emileceğini hesapladılar! Burada
fiziksel yönden alışılmadık bir durum söz konusudur. (Morötesi felaket;
enerji durmaksızın giderek artan frekanslarda alana yönelmelidir.) Ancak
doğa kendisini bu felaketten sakınabilmektedir. Düşük alan salınım
frekanslarında, enerji Rayleigh ve Jeans tarafin- dan hesaplandığı gibidir;
fakat morötesi felaketini öngördükleri yüksek frekanslarda, enerji
dağılımının sonsuz artmadığını, ak- sine frekans arttıkça sıfıra
yaklaştığını gözlemler göstermiştir. Verilen bir ısıda, çok özgün bir
frekansda (renk) enerji en yüksek değerine ulaşır;
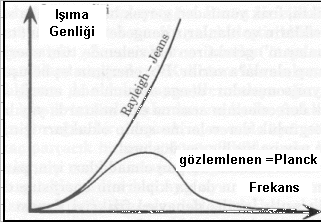
(Akkor halindeki bir demir parçasının ışıması veya güneşin sarı-beyaz ışığı,
aslında, bunun en bilinen örnekleridir.)
Kuantum Kuramının Başlangıcı
Bu sorunlar nasıl çözümlenecek? Newton'un parçacıklar resmi nin, kuşkusuz,
Maxwell alanları nın desteğine gereksinimi var. Daha ileriye giderek
herşeyin bir alan olduğunu, parçacıkların herhangi bir alanın, küçük fakat
sonlu boyutlu, `düğümleri' olduklarını varsayabilir miyiz? Bunun da bazı
zorlukları var çünkü parçaciklar kıvrılarak, salınarak, durmadan değişerek
sonsuz biçim değiştirebilirler.
Fakat, gözlemlenen hiç böyle değildir. Fizik dünyasında aynı türden tüm
parçacıklar birbirine özdeştir. Örneğin, iki elektron birbirinin tamamen
aynıdır. Atomlar veya moleküller bile ancak sonlu sayıda farklı düzenlemeler
oluşturabilirler. Eğer parçacıklar alanlar olarak kabul edilirse, alanları
sonlu ve kesikli özelliklere kavuşturacak yeni bazı öğelere gereksinim var
demektir.
1900'de, zeki fakat tutucu ve tedbirli bir Alman fizikçisi olan Max Planck ,
yüksek frekanslı `siyah cisim' kiplerinden kurtulmak için devrimsel
nitelikte bir görüş sundu: Elektromanyetik salınımlar yalnız, E enerjisi ile
v frekansı arasında belli bir ilişki bulunan kuantumlardan oluşur:
E=hv
Burada h, Planck sabiti olarak bilinen, Doğanın yeni bir temel sabitidir.
Böyle bir zorlama varsayım yoluyla Planck'ın, bugün Planck ışıma yasası adı
verilen kuramı ile, ışıma genliğinin frekansa bağımlılığını gözlemlerle
bağdaştırması şaşırtıcıdır. (Planck sabitinin değeri normal standartlara
göre çok küçüktür: yaklaşık 6.6 x 10-34 Joule-saniyedir.)
Planck bu cesur atılımıyla kuantum kuramının perdesini aralamış oldu.
Einstein başka bir şaşırtıcı öneride bulununcaya kadar fazlaca bir dikkat de
çekmedi. Einstein'ın buluşu şöyleydi: Elektromanyetik alan tamamiyle bu tür
bağımsız birimlerden oluşur! Maxwell ve Hertz 'in, ısığın elektromanyetik
alan salınımlarından oluştuğunu gösterdiklerini anımsayın. Böylece,
Einstein'a -ve Einstein'dan iki yüzyıl kadar öncesi Newton 'a- göre ışık
aslında parçacıklardır! (Ondokuzuncu yüzyılın başlarında İngiliz kuramcı ve
deneycisi Thomas Young ışığın dalgalardan oluştuğunu göstermişti. )
Işığın aynı zamanda hem parçacıklardan hem alan salınımlarından oluşması
nasıl olasıdır? Bu iki kavram yadsınamaz kadar birbirine terstir. Yine de
bazı deneysel sonuçlar ışığın parçacıklardan oluştuğunu gösterirken bazıları
dalgalardan oluştuğunu göstermiştir.
1923'te Fransız aristokrat ve fizikçi Prens Louis de Broglie ,
parçacık-dalga karmaşasına bir aşama daha katarak, doktora tezinde (bu tez
için Einstein'ın onayını almak istemişti!), madde parçacıklarının bazen
dalgalar gibi davrandıklarını savundu! De Broglie'nin, m kütlesine sahip
herhangi bir parçacık için dalga frekansı v , Planck'ın bildirimini bir kez
daha doğrular. Einstein'ın E = mc2'si ile birleştirildiğinde ortaya çıkan
eşitlik v nin m ile bağlantısını gösterir:
hv=E=mc2
de Broglie'nin önermesine göre klasik kuramın bir niteliği olan
parçacık-alan ikiliğini Doğa tanımamaktadır. Gerçekten, v frekansıyla
salınan her neyse yalnız kesikli hv/c2 kütle birimlerinden oluşabilir. Nasıl
oluyorsa oluyor Doğa, parçacıkların ve alan salınımlarının aynı seyler
oldukları tutarlı bir dünya inşa etmeyi başarıyor! Veya, daha doğrusu,
Doğa'nın dünyası, `parçacık' veya `dalga' diye uygun tanımlar yapmamıza
ancak kısmen olanak veren daha incelikli bir içerik taşıyor.
Planck bağıntısı, yirminci yüzyıl bilimsel düşününün ünlü simalarından
Danimarkalı fızikçi Niels Bohr tarafından (1913) parlak bir biçimde
kullanıldı. Bohr'un açısal momentum kuralında öngörülen fikir, çekirdeğin
yörüngesindeki elektronların açısal momentumunun yalnızca h/2pi'nin tam
katları değerler alabileceği idi.
Sonradan Dirac, daha kullanışlı bir simge olan h1 tanımını verdi:
, h1=h/2pi
Buna göre, açısal momentum (hangi eksene göre ölçülürse ölçülsün) sadece şu
değerleri alabilir:
0, h1,2h1,3h1,4h1
Bu yeni içeriğiyle atomun `Güneş sistemi' modeli, oldukça doğru bir şekilde,
birbirinden ayrık kararlı enerji düzeylerini ve Doğanın gerçekten uyduğu
`çılgın' kuralları vermekteydi!
Bu çarpıcı başarısına karşın Bohr'un parlak önerisi, `eski kuantum kuramı'
olarak anılan, ancak geçici bir yararı olan `yamalı bohçadır
Bugün bildiğimiz şekliyle kuantum kuramı, biri Alman Werner Heisenberg ,
diğeri Avusturyalı Erwin Schrödinger olmak üzere dikkate değer iki fızikçi
tarafından birbirinden bağımsız olarak başlatılmıştır. Önceleri, iki
yaklaşım, 1925'te Heisenberg'in `matriks mekaniği' ve 1926'da Schrödinger'in
`dalga mekaniği' olarak birbirinden ayrı kuramlar olarak görülmüşse de, daha
sonra aralarındaki yakın ilişki anlaşılmış; büyük Ingiliz teorik fızikçisi
Paul Adrien Maurice Dirac tarafından kapsamlı tek bir kuram halinde
geliştirilmiştir.
Çift Yarık Deneyi
Kuantum mekaniğinin ilk ana deneyini inceleyelim. Bu deneyde bir elektron
veya ışık demeti, veya başka tür `parçacık- dalga'demeti bir çift dar ve
uzun yarıktan geçirilerek arkadaki ekrana düşürülür
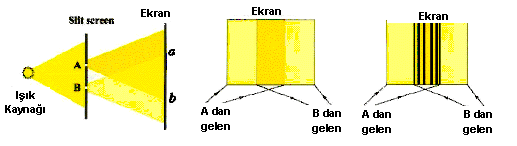
Daha açık örneklemek için, ışığı ele alalım ve ışığın kuantumlarına bilinen
isimlendirmeye uyarak, `fotonlar' diyelim. Işığın, parçacıklar (yani,
fotonlar) olduğunun en açık belirtisi ekranda gözükür. Işık, aralıklı olarak
yerelleşmiş enerji birimleri halinde ekrana ulaşır; ışık enerjisi, E = hv
Planck formülü uyarınca frekansı ile ilişkilidir. Ekrana ulaşan enerji asla
bir fotonun yarısı (veya herhangi bir başka oranı) kadar değildir. Işık
düşümü, foton birimleri cinsinden bir ya- hep-ya-hiç olayıdır. Sadece tam
sayıda foton görülebilir.
Ancak, fotonlar yarıklardan geçerken bir dalga davranışı ortaya çıkar,
yalnız bir yarığın açık (diğerinin kapalı) olduğunu varsayın. Işık açık
kalan yarıktan geçtikten sonra dalga yayılma olayının bir özelliği olarak
kırınım sonucu dağılır. Fakat bu durumda bile parçacık niteliklerini önde
tutabiliriz.
Yarığın kenar çevresinin bir etki yaratarak, fotonları rasgele miktarlarda
bir tarafa veya öteki tarafa saptırdığını düşünebiliriz. Yarıktan geçen ışık
hatırı sayılır büyüklükte bir genliğe sahipse, yani oldukça fazla miktarda
foton içeriyorsa, ekrandaki aydınlanma düzgün bir dağılım gösterir. Işık
genliği iyice azaldığından, parçacık niteliklerine uygun olarak, fotonların
ekrana vurduğu yerlerde bireysel noktalar halinde aydınlanma oluşur.
Aydınlanmanın düzgün görünümü ışığın içerdiği fotonların çok fazla sayıda
olması nedeniyle istatistiksel bir etkidir (Kıyaslama amacıyla belirteyim:
Altmış mumluk bir ampul saniyede yaklaşık 100 000 000 000 000 000 000 foton
üretir!) Gerçekten de fotonlar yarıktan geçerken rasgele dağılıyorlarmış
görüntüsü verirler; değişik sapma açılarında değişik olasılıklarla dağılma,
ekrandaki aydınlanmanın gözlemlenen görüntüsünü verir.
Ancak, parçacık nitelikleri ile ilgili esas problem, her iki yarığı da
açtığımız zaman başgösterir! Yalın, katıksız bir renk, teknik adıyla
monokromatik (yani, tek bir dalga uzunluğuna veya frekansa sahip; parçacık
görüntüsünde ise fotonlarının tümünün aynı enerjiye sahip oldukları ışık)
sağlayan sarı sodyum lambası ışık kaynağımız olsun. Burada, dalga uzunluğu 5
x 10-' m kadardır. Yarıkların her birinin açıklığı 0.001 mm kadar ve
birbirleıinden uzaklığı 0.15 mm kadar olsun. Ekran yaklaşık bir metre uzakta
yer alsın. Oldukça güçlü bir ışık genliğinde, yine düzgün görünümlü bir
aydınlanma elde ederiz, fakat bu kez girişim deseni adı verilen bir dalga
niteliği belirgindir. Ekranın ortasına yakın yerde yaklaşık üç milimetre
eninde şeritler olmuştur
Oysa, ikinci yarığı da açtığımızda sadece ekrandaki aydınlanmanın iki katına
çıkmasını beklerdik. Toplam genel aydınlanma yönünden beklentimiz
gerçekleşmiştir. Fakat şimdi genliğin ayrıntılı dağılımı, tek yarıkla yapmış
olduğumuz deneyle elde ettiğimiz genlikten tamamiyle farklıdır. Ekranın bazı
noktalarında, girişim deseninin en parlak olduğu
. Bir yarık açık olduğunda ekranda görülen genlik dağılımı tek tek küçük
noktalar şeklindedir.
noktalarda, aydınlanma genliği, ilk deneydeki genliğe kıyasla, iki kat değil
tam dört kat artmıştır. Desenin en fazla silikleştiği diğer yerlerde genlik
sıfıra iner.
Sıfır genlikli noktalar parçacık yorumu için belki en büyük problemi
yaratmaktadır. Yarıklar- dan birinin açık olması durumunda fotonun güle
oynaya ulaştığı bu noktalar, ikinci yarığın da açılmasıyla birdenbire fotona
yasaklanıverdi. Fotona izleyeceği yol için ikinci bir seçenek sunarak nasıl
oluyor da onun öteki yolu da izlemesini önlüyoruz? Fotonun dalgaboyunu,
fotonun `büyüklüğü' olarak alırsak, ikinci yarık birincisinden 300 foton
büyüklüğü kadar uzaktadır (her bir yarık birkaç dalgaboyu kadar açıktır ) .
Öyleyse foton, yarıklardan birinden geçerken öteki yarığın açık olup
olmadığını nasıl biliyor? Aslında, ilke olarak, söz konusu `yapıcı' veya
`yıkıcı' girişim olaylarının oluşması için iki yarığın birbirinden uzaklığı
konusunda bir sınır yoktur.
Işık yarıktan (yarıklardan) geçerken, öyle görünüyor ki, bir parçacık olarak
değil bir dalga gibi davranmaktadır!
Yıkıcı girişim dalgaların bir özelliği olarak bilinir. Dalganın yayılması
için iki ayrı yol varsa ve her iki yol da dalgaya açıksa, iki ayrı yoldan
gelen dalgaların birbirini söndürmesi olasıdır.
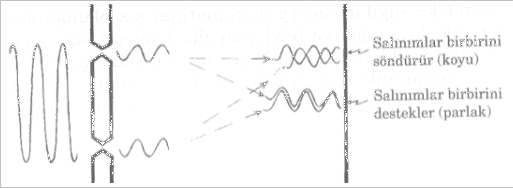
. Dalganın yarıklardan birinden geçen kısmıyla, öteki yarıktan geçen kısmı
tekrar biraraya geldiklerinde aynı `fazda' iseler, birbirlerini
güçlendireceklerdir (başka deyişle, üst üste gelen iki dalganın tepeleri
tepelerine ve, çukurları çukurlarına oturuyorsa), fakat tamamen ayrı `fazda'
iseler birbirlerini söndüreceklerdir. (Başka deyişle, iki dalgadan birinin
dalga tepeleri öteki dalganın dalga çukurlarına oturuyorsa.)
Çift yarık deneyinde, iki yarığa olan uzaklıkları farkı, dalgaboyunun tam
sayı katına eşitse ekranda parlak yerler oluşur ve bu durumda dalga tepeleri
ile çukurları gerçekten birlikte oluşmuşlardır; iki uzaklık arasında fark,
bu değerlerin tam yarılarına eşit ise ekranda siyah yerler oluşur ve bu
durumda dalga tepesi dalga çukuruyla ve dalga çukuru dalga tepesiyle
buluşmuştur. Basit bir makroskopik klasik dalganın, iki yarıktan aynı anda
bu şekilde geçmesinde olağanüstü bir şey yoktur. Ne de olsa bir dalga, ya
sürekli bir ortamın (alan) ya da milyonlarca minik noktamsı parçacıktan
oluşan bir maddenin `bozulmuş' halidir ve kısmen bir yarıktan, kısmen öteki
yarıktan geçebilir.
Fakat burada durum farklıdır: Her bir foton, tamamen kendi başına bir
dalgaymışcasına davranmaktadır! Bir anlamda, parçacık her iki yarıktan aynı
anda geçerek kendi kendisiyle girişim yapmaktadır! Çünkü ışık genliğinin
tümünü yeterince azaltarak, bir anda birden fazla fotonun yarıklardan
geçmesini engelleyebiliriz. Fotonun izleyebileceği iki ayrı yolunun bilinen
olasılıkları alarak birbirlerini yok ettikleri yıkıcı girişim olgusu tek tek
fotonlar için geçerlidir. İki yoldan sadece birisi fotonun yönlenmesi için
açık durumdaysa, foton bu yolu izleyecektir. Öteki yol tek başına açıksa, bu
kez foton o yolu izleyecektir.
Fakat her ikisi birden fotonun önünde açılıyorsa, bu durumda iki olasılık
mucizevi bir şekilde birbirini geçersizleştiriyor ve foton iki yolun
hiçbirini izleyemiyor!
Okuyucu bir an durmalı, bu olağanüstü olayı düşünmelidir. Işığın bazen
parçacıklar bazen de dalgalar gibi davranmasında olağanüstü bir durum
yoktur. Olağanüstü olan, her bir parçacığın, tamamen tek başına, bir dalga
gibi davranması ve bir parçacıkla ilgili değişik olasılıkların bazen
birbirini yoketmeleridir.
Foton gerçekten ikiye ayrılarak kısmen bir yarıktan, kısmen ötekinden
geçebilir mi?
Fizikçilerin çoğu deneyin bu şekilde yorumlanmasına itiraz edeceklerdir.
Yolların yalnızca alternatif olmaları nedeniyle ekranda beliren etkiye
katkıda bulunamayacaklarını, ve yarıklardan geçmek için parçacığın ikiye
bölünemiyeceğini ısrarla savunacaklardır.
Parçacığın kısmen bir yarıktan kısmen öteki yarıktan geçmediği görüşünü
desteklemek için, yarıklardan birine bir parçacık detektörü konulduğunu
varsayalım. Gözlemlendiği zaman bir foton -veya başka bir parçacık- daima
bir bütün olarak görünür, bir bütünün parçası olarak görünmez ve bu nedenle
böyle bir detektör ya tek bir foton saptar ya da hiç bir foton saptayamaz.
Ancak, böyle bir detektör fotonun hangi yarıktan geçtiğini söyleyebilmek
için yarıklardan birine konulduğu zaman, ekrandaki girişim deseni kaybolur.
Bu görüntünün oluşabilmesi için parçacığın `aslında' hangi delikten geçtiği
ile ilgili bir `bilgi eksikliği' olmalı.
Girişim görüntüsünü elde etmek için, seçeneklerin her ikisinin de bazen
`yapıcı' yani beklenenin iki katı kadar bir miktarda birbirlerini
güçlendirerek, veya `yıkıcı', yani birbirlerini gizemli bir şekilde `yok
ederek', katkıda bulunmaları gerekir. Gerçekte, kuantum mekaniğinin
kurallarına göre olup bitenler bundan da gizemlidir!
Seçenekler yapıcı girişimde bulunabilirler (ekrandaki en parlak noktalar)
veya yıkıcı girişimde bulunabilirler (koyu noktalar); fakat daha başka tuhaf
birleşimler de verebilirler, örneğin, `A seçeneği' artı i kere `B seçeneği'
gibi bir birleşimde olabilmelidir; burada `i', 3. Bölümde tanıştığımız eksi
birin kare köküdür (= kök -1) (ekrandaki gri noktalar- da). Gerçekte,
herhangi bir kompleks sayı `seçeneklerin birleştirilmesinde' böyle bir rol
alabilir!
Kompleks sayılar, `kuantum mekaniğinin yapısı için kesinlikle temel
niteliktedir.' Kompleks sayılar sadece matematiğin şık elemanları değildir.
Bir çok ikna edici ve beklenmedik deneysel olgu sayesinde fızikçilerin
dikkatlerini zorla üzerlerine çekmişlerdir. Kuantum mekaniğini anlamak için,
katsayıların kompleks sayılar olabilmesini anlamalıyız.
Yukarıdaki tanımlamalarda fotonları kullanmamızın özel bir amacı yoktur.
Elektronlar veya her hangi bir parçacık, hatta bütün halinde atomlar da aynı
amaçla kullanılabilirdi. Kuantum mekaniğinin kuralları uyarınca, farklı
seçenekli olasılıkların kompleks katsayılarla toplanarak birleşmeleri
bağlamında kriket toplarıyla fıller de toplanabilirler (süperpozisyon).
Ancak biz, kriket toplarının ya da fıllerin böyle alışılmadık şekilde
toplanmalarını asla göremeyiz. Neden göremeyiz? Zor ve tartışması çok uzun
olduğu için bu aşamada sorunun yanıtıyla tanışmanızı istemiyorum. Şu an
için, bir iş kuralı olarak yalnızca, kuantum düzeyi veklasik düzeyolarak
adlandırılan, olası iki farklı fiziksel tanım düzeyinin bulunduğunu
varsayalım.
Kompleks katsayılarla toplanmayı sadece kuantum düzeyinde kullanacağız.
Kriket topları ve filler klasik düzey nesneleridir çünkü.
Kuantum düzeyi, moleküllerin, atomların, atom-altı parçacıkların, vb.
düzeyidir. Genelde bunun çok `küçük ölçekli' olguların düzeyi olduğu
düşünülürse de, `küçük' kavramı aslında fıziksel boyutu bildirmez. Kuantumun
sonuçları metrelerce, veya hatta ışık yılları boyunca oluşabilir. Birşey çok
küçük enerji farklarını içeriyorsa kuantum düzeyinde yer alabilir şeklinde
bir açıklama, belki daha doğru fıkir verecektir. KIasik düzey `makroskopik'
düzeydir ve alışık olduğumuz tanımlar, çevremizde olup bitenlerin, alışıldık
nesnelerin ve fıkirlerin olasılıkları bu düzeyde yer alır.
Bir Parçacığın Kuantum Durumu
Bir sisteme ait farklı seçeneklerin, bunlara karşı gelen olasılıkların
kompleks katsayılarla çarpılarak garip bir şekilde toplanmasıyla kuantum
düzeyinde daima birarada olabilmeleri ne tür bir fiziksel gerçeklik tanımına
yol açar?
Bir çok fizikçi böyle bir tanım bulmaktan umutlarını kesmiş görünüyorlar.
Umutlarını yitirdikleri için kuantum kuramının, sadece olasılık hesaplarını
yapmak için bir yöntem olduğu, fiziksel dünyanın nesnel bir tanımını
yapamayacağı görüşüyle kendilerini avutuyorlar.
Bazıları, kuantum kuramının nesnel bir tanımının yapılmasının, en azından
fiziksel gerçeklerle uyumlu bir tanımının yapılmasının, mümkün olmadığını
bildirdiğini savunuyorlar. Bana sorarsanız, böylesi bir karamsarlığın hiç
bir gerekçesinin olmadığını söylerim. Şu ana kadar yaptığımız tartışmalara
bakarak onların görüşlerine katılmayı çok erken buluyorum. ilerleyen
tartışmalarımızda kuantum etkileri ile ilgili çok daha çarpıcı açmazlarla
karşılaştığımızda belki de bu umutsuzluğun nedenlerini daha iyi
değerlendirebileceğiz. Fakat şimdilik iyimserliğimizi elden bırakmıyarak
kuantum kuramının bize sunduklarını cesurca karşılamaya hazırlanalım.
Bu bize sunulan kuantum durumu ile verilendir. Bir tek kuantum parçacığını
düşünmeye çalışın. Klasik düzeyde, bir parçacık uzaydaki konumuyla
tanımlanır ve bir sonraki evredeki davranışını bilmek için, hızım (veya,
eşdeğer olarak momentumunu) bilmeliyiz. Kuantum mekaniksel açıdan, bir
parçacığın bulunabileceği her bir konum, ona sunulan bir `seçenektir'. Tüm
seçenekler, biraz önce gördüğümüz gibi, kompleks katsayılarla çarpılıp
toplanabilirler.
Bu kompleks katsayılar kümesi, parçacığın kuantum durumunu tanımlar. Kuantum
kuramında, konumun bir kompleks değerli fonksiyonu kabul edilen ve
parçacığın dalgafonksiyonu denilen bu katsayılar kümesini Yunan harfi #968;
(`psi' okunur) ile göstermek standart uygulamadır.
Herhangi bir x konumu için, dalgafonksiyonu #968; (x) değerine sahiptir ve
bu parçacığın x konumunda bulunması olasılığının genliğidir. Kuantum
durumunu bir bütün olarak göstermek için sadece psi harfini kullanabiliriz.
Parçacığın konumunun fiziksel gerçekliğinin, aslında, onun #968; kuantum
durumu olduğu görüşünü benimsiyorum.
Kompleks değerli psi yi nasıl tarif edilir? Üç boyutlu uzayda bu biraz zor
olacağı için parçacığın, tek boyutlu bir doğru üzerinde, örneğin, standart
(kartezyen) koordinat sisteminin x-ekseni boyunca kalmaya kısıtlandığını
varsayalım. psi reel değerli bir fonksiyon olsaydı, x-eksenine dikey bir
`y-ekseni' gibi alınarak psi 'nin grafıği çizilebilirdi Ancak, psi kompleks
değerli bir fonksiyon olduğu için bir `kompleks y-eksenine' -Argand düzlemi
olabilir- gereksinimimiz var.
Hayalimizde, bu amaçla, farklı iki uzaysal boyut daha canlandırabiliriz:
Diyelim ki, uzaydaki y-yönü, Argand düzleminin reel eksenini oluştursun
z-yönü ise sanal eksen olsun. Dalgafonksiyonunun doğru tasarımlanması için
psi (x)'i Argand düzleminde bir nokta olarak (yani, x-eksenindeki her konuma
karşı (y, z)-düzleminde bir nokta) işaretleyebiliriz.
x değiştikçe bu nokta da değişir, ve izlediği yol, x-ekseninin yakın
komşuluğu içinde dolanarak uzayda bir eğriyi tanımlar
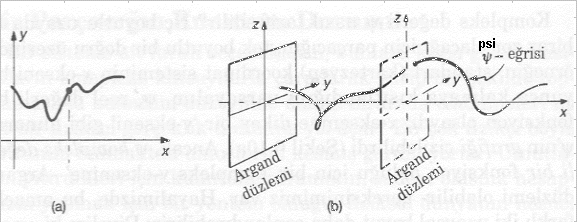
Bu eğriye, parçacığın psi eğrisi diyelim. Parçacığı belirli bir x noktasında
bulma olasılığı, -bu noktaya bir parçacık detektörü yerleştirilmiş gibi
düşünelim- psi (x) genliğinin mutlak değer karesini almak suretiyle
bulunabilir:
psi (x) I kare
Bu ifade, psi eğrisinin x-ekseninden uzaklığının karesidir.
Üç boyutlu fiziksel uzaydaki bir dalga fonksiyonu ile ilgili olarak bu tür
eksiksiz bir resim oluşturmak için, üç boyutu fıziksel uzaya ve iki boyutu
psi (x)'in işaretlendiği her noktadaki Argand düzlemi için olmak üzere beş
boyut gerekir. Ancak, bizim basitleştirilmiş tek boyutlu resmimiz hâlâ
yardımcı olabilir. Eğer bir dalgafonsiyonun fıziksel uzayda herhangi bir
doğru boyunca davranışını incelemek istersek, x-eksenini bu doğru boyunca
alabilir ve buna dik öteki iki uzay yönünü, gerekli Argand düzleminin tanımı
için kullanabiliriz. Çift yarık deneyini daha iyi yorumlamak için bu resmin
gerçekten yararlı olacağını göreceğiz.
Daha önce söylediğim gibi, klasik fizikte, bir sonraki davranışın belirlemek
için bir parçacığın hızının (veya momentumunun) bilinmesi gerekir.
Bu konuda kuantum mekaniği bize önemli ölçüde ekonomi sağlar. psi
dalgafonksiyonu zaten olası momentum değerlerine karşı gelen genlikler
içerir! (Bazı hoşnutsuz okuyucular, parçacığın basit klasik tanımını fazla
büyüttüğümüzü düşünerek biraz ekonomi yapmanın zamanının çoktan geldiğini
düşünüyor olabilirler. Onları anlayışla karşılamakla birlikte önlerine
konulan lokmaları iştahla yemelerini öneririm, çünkü daha da beteri gelmek
üzere!)
Hız genlikleri psi ile nasıl belirlenir? Aslında, momentum genliklerini
dikkate almak daha iyi olur. (Momentumun, parçacığın kütlesi ile hızının
çarpımı olduğunu anımsayın; ) Yapılması gereken, harmonik analiz denilen
yöntemin psi fonksiyonuna uygulanmasıdır. Burada bunu ayrıntılandırmam
yersiz olur, ama şu kadarını söyleyeyim; müzikte seslere uygulanan yöntem de
budur. Herhangi bir dalga formu, farklı `harmoniklerin' bir toplamı olarak
ayrıştırılabilir (`harmonik analiz') ve farklı tınılarda (yani, farklı yalın
frekanslarda) yalın ses tonları elde edilir. psi dalgafonksiyonuna gelince
`yalın tonlar', parçacığın sahip olduğu olası momentum değerlerinin
karşılığıdır, ve her `yalın ton' büyüklüğünün psi 'ye katkısı, bu momentumun
genliğidir. `Yalın tonlara' , momentum durumları denir.
Belirsizlik İlkesi
Pek çok okuyucu Heisenberg belirsizlik ilkesi ni duymuş olmalıdır. Bu ilkeye
göre bir parçacığın hem konum ve hem momentumunu aynı anda ölçmek (yani
klasik düzeye büyütmek) mümkün değildir. Bundan da kötüsü, delta x ve delta
p ile göstereceğimiz bu ölçüm kesinsizliklerinin çarpımlarında,
delta x. delta p> h
bağıntısıyla gösterilen mutlak bir alt sınır vardır.
Bu formül bize, eğer x konumunu ölçerek ne kadar kesin belirliyorsak, p
momentumunun o oranda belirsiz kalacağını söylemektedir. Aynen kesin p
momentum ölçümleri de x konumunu belirsiz bırakacaktır. Eğer konumu sonsuz
duyarlılıkta ölçmüş olsaydık momentum bütünüyle belirsiz kalırdı; tersine
eğer momentumu kesin olarak ölçseydik parçacığın konumu tamamen belirsiz
kalırdı. Heisenberg bağıntısının getirdiği alt sınırın büyüklüğü hakkında
bir fıkir edinmek için bir elektronun konumunun nanometre (10üzeri9m)
mertebesinde duyarlılıkta ölçüleceğini düşünün; bu durumda momentumu o denli
belirsiz kalır ki ölçümden bir saniye sonra elektronun bize 100 km'den daha
yakın olmasını bekleyemeyiz.
Bazı tanımlamalarda, ölçme sürecine has bir tür içten beceriksizliğin
bulunduğunu sanabiliriz. Dolayısıyla, biraz önce düşündüğümüz elektronun
konumunu belirlemek istersek, bu görüş açısına göre, ölçme süreci sırasında
elektron öyle bir rasgele `darbe' alır ki, büyüklüğü Heisenberg ilkesi yle
bulunacak bir hızla uçup gitmesi olasılığı büyüktür.
Diğer tanımlamalarda ise belirsizliğin parçacığa has bir nitelik olduğunu
öğrenmekteyiz; hareketinde öyle bir rastgelelik var ki kuantum düzeyinde
davranışını öngöremeyiz.
Bundan da farklı tanımlamalarda, kuantum parçacığının klasik konum ve klasik
momentum kavramlarının uygulanamadığı anlaşılamaz bir şey olduğu söylenir.
Bu tanımlamaların hiç birisinden hoşlanmıyorum. Birincisi yanıltıcıdır,
ikincisi kesin yanlıştır, üçüncüsü ise gereksiz yere karamsardır.
Dalgafonksiyonu tanımı, gerçekte bize ne bildirir? Momentum durumunun
tanımını anımsayınız. Momentumun en belirgin olduğu durum budur. psi -eğrisi
bir sarmaldır ve ilerlediği tüm yol boyunca eksenden uzaklığı sabit kalır.
Farklı konum değerleri ile ilgili genliklerin, bu nedenle, mutlak değer
kareleri eşittir. Öyleyse, bir konum ölçümü yapılırken parçacığı herhangi
bir noktada bulma olasılığı, bir başka noktada bulma olasılığıyla aynıdır.
Parçacığın konumu gerçekten tümüyle belirsizdir! Peki, bir konum durumu
nedir? şimdi, psi eğrisi bir delta fonksiyonudur. Tüm öteki konum değerleri
için genlikler sıfır olduğu için parçacık kesinlikle delta fonksiyonun
tepesindeki konumda yer alır. Momentum genlikleri, momentum uzayı
tanımlarına bakılarak elde edilir; momentum uzayında psi eğrisi artık öyle
bir sarmaldır ki, farklı momentum genliklerinin tümünün mutlak değer
kareleri eşittir. Parçacığın momentumun ölçülmesi tamamlandıktan sonra elde
edilecek sonuç şimdi tamamen belirsizdir!
Konumların ve momentumların, Heisenberg bağıntısına göre belirli bir
derecede de olsa sınırlandığı bir ara durumu incelemek ilgi çekici olabilir.
Bu duruma ait psi -eğrisi ile psi -eğrisi (birbirlerinin Fourier
dönüşümleri), .

Dikkat ederseniz, her bir eğrinin eksenden uzaklığı yalnız dar bir bölgede
hatırı sayılır büyüklüktedir. Uzaklaştıkça, eğri ekseni çok daha sıkı
sarmaktadır. Başka bir deyişle, mutlak değer kareler, gerek konum uzayında
gerekse momentum uzayında, yalnız çok sınırlı bir bölgede
değerlendirilebilecek boyuttadır. Bu şekilde parçacık uzayda oldukça dar bir
bölge içine sınırlandırılabilir, fakat yine de belirli bir yayılma vardır;
aynı şekilde momentum oldukça belirlidir ve böylece parçacık oldukça belirli
bir hızla hareket eder ve olası konumlarının yayılması zamanla çok fazla
artmaz. Böyle bir kuantum durumuna dalga paketi adı verilir; çoğu kez,
kuantum kuramının klasik parçacığa en yaklaştığı durum olarak kabul edilir.
Ancak, momentum (yani, hız) değerlerindeki yayılma, dalga paketinin zamanla
yayılacağı izlenimini verir. Başlangıç konumunda ne kadar çok yerel
başlanırsa yayılma o kadar hızlı olacaktır.
U ve R Evrim Yöntemleri
Bir dalga paketinin zamanla evriminin yukarıdaki tanımlaması;
dalgafonksiyonunun zaman içerisinde nasıl evrimleştiğini bildiren
Schrödinger denklemi ni çağrıştırmaktadır.
Schrodinger denklemine göre, psi 'yi momentum durumlarına (`yalın tonlar')
ayrıştırırsak, her bir bileşen, c2 bölü ele alınan momentumuna sahip klasik
bir parçacığın hızı kadar bir hızla hareket edecektir. Aslında
Schrödinger'in matematik denklemi bu açıklamadan daha öz yazılmıştır.
Denklemin kendisini daha sonra irdeleyeceğiz. Hamilton veya Maxwell
denklemleri ne (her iki denklemle yakın benzerlikleri vardır) benzeyen bu
denklem, aynı adı geçen denklemler gibi herhangi bir zamanda belirlenmiş
dalgafonksiyonunun tamamiyle belirleyici evrimini verir!
psi 'nin dünyanın `gerçekliğini' tanımladığı kabul edilirse - psi ,
belirleyici Schrödinger evrimi tarafından yönetildiği sürece kuantum
teorisinde doğuştan varolduğu düşünülen belirleyici olmama özelliğinden bir
iz bile kalmaz. Bu evrime U diyelim.
Ancak, kuantum genliklerini klasik düzeye yükseltmek için ne zaman `bir
ölçüm yaparsak', bu kuralları değiştiririz. şimdi U kullanmıyoruz ama
yerine, tamamen farklı bir yöntemi, R - klasik olasılıkları elde etmek için
kuantum genliklerinin mutlak değer karelerini oluşturma yöntemini
kullanıyoruz."
Kuantum kuramına belirsizlikleri ve olasılıkları getiren yalnız ve yalnız R
yöntemidir.
Belirleyici U süreci uygulayıcı fızikçiler açısından kuantum kuramının ilgi
çeken kısmıdır; fakat felsefeciler daha çok belirleyici olmayan R durum
vektörü indirgenmesi ile (veya, süreci gözümüzde canlandıran tanımı
dalgafonksiyonunun çöküşü ile) ilgilenirler.
R 'yi istersek bir sistemle ilgili eldeki bilgide ani bir değişiklik olarak
kabul edelim veya istersek (benim yaptığım gibi) `gerçek' bir kavram olarak
kabul edelim, aslında birbirinden tümüyle farklı iki matematik yaklaşımla,
bir fızik sisteminin durum vektörünü zamanla evrimleşen bir vektör olarak
tanımlayan bir yöntemle karşı karşıyayız.
U 'nun tümüyle belirleyici olmasına karşın R bir olabilirlik yasasıdır; U
kompleks kuantum toplamlarını her zaman korurken R asla umursamaz; U'nun
davranışının sürekli olmasına karşı R açık bir süreksizlik gösterir. Kuantum
mekaniğinin standart yöntemlerine göre R sürecini, U sürecinin karmaşık bir
ifadesi diye `yorumlamak' olası değildir. Gerçekten U sürecinden farklı bir
yöntemdir; kuantum biçimciliğinin yorumunun öteki `yarısını' oluşturur.
Kuramın belirleyici olmaması özelliği tümüyle R'den kaynaklanır; U'nun bu
konuda bir katkısı yoktur. Kuantum kuramının gözlemsel gerçeklerle kurduğu
harika uzlaşma için hem U hem de R gereklidir.
Yine psi dalgafonksiyonuna dönelim ve bir momentum durumu olduğunu
varsayalım. Parçacık herhangi bir başka nesneyle karşılıklı bir ilişkiye
girmediği sürece bir momentum durumu olarak kalmakta bir sıkıntısı
olmayacaktır. ( Schrödinger denklemi nin bildirimi budur.)
Momentumu ne zaman ölçersek ölçelim aynı kesin yanıtı alırız. Olçüm
sonuçlarında olasılıklara yer yoktur. Öngörüler, klasik kuramdakiler kadar
kesindir. Ancak, herhangi bir aşamada parçacığın konumunu ölçmeğe (yani,
klasik düzeye ulaşıncaya kadar yükseltmeye) kalkışırsak, mutlak değer
karelerini almamız gereken bir dizi olasılık genliğiyle karşılaşırız. Bu
aşamada, bir yığın olasılığın arasında ölçümün ne gibi bir sonuç vereceği
tümüyle belirsizdir. Bu belirsizlik Heisenberg ilkesi ne uygundur.
Öte yandan psi fonksiyonunu bir konum durumunda (veya ilk yaklaşıklıkta bir
konum durumunda) başlattığımızı varsayalım. Şimdi, Schrödinger denklemi
bize, psi 'nin bir konum durumunda kalamayacağını, hızla yayılacağını
bildirir. Ne var ki bu yayılma ,sekli tümüyle belirlenmiştir. Davranışında
belirlenemezlik veya olasılık söz konusu değildir. İlke olarak, bu gerçeği
doğrulayacak deneyler yapabiliriz. (Daha sonra ayrıntılandıracağım.) Fakat
tutar momentumu ölçmeğe kalkışırsak, eşit mutlak değer karelere sahip tüm
farklı olası momentum değerleri için katsayılar buluruz, ve yine Heisenberg
ilkesi uyarınca, deneyin sonucu ile ilgili tam bir belirsizlikle
karşılaşırız.
Aynı şekilde, psi fonksiyonunu bir dalga paketi olarak başlatırsak,
gelecekteki evrimi tümüyle Schrödinger denklemi yle belirlenir, ve bu
gerçeği izlemek için, ilke olarak, deneyler yapılabilir. Fakat parçacık
üzerinde farklı bir ölçme, diyelim konum veya momentum ölçümü, yapmaya
kalkışır kalkışmaz, yine Heisenberg ilkesi uyarınca, genliklerin mutlak
değer kareleriyle tanımlanan olasılıklar ve bunların yanısıra belirsizlikler
devreye girecektir.
Kuşkusuz alışılmadık ve gizemli bir olay bu. Ama dünyanın anlaşılamaz bir
tanımı da değil. Bu tanımda, çok açık ve ke- sin yasalar var. Ancak
belirleyici U sürec inin yerine olasılıkcı R sürecinin hangi aşamada devreye
alınacağını öngören açık bir kural yok henüz.
Bir ölçüm sürecinin' öğeleri nelerdir? Genliklerin mutlak değer kareleri
niçin (ve ne zaman) `olasılıklara dönüşür ?
Alıntı:
http://www.felsefeekibi.com/forum 'notlarından
alınmıştır
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru