Feature: November 2000

The idea that the universe is trapped on a membrane in some high-dimensional space-time may explain why gravity is so weak, and could be tested at high-energy particle accelerators.

The possibility of extra dimensions, beyond the three dimensions of space of our everyday experience, sometimes crops up as a convenient, if rather vague, plot in science fiction. In science, however, the idea of extra dimensions has a rich history, dating back at least as far as the 1920s. Recently there has been a remarkable renaissance in this area due to the work of a number of theoretical physicists. It now seems possible that we, the Earth and, indeed, the entire visible universe are stuck on a membrane in a higher-dimensional space, like dust particles that are trapped on a soap bubble.

In this article we look at the major issues behind this new development. Why, for example, don't we see these extra dimensions? If they exist, how can we detect them? And perhaps the trickiest question of all: how did this fanciful idea come to be considered in the first place?

A long-standing idea

The whole notion of extra dimensions has its origin in the search for a unified theory of the forces observed in nature. The story began in the 1860s with the unification of the electric and magnetic forces by James Clerk Maxwell. As well as the extraordinary prediction that light is an electromagnetic wave, Maxwell's theory had a hidden property that was not realized until much later. It has what we now call a "gauge symmetry".

Gauge symmetry can be visualized in the following geometrical way. Suppose that every charged particle has associated with it an arrow that can rotate round in a circle like one of the hands of a clock. This rotation does not take place in the 3-D space that we observe, so the circle is - for the moment - purely mathematical, and the symmetry, known as U(1), is deemed "internal". The symmetry principle states that the absolute positions of these arrows can never be determined. Moreover, the symmetry is said to be "gauged" or "local" - meaning that the definition of absolute arrow position can change with time and location. Allowing such variations introduces a spurious current unless we add an extra ingredient to exactly compensate for it. This extra mathematical ingredient is the electromagnetic field.

The presence of this field explains the physical properties we associate with electromagnetism. For example, the field carries pulses of energy that we observe as particles of light - photons - and the exchange of photons results in the net electromagnetic force between charged particles.

In the 1920s Maxwell's unification of electricity and magnetism, together with Einstein's new general theory of relativity, inspired Theodor Kaluza and Oskar Klein to suggest that it might be possible to unify electromagnetism and gravity in an overarching geometrical scheme involving extra dimensions.

General relativity is a wonderful example of a geometrical theory. It too is derived from a local symmetry, known as Lorentz symmetry, that involves the four dimensions (three space plus one time) of everyday experience. In this case, velocities are like the arrows of the U(1) symmetry. So Lorentz symmetry incorporates the fact that the results from physical experiments are independent of the direction from which we view them and of our velocity. General relativity makes the symmetry local and, as for electromagnetism, that requires a field - which in this case is the geometry of space-time itself. Local "ripples" in space-time are the gravitational equivalent of photons - gravitons.

 

Hidden symmetries-Figure 1

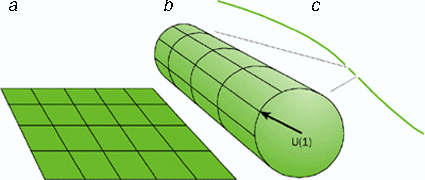
(a) Compactifying a 3-D universe with two space dimensions and one time dimension. This is a simplification of the 5-D space­time considered by Theodor Kaluza and Oskar Klein. (b) The Lorentz symmetry of the large dimension is broken by the compactification and all that remains is 2-D space plus the U(1) symmetry represented by the arrow. (c) On large scales we see only a 2-D universe (one space plus one time dimension) with the "internal" U(1) symmetry of electromagnetism.

Inspired by this idea, Kaluza and Klein proposed including the U(1) symmetry of electromagnetism into this geometric scheme by adding a fourth spatial dimension, giving a total of five. The 5-D space-time begins with the full 5-D Lorentz symmetry. However, if the extra dimension is curled up on itself, or "compactified", part of the symmetry is lost. What remains is precisely the 4-D Lorentz symmetry of general relativity and the U(1) gauge symmetry of electromagnetism. In this picture, the "internal space" of electromagnetism is actually a real extra dimension that is curled up, and the photon is really a component of the higher-dimensional graviton (see figure 1).

The Kaluza-Klein theory was a beautiful and audacious idea, and today seems remarkably prescient. Indeed, our modern geometric picture of gauge theories makes it seem almost natural. However, the Kaluza-Klein theory suffered from a number of serious faults. First, it failed to explain why the strength of the electromagnetic force is quite large while the gravitational force is fantastically weak. Second, quantum mechanics, which was developing rapidly at the time of Kaluza and Klein, could be incorporated into the theory of electromagnetism rather neatly, but not into the theory of gravity. Quantum gravity seemed to be plagued by infinities, which rendered calculations of physical processes useless. Finally, two more forces - the weak and strong forces - were discovered, and these did not seem to fit easily into the Kaluza-Klein picture.

Superstring theory: dimensions galore

Given some artistic licence, it is probably fair to say that interest in extra dimensions waned until the advent of supersymmetry and string theory in the 1970s and 1980s. Supersymmetry is a theory that relates the two different kinds of particles allowed by quantum mechanics - fermions and bosons. Fermions are particles that have half-integer values of intrinsic angular momentum or "spin", and include all the known particles of matter, such as electrons and protons. Meanwhile, bosons are particles with integer values of spin, including photons and gravitons.

Supersymmetry has a number of remarkable properties. In particular, it removes some of the infinities of quantum gravity. Moreover, the most symmetric forms of supersymmetry are naturally formulated in 10 or 11 dimensions.

 

Particles, forces and strings-Figure 2

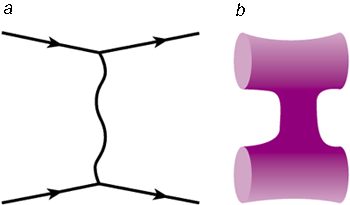
(a) Two charged particles, represented by straight lines, exchanging a photon. (b) In heterotic string theory this process is seen as two loops of a string exchanging a third loop.

String theories were a curiosity that had been around since the early 1970s. In these theories, the world is described by the interactions of 1-D objects called strings, rather than by the interaction of particles (figure 2). In string theory, the different "particles" can be thought of as different modes of vibration of the string. Moreover, there is one mode that has the properties of the graviton, which means that gravity is automatically included in the theory.

In the mid 1980s Michael Green, then at Queen Mary College in London, and John Schwarz of the California Institute of Technology, and others made a fortunate discovery. They realized that when supersymmetry and string theory are combined, the resulting "superstring" theory rather successfully incorporates quantum mechanics without the troublesome infinities, provided there are 10 space-time dimensions. So here, at last, was a candidate theory of quantum gravity - as long as we could accept that our apparently 4-D world has an extra six dimensions that are very tightly rolled up or compactified as in the old Kaluza-Klein idea.

Shortly after this breakthrough, a certain type of superstring theory - known as "heterotic" - became the focus of attention, since it possessed a gauge symmetry that was large enough to include all the known forces in a unified way.

These marvellous properties led to an explosion of interest. However, in a sense, string theory was a victim of its own theoretical success. There were simply far too many consistent solutions to the equations of string theory. Many of these solutions resembled our world, but many more did not. Worse, there was no dynamical mechanism that preferred one solution to any of the others, so string theory provided no explanation of the detailed properties of our world. It even failed to explain why the universe has three large space dimensions and not nine or ten. This problem, which is still with us today despite considerable progress, is called the "degeneracy problem".

There was another feature of heterotic string theories that was discouraging. General arguments suggested that it would probably never be possible to test string theory directly. These arguments involve dimensional analysis. For example, what is the typical size of a string - the so-called string length? Since string theory is a theory of quantum gravity, we can construct a unit of length lPlanck = (GNh-bar/c3)1/2, where GN is Newton's constant, h-bar is the Planck constant divided by 2 pi and c is the speed of light. Because gravity is such a weak force, this length turns out to be an extraordinarily small number, some 10-35 m - about 1019 times smaller than an atomic nucleus. The energy we would need to probe such a small size is described in terms of the equivalent mass, known as the Planck mass. At 1.2 x 1019 GeV c-2, the Planck mass is a dismayingly large number.

The huge Planck mass means that if such a string theory provides the correct description of quantum gravity, then everything we see today is essentially massless as far as the theory is concerned. String-theory effects would only show up if particle accelerators could reach Planck energies and "pluck" some of the higher modes of the string. Such high energies are some 1016 times higher than those that can be achieved at current particle accelerators and are almost certainly beyond our capabilities.

However, there are loopholes in these general arguments, which models constructed independently by Ignatios Antoniadis, then at the Ecole Polytechnique in Paris, and Joe Lykken of Fermilab in the US tried to exploit in the early 1990s. In estimating the string length and the Planck mass, many theorists assumed that all the dimensionless parameters of the theory were of order one. In particular, this assumption led to the prediction that the typical size of the compactified extra dimensions is the same as the typical string scale.

However, Antoniadis and Lykken argued that the theory can dynamically generate very large or very small numbers as a consequence of the degeneracy problem. As a result, the size of the compactified extra dimensions could be much larger. And if they were large enough, string-theory effects would become visible at accessible energies.

Unfortunately, these early models of Antoniadis and Lykken had severe difficulty incorporating the three well-measured gauge forces - electromagnetism, the weak and the strong force - in a successful way. But they were important and interesting precursors to the more recent remarkable developments.

The world as a brane

Up to this point, people had assumed that gravity - together with the electromagnetic, strong and weak gauge forces - lives everywhere in 10-D space-time. However, a new possibility was brought to light in 1998 by Nima Arkani-Hamed at the Stanford Linear Accelerator Center in California, Savas Dimopoulos of Stanford University and Gia Dvali of the International Centre for Theoretical Physics in Trieste, Italy. They asked a rather general question: could gravity be the only force that is aware of extra dimensions? And if so, how large could the extra dimensions be?

 

The world on a brane-Figure 3

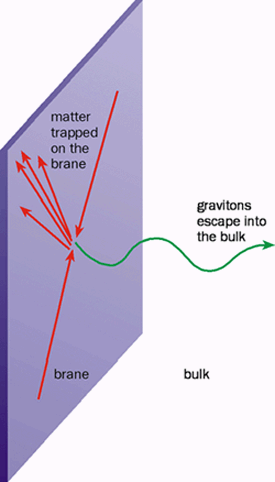
Matter and gauge particles are trapped on the brane. Only gravitational particles travel in the extra dimensions ­ the bulk. A collision between a proton and an antiproton can produce, for example, a single jet of matter particles plus graviton emission into the bulk. Such collisions might be seen in high-energy physics experiments.

If this were the case, the world would look as shown in figure 3. The electromagnetic, weak and strong forces, as well as all the matter in the universe, would be trapped on a surface with three spatial dimensions, like dust particles on soap bubbles. Only gravitons would be able to leave the surface and move throughout the full volume. This 3-D surface is known as a "brane", a name derived from membrane, the 2-D equivalent.

If the strong, electromagnetic and weak gauge forces are trapped on a brane, the answer to how large the "gravity-only" extra dimensions could be is surprising. Since we do not see extra dimensions in everyday life, we naturally assume that they must be tiny. However, our everyday experiences are prejudiced by electromagnetism, which is trapped on the brane. Meanwhile, the highest energy particle accelerators extend our range of sight to include the weak and strong forces down to small scales, around 10-15 mm. We may therefore be blissfully unaware of any extra dimensions.

The only force we can use to probe gravity-only extra dimensions is, of course, gravity itself. Remarkably we have almost no knowledge of gravity at distances less than about a millimetre. This is because the direct tests of the gravitational force are based on torsion-balance experiments that measure the attraction between oscillating spheres (see Long et al. in further reading). The smallest scale on which this type of tabletop experiment has so far been performed is 0.2 mm.

Hence, below about 1 mm, objects could be gravitating in five or more dimensions. However, we know that the strong, weak and electromagnetic forces cannot be modified at distances larger than about 10-15 mm. This prompted Arkani-Hamed, Dimopoulos and Dvali to suggest that these forces might be trapped on a brane that has three spatial dimensions large enough to incorporate the entire visible universe, yet a "thickness" of at most 10-15 mm in the extra-dimensional world.

Let's look in more detail at how forces behave in a brane world with a single extra dimension of size L. The electromagnetic, weak and strong forces, trapped within the 3-D brane, are not aware of the extra dimension and so maintain their usual behaviour. Gravity, on the other hand, behaves rather differently. If we approach a massive body closer than a distance L, we would feel the effects of a force law in four spatial dimensions rather than three. In this case, the gravitons from the massive body are spread over a 4-D sphere with radius r, the surface area of which grows as r3. We would then find that the gravitational force follows a 1/r3 law.
 

Gravity in higher dimensions-Figure 4

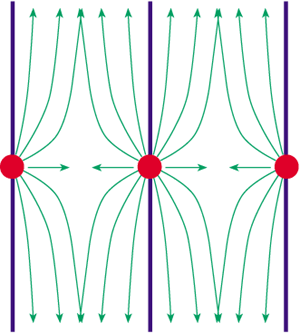
Gravity from a massive body stuck on a brane. The brane dimensions are represented by the single vertical dimension on the page, while the extra dimension is along the horizontal direction. When the bulk is compactified, the body can "see" images of itself gravitationally. Close to the original body, space is bent radially and gravity looks five dimensional. Far away from the body, however, space is bent equally by the body and the infinite line of mirror images. Gravity becomes four dimensional and behaves as it does according to the 1/r² force law of our everyday experiences.

However, as we move further away from the body (i.e. r > L) the usual 1/r2 behaviour is restored. The reason for this is as follows. Adding a compactified extra dimension is rather like standing between two mirrors; we see images of ourselves stretching to infinity. In the Arkani-Hamed-Dimopoulos-Dvali picture the same is true, except the images of the original brane are spaced every L apart and are only "seen" by the gravitational force (see figure 4).

Now consider the gravitational force coming from a massive body trapped in the brane. If we are much further away than L, then we are gravitationally attracted by the original body plus all its mirror images. When we are at a distance r > L along the brane from the original body, the gravitons from it and its infinite line of mirror images are spread out evenly over a 4-D "cylinder" of radius r, and the gravitational force follows the usual 1/r2 behaviour. However, as a result of the initial higher-dimensional spreading, the force of gravity is much weaker than it would otherwise be.

In other words, the only reason the gravitational force appears to be so weak could be because it is diluted by the extra dimensions. This aspect of the world-as-a-brane scenario particularly interested Arkani-Hamed, Dimopoulos and Dvali precisely because it reformulated the question of why gravity is so much weaker than the other forces (or equivalently, why the Planck energy of 1019 GeV is so much larger than the energy scale of weak interactions, around 1000 GeV).

In this picture, Newton's constant is a derived quantity that depends on the volume of the extra dimensions. When viewed from the higher-dimensional space, known as the "bulk", there might be only one fundamental scale. The most radical suggestion lowers the fundamental scale of gravity to the weak energy scale, about 1000 GeV. This assumption leads to an estimate for the size of the extra dimensions in terms of their number, with higher numbers of extra dimensions implying smaller compactification scales.

If there is only one extra dimension then it turns out that it must be larger than the solar system and this possibility can be safely excluded. Two extra dimensions, on the other hand, give a compactification scale of roughly 1 mm, which is close to the current experimental limit. This experimental possibility is one of the most exciting aspects of the world-as-a-brane picture. Suddenly, from believing that a theory of quantum gravity would for ever be beyond the reach of experiments, it seemed as if we might be able to test the theory in tabletop experiments. Such experiments might show the usual Newtonian 1/r2 force law switch to a 1/r4 law, which would characterize two extra dimensions.

The theoretical constructs necessary for the brane-world picture mirrored the developments that had been independently taking place in string theory. One aspect of these developments was the mathematical discovery that extended objects of various dimensionalities are integral to string theory. There turned out to be many well defined examples of such objects, generically called p-branes, where p is the number of spatial dimensions of the object. For example, a 0-brane is similar to a normal point-like particle, a 1-brane is like a string, a 2-brane resembles a membrane, and so on.
 

Strings band together-Figure 5

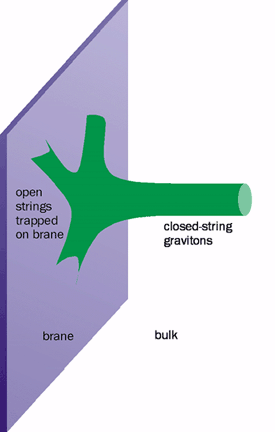
The string theory view of a body trapped on the brane. Matter and gauge particles correspond to open strings, the ends of which are stuck on the brane. Graviton emission can occur when open strings collide and form closed strings that are free to go into the bulk.

Intense interest was stimulated in p-branes following work in 1995 by Joe Polchinski of the University of California at Santa Barbara among others. String-theory p-branes are good candidates for brane worlds because they possess gauge symmetries on their "surfaces" and automatically incorporate a quantum theory of gravity, namely string theory. The gauge symmetry arises from "open" strings, strings that have their endpoints stuck on the brane. Meanwhile, two of these open strings can collide to form a loop of closed string that can travel into the higher-dimensional bulk (figure 5). The simplest excitation modes of these closed strings correspond precisely to gravitons.

-------------------------------------------------------------

The search for extra dimensions
Feature: November 2000

The problems with branes

As an explanation of the weakness of gravity, the world-as-brane idea is striking. However, there are a number of problems and constraints, many of which were first pointed out by Arkani-Hamed, Dimopoulos and Dvali. Many have to do with cosmology, some with astrophysics, and some problems are more aesthetic.

First, the naive statement that two extra dimensions, 0.2 mm in size, are allowed is not quite correct. Such large dimensions would significantly affect the behaviour of astrophysical objects, such as supernovae, because they would cause the object to lose energy by emitting gravitons into the bulk. This graviton emission would show up as an anomalous cooling of the objects' interiors. A precise calculation shows that the two extra dimensions must be smaller than the sub-millimetre size currently accessible in tabletop experiments.

However, the bulk almost certainly has other fields besides gravity. For example, if there are gauge fields in the bulk that are associated with "new forces", then their strength is predicted to be roughly a million times stronger than the gravitational force. It would therefore be possible to detect these stronger forces in tabletop experiments. In addition, gauge forces between like-charged objects are naturally repulsive, so we may even find that gravity seems to become repulsive on sub-millimetre distance scales.

Secondly, although it is inspired by particle physics, the world-as-a-brane picture has dramatic implications for the early evolution of the universe. Conversely, cosmology can place severe constraints on the brane picture. To understand why, recall that in the traditional cosmological view, what we see when we look at the sky today is the remnant of an earlier epoch when the universe was much smaller and hotter. Moreover, the traditional picture of the universe's evolution since the big bang is remarkably successful in many details. For example, it is possible to calculate the synthesis of the light elements - hydrogen, helium, deuterium, lithium and beryllium - using physics that is very well understood. The relative abundances of these light elements agree with measurements, provided that the universe evolved in a conventional way from temperatures below about 3 MeV. (Note that 1 MeV is approximately 1010 kelvin.) This poses a potential problem for the brane-world idea because of a striking new effect that limits how far back our universe can evolve normally.

If our universe, with its three spatial dimensions, is trapped on a brane then it could cool by emitting gravitons into the higher-dimensional bulk, just like a hot object - such as an ember from a fire - typically cools through the emission of infrared radiation in our 3-D world. In the conventional picture, this process does not occur since there is no space "outside" our universe into which the radiation can evaporate. However, for a brane world there are now two processes by which our world with its three spatial dimensions can cool: expansion, plus evaporation into the bulk.

Our conventional view of the evolution means that the first form of cooling should dominate. However, evaporative cooling prevailed at early times when the universe was very hot. Consequently there is a maximum temperature, T*, above which the universe would have evolved in an unconventional way. Calculations show that T* varies from about 1 MeV to 500 MeV as the number of extra dimensions increases from two to six. For two extra dimensions, this is below the temperature at which nucleosynthesis begins, which leads to an unacceptable modification of the light-element abundances.

One way around this is to raise the new fundamental scale of gravity above 1000 GeV, in which case the modification of the evolution of our universe is pushed to higher, and safer, temperatures.

Furthermore, such evaporation is dangerous for another reason. It fills the bulk with energetic gravitons, which can later decay into energetic photons on the brane, thus leading to an unacceptable distortion of the diffuse gamma-ray background that astronomers observe.

The upshot of this analysis is that the universe should never have had a temperature that exceeded about 1 GeV. Moreover, it is difficult, but not impossible, to accommodate the other necessary cosmological ingredients - including inflation and baryogenesis - in such a constrained scenario.

The quest for unification

The third problem is more aesthetic and has to do with the unification of the electromagnetic, weak and strong forces into a single force. One of the most successful and appealing aspects of the traditional view of the world at energy scales above 1000 GeV is that the full unification of these forces comes almost for free. Using conventional physics in 4-D space-time, we can predict how the strengths of the forces change as we increase the energy of an interaction. For example, in the supersymmetric version of the Standard Model - a collection of theories that describes our current understanding of the building blocks of matter and their interactions - the strengths of the three gauge forces become identical (or unify) when we extrapolate the energy to 1016 GeV.

In addition, this unification satisfies a number of non-trivial theoretical and experimental consistency tests. For example, it predicts one of the most important parameters of the Standard Model - the ratio of the strengths of weak interactions to electromagnetic ones. Furthermore, the scale of unification is high enough to prevent the decay of protons.

There are a number of extensions and refinements to this theory that also work well, and it is rather hard to give up this success. Does the would-be new paradigm do as well in this regard? Unfortunately, at the moment, the answer is no, but there are glimmers of hope.

At first glance, the success of the unification of forces seems to be absolutely destroyed by the world-on-a-brane picture. According to this theory, our usual description of the world would break down above 1000 GeV, the new fundamental scale of gravity, and the strengths of the forces would no longer evolve in a way that leads to successful unification.

One possibility emerged a few months after the appearance of Arkani-Hamed, Dimopoulos and Dvali's paper. Keith Dienes, Emilian Dudas and Tony Gherghetta, then all based at the CERN laboratory in Geneva, suggested that the gauge forces can feel some extra dimensions, but not the very large ones that explain the weakness of gravity. They showed that in some cases it was possible to regain a different form of unification that now occurred close to the fundamental scale of gravity of 1000 GeV or above. The concern with this approach is that the calculations, and the possibilities for proton decay, are now very sensitive to the exact theory at the new fundamental scale of gravity, so reliable predictions are difficult to obtain. Also there was no explanation of why the unification of forces in the standard 4-D world was so successful. We are forced to assume that its success was just a lucky accident.

Another approach was initiated at roughly the same time by Antoniadis and by Costas Bachas at the Ecole Normale Supérieure in Paris, and later developed by Arkani-Hamed, Dimopoulos and one of us (JMR). The idea uses some special features of two large extra dimensions. The strengths of the gauge forces on a string-theory brane depend on the properties of the bulk. For two extra dimensions, the variation of this strength can mimic the way that the electromagnetic, weak and strong forces vary with energy in the supersymmetric version of the Standard Model. Thus in Antoniadis and Bachas's approach it might be possible to keep the attractive unification prediction of the standard approach and explain its success. However, no model has been constructed that is successful in detail.

New solutions to old problems

As well as these difficulties, however, the brane-world picture offers new solutions to old problems. One example is the dark-matter problem - why does most of the matter that gravitates in the universe seem to be invisible? (see Smith and Spooner in further reading). An interesting possibility raised by the brane-world proposal is that this mysterious form of matter is trapped on another brane. Such matter would be invisible since it can only communicate to us through the bulk via gravity. In particular, matter on a different brane cannot emit photons by which we could observe it. The existence of other parallel branes in the bulk is very natural, and indeed string theories typically require multiple sets of such branes.

The brane-world picture also offers an intriguing explanation for why the fundamental particles vary so widely in mass. Neutrinos, for example, seem to weigh less than a few electronvolts while other particles are over a billion times heavier. These ideas were originally suggested by Arkani-Hamed, Dimopoulos, Dvali and one of us (JMR) and also by Dienes, Dudas and Gherghetta. In these scenarios, the large size of the extra-dimensional bulk suppresses the interactions that give rise to particle masses. This suppression is possible if there are new fields, in addition to the graviton, that propagate in the bulk and do not feel the influence of the electromagnetic, weak and strong forces. In this picture, the observed neutrinos have such a small mass for precisely the same reason that gravity is very weak.

Finally, the most serious of all problems in particle physics and cosmology is the cosmological constant (see the article by Caldwell and Steinhardt, this issue). This term in Einstein's equations of general relativity is roughly a measure of the mass density of the vacuum. Although the cosmological constant is predicted by our current theories and by world-on-a-brane scenarios to be very large, nature appears to have tuned it to be incredibly small. In fact, the existence of a large long-lived universe demands that the cosmological constant is tiny. Consequently this number is the most constrained and the smallest constant in nature.

Explaining why the cosmological constant is so small has occupied cosmologists and particle physicists ever since Einstein first introduced it. Many proponents of the brane-world picture are tackling this problem again. One recent approach, motivated by a variation of the brane-world idea developed by Lisa Randall of the Massachusetts Institute of Technology and Raman Sundrum of Boston University, is to look at branes in which the bulk dimensions are extremely curved or "warped", but not necessarily compactified. By warping the extra dimensions in the right way, it may be possible to explain why the cosmological constant appears to be so small.

Kaluza-Klein gravitons and black holes

What other experimental signatures might arise from our world being a brane embedded in a higher-dimensional space? One possibility is the appearance of new states, called Kaluza-Klein excitations, at high-energy colliders. These excited states are a feature of models with compactified dimensions, and can be understood by drawing an analogy with water.

Imagine a swimming pool that is infinitely long and just 1 mm wide. Not much use for swimming in admittedly, but the infinitely large side is a good analogy for the large dimensions we experience every day, while the short side is like a compactified dimension. Waves moving in the long direction can have any wavelength, and this is analogous to particles being able to take any energy. However, it is much harder to excite waves in the short direction. In fact, the waves must be smaller than 1 mm to exist at all. Shorter waves are more energetic, so a single wavelength of a 1 mm wave corresponds to the first Kaluza-Klein state, the next state has two 0.5 mm wavelengths and so on.

The large extra dimensions that are felt only by gravity can reveal themselves through the emission of gravitational Kaluza-Klein states into the bulk. This emission is another way of describing the process of graviton "evaporation". Moreover, because of the relatively large size of the extra dimension, the mass difference between one Kaluza-Klein state and the next is very small. There is therefore a huge number of such Kaluza-Klein excitations below the new fundamental scale of gravity. The combined effect of these excitations might be observable close to the new fundamental energy scale. If this fundamental scale is about 1000 GeV then we could see evidence for Kaluza-Klein states in experiments at the Tevatron collider at Fermilab or at the Large Hadron Collider (LHC) at CERN, which will be completed in 2005.

A typical process might involve a proton and antiproton colliding to produce a single spray or jet of particles plus a graviton, which is emitted into the bulk. Since the energy of the graviton would be lost from our 4-D world, the telltale sign for such a process would be an excess of collisions with one jet and "missing" energy above the expectations of the Standard Model.

The particles that are confined to the brane also have Kaluza-Klein or higher string-excitation states, but for them the relevant scale (i.e. the width of the pool) is either the brane thickness or the new fundamental string scale. Both of these scales should correspond in energy to the new gravity scale of 1000 GeV or higher. The LHC could well produce fundamental string or brane relations of our familiar particles. For example, whole towers of Kaluza-Klein states that look like very heavy versions of electrons, photons and so on could be produced. Since these states feel the forces of the Standard Model they would be easy to detect, giving dramatic signals.

As yet, however, there is no evidence for Kaluza-Klein states up to energies of roughly 1000 GeV from high-energy colliders. And this is how we know that the strong, weak and electromagnetic forces do not feel extra dimensions.

Even more strikingly, due to the now much stronger gravitational interactions at short distances, there is also a slight possibility that microscopic black holes could be produced. Fortunately, such small black holes would quickly evaporate and would not be dangerous. In fact they would resemble exotic particles that decayed quite quickly. Nevertheless, it would be truly extraordinary if nature gave us the chance to study objects such as black holes directly in the laboratory.

About the author
Steven Abel is in the Centre for Theoretical Physics, University of Sussex, Brighton, BN1 9QJ, UK, e-mail s.a.abel@sussex.ac.uk. John March-Russell is in the Theory Division, CERN, CH-1211 Geneva 23, Switzerland, e-mail jmr@mail.cern.ch

Further reading
N Arkani-Hamed, S Dimopoulos and G Dvali 1998 The hierarchy problem and new dimensions at a millimeter Phys. Lett. B 429 263

J Ellis 1999 Particle physics: the next generation Physics World December pp43­48

J C Long, H W Chan and J C Price 1999 Experimental status of gravitational strength forces in the subcentimeter regime Nucl. Phys. B 539 23

N Smith and N Spooner 2000 The search for dark matter Physics World January pp23­28

Alıntı: http://physicsweb.org/articles/world/13/11/9

Yasal Uyarı: !!

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir.

Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

 Copyright (c) Cetinbal

   Ana Sayfa / İndex / Ziyaretçi Defteri /  E-Mail / Kuantum Fiziği

     Time Travel Technology /  Kuantum Teleportation /Duyuru

     UFO Technology / Roket bilimi / CetinBAL

     Quantum Teleportation-2