Time Travel Research Center © 2005 Cetin BAL - GSM:+90  05366063183 - Turkey / Denizli 

           

 

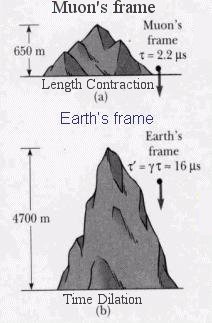  • The time interval T' = t'2 - t'1 of a clock sitting in the S' system at x' = x'o appears to take longer to tick with respect to a stationary observer in the S system. According to the 4th formula in Eq.(8b), the relation is given by T = t2 - t1 =
    T' / (1 - V2/c2)1/2. The effect is known as time dilation and T' is referred to as the proper time - the time experienced in the clock's rest frame. The phenomenon is demonstrated in the decay of unstable particle moving at near the speed of light. The lifetime of such particle appears to be much longer than the one measured in a stationary lab. The diagrams in Figure 04a (where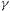 = (1 - V2/c2)-1/2), show the muon decay as experienced in its own frame and from the view point
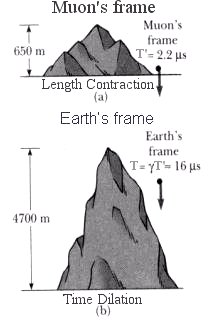
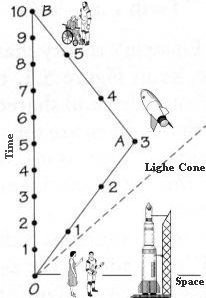
    of a stationary observer on Earth. The twin paradox is another consequence of time dilation. As shown in Figure 04b, one of the twin (at O) leaves on a space journey during which he travels close to the speed of light, while his sister remains on Earth. Because of his motion, time runs more slowly in the spacecraft as seen by the earthbound twin. So on his return the space traveler (at B) will find that his sister has aged more than himself as indicated by the clock readings in line OB (for the sister) and OAB (for the brother). The paradox arises because it can be argued that the sister is moving near the speed of light relative to her brother and so the brother should be getting older instead. A number of experiments have confirmed that the traveling twin would indeed be younger. The two world-

    Figure 04a Dilation

    Figure 04b Twin Paradox

    		lines are different, and not interchangeable, as there is no inertial frame in which the traveling twin is always at rest.

     
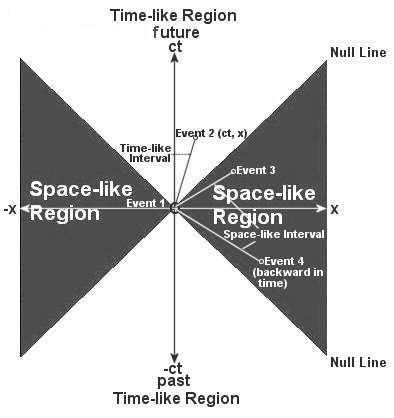
  • Events (a point in the four dimensional space-time as shown in Figure 05) that take place simultaneously to an observer in S, e.g., t = to at x = x1 and x = x2, are separated by a time interval t'2 - t'1 = (V(x1 - x2)/c2) / (1 - V2/c2)1/2 in S' according to the fourth formula in Eq.(8a) (see Figure 06).

     
  • For an infinitesimal interval of space-time, Eq.(6) can be written in the form:

    dx2 + dy2 + dz2 - c2 dt2 = 0 ---------- (9)

    This is called the null line for object moving at the speed of light. In place of the

    • Figure 05 Minkowski Space- time

    		invariant lenght dl in Eq.(5) under the Galilean Transformation, it can be shown that for object moving below the speed of light, the space-time interval

     

    ds2 = dx2 + dy2 + dz2 - c2 dt2 ---------- (10)

    is invariant under the Lorentz transformation. ds is called the proper time since it is the time interval for a clock at rest in a reference frame with dx = dy = dz = 0. In general, denoting v2 = [(dx/dt)2 + (dy/dt)2 + (dz/dt)2], Eq.(10) can be re-written into the form: ds2 = - (1-v2/c2)c2dt2. The interval is called time-like if ds2 < 0 for v < c. As shown in figure 05,

    event 2 can be related causally (temporal sequence cannot be reversed) in some way to event 1 provided that a signal (traveling slower than the speed of light) is available. If ds2 > 0, then it is called space-like, which implies Event 3 is entirely unrelated to Event 1. Alternatively it can be interpreted that two events joined by a space-like interval can never influence each other, since that would imply a flow of information at speeds faster than the speed of light. For some space-like interval, e.g., to event 4, the signal signifies backward in time as well. The interval ds plays the role of the time parameter in Newtonian mechanics to keep track of the development of events such as in the generalized equation of motion in Eq.(12b).

    Figure 06 Minkowski Spacetime Transformation

    		Note that the velocity of light c is constant in all Lorentz frame of references in Figure 06 as originally envisioned.

     
  • Closer examination reveals that Eq.(10) is not a sum of squares of the coordinate differentials. One of these is associated with an opposite sign. This is called pseudo-Euclidean geometry and is the reason for the un-usual appearance of the space-time axes when subject to a rotation in the Minkowski space-time as shown in Figure 06. Mathematically, the Minkowski space-time rotation can be expressed in a form resembling to the 2-dimensional rotation by re-writing Eq.(8b) in term of the hyperbolic functions:

    x = x' cosh(A) + c t' sinh(A)
    ct = x' sinh(A) + c t' cosh(A)

    where tanh(A) = (V/c), sinh(A) = (v/c)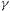 , cosh(A) = 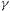are the hyperbolic functions, and 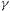= 1 / (1 - V2 / c2)1/2. As v approaches c, tanh(A) ~ 1, the x' and ct' axes merge together at the null line (see Figure 06).
  • In Galilean transformation, the velocity with respect to the S' system is v' = v -V, which is now replaced by
    v' = (v - V) / (1 - vV/c2) in special relativity. Incidentally, this formula yields correctly v'  -c as V c.
  • The mass for a particle moving at velocity v is given by m = mo / (1 - v2/c2)1/2, where mo is the rest mass (relative to the observer's rest frame). This formula shows that m 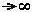as v c. Thus objects with mass can never be accelerated to the speed of light or greater.
  • Mass and energy are equivalent. They can be converted to each other. The total energy E of a particle is given by the formula E = m c2 = mo c2 + T. The first term is the rest mass energy, and the second term is the kinetic energy.
  • In term of the momentum p, E = (mo2 c4 + p2 c2)1/2. The three-momentum and energy together form a four-vector
    (px, py, pz, E/c) in the Minkowski space. The negative of its magnitude - mo2 c2 = p2 - E2 / c2 is an invarant quantity under Lorentz transformation.
  • For particle with zero rest mass, i.e., mo = 0, we can write pc = E = mo c2 / (1 - v2/c2)1/2. This is possible only if v = c; thus all particles with zero rest mass must move at the speed of light.
  • Tachyons are hypothetical objects moving faster than the speed of light. Since E = moc2 / (1 - v2/c2)1/2, the rest mass mo has to be imaginary (that is, mo = i |mo|) in order to cancel out the imaginary part in the denominator (if we want to keep E real). Such superluminal particles would mirror many of the properties of everyday particles. For example, they would move faster as they lost energy (since E = |mo|c2 / ( v2/c2 - 1)1/2), and they would travel backwards in time (event 4 in Figure 05). There is no direct evidence that tachyons exist, and most physicists believe that there is something wrong or it requires some sort of interpretation when they appear in a theory.
  • In special relativity the equation of motion for a particle is:

    fi = m dui / ds

    where the space component of the velocity is u = v/(1-v2/c2)1/2, the time component is u4 = ic /(1-v2/c2)1/2, while the space components of the four vector fi form a vector f / c(1-v2/c2)1/2, the time component is f4 = i fv / c2(1-v2/c2)1/2.
  • Table 01 illustrates the differences between timelike and spacelike objects, where x and k denote the 3-D spacetime vector and 3-D momentum respectively, and v = |dx/dt|. In quantum field theory, the virtual particles possess spacelike or off mass-shell characteristics, which enable physicists to resolve a variety of problems. Off mass-shell means that the relation -mo2c2 = -E2/c2 + k2 is no longer valid. For a real photon ds = 0, and mo = 0, otherwise it is an off mass-shell virtual photon.

     
    Mathematical Entity Timelike Spacelike Spacelike Property
    4-D Spacetime Vector x = (ict, x) x = (ict, x) Outside light cone
    Spacetime Interval ds2 = -c2dt2 + dx2 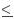0 ds2 = -c2dt2 + dx2 > 0 v > c - tachyon
    4-Momentum k = (iE/c, k) k = (iE/c, k) Outside light cone
    4-Momentum Squared -mo2c2 = k2 = -E2/c2 + k2 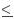0 k2 = -E2/c2 + k2 > 0 Off mass-shell
    4-Momentum Transfer k - k' = [i(E - E')/c, (k - k')] = q k - k' = [i(E - E')/c, (k - k')] = q Outside light cone
    Momentum Transfer Squared (k - k')2 = -(E - E')2/c2 + (k - k')2 = q2 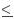0 (k - k')2 = -(E - E')2/c2 + (k - k')2 = q2 > 0 Off mass-shell
    4-Vector Product kx = -Et + kx kx = -Et + kx  

    Table 01 Spacelike Characteristics

                           Ana Sayfa ·  İndex·  Ziyaretçi Defteri    E-Mail  Roket bilimi CetinBAL

                          Time Travel Technology   UFO Technology   Kuantum Fiziği