Quantum Theory - Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli

Quantum Theory, Blackbody Radiation

Quantum Theory, Blackbody Radiation
Correspondence Principle
Uncertainty Principle
Exclusion Principle
Path Integral, Transition to Qunatum Theory
First Quantization, Schrodinger Equation
Hydrogen Atom
References
Index

Molecules are small objects not susceptible of direct observation even under the most powerful microscope. However, their properties can be deduced indirectly from experiments. These objects are different on the conceptual level as well. Classical physics can no longer offer a consistent description. It is replaced by quantum theory, which describes the objects only in term of probability, energy levels, and other quantum numbers. A well-defined orbit such as the path of a planet around the Sun becomes the probability of finding the object at a certain location in the microscopic world. Thus, all the illustrations related to these objects would be just a schematic diagram conveying some ideas, they should never be taken literally as the real thing.

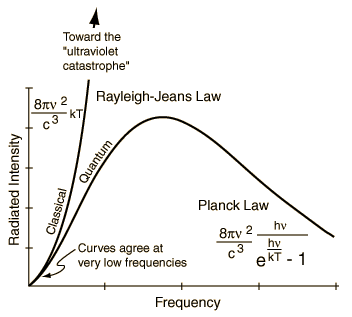Historically, the quantum theory began with the attempt to account for the discrepancy between the theoretical and observational blackbody radiation. The classical theory of Rayleigh-Jeans failed to fit the observation of the radiation energy distribution from a blackbody at high frequency. In searching for a modification that would reduce the contribution of the high frequencies to the energy, Planck was led to make an assumption: The energy of the radiation with frequency v is restricted to integral multiples of a basic unit hv (a quantum), i.e., E_v = nhv where h = 6.625x10^-27 erg-sec is the Planck constant and n is an integer. With this assumption, Planck obtained an exact fit to the observed distribution of radiation energy. According to classical theory, electromagnetic radiation is a wave phenomenon. The Planck's assumption endows a particle aspect to the same entity. Such wave-particle duality requires radical changes in the fundamental concepts of the properties of matter and energy. An introduction on the subject of "wave" can be found in the appendix:Wave, Sound, and Music.

Figure 12-01 Blackbody Radiation

Correspondence Principle

The first difference is that whereas classical theory always deals with continuously varying quantities, quantum theory must also deal with discontinuous or indivisible processes (e.g., the unit of energy packed in a quantum). The second difference is that whereas classical theory completely determines the relationship between variables at an earlier time and those at a later time, quantum laws determine only probabilities of future events in terms of given conditions in the past.

The Correspondence Principle states that the laws of quantum physics must be so chosen that in the classical limit, where many quanta are involved (e.g., n is a large integer in E_v=nhv), the quantum laws lead to the classical equations as an average. This requirement combined with indivisibility, and incomplete determinism define the quantum theory in an almost unique manner.

Uncertainty Principle

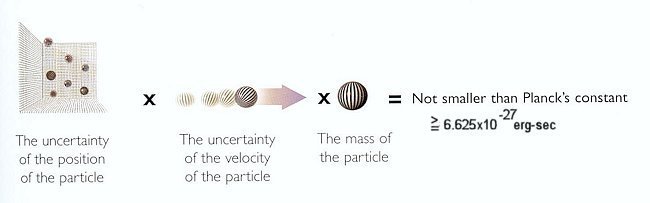
Figure 12-02 Uncertainty Principle

The Uncertainty Principle is derived from three elements: the wave-particle duality, the indivisibility of energy and momentum transfers, and the lack of complete determinism. It states that for a pair of conjugate variables such as position/momentum and time/energy (including the rest mass energy mc²),

it is impossible to have a precisely determined value of each member of the pair at the same time. This statement is illustrated with a schematic representation in Figure 12-02. The corresponding formula is: x p_x > h, where denotes the uncertainty, x is the position of the point mass m along the x-axis, p_x = m v_x is the momentum along the x-axis, v_x is the velocity along the x-axis, and h = 6.625x10^-27 is the Planck's constant. A similar relation exists for the uncertainty of the time t and energy E -- t E > h. In case of heavy mass (such as a macroscopic object), the uncertainties and thus the quantum effect becomes very small, classical physics is applicable once more.

Many quantum phenomena such as superposition, probability density (or wave), vacuum fluctuation, and virtual particles are direct consequence of the uncertainty principle:

Since the quantum state is specified by momentum, energy, angular momentum, or spin and there is an uncertainty in determining their value, it implies that a particle can occupy many quantum states (with different probability). This is called superposition. Figure 12-03a illustrates a very simple superposition of two spin states - one parallel and the other anti-parallel to the direction of a magnetic field, where |a|² and |b|² are probabilities of finding the particle in the corresponding state.

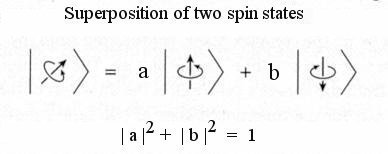
Figure 12-03a Superposition

It is only when the state of the particle, e.g. the spin in this case, is measured that it settles into a definite state. But as soon as we stop monitoring its behavior, the particle dissolves into a superposition again.

Note : Probability = |Probability Amplitude|², e.g., a and b in Figure 12-03a are the probability amplitudes, the corresponding probabilities are |a|² and |b|².

The uncertainty in space and time is interpreted as the probability of finding the particle at a certain time and place. For example, the electron within the confine of the nucleus exhibits a certain probability pattern. Figure 12-03b shows the probability distribution of an electron in the 3d state (m_l=0) of the hydrogen atom. When the electron moves in free space with a certain momentum p, the probability pattern displays a wave-like form with the wavelength 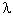= h/p, which is known as the de Broglie wavelength. Since there is a spread of momentum according to the uncertainty principle, the electron wave is described by a wave packet, which is the combination from waves of different wavelengths and amplitudes (Figure 12-03c). If an object's wavelength is of a similar order to the size of the objects around it, the wave nature comes to the fore.

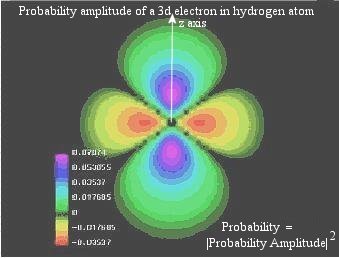Figure 12-03b Probabilty Pattern

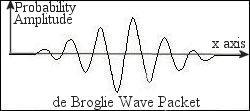	The wavelength of a macroscopic object such as a moving car is something around 10^-36 cm; thus it takes some pretty tiny objects to expose the car's wavelike properties. Only microscopic
Figure 12-03c de Broglie Wave	objects such as electron has a large enough wavelength to show its wavelike property with objects in manageable size, e.g. a diffraction grating.

In classical physics, empty space-time is called the vacuum. The classical vacuum is utterly featureless. However, in quantum mechanics, the vacuum is a much more complex entity. It is far from featureless and far from empty. The quantum vacuum is just one particular state of a quantum field. It is the quantum mechanical state in which no field quanta are excited, that is, no real particles are present. Hence, it is the "ground state" of the quantum field, the state of minimum energy. Figure 12-03d illustrates the kind of activities going on in a quantum vacuum. It shows virtual particle pairs appear, lead a brief existence, and then annihilate one another in accordance with the Uncertainty Principle.

Figure 12-03d Vacuum Fluctuation

There are two kinds of virtual particle. One kind are particles produced out of the vacuum as mentioned above. Many such particles can be produced only in virtual pairs (as shown in Figure 12-03d) in order to preserve the existing balance of properties such as electric charge in the Universe. But particles, which are not constrained by these conservation laws, notably photons, can be produced without any mirror image counterpart (such as in the Casimir effect below).

The particles which join the vertices in a Feynman diagram (Figure12-03e) are also virtual particles and can never be detected directly, even though they are of key importance in determining the way "real" particles interact. This kind of virtual particle can be generated in violation of conservation laws, which are obeyed overall during the interaction. All quantum particles can be thought of as being surrounded by a cloud of virtual particles (and pairs) of various kinds, which are being created and (usually) reabsorbed by the parent particle. The lifetime of each of these virtual particles

	(and therefore the distance it can travel from its parent particle) depends on its mass-energy and the leeway allowed by the uncertainty principle. Interactions occur when a real particle come close enough (as in high energy collision) for one or more of the virtual particles in the cloud to be absorbed by the other real particle.
Figure 12-03e Feynman Diagram

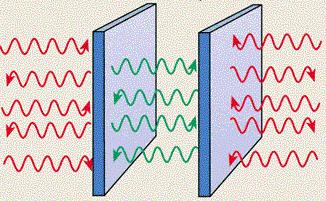Since the virtual photons in between two parallel metal plates placed a short distance apart can exist only when they can form a standing wave , there are fewer photons in each cubic centimeter of vacuum between the plates than there are in the vacuum outside. So, in effect, there is an excess pressure from outside pushing the plates together. This is known as Casimir effect (see Figure 12-03f). The resulting force is very small, but it has been measured (for plates separated by gaps of a few nanometers), proving that quantum fluctuations of the vacuum are a real phenomenon.

Figure 12-03f Casimir Effect

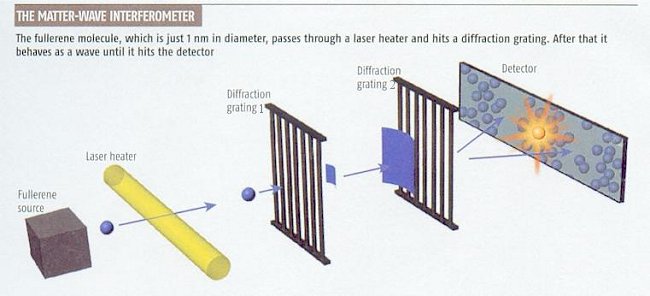
Figure 12-03g Matter-Wave Experiment

Recently in 2004, half-a-dozen experiments have been designed to determine the boundary between the classical and quantum world. One experiment shown in Figure 12-03g fires C₇₀ (70 carbon atoms in the soccerball-like crystal of about 1 nm across) fullerene balls at 190 m/sec toward two diffraction gratings. The first grating creates the matter wave from the fullerenes. The wave is then diffracted by the second grating and the interference pattern is formed on the detecting screen demonstrating

the wave property of the fullerenes. However, the interference pattern fades away if the fullerenes are heated by a laser heater (to about 2700^oC) or collide with gas (leaking into the vacuum chamber of the

experiment). No one has a definitive answer for how the striking photons or molecules switch between quantum and classical behavior. One explanation is that the interaction causes an uncertainty in the position of the fullerenes, blurring the interference pattern. Another idea asserts that the disappearance of the quantum property is caused by entanglement between the photons/molecules, the fullerenes, and the rest of the world (via the wall of the chamber). It goes on further to speculate that if an apertures can be created on the scale of a person's de Broglie wavelngth (~ 10^-33 cm) and an isolated environment can be set up, then that person can turn quantum as described in the "quantum world".

Exclusion Principle

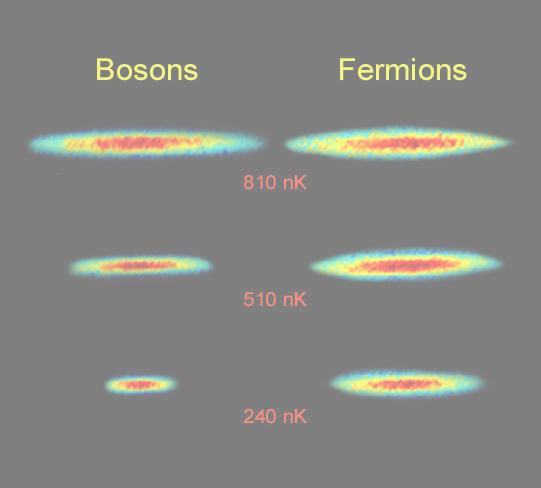The Pauli Exclusion Principle states that identical fermions -- one type of fundamental matter with 1/2 integer spin quantum number -- cannot be in the same place at the same time and with the same orientation (i.e., cannot have the same quantum state). It is this Exclusion Principle that requires the electrons in an atom to occupy different energy levels instead of all congregating in the lowest energy level. Chemistry would be very different without this rule. The exclusion principle is also responsible for the degenerate pressure, which prevents the White Dwarf from complete collapse. The other type of matter, bosons (particles with integer spin quantum number), do not have this property. The boson gas can form Bose-Einstein condensate near absolution zero temperature. They are all in the same quantum state, and behave like a single entity. Figure 12-04 shows the bosons bunch together, while the fermions keep their distance at temperature a few hundreds billionths of a degree above absolution zero (nanoKelvin=nK).

Figure 12-04 Fermions and Bosons

Superfluidity refers to frictionless flow of spin 0 boson, e.g., helium-4 at low temperature.

Path Integral, Transition to Quantum Theory


	Richard Feynman (1918-1988), American physicist Richard Feynman was well known for both his contributions to quantum electrodynamics and his enthusiastic teaching methods.

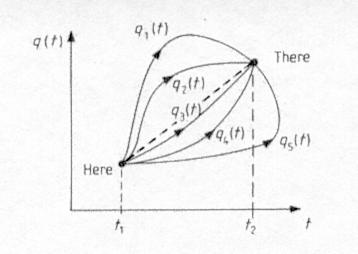The transition from classical to quantum in theoretical physics is most elegantly prescribed by path integral. According to classical physics the movement from "here" at time t₁ to "there" at time t₂ in Figure 12-05 is through the shortest path (the dash line) in evaluating the Action. In quantum theory all paths are possible. However, the classical path (the dash line) does occur with higher probability, the probability for the other paths vary according to a weighting factor. The probability of going from "here" to "there" is the sum of the probability for all paths. This formulism was originally devised by Richart Feynman in his PhD thesis in early 1940s. Twenty years earlier the transition from classical to quantum had to be formulated with a more ad hoc assumption which can be shown to be equivalent to the method of path integral.

Figure 12-05 Path Integral

First Quantization, Schrodinger Equation

It was postulated that the momentum p and position q are no longer mere numbers but are operator satisfying the commutative relation: pq - qp ~ h. This is called the first quantization, which endows wave property to a particle. Actually only p is treated as an operator - a differential operator (~ d/dq) operating on a function called wave function, q remains to be a number. Applying this change to the equation relating the total energy E to the kinetic energy p²/2m and the potential energy V, e.g., E = p²/2m + V yields the time-independent Schrodinger Equation for one particle with mass m and interaction V:

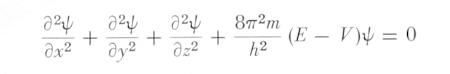		For a given interaction V the problem is to find the Energy E and the corresponding wave function psi. The wave function is related to the probability of finding the particle at certain position. The Schrodinger Equation can be expanded to a system of many particles and more than one source of interaction. However, it becomes rapidly un-manageable beyond one particle and one interacting source locating at the center (of the coordinate frame).
Figure 12-06 Energy Levels	Figure 12-07 Probability Density

Hydrogen Atom

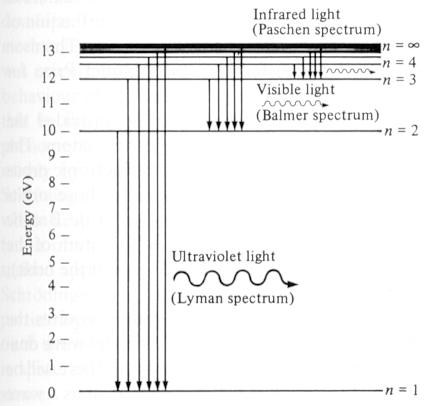
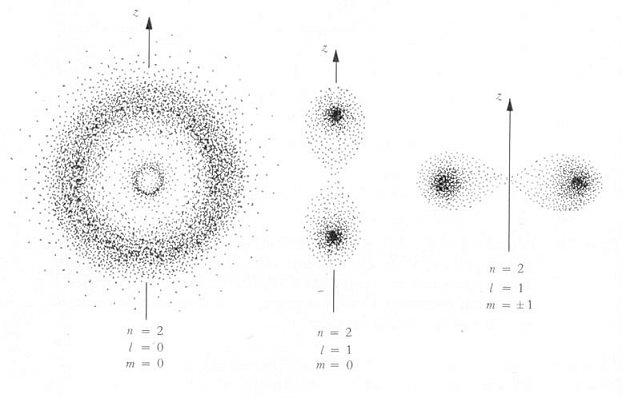
Beside some idealized cases, analytical solution can be obtained only for hydrogen atom which has one electron moving about an atomic nucleus. The energy levels are shown in Figure 12-06 while the probability density corresponding to different quantum states are shown in Figure 12-07 where n, l, and m are the total, orbital, and magnetic quantum number respectively; the probability densities have either spherical symmetry or rotational symmetry about the z axis. When the electron jumps from a higher energy level E_n+1 to a lower one E_n, a photon with frequency v = (E_n+1 - E_n)/h is released. Excitation is the reversed process when the electron in energy level E_n absorbs a photon with frequency v.

The state of the electron in an atom is specified by four quantum numbers. The principal quantum number n determines the energy level; its value runs from 1, 2, 3, ... For each n, the orbital quantum number l = 0, 1, 2, ... (n-1); it is related to the magnitude of angular momentum. Then for each l, the magnetic quantum number m can be -l, -l+1, ...l-1, l; it is related to the z component of the angular momentum. The spin quantum number s is either +1/2 or -1/2. For n = 1, l = 0, m = 0, there is only 2 possible quantum states for the electron, with s = +1/2 and -1/2 respectively. For n = 2, l = 0, m = 0 and l =1,
m = -1, 0, +1; there is a total of 2 + 6 = 8 possible quantum states. Therefore, it requires 2 electrons to complete the shell for n = 1, and 8 electrons to complete the shell for n = 2, ...and so on. The orbital quantum number l is often designated by a letter, s for l = 0, p for l = 1, d for l = 2, and f for l = 3 ... The quantum number l is non-additive while m is additive and relates to an Abelian group (e.g., the two dimensional rotation about the z-axis). Particles having the same non-additive quantum numbers but differing from each other by their additive quantum numbers are said to belong to the same multiplet. The number of members of a multiplet is called its multiplicity. For a given multiplet l the multiplictiy is equal to 2l+1.

Ionic Bond, Atomic Shells

References:

Quantum Theory, Overview -- http://www.levity.com/mavericks/quantum.htm
Quantum Theory, more detail -- http://www.srikant.org/core/node12.html
Path Integral -- http://www.chem.unc.edu/lectures/2003Hermans/notes3/pathintegral.pdf
Schrodinger Equation -- http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/schr.html#c1
Hydrogen Atom, Schrodinger Equation -- http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydsch.html#c2
Hydrogen Atom, Energy and Wave Functions -- http://www.kw.igs.net/~jackord/bp/i6.html

Index

Bose-Einstein condensate
Bosons
Casimir effect
Conjugate variables
Correspondence Principle
Covalent bond, hydrogen molecule
de Broglie wavelength
Exclusion Principle
Fermions
First quantization, Schrodinger Equation
Hydrogen atom
Hydrogen bond, molecular orbital
Ionic bond, atomic shells
Molecular Orbital theory
Orbitals
Oxidation

Path integral, transition to Qunatum Theory
Planck
Potential curve
Probability density
Quantum numbers
Quantum Theory, blackbody radiation
Reduction
Solution
Uncertainty Principle
Vacuum
Valence
van der Waals force, dipole-dipole interaction
Wave
Wave function
Wave-particle duality

[Home Page] The Observable Universe - Elemantary Particles -

Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.

Ana Sayfa /i ndex /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2