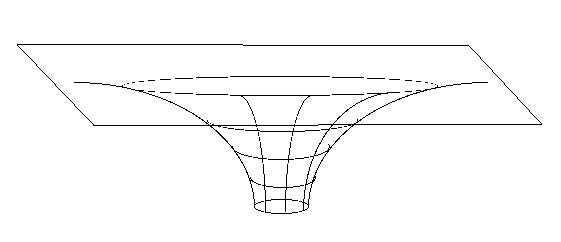
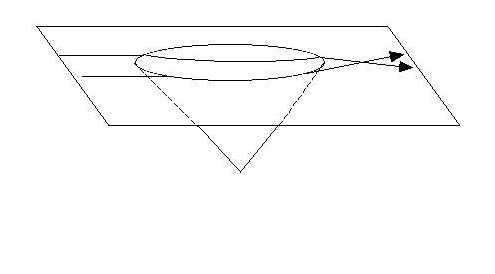
..::Paper "embedding diagram models" of black holes::..IntroductionThis page shows how to make a paper model that shows straight lines (such as light rays) bending together in the vicinity of a black hole, and shows the "geodetic precession" effect predicted by general relativity. Black holes are described by the theory of General Relativity. General relativity is a theory based on non-Euclidean geometry in four dimensions. While the full general theory of relativity is something that will require a long period of study for you to completely understand, a few of the interesting predictions of the theory can be understood if you simply understand some of the basics of non-Euclidean geometry. One way of picturing non-Euclidean geometry is by the use of embedding models. What is Euclidean geometry? What is non-Euclidean geometry?Euclidean geometry (in two dimensions) is the geometry of figures drawn on a flat piece of paper. Therefore, non-Euclidean geometry is geometry drawn on paper that is not flat. Examining the geometry on paper that is not flat is one way to learn some of the basics of non-Euclidean geometry (although you have to keep in mind that General Relativity is a theory of four dimensions, so it cannot be completely described on a 2-dimensional piece of paper.) For example, you have probably seen pictures like this one, that's supposed to be a black hole. Do black holes really look like this? No. But if you were a two-dimensonal person who lived on the surface of the paper, this is what a two-dimensional black hole would be like.
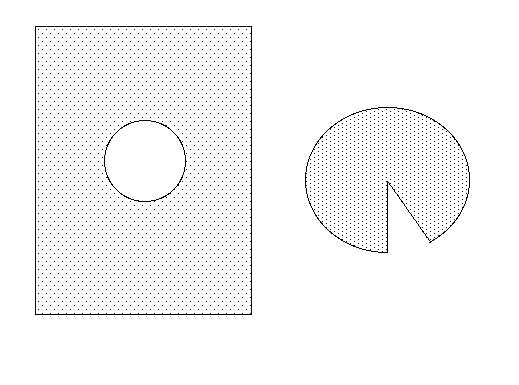
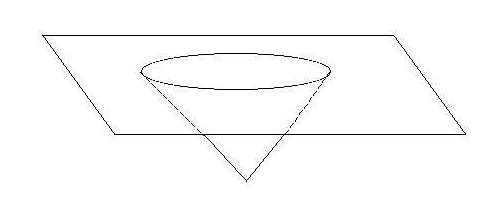
Figure 1. "embedding" diagram of black holePaper model of black holeThis black hole is too difficult to make from a piece of paper, because the paper is itself curved. However, you can make a simplified model of a black hole To make the simplified black hole, you need two pieces of paper. Cut a circle out of one piece of paper, and throw the circle away, keeping the paper it was cut out of. Using the other piece of paper, cut out a circle that is about half again bigger than the circle cut out of the first piece of paper. Cut a triangular slit out of that new circle. What you have will look like figure 2. Now roll the circle-with-a-wedge-cut-out into a cone so that the base of it just fits the hole in the first piece of paper. (the edges may have to overlap a bit to make it fit). Tape it together like this (but use only a small piece of tape, because you will have to untape it later) Now tape this cone onto the flat-paper-with-a-hole-cut-out to make the model of a black hole. This should look like figure 3. This may seem very simple, but you can use this paper model to see something very important to general relativity: the fact that light bends around a black hole (or any massive object) by gravity. This is the famous "light bending" experiment, observed by Eddington during the solar eclipse of 1919, that made Einstein famous. link
Figure 2: left: sheet of paper with a circle cut out. Right: larger circle ("disk") with a wedge cut out. Roll this into a cone with a base exactly the size of the hole in the paper, and tape it closed.
Figure 3: Paper model of a black hole.Demonstration: Bending of Light in non-Euclidean spaceIn general relativity, light is defined as traveling in straight lines (known as "geodesics"). But how do you define a straight line on a curved surface? This is a difficult question, but the simplest solution is that at every little point on the surface, the line is "straight" if it is the shortest path between two nearby points. Hypothesis: When drawn on a sheet of paper that flat, parallel
lines never meet. when drawn on a sheet of paper that is not flat, parallel
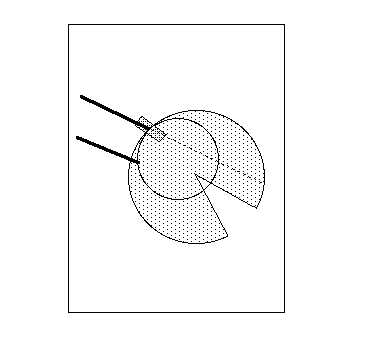
"straight" lines will converge. Turn the paper model upside down, so that the cone points upward instead of downward (this will make things simpler later). Draw two parallel lines on the flat part of the paper. The lines should go toward the "black hole" so that one will go into the "well" on either side of the center. Don't continue drawing yet into the cone part of the well. Put a piece of tape right exactly where the line enters the "cone" part of the black hole, and then remove all of the rest of the tape, so that you can unroll the cone, and you can fold it and the rest of the paper flat, held together just at the one point. It should look a little like figure 4. Although at every point the line on the paper is straight, the (initially parallel) lines cross.
Figure 4: The disk of paper (shown shaded) is held on to the flat sheet of paper at just one point, where the tape is.Now that you have done this, use a straightedge to continue the straight line on the disk. (this is shown as the dashed line in figure 4.) Now--without removing that little piece of tape-- roll the disk back up into a cone. Put a new little piece of tape where the second line starts to enter the black hole, then remove the first piece of tape, flatten out the cone into a disk, and use your straightedge to continue the second line straight. Since it entered the disk of paper at a different point, it will not be parallel to the first one. Now roll the cone back up, and put it back in position. Put a new piece of tape where the line comes out of the well. Now remove all the other pieces of tape, flatten everything out, and use the straightedge to draw the continuation of the line. When you are done, roll the cone back up, put a piece of tape where the second line comes out of the well, and repeat everything. Now that you have continued the straight line through the "gravity" well of your cone model, you can roll the cone back up and tape it together. You should see something like figure 5: even though the lines are straight at every part of their length, they start out parallel, and end up meeting and crossing.
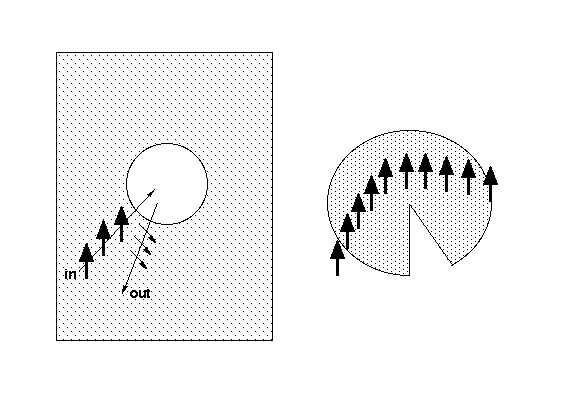
Figure 5: straight lines that pass on either side of the center of the paper "black hole" converge.Geodetic precessionThe phenomenon of geodetic precession was predicted by De Sitter in 1916. A gyroscope, according to Newton's laws of motion, always points in a fixed direction in space. But if you take a gyroscope and move it in a circular orbit around a gravity well, when you bring it back to the place that it started, it will not be pointing in the same direction! You can see how this effect works in your black hole paper model. Draw an arrow on the flat sheet of paper. Then move this arrow into the conical "gravity well" of the model without rotating it. Untape and flatten out the cone, so you can move the arrow around the center without rotating it, and then roll the cone back up. You will see that when the arrow got back to where it started, it's not pointing the same way! The arrows on your flat paper and the flattened-out cone should look something like this:
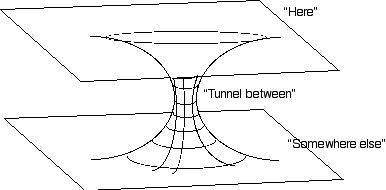
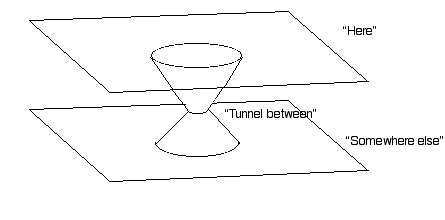
Figure 6: Arrows drawn on paper to show geodetic precession. The arrows coming out of the "gravity well" point in a different direction from the arrows going in, although at no point was the arrow rotated.This effect will be tested by the NASA spacecraft Gravity Probe B (along with another test of relativity, "frame dragging".) Wormhole ModelFor an extra bonus: make a paper model of a wormhole. Use this model to show that parallel lines that go through the wormhole actually diverge. The conventional embedding diagram of a wormhole is shown in figure 7. Note that the wormhole connects one region of space (labelled "here") with another one (labelled "somewhere else"). Figure 8 shows a simplified embedding model of a wormhole that can be made from paper. Good luck!
Figure 7: conventional embedding model of a "wormhole".
Figure 8: paper embedding model of a "wormhole".If you are interested in seeing what some paper embedding models look like, Hollister ("Hop") David has made some models according to these instructions, and you can see photographs on his web page. (The model he made is an embedding of an wormhole with the throat extended into a cylinder.) All of the lines in the photograph are "straight" lines (technically, that is, they are geodesics). In the left-most photo you can clearly see the straight lines coming from the right appearing to bend when they encounter the conical "gravity well" and converging at the right. Learning about General Relativity, Black Holes, and WormholesOnce you keep firmly in mind that I am not claiming to personally be an expert on general relativity, I would like to say that general relativity is an extremely interesting study, and I suggest that anybody interested should dive in! Here are some entry points.
Some books about black holes and general relativityFor people who want to know more about General Relativity and Black Holes, there seem to be literally tons of books about black holes, and I can't claim to be an expert on all of them. Here is a review of a few that are on my desk. For a readable overview, I recommend: A nice book about black holes in astrophysics (not a whole lot of
explanation about general relativity, but superb pictures) is: If you want to learn some of the mathematical background about general relativity, but without hitting the heavy parts of the math, you might try Robert Geroch's book General Relativity from A to B, University of Chicago Press 1978. He shows how relativity is a theory of four-dimensional geometry, and in doing so gives a mostly readable introduction that does exactly what the title says: it gets you to the starting point of understanding the background concepts of relativity. If you are actually serious about learning the subject, let me urge you to learn physics from textbooks, rather than from popularizations: the popularizations of physics are often good entertainment, but in trying to make physics accessible to a general audience, popular physics books often treat the subject at a level of superficiality that ends up being misleading (or even downright incorrect). There is no substitute for an actual physics textbook, both reading through a textbook and doing the problems. Before you start to learn general relativity, you ought to have a working knowledge of special relativity. E.F. Taylor and J.A. Wheeler's Spacetime Physics (W H Freeman & Co.; ISBN: 0716723271) is one classic textbook on the subject. There are also many other texts on the subject. Again, let me urge you to learn from a textbook, not from a popular science article. There is an introductory text about special and general relativity available on the web: Reflections on Relativity. For technical reference, if you want the real physics of general relativity, undiluted by popularization and with the equations intact, I recommend several text books: I.R. Kenyon, General Relativity, Oxford Science Publications, Oxford 1990, hardcover/trade paper. This would be my recommendation for a textbook to learn GR. A thin book that is quite readable, focusing on the physics and leaving out the heavy details of the derivation of the mathematics. It also has the great advantage that Kenyon leaves the factors of G and c in, instead of dropping them in the assumption that the physicist can put them in later. The section on black holes is much briefer than that in Wald, and for this reason I don't find it as good a reference. Robert Wald, General Relativity, University of Chicago Press, Chicago 1984. This is a commonly-used textbook about general relativity. It takes a mathematics approach, rather than a physics approach, and is going to be mighty tough sledding for anybody without a physics or math background. Chapter 6, "The Schwarzschild Solution," is a good reference about black holes. W. Pauli, General Relativity, Dover books, paperback. A very old book still in print, quite concise. Good as a reference book on general relativity, not very useful as a reference book about black holes. C. Misner, K. Thorne and J.A. Wheeler, Gravitation, Freeman, San Francisco, 1973. This is the classic textbook about general relativity, a textbook thicker than most dictionaries that covers everything. As an undergraduate, I found MTW written in an attempt at a breezy style that was hard to follow. As a physicist, I find their notation idiosyncratic. As a reference book, this is the book that all the other textbooks refer to with words such as "for a more complete discussion, see Misner, Thorne and Wheeler." If you actually want to learn general relativity, I suggest trying John Baez's General Relativity Tutorial on the internet. This won't tell you anything about black holes or wormholes, but general relativity is worth learning just as a chance to stretch your mind, and this tutorial is the most readable introduction to the subject I've ever come across. Some other non-technical books include: John Gribbin, Unveiling the Edge of Time. Harmony Books, NY, 1992, $20 hardcover. One of the better popular books; covers much of the territory of Thorne, with a long historical discussion of the development of the ideas behind black holes (starting with Newton) and ending with wormholes, but from a different view. Stephen Hawking, A Brief History of Time. One of the most celebrated books of the last decade. It is not per se about black holes, but is a historical overview of the development of modern cosmology with Hawking's commentary and doses of philosophy interspersed. I found it a little irritating: in working to make the book accessible to a non-technical audience, Hawking simplified some parts so much that what he says borders on being incorrect. This is an good book to read for pleasure, but not a good one from which to learn about black holes from, it is written at a rather low level for non-specialist audience. Stephen Hawking, Black Holes and Baby Universes, trade paper. This one is a series of essays, loosely connected. I hoped from the title that it might tell me a lot about wormholes, but I found it very superficial. Clifford Pickover, Black Holes: A Traveler's Guide. Wiley, New York, 1996, $24.95 hardcover. The smarmy "sci-fi" sections that punctuate the chapters are absolutely horrible, much of the book consists of pretty but irrelevant color computer graphics, and about half of the book has nothing to do with the subject. But, despite these flaws, the book has one overwhelming feature that endears it to me: it actually includes equations. It doesn't just tell you about black holes, it gives you the equations and encourages you to work things out yourself. Some other technical books include: S. Hawking and G. Ellis, The Large-Scale Structure of Space Time, Cambridge University Press, 1973. If you want to see Hawking when he is not being superficial, this is the book for you, dense with math. Too dense for me, alas. Matt Visser Lorentzian Wormholes, AIP Press 1995. This one is the premier textbook on the subject of wormholes. It is extremely mathematics heavy, but in between the mathematics he makes it a specific point to make clear exactly what we know and what we do not know. Some web references
Page by Geoffrey A. Landis November 23, 2001 Alıntı: http://www.sff.net/people/geoffrey.landis/blackhole_models/paper_blackholes.html Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir. The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi / Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru |