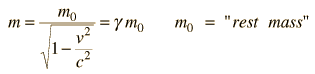Ether Technology
A Rational Approach to Gravity Control
by Rho SigmaETHER TECHNOLOGY: A Rational Approach to Gravity Control, by Rho Sigma. This classic book on anti-gravity & free energy is now back in print. Written by a well-known American scientist under the pseudonym of "Rho Sigma," this book delves into international efforts at gravity control and discoid craft propulsion. Before the quantum field, there was "ether." This small, but informative book has chapters on John Searle and "Searle discs;" T. Townsend Brown and his work on anti-gravity and ether-vortex-turbines. Includes a forward by former NASA astronaut Edgar Mitchell. Don't miss this one.
A great overview of basic electrogravitic theory, January 24, 2000
Reviewer: James Batchelor (Colchester, England) - See all my reviews
Well, what can I say?
The anonymous "Rho Sigma" (come on, it's not that hard to work out) brings us a brilliant compendium of devices and electrogravitic theory. Many of the illustrations within the book have been on a number of T T Brown websites without me even knowing it! The quality is superb, offering a balanced slice of the development of overunity and UFO physics. Anyone else know that one of Brown's electrogravitic motors provided an overunity of over 100,000:1?
One or two gripes - why call the Searl Effect Generator an "Ether Vortex Turbine" and then describe them as if they were two separate devices in the foreword and contents of the book? Having met Searl personally, I am pretty sure that he never referred to the SEG as such.
These aside, it offers some interesting details about the subject, and would be good for anyone interested in Brown's time spent with Agnew Bahnson too. Don't expect ancient lost secrets or Do-It-Yourself UFO instructions, but a savvy reader with this book will certainly be helped along the way to an understanding of the link between electricity and gravitation. It is extremely good value, and well worth adding to your scientific library.
Biefeld-Brown Effect
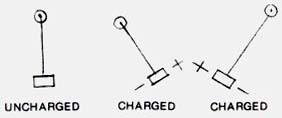
The first empirical experiments by Townsend Brown had the characteristic simplicity which has marked most other great scientific advancements, and concerned the behavior of a condenser when charged with electricity. The startling revelation was that, if placed in free suspension with the poles horizontal, the condenser, when charged, exhibited a forward thrust toward the positive pole! A reversal of polarity caused a reversal of the direction of thrust.
Rho Sigma's classic book on Anti-Gravity and Free Energy is back in print! First published in 1977, this ground-breaking book delves into the international efforts at gravity control and discoid craft propulsion. Before the Quantum Field was the "Ether."
Neither scientist nor layman can he expected to know the details of electrogravitation, in as much as it is a comparatively recent and unpublished development. Townsend Brown is the only known experimental scientist in this new area of scientific development. Thus anyone who wishes to understand electrogravitation and its application to astronautics must be prepared to expand the commonly known principles of electromagnetics in order to grasp the essentially different principles of electrogravitation. Electrogravitation must be understood as an entirely new field of scientific endeavor and technical development, which does not obey the known principles of electromagnetism.
In the Quantum Field or Ether Field of Physics, energy is all around us. Energy can theoretically be drawn from a Unified Fleld of Magnetism, Electricity and Gravity to propel a spacefcraft through space. Rho Sigma (the youngest member of Von Braun's World War II German team of rocket researchers) explains how the technology already exists to control gravity and takes us through the world of Ether-Vortex Turbines, T. Townsend Brown, Searl Discs, Electric Wind, German anti-gravity research, and more.
Rho Sigma also delves into prophecies of coming earthchanges and how "Ether Technology" may help in this period of change. Former astronaut Capt. Edgar D. Mitchell, Ph. D. has written the forward to the book, "A Change of Conciousness." Don't miss this Informative book on the "New Science" that is sweeping the world!Analysing the real Biefeld Brown effect
By Engineer Saviour - Blaze Labs
Note: In the following discussion, all equations have been derived from well accepted conventional physics laws and equations. The main difference you will find is in the interpretation of such equations, enabling you to understand better how many physical effects may relate to each other.
Introduction to the theory
Biefeld Brown effect analysis
Biefeld Brown thrust calculations
Newton vs Einstein laws
Spacetime warping
Speed of light in dielectrics
Energy storage & flow within dielectrics
Symmetric vs Asymmetric energy fields
Biefeld Brown craft efficiency
The Biefeld-Brown Effect (A)
What is antigravity? An artificially generated gravity field that can oppose earth’s own and provide propulsion.
The earliest modern discovery of antigravity belongs to Dr Alfred Biefeld, professor of physics and astronomy at Denison University. According to an old article in FATE magazine, in the early 1920s Dr Biefeld performed laboratory experiments involving capacitors charged with high voltage alternating currents. When charged, these capacitors would violently “twist and lurch” before burning out. This indicated that charged high voltage capacitors exhibited self-propulsive effects. Further research into this anomalous phenomenon was taken up by Thomas Townsend Brown, then a physics student at Denison University working for Dr Biefeld. This began Townsend Brown’s life-long research into antigravity.
Brown’s first experiments consisted of two lead spheres connected by a nonconductive glass rod, like a dumbell. One sphere was charged positive, the other negative, with a total of 120 kilovolts between them. This formed a large electric dipole. When suspended, the system moved toward the positive pole, arcing upwards and staying there against the force of gravity tugging downward. This showed that electric dipoles generate self-acceleration toward the positive pole. This experiment was repeated in oil, in a grounded tank, proving that ion wind was not responsible.
Improved versions of this setup replaced the lead spheres with metal plates, and glass rod with dielectric plates or blocks. This created a high voltage parallel plate capacitor with one or more layers. Brown’s British patent #300,111 – issued in 1927 – described what he termed a “cellular gravitator” consisting of numerous metal plates interleaved with dielectric plates, the entire block wrapped in insulating material and end plates connected to output electrodes and a spark gap to limit the input voltage. This device produced significant acceleration.
Later, Brown experimented with saucer-shaped disks with positive and negative electrodes on opposite sides. This created an open-air high voltage capacitor that combined the electrogravitational effect with ion wind phenomena for propulsion. They worked well in air, and they worked well in vacuum.
Interestingly, the majority of modern articles investigating Brown’s work tend to focus on disk gravitators. Because they include ion wind as part of their operation, debate has arisen whether the Biefeld-Brown effect cannot be explained away entirely by ion wind. Brown’s 1927 patent, however, described a self-contained device that exhibited no ion wind effects and relied solely upon the electrogravitational action arising from the electric dipoles within the gravitator-capacitor.
In my opinion, the cellular gravitator is far more important in demonstrating the validity of the Biefield-Brown effect than the debatable disk-shaped gravitators. Why did Brown never mention cellular gravitators again after the 1930s, considering they unequivocally proved electrogravitation? Maybe because that part of his research became classified. The remaining public aspect, particularly his later patents, were limited to ion wind type devices, or at least those that included that possibility so as to make the electrogravitational aspect more ambiguous. We should remember that Brown was allegedly involved in Project Rainbow, suggesting that much of what we know publicly of his work may only be the “soft” stuff.
Let us therefore focus on the more important part of his research, the cellular gravitators. There were several factors Brown recognized affecting their behavior and the strength of the electrogravitational effect. These are listed as follows:
- applied voltage—greater the voltage, greater the gravitator swings toward the positive end. However, in his British patent, Brown explained that beyond a critical voltage the gravitator would reverse motion and swing toward the negative electrode instead. Perhaps this was due to dielectric breakdown.
- applied current—current is necessary only to overcome leakage of the capacitor. If current is insufficient, the gravitator will not maintain its voltage and therefore the electrogravitational effect will either wane or not manifest noticeably. Van de Graff generators provide microamps of currents, which is normally not enough to power a gravitator. A solid state high voltage DC generator utilizing a cockroft-walton multiplier would be needed instead.
- mass of the dielectric—determines only the total energy of the gravitator once it swings to a given height. Some sources state that the greater the mass, the stronger the electrogravitational effect, but this is debatable since Brown never mentioned this and said instead that only the gravitational potential energy increases with mass since E = m g h.
- duration of impulse—the gravitator’s impulse fluctuates with time, apparently due to environmental gravitational conditions – particularly those arising from position of the sun and moon. This effect was later employed by Greg Hodowanec in his gravitational wave detector circuits, which monitored the voltage across an electrolytic capacitor that fluctuated as the gravitational influence of heavenly bodies changed with time. Just as capacitors charged with electricity generate a gravity field, so can gravity fields affect the electrical charge of a capacitor.
- strength of the dielectric—higher the dielectric constant, stronger the effect. The dielectric constant measures a material’s ability to store electricity in the form of electric displacement or polarization. The more energy is stored via electric polarization, the greater the electrogravitational effect.
- capacitance of the gravitator—higher the capacitance, greater the effect. So the closer the metal plates, the larger the plates, the greater the number of cells (and as mentioned, higher the dielectric constant of the insulator between metal plates, as this also determines total capacitance), the stronger the Biefield-Brown effect.
- geometry of electrodes—increased asymmetry between electrodes increases the effect. This will be explained below.
How it Works
To understand the Biefeld-Brown effect, we must understand why electric dipoles (positive and negative charges separated by a fixed distance) accelerate toward the positive pole. The answer is simple:
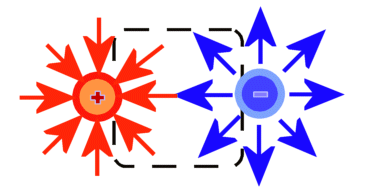
Positive and negative charges, in addition to creating an electric field, also generate slight gravitational fields. You could say charged masses warp space more than uncharged masses do. Positive charges induce a convergence in space and negative charges inducing a divergence in space. Thus, positive charges emit a gravitational field while negative charges emit an antigravitational field. This arises purely from the geometry of the electric field, which happens to include a component that shares the same geometry as a gravity field and thus gives rise to one.
Now, an electric charge by itself emits a symmetric field, whether it’s gravitationally attractive or repulsive. So left to itself, the charge goes nowhere. However, in an electric dipole, an interesting situation arises as shown in the following diagram:
Consider positive charges “sucking in” the surrounding space, and negative charges “blowing out” the surrounding space. By separating them at a fixed distance, the fields between the poles “occupy” or “cancel” each other, while the flow/distortion surrounding the entire dipole is biased in one direction. The positive pole sucks in from the left, the negative pole blows out to the right, and thus the entire dipole propels itself leftward toward the positive pole.
In a parallel plate capacitor, the electric fields outside the capacitor cancel, but the divergent and convergent gravity fields do not, which is why a cellular gravitator can accelerate toward the positive pole without inducing or utilizing any external ion wind effects.
Because electric fields are immensely stronger than gravity fields, it is not generally recognized by modern physics that electric charges contain net gravity fields because the latter are difficult to detect. Nevertheless, certain experimental setups confirm that it is so, such as the gravitator experiment, the different fall rates or pendulum swing periods of oppositely charged objects.
Asymmetric Electrodes
It should now be clear that electrogravitational self-acceleration requires a difference in the gravitational divergence between two poles. Using symmetric electrodes, this is done as simply as giving one a positive charge and the other a negative one. But it’s also possible to create additional asymmetry by making the electrodes themselves asymmetric. This changes the spread of the electric field, which in turn affects the geometric component giving rise to the gravity field.
Toward this end, Brown experimented with umbrella and disk shaped gravitators. The umbrella devices consisted of two electrodes, one positive and one negative, with one electrode shaped like a large bowl and the other like a smaller bowl. Overall, this formed an open-air capacitor but with asymmetric electrodes, whose asymmetric electric fields generated unbalanced gravitational divergences and increased acceleration. The disk gravitators, described earlier, did the same except one electrode formed the leading edge of the disk, while the other electrode formed the body and trailing edge.
Lifters
One common application of the Biefeld-Brown effect is in the form of “lifters”—these are constructions made of balsa wood frames, wire, and aluminum foil. Lifters separate a grid of negatively charged wires from a grid of grounded or positively charged aluminum foil fins. They rely upon a principle patented in 1957 by Townsend Brown (US patent #3,018,394 titled “Electrokinetic Transducer”). While they have been around since the late 50s, lifters haven’t become popular until recently. They are easy to assemble and require only a moderate high voltage supply, around 30 kilovolts.
How do lifters work? The same way Brown’s later devices worked: through a combination of electrogravitational and ion wind mechanisms. The asymmetry of electrodes alone guarantees a genuine electrogravitational component to the propulsion, while it is clear from observing them in action that ion wind is also involved.
Some say that ion wind cannot explain the level of wind generated by lifters. That much I agree with – however, one must also take into account that negative ions create an electrostatic cooling effect, converting thermal energy to kinetic energy, cooling the air while speeding it up. Thus, the wind results not only from air becoming negatively ionized and attracting toward the positive electrode, but also because it gains additional kinetic energy thanks to the negentropic electrostatic cooling phenomenon.
Nevertheless, for those wishing to debunk the Biefeld-Brown effect by attributing it entirely to ion wind, it must be pointed out that closed capacitors, the cellular gravitators, also self-accelerate without any ion wind effects. Electrogravity arises primarily from the gravitational component of the electric field, harnessed for propulsion via the asymmetrical gravitational field of electric dipoles. Brown also experimented with disk gravitators in vacuum chambers and observed them accelerating nearly as quickly as when run at atmospheric pressure.
Experimental Set up
Confirming the Biefeld-Brown effect would require the following:
- 200 kilovolt DC, minimum 200 microamps, solid state high voltage generator—these consist primarily of an autotransformer, a TV flyback transformer and transistor circuit, and a many-staged cockroft-walton voltage multiplier and rectifier. You can buy them from Information Unlimited.
- metal capacitor plates—made from aluminum foil or aluminum flashing cut into rounded squares. The rounded edges are needed to prevent arcing and corona leakage.
- dielectric sheets—made from the best dielectric material available. These must be cut into squares that are larger than the metal plates. Polypropylene, polystyrene, mica, and if available, high-K ceramic plates, are appropriate materials. Make sure the sheets are thick enough to prevent dielectric breakdown or your gravitator will burn out.
- paraffin wax or transformer oil—because the metal plates take up space due to their thickness, there will be slight spaces between one dielectric sheet and another. Once all the plates and sheets are interleaved and bound together, the entire thing is best immersed in transformer oil, or cast in paraffin wax or resin.
These are just the basics…examine Brown’s 1927 patent for more information. Also beware that while a high voltage generator gently zaps you should you touch it, once this electricity is stored in a capacitor it reaches lethal power levels. Once I was stupid enough to peel apart a gravitator capacitor days after charging it with a Van de Graaf generator…thought it was discharged, but the shock I received as I stuck my fingers in there to pry it apart threw me back against the wall. So—only do this experiment if you’re a responsible and smart hobbyist, as I’ll take no responsibility for what you do with this info.
Conclusion
The Biefeld-Brown effect demonstrates a link between electricity and gravity. Given the explanation above, it should be clear why electric dipoles self-accelerate toward the positive pole; the positive pole converges space, the negative poles diverges space, and being that between poles these distortions cancel while outside these poles they point in one direction, the dipole as a whole should accelerate in one direction.
Introduction to the theory
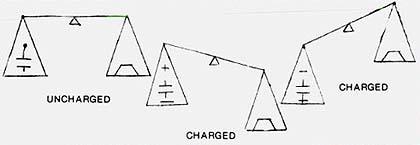
Working in conjunction with Dr. P. A. Biefeld, Thomas Townsend Brown found that highly charged capacitors, when properly suspended, showed a tendency to move relative to the gravitational force.
When the poles of a freely suspended charged capacitor (even in vacuum) were placed on a horizontal axis, a forward thrust would be produced which would move the capacitor in the direction of the positive pole. The direction of thrust would reverse in conjunction with a polarity change. This is the phenomenon known as the Biefeld-Brown Effect.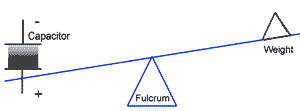
Anti-gravity was demonstrated by placing the capacitor on a beam balance and charging it. When the positive pole pointed upwards, the condenser would move to a point of equilibrium. When the positive pole was pointed downwards, the balance would show a downward deflection.
Experiments show the intensity of the effect to be dependent on several factors:
- the surface area of the plates
- the voltage differential between the plates
- the proximity of the plates to each other
- the material mass between the plates
- the dielectric capacity between the plates
Biefeld Brown effect analysis
The main problem in analysing the real Biefeld Brown effect, is that when tested in air, these devices will be acted upon by the air ions, which will contribute to thrust and thus result in erroneous results of the measured thrust. Testing these charged devices in vacuum is the only way to separate the ion thrust from the effect under study.
As you may note all points (1-5) mentioned above contribute to the total charge stored in a capacitor, which is the total charge flow that occurs in the capacitor during its charging process. When a capacitor is connected to a dc supply, the positive terminal will attract electrons from the negative terminal (even through vacuum). The electron flow stops when the electrons on the negative plate repel other electrons and stop them from reaching the plate. At this point a capacitor is said to be fully charged. No dielectric is a perfect insulator, and so a charging current will always be present, with the greatest flow occuring during initial charging.Biefeld Brown thrust calculations
In many of Thomas Townsend Brown's patents we read that it was not unusual to perform the tests at 300 kV and even Megavolts. Why are such high voltages required? If a device can produce 1 N of thrust at 300 kV then why should it produce no thrust at all (in vacuum) at 30 kV ?
Assume two opposite plates are being charged from zero to a high voltage. Electrons leave the metal surface on the negative plate and are accelerated towards the positive plate. As the electron accelerates, its speed increases steadily to very high values until it hits the opposite surface, at which conservation of momentum makes the positive plate acquire the kinetic energy of the electron. Let's analyse this mathematically:
Electric field energy E=qV , where q = electron charge and V = potential difference.
Lets assume no losses, and that most of this electric energy is used to accelerate the electrons, resulting in kinetic energy.
E = qV = 1/2mv2, where m = mass of electron, v = velocity at positive plate.
Velocity acquired v = sqrt(2qV/m)
So, the velocity acquired by an electron accelerated through a p.d. of 30 kV is 102.7E6 m/s, or 0.34c, where c = speed of light.
Number of charges hitting positive plate per second n = I/q = P/(Vq), where I = current flow, P = Power in Watts.
Thrust on positive plate due to impact momentum p per unit time is:
F = np = nmv = (P/(Vq))m sqrt(2qV/m) = (mP/(Vq)) sqrt(2qV/m)
So, thrust at 100 W, 30 kV would be 1.9E-6 Newtons. Far too small to be detected by a simple mechanical balance as in the experiment described above. This much low value for thrust is mainly due to the low mass value of the electron.
Let's now increase the voltage to reach relativistic speeds, say .999990c
The voltage required to obtain such speed would be mv2/(2q) = 255 kV
So, at approximately 255 kV, electrons would hit the target positive plate at more or less the speed of light.
The relativistic mass of any particle is given by:
Substituting v for 0.99999c, we get y = 223.6, that is the effective electron mass is now 223.6 times its rest mass. Note that the relativistic mass increases sharply to a theoretically infinite value when v increases from 0.9c to 1.0c.
Let's rework the thrust at 100 W, 256 kV with a new mass m'=1E11 x m:
F = (m'P/Vq) sqrt(2qV/m') = 0.21 N
That would be 0.21 N released upon impact. The closer the plates, the higher the current. Force is directly proportional to the current input. Note that as the voltage reaches 255 kV, electrons reach relativistic speeds at increased effective masses and the original equation qV = 0.5mv2 will be subject to an increasing effective mass, which will therefore require a higher electric field to keep accelerating. Thus it should be understood that the above calculations have been worked out to show that Newton's laws cannot be applied to explain the concept of the Biefeld Brown effect.
However, we are here assuming that the effective electron mass can act as a real heavier mass. In such a case, the total averaged momentum would still cancel the impact momentum, and thus cancel the lift, so Einstein's relativistic mass is not a better option to describe the B-B effect. BUT ... as you'll see below, the Biefeld Brown effect may still take place with no particles hitting the boundary wall.Newton's vs Einstein's laws
We know that a big part of textbook physics is based on Newton's laws. If we define a false theory as one which doesn't apply under all conditions, then Newton's laws are false - no way out around this. But similarly we would conclude that most of the other physics laws are false. So, in order not to scrap all our years of studying, we shall better define laws as quite accurate or not accurate, depending on the application. In our case, Newton's laws are not accurate at all, whilst Einstein's laws are quite accurate. Since we are dealing with relativistic speeds within a high voltage capacitor in vacuum, Newton's laws will result in huge errors in our calculations. The higher the applied voltage, the higher our input energy E=Vq, the less accurate will be Newton, and here we are not talking of small errors, but in the scale of 10x.
But let's say, all this error goes in extra mass, then, the capacitor should still not move, due to cancellation of averaged momentum gained with that imparted during the collision. This would also go against Einstein's teachings, that the retardation of acceleration at close to light speeds, is simply due to an increase in mass. In this case, momentum would be preserved because it is a product of mass. But, even Einstein's theories must be questioned in this environment.
Spacetime warping
O.K. so let's face Einstein. His theory yields much more accurate results for the actual particle speeds within a high voltage gradient, their effective mass and total energy.
Effective mass at relativistic speeds = m / (1-v2/c2)1/2 = ym
Total energy = ymc2
Energy used during acceleration = (y-1)mc2
1mc2 is equivalent to the energy stored within the mass of particle at rest and is not part of the input energy.
In many textbooks, the above equation is explained as a gain in mass of the particle of stationary mass m at speed v. I do not know if Einstein himself would be in agreement with this explanation. Here are my other versions of describing the same equation:
- The energy required to move stationary mass m at velocity v is equivalent to that moving a much higher effective mass at velocity v.
- The energy required to move stationary mass m for a distance d is equivalent to that moving the same stationary mass m for a much longer effective distance than d.
- The energy required to move stationary mass m for a distance d during time t is equivalent to that of moving the same stationary mass m for the same distance in a much shorter time.
- The energy required to move stationary mass m at velocity v, is equivalent to the energy required to move the same mass at velocity v, plus an energy doing work against radiation pressure difference (vacuum mod / ether mod / spacetime warp..) between the front and rear sides of the particle.
The apparent mass increase is ALL due to the energy going into the space fabric, and none of it actaully increases the real mass. The mass increase (as shown by points 1,2,3,4) is only a virtual description of the effect best described by point 4.
The above is a pictorial representation of what happens to the space-time fabric when a relativistic particle travels through. This pinching effect is known as space-time warping, the greater the 'effective' mass or energy input, the greater the warping effect. So, does antigravity really exist in capacitors charged in vacuum ? Are these really electrogravitic devices ? Any particles with relativistic speeds undergo time dilation, that is when viewed from an external inertia reference frame, the particles seem to be going slower, and so energy from outside this frame seems to be going in for a longer time. Even if the effect might be very small, the speed of electrons in capacitors in vacuum do undergo time dilation, which is a good indication of space-time warping, same kind of space-time warping as that created by earth's gravity field. So in my opinion Biefeld Brown capacitor in vacuum do produce a gravity field. The higher the voltage, the greater the field, and the greater the deviation between the capacitors' inertial reference frame to its ambient (our ambient).
Speed of light in dielectrics
So how does this explain the B-B effect in a solid dielectric, such as a Mica capacitor. First of all we should put into question the textbook law that states that light slows down in a dielectric. Remember the first time in your life you went swimming and looked at your feet, and thought 'oh my god ... my legs got shorter'. You might have been more correct with that statement than with the textbook laws. Physics thus introduced the refractive index 'n' to try to explain this. It states that n = c/v, v being the velocity of light in the dielectric. Do you think that c does not change, even for an observer travelling near the speed of light, or for any observer in any part of the universe, and then it would easily change by simply passing through a piece of glass? - I don't.
Suppose an astronout is travelling at the speed of light in a transparent spaceship sitting down at the back, and he beams the light of his laser pointer towards the front of his ship. From earth you would see the laser beam travelling very slowly until it arrives at the front. That's because he is within a different inertia (or space-time) reference frame. Now consider the dielectric as a different space-time reference frame and you should get the refractive index, the slowing down of light and all nonsense laws of physics. As I see it, putting mica, glass, air or vacuum within the capacitor will still generate the same effect. Did you know that a high electric field changes the refractive index of a material? I guess Newton will not be of much help to explain this.
It is also interesting to note that dielectric constants increase with refractive index for different materials. The dielectric constant, K, is equal to the sum of the real (E') and imaginary (E'') permittivity of a material and is the square of the refractive index, or K = n2=c2/v2.
This is quite interesting, as the effective mass increase factor y, is now clearly related to the dielectric constant K of the dielectric as follows:
y = (1-v2/c2)-1/2
y = (1-K-1)-1/2
This most clearly shows that the effective increase in energy required to accelerate the particle at relativistic speeds is not due to an increase in the real mass, but due to the changes undergone by the surrounding medium/dielectric properties. The extra energy involved is being used up to modify the dielectric constant within the dielectric.Energy storage & flow within dielectrics
Total energy in the accelerating system = (y+1)mc2
Note the +1mc2 is equivalent to the energy stored within the mass of the moving particle, and is not part of the input energy.
Input energy = ymc2, where m is the stationary mass, which is a constant
Input energy = (1-K-1)-1/2mc2
But we know that as speed gains up, input energy goes up, but the actual resulting acceleration goes down, until it zeroes at v=c. So where is all this input energy going? Well, if it is not being converted into real mass within the particle, and it is neither being used as kinetic energy, then it must be given out to the surrounding space. This seems weird at first, but those of you who ever charged a capacitor or inductor, know that energy can be stored within the dielectric, even in vacuum. If all this amount of energy is being somehow stored within the dielectric (space, air, mica or whatever), some parameters of the dielectric should make up for this, otherwise this energy would have been lost forever, which is impossible. A dielectric is defined by its permittivity, and it is this value which must be expanded or compressed as the energy fills up this space.
Note that in the expression:
Input energy = (1-K-1)-1/2mc2,
the only variables are the energy and the dielectric 'constant' which is not constant at all.
We already know that the dielectric constant, K, of a capacitor changes with temperature and frequency, so this should not be a big shock for us. As shown in the prism colour separation, the refractive index (n) varies with frequency (and K=n2). This suggests that as we input energy in a device containing relativistic speed particles, its dielectric constant (and its refractive index) will change. Of course, this will not be the 'relaxed' condition of the dielectric, and it will be in a stressed condition, until the internal energy is dissipated, and the dielectric gives back this energy and acquires back its normal permittivity. This process is very similar (actually the same) to the process of charging a capacitor.
A high voltage capacitor is thus changing its internal permittivity with electrical energy input, and thus modifying space-time within its plates. From the above discussion, it follows that a change in space-time is normally accompanied by a change in dielectric constant, a change in refractive index, a change in the properties of its inertia reference frame and a change in gravitational field within its plate. In fact, it is known that when an isotropic substance is placed in an electric field, a change in refractive index occurs, which is better known as the Kerr Effect. The effect is quadratic with respect to the electric field strength.
This supports the idea that a capacitor charged at high voltage will gain inertia, not because of its speed or mass, but because of the modified space-time within it. The highest gain in inertia, or gravity field, will be nearest to the positive plate, where most particles would have accelerated to their maximum speeds, and thus left the most stressed space-time. The situation can be explained as 'elastic potential energy within the space-time fabric', and this potential energy will be present as long as the capacitor stores the energy within its dielectric.
Symmetric vs asymmetric energy fields
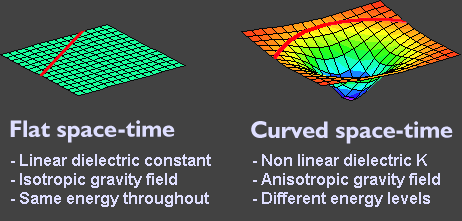
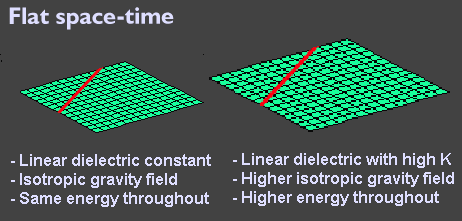
The above diagram shows the difference, using space-time plots, between two different space-time frames having different dielectric constants. In both frames, the dielectric is uniform (no stress, no curved space-time), resulting in a flat space-time. A simple example would be a volume of vacuum in space (left plot) and the same volume of glass (right plot). This can help you understand why a light ray (red path) travelling in vacuum 'seems' to be faster than a light ray travelling in glass. Both rays are travelling at the same speed, but an observer outside the frame will see the one on the right go slower, or travel less distance over the same time. The plot on the right depicts the situation of a highly, but uniformly, energised space-time frame, and is similar to the plot we would get from a highly energised dielectric within a symmetric electric field. A mass or localised energy field within such flat space-times, will not be subject to any external force, other than its own gravity field pointing towards the centre of the mass in all directions.
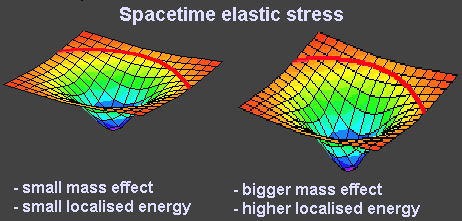
As Thomas Townsend Brown explained, the thrust is higher in an asymmetric electrode configuration. In a symmetric capacitor, the only asymmetry in its energy field is due to the fact that the motion of the electrons at the positive plate is at a higher kinetic energy than that of the electrons leaving the negative plate. This results in very small space-time curvature, having a very small interaction with external energy points or masses, resulting in very small thrust. The above diagram shows the space-time elastic stress of (left) a small mass or localised energy source and that of (right) a bigger mass or localised higher energy source.
The same plot would be obtained for a dielectric in which the energy distribution is asymmetric, for example in an asymmetric electric force field. This asymmetric energy distribution is the key for the generation of space-time elastic stress without the requirement of any particles flowing within the system. This would also explain the fact why a graded dielectric would amplify this elastic stress within such a field. The result of this space-time curvature on masses or energies within the frame (the B-B device) would be similar to a mass entering earth's gravity field. No particles are required to hit the subject, but the subject will tend to be accelerated towards the slower time, i.e. the highest energy level. The greatest effect will be obvious on any matter within the field itself, but also on the walls within reach of the electric field force. In case of such a device operating in vacuum, with no mass or walls in the vicinity, the only propulsion would be achieved by the space-time curve acting on the surrounding energy within the vacuum (vacuum energy, ether,...) which is abundant of high cosmic energy, the same energy causing gravity on any planet in the universe.Biefeld Brown craft efficiency
By now you should have a clear picture of how the real Biefeld Brown generates its elastic potential energy within the dielectric. Efficiency of this mechanism can reach near 100% if the elastic limit of the dielectric is reached on the positive electrode side. The elastic limit of all dielectrics is the same and equates to the condition v=c. So, we know that 100% is impossible, but >99% efficiencies could be obtained by using a very high voltage to charge the capacitor. At such a limiting voltage we get:
Input energy = (1-K-1)-1/2mc2 = 1/2CV2, where C is the capacitance and V is the terminal voltage.
Interesting to note that here we got an alternative formula for capacitance:
C = (2x(1-K-1)-1/2mc2)/V2
It is now clear why the Biefeld Brown effect depends on the mass of the dielectric, other than the 'conventional physics' parameters making up capacitance. The above equation shows that at such high voltages, capacitance is related to dielectric mass as well.Both potential energy within the charged capacitor and earth's gravitational potential energy are the same mechanism, they are both gravity fields. And if their gradients are pointed against each other, their elastic potential energies can do work against each other. Similar to pressing two springs together and releasing both. The lighter spring will move faster (our craft) as opposed to the 'earth'. Their is no energy conversion in this process since they are both gravitational potential energies. This would imply that:
Electrical input energy = Input energy = (1-K-1)-1/2mc2 = 1/2CV2 = mgh
where h would be the change in altitude of the powered craft.
This shows that the small effect noticed by Biefeld Brown during the experiments, can eventually become the solution for the most efficient ether drive. This method could eventually obtain efficiencies of over 99% for the conversion of electrical to kinetic energy within any dielectric medium including space. Unlike ion-air dependent crafts, its maximum speed would not be limited by the ion drift velocity but only by the speed of light.The Biefeld-Brown Effect (A):
Further Information
Thomas Townsend Brown Website – excellent collection of documents, articles, and pictures of Brown and his research.
Rex Research, T. T. Brown – an important article by Brown himself, and a copy of his 1927 British patent.
Jean Naudin Lifter Page – theory, documentation, and pictures of the “lifter” experiment.
Alýntý: http://blazelabs.com/f-biefeld.asp
Çetin BAL, warpdrive, wormhole, electrogravity, zamanda yolculuk, time travel, time machine
H
içbir yazý/ resim izinsiz olarak kullanýlamaz!! Telif haklarý uyarýnca bu bir suçtur..! Tüm haklarý Çetin BAL' a aittir. Kaynak gösterilmek þartýyla siteden alýntý yapýlabilir.The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru