Time Travel Research Center © 2005 Cetin BAL - GSM:+90  05366063183 - Turkey/Denizli 

Contents
Superconductivity
Laser
Plasma
Quantum Computing
Footnotes
References
Index

Superductivity

Superconducting Elements If mercury is cooled below 4.1 K, it loses all electric resistance. This discovery of superconductivity by H. Kammerlingh Onnes in 1911 was followed by the observation of other metals which exhibit zero resistivity below a certain critical temperature Tc. The fact that the resistance is zero has been demonstrated by sustaining currents in superconducting lead rings for many years with no measurable reduction.

Ceramic materials are expected to be insulators -- certainly not superconductors, but that is just what Georg Bednorz and Alex Muller found when they studied the conductivity of a lanthanum-barium-copper oxide ceramic in 1986. Its critical temperature of 30 K was the highest, which had been measured to date. Their discovery started a surge of activity which discovered superconducting behavior as high as 125 K. Table 13-02 shows the elements, which can become superconducting at the indicated critical temperature.

Table 13-02 Superconducting Elements

 
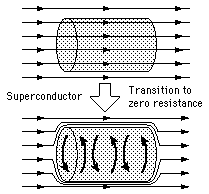Superconductivity Meissner Effect The effect of superconducting is often demonstrated by cooling a disk made of superconducting material with liquid nitrogen to below the critical temperature Tc. A magnet placed above the disk is repelled, i.e., it is levitated above the superconductor. (See Figure 13-07.) This phenomenon is caused by the Meissner effect which is related to the fact that a superconductor will exclude magnetic fields within the superconducting material

Figure 13-07 Superconductivity

Figure 13-08 Meissner Effect

(see Figure 13-08).

 

Suppose, as in Figure 13-07, a magnet is placed above a superconductor. The induced magnetic field inside the superconductor is exactly equal and opposite in direction to the applied magnetic field, so that they cancel within the superconductor. The result are two magnets equal in strength with poles of the same type facing each other. These poles will repel each other, and the force of repulsion is enough to float the magnet. However, the magnet's magnetic field must be below the superconductor's critical magnetic field Hc. If the magnetic field is stronger than Hc it would penetrate the superconductor and extinguish the superconductivity.

In 1956 L. Cooper offered an explanation for this phenomenon of superconductivity. The process starts in some materials at very low temperature when two electrons near the Fermi energy level could couple to form an effective new particle, under a very weak attractive force. This particle was subsequently called the Cooper pair. It can be shown that the most energetically favourable situation for this to occur was when the two electrons had a total spin of zero. Since the Exclusion principle does not apply to particle with integer spin, there is no restriction on the energy state that the Cooper pair can occupy. In particular, at low temperatures thermal agitation is minimal, and all of the Cooper pairs can occupy the lowest possible energy state. Thus no energy exchanges can take place (nothing to give), the normal resistive energy losses are not possible. The Cooper pairs move unimpeded through the superconducting material: it has zero electrical resistance and exhibits superconductivity.

Laser

     
Figure 13-09 Ruby Laser Figure 13-10 Laser, Energy
Levels
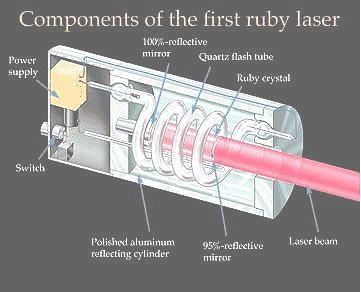
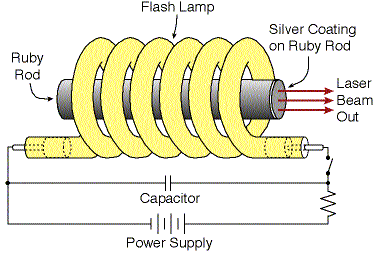
Finding substances in which a population inversion can be set up is central to the development of new kinds of laser. The first material used was synthetic ruby. Ruby  is crystalline aluminum (Al2O3) in which a small fraction of the Al3+ ions have been replaced by chromium ions, Cr3+. It is the chromium ions that give rise to the characteristic pink or red colour of ruby and it is in these ions that a population inversion is set up in a ruby laser.
   

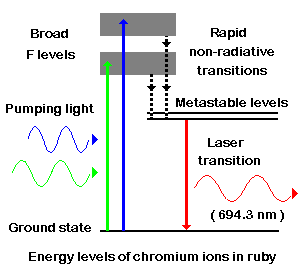
In a ruby laser, a rod of ruby is irradiated with the intense flash of light from xenon-filled flashtubes. (See Figure 13-09.) Light in the green and blue regions of the spectrum is absorbed by chromium ions, raising the energy of electrons of the ions from the ground state level to the broad F bands (See Figure 13-10). Electrons in the F bands rapidly undergo non-radiative transitions to the two metastable E levels. A non-radiative transition does not result in the emission of light; the energy released in the transition is dissipated as heat in the ruby crystal. The metastable levels are unusual in that they have a relatively long lifetime of about 4 milliseconds (4 x 10-3 s), the major decay process being a transition from the metastable level to the ground state. This long lifetime allows a high proportion (more than a half) of the chromium ions to build up in the metastable levels so that a population inversion is set up between these levels and the ground state level. This population inversion is the condition required for stimulated emission to overcome absorption and so give rise to the amplification of light. The stimluating photon and the stimulated photon leave the atom in the same direction, same frequency, same polarization and in phase. This light can then interact with other chromium ions that are in the metastable levels causing them to repeat the same process. As each stimulating photon leads to the emission of two photons, the intensity of the light emitted will build up quickly. This cascade process in which photons emitted from excited chromium ions cause stimulated emission from other excited ion, will create a very intense and coherent red light beam of wavelengths 694.3 and 692.7 nm.

 

Laser cooling utilizes the collective momentum of many photons to reduce the thermal motion of an atom. Since the approaching and recessing speed of the atoms differs slightly due to the Doppler effect and the atoms can only absorb a certain frequency, the laser beam can be tuned such that it slows down only the approaching atoms. The six crossed laser beams shown in Figure 13-10a create a space in which atoms moving in this region (the bright area in the center of the picture) are trapped and cooled by absorption of photons from the crossed beams. With this technique, researchers have already reached temperatures lower than a millionth of a degree Kelvin. That's an average atomic speed on the order of a few cm/sec.

Figure 13-10a Laser Cooling

 

Plasma

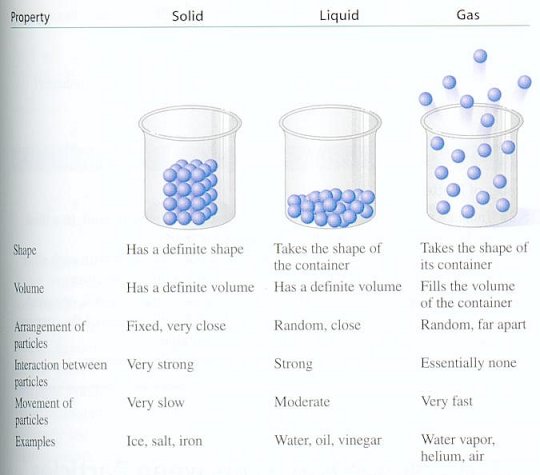
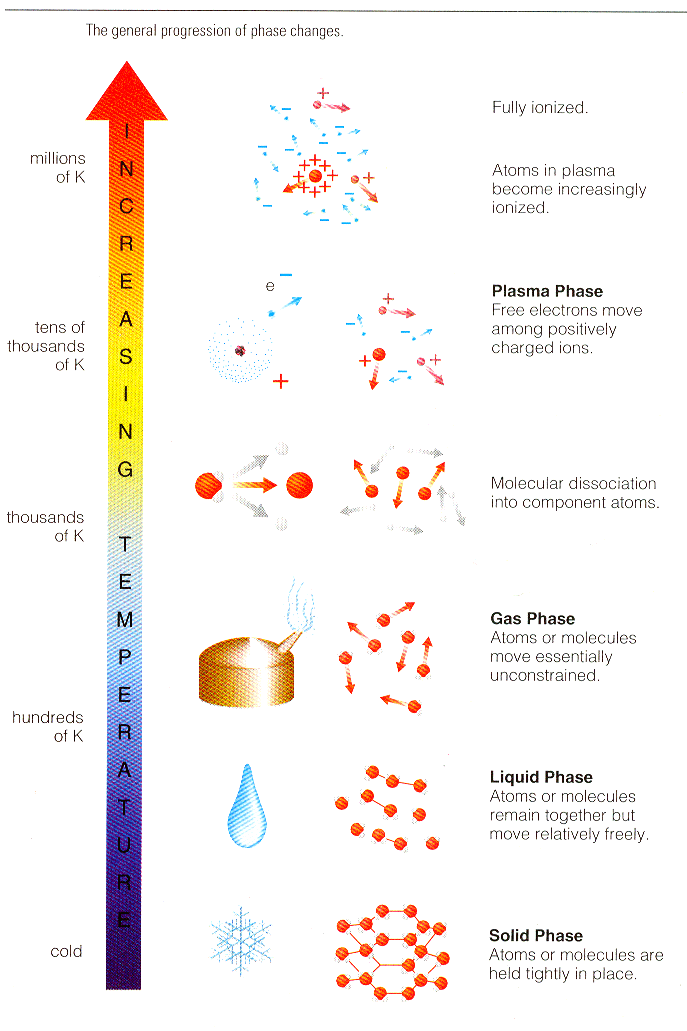
Phases, the Three Fourth Phase In the solid state, the atoms are firmly imprisoned inside a rigid network (like ice for example). When we raise the temperature, they go into a liquid state (the ice melts), where the atoms may slide around in relation to the others, thus enabling a liquid to adapt to the shape of a container. If we heat it up even more, we arrive at the gas state: atoms then move around freely and independently of each other (water turns into steam). 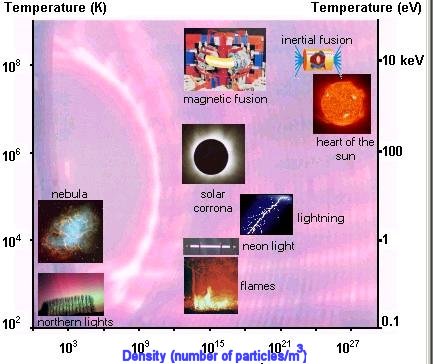(See Figure 13-11.) Finally, when we get to very high temperatures (typically several million degrees), the ingredients of the atom separate, nuclei and electrons move around independently and form a globally neutral mixture: this is the plasma state (See Figure 13-12).

Figure 13-11 The Three Phases

 

Figure 13-12 The Fourth
Phase

  
This fourth state of matter, found in the stars and the interstellar environment, makes up most of our universe (around 99 %). On Earth, it does not exist in a natural form, apart in lightning and the Aurora Borealis. In our everyday life, plasmas have many applications (micro-electronics, television flat screens and so on), of which the commonest is the neon tube. (See Figure 13-13.)

Depending on the temperature, the atoms may be partially or wholly ionized. A plasma may thus be considered as a mixture of positively charged ions and negatively charged 		  electrons, possibly co-existing with neutral atoms and molecules. For example, in our luminescent tube, the ions and electrons is a small proportion in relation to atoms and molecules. On the other hand, in plasmas produced for fusion experiments, the gas is strongly ionised, and the atoms and molecules are in low proportion, even completely absent in the heart of the pulse. In both cases, the description of plasmas comes from the physics of fluid mechanics and controlled by the force of electromagnetic interaction. The system is described by the usual macroscopic features such as density, temperature, pressure and rate of flow.
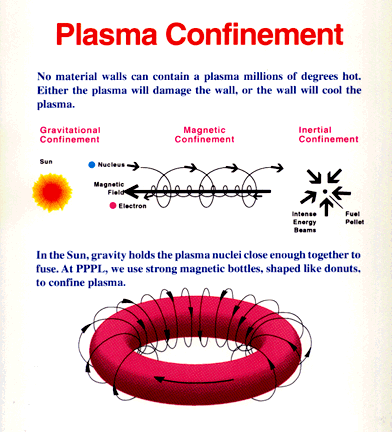
Plasma Fusion The vast power radiated by the Sun is generated by the fusion process wherein light atoms combine with an accompanying release of energy. In nature, proper conditions for fusion occur only in the interior of stars. Researchers are attempting to produce the conditions that will permit fusion to take place on earth.

Since nuclei carry positive charges, they normally repel one another. The higher the temperature, the faster the atoms or nuclei move. When they collide at these high speeds, they overcome the force of

Figure 13-13 Plasma Occurrence
 

Figure 13-14 Plasma Con-
finement

repulsion of the positive charges, and the nuclei fuse. In such collisions, energy is released. The
difficulty in producing fusion energy has been to develop a device which can heat the deuterium-tritium fuel to a sufficiently high temperature and then confine it for a long enough time so that more energy is released through fusion reactions than is used for heating.

 

In order to release energy at a level of practical use for production of electricity, the gaseous deuterium-tritium fuel must be heated to about 100 million degrees Celsius. This temperature is more than six times hotter than the interior of the sun, which is estimated to be 15 million degrees Celsius. Scientists have already passed the task of achieving the necessary temperatures. In some cases, they have attained temperatures as high as 510 million degrees, more than 20 times the temperature at the center of the sun.

The problem is how to confine the deuterium and tritium under such extreme conditions. A part of the solution to this problem lies in the fact that, at the high temperatures required, all the electrons of light atoms become separated from the nuclei. The fuel is in a plasma state. Because of the electric charges carried by electrons and ions, a plasma can, in principle be confined by a magnetic field. In the absence of a magnetic field, the charged particles in a plasma move in straight lines and random directions. Since nothing restricts their motion the charged particles can strike the walls of a containing vessel, thereby cooling the plasma and inhibiting fusion reactions. In a tokamak, the high-temperature plasma are confined by the magnetic field around the doughnut-shaped nuclear reactor as shown in

  the lower section of Figure 13-14.

However, long-lived pinched plasmas are extremely difficult to maintain. The plasma column is observed to break up rapidly. The reason for the disintegration of the column is the growth of instabilities. The column is unstable against various departures from cylindrical geometry. Small distortions are amplified rapidly and destroy the column in a very short time. The mechanisms of instability in plasma physics are nearly unlimited. Some instabilities are comparable to examples borrowed from fluid mechanics, as the Rayleigh Taylor’s instability, which consists of superposing two fluids with the heaviest on top. Imagine for example a vessel in which you pour water and then carefully add oil over the top. The system is then in a state of meta-stable equilibrium. The slightest nudge will provoke a change with the heavier fluid dropping to the bottom, which corresponds to a stable equilibrium. Another type of instability are kink instabilities, which occur when a current parallel to the magnetic field cause twisting of the field lines, recalling the effect obtained if we twist a rope too much: the rope twists out and kinks. The sausage or neck instability causes a greater inwards pressure at the neck of a constriction. This serves to enhance the existing distortion.

The Tokamak Fusion Test Reactor has produced significant quantities of fusion power (up to 10 Million Watts) from the fusion of DT (Deuterium and Tritium). However, this has not yet equaled the input heating power -- the breakeven condition.

  

Quantum Computing

Quantum Computing Physics and Computer science have combined to create a new field: quantum computing and quantum information. The spark that ignited world wide interest in this new field sprang forth in 1994 with Peter Shor's discovery of a theoretical way to use quantum mechanical resources to unravel a mathematical problem at the heart of electronic commerce and cryptography.

Basic steps towards the creation of a quantum computer have been taken, with the demonstrations of elementary data storage and manipulation using photons and atoms or trapped ions as the quantum bits, or "qubits". Recently, it has been shown that it is possible to build solid-state qubits made from tiny samples of superconducting material. Figure 13-15 shows some of the subjects, which are currently being investigated in the field of quantum computing.
 

Figure 13-15 Qunatum Computing

 
Qubit Qunatum computing exploits two resources offered by the laws of quantum mechanics: the principle of superposition of states and the concept of entanglement. Superposition is a "one-particle" property; while entanglement is a characteristic of two or more particles.

Consider a particle with spin such as the electron. With reference to a given axis (say along the z axis), the spin of the particle can point in two opposite directions, say "up" and "down", and the spin states can be denoted as |1 > and |0 >. But by the laws of quantum mechanics, the particle can exist in a superposition of these two states, corresponding to arbitrary orientation as shown in Figure 13-16.

Figure 13-16 Qubit

 
Mathematically, the superposition of these two states can be written as:
|f > = a |1 > + b |0 > ------ (1)
where a and b are related to the probability of finding the electron in state |1 > and |0 > respectively satisfying
|a|2 + |b|2 = 1. This normalization defines the total probability of finding the electron to be 1. In general, the
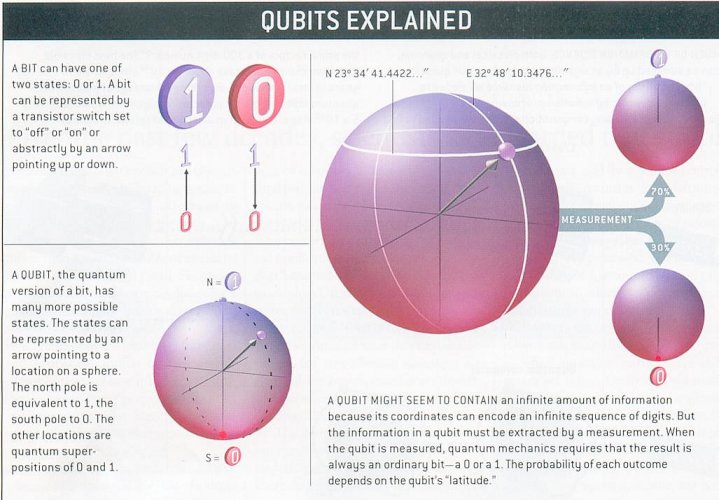
|1 > and |0 > states can be represented by any two-states entity such as "on" and "off", horizontal and vertical polarization of a photon, one particle vs no particle, ... etc. 		  |f > is called a qubit. If a photon in state |f > passes through a polarizing beamsplitter -- a device that reflects (or transmits) horizontally (or vertically) polarized photons -- it will be found in the reflected (or transmitted) beam with probability |a|2 (or |b|2). Then the general state |f > has been projected either onto |1 > or onto |0 > by the action of the measurement (sometimes it is referred as collapse or decoherence of |f >). Thus according to the rule of quantum mechanics, a measurement of the qubit would yield either
|1 > or |0 > but not |f >.(See Figure 13-16.)
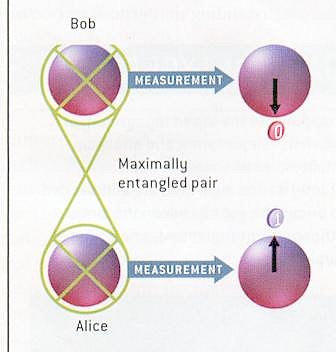
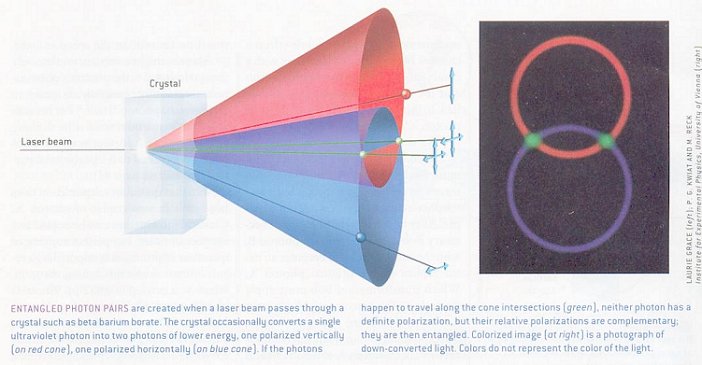
Entanglement1 Entanglement2 Now, consider a two-particle state: there are four "basis states",
|1 >1|1 >2, |0 >1|0 >2, |1 >1|0 >2 and |0 >1|1 >2, where the subscript indicates particle 1 and 2. Again, superpositions can be made of these states, including in particular, the four "maximally entangled Bell states":
|1 >1|1 >2 + |0 >1|0 >2 ------ (2)
|1 >1|1 >2 - |0 >1|0 >2   ------ (3)
 

Figure 13-17 Entanglement

Figure 13-18 Entanglement Implementation
 

 |1 >1|0 >2 + |0 >1|1 >2  ------ (4)
|1 >1|0 >2 - |0 >1|1 >2   ------ (5)
 

Such Bell states have the peculiar property that the particles always "know" about each other, even if they are separated by huge distances; this property is commonly associated with the "non-locality" of quantum mechanics. Entanglement such as this is a basic ingredient of quantum computing. Figure 13-17 shows that a measurement of one entangled member will determine the outcome for the other member -- either in the same state if the Bell state is Eq.(2), Eq.(3) or in the opposite state if the Bell state is Eq.(4), Eq.(5). Figure 13-18 shows an experiment that implements the entangled state of two photons.

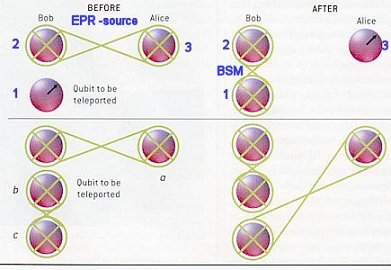
Teleportation Suppose particle 1 which Bob wants to teleport is in the initial state:
|f >1 = a |1 >1 + b |0 >1 ------ (6)
and the entangled pair of particles 2 and 3 shared by Bob and Alice is in the state:
|f >23 = (|1 >2|0 >3 - |0 >2|1 >3)/21/2 ------ (7)
which is produced by an Einstein-Podolsky-Rosen (EPR) source.
The teleportation scheme works as follows. Bob has the particle 1 in the initial state |f >1 and particle 2. Particle 2 is entangled with particle 3 in the hands of Alice. The essential point is to perform a joint Bell-state measurement (BSM) on particles 1 and 2 which projects them onto the entangled state:
 

Figure 13-19 Teleportation

 |f >12 = (|1 >1|0 >2 - |0 >1|1 >2)/21/2 ------ (8)
This is only one of four possible Bell states into which the two particles can be entangled. The state given in Eq.(8) distinguishes itself from the others by the fact that it changes sign upon interchanging particle 1 and 2. This unique antisymmetric feature plays an important role in the experiment.

According to the rule of quantum physics once particles 1 and 2 are projected into |f >12, particle 3 is instantaneously projected into the initial state of particle 1. (See top portion of Figure 13-19.) This is because when we observe particles 1 and 2 in the state |f >12 we know that whatever the state of particles 1 is, particle 2 must be in the opposite state. But we had initially prepared particle 2 and 3 in the state |f >23, which means particle 2 must be in the opposite state of particle 3. This is only possible if particle 3 is in the same state particle 1 was initially. The final state of particle 3 is therefore:
|f >3 = a |1 >3 + b |0 >3 ------ (9)
Note that during the Bell-state measurement particle 1 loses its identity because it becomes entangled with particle 2. Therefore the state |f >1 is destroyed on Bob's side during teleportation.

The transfer of quantum information from particle 1 to particle 3 can happen instantly over arbitrary distances, 		  hence the name teleportation. Experimentally, quantum entanglement has been shown to survive over distances of the order of 10 km. In the teleportation scheme it is not necessary for Bob to know where Alice is. Furthermore, the initial state of particle 1 can be completely unknown not only to Bob but to anyone. It could even be quantum mechanically completely undefined at the time the Bell-state measurement takes place. This is the case when particle 1 itself is a member of an entangled pair and therefore has no well-defined properties on its own. This ultimately leads to entanglement swapping. (See lower portion of Figure 13-19, "e-bit" means entangled bit)

A complete Bell-state measurement not only give the result that the two particles 1 and 2 are in the antisymmetric state in Eq.(8), but with equal probabilities of 25% we could find them in any one the remaining three Bell states. When this happens, the state of particle 3 is determined by one of these three different states. Therefore Bob has to inform Alice, via a classical communication channel, which of the Bell state result was obtained; depending on the message, Alice leaves the particle unaltered or changes it to the opposite state. Either way it ends up a replica of particle 1. It should be emphasized that even if it can be demonstrated for only one of the four Bell states as discussed above, teleportation is successfully achieved, albeit only in a quarter of the cases.

 

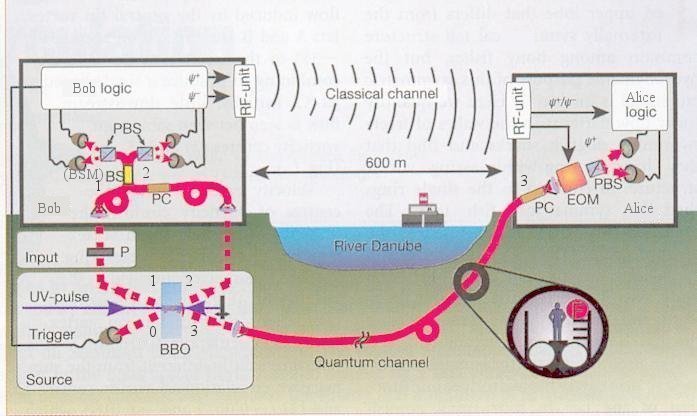
The actual experimental setup is shown in Figure 13-20 with a demonstration successfully completed over a distance of 600 meters across the River Danube. Alice's photon 3 was transported inside an 800 meter long optical fibre in a public sewer located underneath the river, where it is exposed to temperature fluctuations and other environmental factors (the real world). In Figure 13-20, the entangled photon pairs (0,1) and (2,3) are created in the beta-barium borate (BBO) crystal by a pulsed UV laser. Photon 0 serves as the trigger. Photons 1 and 2 are guide into a optical-fibre beam splitter (BS) connected to

Teleportation over River Danube polarizing beam splitters (PBS) for Bell-state measurement (BSM). The logic electronics identify the Bell state and convey the result through the microwave channel (RF unit) to Alice's electro-optic modulator (EOM). Depending on the message, it either leaves the photon state unaltered or changes it to the opposite state. Note that because of the reduced velocity of light within the fibre-based quantum channel, the classical signal arrives about 1.5 microseconds before photon 3. Thus, there is enough time to set the EOM correctly before photon 3 arrives. Polarization rotation (which introduces errors) in the fibres is corrected by polarization controllers (PC) before each run of measurements.

Figure 13-20 Teleportation over River Danube

Polarization stability proved to be better than 10o on the fibre between Alice and Bob, corresponding to an ideal teleportation fidelity of 0.97.

 

Footnotes

1Deuterium and tritium are the isotopes of hydrogen. While the hydrogen nucleus contains only 1 proton, the deuterium contains 1 proton and 1 neutron, and the tritium contains 1 proton and 2 neutrons.

2An EPR-source is used to provide an entangled pair. An example is the decay of the pi meson into an electron-positron pair. Since the spin for the pi meson is 0, the spin for the electron-positron pair must be opposite according to the conservation of angular momentum. Therefore, no matter how far apart are the members of this pair, if the spin is flipped for one of the member, the spin for the other member will also be flipped to the opposite at precisely the same moment. This non-local influence (non-locality) occur instantaneously, as if some form of communication, which Einstein called a "spooky action at a distance", operates not just faster than the speed of light, but infinitely fast. Figure 13-18 is another method to prepare entangled pair. In this case, it is the entanglement of the horizontal and vertical polarizations of the photon. It has been demonstrated recently in 2004 that entanglement and teleportation is possible using pair of trapped ions such as Ca+ or Be+.

3To achieve projection of photon 1 and 2 into a Bell state the two photons are superposed at a beam splitter.

Index


Atomic mass
Atomic number
Band theory, metal
Bell state measurement
Bell states
Carbon
Conduction band
Cooper pair
Deuterium-tritium fuel
Einstein-Podolsky-Rosen (EPR) source
Entanglement
Fermi energy
Fourier series
Fusion
Glass
Instabilities
Insulator
Isotopes
Laser		  
Laser Cooling
Meisser effect
Metastable levels
Periodic table
Phonon
Plasma
Population inversion
Quantum computing
Qubits
Ruby laser
Semiconductor
Specific Heats of Solids
Stimulation emission
Superconductivity
Superposition
Teleportation
Tokamak
Valence Band
Valence electrons
 

Wormhole, Time Travel, Time Machine, Zamanda Yolculuk, Zaman Makinası, Warp drive, UFO, Antigravity, Free energy

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

Ana Sayfa /index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy) /Astronomy