Matter curves spacetime. This curvature is observed as forces acting on every kind of matter. A consequence of this is the existence of black holes: A star may collaps under its own gravitational force leading to an enormous energy density in the interior and thus to a vast curvature. When this evolution has reached the point where no particle in the vicinity, not even light, can escape, a black hole is formed. In its interior the mass density is infinite and perfectly concentrated in the center.

The occurence of infinities is an indication that the known laws of physics may break down at that point. Are there similar solutions of the Einstein equations but without a deadly singularity? Imagine a spacetime that does not contract into one point like a black hole, but widens up again after some minimal radius. It may be visualized as in the following diagram, showing a three-dimensional cut of some higher-dimensional embedding.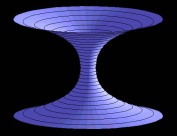

 

Aspacetime of such a form may be called a wormhole. Its name suggests that an observer once fallen into the hole will not be sucked into the center and crunched by the immense forces present but instead continue his way until he reaches the other end of the wormhole. Having left the tunnel the observer may have entered a completely new universe, but also distant regions of the same universe could be connected. This is shown in the next figure.

 

An observer travelling from one mouth to the other can choose between two paths. Either he takes the usual route or he uses the tunnel created by the wormhole. This tunnel can be arbitrarily short allowing the distance to be covered in a much shorter time, viewed in the inertial system of one of the mouths. Thus a possibility for travelling over large distances is provided.

Acommon ansatz for a spacetime, i.e. a solution to Einstein’s equations, with the desired properties is the metric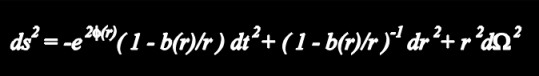

 

For phi(r)=0 and b(r)=2mr the metric describes a black hole. A wormhole emerges when phi and b fulfill several properties, such as lim_r->oo phi(r)= const, b₀(r₀) = r and b(r) ^>_< r for r ^<_> r₀ . A special choice compatible with these contraints yields an energy distribution thus:

 

Obviously there is a region where the energy density becomes negative. The exotic matter is located in a sphere around the wormhole interior. The absolute amount of negative energy can be arbitrarily small, but must always be greater than zero. This is a constraint for the existence of wormholes.

The strength of tidal forces depends on the energy distribution and can be minimized through an appropriate choice of b(r) and phi(r).

 09'2000 ©Marcus Baumgartl