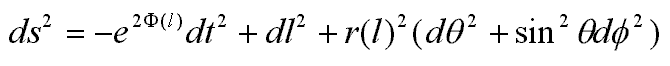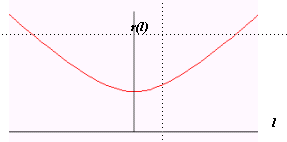
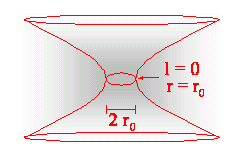
The Morris-Thorne-wormhole is a good basis for a fundamental examination of a womhole’s properties and can also be a starting point for further generalizations. Usually its metric looks like.

This describes a wormhole which can be visualized as in fig.2/5. r(l) denotes the distance from the center, but the proper radial distance for a traveller moving through the wormhole is measured by the coordinate l.

As the wormhole connects two asymptotically flat space-times, the coordinate l covers the entire range from to . The absence of event horizons, which makes the wormhole traversible, depends on the proper choice of . Note that r(l) has a minimum value r₀. This makes sure that the traveller does not encounter a singularity within.

The fact that such a (unique) minimal value exists can be assumed as a general feature, at least for a large class of wormholes. The space-like 2-sphere with the radius r₀ is called ‘throat’ or ‘horizon’.

This leads to the so-called ‘flare-out’ condition, which gives us a possible definition of a wormhole-throat at hand:

In a space-time containing a wormhole there exists a space-like 2-sphere with minimal area (see also fig.6).

Obviously this definition is independent of the employed theory of gravity.