Mathematics of Time Travel - Cetin BAL/Denizli

Mathematics of Time Travel

The Lorentz Transformations: according to relativity theory the length of a body as measured by an observer in uniform relative motion is less than that measured by an observer at rest with respect to the body. There's not a physical change in the body, but a consequence of the Lorentz Transformation. For simplicity it has been assumed throughout than Z is the direction of motion, consequently:

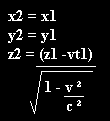
Where i = square root of -1

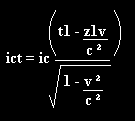
This Lorentz invariant applies to the four vectors: distance, velocity, acceleration and momentum and each will be discussed below:

Distance

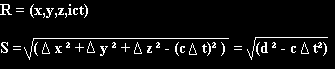
Velocity

In Newtonian mechanics velocity is derived by differentiating the position with respect to time. The relative nature of time in Einstein's relativity appears at first glance to pose something cause problem. The solution is to use the "proper time", i.e. the time measured by an observer attacks to the moving object. This has the advantage that the differences in x, y and z are zero nd that the "proper time" is orthogonal to the other three axes; which is an intrinsic properly of "proper time" Newtonian mechanics, considered as the fourth Euclidean ordinate.
Differentiating using the proper time gives the four-velocity expression below, where uu is the familiar three-space velocity of Newton:

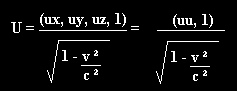
Acceleration

Again, this is obtained by differentiating the four velocity with respect to the "proper time" giving A = (a, 0) where a is the three-space acceleration of Newton.

Momentum

The Lorentz Transformation invariant four momentum expression where p is the magnetude the three momentum of Newtonian mechanics is shown below. The conservation both of the three momentum and of mass energy is contained within the conservation of four momentum:

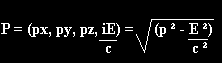
Dirac's Derivation of Negative Mass Energy: In classical Newtonian physics the energy E of an object is given by:

Where m is mass and v is velocity. As both mass and any quantity squared must be positive, energy also must be positive. Classical Newtonian momentum is simply the product of the mass and the velocity.
Both classical energy and momentum are conserved. In relativistic Einsteinian physics, four momentum, P, is of the form (px, py pz, iE/c). It is now this four momentum, momentum energy that is conserved. As a vector its magnetude is Lorentz invariant. If in one frame of reference the rest frame, an object is at rest then:

P² = m²oc²

Where m is now the rest mass. In a frame in which it is moving then:

P² = p² - E²
ccccccacc²

Where p is just the magnitude of Newton's three momentum, and E is the corresponding energy. Each component of P is conserved, which consequently implies the conservation of both mass energy and momentum, similarly to Newtonian mechanics. Additionally, as P is invariant, the last two equations must be equal, i.e. after rearranging:

We are at liberty to take either the positive or negative square root of the right hand side for energy; the latter of these gives rise to negative mass energies.

Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.

Ana Sayfa / İndex / Ziyaretçi Defteri / E-Mail / Kuantum Fiziği / Quantum Teleportation-2

Time Travel Technology / Kuantum Teleportation / Duyuru / UFO Technology /

Roket bilimi / CetinBAL / Astronomy