Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey/Denizli
![]()
Time Travel Physics
Space-Time Engineering |QuantumTheory| Home | Parallel Universes | Wormhole | Time Machines | Reversing Time | ÇetinBAL: Time Travel | Time Travel Research | UFO Technology | New Theories of Space-Time |Reversing Time at Sub-light Speed (Part 1 of 3)
by David Anderson, Ph.D.
In this series of articles we will show a solution using a rotating cylinder model that demonstrates how time travel is possible within the context of general relativity. This solution clearly permits time travel and communication not only to the future, but also to the past. Most important, it will show how reverse time travel can be achieved without having to travel faster than the speed of light. The advanced computer simulations we have run at the Time Travel Research Center have confirmed this model as a valid approach for actual time travel to the past.
Introduction
The rotating cylinder model is based on a conclusion of general relativity that shows rotation of matter causes a distortion in space-time. This distortion can become powerful enough to actually twist time around a rotating cylinder.
With the right amount of mass and speed, a pattern of what are referred to as "closed time-like curves" can be created.
Navigating through this pattern of closed time-like curves will permit time travel to both the future and the past without violating the laws of mathematics and physics.
To understand time control using rotating cylinders requires some understanding of general relativity. An overview of the "General Theory of Relativity" has been included as a separate article in this issue of The Space-Time Journal. It also requires a basic understanding of space-time physics, including the ideas of space-time diagrams, light-cones and closed time-like curves. Following is a brief review of these topics.
Space-Time Diagrams
A common tool we use to discuss space-time is the space-time diagram. This diagram plots the position of a particle as it moves through space-time. By connecting all the plotted positions, a line called the "world line" of the particle is created.
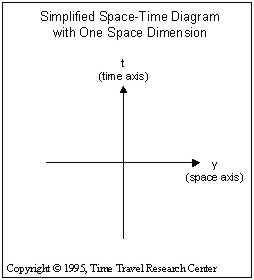
In reality, a true space-time diagram would have four dimensions including three space dimensions and one time dimension. This type of diagram is very difficult to illustrate and visualize. Wherever possible we use a simpler convention to illustrate concepts in space-time.
The illustration to the right shows a simplified space-time diagram with just one space axis (y) representing motion through one space dimension, and one time axis (t) representing motion through time.
Lets look at the example of a particle starting at rest on the origin of the y and t axes. If the particle does not move over time in the space dimension (y) it will not move off the time axis (t).
So for a particle at rest in some observers? frame of reference, its space-time diagram for that observer is a vertical world line. This is illustrated in the space-time diagram to the right showing a particle at rest.
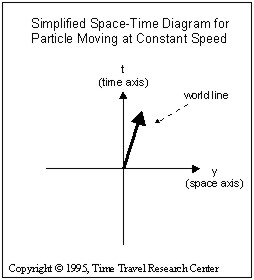
The path the particle follows, whether it moves in the space dimension (y), time dimension (t), or both represents what we call its world line. The world line represents the path the particle follows in space-time as a whole.
If the particle moves in the space dimension (y), its world line tilts away from the vertical as is illustrated in the space-time diagram of a particle moving at constant speed shown to the left. Straight (un-curved) world lines like this represent un-accelerated particles (i.e.) particles experiencing no forces.
If a particle experiences acceleration, its world line will curve away from the vertical time axis. If the same particle experiences decceleration, its world line will curve back towards the vertical time axis.
The resulting world line will be curved as is illustrated in the space-time diagram of an accelerating/deccelerating particle on the left.
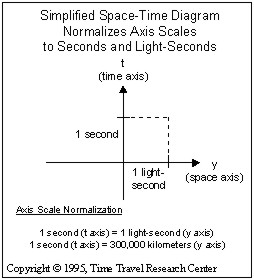
In order to make a space-diagram more meaningful in has become common practice to normalize the axis to a specific standard.
Each unit on the time axis (t) is set to a second and each unit on the space axis (y) is set to one light-second. A light-second is the distance that light can travel in one second, which is 300,000 kilometers. This normalization of axes is illustrated to the left.
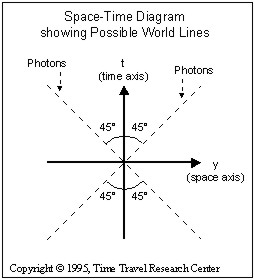
Since photons travel at the speed of light, this means that the world line of a photon is tilted away from the vertical time axis by and angle of 45 degrees, or 300,000 km/sec.
If we accept a speed limit of the speed of light as is general believed, the area between the world lines of the photons represents the area where all possible world lines must be contained. The illustration to the left shows that the paths of all possible world lines will never tilt more than 45 degrees away from the vertical.
Light Cones:
As we recall, a true space-time diagram would have the time dimension plus three space dimensions. But again, this can be extremely difficult to both draw and visualize. But by adding another dimension, our 45? area around the time axis wraps around the time axis and also upward and downward becoming a three dimensional "light cone." This light cone with two space dimensions is illustrated below.
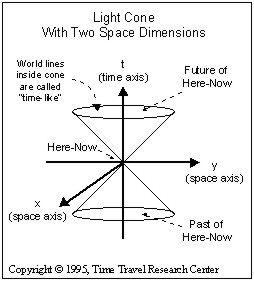
Lets call the point in space-time located at the origin of all three axes (x=0, y=0, and t=0) the Here-Now. Then all points in the upward region are located in the future of Here-Now. Also, all points in the downward region are located in the past of Here-Now.
From Here-Now a particle can travel to any other point in the future light cone by traveling at a speed less than the speed of light.
Also, any particle inside the past light cone can travel to Here-Now by traveling at less than the speed of light.
In this diagram the present is represented by the point where the two cones meet in the middle (i.e. here-now). Since we generally assume that we are restricted to at most the speed of light, the cone above here-now represents the only possible "future" states of the event, while the bottom cone represents restrictions on possible pasts of here-now.
Space-Time Intervals
The distance between any two space-time points on a world line on this space-time diagram is defined as:
The future cone represents those areas where "ds" is positive and "t" is also positive. The past cone includes space-time points with "ds" positive and with "t" negative.
Those volumes outside the two cones represent what is sometimes called "Elsewhere," since they are events for which the metric "ds" is imaginary. For one event to influence another event, it is necessary that the event that is to provide the influence lie in the past cone of the event being influenced.
We typically refer to three different types of space-time intervals. These are commonly called time-like, space-like and light-like.
On our space-time diagrams a time-like displacement is one with an angle to the time axis of less than 45?. A time-like displacement represents an object traveling at a speed of less than the speed of light. Time-like intervals have positive ds values.
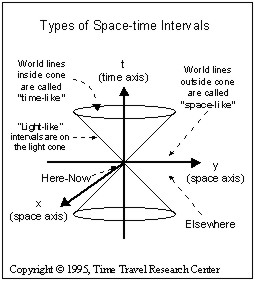
A light-like interval is one that makes an angle of 45? to the time axis. Light of course travels on light-like intervals.
The third possibility is a space-like interval, which represents a line that makes an angle of more than 45? to the time axis. Space-like intervals have negative ds values. Events joined by a space-like interval can never influence each other, since that would imply a flow of information at speeds faster than the speed of light.
Its very important to note that every point in space-time has its own, and potentially differently-oriented light cone.

Space-time diagrams can also be used to represent world lines that travel into the past instead of the future. As shown in the illustration to the right a world line can loop back on itself. In this example the world line curves back and comes close to itself. On a world line it is important to remember that the direction of the world line is in the direction of the local future of the particle. Events happen in a sequence and direction of the world line. If the particle is a living person then memories would also be formed in the direction of the world line.
A subtle implication of this "loop back" is that it is only possible by both moving through space and also exceeding the speed of light. As soon as the loop bends more than 45 degrees away from the time axis the particle must be traveling at a faster than light speed.
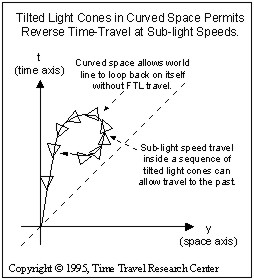
Closed Time-like Curves
So how can reverse time travel be possible at sub-light speed? By understanding and using curved space-time. There are two important points here that we will use later to show how reverse time travel is indeed possible at sub-light speed.
First, general relativity shows that space-time can be curved by heavy gravity. Second, every point in space-time has its own light cone. In a curved space-time it is possible to "tilt" or "tip over" light cones. With a sufficient amount of space-time curvature a particle or person could continue to move into their own local future at sub-light speed but actually travel along a world line that loops back on itself as shown in the illustration. This loop back is commonly referred to as a closed time-like curve, a concept introduced by Kurt Godel in 1949.
This world line could carry the particle or person backwards into time without violating the laws of mathematics and physics? and without having to travel faster than light!
Lets now take detailed look at a rotating cylinder model that could create a curved space-time like this, permitting time travel to the future, the past, and back again.
The Rotating Cylinder
In 1974 Frank Tipler published what appeared to be the construction details for a time machine. His paper even concluded with the quote, "In short, general relativity suggests that if we construct a sufficiently large rotating cylinder, we create a time machine."
Tipler was continuing to build upon the study of rotating cylinders and the relation of general relativity that actually been around for decades. References can even be found for literature on rotating infinite cylinders dating back to 1932.
However, Tipler was the first to publish his work in a respectable scientific journal and show a solution free of singularities and other problems associated with black hole models. Tipler was also the only scientist at the time to show a solution that violated causality.
What does this rotating cylinder look like? Let?s take a look.
The one result from general relativity that we will be using is that the rotation of matter causes a distortion in space-time that results in the tipping over of light cones. The rotating, infinite cylinder is a method that can be used to artificially produce the tipped-over light cone effect creating closed time-like curves.
The best way to picture a rotating cylinder would be to take a piece of material ten times the mass of the Sun and compress it into a long, thin, super-dense cylinder. Then spin the cylinder up to a few billion revolutions per minute. The cylinder must rotate with a surface speed of at least half the speed of light. This is necessary to create centrifugal forces that will balance the gravitational attraction of the super-dense material used to construct the cylinder to prevent collapse or explosion.
By moving around the surface in a carefully plotted spiral course one could travel through time into the past. One could also make the return trip back to the original time of departure. The integrity of this model holds on paper and it does not violate the laws of mathematics and physics.
How does it work
General relativity shows how rapid rotation can actually twist space-time creating and allowing movement through closed time-like curves into the past. This is again accomplished at sub-light speed travelling through a series of tipped light cones in curved space. One method to artificially produce closed time-like curves is to use a rotating, super-dense cylinder.
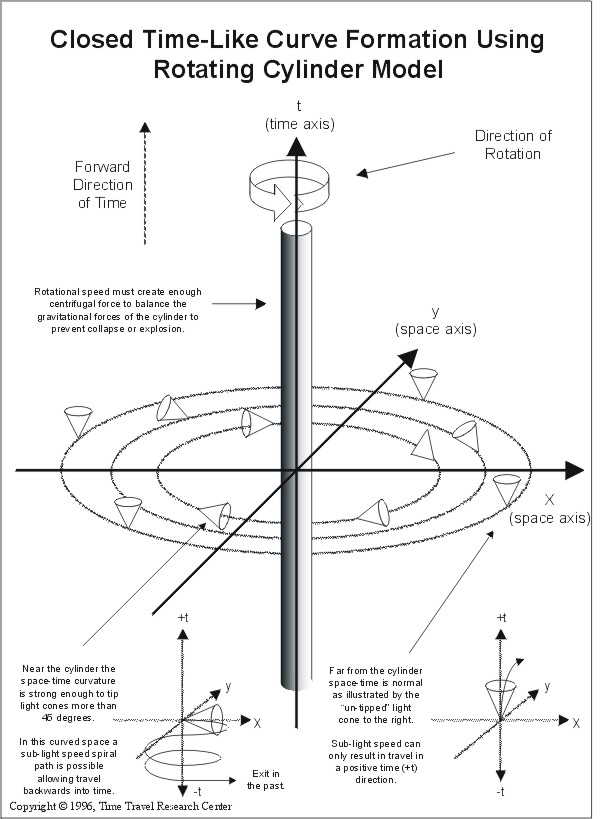
We will use the diagram titled "Closed Time-like Curve Formation using a Rotating Cylinder Model" to illustrate how this works.
The rotating cylinder will spin along the vertical time axis shown in the illustration. The gravitational effects on space-time curvature are weaker distant from the cylinder but grow stronger the nearer one approaches the cylinder.
At a distance from the cylinder the resulting curvature of space-time is small and the light cones are upright pointing almost directly in the positive time (+t) direction. This is the typical orientation for any point a normal or flat space-time.
The closer one approaches the rotating cylinder the stronger the space-time curvature which can be illustrated by the tipped over light cones. The effect of the rotating cylinder is to curve space-time, which can be illustrated by the light cones that tip further in the direction of rotation as we come closer to the cylinder.
The light cones closest to the cylinder are tipped more than 45 degrees. This is far enough that part of the inside of their cone actually is tipped through the x,y plane and into the negative time (-t) direction. With part of our future light cone now tipped into the past we now are in a region where the roles of space and time interchange and time itself is twisted around the cylinder.
Backwards in Time at Sub-light Speeds.
To travel back in time the time traveler would approach the cylinder and carefully navigate into a region of high space-time curvature. Following a helical path around the cylinder the time traveler would spiral down into the negative time (-t) direction. Notice that the time traveler's motion only needs to be a sub-light speed and stays completely within the local future of his light cone.
By navigating a course that always moving into his local future the time traveller can follow a path at sub-light speeds that will carry him backwards into time where he can steer away from the cylinder and then exit in his own distant past.
Time travel to the future, time travel to the past? even travel to the past and return to the future. This is all possible within the laws of mathematics and physics. Within general relativity are secrets that will allow us to unlock the possibilities of interstellar travel and time travel.
Look for part two of the three-part article in the next issue (Volume 21, Winter 2000) of the Space-Time Journal. In part two we will:
- Explore how to navigate the Cylinder for forward and reverse time travel.
- Examine some detailed mathematical models of the rotating cylinder Model
- Study some other interesting implications and uses of the rotating cylinder.
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa / index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru