Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
Time dilation
Time dilation is the phenomenon whereby an observer finds that another's clock which is physically identical to their own is ticking at a slower rate as measured by their own clock. This is often taken to mean that time has "slowed down" for the other clock, but that is only true in the context of the observer's frame of reference. Locally, time is always passing at the same rate. The time dilation phenomenon applies to any process that manifests change over time.
-In Albert Einstein's theories of relativity time dilation is
manifested in two circumstances:
In special relativity, clocks that are moving with respect to an inertial
system of observation (the putatively stationary observer) are found to be
running slower. This effect is described precisely by the Lorentz
transformations.
-In general relativity, clocks at lower
potentials in a gravitational field-- such as in close proximity to a
planet --are found to be running slower. This
gravitational time dilation is only briefly mentioned in this
article but is described elsewhere (see also
gravitational red shift).
In special relativity, the time dilation effect is reciprocal: as observed from the point of view of any two clocks which are in motion with respect to each other, it will be the other party's clocks that is time dilated. (This presumes that the relative motion of both parties is uniform; that is, they do not accelerate with respect to one another during the course of the observations.)
In contrast, gravitational time dilation (as treated in General Relativity) is not reciprocal: an observer at the top of a tower will observe that clocks at ground level tick slower, and observers on the ground will agree. Thus gravitational time dilation is agreed upon by all stationary observers, independent of their altitude.
- length contraction and time dilation
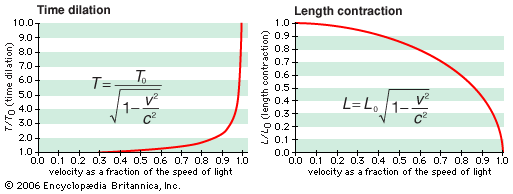
Length contraction and time dilation
As an object approaches the speed of light, an observer sees the object become shorter and its time interval become longer, relative to the length and time interval when the object is at rest.
Images from other articles related to the topic speed of light
- invariance of the speed of light
- Fizeaus method for measuring the speed of
light
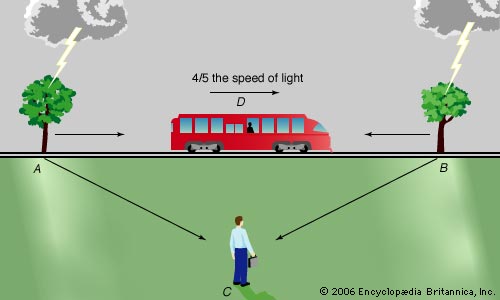
Invariance of the speed of light Arrows shot from a moving train (A) and from a stationary location
(B) will arrive at a target at different velocitiesin this case, 300
and 200 km/hr, respectively, because of the motion of the train. However,
such commonsense addition of velocities does not apply to light. Even
for a train traveling at the speed of light, both laser beams, A and B,
have the same velocity: c.
Simultaneous events
Simultaneous events may appear to coincide in time for one observer but not for another because of differences in their spatial positions.
Encyclopædia Britannica, Inc.
Related Articles:
relativity : Relativistic space and time (Encyclopædia Britannica)
In order to make the speed of light constant, Einstein replaced
absolute space and time with new definitions that depend on the state
of motion of an observer. Einstein explained his approach by
considering two observers and a train. One observer stands alongside a
straight track; the other rides a ...
Overview
The formula for determining time dilation in special relativity is:
-
-
-
- where
- Δ t is a time interval measured by an observer in a stationary frame of reference,
- Δ t0 is that same time interval as measured by an observer in the moving frame,
-
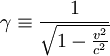 is
the Lorentz factor,
is
the Lorentz factor,
- v is the relative speed between the clock and the stationary system, and
- c is the speed of light.
-
Thus the duration of the clock cycle of a moving clock appears to be increased: it is "running slow." As indicated, the Lorentz transforms can be used for more general cases.
As shown, the effect increases in an exponential manner with respect to relative speed or gravitational differences. The range of such variances in ordinary life, even considering space travel, are not great enough to produce easily detectable time dilation effects, and such vanishingly small effects can be safely ignored. It is only when an object approaches speeds on the order of 30,000 km/s (1/10 of the speed of light), or lies deep within the gravitational "well" of massive stellar objects, that it becomes important.
Time dilation by the Lorentz factor was predicted by Joseph Larmor (1897), at least for electrons orbiting a nucleus. Thus
"... individual electrons describe corresponding parts of their orbits in
times shorter for the [rest] system in the ratio :![]() "
(Larmor 1897). Time dilation of magnitude corresponding to this (Lorentz)
factor has been experimentally confirmed, as described below.
"
(Larmor 1897). Time dilation of magnitude corresponding to this (Lorentz)
factor has been experimentally confirmed, as described below.
Experimental confirmation
Time dilation has been tested a number of times. The routine work carried on in particle accelerators since the 1950s, such as those at CERN, is a continuously running test of the time dilation of special relativity. The specific experiments include:
Velocity time dilation tests
- Ives and Stilwell (1938, 1941), An experimental study of the rate of a moving clock, in two parts. These experiments measured the Doppler shift of the radiation emitted from cathode rays, when viewed from directly in front and from directly behind. The high and low frequencies detected were not the classical values predicted.
-
-
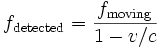 and
and
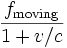 =
=
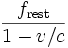 and
and
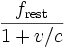
-
- i.e. for sources with invariant frequencies
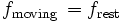 The high
and low frequencies of the radiation from the moving sources were
measured as
The high
and low frequencies of the radiation from the moving sources were
measured as
-
 and
and
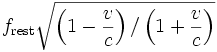
-
- as deduced by Einstein (1905) from the Lorentz transformation, when
the source is running slow by the Lorentz factor. Thus, the experiment
shows that the frequency of the moving sources is reduced and given by
-
- Rossi and Hall (1941) compared the population of cosmic-ray produced muons at the top of a mountain to that observed at sea level. Although the travel time for the muons from the top of the mountain to the base is several muon half-lives, the muon sample at the base was only moderately reduced. This is explained by the time dilation attributed to their high speed relative to the experimenters. That is to say, the muons are decaying about 10 times slower than they would in a rest frame (that is, for "stationary observers").
- Hasselkamp, Mondry, and Scharmann (1979) measured the Doppler shift from a source moving at right angles to the line of sight (the transverse Doppler shift). For an invariant source frequency, there is no classical transverse Doppler shift, so, unlike the Ives-Stillwell experiment, the lower frequency of the moving source can be attributed to the time dilation effect alone. This is a striking illustration of the fact that the time-slowdown is observed to be affecting the object as an object, not merely the particular ancillary effects used in instrumental measurement procedures.
Gravitational time dilation tests
- Pound, Rebka in 1959 measured the very slight gravitational red shift in the frequency of light emitted at a lower height, where Earth's gravitational field is relatively more intense. The results were within 10% of the predictions of general relativity. Later Pound and Snider (in 1964) derived an even closer result of 1%. This effect is as predicted by gravitational time dilation.
Velocity and gravitational time dilation combined-effect tests
- Hefele and Keating, in 1971, flew cesium atomic clocks east and west around the Earth in commercial airliners, to compare the elapsed time against that of a clock that remained at the US Naval Observatory. Two opposite effects came in to play. The clocks were expected to age quicker (show a larger elapsed time) than the reference clock, since they were in a higher (weaker) gravitational potential for most of the trip (c.f. Pound, Rebka). But also, contrastingly, the moving clocks were expected to age more slowly because of the speed of their travel. The gravitational effect was the larger, and the clocks suffered a net gain in elapsed time. To within experimental error, the net gain was consistent with the difference between the predicted gravitational gain and the predicted velocity time loss. In 2005, the National Physical Laboratory in the United Kingdom, report their limited replication of this experiment. The NPL experiment differed from the original in that the cesium clocks were sent on a shorter trip (London-Washingon D. C. return), but the clocks were more accurate. The reported results are within 4% of the predictions of relativity.
- The Global Positioning System can be considered a continuously operating experiment in both special and general relativity. The in-orbit clocks are corrected for both special and general relativistic time-dilation effects so they run at the same (average) rate as clocks at the surface of the Earth. In addition, but not directly time-dilation related, general relativistic correction terms are built into the model of motion that the satellites broadcast to receivers -- uncorrected, these effects would result in an approximately 7-metre oscillation in the pseudo-ranges measured by a receiver over a cycle of 12 hours.
Time dilation and space flight
Time dilation would make it possible for passengers in a fast moving vehicle to travel into the further future while aging very little, in that their great speed retards the rate of passage of onboard time. That is, the ship's clock (and according to relativity, any human travelling with it) shows less elapsed time than stationary clocks. For sufficiently high speeds the effect is dramatic. For example, one year of travel might correspond to ten years at home. Indeed, a constant 1 g acceleration would permit humans to circumnavigate the known universe (with a radius of some 13.7 billion light years) in one human lifetime. The space-travellers could return to earth billions of years in the future (provided the Universe hadn't collapsed and our solar system was still around, of course). A scenario based on this idea was presented in the novel Planet of the Apes by Pierre Boulle.
A more likely use of this effect would be to enable humans to travel to nearby stars without spending their entire lives aboard the ship. However, any such application of time dilation would require the use of some new, advanced method of propulsion. A further problem with relativistic travel is that at such velocities dispersed particles in the rarefied interstellar medium would turn into a stream of high-energy cosmic rays that would destroy the ship unless extraordinary radiation protection measures were taken.
Current space flight technology has fundamental theoretical limits based on the practical problem that, per other aspects of Einsteinian relativity affecting mass, an increasing amount of energy is required for propulsion as a craft approaches the speed of light. The likelihood of collision with small space debris and other particulate material is another practical limitation. At the velocities presently attained, however, time dilation is not a factor in space travel.
Time dilation at constant acceleration
In Special Relativity, time dilation is most simply described in circumstances where relative velocity is unchanging. Nevertheless, the Lorentz equations allow one to calculate proper time and movement in space for the simple case of a spaceship whose acceleration, relative to some referent object in uniform (ie, unaccelerating) motion, equals G throughout the period of measurement.
Let t be the time in an inertial frame subsequently called the rest frame. Let x be a spatial coordinate, and let the direction of the constant acceleration as well as the spaceship's velocity (relative to the rest frame) be parallel to the x-axis. Assuming the spaceship's position at time t = 0 being x = 0 and the velocity being v0, the following formulas hold:
Position:
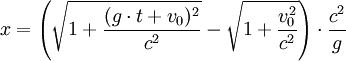
Velocity:
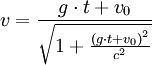
Proper time:
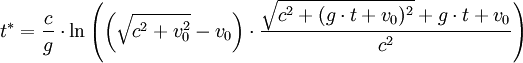
Time in the rest frame as a function of x:
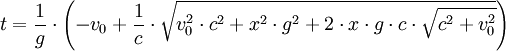
Simple inference of time dilation
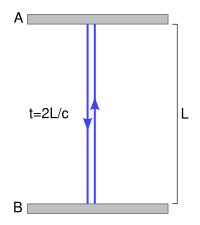
Observer at rest sees time 2L/c
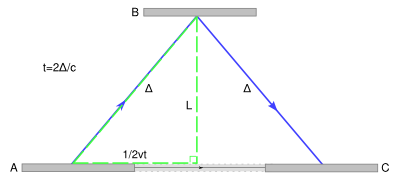
Observer moving right, sees longer path, time > 2L/c, same speed c
Time dilation can be inferred from the constancy of the speed of light in all reference frames as follows:
Consider a simple clock consisting of two mirrors A and B, between which a photon is bouncing. The separation of the mirrors is L, and the clock ticks once each time it hits a given mirror.
In the frame where the clock is at rest (diagram at right), the photon traces out a path of length 2L and the period of the clock is 2L divided by the speed of light.
From the frame of reference of a moving observer (diagram at lower right), the photon traces out a longer, angled, path. The second postulate of special relativity states that the speed of light is constant in all frames, which implies a lengthening of the period of this clock from the moving observer's perspective. That is to say, in a frame moving relative to the clock, the clock appears to be running slower. Straightforward application of the Pythagorean theorem leads to the well-known prediction of special relativity.
![]()
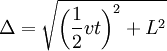
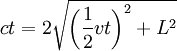
c2t2 = v2t2 + 4L2
![]()
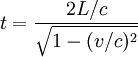
Time dilation is symmetric between two inertial observers
One assumes, naturally enough, that if time-passage has slowed for a moving object, the moving object would find the external world to be correspondingly "sped up." But counterintuitively, Einsteinian relativity predicts the opposite, a situation difficult to visualize. This is based on an essential principle of the overall theory: if one object is moving with respect to another (at an unchanging velocity), the other is equally moving with respect to it.
We're accustomed to this notion of relativity with respect to distance: the distance from Los Angeles to New York is, and must be, the same as the distance from New York to Los Angeles. But when we consider speeds, we think of an object as "really" moving, overlooking that its motion is always relative to something else--to oneself, the ground, the stars, etc. A camera "panning" along with a moving object against a blank background would reveal no motion.
The Einsteinian takes seriously the thesis that all motion is indeed relative to some actual (if specified only by implication) "benchmark" that is regarded as stationary, setting aside any issue as to whether what is treated as stationary "really is". You regard it as stationary, and are justified in so treating it, if you yourself are maintaining a fixed distance from it. And this is true even if, for someone else, both you and the benchmark are moving along side-by-side.
But if motion is thus understood as purely relative, it can be divided-up between "mover" and "benchmark" in any way one pleases, even allowing them to completely switch roles. All that matters is the rate at which they are approaching, or departing from, one another, a grand total which re-distributing the speed-contribution of each one doesn't change. And if that is true, the consequences of relative motion predicted by the theory must also "add up" to an unchanging total effect. If A finds that B has undergone a slowdown-in-time during the period of relative motion, it must work out that B will also find that A has a relatively slower "clock." It seems an inconceivable situation: yet the math works out, and actual tests confirm it.
With respect to constant relative motion between two "clocks", a
measurement of relative time must choose one clock as being "stationary"
in spacetime, and that clock is the basis of a temporal coordinate system
where time throughout is treated as synchronized with the stationary clock.
The other "moving" clock is in motion with respect to this treated-as-stationary
coordinated system, and its relative motion is the velocity value used in
the applicable equations.
In the Special Theory of Relativity, the moving clock is found to be
ticking slow with respect to the temporal coordinate system of the
stationary clock. And as indicated, this effect is symmetrical: In a
coordinate system synchronized, by contrast, with the "moving" clock, it
is the "stationary" clocks that is found (by all methods of measurement)
to be running slow. (Neglecting this principle of symmetry leads to the so-called
twin paradox being regarded as paradoxical.)
Note that in all such attempts to establish "synchronization" within the
reference system, the question of whether something happening at one
location is in fact happening simultaneously with something happening
elsewhere, is of key importance. Calculations are ultimately based on
determining what is simultaneous with what.
It is a natural and legitimate question to ask how, in detail, Special
Relativity can be self-consistent if clock A is time-dilated with respect
to clock B and clock B is also time-dilated with respect to clock A. It is
by challenging the assumptions we build into the common notion of
simultaneity that logical consistency can be restored.
Within the framework of the theory and its terminology, the short
answer is that there is a relativity of simultaneity that affects how the
specified "benchmark" moments of "simultaneous" events are aligned with
respect to each other by observers who are in motion with respect to one
other. Because the pairs of putatively simultaneous moments are
differently identified by the different observers (as illustrated in the
twin paradox article), each can treat the other clock as being the slow
one without Relativity being self-contradictory. For those seeking a more
explicit account, this can be explained in many ways, some of which follow.
Temporal coordinate systems and clock synchronization
In Relativity, temporal coordinate systems are set up using a procedure for synchronizing clocks, discussed by Poincaré (1900) in relation to Lorentz's local time (see relativity of simultaneity). It is now usually called the Einstein synchronization procedure, since it appeared in his 1905 paper.
An observer with a clock sends a light signal out at time t1 according to his clock. At a distant event, that light signal is reflected back to, and arrives back to the observer at time t2 according to his clock. Since the light travels the same path at the same rate going both out and back for the observer in this scenario, the coordinate time of the event of the photon being reflected for the observer tE is tE = (t1 + t2) / 2. In this way, a single observer's clock can be used to define temporal coordinates which are good anywhere in the universe.
Symmetric time dilation occurs with respect to temporal coordinate systems set up in this manner. It is an effect where another clock is being viewed as running slow by an observer. Observers in rest in their coordinate system do not consider their own clock time to be time-dilated, but may find that it is understood to be time-dilated in another coordinate system.
The spacetime geometry of velocity time dilation
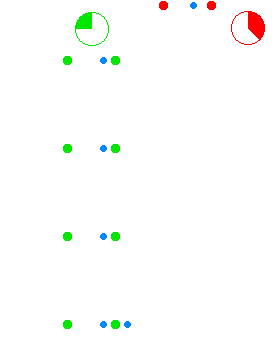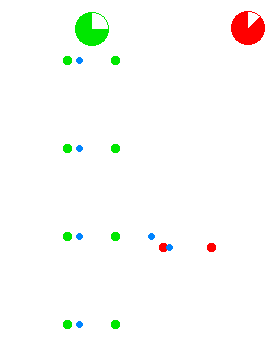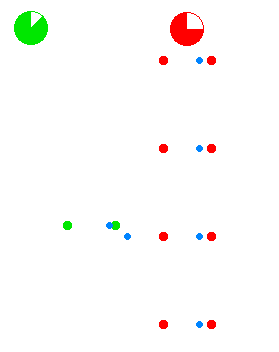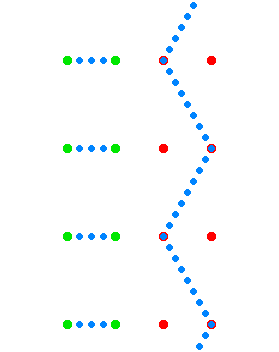
The green dots and red dots in the animation represent spaceships. The ships of the green fleet have no velocity relative to each other, so for the clocks onboard the individual ships the same amount of time elapses relative to each other, and they can set up a procedure to maintain a synchronized standard fleet time. The ships of the "red fleet" are moving with a velocity of 0.866 of the speed of light with respect to the green fleet.
The blue dots represent pulses of light. One cycle of light-pulses between two green ships takes two seconds of "green time", one second for each leg.
As seen from the perspective of the reds, the transit time of the light
pulses they exchange among each other is one second of "red time" for each
leg. As seen from the perspective of the greens, the red ships' cycle of
exchanging light pulses travels a diagonal path that is two light-seconds
long. (As seen from the green perspective the reds travel 1.73 (![]() )
light-seconds of distance for every two seconds of green time.)
)
light-seconds of distance for every two seconds of green time.)
One of the red ships emits a light pulse towards the greens every second of red time. These pulses are received by ships of the green fleet with two-second intervals as measured in green time. Not shown in the animation is that all aspects of physics are proportionally involved. The lightpulses that are emitted by the reds at a particular frequency as measured in red time are received at a lower frequency as measured by the detectors of the green fleet that measure against green time, and vice versa.
The animation cycles between the green perspective and the red perspective, to emphasize the symmetry. As there is no such thing as absolute motion in relativity (as is also the case for Newtonian mechanics), both the green and the red fleet are entitled to consider themselves as "non-moving" in their own frame of reference.
Again, it is vital to understand that the results of these interactions and calculations reflect the real state of the ships as it emerges from their situation of relative motion. It is not a mere quirk of the method of measurement or communication.
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru