
 Stellen
wir uns die Raumzeit nochmals als ein gespanntes Tuch vor. Ist keine
Materie zugegen, ist es flach und glatt. Legt man aber einen Gegenstand
darauf, so wird das Tuch je nach Gewicht des Gegenstandes mehr oder
weniger stark ausgebeult - es wird gekrümmt. Ein Schwarzes Loch
beeinflusst die Raumzeit so stark, dass die Krümmung in dessen Zentrum
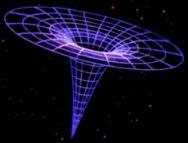
unendliche Werte annimmt. Im nebenstehenden Diagramm sind der Horizont und
die Singularität angedeutet, letztere befindet sich am untersten Punkt. In
Wirklichkeit kann man das Geschehen nicht zeichnerisch darstellen, weil
der Trichter unendlich lang und dünn werden müsste.
Stellen
wir uns die Raumzeit nochmals als ein gespanntes Tuch vor. Ist keine
Materie zugegen, ist es flach und glatt. Legt man aber einen Gegenstand
darauf, so wird das Tuch je nach Gewicht des Gegenstandes mehr oder
weniger stark ausgebeult - es wird gekrümmt. Ein Schwarzes Loch
beeinflusst die Raumzeit so stark, dass die Krümmung in dessen Zentrum
unendliche Werte annimmt. Im nebenstehenden Diagramm sind der Horizont und
die Singularität angedeutet, letztere befindet sich am untersten Punkt. In
Wirklichkeit kann man das Geschehen nicht zeichnerisch darstellen, weil
der Trichter unendlich lang und dünn werden müsste.
Wir wissen jetzt, was beim Kollaps eines Sterns zum Schwarzen Loch geschieht und was Beobachter an verschiedenen Orten ("Bezugssystemen") sehen würden. Aber bemühen wir doch noch einmal unseren armen Astronauten und lassen ihn eine Reise in das "fertige" Schwarze Loch unternehmen! Dazu muss er ungewöhnliche, übermenschliche Eigenschaften aufweisen, die es in der Realität natürlich nicht gibt. Doch er ist ja schon recht gut abgehärtet...
Der Schwarzschildradius stellt also eine Grenze dar, mit der sich das Schwarze Loch vom Rest des Universums abschneidet. Unterhalb dieser Grenze kann kein Signal das Loch verlassen, ein außenstehender Beobachter kann deshalb kein Ereignis mehr erkennen. Und auch die Zeit bleibt unterhalb des Ereignishorizontes einfach stehen.
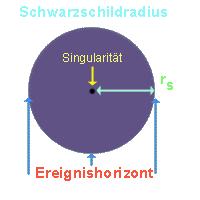 Nebenstehend
ist nochmals ein Schwarzes Loch skizziert um zu verdeutlichen, dass der
Ereignishorizont bzw. Schwarzschildradius seine Ausdehnung bestimmt. Diese
Größe ist ausschließlich von der Masse der Singularität im Zentrum
abhängig. Alles was sich innerhalb dieser Grenzen abspielt, bleibt uns für
immer verborgen.
Nebenstehend
ist nochmals ein Schwarzes Loch skizziert um zu verdeutlichen, dass der
Ereignishorizont bzw. Schwarzschildradius seine Ausdehnung bestimmt. Diese
Größe ist ausschließlich von der Masse der Singularität im Zentrum
abhängig. Alles was sich innerhalb dieser Grenzen abspielt, bleibt uns für
immer verborgen.
Wie oben gezeigt, ist die Krümmung der Raumzeit
bereits in der Umgebung des Ereignishorizonts recht groß. Der Astronaut
beginnt also seinen Abstieg zum Loch, indem er es vorsichtig umkreist. Er
beginnt mit einer Umlaufbahn von z.B. 100 000 km Länge. Bereits jetzt
spürt er deutlich, dass seine Füße stärker angezogen werden als sein Kopf,
doch diese mörderischen Kräfte, die ihn am Ende zerreißen werden, ist er
ja bereits gewohnt.
Während er jetzt weiter sinkt, beobachtet er, wie unter ihm das Schwarze
Loch immer mehr an Größe zunimmt. Seltsamerweise nimmt nun der sichtbare
Himmelsausschnitt im selben Maße ab, wie das dunkle Loch unter dem
Astronauten anwächst. Das geht sogar so weit, dass sich das Schwarze Loch
scheinbar auch seitlich um den Astronauten schließt, obwohl er noch weit
vom Horizont entfernt ist. Wie ist das möglich?
Der Astronaut sieht den Himmel in einem immer
kleiner werdenden Durchmesser, je tiefer er zum Loch absinkt. Durch die
ungeheure Gravitation in der Nähe des Horizonts werden die Lichtstrahlen
immer mehr abgelenkt. Selbst das Licht von Sternen, die sich querab in
horizontaler Position (90° vom Zenit) befinden, sieht der Astronaut nun
direkt von vorn kommen. Anders ausgedrückt: Die Lichtstrahlen werden
gezwungen, den immer stärkeren Krümmungen der Raumzeit zu folgen!
 Hier
eine Skizze, in die wir verschiedene Abstände von der Singularität
eingezeichnet haben. Der Ereignishorizont befindet sich im Abstand von
einem Schwarzschildradius, also 1 rS. Im Abstand von 1,5 rS
finden wir eine Bahn, auf der ein unter günstigstem Winkel eingebrachtes
Photon sich gerade noch aufhalten kann. Man nennt diese Bahn daher auch
Photonensphäre. Das Photon würde hier unendlich lang das Loch
umkreisen. Bei geringster Unterschreitung dieses Abstandes wäre sein
Absturz ins Loch allerdings besiegelt. Für den Astronauten gilt etwas
anderes: will er das Loch nur umkreisen und sich eine Chance zur Rückkehr
offen halten, so darf er sich in einer Distanz von höchstens 3 rS
aufhalten, ansonsten ist er für immer verloren!
Hier
eine Skizze, in die wir verschiedene Abstände von der Singularität
eingezeichnet haben. Der Ereignishorizont befindet sich im Abstand von
einem Schwarzschildradius, also 1 rS. Im Abstand von 1,5 rS
finden wir eine Bahn, auf der ein unter günstigstem Winkel eingebrachtes
Photon sich gerade noch aufhalten kann. Man nennt diese Bahn daher auch
Photonensphäre. Das Photon würde hier unendlich lang das Loch
umkreisen. Bei geringster Unterschreitung dieses Abstandes wäre sein
Absturz ins Loch allerdings besiegelt. Für den Astronauten gilt etwas
anderes: will er das Loch nur umkreisen und sich eine Chance zur Rückkehr
offen halten, so darf er sich in einer Distanz von höchstens 3 rS
aufhalten, ansonsten ist er für immer verloren!

Nun können wir ein plastisches "Bild" eines
Schwarzen Lochs zeichnen. Dass die Singularität eigentlich nicht
dargestellt werden kann ist uns klar: Sie ist (fast) unendlich klein. Der
Schwarzschildhorizont ist die absolute Grenze zwischen dem uns bekannten
Weltraum und einem "irgendwas dahinter". Es ist ein "point of no return",
wer ihn überschreitet, kann nie mehr zurück. Umschlossen wird das Loch im
Abstand von 1,5 Schwarzschildradien von einer weiteren Grenze, der schon
genannten Photonensphäre. Sobald diese Distanz minimal unterschritten wird,
gibt es auch für das Licht kein Entrinnen mehr.
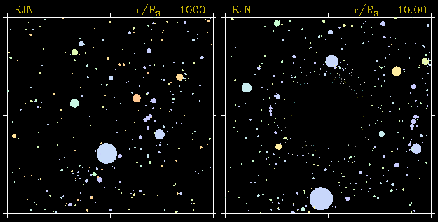 In
dieser Computersimulation ist ein künstlicher Himmelsauschnitt dargestellt,
wie der Astronaut das Schwarze Loch bei seiner Annäherung erblicken würde.
Im linken Bild erkennt man die drei Gürtelsterne des Sternbilds Orion. In
die rechte Bildhälfte wurde ein Schwarzes Loch "eingerechnet". Das Loch
selbst ist natürlich nicht sichtbar, man sieht aber deutlich die
Verzerrungen, die von seinem Gravitationsfeld hervorgerufen werden. Es
wirkt aus dieser Distanz bereits als Gravitationslinse und erzeugt
Doppelbilder der hinter ihm liegenden Sterne. Würde man sich dem Loch noch
weiter nähern, so könnte man aus einem Blickwinkel das gesamte Weltall
überschauen.
In
dieser Computersimulation ist ein künstlicher Himmelsauschnitt dargestellt,
wie der Astronaut das Schwarze Loch bei seiner Annäherung erblicken würde.
Im linken Bild erkennt man die drei Gürtelsterne des Sternbilds Orion. In
die rechte Bildhälfte wurde ein Schwarzes Loch "eingerechnet". Das Loch
selbst ist natürlich nicht sichtbar, man sieht aber deutlich die
Verzerrungen, die von seinem Gravitationsfeld hervorgerufen werden. Es
wirkt aus dieser Distanz bereits als Gravitationslinse und erzeugt
Doppelbilder der hinter ihm liegenden Sterne. Würde man sich dem Loch noch
weiter nähern, so könnte man aus einem Blickwinkel das gesamte Weltall
überschauen.
Mit freundlicher Genehmigung von Robert Nemiroff (MTU)
Unser armer Astronaut ist dem Ereignishorizont
nun schon ziemlich nah gekommen. Die Raumzeitkrümmungen wirken sich immer
stärker aus und das Licht des ganzen Universums wird in einen kleinen
hellen Abschnitt seines Sichtfelds gebündelt. Selbst das Licht der hinter
dem Beobachter liegenden Quellen kommt nun von vorn auf ihn zu (das wäre
nicht der Fall, könnte er anhalten). Je tiefer er sinkt, umso kleiner wird
die Sichtöffnung, dafür schließt sich immer mehr der schwarze
Ereignishorizont des Lochs um den Astronauten.
Raum und Zeit werden mit dem Licht und unserem Astronauten ins Schwarze Loch gezogen. Genau in dem Moment, als er den Ereignishorizont überquert, wirft er einen Blick in die Unendlichkeit! Die Beeinflussung der Zeit durch die Gravitation erfährt er nun in voller Pracht. Obwohl seine Uhr für ihn völlig "normal" weiterläuft, sieht er jetzt die Vorgänge im Universum wie in einem wahnsinnigen Zeitraffer ablaufen. Doch schon ist dieser Anblick vorüber, denn nun ist der tapfere Astronaut im Innern des Schwarzen Lochs.
 Jetzt wird es noch exotischer! Immer noch kann er
Licht aus unserem Universum sehen, vielleicht als verschwommenes Halo.
Wenn er genau hinsieht, kann er denselben Film wie zuvor anschauen, nur
läuft dieser jetzt rückwärts. Nach einer Weile kann er sogar sehen, wie er
aus dem Schwarzen Loch steigt und erlebt rückwärts noch einmal alle
Ereignisse bis zu seinem Start. Erst wenn unser Held in die Mitte des
Lochs gelangt, wird er nichts mehr von unserem Universum sehen, denn nun
gelangt er in die fürchterliche Singularität, in der die physikalischen
Gesetze ihre Gültigkeit verlieren.
Jetzt wird es noch exotischer! Immer noch kann er
Licht aus unserem Universum sehen, vielleicht als verschwommenes Halo.
Wenn er genau hinsieht, kann er denselben Film wie zuvor anschauen, nur
läuft dieser jetzt rückwärts. Nach einer Weile kann er sogar sehen, wie er
aus dem Schwarzen Loch steigt und erlebt rückwärts noch einmal alle
Ereignisse bis zu seinem Start. Erst wenn unser Held in die Mitte des
Lochs gelangt, wird er nichts mehr von unserem Universum sehen, denn nun
gelangt er in die fürchterliche Singularität, in der die physikalischen
Gesetze ihre Gültigkeit verlieren.
Eine solche Reise in ein Schwarzes Loch ist natürlich nur fiktiv. Wie wir noch sehen werden, sind die meisten Schwarzen Löcher von einer Scheibe glühend heißen Plasmas umgeben. Hinzu kommen Gezeitenkräfte, die jeden noch so stabilen Körper bis zur Unkenntlichkeit zerfetzen. Selbst bei superschweren Ausgaben dieser Objekte, bei denen die Gezeitenkräfte am Horizont noch erträglich wären, stürzt jede Materie ab dem Horizont unweigerlich mit Lichtgeschwindigkeit zur Singularität. Falls man überhaupt bis zum Horizont gelangen würde, denn die meisten Löcher rotieren, sehr schnell, und die mitrotierende umgebende Raumzeit zwingt allem diese Bewegung mit bis zur halben Lichtgeschwindigkeit auf...
Die Folgerungen der Allgemeinen Relativitätstheorie Einsteins lassen noch weitere, interessante Aspekte zu: es gibt Symmetrien der Zeit. Das bedeutet, dass Zeit vorwärts und rückwärts laufen könnte (siehe hierzu auch Hawkings Universum). Daraus lässt sich folgern, dass die Zeit, wenn sie am Ereignishorizont eines Schwarzen Loches bereits stehen bleibt, sich in der Singularität umkehrt und dann rückwärts laufen könnte. Wenn man diesen Gedanken weiter verfolgt, kommt man zum Schluss, dass es auch "umgekehrte" Schwarze Löcher geben könnte.
Ein Schwarzes Loch ist ein Objekt, aus dem nichts
mehr entweichen kann. So wäre es denkbar, dass irgendwo im Universum ein
Ort existiert, an dem die umgekehrte Version zu Tage tritt und in welche
nichts hineingeraten, nichts eindringen kann. Im Gegenteil: es müsste
Materie und Energie emittieren. Das könnte man als Weißes Loch
bezeichnen. Das größte Weiße Loch war sicherlich unser Kosmos zum
Zeitpunkt des Urknalls, ein winziger Ort, aus dem Energie nur so "sprudelte".
Manche Astrophysiker glauben, dass die Materie und die Energien, die ein
Schwarzes Loch aufsaugt, an einem ganz anderem Ort des Kosmos, vielleicht
sogar in einem anderen (Parallel-) Universum oder in einer unbekannten
Dimension wieder "ausgespuckt" werden.
Dies ist jedoch ein rein theoretisches, mathematisches Modell, ob Weiße
Löcher tatsächlich existieren, ist niemandem bekannt.
Das stört unseren Astronauten jetzt aber nicht. Er stürzt weiter zur Singularität. Wenn er in ihre Richtung sieht, erkennt er einen winzigen Lichtpunkt in der Mitte.
Dieses Licht in der Mitte kommt aus einem anderen
Universum. Umgeben ist es von tiefer Schwärze, doch sieht er immer noch
einen Halo, Licht aus unserem Universum. Je tiefer der Astronaut sinkt,
umso schmaler wird der dunkle Rand. Kurz bevor er endgültig in der
Singularität verschwindet, sieht er vor allem Licht und er kann erkennen,
was sich im anderen Universum abspielt. Nur - die Zeit dort verläuft der
unseren genau entgegengesetzt.
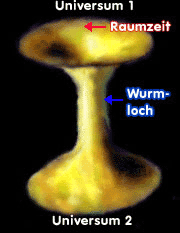 Schon
1935 erkannten Einstein und Nathan Rosen, dass die Allgemeine
Relativitätstheorie "Brücken" in der Raumzeit zulässt (Einstein-Rosen-Brücke).
Heute bezeichnen wir diese als
Wurmlöcher. Sie
stellen quasi einen Verbindungstunnel dar zwischen einem Schwarzen und
einem Weißen Loch, möglicherweise könnten Wurmlöcher sogar zwei Universen
miteinander verbinden. Durch diesen Tunnel könnte das Licht gelangen, das
unser Astronaut sah, kurz bevor er auf Nimmerwiedersehen in der
Singularität verschwand. Bitte planen Sie nun aber keine Reise durch ein
Wurmloch in ein anderes Universum! Solche Wurmlöcher schnüren sich in der
Mitte fast unendlich dünn ein, und bei der geringsten Störung reißt die
Brücke sofort ab. Zudem: Nicht einmal unser äußerst robuster Astronaut hat
den Sturz in die Singularität überlebt...
Schon
1935 erkannten Einstein und Nathan Rosen, dass die Allgemeine
Relativitätstheorie "Brücken" in der Raumzeit zulässt (Einstein-Rosen-Brücke).
Heute bezeichnen wir diese als
Wurmlöcher. Sie
stellen quasi einen Verbindungstunnel dar zwischen einem Schwarzen und
einem Weißen Loch, möglicherweise könnten Wurmlöcher sogar zwei Universen
miteinander verbinden. Durch diesen Tunnel könnte das Licht gelangen, das
unser Astronaut sah, kurz bevor er auf Nimmerwiedersehen in der
Singularität verschwand. Bitte planen Sie nun aber keine Reise durch ein
Wurmloch in ein anderes Universum! Solche Wurmlöcher schnüren sich in der
Mitte fast unendlich dünn ein, und bei der geringsten Störung reißt die
Brücke sofort ab. Zudem: Nicht einmal unser äußerst robuster Astronaut hat
den Sturz in die Singularität überlebt...
Vieles von dem, was der tapfere Astronaut auf seiner Reise sah, ist Spekulation. Niemand weiß, ob es andere Universen gibt, ob Weiße Löcher oder Wurmlöcher existieren oder wie es im Innern Schwarzer Löcher aussieht. Aber wir erkennen, welche Faszination von diesen simplen Gebilden ausgeht. Sehen wir nun, was geschieht wenn Schwarze Löcher auch noch rotieren!
Bis jetzt haben wir Schwarze Löcher als einfache, simple Gebilde kennen gelernt, was sie im Grunde auch sind. Man kann sie recht kurz beschreiben durch ihre Masse und dem daraus folgenden Radius. Eine Lösung der Einsteinschen Feldgleichung ("Reissner-Nordström-Lösung") weist darauf hin, dass Schwarze Löcher eine elektrische Ladung besitzen können, was ein weiterer Aspekt ihrer Beschreibung wäre. Es spricht nichts dagegen, dass aus dem Loch elektrische Feldlinien herausragen. Wären sie positiv geladen, würden z.B. Elektronen angezogen, bei negativer Ladung Protonen. Diese Teilchen würden bei ihrem Sturz ins Loch dessen Ladung recht schnell neutralisieren. Das aus dem Grund, weil Schwarze Löcher im Kosmos stets von Materie umgeben sind. Materie besteht aus Elektronen und Protonen (sowie Neutronen), also positiven und negativen Ladungen. Die elektrostatischen Anziehungskräfte eines geladenen Schwarzen Lochs sind eine Milliarde Milliarden mal stärker als seine Gravitation, daher wäre seine Ladung in kürzester Zeit durch Anziehung der entgegengesetzt geladenen Teilchen neutralisiert. Eine weitere Betrachtung geladener Löcher erübrigt sich daher, denn in der Natur werden wir sie kaum antreffen.
Etwas sehr Wichtiges wurde bei den bisherigen Betrachtungen allerdings noch nicht beachtet: Alle Sterne, die wir beobachten können, rotieren! Bis jetzt führte unsere Reise lediglich zu "statischen" Schwarzen Löchern, also solchen, die nicht rotieren. Doch wenn ein Stern kollabiert, dann muss nach dem physikalischen Gesetz der Drehimpuls erhalten bleiben, es sei denn, er wird durch eine äußere Kraft gebremst. Weil es keine "Bremse" bei einem solchen Ereignis gibt, werden somit die allermeisten Schwarzen Löcher rotieren!
Damit haben wir alles beisammen, um ein Schwarzes Loch zu beschreiben:
Masse Drehimpuls Ladung
Mehr als das kann man niemals über ein Schwarzes Loch erfahren. Man kann hinfliegen und diese Größen messen, aber man wird nie herausbekommen, ob das Loch z.B. aus einem Stern entstanden ist oder vielleicht sogar aus Antimaterie besteht. Nun wird man sich fragen, was passiert denn mit dem Magnetfeld des Sterns, wenn er kollabiert? Es müsste doch zu ungeheurer Stärke verdichtet werden, noch viel mächtiger als bei den Magnetaren. Doch auch hier siegt die Gravitation. Die magnetischen Feldlinien werden immer mehr nach unten gebogen und wenn der Stern den kritischen Radius erreicht hat, ragt keine einzige mehr aus dem Loch heraus. Die Gravitation lässt es nicht zu, dass wir mehr als die drei oben genannten Größen erfahren! Diese Eigenschaften, die ein Schwarzes Loch zu einem "simplen" Gebilde machen, beschrieb 1971 John Wheeler mit dem prägnanten und durchaus zweideutigen Satz
Schwarze Löcher haben keine Haare!
Mit den Haaren ist natürlich all das gemeint, was aus dem Schwarzen Loch, dem Horizont, herausragen könnte. Mit seinem Satz erregte John Wheeler verständlicherweise einige Unruhe unter seinen Wissenschaftskollegen, doch bald legte sich die Aufregung über diese "Obszönität". Heute findet dieser Ausspruch in jeder Abhandlung über Schwarze Löcher seinen selbstverständlichen Platz.
Gegenstände wie Sterne, Hühner oder Autos sind
komplizierte Gebilde. Um jedes noch so kleine Detail, bis in den atomaren
Aufbau, beschreiben zu können, würde man viele Milliarden von Parametern
benötigen. Ein Schwarzes Loch dagegen reduziert alles auf die drei
genannten Größen. Es "vergisst" praktisch alles, woraus es entstanden ist
und wie der ursprüngliche Aufbau beschaffen war. Masse, Drehimpuls und
elektrische Ladung sind alles, was von Sternen, Hühnern oder Autos übrig
bleibt, fallen sie in ein Schwarzes Loch. Schwarze Löcher sind die
effektivsten Informationsvernichter im Universum!
Doch zurück zu Schwarzen Löchern, die rotieren.
Die Einsteingleichungen für rotierende, nicht geladene Schwarze Löcher sind vom neuseeländischen Mathematiker Roy Kerr erst 1963 gelöst worden, und man nennt solche Objekte nach ihm Kerrsche Löcher. Zunächst beschrieb seine Lösung die Krümmungen der Raumzeit um einen rotierenden Stern. Doch schon bald konnten Brandon Carter, Roger Penrose sowie R.Boyer und R. Lindquist nachweisen, dass Kerrs Lösung alle rotierenden Schwarzen Löcher umfasste. Und was ist an diesen Objekten nun anders als bei den Schwarzschild- Löchern?
Karussell der Raumzeit
Kerrsche Löcher rotieren nicht nur selbst, sondern zwingen allem in ihrer Umgebung diese Rotation auf! Alles, was sich in der Nähe des Horizonts aufhält. Licht oder andere Strahlung, Materie jeder Form und sogar die Raumzeit werden gezwungen, der Rotation des Lochs mit derselben Geschwindigkeit zu folgen. Man kann sich diesen Effekt (genannt frame-dragging) wie einen Strudel vorstellen. Das Mitreißen der Raumzeitgeometrie gilt im Prinzip für jeden rotierenden Körper ("Lense-Thirring-Effekt"), ist aber verschwindend gering, solange der Körper nicht zum Schwarzen Loch kollabiert ist.
 Wenn
Sie einmal den Stöpsel aus der Badewanne ziehen, sehen Sie, dass entfernt
vom Abfluss die Wasseroberfläche (die "Raumzeit") noch relativ ruhig ist.
Je näher man an den Abfluss herangeht, umso schneller und so wirbelnder
werden die Bewegungen. Ähnlich auch beim Schwarzen Loch, direkt an der
Oberfläche des Horizonts muss alles mit der Geschwindigkeit des Lochs
rotieren. Hier zunächst in einem so genannten Einbettungs- Diagramm die
umgebende Raumzeit eines nichtrotierenden Schwarzen Lochs, die Rotation
entspricht a = 0. a ist der so genannte Kerr-
Parameter, mit dem die Rotation Schwarzer Löcher bezeichnet wird. Er kann
Werte zwischen 0 und +1 oder -1 annehmen. Der rote Kreis zeigt jeweils den
Ereignishorizont.
Wenn
Sie einmal den Stöpsel aus der Badewanne ziehen, sehen Sie, dass entfernt
vom Abfluss die Wasseroberfläche (die "Raumzeit") noch relativ ruhig ist.
Je näher man an den Abfluss herangeht, umso schneller und so wirbelnder
werden die Bewegungen. Ähnlich auch beim Schwarzen Loch, direkt an der
Oberfläche des Horizonts muss alles mit der Geschwindigkeit des Lochs
rotieren. Hier zunächst in einem so genannten Einbettungs- Diagramm die
umgebende Raumzeit eines nichtrotierenden Schwarzen Lochs, die Rotation
entspricht a = 0. a ist der so genannte Kerr-
Parameter, mit dem die Rotation Schwarzer Löcher bezeichnet wird. Er kann
Werte zwischen 0 und +1 oder -1 annehmen. Der rote Kreis zeigt jeweils den
Ereignishorizont.
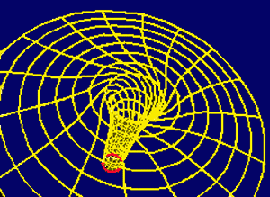 Bei
einem mit maximaler Geschwindigkeit (a = 1) rotierenden Loch wird
die umgebende Raumzeit in einer strudelartigen Form mitgerissen. Ein
anderer anschaulicher Vergleich ist etwa ein Tornado, der einen ähnlichen
Wirbel erzeugt. Wieso gibt es eigentlich eine maximale
Rotationsgeschwindigkeit? Theoretisch könnte man doch einfach mit
Drehimpuls behaftete Materie in das Loch werfen, um seine Rotation immer
schneller werden zu lassen (der Drehimpuls muss ja erhalten bleiben). Da
aber macht uns die Natur einen Strich durch die Rechnung.
Bei
einem mit maximaler Geschwindigkeit (a = 1) rotierenden Loch wird
die umgebende Raumzeit in einer strudelartigen Form mitgerissen. Ein
anderer anschaulicher Vergleich ist etwa ein Tornado, der einen ähnlichen
Wirbel erzeugt. Wieso gibt es eigentlich eine maximale
Rotationsgeschwindigkeit? Theoretisch könnte man doch einfach mit
Drehimpuls behaftete Materie in das Loch werfen, um seine Rotation immer
schneller werden zu lassen (der Drehimpuls muss ja erhalten bleiben). Da
aber macht uns die Natur einen Strich durch die Rechnung.
Wenn Sie ihren Kaffee einmal extrem schnell umrühren, so wird ab einer bestimmten Drehzahl durch die Zentrifugalkraft das herrliche Getränk aus der Tasse spritzen, der Zusammenhalt der Flüssigkeit zerreißt 1. Auch Sterne können nicht mit jeder beliebigen Geschwindigkeit rotieren, denn sonst würden sie durch die Zentrifugalkräfte zerissen. Das gilt auch für Weiße Zwerge, genauso wie für Neutronensterne, die nicht mehr als etwa 1000 Umdrehungen pro Sekunde durchführen können. Gilt das auch für ein Schwarzes Loch?
Durch die Zentrifugalkraft wird der Horizont (exakt ausgedrückt: die Ergosphäre, siehe weiter unten, der eigentliche Ereignishorizont wird nicht verformt) eines Schwarzen Lochs zusammengepresst, abgeplattet wie die Erde durch ihre Rotation. Irgendwann sollte er doch zerreißen, wenn wir immer mehr Materie mit Drehimpuls hineinwerfen? Leider nein. Es gibt für ein rotierendes Schwarzes Loch eine maximale Geschwindigkeit: Wenn es mit halber Lichtgeschwindigkeit rotiert (a = 1, = "Maximal-Kerr"), lassen es die Zentrifugalkräfte nicht mehr zu, dass Materie ins Loch fällt. Sie wird vom Horizont fortgeschleudert. Würde allerdings Maximal-Kerr tatsächlich exakt erreicht werden, könnten die Zentrifugalkräfte die Gravitation aufheben. Wir hätten dann ein Schwarzes Loch ohne Horizont geschaffen, denn der würde jetzt zerplatzen und wir könnten direkt auf die Singularität sehen!
 Man kann aber noch so trickreich vorgehen, wir können weder den Horizont
zerstören, noch die Rotation beliebig steigern. Roger Penrose hat
1969 eine Hypothese aufgestellt, die so genannte Kosmische Zensur (cosmic
censorship). Demnach ist es einem außenstehenden Beobachter zu keiner
Zeit und an keinem Ort des Universums möglich, eine nackte Singularität
zu erblicken, also eine Singularität ohne Ereignishorizont. Die Natur
scheint uns das generell verwehren zu wollen. Jede echte ("intrinsische",
~aus sich selbst heraus) Singularität muss sich nach der Kosmischen
Zensur hinter einem Ereignishorizont verbergen, vom Rest des Universums
isolieren. Ein Beobachter kann eine Singularität nur erblicken, wenn er
sich in das Schwarze Loch begibt. In der "Praxis" ist es also nicht
möglich, dass ein Loch mit maximaler Geschwindigkeit rotiert, jedoch
können viele Schwarze Löcher dem maximalen Drehimpuls sehr nahe kommen.
Man kann aber noch so trickreich vorgehen, wir können weder den Horizont
zerstören, noch die Rotation beliebig steigern. Roger Penrose hat
1969 eine Hypothese aufgestellt, die so genannte Kosmische Zensur (cosmic
censorship). Demnach ist es einem außenstehenden Beobachter zu keiner
Zeit und an keinem Ort des Universums möglich, eine nackte Singularität
zu erblicken, also eine Singularität ohne Ereignishorizont. Die Natur
scheint uns das generell verwehren zu wollen. Jede echte ("intrinsische",
~aus sich selbst heraus) Singularität muss sich nach der Kosmischen
Zensur hinter einem Ereignishorizont verbergen, vom Rest des Universums
isolieren. Ein Beobachter kann eine Singularität nur erblicken, wenn er
sich in das Schwarze Loch begibt. In der "Praxis" ist es also nicht
möglich, dass ein Loch mit maximaler Geschwindigkeit rotiert, jedoch
können viele Schwarze Löcher dem maximalen Drehimpuls sehr nahe kommen.
Gravitonen kann man sich also als winzigste Teilchen, oder besser nach der Quantenmechanik, als Feldquanten vorstellen, die eine gewisse Ähnlichkeit mit den Photonen aufweisen.
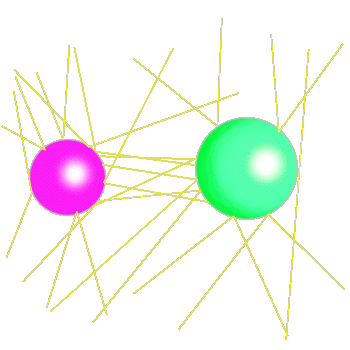 Hier
sieht man, wie Gravitonen zwischen zwei Körpern ausgetauscht werden
könnten. Man kann diesen ruhemasselosen Feldquanten, genau wie den
Photonen, einen Impuls zuordnen. Daraus folgt, dass sich auch Gravitonen
ausschließlich mit Lichtgeschwindigkeit bewegen. Entgegen vielen anderen
Behauptungen breiten sich damit Gravitationsfelder nur mit c
aus.
Hier
sieht man, wie Gravitonen zwischen zwei Körpern ausgetauscht werden
könnten. Man kann diesen ruhemasselosen Feldquanten, genau wie den
Photonen, einen Impuls zuordnen. Daraus folgt, dass sich auch Gravitonen
ausschließlich mit Lichtgeschwindigkeit bewegen. Entgegen vielen anderen
Behauptungen breiten sich damit Gravitationsfelder nur mit c
aus.
Nun werfen wir einen Blick durch ein Elektronenmikroskop und betrachten ein Wasserstoffatom. In einfachster Vorstellung wird hier ein Proton von einem Elektron umkreist. Das Elektron könnte nun ein kleines Energiepaket, ein Photon, abstrahlen und dadurch von einer hohen auf eine niedrigere Bahn fallen. Ebenso gut könnte das Elektron auch ein Graviton abstrahlen! Doch wir haben ja schon festgestellt, dass im atomaren Bereich die Gravitation nichts zu melden hat, vielmehr ist hier das Reich der elektromagnetischen Wechselwirkung. Und so kommt es, dass wir auf 1044 (!) beobachtete, vom Elektron abgegebene Photonen nur ein einziges Graviton feststellen könnten.
Wir brauchen also etwas Massiveres als ein Elektron, um den Gravitonen auf die Spur zu kommen.
Beschäftigen wir uns nun ein wenig mit dem Horizont Kerrscher Löcher, besser gesagt den Horizonten:
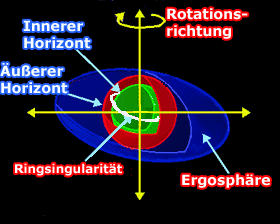 Wie
die Skizze schon andeutet, ist der Aufbau stark verändert gegenüber einem
nicht rotierenden Loch. Außen umschließt eine so genannte Ergosphäre
das Gebilde. Sie hat die abgeplattete Form eines Ellipsoids und stellt ein
Gebiet um das Loch dar, in dem keine statisch ruhige Lage mehr in Bezug
auf ein fernes, äußeres Bezugssystem möglich ist. Die äußere Begrenzung
der Ergosphäre wird deshalb auch statische Grenze genannt. Selbst
wenn ein Körper Lichtgeschwindigkeit erreicht, kann er innerhalb der
Ergosphäre keine statische Lage mehr einnehmen. Nicht eingezeichnet ist
der Übersichtlichkeit halber hier die schon bekannte Photonensphäre, ein
Bereich, in dem ein unter günstigem Winkel hinein gelenktes Photon gerade
noch auf einer stabilen Bahn umlaufen kann, ohne in das Loch zu fallen.
Wie
die Skizze schon andeutet, ist der Aufbau stark verändert gegenüber einem
nicht rotierenden Loch. Außen umschließt eine so genannte Ergosphäre
das Gebilde. Sie hat die abgeplattete Form eines Ellipsoids und stellt ein
Gebiet um das Loch dar, in dem keine statisch ruhige Lage mehr in Bezug
auf ein fernes, äußeres Bezugssystem möglich ist. Die äußere Begrenzung
der Ergosphäre wird deshalb auch statische Grenze genannt. Selbst
wenn ein Körper Lichtgeschwindigkeit erreicht, kann er innerhalb der
Ergosphäre keine statische Lage mehr einnehmen. Nicht eingezeichnet ist
der Übersichtlichkeit halber hier die schon bekannte Photonensphäre, ein
Bereich, in dem ein unter günstigem Winkel hinein gelenktes Photon gerade
noch auf einer stabilen Bahn umlaufen kann, ohne in das Loch zu fallen.
Weder die Ergosphäre, Photonensphäre noch die statische Grenze stellen einen Ereignishorizont dar. Erst bei weiterem Eintauchen in das Kerr- Loch stoßen wir auf - zwei - Horizonte! Der äußere Horizont befindet sich vollständig innerhalb der statischen Grenze, an den Polen können Ergosphäre und äußerer Horizont sich überschneiden (bei a = 1). Dieser Horizont ist die eigentliche Grenze des Lochs, aus der keine Informationen mehr entweichen können. Zwischen äußerem und innerem Horizont stoßen wir nun auf eine ringförmig aufgeblasene Singularität in der äquatorialen Ebene. Bei Maximal-Kerr liegt sie, wie dann auch der innere auf dem äußeren Horizont. Über die Bedeutung des inneren Horizonts ist man sich noch nicht ganz im klaren.
 Hier
eine weitere Darstellung, wie ein Kerr- Loch die Raumzeit und alles andere
mit sich reißt (frame-dragging) und seine Rotation aufzwingt.
Vielfach wird gesagt, dass durch die Ringsingularität völlig neue
Möglichkeiten eröffnet werden: Man könnte sich oberhalb der Ringebene
aufhalten oder sogar durch den Ring hindurch fliegen, zumindest bei
supermassiven Löchern, da hier die Gezeitenkräfte noch erträglich wären.
Der Ring stelle nicht das Ende der Raumzeit dar, wie es bei einer
intrinsischen Punktsingularität der Fall ist. Prinzipiell könnten wir
unseren Astronauten also wieder auf die Reise schicken, und nach manchen
Vermutungen sollte er durch die Ringsingularität sogar andere Universen
erreichen. Allerdings liegen solche Spekulationen jenseits jeder Realität,
niemand kann den Sturz in ein Schwarzes Loch überleben! Zunächst einmal
dürfte es keine Konstruktion und keinen Organismus geben, die den
Belastungen der Rotation mit evtl. relativistischen Geschwindigkeiten
schon in Horizontnähe widerstehen könnten. Direkt am Horizont hätte jeder
Gegenstand Lichtgeschwindigkeit, um dann überlichtschnell weiter zu
stürzen! Materie in der uns bekannten Form kann hier wohl nicht mehr
existieren, weil die Geodäten der Teilchen raumartig werden. Das bedeutet,
dass die Teilchen
tachyonische
Eigenschaften annehmen, sich außerhalb aller von uns fassbaren Grenzen
bewegen. Deshalb bleibt fortan unser Astronaut von allen Blessuren
verschont.
Hier
eine weitere Darstellung, wie ein Kerr- Loch die Raumzeit und alles andere
mit sich reißt (frame-dragging) und seine Rotation aufzwingt.
Vielfach wird gesagt, dass durch die Ringsingularität völlig neue
Möglichkeiten eröffnet werden: Man könnte sich oberhalb der Ringebene
aufhalten oder sogar durch den Ring hindurch fliegen, zumindest bei
supermassiven Löchern, da hier die Gezeitenkräfte noch erträglich wären.
Der Ring stelle nicht das Ende der Raumzeit dar, wie es bei einer
intrinsischen Punktsingularität der Fall ist. Prinzipiell könnten wir
unseren Astronauten also wieder auf die Reise schicken, und nach manchen
Vermutungen sollte er durch die Ringsingularität sogar andere Universen
erreichen. Allerdings liegen solche Spekulationen jenseits jeder Realität,
niemand kann den Sturz in ein Schwarzes Loch überleben! Zunächst einmal
dürfte es keine Konstruktion und keinen Organismus geben, die den
Belastungen der Rotation mit evtl. relativistischen Geschwindigkeiten
schon in Horizontnähe widerstehen könnten. Direkt am Horizont hätte jeder
Gegenstand Lichtgeschwindigkeit, um dann überlichtschnell weiter zu
stürzen! Materie in der uns bekannten Form kann hier wohl nicht mehr
existieren, weil die Geodäten der Teilchen raumartig werden. Das bedeutet,
dass die Teilchen
tachyonische
Eigenschaften annehmen, sich außerhalb aller von uns fassbaren Grenzen
bewegen. Deshalb bleibt fortan unser Astronaut von allen Blessuren
verschont.
Mit freundlicher Genehmigung
von J. Bergeron/Sky & Telescope
Damit kennen wir jetzt alle Arten von Schwarzen Löchern, die denkbar sind:
- Das Schwarzschild- Loch. Es ist statisch, rotiert also nicht und ist kugelsymmetrisch. Für seine Beschreibung genügt die Masse
- Das Schwarze Loch nach Reissner-Nordström: Es rotiert auch nicht, ist ebenfalls kugelsymmetrisch, aber elektrisch geladen
- Das Kerrsche Loch. Zu seiner Beschreibung braucht man Masse und Drehimpuls
- Die wahrscheinlichste Lösung eines Gravitationskollapses: Ein im Gleichgewicht befindliches, rotierendes Loch mit einer geladenen Masse. Es wird Kerr-Newman- Loch genannt.
Für die Masse eines Schwarzen Lochs ist keine Begrenzung bekannt, sie kann beliebige (!) Größen annehmen. Das gilt jedoch nicht für die Ladung und den Drehimpuls, ihnen ist ein oberes Limit gesetzt. Würde es überschritten, z.B. beim Kollaps eines Sterns, so könnte kein Schwarzes Loch entstehen, sondern eine nackte Singularität. Das aber verbietet die Kosmische Zensur!
Jetzt wollen wir uns ansehen was passiert, wenn Materie zu engen Kontakt mit Schwarzen Löchern hat.
1
Bitte verwenden Sie für diesen Versuch höchstens einen Kaffee aus der
Kaffeemaschine. Ein von Hand aus ganzen Bohnen gemahlener und von Hand
gefilterter Kaffee sollte Ihnen für solche Experimente zu kostbar sein!
Zurück zum Text.
Weitere Informationen: http://www.lsw.uni-heidelberg.de/users/amueller/astro_sl.html#kerr
Erstellt: 30. November 2003
Ana Sayfa /
index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru
Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)