Today we examine the second of Einstein's great achievements - The General Theory of Relativity (GR)

(actually it was his third, he contributed to QM with his theory of the photo-electric effect)

We are also going to focus on the strangest of GR's offspring - Black Holes

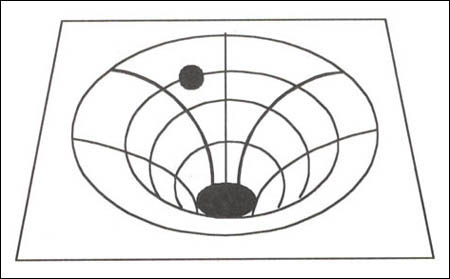
Distorted space-time and a 'new' interpretation of the fall of an object to Earth. The space-time is distorted by mass or energy, thus (the mass of) the Earth distorts the space-time around it. A 'falling' object rolls along the geodesic of curved space-time near the Earth.
 

The Death of Action at a Distance

Remember that Newton's great achievement was to unite Heaven and Earth with a single Universal Law of Gravitation.

This law

made gravity into a specific and quantifiable force.

But how did this force reach out across space to act on massive bodies? This almost occult-like property of Newtonian gravity bothered everyone, most of all Newton himself.
 

Einstein built on his special theory of relativity and constructed a way of viewing gravity that did away with the problem of action at a distance.

In special relativity Al considered bodies in Uniform (constant velocity) Motion. In general relativity Einstein considers bodies that accelerate.

Al recognized that if you are in a closed elevator that was accelerating through space you would feel a force down towards the floor just as if you where standing on the Earth.
 

Einstein realized that there was an equivalence between an accelerating frame of reference and a stationary one which experiences a gravitational field.

From this Einstein inferred something quite amazing.

 Gravity was intimately linked to the structure of Space-Time.

Special Relativity had taught him to think of Space-Time and malleable entity. He now explored how Space-Time's elastic properties could be used to embrace the phenomena of gravity.

In his new theory gravity becomes the Geometry of Space-Time: this is why understanding 4-D geometry becomes so important.

General Relativity says:

• Space-Time tells matter how to move (fall).
• Matter tells Space-Time how to bend.

In GR's perspective something falls because that is the way Space-Time "goes". That is the way it is bent

A chunk of matter left on to its own device's (no external forces) will follow the curve of space-time.

But what determines the curvature of Space-Time? Its the amount of matter present.

Actually its Matter-Energy (E=mc² after all).

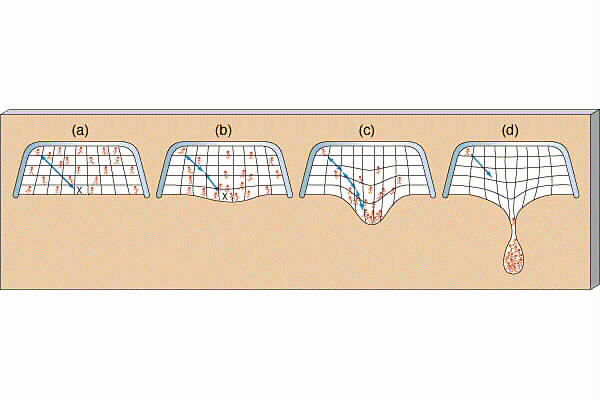
Now this happens in 4-D which is impossible to visualize. But we can play the 1-2-3 game again.

Imagine a 2-D Space-Time, i.e. the surface of a trampoline.

If you drop a bowling ball onto the trampoline it distorts the elastic fabric creating a depression.
 
 

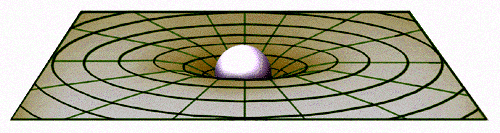
Shoot a BB across the trampoline's surface and it gets defected, perhaps even caught in the bowling ball's "well".

Just like a orbiting satellite or falling meteor!

Space-Time is an elastic fabric which permeates your being.

Since its Space-Time we are talking about, both the space and time parts change character depending on where you are in the well.

For instance, time runs slower the deeper you are in the well.
 
 

Experimental tests of GR.

This is a pretty freaky theory. How do we know its true?

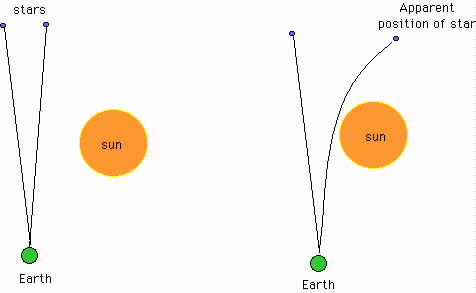
The confirmation of GR came in 1918 during a solar eclipse.

If Space-Time gets bent by matter then even light rays should have their paths altered as they travel near a massive body.

By looking at the relative positions of two stars before and during a solar eclipse astronomers could actually confirm that light paths did indeed get bend by exactly the amount Einstein predicted.

It works like this.  

An extreme form of this is "Gravitational Lensing" where light from a distant object gets bend by a foreground objects' gravity the ways a lens focuses light. This produces multiple images of the distant object.
 
                               
 

You can also take two synchronized atomic clocks, put one on a plane and leave the other on the ground.

After the plane flies at high altitude for a while you bring the clocks back together and the
clocks are out of synch by exactly the amount Einstein predicted.

Why is GR so hard?

Einsteins' equations relating space-time curvature and matter-energy can appear quite elegant.
 


 

But if you want to actually work with them you end up with stuff like this....
 

Black Holes:

OK so what is a black hole?

Remember the collapse of a massive star.... If the core is too massive nothing can hold it up and it collapses to a point.

There are also super massive black holes at the center of galaxies. They can contain more than 10 ⁶ times the mass of the sun

There are two parts to a black hole -An event horizon which surrounds a singularity.
 
                                                       

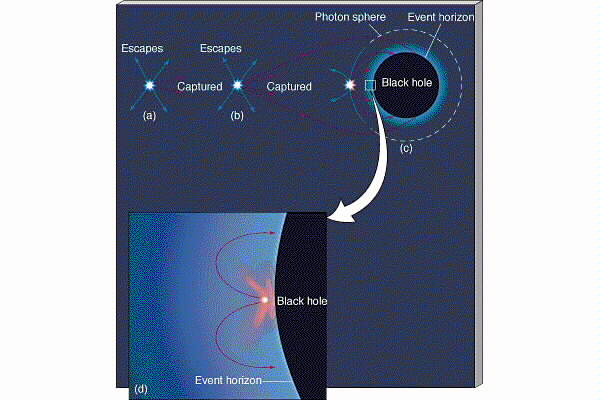
The event horizon is the place where the escape velocity from the "star" equals the speed of light.

Photons at the event horizon orbit it forever.
 

                                                          
 

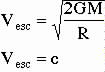
Nothing, not even light, can escape from inside the event horizon.
 

In terms of the bending of Space-Time, a black hole represents so extreme a curvature that Space-Time "tears"

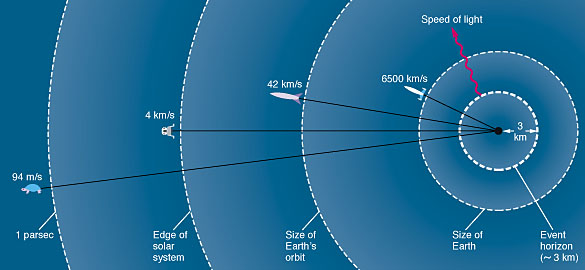
The size of the event horizon is determined from the escape velocity formula. Its radius is called the "Schwarzschild radius" (R_s).
 
                                                      

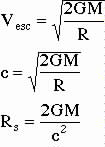
A 1 solar mass black hole would have a "Schwarzschild radius" of about 3 kilometers across.

At the center of the event horizon is the singularity. This is the geometrical point into which all the mass of the original star has collapsed.

A point has no dimensions! Yet that is where all the mass is! This is an abomination to physics. We just don't understand what happens here. The laws we understand break down.

The event horizon protects our universe from the singularity. Anything that falls past the event horizon can't get out.

Actually the roles of space and time reverse inside a event horizon. The coordinate for distance from the center (r) acts like negative time (-t) and visa versa.

This means that once inside the event horizon you are pulled towards the singularity in the same way you are "pulled" towards the future.

Once inside the event horizon you have to hit the singularity.

In a sense the event horizon protects our universe from the singularity (where all hell could literally break loose)

Can there be singularities without event horizons surrounding them?

Physicists wet their pants in terror just thinking about. They have even invoked something called "cosmic censorship" which states singularities must always have event horizons around them.

What is life like near a black hole.

First off - black holes do not suck the entire universe in. If you are not at the event horizon you can, with enough force escape a black hole. Its just like any other gravitating body until you get near R = R_s.

Photons which do make it out from close to a black hole do get very strongly redshifted because the must fight to escape the enormous pull. They lose energy by becoming weaker (longer wavelength) photons.
 

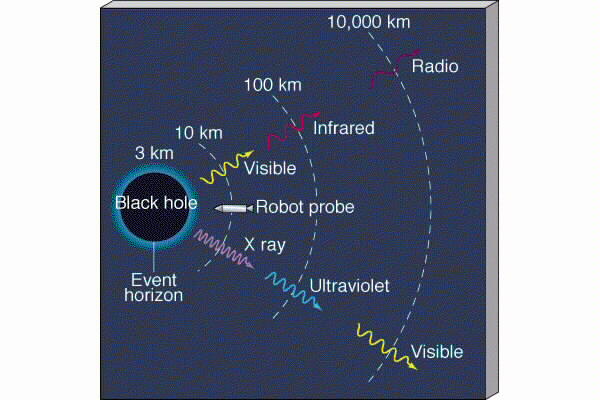
If you fell into a black hole you would get torn apart before you actually hit the event horizon.

This occurs because of "tidal forces" which are the difference in the gravitational force between two points.

Near the event horizon the stretching of space-time is so extreme that your feet feel a much stronger acceleration than your head.

You get pulled into long strand of spaghetti.

These extreme forces pull matter apart down to the subatomic level. The violence of this produces and enormous amount of heat. The radiation from this heat is a signature of black holes.

A person watching from the outside would watch as you fell into the black hole and would see the sequence of events slow down as you approached the event horizon.

At the event horizon time would appear to stand still.

You would appear, however, forever at the lip of the black hole. Of course the light be would be "redshifted" so strongly that it would be impossible to detect.

If you were indestructible and could survive the tidal forces everything would look OK to you just like in Special Relativity.

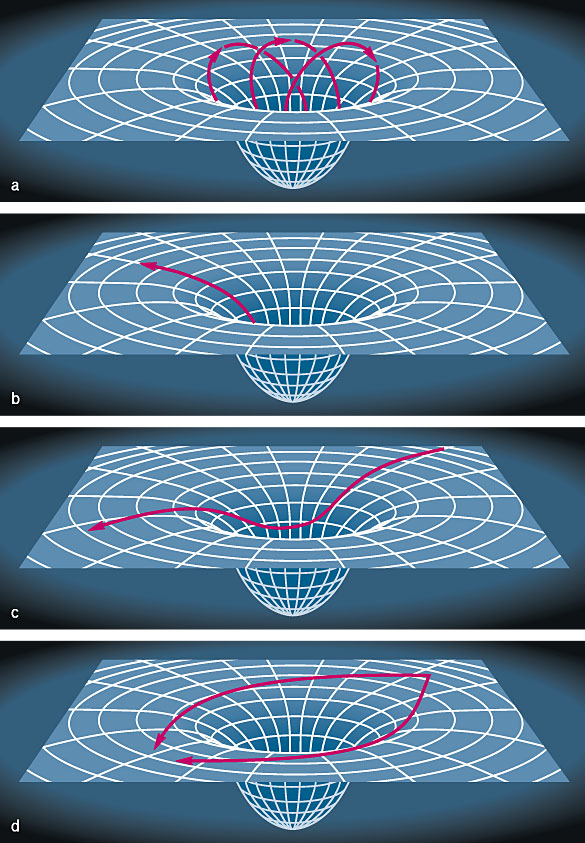
Wormholes and White Holes.

The equations of GR have the properties that they are time invariant. You can run them one way or the other. It doesn't matter.

That means that the opposite of a black hole, a time-reversed black hole, a white hole, can mathematically exist.

A black hole can only swallow things. A white hole can only spit things out.

It is hard to see how to make one of these.

On the other hand a charged or rotating black hole has the property that in can join up with a white hole in such a way that you can fall into the black hole and pop out of the white hole.

This is a wormhole.
 

The worm hole could lead anywhere, to distant parts of the universe, into the past, even to different universes.

Problem is its hard to make one of these, they don't form from ordinary collapse.

The wormholes are also unstable. Any little jolt and they close up. But who knows.....

Black Hole Evaporation:

Black Holes are not totally black! They can actually emit radiation and in doing so they evaporate!

This can happen because of Quantum Mechanics.

Near the event horizon quantum fluctuations can produce pairs of matter and anti-matter particles

electrons (e-) and positrons (e+).

This would not normally violate the conservation of energy because the two particles would collide and annihilate.

But if one of the particles get swallowed by the event horizon and the other escapes then this is a net lose of energy which must come from the black hole's mass.
 
 
                                  

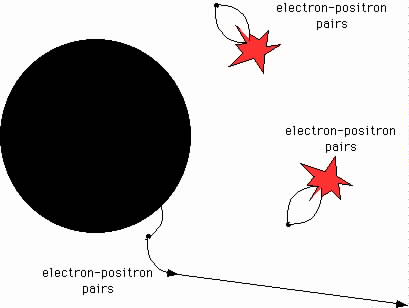
The radiation which is produced this way is called Hawking Radiation .

When a black hole evaporates all the photons stuck at the event horizon get freed. Now you would see all that stuff fall into the black hole.
 

Detecting Blackholes

The most important way of detecting balckholes is by watching how fast things rotate around them
   

With the doppler shift you can measure rotation (orbital )speeds of material in accretion disks.
rotation speed depends on the mass of thing being orbited.

Create your own universe

From issue 2559 of New Scientist magazine, 10 July 2006, page 32

• 10 July 2006
• Exclusive from New Scientist Print Edition.

One of the good things about being God is that there's not much competition. From time immemorial, no one else has boasted the skills necessary to create a universe. Now that's about to change. "People are becoming more powerful," says Andrei Linde, a cosmologist based at Stanford University in California. "Maybe it's time we redefine God as something more sophisticated than just the creator of the universe."

Linde was prompted to make this wry observation by the news that a glittering prize is within physicists' reach. For decades, particle accelerators have been racking up an impressive list of achievements, including creating antimatter and exotic particles never seen in nature. The next generation of these giant colliders will provide the hunting ground for the elusive Higgs boson, thought to be the source of all mass. These machines might even create mini black holes. Mighty as those discoveries and creations are, however, they pale into insignificance beside what Nobuyuki Sakai and his colleagues at Yamagata University in Japan have now put on the table. They have discovered how to use a particle accelerator to create a whole new universe.

The idea of creating another cosmos is not a new one; in fact it has a long history. "The story really begins with the question of the origin of our own universe," says Eduardo Guendelman, a physicist at Ben Gurion University, in Beer Sheva, Israel. As physicists began to research what kick-started our universe, they realised that if it happened once, maybe it could happen again. The growing acceptance of the big bang model in particular, which suggested that space-time burst forth in an explosion of energy concentrated in a tiny space, opened up a new set of tantalising possibilities. "People immediately started to wonder what would happen if you put lots of energy in one space in the lab - shot lots of cannons together," Linde says. "Could you concentrate enough energy to set off a mini big bang?"

For theoretical physicists the initial answer was a resounding "no". All of the particles that you would create in such a process would have their own gravity, pulling them together. So, instead of creating a baby universe in the lab, you would just create a black hole. The idea came back to life in 1981, however, when Alan Guth at the Massachusetts Institute of Technology proposed the theory of inflation, which suggests the universe went through a period of rapid expansion just after the big bang.

Guth's idea solves many cosmological puzzles, but no one really knew how or why it happened. So he and his colleagues set about trying to find out what might have made our universe inflate - exactly the question that would help us create a new universe using our own tools.

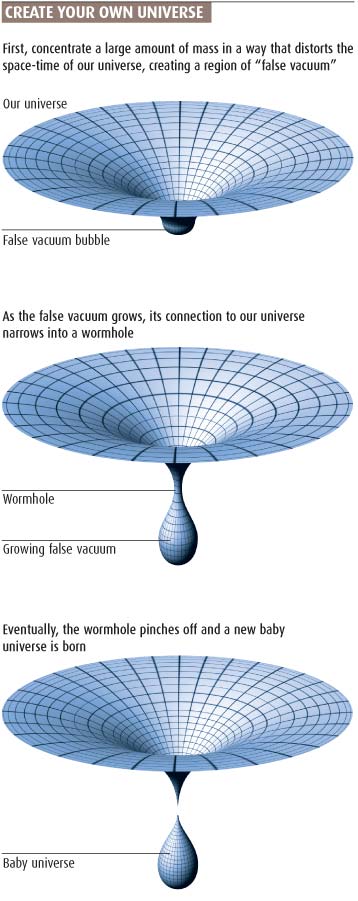
Inflation theory, subsequently modified by Linde, relies on the fact that the "vacuum" of empty space-time is not a boring, static place. Instead, it is subject to quantum fluctuations that cause strange bubbles to appear at random times. These bubbles of "false vacuum" contain space-time with different - and very curious - properties.

According to our best understanding of physics, the universe's energy is stored in different kinds of fields. One of these is the Higgs field, which plays a vital role inside bubbles of false vacuum: it keeps the energy density within the bubbles constant.

That has two effects. First, it creates a repulsive gravitation within the bubble, which causes the bubble's space-time to swell. Though that might seem just what a budding creator requires, the effect doesn't change the size of the bubble to an observer on the outside - the growth is only noticeable within the body of the false vacuum bubble. Nor are things improved by the second consequence of a constant energy density.

In 1987, Guth and Ed Farhi, also at MIT, demonstrated that bubbles which start out below a certain size collapse under the tension of the bubble walls before the space they enclose has a chance to expand. That happens because the pressure inside the bubble of false vacuum is always lower than the pressure of the true vacuum outside. In other words, if the bubble is too small, its walls will always have a tendency to collapse inwards.

Frustratingly, there's even a problem with the larger bubbles. Although they could grow to cosmological scales in theory, they also need a kick-start before they will expand. In our early universe, that kick was provided by the big bang, a point with infinite energy density. Reproducing one of those in the lab isn't exactly plain sailing.

In 1989, however, Willy Fischler, a cosmologist at the University of Texas in Austin, and his colleagues found a way out. They showed that the same random quantum processes that create a false vacuum bubble would also allow it to spontaneously turn into a larger one. Their calculations showed that once this larger bubble had been burped out, it could inflate into a new universe without a kick-start from infinite energy.

Only one problem remained for the wannabe creators of the universe: a crippling time delay. The spontaneous transition from small bubble to large bubble can take a long time to occur, and the initial bubble tends to collapse under the tension of its walls before it can transform itself into a larger bubble.

Guendelman and his colleague Jacov Portnoy, also at Ben Gurion University, took matters into their own hands, and came up with some ways to prop the bubble walls apart. They factored in fields of energy known as "gauge fields" to the small bubble's surface to keep its skin taut, holding it at a constant radius. "With that in place, all you need to do is sit there, watch the small bubble and wait for the large bubble to appear," says Guendelman.

By this point, however, the home-made universe was starting to look rather cobbled together, to say the least. Though Guendelman and Portnoy's trick was neat, no one knew how you might add these gauge fields into an experiment. Plenty of other obstacles remained, too. For a start, although Guth had calculated that the size of bubble needed was invitingly small - just 10^-26 centimetres across - there still wasn't any realistic way to create the bubble in the first place. What's more, one unfortunate consequence of quantum mechanics is that, even if you set up the right conditions for the process to occur and stop the bubble imploding, you still don't know exactly when the inflation will happen. So even with a small bubble in place, and Guendelman and Portnoy's theoretical fields doing their job, there was no guarantee it would turn into a baby universe any time soon. "You could be sitting and waiting from here to eternity," says Guendelman.

Blowing bubbles

For years, Guendelman and his colleagues sought to break through this impasse. What they needed was something that would create the bubble, then quickly blow it up into a universe.

And that is what Sakai has just found. The vital part of the new universe-creation tool kit is a magnetic monopole - a strange spherical particle that encapsulates an isolated north or south magnetic field. For would-be universe builders, the big attraction of a monopole is that it has a huge mass concentrated into a tiny volume, with an enormous energy density created by the Higgs field - just like false vacuum bubbles.

Sakai and his team realised that a seemingly stable monopole in our universe is always teetering on the brink of expansion - needing just a nudge to start it inflating. Hurling mass onto the monopole - increasing its energy density - will push it over the edge, leading to runaway inflation . "Our calculations show that, given enough energy, the monopole will inflate eternally," Sakai says.

This process could be triggered naturally. According to Sakai, if a monopole floating through space collided with another massive object it would gain the mass needed to trigger inflation. One candidate is a cosmic string - a kind of high-energy rip in space-time. Though we have yet to see one, cosmic strings may have been created as a by-product of the big bang.

But since we have no cosmic strings - and we'd like to remain in control of the project - Sakai suggests we might be able to trigger inflation by hurling particles onto a monopole in an accelerator. This would add mass, and thus energy, to the monopole, and make it blow up into an entirely new universe.

It would be an extraordinary achievement, of course, but what happens then? It's one thing to create a universe, but quite another to know where to keep it. After all, an eternally inflating universe might be expected to take up quite a bit of space - the cupboard under the stairs simply won't do.

Actually this wouldn't be a problem, Sakai says. For a start, the process warps space-time enormously, so that it is no longer the Euclidean space we are familiar with. This highly distorted space doesn't have the same geometry as normal space, so it's not as if the universe would blow up and engulf us.

Also, the baby universe has its own space-time and, as this inflates, the pressure from the true vacuum outside its walls continues to constrain it. As these forces compete, the growing baby universe is forced to bubble out from our space-time until its only connection to us is through a narrow space-time tunnel called a wormhole (see Graphic).

In the end, space-time becomes so distorted that even this umbilical cord is severed. The baby universe's space-time is left entirely divorced from our own. If you were sitting inside the monopole, you would see space expanding, rushing out in every direction - just as it did after the big bang in our universe. The view from our universe, outside the monopole looking in, would be rather less spectacular.

Sakai's calculations show that, once disconnected, the baby universe will be locked inside a microscopic black hole which will not appear to grow in size. This mini black hole will emit Hawking radiation and quickly evaporate from our universe. It will continue to grow its own space-time, but will leave behind little trace of its presence in our universe. "We would make this tiny little thing and before we know it, it has flown away - escaped from our grasp," Linde laments.

Vanishing trick

In fact, it will disappear so fast it may even be difficult to tell if we've managed to create it at all, Sakai says. Plans are under way to detect mini black holes in the next generation of particle accelerators, such as the Large Hadron Collider at CERN, in Switzerland, so Sakai is hopeful that in the future we will be able to detect the fleeting birth cries of a baby universe (New Scientist, 23 April 2005, p 38).

Everyone agrees it's an enticing idea, though Fischler is not counting his baby universes before they're hatched. "The real question is whether it is doable," he says. There's still a problem of raw materials, he points out. As yet, not even one monopole has been detected in nature.

Ironically, one of inflation theory's greatest successes was to explain why we have had such difficulty finding these elusive monopoles, despite theoretical predictions that they should exist all around us. Inflation argues that our visible universe grew from a quantum fluctuation so small it contained only one monopole. That particle is out there somewhere, but the odds are against our bumping into it.

So if we aren't likely to run into a natural monopole any time soon, just how will we get our hands on one? Maybe we could make one in the lab, Fischler concedes. Colliding an electron with a positron in a particle accelerator could, in principle, create a monopole-antimonopole pair. And, according to Sakai, we could then trigger inflation by crashing other particles onto our new monopole, adding more and more mass to it.

Generating a monopole-antimonopole pair in the lab is, however, incredibly problematic. Monopoles have huge masses compared to electrons and positrons. To make up this mass difference we would have to smash the initial particles together with far greater energies than are available in today's accelerators. Even assuming that at some future time we would have the technology to reach these energies, the chances of success are still slim. "You would be colliding two ping-pong balls and hoping that two perfectly formed bowling bowls fall out," says Fischler. "I would say that in practical terms this is even worse than hopeless."

OK, so it's not exactly a school science project, but the budding universe creators are excited, nonetheless. "I think our model is one of the most realistic for creating a universe in the lab because it uses materials that may well already be out there," Sakai says. Guendelman agrees. "Ours was just a theoretical idea, but they get a similar effect using something that is predicted to exist by well-known theories," he says. In addition, Sakai's mechanism solves the waiting problem, Guendelman says.

The question is, would it be worth all the effort? Linde thinks so. "I sat down and really thought about why we should even care about creating a universe in the laboratory," Linde says. "We put energy into the baby universe to create it, but we can't get any energy out of it - we can't mine its resources." Once it's formed, he adds, its space and time - though growing - is entirely divorced from our own. "We can't jump into this tiny thing and visit it," says Linde. "We don't seem to be able to communicate with it at all."

In the end, Linde realised he had overlooked the obvious motivation: good old-fashioned megalomania. "Just imagine if it's true and there's even a small chance it really could work," he says. "In this perspective, each of us can become a god."

The elephant and the event horizon - By Amanda Gefter

What happens when you throw an elephant into a black hole? It sounds like a bad joke, but it's a question that has been weighing heavily on Leonard Susskind's mind. Susskind, a physicist at Stanford University in California, has been trying to save that elephant for decades. He has finally found a way to do it, but the consequences shake the foundations of what we thought we knew about space and time. If his calculations are correct, the elephant must be in more than one place at the same time.

In everyday life, of course, locality is a given. You're over there, I'm over here; neither of us is anywhere else. Even in Einstein's theory of relativity, where distances and timescales can change depending on an observer's reference frame, an object's location in space-time is precisely defined. What Susskind is saying, however, is that locality in this classical sense is a myth. Nothing is what, or rather, where it seems.

This is more than just a mind-bending curiosity. It tells us something new about the fundamental workings of the universe. Strange as it may sound, the fate of an elephant in a black hole has deep implications for a "theory of everything" called quantum gravity, which strives to unify quantum mechanics and general relativity, the twin pillars of modern physics. Because of their enormous gravity and other unique properties, black holes have been fertile ground for researchers developing these ideas.

It all began in the mid-1970s, when Stephen Hawking of the University of Cambridge showed theoretically that black holes are not truly black, but emit radiation. In fact they evaporate very slowly, disappearing over many billions of years. This "Hawking radiation" comes from quantum phenomena taking place just outside the event horizon, the gravitational point of no return. But, Hawking asked, if a black hole eventually disappears, what happens to all the stuff inside? It can either leak back into the universe along with the radiation, which would seem to require travelling faster than light to escape the black hole's gravitational death grip, or it can simply blink out of existence.

Trouble is, the laws of physics don't allow either possibility. "We've been forced into a profound paradox that comes from the fact that every conceivable outcome we can imagine from black hole evaporation contradicts some important aspect of physics," says Steve Giddings, a theorist at the University of California, Santa Barbara.

Researchers call this the black hole information paradox. It comes about because losing information about the quantum state of an object falling into a black hole is prohibited, yet any scenario that allows information to escape also seems in violation. Physicists often talk about information rather than matter because information is thought to be more fundamental.

In quantum mechanics, the information that describes the state of a particle can't slip through the cracks of the equations. If it could, it would be a mathematical nightmare. The Schrödinger equation, which describes the evolution of a quantum system in time, would be meaningless because any semblance of continuity from past to future would be shattered and predictions rendered absurd. "All of physics as we know it is conditioned on the fact that information is conserved, even if it's badly scrambled," Susskind says.

For three decades, however, Hawking was convinced that information was destroyed in black hole evaporation. He argued that the radiation was random and could not contain the information that originally fell in. In 1997, he and Kip Thorne, a physicist at the California Institute of Technology in Pasadena, made a bet with John Preskill, also at Caltech, that information loss was real. At stake was an encyclopedia - from which they agreed information could readily be retrieved. All was quiet until July 2004, when Hawking unexpectedly showed up at a conference in Dublin, Ireland, claiming that he had been wrong all along. Black holes do not destroy information after all, he said. He presented Preskill with an encyclopedia of baseball.

What inspired Hawking to change his mind? It was the work of a young theorist named Juan Maldacena of the Institute for Advanced Study in Princeton, New Jersey. Maldacena may not be a household name, but he contributed what some consider to be the most ground-breaking piece of theoretical physics in the last decade. He did it using string theory, the most popular approach to understanding quantum gravity.

In 1997, Maldacena developed a type of string theory in a universe with five large dimensions of space and a contorted space-time geometry. He showed that this theory, which includes gravity, is equivalent to an ordinary quantum field theory, without gravity, living on the four-dimensional boundary of that universe. Everything happening on the boundary is equivalent to everything happening inside: ordinary particles interacting on the surface correspond precisely to strings interacting on the interior.

This is remarkable because the two worlds look so different, yet their information content is identical. The higher-dimensional strings can be thought of as a "holographic" projection of the quantum particles on the surface, similar to the way a laser creates a 3D hologram from the information contained on a 2D surface. Even though Maldacena's universe was very different from ours, the elegance of the theory suggested that our universe might be something of a grand illusion - an enormous cosmic hologram (New Scientist, 27 April 2002, p 22).

The holographic idea had been proposed previously by Susskind, one of the inventors of string theory, and by Gerard't Hooft of the University of Utrecht in the Netherlands. Each had used the fact that the entropy of a black hole, a measure of its information content, was proportional to its surface area rather than its volume. But Maldacena showed explicitly how a holographic universe could work and, crucially, why information could not be lost in a black hole.

According to his theory, a black hole, like everything else, has an alter ego living on the boundary of the universe. Black hole evaporation, it turns out, corresponds to quantum particles interacting on this boundary. Since no information loss can occur in a swarm of ordinary quantum particles, there can be no mysterious information loss in a black hole either. "The boundary theory respects the rules of quantum mechanics," says Maldacena. "It keeps track of all the information."

Of course, our universe still looks nothing like the one in Maldacena's theory. The results are so striking, though, that physicists have been willing to accept the idea, at least for now. "The opposition, including Hawking, had to give up," says Susskind. "It was so mathematically precise that for most practical purposes all theoretical physicists came to the conclusion that the holographic principle and the conservation of information would have to be true."

All well and good, but a serious problem remains: if the information isn't lost in a black hole, where is it? Researchers speculate that it is encoded in the black hole radiation (see "Black hole computers"). "The idea is that Hawking radiation is not random but contains subtle information on the matter that fell in," says Maldacena.

Susskind takes it a step further. Since the holographic principle leaves no room for information loss, he argues, no observer should ever see information disappear. That leads to a remarkable thought experiment.

Which brings us back to the elephant. Let's say Alice is watching a black hole from a safe distance, and she sees an elephant foolishly headed straight into gravity's grip. As she continues to watch, she will see it get closer and closer to the event horizon, slowing down because of the time-stretching effects of gravity in general relativity. However, she will never see it cross the horizon. Instead she sees it stop just short, where sadly Dumbo is thermalised by Hawking radiation and reduced to a pile of ashes streaming back out. From Alice's point of view, the elephant's information is contained in those ashes.

Inside or out?

There is a twist to the story. Little did Alice realise that her friend Bob was riding on the elephant's back as it plunged toward the black hole. When Bob crosses the event horizon, though, he doesn't even notice, thanks to relativity. The horizon is not a brick wall in space. It is simply the point beyond which an observer outside the black hole can't see light escaping. To Bob, who is in free fall, it looks like any other place in the universe; even the pull of gravity won't be noticeable for perhaps millions of years. Eventually as he nears the singularity, where the curvature of space-time runs amok, gravity will overpower Bob, and he and his elephant will be torn apart. Until then, he too sees information conserved.

Neither story is pretty, but which one is right? According to Alice, the elephant never crossed the horizon; she watched it approach the black hole and merge with the Hawking radiation. According to Bob, the elephant went through and floated along happily for eons until it turned into spaghetti. The laws of physics demand that both stories be true, yet they contradict one another. So where is the elephant, inside or out?

The answer Susskind has come up with is - you guessed it - both. The elephant is both inside and outside the black hole; the answer depends on who you ask. "What we've discovered is that you cannot speak of what is behind the horizon and what is in front of the horizon," Susskind says. "Quantum mechanics always involves replacing 'and' with 'or'. Light is waves or light is particles, depending on the experiment you do. An electron has a position or it has a momentum, depending on what you measure. The same is happening with black holes. Either we describe the stuff that fell into the horizon in terms of things behind the horizon, or we describe it in terms of the Hawking radiation that comes out."

Wait a minute, you might think. Maybe there are two copies of the information. Maybe when the elephant hits the horizon, a copy is made, and one version comes out as radiation while the other travels into the black hole. However, a fundamental law called the no-cloning theorem precludes that possibility. If you could duplicate information, you could circumvent the uncertainty principle, something nature forbids. As Susskind puts it, "There cannot be a quantum Xerox machine." So the same elephant must be in two places at once: alive inside the horizon and dead in a heap of radiating ashes outside.

The implications are unsettling, to say the least. Sure, quantum mechanics tells us that an object's location can't always be pinpointed. But that applies to things like electrons, not elephants, and it usually spans tiny distances, not light years. It is the large scale that makes this so surprising, Susskind says. In principle, if the black hole is big enough, the two versions of the same elephant could be separated by billions of light years. "People always thought quantum ambiguity was a small-scale phenomenon," he adds. "We're learning that the more quantum gravity becomes important, the more huge-scale ambiguity comes into play."

All this amounts to the fact that an object's location in space-time is no longer indisputable. Susskind calls this "a new form of relativity". Einstein took factors that were thought to be invariable - an object's length and the passage of time - and showed that they were relative to the motion of an observer. The location of an object in space or in time could only be defined with respect to an observer, but its location in space-time was certain. Now that notion has been shattered, says Susskind, and an object's location in space-time depends on an observer's state of motion with respect to a horizon.

What's more, this new type of "non-locality" is not just for black holes. It occurs anywhere a boundary separates regions of the universe that can't communicate with each other. Such horizons are more common than you might think. Anything that accelerates - the Earth, the solar system, the Milky Way - creates a horizon. Even if you're out running, there are regions of space-time from which light would never reach you if you kept speeding up. Those inaccessible regions are beyond your horizon.

As researchers forge ahead in their quest to unify quantum mechanics and gravity, non-locality may help point the way. For instance, quantum gravity should obey the holographic principle. That means there might be redundant information and fewer important dimensions of space-time in the theory. "This has to be part of the understanding of quantum gravity," Giddings says. "It's likely that this black hole information paradox will lead to a revolution at least as profound as the advent of quantum mechanics."

That's not all. The fact that space-time itself is accelerating - that is, the expansion of the universe is speeding up - also creates a horizon. Just as we could learn that an elephant lurked inside a black hole by decoding the Hawking radiation, perhaps we might learn what's beyond our cosmic horizon by decoding its emissions. How? According to Susskind, the cosmic microwave background that surrounds us might be even more important than we think. Cosmologists study this radiation because its variations tell us about the infant moments of time, but Susskind speculates that it could be a kind of Hawking radiation coming from our universe's edge. If that's the case, it might tell us something about the elephants on the other side of the universe.

Einstein's Relativity.

Some gravitational fields are so strong, that not even light itself can escape! These are called black holes.

Einstein realized that one way to descrive gravity was to consider how it warped space. A black hole warps space so much that even photons are "sucked in".

A BLACK HOLE is the final state of matter for stellar remnants > 3 Msun. Remember - it is the FINAL mass that matters...

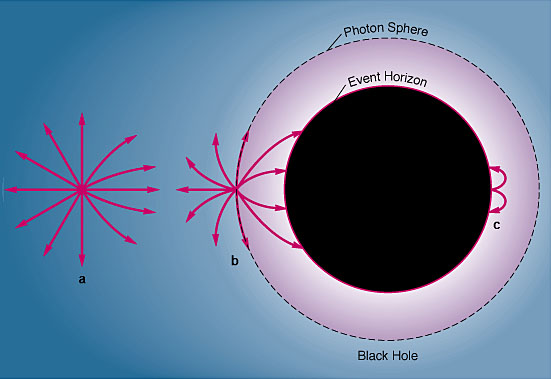
We can define something called the EVENT HORIZON where no information (from light or anything else) can escape. A photon release there would simply "orbit" the black hole forever.

These exotic objects can be surrounded by massive accretion disks. When matter falls into the black hole energy can be released at the boundary causing a burst of high energy radiation as x-rays or gamma rays. While interesting and amazing in their own right, black holes could be telling us a lot about galaxy formation and evolution - most massive galaxies appear to contain supermassive black holes at their centers!

This is the final chapter in the story of stellar evolution. While interesting and amazing in their own right, these stellar remnants could be telling us a lot about galaxy formation and evolution - our next topic in the course!

Sayfa başına dön

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

Ana Sayfa / index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)