Zaman Yolculuğunu Araştırma Merkezi © 2005 Cetin BAL - GSM:+90  05366063183 - Turkey / Denizli

 

Giriş

Tarih: 19:27 on 11/2/2006

Bu Blog konusuna girmeden bir hayli düşündüm. Acaba ilgi çekici birtakım söyleyeceklerim var mı? Okuyucu ilgilenir mi? Söyleceklerim önemli mi? türünden sorular kafamda idi. Fakat sonunda karar verdim.

Evet, söyleyeceklerim var. Bir bakış açım, bir dünya görüşüm, bir düşünce duruşum var. Bunlar ilginç mi? siz karar vereceksiniz. İsterseniz, başlıkları şöyle bir gelişi-güzel sıralayayım. Yazılarım aynı sırayı takip etmese de değineceğim konular şunlardır:

Bilim düşüncesi, Fizik bilimi, Modern Fizik kuramları, Evren, Zaman ve mekan, Düşüncenin yapısı, Mantık çeşitleri, Sonsuzluk kavramı, Sonsuzluk Çeşitleri, Varlık ve Yokluk hakkında, İnsan Düşüncesi ve Psikolojisi, Metafizik, Matematik, Geometri, Evrenin Geometrisi, Evrenin yapısı ve Modelleri, Canlılık ve cansızlık, Hareket ve duraganlık, .........gibi daha birçok benzer konu.

Eğer bilim ve bilim felsefesi ile ilgili iseniz sizin için ilginç olabilir. Ama, güncel konular peşinde iseniz, gündemle ilgili pek fazla yorum bulmayabilirsiniz.

Karar sizin, hadi hayırlısı..

 

Enerji ve Entropi

Tarih: 07:25 on 5/4/2006

Bir önceki yazımda etki-tepki yasası doğru yorumlandığı taktirde bu yasa yardımıyla birçok farklı yasanın türetilebileceğini söyledim. Şimdi doğanın önemli iki yasasından söz edeceğim. Bunlar, “Enerji” ve “Entropi” yasalarıdır. Her ikisini de etki-tepki yasasından türetmek mümkündür.

Kapalı bir sistem içinde enerjinin korunduğunu hemen herkes duymuştur. Öncelikle “kapalı sistem”  kavramının bir yaklaşım olduğunu, hiçbir sistemin tümüyle kapalı olamayacağını belirtmekte yarar var. Kapalı sistemi tanımlamak bize kalmış bir durumdur. Herhangi bir hacim, kısa bir süre için kapalı olarak tanımlanabilir. Şu halde kapalı sistem göreli bir kavramdır. Üstelik hem enerji hem de entropi kavramları bir başlangıç durumu bir de son durum tanımı gerektirdiklerinden iki “an” veya iki “durum” arasındaki değişim göz önüne alınmalıdır. Bu iki durumun birer “denge durumu” olduklarını varsayıyoruz.

Etki-tepki yasası statik bir yasa gibi görünse de sistemlerin hareket etmelerine neden olan dinamik bir yasadır. Yani her “an” geçerli olan ve bu bakımdan ne bir başlangıç ne de bir sonuç noktası tanımı gerektirmeyen bir yasadır. Çünkü başlangıç ve sonuç anlarını tanımlamak bizim elimizde olan karardır. Etki-tepki yasası (bir önceki yazımda gösterdiğim gibi) kuvvet kavramını gerektirmez, kuvvet kavramı bu yasadan türer.

Her “var olan” nesne veya olay için şu noktaları hatırlatmakta fayda vardır:

1. Her var olan (nesne veya olay) birçok düğümden oluşmuştur. Tek parçacık kavramı geçerli olmayan bir yaklaşımdır.
2. Bu bakımdan doğada gördüğümüz her türlü olay veya nesne için istatistik mekanik kavramları geçerlidir. Klasik mekanik kavramları devre dışı kalabilir.
3. Her “var olan” olay veya nesne bir çeşit gruplaşma (dolayısıyla anlık kapalı sistem) veya yerel olarak yoğunlaşma olarak değerlendirilmelidir.
4. Her gruplaşma veya yoğunlaşma örgü alan dengesinin yerel olarak bozulması anlamına gelir.
5. Örgü alanın bozulması bir etki olarak görülmelidir. Bu etki gizli olan simetrinin, veya dengenin, bozulması anlamını taşır.
6. Etki-tepki yasasına göre her etki bir tepki yaratacağından, tepki kuvvetinin görevi etkiye karşı koymak ve dengenin bozulmasına engel olmaktır.
7. Etki-tepki dengesi sürekli gibi görünse de, her an kendini yenileyen süreksiz bir oluşumdur.
8. Doğada her etkiye karşı tepki verip düzen oluşturma ve dengeyi geri getirme görevini Takiyon adı verilmiş olan ara “parçacıklar/dalgalar” yüklenmiştir. Takiyonlar kuvvet ileten parçacıklar olarak görülebilir.

Bu 8 noktaya şimdiye kadar yazmış olduğum bölümlerde çeşitli fırsatlarda değindim. Örgü alanında bulunan gizli simetrinin bozulmasında alanın yapısında bulunan vakum titreşimleri önemli bir etkendir. Vakum titreşimleri çizgisel olmayan bir şekilde eklenip yerel olarak bir yoğunluk farkına neden olurlar.

Kısa bir süre için kapalı bir sistem oluştuğunu düşünelim. Bu kısa sürenin t₁ başlangıç anında sistemin belli bir E₁ enerjisi ve S₁ entropisi bulunsun. Sistemi “kapalı” olarak tanımladığımızdan belli bir V₁ hacmi içinde dıştan herhangi bir etki olmadığını kabul ediyoruz. Şu halde iç dinamiklerden dolayı sistemde bir değişim olduğunda, değişimin hem enerjiyi hem entropiyi hem de hacmi değiştirdiğini varsayalım.

Etki-tepki yasası gereği etkiye eşit ve zıt yönde derhal bir “tepki” oluşacaktır. İkinci “an” olarak tanımladığımız son durumda, yani t₂ anında, enerji E₂ entropi S₂ ve hacim V₂ olur. Fakat tepki etkiye zıt olduğundan E₂ = - E₁ olacağından E₂ + E₁ = 0, dolayısıyla toplam enerjinin değişmediğini görmekteyiz. Enerji de göreli olduğundan toplam enerjiye bir sabit değer eklemek sonucu değiştirmez. Şu halde E₂ + E₁ = Sabit dersek enerji korunumu yasasını elde etmiş oluruz.

Entropi ise hacım ile ilgilidir. Çünkü Entropi tanımı sistem içindeki düğüm noktalarının erişebildiği durumların olasılığı ile ilgilidir. Tepki sonucu hacim büyürse yani V₂ > V₁ ise entropi artar, V₂ < V₁ ise entropi azalır. Entropi değişimi de etki-tepki yasası gereği oluşmaktadır.

 

Etki-tepki yasası

Tarih: 15:42 on 3/4/2006

Newton (1643-1727), doğayı açıklamak için ileri sürdüğü ilk yasaya göre: “Her etkiye karşı eşit ve ters yönde bir tepki oluşur”. Etki-tepki yasası olarak da adlandırabileceğimiz bu yasa, doğanın en temel yasası olup varlığın varlığını sürdürmesi için gereklidir. Eğer hareket bir etki sonucu oluşmakta ise her nesne doğal olarak harekete karşı bir tepki verir. Yani, nesneler harekete karşı direnç gösterirler.

Bir önceki yazımda akımın zamanla değiştiğini ve sabit bir I₀ değerine yaklaştığını fakat asla tam olarak ulaşmadığını söyledim. I₀ değeri bir üst limit değer olması bakımından akım o değer etrafında küçük salınımlar yapar. Bu salınımlar o kadar hızlı ve küçüktürler ki pratikte akım bize sabit imiş gibi görünür. Akımın salınımlar yapması hem etki-tepki yasası ile ilgilidir, hem de akımın dalgasal bir hareket olması ile ilgilidir. Şu halde sadece alternatif akım dalgalı hareket yapmıyor, aynı zamanda doğrusal akım da dalgasal hareket yapıyor.

Akım henüz üst kritik limit değere ulaşmadan değişim halinde olduğunu gördük. Bu süre içinde etki-tepki denklemi E₀ - L(∆I / ∆t) = RI₀ şeklinde yazılabilir. Bu ifadede E₀  = V elektronlara etki eden pilin itici kuvveti, L devrenin fiziksel yapısından kaynaklanan ve “Endüktans” denen bir sabit değerdir. Akımın artmasını sağlayan E₀ değerine “etki eden kuvvet” diyebiliriz. Bu kuvvete karşı F_t = L(∆I / ∆t)  tepki kuvveti olarak tanımlanabilir. Eksi işaret ile belirtilmesinin nedeni etkiye karşı ve zıt yönde bir tepki kuvveti oluşundandır. Sağdaki terim ise akımın pratik olarak ulaştığı I₀ değeri ile sabit bir R sayısından oluşur. Akım sabitlenince ∆I = 0 olacağından Ohm yasası V = R.I elde edilir. Eğer t =0 anından t = t(kritik) anına kadar yapılan işi hesaplamak istersek İş = Kuvvet çarpı yol tanımından iş = W = F.I .

               W(0,m) = ∑^m I L(∆I / ∆t). ∆t = L ∫ I dI = (1/2) L I²

elde edilir. Burada toplam 0’dan başlayıp m değerine ulaştığında I akımı da sabit I₀ değerine ulaşmış veya çok yaklaşmış olmaktadır. W(0,m) ifadesi devrenin enerjisi olmaktadır.

Hareket halindeki parçacıklar için aynı mantıkla p = m.v (momentum = kütle çarpı hız) eşitliğini kullanırsak yukarıdaki denkleme benzer şekilde:

                 W(0,r) = ∑^r v m(∆v / ∆t). ∆t = m ∫ v dv = (1/2) mv² = K

 

olup K ifadesine kinetik enerji demekteyiz. Görüyoruz ki “Kinetik enerji” v sabit hızına yaklaşan ve pratikte ulaşan m kütleli parçacığın 0 ile belli bir r aralığında yaptığı iş olmaktadır.

Hem mekanik hem de elektrik enerjinin aynı temel görüşten türeyerek aynı yapıda oluşları tesadüf değildir. Her ikisi de benzer olan “tepki kuvveti” sayesinde belirmektedir. Elektrikteki tepki kuvveti F_t (elektrik)= L(∆I / ∆t) olduğu gibi, mekanik tepki kuvveti F_t (mekanik)= m(∆v / ∆t) olur. Burada m kütle ve v hız olduğuna göre tepkime kuvveti:

       F_t (mekanik)= m(∆v / ∆t) =  ma = ∆(mv) / ∆t = ∆p / ∆t = F

olur. Böylece Newton’un ikinci yasası olan F = ma denklemi doğrudan etki-tepki yasasından elde edilmektedir. Yani, ikinci yasa aslında birinci yasadan türetilebilir.

Bu denklemler sayesinde şu sonuçlara ulaşmaktayız:

1. Doğanın en temel yasası etki-tepki yasasıdır. Bu yasa doğru yorumlandığı taktirde birçok farklı yasa bu temel yasadan türetilebilir.
2. Elektrik ve mekanik olaylar, dış görünüşte çok farklı oldukları kanısını uyandırsalar dahi, temelde aynı yapının farklı görüntüleridir.
3. Bir elektrik devrede “endüktans” adı verilen L sabiti ile mekanik yapılarda “kütle” dediğimiz m sabiti aynı temel kavramın farklı yansımalarıdır.
4. Elektrik akımı dalgasal olarak yayılmaktadır. Şu halde, benzer şekilde, madde dediğimiz kütle içeren yapılar da dalgasal hareket ile yayılırlar.
5. Her nesnenin hem madde hem de dalga olduğu sonucu klasik olarak (Görelilik kuramına gerek duyulmadan) elde edilebilmektedir.

 Köpek ve sahibi

Tarih: 09:06 on 3/4/2006

Çok parçacıktan oluşmuş her sistem için bir “Üst kritik nokta” tanımlanabilir. Üst kritik noktanın sabit ve mutlak bir nokta olduğunu düşünmemek gerekir. Her sistem için farklı olabileceği gibi hareketli bir nokta olabilir.

Bir örnek vereyim. Yukarıda görülen grafiği bir düz tarla olarak düşünün. O noktasında bir köpek ve A noktasında sahibi olan Ahmet (A) bulunsun. A sabit hızla (mavi renkle gösterilen) düz bir çizgi boyunca yürümeye başlıyor. Aynı anda köpek sahibinin yürüdüğünü görünce ona doğru kendi hızında yaklaşmak ve A’ya ulaşmak istiyor. Köpek kendi hareketini her an sahibine göre değiştirmekte ve kendisi ile A arasındaki düz çizgi boyunca ilerlemektedir. Bu düz çizgileri belli aralıklar için gösterdim. Çizim tümüyle geometrik olup matematik herhangi bir katkı yoktur.

Köpeğin izlediği yolu kırmızı bir çizgi halinde görmekteyiz. Bu çizgi tam bir üstel (eksponansiyel) eğridir. Kanıt olarak da daha küçük bir grafik olarak, gri zeminde çizilmiş olan matematikten elde edilmiş üstel fonksiyonun köpeğin izlediği yolla nasıl da çakıştığını görmekteyiz.

Bu örnekten 3 sonuç çıkarabiliriz.

1. Köpeğin ulaşmak istediği hedef sahibi olduğuna göre sahibinin har an içinde bulunduğu nokta  kendisi için üst kritik noktayı oluşturmaktadır. Şu halde yatay eksen zaman ekseni olarak tanımlanabilir. Zaman arttıkça köpek ile sahibi arasındaki mesafe azalmaktadır.
2. Köpek her ne kadar sahibine yaklaşsa da asla erişemeyecektir. Çünkü üstel fonksiyon ancak sonsuzda limite ulaşır. Demek ki üst kritik noktaya yaklaşılabilir ama ulaşılamaz. Bunun anlamı şudur: Eğer üst kritik noktaya ulaşılırsa sistemde ani bir değişiklik oluşur. Yani verili şartlarda ani bir değişiklik oluşmadıkça üst kritik noktaya ulaşılamaz. Bu örnekte köpek A’ya henüz ulaşmamıştır. Ulaştığında artık şartlar değişmiş, sistem ani bir sıçrayışla farklı bir yapıya dönüşmüş olacaktır. 
3. Köpeğin hareketi doğrusal olmayıp bir üstel fonksiyonla tanımlanabilir. Bu da köpeğin dalga fonksiyonudur. Çünkü daha önceki bir yorumumda hareketi oluşturan en genel dalga fonksiyonun

          V(t) = a_n e^-iktEn  şeklinde yazılabileceğinden söz etmiştim (Bakınız Farklı bir yorum başlıklı yazım). Şu halde dikey eksen enerjiyi belirten V-ekseni olarak tanımlanabilir. Üstel fonksiyon da karmaşa ve düzen yaratan dalga fonksiyonundan başka bir şey değildir.

Demek ki her hareketin temelinde bir dalga fonksiyonu bulunmaktadır. Bunu her düzeyde görmekteyiz. Örneğin, kondansatör denilen elektrik yükü biriktirmeye yarayan nesneyi düşünelim. Bu nesne (en basit şekliyle) aralarında bir boşluk bulunan iki düz metal levhadan oluşmuştur. Bir pilin iki kutbunu bu iki levhaya bağlarsak bir süre sonra yükler bu levhalarda birikir. Fakat birikim aniden olmaz. Birikimin zaman içindeki değişimini ölçmek için telden geçen elektrik akımını ölçmemiz yeterlidir. Telden geçen akım I ise:

          I = I₀ (1 – e^-kt) şeklinde olup burada k = R/L şeklinde bir sabittir. Bu denklemde I₀ üst kritik noktayı oluşturmaktadır. Çünkü t sonsuza yaklaştıkça I = I₀ ve en başta, yani t = 0 da, akım olmaması gerektiğinden I = 0 olur. Fakat kondansatör içine yüklerin birikimi çizgisel olmayıp, üstel fonksiyonun gerektirdiği şekildedir. Yani, kondansatörün yapısı bize akımın ulaşabileceği üst kritik nokta olan I₀ değerini belirler.

Bu üst kritik nokta aynı zamanda bir “acayip çekici” nokta olmaktadır. Kuramsal olarak bu noktaya ancak sonsuzda ulaşılabilir. Pratikte ise ulaşıldığında aniden çatallaşma oluşur ve sistem farklı bir yapıya dönüşür. Örneğin kondansatör örneğinde fazlaca kuvvetli bir pil bağlanırsa yükler birikmekte devam edip üst kritik noktayı aşarlar. Bu durumda iki levha arasında yük sıçraması oluşur. Bu durum (pratikte) kondansatörün aşırı yükten dolayı bozulmuş olduğu şeklinde tanımlanır. Çünkü bir kere iki levha arasında yük sıçraması (şerrare) oluştuktan sonra levhalar arasındaki dielektrik ortamın (mum,plastik,bakalit) özelliği bozulmuş olur ve kondansatör eskisi gibi yük biriktiremez.

Sonuç olarak, bir sistemi oluşturan parçacıkların hareketi, mümkün olan en kısa yol boyunca olsa da, söz konusu hareket daima bir üstel dalga fonksiyonu içermektedir.

 

Kristallerin oluşumu

Tarih: 10:12 on 1/4/2006

Kuantum kuramına göre kuvvet kavramının klasik fiziktekinden farklı olduğunu söyledim. Kuantum kuramında kuvvet daima bir parçacık (veya dalga) alışverişi ile oluşmaktadır. Elektromağnetik kuvvetin ortaya çıkışı bir veya birkaç foton alışverişi sayesindedir. Diğer kuvvetlerin oluşumu da parçacık alışverişi sayesindedir (Bakınız Feynman çizimi başlıklı yazım).

Kimyasal bağlar da aynı şekilde elektron alışverişi olarak görülmelidir. Bir önceki yazımda sözünü ettiğim NaCl molekülünün bağını bir elektron oluşturmaktadır. Ancak bu elektron sürekli bir titreşim içinde bir atomdan diğerine sıçrar. Her sıçramada molekül bir anda nötr (yüksüz) durumdan artı ve eksi yüklü iki iyona dönüşmekte, bir an sonra tekrar nötr olmaktadır. Yukarıdaki şekilde bu farklı durumları gösteriyorum.

En üstte görülen Sodyum atomu ve Klor atomu birbirleri ile etkileşmedikleri sürece nötr durumdadırlar. Etkileşince aralarında bir bağ oluşur. Bu bağ Kritik kuvvet kavramı başlıklı yazımda gösterdiğim şekildeki gibi oluşur. Fakat bağ statik bir ip gibi değil, bir yay gibi veya iki atom arasında el değiştiren bir top gibi düşünülebilir. İki atom arasında gidip gelen bir dalga olarak düşünebiliriz.

Elektron Klor atomuna geçtiğinde atom bir fazla elektron sahibi olacağından (-) eksi yüklü olurken, Sodyum atomu bir eksik elektron sahibi olacağından (+) artı yüklü olur. İki atom ayrılıp iyon haline dönüştüklerinde dahi birbirleri ile uzaktan ve anında etkileşmekte devam ederler. Çünkü Klor atomundan Sodyum atomuna geçmiş olan elektron yeni bir ortamda bulunmasına rağmen eski ortamının da bilgisini içermektedir. Yani, elektronun da hafızası vardır.

Şimdi diyeceksiniz ki: “küçücük elektronun hafızası olabilir mi?”. Evet, olabilir. Hatta sadece elektronun değil, her parçacığın kendi hafızası vardır. Bu hafıza sayesinde bilgi birinden diğerine anında ve ışıktan hızlı bir şekilde ulaşmaktadır. Bilgiyi aktaran parçacık da Takiyondur. Bunun anlamı bilginin asla kaybolmadığıdır.

Elektron Sodyum atomundan Klor atomuna geçtiğinde her iki atomun valans bandı 8’er elektron sahibi olduğundan her iki atom daha dengeli bir yapıya ulaşmış olurlar. Fakat, öte yandan her iyonda proton sayısı ile elektron sayısı eşit olmadığından yeni bir dengesiz durum ortaya çıkar. Demek ki iyonlar da dengesiz yapılardır ve en küçük fırsatta tekrar birleşip molekül haline dönüşmek isterler. Hatta moleküllerden de daha sağlam yapılar olan kristallere dönüşmek isterler.

Kristaller aynen bir örgü alanına benzerler. Kristal yapıların simetrisi oldukça ileri düzeydedir ve her kristal kendini tekrarlayan bir yapı içerir. Yukarıda görülen tuz kristalindeki küçük küreler Sodyum atomunu, büyük küreler Klor atomunu simgeliyorlar. Fakat aralarındaki bağ öyle güçlüdür ki tuz kristali sudan arındığında katı bir görünüm sergiler. Kristal yapı, titreşimler sonucu birbirlerine yaklaşan iyonların belirgin bir şekilde bağlanmaları olarak açıklanır. Birbirlerine yaklaştıran veya iten kuvveti de yük kavramı ile açıklamaktayız. Oysa ki Takiyon Evren modeline göre aynı olayları farklı bir yorumla açıklayabiliriz.

TE modelinde amaç sürekli denge durumunu korumak veya bozulan dengeyi yeniden sağlamaktır. Eriyik içinde ayrılmış olarak yüzen iyonlarda elektron-proton dengesi bozulmuş olduğundan yeni bir denge durumunu sağlamak görevi Takiyonlara düşmektedir. Bu yeni denge durumu da sistem kritik noktaya ulaştığı anda aniden (veya çok kısa bir sürede) Takiyonlar sayesinde oluşmaktadır.

Bu oluşumu yine NaCl kristali ile örnekleyeyim. Eğer bir kap su içine tuz eriterek suyu tuza doymuş hale getirirseniz eriyik üst kritik noktaya ulaşmış olur. Çünkü su kütlesi kabul edebileceği en fazla sayıda Sodyum ve Klor iyonlarına sahiptir. Şimdi bir pamuk ipliğine bağlı küçük bir tuz kristalini suyun içine sallandırın. Su tuza doymuş olduğundan tuz kristali suda erimeyecek, aksine serbest dolanan iyonlar bu kristale yapışarak kristalin büyümesine neden olacaklardır. Yani, eriyikte ani bir faz değişimi oluşmaktadır. İşte, üst kritik noktaya ulaşan bir sistemde yeni bir dengeli ve düzenli  durum, bir faz değişimi şeklinde, aniden ortaya çıkmakta ise bunun nedeni Takiyonların düzen sağlayıcı etkisidir.

 

Kimyasal etkileşmeler

Tarih: 07:25 on 1/4/2006

Var olanların varlıklarını sürdürmeleri için zorunlu olarak işbirliğine girdiklerini söyledim. Her düzeyde ve boyutta işbirliğine rastlamaktayız. İnsanlar her ne kadar bu işbirliğinin istek sonucu oluştuğunu sansalar dahi, var olmayı dengeli ve tutarlı bir şekilde sürdürebilmek için işbirliği yapmaktan başka çare yoktur.

Size şimdi, atomların yaptığı işbirliğinden söz edeceğim. Kimya biliminin esas konusu moleküllerin oluşumunda atomlar-arası bağları incelemektir. Her atom merkezde bir çekirdek ve etrafında dönen elektronlardan oluşur. Bu elektronlar belirli yörüngelerde toplanırlar. Kimyasal reaksiyonlarda bağları oluşturan elektron tabakası en dışta bulunan tabakadır. Bu elektron tabakasına “Valans bandı” veya “değerlik tabakası” denir. Çünkü bu tabakada bulunan elektronların adedi o atomun değerliğini belirler.

Yukarıdaki şekilde Sodyum ve Klor atomlarının sadece valans bandı gösterilmiştir. Bu bandların dolması için her birinde 8’er elektron bulunması gerekir. Sodyum atomunun 8 elektronluk bandı dolduktan sonra bir tane de fazladan elektron bulunduğundan valans bandında tek bir elektron vardır. Klor atomunun valans bandında ise 7 adet elektron bulunmaktadır. Bu iki atom yaklaştıklarında işbirliği yapıp bir elektronu paylaşırlar. Böylece Sodyum atomu fazla elektronunu Klor atomuna ödünç verir ve her iki atom da valans bandında 8’er elektron sahibi olmuş olurlar.

Fakat ödünç verilen elektron hala Sodyum atomuna aittir. Yani Sodyum “elektronumu verip kurtulayım” demek yerine Klor atomuna “elektron senle ben arasında titreşsin, böylece hem sen bir elektron sahibi olmuş olursun, hem de ben elektronuma sahip olmaya devam ederim” demektedir. Böylece Sodyumklorür, yani Tuz molekülü oluşmuş olur.

Fakat suda bu elektron bağı kolaylıkla kopar. Tuzun suda kolayca eridiğini hepimiz biliyoruz. Tuz eriyince Sodyum elektronundan kolaylıkla vazgeçer ve bir eksik elektron sahibi olduğundan +1 yük sahibi olur. Çünkü çekirdeğindeki proton adedi şimdi elektron adedinden bir fazladır. Benzer şekilde Klor atomu bir fazla elektron kazanarak valans bandını tamamlamıştır ama elektronların toplam sayısı protonlardan bir fazla olduğundan yükü de –1 olur. Değerliği -1 olan atomun bir fazla elektrona sahip olduğu ve değerliği +1 olan atomun bir eksik elektrona sahip olduğunu ifade etmekteyiz. Bu durumda iki atom arasındaki bağ kopmuş olduğundan eriyik içindeki serbest dolanan bu tür atomlara "iyon" denmektedir.

Eğer valans bandında birden fazla elektron eksikse ne olur? Gene aynı şekilde elektron paylaşımı ile atomlar bağ kurarlar. Resimde bir Oksijen molekülü görmekteyiz. Her bir Oksijen atomunun valans bandında 6’şar elektron bulunmaktadır. Şu halde 2 adet elektron paylaşmaları gerekmektedir. İki adet elektronun paylaşımı sonucunda oluşan O₂ molekülü tuz molekülüne göre daha sağlam ve dayanıklıdır. Çünkü tek elektron bağını koparmak kolay, iki adet elektronun oluşturduğu bağı koparmak zordur.

Yukarıda görülen Oksijen molekülü ile Feynman çizimi başlıklı yazımda göstermiş olduğum şekli karşılaştırırsak aynı bağ yapısının değişik boyutlarda tekrarlandığını görürüz. Demek ki paylaşım ve işbirliği doğanın temel bir özelliğidir. Varlığın varlığını sürdürmesi için gerekli ve zorunlu bir etkileşim şeklidir.

İnsanlar da aynı davranışları sergileyerek bağlar kuruyorlar. Aileler, şirketler, vakıflar, politik partiler hep işbirliği gereği ortaya çıkmışlardır. “Birlikten kuvvet doğar” sözü hepimizin bildiği eski bir atasözüdür. Eskiden büyük aileler vardı, çünkü işbirliği gerektiren tarım veya toplu avcılık ile uğraşan insanlar için en dengeli yapı büyük aileler, klanlar ve boylar idi. Zamanla toplu davranma gereği azalınca ailelerin de boyu küçüldü. Günümüzde aile “çekirdek aile” olarak tanımlanan en küçük haline indirgenmiş durumdadır.

Devletler ve devletlerin toplamından oluşan birlikler, hep paylaşım ve güçlü bağlar kurma gereğinden türemiş işbirliği örnekleridir. Günümüzde büyük ailelerin yerini büyük ve uluslararası şirketlerin almakta olduklarını görmekteyiz.

İstatistik mekaniğin yorumu

Tarih: 08:31 on 31/3/2006

Bir önceki yazımda İstatistik mekaniğinden söz ettim. Biraz fazlaca matematik denklemler içerdiğinden şimdi denklemlerin anlamı üzerinde durmak istiyorum. Öncelikle şu noktayı açıklamakta yarar vardır: İleri sürdüğüm yaklaşımda genel kabul görmüş İstatistik mekaniğinden farklı olarak toplamlar sıfırdan sonsuza kadar olmayıp, sıfırdan belli bir kritik sayıya kadardır. Yani, sonlu toplamlar söz konusudur. Ayrıca sıfır enerji yokluk demek değildir. n = 0 dan kasıt, sistemin ilk başlangıç noktasını tanımlamak demektir. Bu başlangıç noktası da mutlak olmayıp görelidir. İstenilen herhangi bir “an” veya herhangi bir “durum” sıfır noktası olarak tanımlanabilir. Zaten “potansiyel enerjinin” en büyük özelliği de sabit bir değer olmayışı ve göreli olmasıdır. V(0,m) fonksiyonu da bir potansiyel enerji fonksiyonudur.

Bu potansiyel enerji yerel değişimlere yol açabilir. Değişimlerin ortaya çıkışı sonlu küçük adımların toplamı sonucunda belirir. Diğer bir ifadesi de “değişimler yerel yoğunluk farkları sonucunda oluşur” şeklindedir. Çünkü, sonlu sayıda birimin etkileşimi sonucu ortaya çıkan yapı, aniden ve yerel olarak oluşmaktadır.

Fakat öte yandan her bir yerel birimin genel yapı ile ışıktan hızlı bir şekilde haberleştiğini de söyledim. Şu halde yerel oluşumlarda yerel olmayan etkiler de var olmak zorundadırlar. Burada bir zorunluluk söz konusudur. Çünkü oluşan yapılar gelişi güzel ve tesadüfi olarak oluşmuyorlar. Altta yatan ve ilk anda görülmeyen, gizli bir simetrinin gerektirdiği şekilde oluşuyorlar. Gizli simetri “eşit dağılım” olarak da düşünülebilir. V(0,m) veya Z (equipartition) fonksiyonu esas itibariyle bir “eşit dağılım” fonksiyonu olup belli bir aralıktaki gizli simetriyi içerir. Çünkü bu gizli simetri sürdüğü sürece sistem dengede ve bozunmadan var olmaya devam eder. n =m noktasına ulaşıldığında veya aşıldığında simetride kırılma oluşur ve ani bir sıçrayışla yeni bir durum ortaya çıkar.

“Yaşam” adını verdiğimiz varlık boyutu da aynı şekilde iki etkinin ortaklaşa işbirliği sayesinde aniden oluşmaktadır. Bir yandan yerel yoğunlaşmalar sonucu sistemin üst kritik noktaya ulaşmasını sağlayan yerel etkiler, diğer yandan kırılan simetri sonucunda belirli yapıların oluşmasına izin veren genel etkiler. Genel etkiden kasıt, örgü ağını oluşturan küçük düğümlerin yapısında bulunan “non-lineer” (çizgisel olmayan) özellik.

Eğer bu özellik bulunmasaydı hiçbir etki kalıcı olamazdı. Bir süre sonra Termodinamiğin ikinci yasası icabı genel örgü ağı içinde dağılıp giderdi. Çünkü, Takiyonların görevi örgü ağında oluşan pürüzleri ütülemek ve ağın yeniden düzgün bir ağa dönüşmesini sağlamaktır. Etkiler çizgisel olmazlarsa toplam etki kritik bir noktaya ulaşabilir ve, yine Takiyonlar sayesinde, ani bir sıçrayışla yeni bir yapıya dönüşebilir.

Varlıkların yapısında bulunan çizgisel olmayan etkileşme türüne “işbirliği” de diyebiliriz. Bu işbirliği, istek sonucu “özgür irade” ile oluşan bir işbirliği değildir. Daha çok zorunlu bir işbirliğidir. Var olanların varlıklarını sürdürmeleri için seçmek zorunda oldukları davranış türüdür, de denebilir. Her varlık kendinde eksik olanı tamamlamak zorundadır. Çünkü, eksik tamamlanmadığı taktirde bu eksiğin getireceği sorunlar artarak büyür ve varlığın kendi varoluşunu tehlikeye atar (Bakınız Yin ve Yang başlıklı yazım).

İşte, eksiğin tamamlanması için girişilen karşılıklı yarar faaliyetlerine “işbirliği” demekteyiz. Bu girişime son yıllarda “kazanç-kazanç stratejisi” adı verilmiştir. Tek tek ve bağımsız gibi görünen varlıkların bir araya gelip işbirliği yapmalarına neden olan birtakım çekim kuvvetlerinden söz ediyoruz. Canlılar için “sembliyoz” terimi kullanılmaktadır. Nesneler için çekim kuvveti, varlığın bir şekilde varlığını sürdürmesini sağlayan Takiyon etkisi olarak görülmelidir. Çünkü, Takiyonlar varlıklar arası iletişimi sağlayan ve evrene düzen getiren nesnelerdir.

Bu düzen hem yerel boyutta hem de genel boyutta oluşmaktadır. Takiyonlar yerel boyutta bize ayrı ve bağımsız gibi görünen varlıkların oluşumunu sağlarken, genel boyutta evrenin tümel olarak varlığını sürdürmesini sağlayan titreşim hareketinin de nedenidirler. Çünkü var olanlar her boyutta titreşim/salınım/dalga hareketi yaparak varlıklarını sürdürmektedirler.

İstatistik mekanik

Tarih: 10:07 on 29/3/2006

Uzam adını verdiğimiz vakum ortamda hiçbir parçacık bulunmasa dahi titreşen küçük yaylar bulunduğunu düşünebiliriz. Bu küçük yaylar büyük çapta  bağımsız titreşimler yaparlar. Fakat her biri bir dalga fonksiyonu ile tanımlanabilir. Belli bir küçük yayın titreşmesi onun enerjiye sahip olduğunu gösterir. Bu titreşimlere “vakum titreşimleri” dendiğinden söz etmiştim (Bakınız Titreşen kuantum düğümler başlıklı yazım).

E_n enerjisine sahip n’inci yayın V_n = e^-ikEn  potansiyeli içinde titreştiğini yazabiliriz. Tüm vakum alan için toplam potansiyel n üzerinden toplam olmalıdır. Ancak bu toplam sonsuza kadar olamaz. Sıfırdan başlayarak bir maksimum “Üst kritik değere” kadar olmalıdır. Çünkü daha önce de belirttiğim gibi, sistem Üst-kritik değere ulaşınca değişim aniden ve kendiliğinden olur. Şu halde üst-kritik değeri m ile gösterirsek, toplam potansiyel

        V = ∑^m e^-ikEn  Burada n=0 dan m’ye toplam kast edilmektedir. Fakat bir a

           n=0

parametresi ilavesiyle toplam işaretini kaldırabiliriz.  V(0,m) = a_n e^-ikEn  denklemi n üzerinden toplam ifade etmekte ve V(0,m) potansiyeli 0 ile m sabit tam sayıları arasında tanımlı olduğu anlaşılmaktadır. Belli bir yayın E_r enerjisine sahip olma ihtimali (olasılığı) toplam potansiyeldeki oranı kadardır. Yani,  V_r  / V(0,m) olup bu orana P_r diyebiliriz.

Böylece P_r(0,m) = e^-ikEr / a_n e^-ikEn  bağıntısını elde ederiz.

Veya aynı ifadeyi şu şekilde de yazabiliriz. P_r(0,m) = e^-ikEr / V(0,m). Belli bir Q değişkeninin beklenen değeri (bu değer enerji veya momentum olabilir) şu olur:

   Q(m) = Q_r . P_r(0,m) = Q_r . e^-ikEr / V(0,m) burada yine r değişkeni 0 dan m ye kadar toplanmaktadır.

Vakumun bir “iç enerjisi” bu yaklaşımla  U(m) = E_r e^-ikEr  / V(0,m) olur.

 

Bu ifadede r sabit tam sayılar üzerinden sıfırdan m ye kadar toplam vardır. Matematik ifadenin anlamı m kritik değerine ulaşan sistemin (vakumun) iç enerjisinin beklenen değeri olmaktadır. 

Statistik mekanikte  V(0,m) yerine aynı anlamda Z fonksiyonu kullanılmaktadır. Eğer enerji sadece sıfır ve sabit bir E değeri alabiliyorsa Z = V(0,1) olur. Bu durumda,

 

Z = 1 + e^-E/kT olur. Bu Z fonksiyonu Fermi-Dirac istatistik fonksiyonudur.

Görülüyor ki, daha önce tanımlamış olduğum en genel dalga fonksiyonu maddesel parçacıkların da istatistiğini vermektedir. Yukarıdaki V(0,m) veya Z potansiyeli ancak kritik değerin altında geçerlidir. Kritik değere ulaşıldığında durum değişir. Üst veya alt kritik değerde devreye Takiyonlar girer ve sistemde ani bir sıçrayışla farklı bir yapı oluşur. Bu yapı her sistemin kendi iç dinamiklerine göre farklı olabilir. Fakat amaç gene de yeni bir denge durumuna ulaşmaktır.

Bu değişimi bir merdivenin basamaklarını tırmanmaya benzetebiliriz. Aynı basamakta durduğumuz sürece yukarıdaki Z fonksiyonu geçerlidir. Bir basamak üste veya alta geçiş durumunda ani bir süreksiz değişim oluşur. Ancak basamak değiştiği anda yeni bir denge durumu oluşmuş demektir.

Denge durumundan uzak durumlara karasız denge durumları da diyebiliriz. İşte, kritik noktalarda sistem kararsız dengededir ve yeni bir denge durumuna ulaşması için gizli olan simetrinin kırılması gerekir.

 

Feynman çizimi

Tarih: 08:42 on 27/3/2006

Elementer parçacıkların etkileşmeleri daima bir ara parçacık (veya dalga) değiş-tokuşu ile oluşmaktadır. Bu ara parçacık maddesel bir parçacık olmayıp enerji taşıyan bir dalga paketi olarak görülmelidir. Ancak bu paketin de kendine has, ölçülebilen özellikleri vardır.

Elektromağnetik etkileşmelerin ara parçacığı bir veya birkaç fotondur. Yukarıdaki resimde iki elektronun elastik çarpışmalarını görmekteyiz. Alttaki çizimde zaman soldan sağa doğru ilerlemektedir. Önce iki elektron birbirlerine doğru yaklaşmakta sonra belli bir mesafeye kadar yaklaşınca aralarında iki bağ oluşmakta ve itici kuvvetlerin etkisiyle ayrılmaktadırlar. Çünkü, elektronlar eksi yüklüdürler ve eksi yükler birbirini iter.

Alttaki gösterim, bir önceki yazıda belirtmiş olduğum gibi, örgü alanın yoğunlaşıp bağ oluşturması durumudur. Üstteki çizim ise aynı etkileşmeyi simgesel olarak göstermektedir. Bu çizim tarzı fizikçi Richard Feynman’a aittir. Bu bakımdan benzer çizimlere “Feynman çizimleri” adı verilmiştir. Her etkileşme köşesinde yük, Baryon sayısı ve Lepton sayısı korunmalıdır. Maddesel parçacıklar düz çizgilerle ve oklarla ifade edilirken, sanal (kuvvet ileten) parçacıklar dalgalı çizgilerle gösterilir ve üzerlerinde ok yoktur. Çünkü onların hareket yönleri belli değildir. Bir parçacıktan diğerine doğru hareket etmezler. İki parçacık arasında değiş-tokuş edilirler. Sanki, selamlaşan iki kişinin birbirlerine doğru el uzatmaları gibi düşünülebilir. Bir kere selamlaştıktan sonra her biri kendi elini geri çeker ve ayrılırlar. Kuantum dünyasının elastik çarpışmalarında sarılıp kucaklaşma yoktur.

Feynman çiziminde zaman aşağıdan yukarı doğru hareket ediyor. İki elektron birbirlerine doğru yaklaşırlarken iki adet gamma ışını değiş-tokuş ediyorlar. Gamma ışınları yüksek enerjili fotonlardır. Bu bakımdan gözle görülmezler. Bir anda bu değişim oluşuyor ve sona eriyor. Böylece “kuvvet” kavramı parçacık değişimlerine indirgenmiş oluyor.

Kuantum kuramında kuvvet tanımı yoktur. Çünkü olaylar sürekli değil, kesikli olarak “anda” oluşurlar. Dolayısıyla her Feynman çizimi anlık bir fotoğraf gibidir. Etkileşme olayına süreksiz bir çarpışma olayı olarak bakabiliriz. Fotonlara da uzayın kendi yapısı içinde bir anda oluşan süreksiz bir yoğunlaşma olarak bakmak yanlış değildir.

Fakat Feynman çizimleri sadece elektromağnetik etkileşmelerde kullanılmaz. Kuantum düzeyinde her türlü etkileşmede kullanılırlar. Zayıf etkileşmelerde değiş-tokuş edilen ara parçacıklar W(+). W(-) ve Z(0) isimli parçacıklardır. Kuvvetli etkileşmelerde Љ (pi) mezonlar ve kuarklar arasında da glüonlardır.

Fakat Kuantum kuramına göre, bir kere etkileşmeye girip bir bütün oluşturmuş olan parçacıklar birbirlerinden ayrıldıktan sonra dahi birbirleri ile ışıktan hızlı haberleşirler. Bu durumu sağlayan parçacıklar değiş-tokuş edilen ara parçacıklar değildir. Bu durumu sağlayan parçacıklar Takiyonlardır. Onlar ara parçacık değildirler. Onlar doğanın düzenini sağlayan polislere benzerler.

İki parçacık birbirlerine doğru yaklaşırken örgü alanda anlık bozulmalar oluşur. Bunlara ara bağlar dedim. Aynı bağlara Kuantum kuramı ara parçacıklar diyor. O bölgeye derhal Takiyonlar ulaşır ve tekrar düzenin oluşmasını sağlarlar. Yani, elastik çarpışma durumunda parçacıkları birbirlerinden uzaklaştırırlar, veya inelastik çarpışma durumunda birleştirirler.

Elastik çarpışma durumunda dahi çarpışma öncesi ile sonrası farklıdır. Çarpışma süresinde değiş-tokuş edilen parçacık sayesinde iki parçacık arasında bilgi alış-verişi olmuştur. Buna fizik terimiyle enerji ve momentumun korunumu diyoruz. Bu yeni bilgi yüzünden, iki parçacık tümüyle bağımsız değildirler. Aralarında ışıktan hızlı bilgi iletimi vardır ve bu bilgiyi ileten de Takiyon adını verdiğimiz ışıktan hızlı hareket eden parçacık veya dalgadır. Takiyonun görevi sadece enerji ve momentum korunumunu sağlamak değil, aynı zamanda o iki parçacık arasında zaman ve uzamdan bağımsız olarak, her türlü bilgi alkışını anında ulaştırmaktır.

 

Kulplu mu kulpsuz mu

Tarih: 10:08 on 26/3/2006

 

 

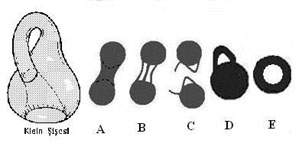
Size Möbius şeridinden söz ettim. Bu şeritin bir özelliği de kendi üzerine dönüşümlü oluşudur. Çünkü, hangi noktadan başlarsanız başlayın tek bir yüzey, dolayısıyla teklik, ile karşılaşmaktasınız. Küre yüzeyi uzayı ikiye ayırır. Kürenin içi ve dışı diye iki ayrı bölge tanımlayabilirsiniz. Sonsuz genişlikte bir yüzey de uzayı, yüzeyin altı ve üstü diye, ikiye ayırır.

Acaba uzayı ikiye ayırmayan 3-boyutlu ve kapalı bir nesne var mıdır? Evet vardır ve adına Klein şişesi denmiştir. Resimde solda görülen Klein şişesi kendi üzerine dönüşümlü 3-boyutlu bir şekildir. Klein şişesi de Möbius şeridi gibi tek yüzeylidir. Yani şişenin içi ve dışı diye iki bölge tanımlamak mümkün değildir.  Möbius şeridine olan bir diğer benzerliği de her ikisinin de bir “kesik” içerdiğidir. Möbüs şeridini yapmak için sonsuz düzlemi kesip yapıştırmanız gerekir. Klein şişesi de kendi içinden geçtiği için bir kesik, dolayısıyla bir çeşit süreksizlik içermektedir.

Fakat kesik bir görüntüdür sadece. Klein şişesine bakarken ona 4-boyutlu uzayda var olan bir varlığın 3-boyutlu uzaydaki yansıması olarak bakınız. Yani, Klein şişesi 4-boyutlu uzayda var olan bir nesnedir. Fakat üç boyutlu uzaydaki yansımasında bir kesik varmış gibi görünmektedir. Ancak, elinizle onun yüzeyini yokladığınızda kapalı ve sonlu fakat hudutsuz 2-boyutlu bir yüzey olduğu sonucuna varırsınız.

Klein şişesine baktığınızda sanki kulpu varmış görüntüsünü verir. Bu sadece bir yanıltıcı görüntüdür. Bu yanılgı 4-boyutlu Klein şişesini bilgisayarda programladığınızda açıkça ortaya çıkmaktadır. Görüntüde Klein şişesi hem kulplu hem de kulpsuz gözükür.

Kulplu bir nesneyi, örneğin bir kahve fincanını sürekli olarak değiştirerek bir simit haline sokabilirsiniz. Ama bir küre haline sokamazsınız. Çünkü iki nesnenin arasında sürekli bir ilişki yoktur. Bizim 3-boyutlu uzayımızda ise değişimler bize sürekli imişler gibi görünmektedirler. Fakat 4-boyutlu veya daha yüksek boyutlu nesneler için böyle bir kısıtlama yoktur.

Sürekli dönüşümleri inceleyen matematik dalına Topoloji adı verilmiştir. Bu dal geometrik şekilleri sınıflandırarak içinde delik bulunmayan nesnelerle delik bulunduran nesnelerin ayrı sınıflara ait oldukları sonucuna varmıştır. Ancak içinde delik bulundurmayan katı bir nesneden içinde delik bulunduran bir nesne fizik olarak oluşturmak mümkündür. Bunun için de süreklilik varsayımından vazgeçmek gerekir.

Yukardaki şekilde A durumuna bakalım. Şekil A’da Birbirinden ayrılmakta olan iki kürenin bağımsızlaşma durumundan hemen önceki halleri görülmektedir. Bu ayrılmadan önceki etkileşme durumundan daha önce Kritik kuvvet kavramı başlıklı yazımda söz etmiştim.

Ayrılırlarken şekil B’de görüldüğü gibi tek bir bağ yerine 3 adet ince bağ oluştuğunu kabul edelim. Topoloji bilimine göre bu değişim süreksiz bir değişimdir. Ancak, evrenin yapısını oluşturan örgü alanını titreşen ve süreksiz küçük yaylarla tanımlamak mümkündür. Bu bakımdan mikro evrende bu tür bağlar oluşabilir.

Bağlar koptuğunda ve nesneler birbirlerinden uzaklaştığında, şekil C’de görüldüğü gibi iki bağ birbirlerine bitişip bir halka oluştururken üçüncü bağ da tek başına kalmış olsun. Daha sonra tek olan uzantı sürekli olarak nesne ile birleşse dahi kulp halini almış olan kısım ayrı bir bölge olarak kaldığını düşünelim. Şekil D’de görülen (büyütülmüş olan) iki nesneden sadece biri olan yeni nesne sürekli dönüşümle şekil E’deki gibi bir simit haline gelebilir.

 

Sonuçta evrende görülen farklı yapıların topolojik (sürekli) değişimlerle oluşmadıklarını ve süreksiz değişimler içerdiklerini kabul etmek durumundayız.

5-boyutlu uzay

Tarih: 09:36 on 24/3/2006

 

İki kritik noktadan bundan önceki iki yazımda söz ettim. “Düzenli varlık” ve “düzenli davranışlar” bu iki kritik nokta arasında kalan salınımlar şeklinde anlaşılmalıdır. Lorenz fraktali iki çekici nokta içeriyor. Bu iki çekici nokta etrafındaki salınımlar çok küçük değişimlerle sürüp gidiyorsa olay sürekli gibi gözükür. “Sürekli  gibi” dedim çünkü burada görünen “gerçek” değildir. Altta yatan gerçek olayın bir karmaşa içerdiğidir. Yani, karmaşa kuramının süreksiz ve kendi üzerine dönüşümlü denklemleri geçerlidir. Fakat yaklaşık olarak sürekli olan bir dalga fonksiyonu kullanılabilir. Önemli olan, bir yaklaşım yaptığımızın farkında olmamızdır.

Lorenz fraktali bize “varlık” hakkında çok şey söylemektedir. Öncelikle, varlığın sonlu fakat hudutsuz olduğunu söylemektedir. Bu konuda Karmaşa ve düzen başlıklı yazıma bakınız. Fakat asıl ilginç yanı fraktalin sonsuzluk belirten yan yatmış 8 işaretine ( ∞ ) benzemesidir. Sonsuzluk ifade eden bu işaret bir dairenin 180 derece katlanmış şeklidir. İki boyutlu bir yüzey içinde var olan tek boyutlu bir çizgidir, sonsuzluk işareti. Öte yandan bu işaret hiçbir yere bizi götürmez. Aynı yerde döner durursunuz. Şu halde boyutsuz bir noktaya benzer.

Sonsuzluğun bir boyut yükselmiş görüntüsünü matematikçi August Ferdinand Möbius (1790-1868) tarafından ileri sürülmüş olan “Möbiüs şeridi” denen yapıda görmekteyiz. Bu şeridin iki boyutu olmasına rağmen tek bir yüzü vardır. Yani, alt yüzü ile üst yüzünü ayrı ayrı tanımlamak mümkün değildir.

Yukarıda görülen Möbiüs şeridini yapmak için bir kağıttan şerit alın. Bu şeridin bir ucunu diğerine göre 180 derece döndürüp yapıştırın. Bu şekilde birleşmiş olan şeridin herhangi bir noktasından başlayıp, parmağınızı hiç şeritten kaldırmadan şerit üzerinde hareket ettirdiğiniz taktirde hem şeritteki tüm noktalardan geçmiş, hem de aynı noktaya ulaşmış olursunuz. Şu halde şerit iki boyutlu olmasına rağmen tek boyutlu bir çizgiye benzer.

Üstelik şerit 3-boyutlu uzam içinde var olan bir nesnedir. Sonsuzluk işareti iki boyut içinde var olan tek boyutlu bir yapı olup boyutsuz bir nokta olarak algılanabildiği gibi, Möbiüs şeridi de üç boyut içinde var olan iki boyutlu bir yapı olup tek boyutlu olarak algılanmaktadır. Evren de benzer şekilde 5-boyut içinde var olan 4-boyutlu olup bize üç boyutlu gibi gözükmektedir. Yani bulunduğu mekan 5-boyutludur ama kendisi 4-boyutludur. Bize olan görünüşü (yansıması) ise 3-boyutludur.

Beşinci boyut ise Takiyonların boyutudur. Biz onları algılamadığımız için beşinci boyutu da algılamamız mümkün değildir. Ancak beşinci boyut matematiksel olarak kuramlara katıldığında ilginç sonuçlar vermektedir. 1920 yılında Theodor Kalutza 5-boyutlu Genel Görelilik denklemlerini çözmeyi denedi. Vardığı sonuç son derece ilginç oldu. 5-boyutlu denklemler çözüldüğünde bir yandan Maxwell’in klasik elektromağnetik denklemleri, diğer yandan Einstein’ın Genel Görelilik denklemleri doğal olarak ortaya çıktıkları görüldü. Daha sonra Oscar Klein da bu konu ile ilgilenince Kalutza-Klein kuramı ortaya çıktı.

Fakat, fizik dünyası bu kuramı kabullenmek istemedi. Çünkü 5-boyutlu uzaya pek bir anlam veremiyorlardı. Onlar için sadece matematik bir oyundu bu kuram. Son yıllarda sicim kuramı ve daha da yeni olan “membrane” yüzey kuramı ile birlikte çok boyutlu uzamlar gene gündeme gelmiş durumdadırlar.

Dört boyutlu uzay-zaman örgü alanı 5-boyutlu bir evren içinde varsa, bu örgüyü oluşturan düğümlerin farklı yoğunluklarda bir araya gelmeleri veya ayrılmaları Takiyonlar sayesinde olmaktadır. Çünkü Takiyonlar ancak beşinci boyutta hareket edebilirler. Daha alt boyutlarda etkileşime girmeleri “Tünel olayı” sayesinde olabilmektedir. Fakat bizim evrenimizdeki parçacıkların beşinci boyuta yükselmeleri mümkün değildir. Çünkü bizim evrenimizdeki parçacıklar ışıktan yavaş hareket eden parçacıklardır. Beşinci boyuta yükselmek için ışıktan hızlı hareket etmek gerekmektedir.

Beş boyutlu bir uzayın içinde bulunan bizim 4-boyutlu evrenimiz böylece hem sonlu hem de hudutsuz olabilmektedir.

Üst kritik nokta

Tarih: 09:34 on 21/3/2006

Gizli Kritik Nokta başlıklı yazımda iki adet kritik nokta bulunduğundan söz ettim. Bunlardan biri alt kritik nokta, diğeri ise üst kritik nokta olarak tanımlanabileceklerini belirttim. Alt kritik nokta durumunu süperiletkenlik olaylarında gözlüyoruz. Şimdi biraz da üst kritik noktayı nasıl gözlemlemenin mümkün olduğu hususu üzerinde duralım.

İlk örnek çok basit. Herkes kendi evinde deneyebilir. Bır yumurtanın sadece sarısını bir kaba koyun. Üzerine yarım limon sıkın ve iki kaşık zeytinyağı ilave edin. Karıştırmaya başlayın. Göreceksiniz ki karışım önce son derece düzensiz bir şekilde karışmayı ret edecektir. Yani homojen olmak istemeyecektir. Fakat karıştırmaya devam edin. Bir süre sonra aniden ve hiç beklenmedik bir şekilde, karışım homojen hale gelip son derece düzgün bir bütünlüğe kavuşacaktır. Bu örnek “mayonez” denen yiyeceğin yapılışıdır.

İşte bu aniden tek bir varlık haline dönüştüğü noktaya “Üst kritik nokta” diyorum. Bu nokta bir “an” olarak da görülebilir, soyut bir çatallaşma noktası olarak da görülebilir. “Çatallaşma” sözü “ikiye ayrılma” ifade etse de asıl önemli olan “eski durumdan aniden farklı bir duruma atlayış” olarak anlaşılması gerekir.

Bir diğer örnek “LASER” denen aletin çalışması. Bir kristalin (örneğin yakut kristali) iki yönüne ayna konmuş olsun. Bu aynalardan biri yarı geçirgen diğeri ise tam yansıtıcı olsun. Eğer bir ışık demeti yarı geçirgen taraftan içeri yollanırsa bir süre sonra çok düzgün, tek bir dalga boyu içeren bir ışık demeti dışarı çıkmaya başlar. Nedeni ise içerdeki ışığın iki ayna arasında gidip gelmesidir. Ani olarak tüm ışık dalgaları aynı dalga-boyunda bütünleşip tek bir dalga olmaya karar vermişlerdir.

Bu durum mayonez yapmak gibidir. Arada fark yoktur. Çünkü birinde siz kendiniz karıştırıyorsunuz, diğerinde aynalar karıştırma işlemini yapıyor. Karıştıkça da bütünlük ve birlik oluşuyor. Bu son dediğimi şimdi insanlara uygulayalım.

İnsanlar ufak guruplar halinde yaşayıp karışmadıkları sürece ayrı kültürler ve diller, dinler, gelenekler oluşur. Karışma ve bir-arada yaşama durumu oluşunca bir süre sonra üst kritik noktaya ulaşılır. Tüm gurup bir rezonansa girer ve ortak bir tek görüş oluşur. Bu durumda ayrı olan guruplar bir millet oluştururlar. Sonda da “devlet” ortaya çıkar.

Demek ki “devlet” gerçeği üst kritik noktaya ulaşılması ile birdenbire oluşur. İnsanlar yavaş yavaş ‘devlet kuralım’ diye bir araya gelmezler. Şartlar uygun olunca devlet kendiliğinden oluşur. Bu bakımdan bu gerçeğin üzerinde durmak gerekir. Eğer sizden bir parçayı ayırıp ona ayrı bir alt kimlik verilirse, bir süre sonra aniden bir yeni devlet ortaya çıkıverir. Osmanlı imparatorluğundan bunca ayrı dil ve dine sahip devletin ortay çıkışı bu “üst kritik nokta” durumuna ulaşılmış olduğu içindir.

Hayvanlar için de durum aynıdır. Hiç küçük serçe kuşu gurubunun havada uçuşunu izlediniz mi? Hepsi “senkonize” olarak aynı hareket içinde, bir bütün olarak uçarlar. Yani benlik kalmamıştır. Sadece birlik kalmıştır. Çünkü onlar sayıca bir üst kritik noktaya ulaşmışlardır. Aynı durum, küçük balıkların yüzüşünde de görülür. Hepsi aynı hareket içinde bir yandan diğer yana sanki tek-vücut imişler gibi yüzerler.

Bir parçacığa da böyle bakabiliriz. Parçacık bir dalga paketidir. Bundan daha önce söz ettim. Eğer dalga paketi içindeki tüm dalgalar tek bir dalga gibi davranırlarsa, yani senkron hale gelip ortak bir davranış içine girerlerse bu dalga paketi bir parçacık olur. Yani parçacık dahi “üst kritik noktaya” ulaşmış dalgaların sergilediği bir davranıştır.

Şu halde, “varlık nedir?” sorusuna geri dönecek olursak varlık, üst kritik noktaya ulaşmış olan birimlerin görüntüsüdür. Evet, sadece bir görüntüdür. Çünkü bu görüntüyü her boyutta farklı olarak algılıyoruz. Bazen parçacık olarak algılıyor ve ona “madde” diyoruz, bazen onu hayvan davranışı olarak algılıyor ve bu duruma “guruplaşma” diyoruz, bazen de insan üretimi olarak algılıyor ve ona “kültür” diyoruz.

 

Düzenli makro sistemler

Tarih: 08:07 on 12/3/2006

En genel dalga fonsiyonu olarak tanımladığım ifadenin her boyutta uygulaması bulunmaktadır. Bu ıfadedeki sabit sayılarda oluşan ufak değişiklikler çok farklı sonuçlara yol açabilmektedirler. Örgü-alan boyutundan molekül boyutuna geçtiğimizde yine aynı denklem karşımıza çıkıyor.

Kimyasal denge durumunda bir yandan kimyasal bileşenler oluşurken, diğer yanda ve aynı hızla bozunmaları gerekmektedir. Böylece her iki olayın (oluşum ve bozunum) hızı eşit olmasa da, son derece yakın olduklarını görürüz. Denge durumunda kimyasal etkileşme yokmuş gibi görünse de bu görüntü yanıltıcıdır. Denge durumu daima bir peryodik titreşim hareketi içerir.

Termodinamik bir sistemde etkileşimleri ve dolayısıyla sistemin zaman içindeki dönüşümünü saptayan fonksiyona “Termodinamik Potansiyel” denir. Bu potansiyel K harfi ile gösterilir. K’nın zaman içindeki değişimi ise:

K(t) = A. K^-Δt/RT  seklindedir. Burada A sabit bir sayı, R gaz sabiti, T sıcaklık ve Δt sonlu bir zaman aralığıdır. K(t) ifadesinin bir önceki yazıdaki (i hariç) ψ(t) ifadesine ne derece benzediği ortadadır. Zaman sonlu aralıklarla arttığında denge oluşumunda etken olan Takiyon dalga fonksiyonu

ψ(t) = a_n e^-ik(Δt)En şeklini almaktadır. Bu ifadenin gerçel kısımları değişik sistemlerin davranışlarını sergilemekte kullanılabilir.

Şimdi biraz daha üst bir düzeyde denge durumunu inceleyelim. Ekoloji denen bilim dalı doğadaki hayvan ve bitki toplulukları arasındaki denge durumu ile ilgilenir. Özelikle av ile avcı gurupların dengesi incelendiğinde oldukça basit bir ilişki ortaya çıkmaktadır. Avcı gurubun belli bir zaman aralığındaki artışı sabit bir katsayı ile belirtiliyor. Böylece avcı topluluğunu R ile belirtirsek,

ΔR / Δt = kR şeklinde bir basit fark denklemi elde ederiz. Bu denklemin çözümü gene bir önceki ifadeye benzer şekilde

R = A. e^-kΔt şeklindedir. Yukarıdaki fark denklemini biraz daha ayrıntılı hale getirebiliriz. Av ile avcının etkileşim terimini de katarsak ΔR / Δt = kR + qRP şeklini alır. Burada P terimi av olan gurubu ifade etmektedir. Aradaki etkileşim sabiti de q ile gösteriliyor. Etkileşim sabitini tespit etmeye etken olan bir özellik, iki gurubun ne derece sık karşılaştıkları olabilir. Bu denkleme Lotka-Volterra denklemi de denmektedir. Ancak bu denklem eksiktir. Zira avcı gurubun azalmasını sağlayacak bir terim eksiktir. Onu da eklersek, en genel Lotka-Volterra denklemi

ΔR / Δt = kR + qRP + ΔP şeklini alır. Şimdi 3 adet (A, k ve q) parametrenin farklı değerleri için denklem çözüldüğünde doğadaki av-avcı ilişkisini bulabilmekteyiz. Belli değerler için ilişki tümüyle dalgasal bir yapı ortaya çıkarmaktadır. Yani av azaldığında avcıların da ölümü arttığından avcı topluluğunun sayısı azalmakta, av sayısı arttığında birlikte avcı topluluğun sayısı da artmaktadır. Böylece av-avcı dengesi dalgasal bir yapı içinde sürüp gidebilmektedir.

Evrende mikro düzeyden makro düzeye kadar her sistem birçok düğüm noktasından oluşmuştur. Bu düğümler sistem büyüdükçe büyür. Sırasıyla elementer parçacıklar, moleküller, hücreler, tek veya az hücreli canlılar, çok hücreli canlılar, canlı ve cansız gurupları, gök cisimleri ve gök adaları hep aynı mekanizma sayesinde oluşurlar. Burada bilgi artışı düğüm sayısı ile orantılıdır. Bir gurubun üyesi (düğümü) ne derece çoksa bilgi birikimi o derece fazla olur. Bu bakımdan çok hücreli canlıların bilgi birikimi tek hücreli canlılardan fazladır.

 

Gök adaları ve karadeliklerde de bilgi birikimi olur. Çünkü bilgi Entropinin zıddına, düzen arttıkça artar. Bu düzeni getiren de Takiyonların etkisidir.

 

Farklı bir yorum

Tarih: 06:39 on 11/3/2006

V(z) = a_n e^izbn  olarak belirtmiş olduğum durum enerjisi, aslında tüm alan içinde oluşabilecek her türlü yapıyı tanımlayabilecek güçtedir. Çünkü, daha önce de belirttiğim gibi V(z) seri içinde seriler içermektedir ve bize çok geniş seçenekler sunmaktadır. Şu halde V(z) bir enerji olmakla beraber alanın ta kendisidir. Yani, hem dalga hem de parçacık kavramını içermektedir.

Artık V(z) durum enerjisini “alan fonksiyonu” olarak tanımlayabiliriz. Yani, alanın ta kendisi olup, dalga paketi veya eşdeğer olarak parçacık yaratma gücüne sahip yapı olduğundan ona ф(z) adını verelim. Artık bizim için “alan”, “enerji” ve “parçacık” kavramları farklı ve bağımsız kavramlar değildirler. Hepsi bir arada ф(z) = a_n e^izbn  ifadesinde bir araya gelmişlerdir.

Bu ifadeyi bir tanım olarak görürsek, a_n belirgin bir parçacığın var olduğunu bildirmekte, b_n parçacığın enerjisini ifade etmekte, z de ister x ister t veya daha farklı bir değişkeni belirtmektedir . Şu halde ф(z) dalga fonksiyonu Kuantum kuramında en önemli yapı olup bize büyük kolaylıklar sağlamaktadır. Zamanı da katarsak  ф(t) = a_n e^iktEn  olur.

ф(t) dalga fonksiyonu bizim dünyamızdaki gözlediğimiz makro olayları tanımlayabileceği gibi, çok daha büyük yapıları, örneğin gök cisimlerini hatta 4-boyutlu uzay-zaman yapısı olan tüm evreni tanımlayabilir. Dalgasal bir yapı içerdiğinden evrenin açılıp kapanmasını da, tüm var olanların tekrarlanan davranışlarını da, canlıların nefes alıp verişlerini de açıklama gücüne sahiptir.

Oysa ki varlığı oluşturan ve düzeni evrene getiren gücün Takiyonlar olduğundan söz etmiştim. Şu halde dalga fonksiyonu Takiyonları da tanımlaması gerekir. Takiyonların en önemli özelliği zamanda geri gidişleridir. Şu halde t yerine eksi t korsak yeni Psi alanı

ψ(t) = a_n e^-iktEn , E_n enerjine sahip a_n parçacığını yaratan “Takiyon alan” olarak yorumlanabilir. Burada yapmakta olduğum sadece Kuantum kuramının denklemlerini değiştirmeden yeni bir yorum getirmektir. a_n  artık alana etki eden bir operatördür.

Aynen Kuantum kuramında olduğu gibi  ψ ψ^† = lψl² parçacığın belli bir yerde var olma olasılığı olarak yorumlanır.

Şu halde Kuantum kuramındaki gibi [a_{n  ,} a_m^†] = δ_nm olmalıdır. Bu işaretten daha önce söz etmiştim (Bakınız Alan Kavramı başlıklı yazım). Kronecker deltayı kullanış nedenim zamanın sonlu ve süreksiz artışından dolayı Dirac delta fonksiyonu kısıtlamasına gerek olmamasından dolayıdır. Kronecker deltanın özelliği n ile m birbirlerinden farklı iseler sıfıra eşit, aynı iseler 1 e eşit olmasıdır. a operatörü üzerindeki küçük haçın anlamı ise “kompleks konjüge” denen özelliği içermesidir.

Bu noktadan sonra fazlaca teknik konulara girmek gerektiğinden ayrıntılardan söz etmek istemiyorum. Önemli olan Kuantum kuramının matematiğini hiç değiştirmeden yeni ve farklı bir yorum getirmiş olmamdır. Zaten fizikçilerin de en çok zorlandıkları konu budur. Matematik denklemlerde tutarlık sağlamak bir şey, onların fiziksel yorumlarını yapıp anlamlandırmak başka şeydir. Pek çok fizikçi matematik denklemleri kullanmakta ustadır ama onlara “Bu denklemler fizik alemde ne anlam taşıyorlar?” diye sorsanız, çoğu yanıt veremez.

Oysa ki biz insanlar sürekli anlam peşindeyiz. Anlam içermeyen davranışlar veya sözler bizi ilgilendirmiyor. Bu konuya kısaca değinmiştim (Bakınız Özne enerjisi başlıklı yazım). Anlamak ile bilmek farklıdır. Bilim adamları deney ve gözlem yapıp akıl ve mantığın da yardımıyla bilebilirler. Fakat bu “bilgi” içselleşirse ancak “anlamak” denilen şekle dönüşür. Dışta ve zihin düzeyinde kalırsa içselleşmiş olmaz. İçselleşmesi için varlığımızın bir parçası haline dönüşmesi gerekir.

Burada yapmaya çalıştığım “varlık” alanı olarak tanımladığımız mikro evrenden makro evrene kadar her türlü yapıya bütünsel olarak bakıp anlamlandırmaktır.

Durum Enerjisi

Tarih: 07:30 on 10/3/2006

Örgü-alan ile ilgili ulaştığımız sonuçları topluca özetlemekte yarar var kanısındayım. Çünkü bundan sonrası biraz daha derin konular içeriyor. Örgü alan her yöne doğru yayılan bir yapı olup düğüm noktalarından oluşur. Nesneler bu örgü alanın içinde değildirler. Onlar örgü alanın kendisidirler. Yani, örgü-alan belli bir bölgede sıkışıp düğümlerin yoğunluğu arttığında “nesne” oluşur. Nesne bir dalga paketidir. Tek bir dalga değildir. Dolayısıyla her nesne, en küçükten en büyüğe kadar, bir dalga sistemidir.

Burada “dalga paketi” ile “sistem” sözcüklerini aynı anlamda kullanıyorum. Yani, tek parçacık fikrinden vazgeçip “düğümlerden oluşmuş bir sistem” kavramına geçmek gerektiği görüşündeyim. Her düğüm küçük bir yay gibi titreşir. Eğer örgü-alanın düzgün bir bölgesinde isek o bölgeye “boşluk” veya “vakum” demekteyiz. Ancak boşluk veya vakum denilen bölge dahi enerjiden yoksun değildir. Çünkü her titreşen düğüm noktası enerji içermektedir.

Titreşen yayların enerjilerine “potansiyel enerji” veya “durum enerjisi” diyoruz. Yaylar (düğümler) vakum bölgesinde küçük titreşimler yaparlar. Bu bakımdan vakum titreşimleri hiçbir şekilde sıfıra eşit olamazlar. Bu titreşimler doğal olarak karmaşa yaratırlar. Karmaşanın oluşması için herhangi bir dış etkinin olması gerekli değildir. Karmaşa oluştuğunda düğümlerde yerel olarak bir miktar yoğunluk artışı belirir. Bu yoğunluk artışı iki farklı durum ile sonuçlanabilir.

Bu iki farklı durumdan biri yoğunluğun dağılması ve düğümlerin eski hallerine dönerek tekrar zayıf titreşim hareketlerine devam etmeleri ile sonuçlanır. Bu sonuç, simetrinin geri gelmesi olarak da tanımlanabilir. Çünkü vakum durumunda tam bir simetri vardır. Her titreşen küçük yay diğer her yay ile aynıdır ve bu bakımdan birbirlerinden ayırt edilemezler.

İkinci durum yoğunluğun artarak çoğalması ve yayların daha çok gerilmeleri sonucu durum enerjisinin yerel olarak birikmesi durumudur. Böylece belli bir örgü-alan bölgesi vakumdan farklı bir yapıya ulaşır. Eğer bu yapı dağılmayıp varlığını sürdürürse o bölgede “parçacık” adını verdiğimiz belirgin bir dalga paketi meydana gelir. Bu yeni durumda artık simetri aniden kırılmıştır.

 

Her parçacık bir “yay sistemi” olduğundan küçük yay enerjilerinin toplamı da parçacığın enerjisini oluşturur. Tek bir klasik yayın durum enerjisini V(x) = kx²/2 şeklinde tanımlamıştım. Öte yandan hem düzenli sistemlere hem de karmaşaya yol açabilecek olan durum enerjisini  V_n+1(z) = a.(z_n)² - b. (z_n)⁴ denklemi ile ifade etmiştim (Bakınız: Titreşen kuantum düğümler başlıklı yazım).

Bu durum enerjisini V = a z² + b z⁴ şeklinde yazarsak bir uzun polinom serinin ilk iki terimi şeklinde düşünebiliriz. En genel halinde ise

 V(z) = a₀ z⁰ + a₁ z¹ + a₂ z² + a₃ z³ + a₄ z⁴ ..........

Şeklinde bir sonsuz seri olur. Bu serinin bazı a sabitleri sıfıra eşittir bazıları değildir. Örneğin, n> 4 için tüm  a_n ler sıfıra eşittir dersek, seriyi ilk 5 terimle kısıtlamış oluruz. Dolayısıyla a sabitelerini belirlemeden V(z) = a_n zⁿ şeklinde yazabiliriz. Burada yapılan kabul şudur: Eğer bir belirleyici (indeks) hem altta hem de üstte tekrarlanıyorsa o belirleyici sıfırdan sonsuza kadar arttığında oluşan terimler toplanmalıdır. Böylece, üstteki uzun seriyi kısa olarak belirtmiş olduk.

Bu mantıkla bir önceki yazımda seri açılımını göstermiş olduğum e^z de V(z) ile aynı yapıda olduğundan a_n parametresi yardımıyla durum enerjisi: 

V(z) = a_n e^izn  = a₀ e^iz0  + a₁ e^iz1 +  a₂ e^iz2  + a₃ e^iz3  ...........

 

Şeklinde serilerden oluşmuş bir seri olarak ifade edebiliriz. Eğer daha da genel hale getirmek istersek bir de b_n parametresi katarak durum enerjisini:

 

V(z) = a_n e^izbn  şeklinde pek çok a_n ve b_n parametrelerine bağımlı bir seri olarak yazabiliriz. Böylece her türlü oluşuma açık ve üstelik gerçel ile sanal terimler içeren bir durum enerjisi oluşmuş olur. Bu durum enerjisi hakkında gelecek yazıda daha ayrıntılı bilgi vereceğim.

 

Tekrarlanan hareketler

Tarih: 09:04 on 9/3/2006

 

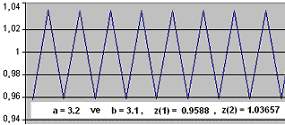
Gizli Kritik noktaya doğru çekilen sistem 3 farklı davranış gösterebilir. a) Sabit bir kritik noktaya doğru gittikçe küçülen adımlarla yaklaşır ve noktasal sonsuzluğa ulaşır. b) Kritik noktaya hiç ulaşamaz ama onun etrafında peryodik (tekrarlanan) salınımlar yapar. c) Karmaşık bir düzen içinde kritik nokta civarında dolanır.

Üçüncü durumu bir önceki yazımda inceledim. Birinci durumu da Altın Oran başlıklı yazımda incelemiştim. Şimdi b durumu üzerinde biraz duralım. Doğada pek çok dengeli yapı sabit aralıklarla tekrarlanan hareketler yapar. Mikro alemdeki atomların yapısından tutun da makro alemdeki gök cisimlerine kadar, varlığını sürdüren yapılarda bu tür tekrarlanan bir hareket görmekteyiz.

Dünyamızda yaşayan tüm canlılar varlıklarını sürdürmek için tekrarlanan hareketler yaparlar. Nefes alıp verme hareketi, kalbin açılıp kapanarak kanı pompalaması, beslenmedeki sürekli tekrar durumu, düzenli olan periyodik hareketlerdir.

Yukarıdaki grafikte V_n(z) fonksiyonunda a = 3.2 ve b = 3.1 değerleri için potansiyelin iki nokta arasında gidip geldiğini görmekteyiz. Ancak, bu iki nokta rasyonel sayılar değildirler. Z(1) ve Z(2) noktaları hiç bitmeyen bir dizi şeklinde sürüp giderler. Yani her iki nokta da irrasyonel sayılardır. Aynen pi ve e sayıları gibi bitmeyen bir yapıları vardır. Şu halde bu durumda dahi bir tür karmaşa vardır ama sistemin dengeli bir yapı gösterip varlığını sürdürmesini sağlayan bir karmaşa türüdür. Fizik kuramlarındaki sabit sayıların irrasyonel olduklarından daha önce söz etmiştim.

Fizik kuramları düzenli olarak kendini tekrarlayan hareketlerin matematik ifadelerinde sinüs ve cosinüs fonksiyonlarını kullanırlar. Her iki fonksiyonda kendini tekrarlayan bir yapı vardır. Sin ve Cos şeklinde kısaltılarak tanımlanan bu iki fonksiyon artı 1 ile eksi 1 arasında sürekli olarak değişirler.

Her iki fonksiyon da e sayısı ile yakından ilişkilidir. e^u = cos(u) + i.sin(u) şeklinde yazılabilir. Burada i = √-1 dir. Bu iki terimden birincisi gerçel ikincisi sanaldır. V_n(z) potansiyelindeki z sayısı da z = a +i.b şeklinde yazılabilir. Z sanal sayısı ile e sayısı arasında belirgin bir benzerlik göze çarpmaktadır. Ayrıca e fonksiyonuna e denmesinin nedeni eksponansyel (geometrik) bir artış içinde oluşundan dolayıdır. Bu artış ile n>1 şartını içeren herhangi bir zⁿ polinomu aynı olmasalar da belli bir değere kadar benzer bir yapı gösterirler. Zaten bizim için de önemli olan belli iki değer arasındaki salınım hareketidir.

Bu bakımdan dalgasal hareketi belirtmek için genelde e fonksiyonu kullanılır. Nitekim, eksponansyel (üstel) fonksiyonun seriye açılımı:

                     e^x = 1 + x + x²/2! + x³/3! + x⁴/4! + ......

şeklinde sonsuza doğru artarak gider. Bu serideki ilk 5 terim göz önüne alındığında karşımıza V_n(x) potansiyelinin davranışına benzer bir yapı ortaya çıkmaktadır. Üstel artışı doğada birçok sistemim artış şeklinde görmekteyiz. Bir beslenme ortamında mikro organizmalar (tek hücreli canlılar) üstel olarak artarlar. Yani, artışları çizgisel değildir. Bulaşıcı hastalıkların yayılımı da çizgisel değildir. Örneğin, çiçek hastalığını taşıyan virüs insanlar arasında üstel olarak yayılır.

Elektrik devrelerde önemli rol oynayan kondansatörler üstel olarak dolarlar ve boşalırlar. Örütbağa bağlanan bilgisayar sayısı da belli saatlerde üstel olarak artar. Her bilgisayar örütbağın bir düğümü olarak görülürse, düğüm sayısının da üstel olarak arttığını görmekteyiz.

Doğada atmosfer basıncı da yükseklik arttıkça üstel olarak azalır. Radyoaktif maddelerin bozunması da  üstel bir değişimin sonucu olduğu saptanmıştır. Kuantum mekaniğinde Schrödinger dalga denklemini sağlayan fonksiyonun da üstel bir fonksiyon olması tesadüf değildir.

Gizli Kritik nokta

Tarih: 17:45 on 8/3/2006

 

Örgü-alanın taban enerjisi olarak tanımlanabilecek olan V_n(z) potansiyeli kendi üzerine dönüşümlü bir yapıya sahiptir. Zira her yeni adımda bir önceki potansiyel değeri esas alınmakta ve yeni değer süreksiz artışlarla oluşmaktadır. Demek ki, başlangıç şartları önemsizdir. Potansiyeli herhangi bir değerden başlayarak hesaplayabiliriz.

Yukarıdaki şekilde V_n(z) potansiyelinin a ve b nin belli bir değeri için karmaşa durumunu oluşturduğu görülmektedir. Vakumun simetrik yapısından aniden ortaya çıkan bu karmaşa durumuna simetrinin aniden kırılması denmektedir. Modern fizik kuramlarında gizli simetrinin aniden kırılması önemli bir yer işgal eder. Vakum dediğimiz örgü-alanın düzgün olan bölgesinde yüksek bir simetri hakimdir. Vakumda hiçbir küçük bölge diğer bir bölgeden ayırt edilemez. Çünkü ayırt etmek için herhangi bir referans (nirengi) noktamız yoktur.

Fakat vakumun doğal titreşimi sonucu çok küçük etkiler dahi büyük ve çok farklı sonuçlara yol açabilmektedirler. Belli şartlar altında örgü-alanda simetri aniden kırılmakta ve alanın bir bölümü “Acayip çekici” adı verilmiş olan noktaya doğru çekilmektedir. Örneğin, mutlak sıfır olan –273 derece C’ye yaklaşınca metallerin elektrik akımına karşı gösterdikleri direnç aniden sıfıra düşmektedir. Bu düşüş tedrici değil çok ani ve süreksiz bir şekilde olmaktadır.

Çok düşük sıcaklıklarda yapılan deneyler beklenmedik sonuçlar vermektedirler. Ani bir değişiklik sonucu oluşan yeni tür maddelerde bir “Kritik Kuantum noktası” bulunduğu gözlenmiştir. Bu nokta civarında maddenin birçok özellikleri değişmekte, sistem tam olarak uyumlu bir davranış içine girmektedir. Bu konu henüz çok yeni olduğundan hem deneysel hem de kuramsal çalışmalar sürmektedir.

Klasik çok parçacıklı termodinamik sistemler de bir Kritik noktaya sahiptirler. Örneğin su ile su buharı normal basınç ve sıcaklıkta iki ayrı faz oluştururlar. Fakat basıncı ve sıcaklığı arttırırsak belli bir noktada iki faz aradan kalkar ve su molekülü sıvı faz ile gaz fazı arasında sürekli titreşir. Yani hem sıvı hem de gaz fazındadır. Bu noktaya Kritik Nokta denir, Suyun kritik noktası 374 derece C ve 218 Atmosfer basınçtır. Yani, normal hava basıncının 218 katına ulaşmak gerekmektedir. Görülüyor ki hem sıcaklık hem de basıncın iki aşırı ucunda kritik noktalar bulunmaktadır. Hava, atmosferin en üst tabakalarında çok düşük basınca sahiptir. O bölgede hava molekülleri yer çekim kuvvetinden kurtulmakla kurtulmamak arası bir ara durum oluştururlar. İşte o bölgede hava basıncı Kritik bir alt değerdedir.

Şu halde iki farklı uçta bulunan Kritik noktalardan söz edebiliriz. Bunları “Alt Kritik nokta” ile “Üst kritik nokta” olarak tanımlayalım. Genel olarak bu iki kritik noktada sistem kararsız denge içindedir. Ufak bir etki ile bir fazdan diğerine geçebilir. Ancak, göz önüne alınan sistem ne olursa olsun, gizli bir kritik noktası daima bulunmaktadır. Bu gizli kritik noktaya doğru hareket eden sistemin gizli olan simetrisi de aniden kırılabilmektedir. Yukarıdaki grafikte sistemin kararsız bir denge içinde Gizli Kritik Nokta etrafında salınışını görmekteyiz.

Gizli kritik noktada hem itici hem de çekici kuvvetlerin etkin oldukları söylenebilir. Çünkü sistem karmaşa içine girse dahi, yine de tümüyle kontrolden çıkmamaktadır. Bu sayede yeni oluşumlar ve her boyutta sistemin kendisine benzeyen yapılar ortaya çıkmaktadırlar. Tek bir parçacık dahi örgü-alan içinde birçok düğüm noktasından oluşmuş olduğundan bağımsız bir nesne olarak değil, bir sistem olarak düşünülmesi gerekir.

Şu halde, “sistem” tanımını en genel anlamda alıp, örgü-alan içinde çatallaşmış herhangi bir yapı olarak anlayabiliriz. Bu yapıyı oluşturan “Acayip çekici” ise Gizli Kritik Noktadır. Bu noktayı her ne kadar matematikten çıkarmış olsak da, doğadaki çeşitli durum ve davranışların yorumunda büyük fayda sağladığını da kabullenmek zorundayız.

Titreşen kuantum düğümler

Tarih: 06:43 on 8/3/2006

Varlığın oluştuğu 4-boyutlu yapıya Örgü-alanı dedim. Bu alanda her nokta “asemtotik anlamda” özgürdür. Yani birbirlerine yakın iken belli bir yön tercihleri yoktur ve her biri komşusu ile zayıf bir şekilde etkileşir. Şu halde aralarındaki uzaklıkta önemli bir değişiklik oluşmadığı sürece örgü alanın yapısı simetriktir. Ancak düğüm noktalarını birbirlerine göre olan uzaklıkları değiştirecek bir etki oluşursa, o zaman simetri bozulmuş olur.

Bu durumu anlamak için bir su kütlesini düşünelim. Su moleküllerini etkileyen herhangi bir enerji kaynağı yoksa su durgun görünür. Oysa ki su molekülleri birer elektrik dipol (iki kutuplu yapı) gibi sürekli titreşirler. Ancak su moleküllerinin herhangi bir tercihli yönleri olmadığından su molekülleri düzenli ve belirgin bir yapı yerine, akışkan ve amorf bir görüntü sergilerler. Dolayısıyla su moleküllerinin oluşturdukları yapı karmaşık ve simetriktir.

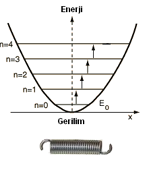
Örgü alanını da aynen su gibi düşünebiliriz. Her bir düğüm noktası su molekülleri gibi titreşir, fakat her bir düğüm komşu düğümlerle zayıf bir etkileşme içinde olduğundan bağımsız bir küçük yay gibi davranır. Yani, her bir düğüm noktası bir “Kuantum harmonik osilatörü” (sabit titreşim frekansı olan küçük bir yay) şeklinde düşünülebilir. Resimde görülen yay düğüm noktalarını simgelemekte ve üstteki grafik yayın enerji seviyelerini göstermektedir. Her bir düğüm noktası bir kuantum titreşeni olduğundan enerji seviyeleri de süreksiz ve sonludur. Grafikte x ekseni yayın gerilim miktarını, y ekseni ise enerji seviyelerini gösteriyor.

Kuantum harmonik titreşeninin enerji seviyelerini hesaplamak mümkündür. Bu seviyeleri sıfırdan başlayan tamsayılarla ifade edersek:    E(n) = (n + ½).hf ,  n = 0, 1, 2, 3, .... şeklinde sonlu tam sayılar olup, h Planck sabiti ve f yayın titreşim frekansıdır. Bu enerji denklemine göre yayın en düşük enerjisi (Taban Enerjisi) n = 0 durumunda E(0) = hf/2 gibi sıfırdan farklı bir değerdir.

Yayın Taban Enerjisi en doğal haline, yani geriliminin çok az olduğu x'in yaklaşık olarak sıfıra yakın olduğu duruma denk gelir. Bu da örgü-alanı için “vakum” durumu demektir. Çünkü, vakum durumunda herhangi bir parçacık bulunmadığından düğüm noktaları arasında gerilim çok az fakat gene de sıfırdan farklıdır. Görüyoruz ki kuantalaşmış yaylarda hiçbir gerilim durumu bulunmasa dahi enerjileri sıfırdan farklıdır. Bu durum, bir yandan daha önce sözünü ettiğim, “vakum titreşimlerinin”  oluşmasına neden olurken, diğer yandan sıfır boyutlu noktasal sonsuzluğun oluşmasına da engel olur.

Kuantum titreşeninin enerji seviyeleri süreksiz olduklarından, bir seviyeden diğerine ani bir sıçrayışla yeni yapılar oluşur. Örgü-alan içinde oluşan parçacıklar ve dalga paketleri sürekli bir şekilde oluşmazlar. Aniden, enerjinin fraktal özelliğe sahip oluşundan dolayı, süreksiz bir şekilde, düzensizlikten düzenli yapılar ortaya çıkar. Enerjinin fraktal bir yapıya sahip olduğunu klasik yayın enerjisini hesapladığımızda görebiliriz.

Klasik yayın potansiyel enerjisi E_p = k.x²/2 şeklindedir. Burada k yay sabiti ve x yayın gerilme miktarıdır. Potansiyel enerji yayın gerilimi ile doğru orantılı olmayıp,  (kuadratik) x’in karesi ile orantılıdır. Daha önce de gördük ki kareli ifadeler içeren denklemler daima karmaşık davranışlara ve düzensiz yapıların oluşmasına neden olmaktadırlar. İşte bu yüzden, düzenli gibi görünen boşlukta (vakumda) daima karmaşaya yol açabilecek ve farklı yapıların ortaya çıkmalarını sağlayacak gizli bir enerji bulunmaktadır.

Karmaşa oluşması için en basit sonlu artış denklemini Karmaşa ve düzen başlıklı yazımda vermiştim. O denklemi tekrar yazarsak  P_n(x+1) = a.P_n(x) – b.P_n(x)² denkleminde sonlu artışları örgü-alanın küçük yaylarına uygulayalım. Bu durumda P(x) ile E_p eşleştiğinde x = z² ve P(x)² ile (E_p)² eşleştiğinde x² = z⁴ ile orantılı olur. Şu halde sonlu artan ve karmaşa içeren potansiyel enerji:

                                V_n+1(z) = a.(z_n)² - b. (z_n)⁴   şekline dönüşür.

Burada z değişkeni “kuantize edilmiş sanal” bir değişken olduğundan z₀ sıfırdan farklı sonlu bir sayıdır. Sistemin Taban Enerji ise n = 0 için herhangi bir başlangıç noktası olan V₁(z) değeridir. Sabit a ve b parametrelerinin değeri enerji denkleminin gelişimini tayin ederler.

Belli a ve b değerleri düzenli yapılara ve enerji seviyelerine doğru sistemi götürürken, az farklı a ve b değerleri sistemi karmaşaya sürükleyebilirler. Ayrıca z_n değeri sonsuza kadar artmayıp, n’nin belli bir değerinde V potansiyelinin çatallaşmasını sağlamaktadır. Böylece sistemde sürekli kendine benzeyen fakat yine de farklı olan yapılar oluşabilmektedir.

  

Kritik kuvvet kavramı

Tarih: 07:17 on 7/3/2006

 

Örgü-alan yaklaşımına göre evren ve tüm var olanlar, bu 4-boyutlu alanın değişik bölgelerdeki değişik yoğunlukları oluyorlar. Fakat bizim yoğunluk kavramının aksine, düğümler arası mesafe ne kadar az ise, yani düğümler ne kadar sık ise, o bölgede o kadar az parçacık vardır. Çünkü örgü muntazam bir kristal yapısında olduğunda her nokta eşdeğerdedir ve yapıda hiçbir yoğunluk farkı oluşmaz.

Yoğunluk farkının oluşması için düğümler arası mesafede bir düzensizlik oluşması gerekir. İşte bu düzensiz yapıyı düzeltmek görevi Takiyonlara düşmektedir. Örgüde düzensiz yapı oluştuğu anda (düğümler arası mesafe değiştiğinde) anında oraya Takiyonlar hücum edip örgüyü tamir etmek için harekete geçerler. Bu da örgüye düzeni geri getirir. Yani düzensizlikten düzen oluşur.

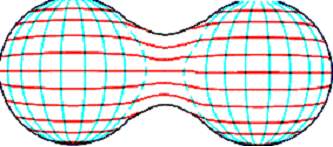
Yukarıdaki resimde örgü-alan içinde oluşmuş iki küresel parçacığın etkileşimini görüyoruz. İki küre birbirlerine yaklaştıklarında (veya bitişik iken uzaklaştıklarında) aralarında bir köprü oluşur. Örgü-alanın kendisi olan bu köprü üzerinde bulunan düğüm noktaları, küreler üzerindeki düğüm noktalarına oranla daha geniş aralıklıdırlar. İşte Takiyonlar bu köprü bölgesinde etkin olup yeniden aralıkları eşitlemekle yükümlüdürler.

Eğer parçacıklar ayrılıyorlarsa tekrar birleşmeleri için kuvvet üretirler. Bu kuvvete bir önceki yazımda Adezyon ve Kohezyon kuvvetleri dendiğinden söz ettim. Eğer parçacıklar bir-araya gelmekte iseler bu bütünleşmeyi bir an önce sağlamak için köprü durumunda etkin olmaya başlarlar. Fakat ayrı olan parçacık sistemlerinde dengenin sağlanması her zaman çekici kuvvetlerle olmaz. Bazen de itici kuvvetlerin devreye girmeleri gerekir. İşte bu yüzden iki tür kuvvetin varlığı gereklidir (Bakınız: Etkenlik-edilgenlik başlıklı yazım).

Takiyonlar bizim vücudumuzdaki koruyucu “Antikor” denen akyuvarlara, savaşan hücrelere benzerler. Nasıl ki yabancı bir canlı (mikrop veya virüs) bedene saldırdığında bu hücreler koruma görevini yükleniyorlarsa, Takiyonlar da uzay-zaman örgüsünü koruma görevini yüklenmişlerdir. Daha önce Takiyon evren ile bizim ışık-altı parçacıkların evreni varlıklarını sürdürmek için birbirlerine muhtaç olduklarını söylemiştim. Evren de bedenimiz gibi korunmaya muhtaçtır. Bedenimizde akyuvarlar bedeni koruyarak varlığını sürdürmesini sağlarlar. Çünkü onların koruyucu etkisi olmasa insan bedeni yabancı organizmaların saldırısına dayanamaz. Takiyonlar da benzer şekilde 4-boyutlu uzam-zaman örgüsünde oluşan dengesizlikleri düzelterek örgüye düzen getirirler ve örgünün varlığını sürdürmesini sağlarlar.

Takiyonların düzen sağladıkları doğru olsa da, bu düzen dış görünüş olarak karmaşaya da benzeyebilir. Çünkü onların düzen sağlayışları bir fraktal yapı oluşturup “acayip çekici” adını verdiğimiz görünmez merkeze doğru sistemi harekete geçirmek şeklindedir. Bu arada karmaşık bir hareket oluşsa da altta gizli olan bir simetri, bir harmoni, bir denge durumu vardır (Bakınız: Doğanın estetiği başlıklı yazım).

Örgü-alan yaklaşımının önemli bir diğer özelliği de tek bir düğüm noktası yerine düğüm noktalarının topluluğu ile ilgilenmesidir. Yani, tek bir parçacık dahi birçok düğüm noktasından oluşmaktadır. Bu bakımdan örgüde düğümler arası etkileşme ve iletişim her boyutta geçerlidir. Nasıl ki bir bedende atomlar, hücreler, dokular ve uzuvlar bir araya gelip birbirlerinden bağımsız davranmıyorlarsa, örgü-alan tarafından oluşturulan yapılar da bağımsız değildirler. Çok düğümlü yapılar parçacıklara, onlar da daha karmaşık madde türlerine dönüşüyor.

Çok-düğümlü bir yapıda geçerli olan kuvvet ikili etkileşme kuvveti değildir. O sistemin kritik bir alt ve üst değerinde devreye giren bir “Kritik Kuvvet” olarak ele alınması gerekir. Zira değişimler sürekli olmayıp ani kırılmalar ve sıçramalar şeklinde olmaktadırlar (Bakınız: Türlerin oluşumu başlıklı yazım). Bu bakımdan gerek mikro alemde gerekse makro alemde etken olan kuvvetler çatallaşma noktasında aniden etken olmaya başlayan “Kritik kuvvetler” olarak görülmeleri gerekir.  Kuvvetlerin etkisini iki parçacık arasında değil, parçacıklar topluluğuna (veya alt düzeyde düğümler topluluğuna) etken olan kuvvetler olarak incelemek gerekmektedir.

Bu bakımdan itici ve çekici kuvvetleri, ancak belli bir kritik değere ulaştıklarında etkinlikleri ortaya çıktığına göre, daha farklı bir yaklaşımla "Kritik" noktada tanımlamak gerekecektir.

 

Adezyon ve Kohezyon kuvvetleri

Tarih: 07:18 on 6/3/2006

Bir önceki yazımda sözünü ettiğim “Asemtotik özgürlük” kavramı Kuarklar için geçerlidir. Baryonları oluşturan Kuark adı verilmiş olan parçacıklar serbest halde görülmüyorlar. Bu durumu açıklamak için ileri sürülen “Asemtotik özgürlük” kavramına göre iki adet Kuark parçacığını birbirlerinden uzaklaştırmaya çalıştıkça aralarındaki çekim kuvveti artmaktadır. Yani hayali bir yay ile bağlı gibidirler. Eğer bir parçacığın içinde bulunuyorlarsa serbest parçacıklar gibi davranırlar. Ancak hayali yay onların serbest olarak gözlenmelerini önler.

Bu durumu klasik fizikte (makro düzeyde) gözlenen Adezyon ve Kohezyon kuvvetlerine benzetebiliriz. Adezyon, bir sıvının (örneğin suyun veya yoğun bir sıvının) cama yapışması durumunda etkin olan kuvvettir. Çay içerken bardağı kaldırdığınızda küçük çay tabağının da birlikte kalktığına çok kere şahit olmuşuzdur. İşte iki cam tabakayı birbirlerine yapıştıran, suyun özelliği olan Adezyon kuvvetidir.

Kohezyon kuvveti ise suyun veya yoğun bir sıvının moleküllerini bir arada tutan kuvvettir. Bir musluktan su damlarken önce küçük bir damla oluştuğunu, sonra damlanın büyüyüp aşağı doğru uzadığını ve nihayet musluktan kopup bağımsız halde, fakat yine de bir bütün olarak yere doğru düştüğünü gözlemişizdir. Yukarıdaki resimde bu üç ayrı durum görülüyor.

Yukarıdaki resimde, ortadaki görüntü üzerinde biraz duralım. Damlanın nasıl da musluktan ayrılmamak için direndiğini, nasıl da yerçekimi kuvvetine karşı koymaya çalıştığını görüyoruz. Uzamış olan boyun kısmında moleküller-arası uzaklık diğer bölgelere göre daha fazladır. Bu durum Alan kavramı başlıklı yazımdaki tepe görüntüsüne benzer.

Örgü-alan yaklaşımında ise aynı durumu düğümler-arası aralığın artışı olarak yorumlamak mümkündür. Asemtotik özgürlük sınırlaması çerçevesinde noktalar (düğümler) arası açıldıkça aralarındaki çekim kuvveti artar. Bu artış deneysel olarak da kanıtlanmış bir durumdur.

Adezyon veya eşdeğer olarak kohezyon kuvvetini deneysel olarak ölçmek için şöyle bir deney yapılmıştır. Yatay duran geniş bir cam yüzeyin altına değişik boyda küçük cam yüzeyler su ile tutturulmuştur. Suyun adezyon kuvveti sayesinde küçük cam levhalar düşmeden yüzeye yapışmışlardır. Daha sonra küçük cam levhalara belirli ağırlıklar yapıştırılmış ve hangi ağırlıkta büyük cam yüzeyden ayrılıp düştükleri saptanmıştır. Böylece yüzey alanı ile adezyon (kohezyon) kuvveti arasında bir ilişki bulunmuştur.

Aradaki sıvı tabakanın her örnekte aynı kalınlıkta olduğunu kabul edersek, sıvının hacımı camın yüzey alanı ile doğru orantılı, dolayısıyla, aynı zamanda, sıvıda bulunan molekül sayısı ile de doğru orantılıdır. Ne kadar fazla su molekülü varsa o kadar fazla adezyon kuvveti oluşmaktadır. Şu halde yer çekim kuvveti ölçüldüğünde adezyon kuvveti de ölçülmüş olur.

Bulunan sonuca göre adezyon kuvveti artan yüzeyle doğru orantılı olarak artmamakta, alanın karesini içeren kareli (çizgisel olmayan) bir yapı göstermektedir. Yani, molekül sayısı arttıkça moleküller-arası çekim kuvveti (kohezyon kuvveti) molekül sayısı ile doğru orantılı olarak artmamaktadır. Bulunan sonuca göre

Kuvvet = 0.0667 S² + 7.7664 S denklemini sağlıyor. Burada S molekül sayısıdır. Yukarıdaki resimde görülen damlada molekül sayısı arttıkça, damlanın yerçekim kuvvetine karşı direnci doğrusal olarak değil, daha güçlü bir şekilde (kuadratik olarak) artmaktadır.

Yukarıdaki denklemde çekici kuvvet aynı zamanda bir “acayip çekici” gibidir. Damlanın ayrılıp düşmesine neden olan kuvvet çizgisel olmadığından karmaşık (belirsiz) bir zaman aralığı içinde düşer. Yani suyun damla halinde birikimi istediği kadar düzgün olsun, yine de bir sonraki damlanın ne zaman düşeceğini kestiremeyiz. Doğanın karmaşık yapısı bu basit örnekte ortaya açıkça çıkmakta, çizgisel ve sürekli fonksiyonların doğayı açıklamakta yetersiz kaldıkları görülmektedir.

Örgü Alan Kuramı

Tarih: 07:57 on 5/3/2006

Bir önceki yazımda alan kavramı üzerinde bir miktar durdum. Alan kavramı biraz yanıltıcı olabilir. Zira “alan” deyince 2-boyutlu bir yüzey akla geliyor. Oysa ki benim kast ettiğim alan 4-boyutlu uzam-zaman yapısıdır. Bu bakımdan göz önüne getirilemez. Çünkü bizim uzayımızda 3-boyutlu uzam ile tek boyutlu zaman ayrılmış durumdadır.

Bu durumu göz  önüne getirmek için şöyle düşünün: Üç boyutlu bir küp olsun. Bu kübün eni ve boyu yüksekliğine göre çok daha fazla olsun. Yani yassı bir kâğıt gibi olsun. Kâğıdın kalınlığı çok az olduğundan bize iki boyutlu bir yapı gibi görünür. İşte zaman da diğer üç boyuta göre çok kısa aralıklarla arttığından bize uzamdan farklı imiş gibi görünüyor.

4-boyutlu uzam-zaman yapısı bir kristaldeki gibi düzgün aralıklardan oluşmuş bir yapıdır. Bu yapıya “Örgü Alan” (Lattice Field) adı verilmiştir. Örgü alanın aynen bir örgüde olduğu gibi düğüm noktaları ve aralarında boşluklar vardır. Bu boşluklar bizim “vakum” adını verdiğimiz boşluklar değildir. Bu boşluklar Takiyon evrenin varlık alanıdır. Yani uzam-zaman konisinin dışında kalan bölgedir (Bakınız: Uzam-zaman konisi başlıklı yazım).

Modern fizik biliminde bu türden bir Örgü-alan kuramı geliştirilmiş durumdadır. Ancak Takiyonlar henüz dahil edilmiş değildir. 4-boyutlu örgü alan ilk olarak 1975 yılında Amerikalı fizikçi Keneth Wilson tarafından ileri sürülmüştür. Bu sayede standart modelin sayısal olarak hesaplanması mümkün olmuştur.

Elementer parçacık fiziğinde kuvvetli etkileşmeler “pertürbasyon” (seriye açılım) metodu ile analitik hesaplara gelmiyorlar. Bu bakımdan sayısal çözümler, özellikle çizgisel olmayan yapılar için, daha uygun bir yaklaşım olmaktadır. Ancak, geniş örgü alanlarını hesaplamak için çok hızlı ve çok büyük bellekli özel bilgisayarlar gereklidir. Önümüzdeki yıllarda bu tür güçlü bilgisayarlar geliştirilecek ve hesaplar yapılabilecektir.

Örgü alanı göz önüne getirmek için bir önceki yazımın üst kısmındaki resme bakın. Bu resimde tepelerin bulunduğu bölgeden uzak olan düz alan oldukça düzgün ve homojen bir yapı gösteriyor. İşte o düzgün bölge bizim “vakum” adını verdiğimiz, maddesel dalgaların (nesnelerin) bulunmadığı bölgedir. Fakat o bölge tümüyle enerjiden yoksun da değildir. Her düğüm noktasında az da olsa bir miktar enerji bulunmaktadır. Örgünün bir bütün olarak varlığı için bu enerji gereklidir.

Tepe kısmına yaklaştıkça örgünün düğüm noktaları arasındaki aralık artmaktadır. En yüksek tepede ise düğüm aralığı bayağı artmış durumdadır. Bu durumu “Asemtotik özgürlük” ile açıklayabiliriz. Bu kavram da yüksek enerji fiziği yapan fizikçiler tarafından kullanılan başarılı bir kavramdır. Asemtotik bağımsızlık kavramını bulan üç fizikçi, Gross, Politzer ve Wilczek 2004 yılında Nobel fizik ödülünü almışlardır.

Bu kavrama göre iki Kuark (bizim modelimizde düğüm noktası) arasındaki uzaklık azaldıkça serbestlik dereceleri artar. Yani örgü aralıkları azaldıkça dalga özgür bir parçacık gibi davranır. Örgü aralıkları arttıkça (tepe noktasına yaklaştıkça) dalga bağımlı duruma geçer ve özgürlüğü azalır. Özgürlüğün azalması bağımlı durumun, dolayısıyla çekici kuvvetlerin artması anlamına gelir. Bu sayede tepenin sonsuz yüksek olmasına ve noktasal sonsuzluğa dönüşmesine de engel olunmuş olunur. 

Bu durumu TE modeli ile daha kolay anlayabiliriz. Örgü alanında düğümlerin arası açıldıkça Takiyonlar için daha geniş bir boşluk oluşur. Bu boşluktan geçen Takiyonlar, 4-boyutlu örgünün düğüm noktaları ile etkileşime girebilirler ve düzen getirirler. Düzenin gelmesi ise bağımsızlığın azalması, yani Entropinin azalmasıdır. Bu sayede parçacık adını verdiğimiz, yerel olarak örgüde yoğunlaşmış yapılar oluşur. Resimdeki tepe bölgesinde iki adet parçacık görülüyor. Yüksek tepedeki parçacığın kütlesi diğerine göre daha fazladır.

Örgü alanının düğümleri arasındaki boşluk azaldıkça Takiyon etkisi de azalır. Dolayısıyla bizim evrenimizde görülen düzensizlik, yani bağımsızlık ortaya çıkar. Böylece etkileşmelerin de gücü azalır. Çok uzun dalga boyları ortaya çıkar ve tepeler belirgin olmaz. İşte bu tür düşük enerjili dalgaların bulunduğu örgü bölgesine biz boşluk veya “vakum” diyoruz.

Alan kavramı

Tarih: 09:06 on 4/3/2006

 

Einstein Özel Görelilik kuramındaki eksiklikleri gidermek için Genel Görelilik (GG) kuramını ileri sürmüştür, ama bu kuram da birtakım sorunlar içermektedir. Bu sorunların ne olduklarından daha önce söz ettim ve onları gidermek için Takiyon Evren Modelini bir miktar (düşünce boyutunda) açıkladım. Bilimsel olarak kabul görmesi için TE modelinin matematik yapısını oluşturmak gerekecektir.

TE modelinde hem GG kavramları hem de Kuantum Kuramının (KK) kavramları yer alıyor. Bir yandan uzay-zaman eğriliği içinde her nesnenin enerji olduğu ileri sürülürken diğer yandan KK’nın sonlu enerji kavramı da varsayılıyor. Yani, uzay-zaman sürekli değil. Bu bakımdan GG sürekliliği yerine Karmaşa kuramındaki süreksiz ve sonlu değişimler içeren matematik yaklaşım geçerli olmalıdır (Bakınız: Karmaşa kuramı başlıklı yazım).

Uzam-zaman yapısını anlamaya yukarıdaki resim yardımcı olabilir. Her “var olan” uzam-zaman yapısında bir “yoğunlaşma” gibi görülebilir. Yani hareket eden bir dalga uzam-zaman içinde hareket etmiyor. Uzam-zamanın kendisi yerel olarak sıkışarak yoğunlaşıyor. Bu yoğunluğun yer değiştirmesi de bize hareket gibi görünüyor. Fakat uzam-zaman var olabilmek için saniyede milyarlarca kere titreşiyor. Bu titreşimler Takiyon evrenle maddesel evrenin etkileşimi sayesinde sürüyor. Yani, TE modelinde iki türlü Takiyon etkisi var. Bir yandan bildiğimiz evrenin çok kısa süreler içinde açılıp kapanmasını sağlarken, diğer yandan bildiğimiz evren içinde düzen sağlayarak, yerel olarak düzenli yapıların oluşmasını sağlıyor.

KK bu arada neden gerekiyor? Çünkü KK olmasa, yani enerjinin sonlu olduğu sınırı getirilmese, yerel olarak sonsuz enerjiye sahip yapılar oluşabilir. Yukarıdaki resimde görülen yerel yapının sonlu yükseklikte oluşu bu nedendendir. Eğer Kuantum sınırı olmasa bu tepe sonsuz darlıkta ve sonsuz yükseklikte olabilir. Bu da yerel olarak noktasal sonsuzluk demektir. Bu konuyu da ayrıntılı inceledim (Bakınız: Noktasal sonsuzluk başlıklı yazım).

Uzam-zamanın sonlu aralıklar içeren hem uzamda hem de zamanda süreksiz bir yapı olduğunu düşünelim. Bu yapının her “düğüm noktasında” bir enerji fonksiyonu tanımlayabiliriz. Uzam-zaman 4-boyutlu olduğundan enerji fonksiyonunun da 4-boyutlu olması gerekir. Bu fonksiyonu daha iyi anlayabilmek için “Kuantum Alan Kuramı” denen KK’nın daha gelişmiş şeklini incelemek gerekir.

Elektromağnetik olayları açıklamak için geliştirilmiş olan Kuantum Elektrodinamiğinde (KE) iki türlü alan tanımlanır. Bunlardan biri skaler alan, diğeri vektör alandır. Skaler alan tek bir sayı içerir ve yönü yoktur. Yani her noktada bulunabilir ve hiçbir yön belirlemez. Vektör alan ise 3  bileşenlidir ve daima bir yön belirtir. Böylece iki alanı içeren 4-boyutlu bir alan tanımlanabilir.

KE’de yer ve momentum değişkenleri sürekli olduklarından sonsuzluklar bu kuramda karşımıza çıkmaktadırlar. Bu sonsuzluklardan kurtulmak için İngiliz fizikçi Paul Dirac tarafından özel bir sınırlayıcı matematik yapı teklif edilmiş ve bu yapıya “Dirac Delta Fonksiyonu” (DDF) denmiştir.

Dirac delta fonksiyonunu anlamak için yukarıdaki resme bakınız. Bu fonksiyon yukarıda görülen tepeye sınır getiriyor ve suni olarak sonsuza kadar yükselmesine engel oluyor. Bu yapay zorlama genel bir kabul görmüştür, çünkü sürekli uzam-zaman başka şekilde kontrol altına alınamamaktadır. Oysa ki süreksiz uzam-zaman durumunda bu sorunla karşılaşmıyoruz. DDF yerine Kronecker Delta (KD) denilen daha basit ve süreksiz sınırlama geçerli olabilir. Böylece zorlama DDF varsayımından kurtuluruz.

4-boyutlu uzam-zaman içinde herhangi iki noktanın yerini n ve m harfleri ile gösterelim. İki nokta farklı ise n ile m farklı, aynı ise n = m olsun. Bu durumda KD için δ harfini kullanırsak  n = m durumunda δ = 1 ve diğer tüm hallerde (n farklı m için) δ = 0   şekilde tanımlanabilir. Bu tanım sayesinde her düğüm noktası için bir yer ve momentum değeri içeren Alan fonksiyonu tanımlanabilir. Böylece her düğüm noktasında belli bir “dalga alanı değeri” (dolayısıyla parçacık) tanımlanabilir. Ancak, bu alanın parçacık özelliğini yansıtması için birtakım özel şartlara da uyması gerekir.

Özelden Genele

Tarih: 06:43 on 3/3/2006

Bir önceki yazımda elde ettiğim zaman aralığı denkleminin üzerinde biraz durmak istiyorum. Artı işaretlisini tekrar yazarsak,

 

                            Δt’ = Δt . (1 – V ² / c ² )^1/2

 

V = 0 durumunda  Δt’ = Δt olur. Yani iki gözlem çerçevesi birbirlerine göre hareket etmiyorlarsa ikisinin de zamanı aynıdır. Bu bakımdan duran çerçevelerde uzunluklar da aynı değerde olur. Bizim gündelik hayatta yaptığımız zaman ve uzam ölçümlerinde aynı sonucu elde etmemizin nedeni budur. Dünyadaki yapılan tüm ölçümlerde göreli hız ışık hızına göre o kadar küçüktür ki fark ihmal edilip sıfır kabul edilebilir. Yani, dünya olaylarında yukarıdaki denklem geçerli olsa da aradaki zaman farkı ölçülemeyecek kadar küçüktür.

İkinci bir değerlendirme V göreli hızın ışık hızına yaklaştığı durumdur. Limit hal olarak V = c alalım. Karakökün içi sıfıra eşit olur. Zaman genleşmesi görebilmek için Δt terimi ile ilgilenmemiz gerekir. Zira bir önceki yazıya bakarsak A’ çerçevesine ait olan q ve q’ noktaları arasındaki uzaklığa qq’ = V.Δt demiştik. Şu halde A’ çerçevesinde geçerli zaman Δt zaman aralığıdır. Bu durumda Δt = Δt’ /  0  yani Δt sonsuz olur. Şu halde göreli hız ışık hızına yaklaştıkça hareketli çerçevede zaman genleşir ve ışık hızında sonsuz olur. Zamanın sonsuz olması ne demektir?

Zaman aralığının sonsuz olması demek, ışık hızında hareket eden bir nesne için zamanın geçmeyeceği, daha doğrusu sürekli bir “an” yaşanacağı demektir. Bunun anlamı ışık hızında zaman kavramının geçersiz olduğudur.

Özel görelilik kuramına “Özel” denmesinin nedeni sadece kısa mesafelerde geçerli olması ve uzay söz konusu olduğunda geçersiz oluşudur. Özel Görelilik kuramının şu zaafları vardır:

1.            Bu kuram sadece sabit hızları göz önüne almaktadır. Oysa ki evrende ivmeli hareket yapan çerçeveler de vardır. Şu halde bu kuram ivmeli hareketi, dolayısıyla kuvvetleri dışlamaktadır.

2.            Bu kuram sadece Öklid geometrisi ile hesap yapmaktadır. Öklid geometrisi sadece düz yüzeylerde geçerlidir. Eğri yüzeyleri içeren bir kuram değildir.

3.            Bu kuramda Kartezyen koordinatlar kullanılmıştır. Oysa ki doğa yasalarını tek bir koordinat sistemi ile açıklamak yanlıştır. Doğa yasaları her türlü koordinat sisteminde aynı sonuçları vermelidir.

4.            Bu kuramda hareketin nedeni açıklanmıyor. Bu bakımdan Kinematik bir kuramdır. Dinamik değildir.

İşte bu 4 zaaf karşısında Einstein kuramı daha genel bir çerçeveye oturtmak istemiş ve 10 yıl kadar uğraştıktan sonra Genel Görelilik kuramını ileri sürmüştür.

İki yönlü zaman

Tarih: 11:51 on 2/3/2006

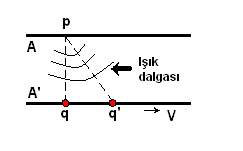
Şekilde görülen iki A ve A’ gözlem çerçeveleri olsun. Bunlardan A’ çerçevesi A ya göre V hızıyla hareket ediyor olsun. Belli bir anda A çerçevesindeki p noktasından bir ışık demeti A’ ne doğru gönderilsin. Işık A dan A’ ne ulaşana kadar q noktası q’ noktasına ulaşmıştır.  Şu halde qq’ = V.Δt (x=vt tanımından) olur. Çünkü A’ çerçevesinden ancak t zamanı ölçülebilir.

Öte yandan bu iki çerçeve hiç kımıldamadan karşılıklı dursalar A dan ölçüldüğü gibi pq = c.Δt’  olması gerekir. Zira c hızı sabittir ve duran iki çerçeve için hareket olmadığından zaman aralıkları aynı olur. V hızı ile hareket eden A’ çerçevesinde ışığın q’ noktasına vardığını ancak A’ de bulunan gözlemci bilebilir. Onun da ölçtüğü zaman kendi zamanı olmayıp Δt aralığıdır. Işık q’ noktasına vardığında pq’ = c.Δt olmalıdır. Pisagor teoremini kullanarak:

                (c. Δt’)² + (V.Δt)² = (c.Δt)² 

 denkleminden her iki tarafı c² ye bölerek.

                (Δt’)² = (1 – V ² / c ² ). (Δt)²    elde ederiz.

Bu denklem Özel Görelilik kuramında zaman genleşmesini hesaplamaya yarayan önemli bir ifadedir. Ancak Δt’ zaman aralığını hesaplamak için her iki tarafın karekökünü almak gerekir. Bu durumda:

Δt’ = Δt . (1 – V ² / c ² )^1/2    ve   Δt’ = - Δt . (1 – V ² / c ² )^1/2

Şeklinde iki denklem edilir. Genelde geriye giden zaman kabul edilmediğinden eksi işaretli ikinci terim yok sayılıp sadece artı işaretli olan birinci terim kabul edilir. Oysa ki bu iki terimin varlığı zamanın iki yönlü akabileceğinin kanıtıdır. Zamanın iki yönlü akabileceğinden daha önce söz ettim (Bakınız: Işıktan hızlı başlıklı yazım)

 Özel görelilik kuramının en önemli sonucu yukarda ifade ettiğim uzunlukların azalması ve zamanın yavaşlaması değildir. En önemli sonuç Enerji ile kütle arasındaki    E = m. c²   bağıntısıdır.  Bu denklem öylesine önemli bir buluştur ki hem teknolojinin hem de felsefenin büyük bir sıçrama yapmasına neden olmuştur.

Teknolojide Nükleer santralların yapımında bu denklemin önemli bir katkısı olmuştur. Eğer bu denklem olmasaydı radyoaktif maddelerin enerji denklemleri yazılamazdı ve sayısal olarak açığa çıkan enerji hesaplanamazdı. Daha sonra atom ve hidrojen bombalarının yapımı da tümüyle bu denklem sayesinde olmuştur.

Felsefe de bu denklemden etkilenmiştir. Artık biliyoruz ki her nesne enerjiye dönüşür. Enerji maddedir, madde de enerji. Şu halde madde anlayışımız da tümden bu denklem sayesinde değişmiştir. Eskiden maddenin 3-boyutlu olması gerektiği inancı vardı. Şimdi biliyoruz ki madde değişik yoğunluklarda enerjidir. Görelilik kuramı sayesinde dünya görüşümüz değişmiş, mutlak kavramların geçersiz oldukları anlaşılmıştır.

İkizler çelişkisi

Tarih: 07:44 on 2/3/2006

Bir önceki yazımda A ve A’ gibi iki gözlem çerçevesinin farklı hızlarda hareket ettiklerini varsaymıştım. A nın hızı V ve A’ nın hızı V’ olsun deyip V’ > V şartını koşmuştum. Bu şart altında birbirlerine göre sabit hızla hareket eden iki gözlem çerçevesinden ölçülen uzunluklar ve zaman süreleri eşit olmadıkları sonucu çıkmıştı.

Her iki gözlem çerçevesinde bulunan gözlemci için kendi gözlem çerçevesi hareketsiz olmasından yararlanarak A nın V hızını sıfır olarak kabul edelim. Yani V = 0 olup A gözlem çerçevesi hareketsiz varsayılabilir. Şu halde Δx > Δx’ ve Δt < Δt’ eşitsizliklerinden ilkine göre hareketli bir çerçevede belli bir uzunluk, duran çerçeveye göre daha kısadır. Aynı mantıkla hareketli çerçevede belli bir zaman süresi, duran çerçeveye göre daha uzundur.

Birinci eşitsizlikte hız arttıkça boyda kısalma olması durumuna “Lorentz-Fitzgerald kısalması”, ikinci eşitsizlikte hız arttıkça zamanda uzama durumuna “Zaman genleşmesi” adı verilmiştir. Hareketli çerçevenin hızı ne kadar ışık hızına yaklaşırsa o derece zaman genleşir. Zamanın genleşmesi saatlerin daha yavaş çalışması demektir. Kime göre daha yavaş? Duran gözlemciye göre daha yavaş. Çünkü mutlak bir zaman kavramını terk ettik.

Δt duran çerçevedeki zaman olduğuna göre, belli bir süreyi belirtsin. Bu süreye T diyelim. Hareketli çerçevede aynı süreye karşılık gelen zaman aralığı Δt’ olduğuna göre ona da T’ diyelim. T’ > T demek, hareketli çerçevede belli bir sürenin, örneğin duran çerçevedeki 1 saniyenin daha uzun sürmesi dolayısıyla zamanın hareketli çerçevede yavaşlaması demektir.

Bu sonuç sadece kuramsal bir sonuç olmayıp, çok hassas atomik saatlerle yapılmış ve uçakta seyahat eden saatin yavaşladığı saptanmıştır. Bu deney yapılmadan önce çok tartışılan ikizler çelişkisinden söz edeyim. İkiz olan iki kardeşten biri yer yüzünde kalmakta, diğeri ışık hızına yakın bir hıza sahip bir uzay gemisi ile bir süre seyahat ettikten sonra yeryüzüne inmektedir. Hızlı hareket eden çerçevelerde zaman yavaşladığına göre hareketli ikizin daha yavaş yaşlanması gerekir. Böylece yeryüzüne döndüğünde duran ikiz kardeşten daha genç olması gerekir.

Fakat çerçeveler eşdeğer olduklarından hareketli ikizin çerçevesinden bakıldığında kendisi durmakta, dünyadaki ikizi ışık hızına yakın hareket etmektedir. Şu halde dünyadaki ikizin zamanı yavaşlamalı ve kendinden genç kalmalıdır. Hareketli ikiz kardeş yeryüzüne döndüğünde duran ikiz kardeşi kendinden daha genç olmalıdır. Bu durum çelişkili midir?

Çelişkinin çözümü iki gözlem çerçevesinin eşdeğer olmadıklarında yatmaktadır. Hareketli ikiz yeryüzünden ayrılıp ışık hızına yakın bir hıza ulaşması için hızının artması gerekir. Yani iki çerçeve birbirlerine göre sabit hızla hareket etmezler. Bu durumda görelilik ilkesi geçersiz olur (çünkü iki çerçeve eşdeğer olmazlar) ve çelişki ortadan kalkar. Eğer yan-yana (bir araya gelmeden) sabit hızla geçiş durumu ileri sürülürse o zaman da hangisinin daha genç kalmış olduğunu saptamak mümkün değildir. Çünkü her bir çerçevede zaman süresi ölçen saatler bir araya gelip karşılaştırılmadıkları sürece hangisinin daha yavaş ilerlediği saptanamaz. Birinden diğerine zaman bildirmek için ışık sinyali gönderildiğini ileri sürebilirsiniz. Fakat ışık bir çerçeveden diğerine ulaşması için de gene zamana gerek duyacağından bu süre hesaba katılmadan zaman tespiti de yapılamaz. Bu süre ise mutlak olmayıp gözlemciye göre değişen göreli bir süredir.

Özel görelilik kuramının ileri sürdüğü zaman genleşmesi deneysel olarak Muon adı verilen bir parçacığın davranışında ortaya çıkmaktadır. Muonlar ağır elektronlardır. Maddesel parçacıklar olmalarına rağmen sabit bir yapıları yoktur. Ömürleri 2.2 mikro saniyedir. Kozmik ışınların hava moleküllerindeki protonlara çarpması sonucu oluşan Muonların yeryüzüne ulaşmadan bozunup yok olmaları gerekir. Oysa ki yeryüzü laboratuarlarında Muonlar gözlenmektedir.

Bu gözlemin açıklaması, hızlı hareket eden Muonların zamanı yavaşladığından bozunma sürelerinin uzadığı ve bu sayede yeryüzüne ulaşabildikleri şeklindedir.

Göreli uzam ve zaman

Tarih: 16:50 on 1/3/2006

Bir önceki yazıda dedim ki: “referans noktası olan A noktası aynı zamanda sonlu ile sonsuzun kesiştiği bir “çatallaşma” noktasıdır. Her nesne bu noktadadır.”  Fakat her nesne kendi referansı olan A noktasındadır. Tüm var olanların tek bir ortak A noktasında bulunmaları düşünülemez. Öncelikle bu durumun böyle olması gerektiğini Kuantum kuramı söylüyor.

Maddesel parçacıklar aynı anda aynı yeri kaplayamazlar (Bakınız: Takiyon etkisi başlıklı yazım). Şu halde her nesnenin kendine ait bir “şimdi” ve “burada” noktası olan A noktası olması gerekir. Bunun anlamı da “bir tek şimdi” kavramının olamayacağıdır. Her var olanın şimdi’si farklıdır. Dolayısıyla aynı anda (şimdiki anda) oluştuğu sanılan olaylar arasında belli bir zaman farkı olması gerekir. Demek ki her var olan için aynı olan, mutlak ve tek, bir zamandan söz edilemez.

Benzer şekilde tek bir uzamdan da söz edilemez. Her var olanın ölçtüğü uzam kendi gözlem çerçevesine bağlı olacağına göre uzunluk ölçümleri de farklı değerler verir. Bu farkı yaratan da gene tek bir ortak A noktasının olanaksızlığıdır. Ancak uzam-zaman konisi içinde kalan noktalar arasında nedensellik geçerli olduğundan farklı dahi olsalar uzamla ve zamanla ilgili ölçümler hesaplanabilir. Uzam-zaman konisi dışındaki olayların ne uzamları ne de zamanları hesaplanamaz.

Uzam-zaman konisi içinde kalan olaylar görelidir. Yani ne tek bir uzamdan ne de tek bir zamandan söz edebiliriz. Bu durumu daha iyi anlayabilmek için “eylemsiz” (birbirlerine göre sabit hızla hareket eden) gözlem çerçevelerine bakalım. Eğer bulunduğumuz odada hareket eden hiçbir nesne yoksa bu odanın hareketsiz mi olduğu, yoksa sabit hızla hareket halinde mi olduğu bilinemez. “Bilinemez” derken, yapacağınız hiçbir deney bu farkı saptayamaz. Şu halde sabit v hızıyla hareket halinde olan bir gözlem çerçevesi duran gözlem çerçevesinden ayırt edilemez. İkisi eşdeğerdir. Tek bir gözlem çerçevesi hareketi de saptayamaz.

Bu tanım aslında Newton’un birinci yasasından farklı bir şey değildir. Çünkü Newton’un birinci yasasına göre: “Bir cisme dış kuvvet etki etmezse o cisim ya sabit yerinde kalır (v =0), veya sabit hızla hareket eder (v = sabit).” Yani, iki durum tamamen eşdeğerdir.

Şu halde eylemsiz gözlem çerçevelerinin eşdeğer oluşu ve birbirlerinden ayırt edilemeyişleri Newton’un birinci yasasından başka bir şey değildir. Demek oluyor ki bir cismin hareket ettiğini saptamak için iki gözlem çerçevesine gerek vardır. Şu halde 2 gözlem çerçevesi ile çalışalım. Bunlara A ve A’ diyelim. Bizim için A ve A’ eşdeğerdir. Çünkü birbirlerine göre sabit hızla hareket halindedirler. Ama, her bir gözlem çerçevesinde bulunan gözlemci için kendi gözlem çerçevesi hareketsizdir.

A gözlem çerçevesinde ölçülen hız kendi hızı olamaz. Ancak A’ nün hızı olabilir. Eşdeğer olarak A’ gözlem çerçevesinde ölçülen hız kendi hızı olamaz. A’ den ölçülen hız A nın hızıdır. Bu durumu şöyle düşünün. Siz bir odadasınız ve odada her nesne hareketsiz. Camın önünden bir kuş geçiyor. Siz kuşun hızını ölçebilirsiniz. Yani kuşun size göre hızını ölçebilirsiniz.

İşte bu noktada görelilik işin içine giriyor. Ölçülen hız, mutlak hız değil, göreli hızdır. Şimdi hızı tanımlayalım. Tanım: Sabit v hızının ifadesi v = Δx / Δt dir. Yani hızı ölçmek için uzunluk boyutundaki değişim miktarını zamandaki değişim miktarına bölmek gerekir. Dikkat ederseniz, “değişim miktarından” söz ediyorum. Tek bir noktada ölçüm yapmaktan söz etmiyorum. Değişim miktarını ölçmek için iki farklı zamanda ölçüm yapmak gerekir.

Bu durumda A gözlem çerçevesinden ölçülen V hızı A’ gözlem çerçevesinin hızı olur. Eşdeğer olarak A’ gözlem çerçevesinden ölçülen V’ hızı da A nın hızı olur.

V = Δx’ / Δt’ ve V’ = Δx / Δt olmak durumundadır. Çünkü A dan ölçülen V hızı A’ nün yolu ve zamanı olmak zorundadır. A çerçevesi içinde tüm cisimler durağan olduğundan, kendi yol ve zamanını ölçemez. Keza A’ den ölçülen yol ve zaman A nın yol ve zamanı olmak zorundadır. Çünkü bu iki gözlem çerçevesi eşdeğerdir.

Şimdi, V’ > V diyelim. Bu tanım tamamen görelidir. Bizim A gözlem çerçevesinde bulunduğumuzu ve diğer gözlem çerçevesinin bize göre hareketli olduğunu ifade etmektedir. V’ hızı V hızından büyüktür demek, bizim penceremizin önünden bir kuş geçti ve biz onun hızını bize göre ölçtük demektir. Hız tanımından (Δx / Δt ) > (Δx’ / Δt’) olmalıdır.

Şu halde Δx > Δx’ ve Δt < Δt’ olmak zorundadır. Çünkü bir oranın diğerine göre büyümesi için ya pay kısmının büyümesi veya paydanın küçülmesi veya hem pay kısmının büyümesi hem de paydanın küçülmesi gerekir. Bu iki eşitsizlikten ortaya çıkan ilk sonuç iki farklı gözlem çerçevesinde uzunluk farklarının ve zaman aralıklarının aynı olamayacağıdır.

Uzam-Zaman konisi

Tarih: 07:49 on 1/3/2006

TE modelinde iki adet, hem bitişik hem de iç-içe olan, evrenden söz ettim. Bu iki evreni göz önüne getirmek için yukarıda görülen Uzam-Zaman konisi şekli yardımcı olabilir. Yatay eksen 3-boyutlu bildiğimiz uzamı ve dikey eksen tek boyutlu zamanı belirtsin. x-ekseni tek boyut olarak çizilmesine rağmen üzerindeki düz çizgi bir 3-boyutlu vektör olduğunu belirtiyor. Dolayısıyla resimdeki koni 4-boyutlu uzay-zaman yapısını tanımlıyor. Üstteki koni geleceği ve alttaki koni geçmişi simgeliyor.

Işık hızı c sabit olduğundan kolaylık olsun diye c = 1 alınabilir. Bu bakımdan x = c.t ile tanımlanan ışığın aldığı yol x = t eşitliğine dönüşür. Resimde x’in t’ye eşit olduğu çizgi koninin yüzeyidir. Çünkü koninin kenarı her iki eksene eşit uzaklıkta olup, her iki eksenle 45 derecelik bir açı yapmaktadır.

Böylece iki ayrı bölge beliriyor. Biri koninin içi, diğeri koninin dışıdır. İçinde bulunan bir nesne için, örneğin B noktasında, daima x < t olur. Herhangi bir ışıktan yavaş hareket eden nesne için yol denklemi x = v.t olup v < c dolayısıyla v < 1 olmalıdır. x / t = v yazıp v < 1 olduğundan x / t < 1 ve x < t buluruz. Şu halde koninin içi ışıktan yavaş hareket eden parçacıkların bölgesi koninin dışı ise ışıktan hızlı hareket eden parçacıkların bölgesidir. C noktasında ancak bir Takiyon bulunabilir.

Bu iki evrenin kesiştiği A noktasında x = 0 ve t = 0 olduğundan bu nokta bizim için referans noktası olup “burada” ve “şimdi” noktasıdır. Yani bizim özümüz (öznemiz) A noktasında durmaktadır. Bu noktada ise hem B bölgesi hem de C bölgesi aynı derecede yakın, aynı derecede iç-içedir.

İnsan tin ve ten bütünlüğü olduğundan daima A noktasında bulunur. Koninin içindeki herhangi bir noktadan A referans noktasına ulaşan bir etki nedensellik ilkesine uyar. Çünkü koninin içinde hareket eden herhangi bir etkinin hızı ışık hızından küçüktür. Oysa ki koninin dışından referans noktasına ulaşan bir etki ışıktan hızlı hareket etmesi gerektiğinden ancak Takiyon etkisi olabilir. Bu tür bir etkinin nedensellik ilkesine uyması gerekmez.

Koninin yüzeyi ışık hızı bölgesidir. Dolayısıyla koninin dışında bulunan Takiyonlar iç bölgeye etki etmeleri için koninin yüzeyinden içe doğru bir etkide bulunmaları gerekir. Bu etkiyi de Kuantum kuramının öngördüğü “Vakum titreşimleri” sayesinde yaparlar.

Özel Görelilik kuramının temel varsayımına göre “Birbirlerine göre sabit hızla hareket eden bütün gözlem çerçeveleri için ışığın hızı sabittir.” Bu durumun oluşması için her bir gözlem çerçevesinin A noktasında bulunması gerekir. Çünkü ancak o zaman koninin yüzeyi 45 derecelik bir açıyla görülebilir. Şu halde birbirlerine göre sabit hızla hareket eden tüm gözlem çerçeveleri eşdeğerdedir. Birinin diğerine göre üstünlüğü yoktur.

Ayrıca A referans noktasında hem zaman hem de uzam sıfıra eşit olduklarından bu noktada duran özne için ne zaman ne de uzam kavramı sürekli değişkenler olabilir. Yani “burada” ve “şimdi” noktasında uzam ve zaman hem sonludur hem sonsuz. Eğer A noktasına gelen etkiler koninin içinden geliyorlarsa uzam ve zaman sonludur. Eğer dışından geliyorlarsa uzam ve zaman sonsuzdur. Çünkü Takiyonların hızı sonsuz olabilir.

Şu halde referans noktası olan A noktası aynı zamanda sonlu ile sonsuzun kesiştiği bir “çatallaşma” noktasıdır. Her nesne bu noktadadır. Ancak insanın durumu biraz farklıdır. İnsan bu A noktasında durduğunun farkındadır. Farkında olduğu için de hem sonlu hem de sonsuz bölgelere doğru etkilerde bulunabilir, oralardan da bilinçli etkiler alabilir. Farkındalığı sayesinde evrensel enerjiyi kullanabilir. Farkındalığı sayesinde uzam ve zamanın süreksiz olduklarını algılayabilir.

Daha da ilginci, farkındalığı sayesinde hayal edip ışık konisinin dışına çıkabilir. Çünkü ışık konisinin dışına çıkabilmek demek, uzam-zaman yapısının nedensellik bağlarını koparmak demektir. Bunu da ancak insan başarabilir.

Çatallaşma noktası

Tarih: 07:00 on 28/2/2006

Bir önceki, Görüngübilim yaklaşımı başlıklı yazımda “öznelerarası etkileşim ile iletişim temelinde öznel olana önem verilir”, dedim. İlk bakışta özneye önem vermek pozitif bilimi ret etmek gibi gelebilir. Çünkü her özne kendi bakış açısından bir “gerçek” tanımı yapacağından ortak bir gerçeklik üzerinde anlaşmaya varmak imkânsız olacaktır.

Oysa ki durum hiç de öyle değil. Eğer özneler arasında belli bir düzenli ilişki varsa, daha doğrusu ikisinin anlaştığı tek bir ortak referans noktası varsa, bu nokta sayesinde ortak bir gerçek üzerinde anlaşmaya varılabilir.

Örneğin, zaman kavramını ele alalım. İngiltere’de trenlerin bir istasyondan belli bir saatte kalkıp diğer bir istasyona hangi saate ulaşacaklarını bilmek hem yolcular bakımından hem de istasyon şefleri bakımından önemli idi. Bunu sağlayabilmek için, 1852’de Londra’daki Greenwich rasathanesi istasyonlara telegrafla trenlerin hareket saatini bildirmeye başladı. Greenwich ortalama zamanı 1855 yılında tüm İngiltere’de ortak referans olmaya başlamıştı. Bir süre sonra tüm Avrupada GMT zamanı ortak bir referans noktası olarak kabul edildi. Günümüzde tüm dünya GMT sayesinde kendi yerel zamanlarını, gerekli saat farkı düzenlemesini yaparak, saptamaktadırlar.  

Demek oluyor ki, tek bir ortak referans noktası tüm dünyada zaman kavramının düzene girmesi için yeterli olmaktadır. Fakat bu pratik çözüm kuramsal olarak da geçerli midir? Yani, farklı gözlem çerçevelerinden izlenen zaman için de ortak bir referans noktası var mıdır?  Evet, vardır ve bu ortak referans noktası ışığın birbirlerine göre sabit hızla hareket eden gözlem çerçevelerinde aynı sabit hıza sahip oluşudur.

Einstein 1905 yılında Özel Görelilik kuramını yayınladığında önemli bir varsayımdan hareket etmişti. Bu varsayıma göre: “Birbirlerine göre sabit hızla hareket eden bütün gözlem çerçeveleri için ışığın hızı sabittir.” Böylece ortak bir referans noktası bulunmuş ve bu ortak nokta sayesinde  sabit hızla hareket eden tüm gözlem çerçevelerinin eşdeğer oldukları ve birbirlerinden ayırt edilemez oldukları görüşü ileri sürülmüştür.

Bu kabul sayesinde her bir farklı gözlem çerçevesi (isterseniz gözlem çerçevesi yerine özne deyin) farklı zamana sahip olsalar dahi, biri bilindiğinde diğeri hesaplanabilmektedir. İşte doğada da her karmaşık sistemin sabit bir referans noktası vardır ve bu noktaya da “acayip çekici” adı verilmiştir. Bu nokta sayesinde karmaşık sistem bir anda düzene girer. Yani, bu nokta sayesinde düzensizlikten düzen ortaya çıkar.

Düzensizlikten düzenin ortaya çıktığı noktaya “çatallaşma noktası” (bifurcation) dendiğini daha önce açıklamıştım (Bakınız: Türlerin oluşumu başlıklı yazım). Demek ki acayip çekici nokta aynı zamanda çatallaşma noktasıdır. Bu bakımdan bundan sonra “acayip çekici” yerine “çatallaşma noktası” terimini kullanacağım, zira “acayip” sözü insanda yanlış çağrışımlara neden olabiliyor.

Doğada sabit değerde hareket eden ışık bir çatallaşma noktasıdır. Bu sabit değerin altında ayrı bir evren, üstünde ayrı bir evren oluşmaktadır. Altında oluşan evren bizim içinde yaşadığımız maddesel parçacıklar evrenidir. Üstünde oluşan evren ise sanal kütleli, Takiyon adını verdiğimiz, parçacıklar evrenidir. Bu iki evren hem ayrı hem iç-içedirler. Ayrıdırlar, çünkü çatallaşma noktası onları ayırmıştır. İç-içedirler çünkü temel yapıda herhangi bir değişiklik yoktur. Aynı gerçekliğin iki ayrı yansıması (kolu) durumundadırlar.  Biz sadece kendi evrenimizi ölçüp Takiyon evreni ölçemiyorsak nedeni bizim kollardan biri üzerinde bulunmamızdandır. Eğer bu evrenin dışına çıkıp gözlem yapma imkânımız olsaydı her iki evreni de gözleyip ölçmek olanağımız olurdu.

Yukarıda da belirttiğim gibi, düzensizlikten düzenin ortaya çıktığı nokta çatallaşama noktasıdır. Bu nokta bizim evrenimiz için sabit olan ışık hızıdır. Takiyonlar ışıktan hızlı hareket ettiklerinden, kendi evrenlerinden bizim evrenimize düzeni ışık hızına  yavaşladıkları anda getirmektedirler (Bakınız: Takiyon etkisi başlıklı yazım).

 

Görüngübilim yaklaşımı

Tarih: 17:56 on 27/2/2006

Jacques Derrida’nın “yapı bozumu” kavramını biraz daha açmak istiyorum. Yapı bozumu derken, kalıplaşmış, tartışması bitmiş, mutlak düşünce kalıplarının bozulmaları gerekliliği anlaşılmalıdır. Örneğin,”nesne” dendiğinde tümüyle tanımlı, sınırları belli olan, kendi başına bağımsız bir varlık düşünmek, belirli bir yapı oluşturmak demektir. Oysa ki bu kavramın içerdiği pek çok ayrıntıyı ele alıp onların bütünsel ilişkisini incelemek, yapı bozmaktır.

Bu yaklaşımın kökünü Edmund Husserl (1859-1938)’in Fenomenoloji (Görüngübilim) felsefesinde bulmaktayız. Husserl’e göre varlığın aslı (özü) hakkında fikir ileri sürerken daima “tırnak içinde” konuşmak gerekir. Çünkü, öz tam olarak bilinemez. Ancak teğetsel veya asemtotik olarak yaklaşan ifadeler kullanılabilir. Dış dünya olarak tanımladığımız nesnelerle olan ilişkimiz onları bir bakıma kendi isteğimiz doğrultusunda şekillendirir. Önemli olan nesnelerin kendi varlıkları değil bizim onlara karşı olan tutumumuzdur.

Nesne, öznenin (çoğu zaman benliğin) dış dünya ile girdiği etkileşim sonucu duyu organlarıyla algıladığı bir durumdur. Benlik, şekil verici ve kendi çıkarları doğrultusunda yönlendirici olduğundan dış dünyayı kendine göre yorumlar. Oysa ki özne, taraf tutmadan, mümkün olduğunca “benlik” iddiasında bulunmadan dış dünyanın yapısını çözümlemeye çalışır. Eğer bu durum sağlanırsa özne “varlığın özüne” ulaşmasa da yaklaşır. Öznenin dış dünya ile ilişkisi sayesinde dış dünyanın özüne yaklaşılabilir.

Dış dünyanın özüne asla ulaşılamaz. Ona ancak asemtotik olarak yaklaşılır. Bu bakımdan hem dış dünya hem de özne tırnak içinde açıklanıp yorumlanabilir. Yani, “varlık” kavramı kısa ve kesin bir tanıma indirgenemez. Tırnak içine alınan kavramı açıklamak, ilişkilerini göstermek ve kapsadığı alanı mümkün olduğunca ayrıntılı bir şekilde açıklamak gereklidir.

Görüngübilim yaklaşımında nesneler artık gerçek nesneler olmaktan çıkmış, düşünce ürünlerine dönüşmüşlerdir. Yani nesneler duyularla algılandıkları gibi değil, birer bilinç ürünü olarak bilinçte ortaya çıkmış nesneler olarak işlenirler. Böylece bilinç özne ile bütünleşmiş olur. Tüm değer yargıları, algılar ve dıştan verilen önyargılar bilinci kısıtlayan örtülerdir. Bu örtüler kalkarsa “aşkın” (transandantal) bilince ulaşılır. Bilinç kendi üzerine katlanmak ve kendini düşünmekle "özne-nesne" ikiliğini ortadan kaldırmış olur.

İşte Descartes’ın “düşünüyorum öyleyse varım” sözünün asıl anlamı, varlığın düşünceden ayrılması mümkün olmadığına işarettir. Görüngübilimin özne-nesne bütünlüğü hakkındaki görüşü modern bilimin, özellikle Kuantum kuramının felsefesi ile tam bir uyum halindedir. Bilinç bir yandan anlam üretirken diğer yandan dış dünyanın özünü sorgulamaktan geri kalmaz. Bilimsel ve felsefi düşünce yapıtları bu sorgulamanın sistematik ve tutarlı görüntüleridir.

Yani hem bilim hem de felsefe görüngüler ilişkisine “inandırıcı bir anlam” verme gayretidir. Yoksa anlam her davranış şeklinde ve her alınan kararda gizlidir. Onsuz insan tek bir söz bile söyleyemez, tek bir hareket bile yapamaz. İnandırıcı anlam özne ile nesnenin ilişkiye geçmesini sağlayan yapıyı açıklamaktan geçer. Bilim (özellikle fizik bilimi) nesnelerin birbirleri ile etkileşimlerini temel kuvvetlere indirgeyerek açıklamaktadır. Ancak, bu kuvvetlerin etkin olmalarını sağlayan yapı nedir? sorusu daha temel ve derin bir yorum gerektirir. Bu yorum da şimdiye kadar genel kabul görmüş “pozitif bilim” anlayışının  içeriğini genişletmeyi (yapısını bozmayı) gerektirir.

Pozitif bilimde nesnellik ve nesnel olanın bilgisine ulaşma amaçlanır. Bu amaç doğrultusunda aynı sonuçlara ulaşabilmek için deneylere ve gözlemlere büyük önem verilir. Buna karşı görüngübilim bütünüyle her öznenin dünyayı farklı bir biçimde yapılandırıp kurma biçimleri üzerine odaklanır. Yani, ortak bir modelden (varsayımdan) hareket etmek yerine, kabul edilmiş olan yapı bozularak katılımcı ve "öznelerarası" etkileşim ile iletişim temelinde öznel olana önem verilir.

İşte, postmodern yaklaşım, insanın bir yandan evrene düşünce boyutunda anlam vermeye çalışmasını, ancak diğer yandan kendi öznesini dışlamaması gerektiğini savunmaktadır.

Postmodern yaklaşım

Tarih: 06:54 on 27/2/2006

Bakış açımızda açılımlar oluşması için öncelikle birtakım varsayımlardan kurtulmak gerekir. Bu varsayımların bazılarından söz ettim. "Yerel gerçeklik" varsayımı bizleri en çok bağlayan ve yorumlarımızı kısıtlayan bir yaklaşımdır. Bu varsayımla birlikte süreklilik ve özdeşlik varsayımları da tartışma konusudurlar.

Modern bilim kuramlarının getirdiği farklı görüşlerin yerleşmesi için klasik yapının bozulması gerekir. Bu durum Fransız felsefeci Jacques Derrida’nın meşhur ettiği “Yapı bozumculuğu” (decontruction) kavramı ile ilgilidir. “Yapı bozumu” yıkım değildir, analiz hiç değildir. Daha çok batı düşünce sisteminin aşkın durumları açıklamakta karşılaştığı zorlukları çözebilmek için başvurulan bir bakıştır.

Bu bakımdan hem Aristo mantığının kabulleri hem de batı metafiziğinin temel varsayımları yeniden yorumlanıp farklı ufuklara doğru yelken açmalarına izin vermek  gerekmektedir. Derrida’nın esas saldırı hedefi ikili (karşıt) kavramlardır. Yani, ikili dialektik yaklaşımın kısıtlayıcı olduğunu iddia etmiştir.

Bu görüş, tamamen benim burada göstermeye çalıştığım klasik dialektik mantığın yetersiz olduğu görüşü ile uyum halindedir. Hem-hem mantığı dialektik (ikili) mantığı aşmak amacını güden, daha esnek bir yapı sergilemektedir. Evreni ve insanı anlamak istiyorsak ikili mantığı aşmamız gerekiyor. Yeni mantığın öngördüğü yaklaşımda şu tercihler öncelik kazanıyor:

-          Gözlem yerine katılım,

-          Tikel yerine tümel,

-          Boşluk ve yokluk yerine varlık,

-          Anlamsız yerine anlam,

-          Mutlak yerine göreli,

-          Bağımsız yerine bütünsel,

-          Nesne yerine enerji,

-          Sürekli yerine süreksiz.

Burada belirttiğim ikili kavramlar tam olarak birbirlerinin karşıtı değiller. Amaç ikilemli mantığı geri getirmek değil, aksine onların kısıtlayıcı yapısını bozmaktır. Derrida bilimsel bir açıklamada kullanılan terimlerin anlamlarının yeni açıklamalarla genişletilmeleri gereği üzerinde durmuştur. Bu sav “Postmodern yaklaşımın” temel iddiasıdır. 

Postmodern felsefeyi geliştirmiş olan  Derrida, Lyotard, Faucault ve diğerleri , anlam dünyamızı (modernizm bağlamında) sarsacak çözümlemelere giriştiler. Kuhn ve Feyarebend de postmodern düşünceye birçok katkıda bulundular. Postmodern yaklaşım bir sorgulamadır. Bu doğru. Fakat neyi sorguluyor? 200 yıla yakın bir süredir batı toplumlarına kesin doğru imiş gibi pompalanan birtakım önyargıları ve varsayımları.

Bunların sorgulanması birinci aşama. İkinci aşama ise bu sorgulamaya bir yanıt bulma gayreti. Yani, anlamsızlıkta israr etmek yerine, anlamsız gibi görünen olgularda gizli olan anlamı ortaya çıkarabilmek önemlidir. Modern bilim kuramları, Kuantum Kuramı ve onun daha ileri modelleri, Özel ve Genel Görelilik Kuramları ve en son Karmaşa Kuramı anlam arayışına önemli katkılarda bulunmuşlardır. Bu kuramlar klasik fizik görüşlerini alt üst etmiş durumdalar. Şu halde elimizde malzeme hazır.

Yapılacak olan, ki benim bu konuda ümidim kuvvetli, bu modern kuramların yeni felsefi açılımlarını geniş halk kitlelerine tanıtmak, basitleştirip anlatmak ve sonuçta eski varsayımlardan kurtulmak. İnsanı dışlamış olan klasik bilime yeniden insan ögesini katmak. Böylece bilim ile bilimadamını bütünleştirerek bilime sorumluluk getirmek.

Sorumluluk konusu günümüzde bilim çevrelerinde oldukça sık tartışılan bir konu haline gelmiştir. Artık, postmodern bilim adamı “ben yaparım isteyen istediği şekilde kullansın” mantığını terk etmek gerektiğini kavramış durumdadır.

Süreksiz gerçeklik

Tarih: 07:19 on 26/2/2006

Einstein kuantum belirsizliğine hiç inanmamıştır. Çünkü nesnelerin bağımsız birimler oldukları görüşünü benimsemiş olduğundan uzaktan etkilenebileceklerini de ret etmiştir. Işığın sabit hızla yayıldığı kanıtlandıktan sonra ışıktan hızlı etkileşmelerin varlığını da ret etmiştir. Bu görüşü savunan bilim adamları halen çoğunluktadır. Savundukları bu görüşe  “Yerel Gerçeklik” adı verilmiştir.

Oysa ki yerel gerçeklik görüşü Kuantum kuramında geçerli değildir. Geçerli olmadığı sadece kuramsal olarak değil deneysel olarak da kanıtlanmıştır. 1982 yılında Fransız fizikçi Alain Aspect tarafından gerçekleştirilen deneye göre: “Bir arada (bir sistem içinde) etkileşmiş olan parçacıklar ayrılsalar dahi ışık hızından daha hızlı bir şekilde –anında- etkileşmelerini sürdürürler”.

Bir arada bir bütün oluşturmuş sistemlerin dalga paketi oluşturduklarından söz ettim (Bakınız Belirsizlik ilkesi başlıklı yazım). Evren bir bütün olarak tek bir dalga paketi şeklinde düşünülmesi mümkün olduğundan evreni oluşturan parçalar arasında anında ve uzaktan etkileşme olabileceğini kabul etmek zorundayız.

Bir yandan yerel gerçeklik kavramını terk etmek, diğer yandan özdeşlik ilkesine bağlı kalmak mümkün değildir. Çünkü etkileşmelerin yerel olduklarını varsaymak için mutlaka bir var olanın kendi ile özdeş, değişmez yapıda olması gerekir. Bir nesne ışıktan hızlı bir şekilde diğer nesnelerle etkileşiyorsa yalıtık ve bağımsız olmak özelliğini kaybeder. Dolayısıyla “kendine özdeş” kavramı da geçersiz olur.

Yerel gerçeklikten vazgeçmekle her var olanın, ister canlı ister cansız olsun, evrensel enerjinin oluşturduğu dalga paketi içinde girişimde bulunan dalgalar olduklarını kabullenmek zorundayız. Bu dalgalardan birini gözlemlersek, o dalgayı (nesneyi) paketin içinden ayrıştırmış oluruz. Farkındalığımız belirli bir dalgaya yöneldiğinde ona anlam kazandırıp etiketlemiş de oluyoruz.

Bu durumu daha iyi kavramak için havadaki radyo dalgalarını düşünün. Hepsi de aynı yapıda elektromağnetik dalgalardır. Tek fark ayrı frekansa (titreşime) sahip olmalarıdır. Radyomuzu belli bir istasyon frekansına ayarladığımızda, yani gözlem yaptığımızda, havadaki karmaşık yapıdan tek bir dalgayı çökertip algılamış oluyoruz.

Şu halde “gerçeklik” kavramını da aynı mantıkla açıklamamız gerekir. Gerçek tek fakat karmaşık bir dalga paketidir. Biz sürekli kendi isteğimiz doğrultusunda bu tek olan gerçeği yerel olarak ayrıştırıp yorumluyoruz. Ancak modern bilim bize yerel gerçekliğin geçerli olmadığını söylemektedir. Eğer “yerel gerçeklik” varsayımını terk edersek yerine ne gibi bir kavram getirebiliriz? Benim görüşüm “süreksiz gerçeklik” kavramının daha uygun olacağıdır. Çünkü ne zaman, ne de uzam süreklidir. Dolayısıyla, etkileşmelerin de süreksiz olabilecekleri gerçeğini göz önüne almalıyız.

An içinde yerel gerçeklikten kopabilen insanlar kısa bir süre trans (vecd) haline geçerek farklı gerçeklik boyutlarına ulaşmışlardır. Örnek olarak, Asya Türklerinin Kam dedikleri şaman kişilerden söz edeyim. Kamlar yerel olmayan bir etkileşme içinde evrensel enerjiden yararlanabilen kişilerdir. Onların evrensel enerjiye hakimiyetleri şu alanlarda belirir.

1.)               Hastalıkların tedavisi (Şifacılık).

2.)               Ruhsal irtibatlar (Medyumluk)

3.)               Kehanet çalışmaları (Duyular ötesi).

4.)               Zaman ve mekân ötesi ilişkiler

 

Tüm bu faaliyetler Maji (İlm-i-Ledun) olarak algılanmış ve pozitif bilim tarafından ret edilmiştir. Ancak yerel gerçeklik görüşünün kısıtlamalarından sıyrılıp süreksiz gerçeklik yaklaşımını benimsersek kamların davranışlarına, diğer insanlara ve evrendeki tüm canlılara olan bakışımız değişir. Dolayısıyla hem mantık yapımızda hem de dünya görüşümüzde açılımlar oluşur.

Canlı mı cansız mı

Tarih: 08:21 on 25/2/2006

İkilikte teklik başlıklı yazımda karşıtların aslında tek bir gerçekliğin iki farklı yansıması olduğundan söz ettim. Bu yazımda canlılık-cansızlık kavramları üzerinde durmak istiyorum. Günümüzde hücre biyolojisi ile ilgilenen bazı bilim adamları yaşam öncesi şartları inceleyerek “yapay yaşam” oluşturma gayretindeler. Bu tür organik yapılara “sentetik organizma” adı veriliyor.

Sentetik organizmalar oluşturmak için hücrenin beslenebileceği bir ortam içinde değişik tek hücrelilerden alınan farklı hücre birimleri bir araya getirilerek (bir lego oyuncağı inşa eder gibi) bir süre canlı gibi beslenmesi sağlanıyor. Araştırmayı yürüten biyolog bu organizmaların canlı olmadıklarını, sadece canlı hücrelerin bazı özelliklerini sergilediklerini iddia ediyor.

Artık canlı-cansız sınırının nerede başlayıp nerede bittiğini kesinlikle tanımlamak mümkün değil. Bir cansız hücre hangi özellikler eklenince canlanıyor? Veya canlı hücre hangi özelliklerini kaybedince cansız hale dönüşüyor? Kesinlikle söylemek mümkün değil. Canlı-cansız ayırımı sadece biyoloji ve genetik biliminde değil, fizikte de önemli bir tartışmaya yol açmıştı.

Kuantum kuramına göre nesnelerin hem dalga hem parçacık oldukları görüşü tartışılırken Erwin Schrödinger’e (1887-1961) şöyle bir düşünce deneyi sorulmuştu:

Kapalı bir kutuya bir kedi, bir zehirli gaz içeren şişe, bu şişenin kırılmasını sağlayacak bir makanizma ve bu mekanizmayı tetikleyecek olan bir radyoaktif madde koyuyoruz. Radyoaktif maddenin çekirdeği dengeli bir yapı olmadığından belirsiz bir anda bir alfa parçacığı salar. Bu parçacık mekanizmayı tetiklesin ve şişe kırıldığında zehirli gaz kutuya yayılsın. Soru: Kutu kapalı olup içini görmediğimize göre, kedi canlı mıdır ölü mü?

Bu sorunun kuantum belirsizliği ile ilgisi vardır. Mikro alemdeki belirsizlik (bakınız Belirsizlik ilkesi başlıklı yazım) bizim 3-boyutlu makro aleme taşındığında çelişkiler içereceğini göstermek için sorulmuştur. Soru Einstein tarafından 1936 yılında Schrödinger’e sorulmuştur. O günden beri de “Schrödinger’in kedisi” adıyla bilinmektedir.

“Kopenhag yaklaşımı” olarak bilinen yanıta göre, kapak kapalı iken “gerçek” ancak potansiyel (bilkuvve) durumdadır. Ancak kapak açılınca kedinin canlı veya cansız olma durumu belirir. Bu durumda artık bir seçenek yapılmıştır. Yani bilkuvve durum bilfiil duruma dönüşmüştür. Kuantum dalga yaklaşımına göre kutu kapalı iken tek bir dalga paketi halindedir. Bu paketin içinde zehirli şişe bir dalga, mekanizma ikinci farklı bir dalga, radyoaktif madde üçüncü bür dalga ve kedi dördüncü bir dalga olarak yazılabilir. Fakat kapak açılmadıkça bu dalga paketi içindeki dalgalar ayırd edilemez. Bu bakımdan kedinin diri veya ölü olup olmadığı bilinemez. Ancak kapak açıldığında belli bir sonuç ortaya çıkar. Bu duruma dalganın çöküşü de denmiştir.

Karmaşa kuramına göre kutu kapalı iken içteki durum karmaşıktır. Yani ister dalga ister parçacık olarak düşünün, karmaşık durumda “gerçek” belirgin ve kesin olarak tanımlanamaz. Fakat kapak açıldığında karmaşa yerini düzene bırakır ve kedinin durumu kesin olarak bilinir.

Bu deney sayesinde gözleyen-gözlenen ikiliğinin aslında ayrılmaz bir bütün oluşturduğunu anlamaktayız. Kapalı kutu durumunda gözleyen insan ve gözlenen kutu vardır. Kedi ve diğer kutu içindekiler belirsiz bir durumdadırlar. İşte mikro alemdeki belirsizliğin makro alemdeki açıklaması bu şekilde olmalıdır. Yani kutu kapalı iken kedi canlı mıdır yoksa ölü mü sorusuna “belirsiz durumdadır” yanıtı verilmelidir. Belirsizliği ancak hem-hem mantığı ile açıklayabiliriz. Yani, kapak kapalı iken kedi hem diridir hem ölü.

Kuantum kuramının dalgasal açıklamasına göre kutu kapalı iken dalga paketini oluşturan dalgalar birbirleri ile girişim durumunda olduklarından tek bir dalga paketi vardır ve bu paketin içindeki dalgalar bağımsız varlıklar olarak tanımlanamazlar.

İkilikte teklik

Tarih: 07:13 on 24/2/2006

Etkenlik-edilgenlik başlıklı yazımda iki zıt kuvvetin varlığından söz ettim. Karmaşa kuramı ışığında bu iki kuvvet tek bir “acayip çekici” ile ilişkilidir. Bu çekicinin görüntüsü Karmaşa ve düzen  başlıklı yazımda göstermiş olduğum Lorenz fraktalidir. Lorenz fraktalinde iki merkez açıkça görülüyor. Ancak bu merkezleri fiziksel, 3-boyut içinde, düşünmek hatalıdır. Onlar her yapının, davranışın ve olgunun oluşumunda rol oynayan temel etkenlerdir. Fraktalin görüntüsü fiziksel olmayıp matematikseldir.

Etken-edilgen çifti olarak tanımladığım acayip çekici insanda ruh-beden, duyu-duygu, iç-dış, bilinç-bilinçaltı, uyku-uyanıklık, yin-yang, dişil-eril şeklinde belirirken doğada gece-gündüz, hareket-durağanlık, aydınlık-karanlık, dalga-madde, zamanda ileri-geri, karmaşa-düzen şeklinde ortaya çıkmaktadır.

İnsan düşüncesi dahi bu ikilik sayesinde işliyor. Doğru-yanlış, güzel-çirkin, iyi-kötü, tez-antitez, gibi ikilemler sayesinde kavramlar üretiyor, kuramlar geliştiriyoruz. Daha derin bilinç boyutunda sonlu-sonsuz kavram çifti sayesinde karmaşa ile düzenin nasıl da iç-içe ve birbirlerini muhtaç olduklarını görüyoruz.

İşte bu ayrılmaz karşıtlığın bilincine vardığımızda bir önceki yazımda sözünü ettiğim: “Daha da ileri bir iddia ile insandan bağımsız nesnel bir dış dünyanın varlığından da söz edilemez” ifadesi açıklanmış oluyor. Nesne-özne karşıtlığı aslında tek bir gerçeğin iki ayrı oluşumudur. Her ikisini oluşturan fraktal yapıda karmaşa-düzen ikilisi bulunur.

Hem dış dünya hem de iç dünyamız aynı yapıda olup ayrılmaz bir şekilde hem karmaşık hem düzenlidir. Bazen karmaşa üstün gelir bazen de düzen. Fakat biz insanların aradığı düzenli yapılardır. Bu düzeni aramakla kalmayıp kendimiz oluşturuyoruz. Hem içimizde hem de dışımızda. Böylece varlığımızı ve yaşantımızı derli-toplu bir şekilde sürdürebiliyoruz. Anlam arayışı içinde karşımıza çıkan her olguya bir anlam yükleme gayreti doğal bir davranıştır. Yapay bir gayret değildir.

Bu bakımdan “evrende ve var oluşumuzda anlam var mıdır?” sorusu dahi bir anlam arayışıdır. “Herşey anlamsızdır” önermesi dahi anlam yükleyen bir önermedir. Demek ki anlamdan kurtuluş yok. Anlamsızlık üzerine ciltlerle yazı yazan ve “varoluşçu felsefe” okulunu geliştiren filozoflar dahi farkında olmadan yaşama ve varlığa anlam yüklemişlerdir. Düşünceyi düşünmek başlıklı yazımda belirttiğim gibi, hem bilimsel düşüncede hem de felsefi düşüncede insanlığı, yaşamı ve doğayı sorgulayıp anlamlı ve tutarlı yanıtlar arama gayreti vardır.

Bir önceki yazıda doğanın estetiğinden söz ettim. Fakat fraktal yapılar sayesinde doğal-yapay ikilemi dahi ortadan kalkmak üzeredir. Yukarıdaki resim yapay bir fraktaldir. Tek bir merkezden yayılan, fakat aynı zamanda tek bir merkeze doğru çekilen estetik bir görüntü sayesinde tüm varlığın oluşumunu kavrayabilmekteyiz. Burada teklikten oluşan çokluk, ve çokluk içinde teklik gerçeği belirmektedir.

İnsanlığın çok eski dönemlerden beri bildiği ve Lao Tzu, Heraklitos, Muhiddin ibnül-Arabi gibi düşünürlerin kendi felsefelerinde belirttikleri bu “teklik-çokluk” özdeşliği günümüzde matematik fraktaller sayesinde görüntülenir olmuştur.

Benim ayrıntılı olarak bu yazılarımla geliştirmeye çalıştığım Takiyon Evren modeli de ikilik altında gizli olan teklik düşüncesine dayanıyor. Çünkü ışık-altı ve ışık-üstü evrenlerin bir bütün oluşturduklarını, birbirleri içinde bulunduklarını ve onları ayırıp farklı iki evren olarak gözlemenin mümkün olmadığını çeşitli yazılarımda belirttim.

Bizim dış dünya olarak gözlediğimiz evren ikili gibi görünen fakat tek olan “acayip çekici” tarafından şekillendiriliyor. Bu merkez hem gerçel parçacıkları hem de sanal parçacıkları oluşturuyor. Hem karmaşa hem de düzen getiriyor. Zamanı hem ileri doğru itiyor hem de geri doğru çekiyor. Hem geçmişi hem de geleceği yaratıyor. Fakat hem-hem mantığı sayesinde biliyoruz ki ikilikler teklikten türüyorlar. Zamanın geçmiş-gelecek ikiliğinin oluşumunda “an” dediğimiz tek bir merkezi nokta vardır.

Doğanın estetiği

Tarih: 14:58 on 23/2/2006

Bir kar tanesinin mikroskop altındaki görünüşü

Bilim, deney ve gözlemlerin gerisinde yatan veya gizli olarak duran ortak özellikleri ve ilişkileri sistematik bir bütünlük içinde açıklamaya çalışan bir disiplindir. Her deney veya gözlem duyularımıza hitap etmek zorunda olduğuna göre sonuç itibariyle her bilimsel açıklama sübjektif bir yapı olup insan şuurunun  ürünüdür. Bu açıdan insandan bağımsız nesnel (objektif) bir bilimden söz edilemez. Daha da ileri bir iddia ile insandan bağımsız nesnel bir dış dünyanın varlığından da söz edilemez. Eğer birçok kişi aynı dış dünyanın varlığı üzerine anlaşıyorsa bunun nedeni yaratmış oldukları zihinsel modelin aynı olmasından dolayıdır. Bu zihinsel model ise insana, farkına bile varmaksızın, çevre ve toplum tarafından “ortak kültür” olarak işlenir, kabul ettirilir.

Ortak kültürün kabulleri, varsayımları, değer yargıları, tercihleri ve tabuları olabileceği gibi güzellik ölçüleri ve estetik anlayışı da vardır. Şu halde bilimsel bir yaklaşım yapmak istersek kültürleraşırı veya farklı kültürlerde ortak olan özelliği bulup çıkarmamız gerekir. Zira bilim, deney ve gözlemlerin gerisinde yatan ortak özelliklere yönelir ve farklı gibi görünen olguları ortak yasalar altında birleştirmek ister.

Batı düşüncesinde yerleşmiş olan Nesnellik, İndirgeyicilik ve Yerellik varsayımlarından söz ettim (bakınız Yerellik ve indirgeyicilik başlıklı yazım).Bu varsayımları ilke olarak kabul eden toplumlarda özne yerini benliğe terk ettiği için “Var ol, kendini belirt, ortaya koy, ifade et” türünden istençler önemli olmuş, varoluşçu bir dünya görüşü, felsefesi ve sanatı ortaya çıkmıştır. Bu yaklaşımı da yadırgamamak gerekir zira sanatçı kendi dönemini ve döneminin kültürünü yansıtır. Aksi takdirde marjinal kalır ve ön saflarda yer alamaz.

Fakat günümüzde sanat gittikçe doğadan kopmaktadır. Resim sanatı belirsiz ve anlamsız şekiller ile renkler karmaşasına, müzik atonal bir yapı içinde melodiden uzak, heykel sanatı dahi soyut ve anlamsız şekillere dönüşmüştür. Yine de tüm bu karmaşık yapılarda bir harmoni, estetik ve denge unsuru var olmaya devam etmektedir. Çünkü insan her ne kadar doğadan kopmuş bir yaşam sürdürse de doğanın bir parçası ve holografik bir özü olması itibariyle tümüyle doğanın dışına çıkamaz.

İnsan doğanın bölünmez bir parçası olmasından dolayı doğadaki güzellik, harmoni ve simetri karşısında hayran kalmaktan kendini alıkoyamaz. Doğada iki türlü simetri vardır. Biri açık simetri diğeri örtülü gizli simetri. Gizli simetri matematiksel ve geometrik simetridir. Onu ortalıkta açıkça görmek kolay değildir. Fakat bu simetrik özelliği kuramlarımızda kullanarak doğanın birçok davranışını açıklayabiliriz.

Örneğin, Enerji korunumu ve Momentum korunumu, duyularımızla gözlemekte güçlük çektiğimiz fakat hesap sonucu var olduklarını kanıtladığımız, doğanın temel bazı gizli simetrilerinden türerler.

Açık simetriye örnek olarak kar kristallerini verebilirim. Kar kristallerinde herkesçe beğenilen estetik bir yapı olduğu kuşkusuzdur. Ayrıca insan tarafından değil, doğa tarafından açıklanamaz bir simetri içinde yaratılan ve süratle erimelerine rağmen her gördüğümüzde bizi hayran bırakan bu kar kristalleri simetri ile güzellik arasındaki bağı açıkça ortaya koymaktadırlar.

Fakat günümüzde kar kristallerinin sırrı da çözülmüş durumdadır. Koch eğrisi denilen bir tür fraktal şekil üzerinde yapılan matematik ayarlamalarla bir kar kristalini bilgisayarda oluşturmak mümkündür. Yukarıdaki resimde solda gerçek bir kar kristali sağında da fraktal bir basit modeli görülüyor.

Çok simetrik bir yapı gösteren kar kristali karmaşadan düzenin ortaya çıktığını gösteren  güzel bir örnektir. Bu basit örnek sayesinde matematik bir karmaşa denkleminden simetrinin ve güzelliğin nasıl da bir anda ortaya çıktığını anlamaktayız. Tüm canlı varlıklarda gözlediğimiz güzellik ve estetik, evrenin temelinde yatan gizli ve simetri içeren fraktal bir yapıya işarettir. 

 Bilkuvve ve bilfiil

Tarih: 08:08 on 23/2/2006

Düşünceyi düşünmek başlıklı yazımda özneyi tanımlarken “Özne, cümle içinde iş yapan, yani fail. Fizikte ise iş yapma gücüne sahip olana “enerji” diyoruz. Şu halde “İş yapan enerji ise, özne = enerjidir”. Bir diğer ifadesi de bizim özümüz enerjidir. Biz (özne) ne maddeyiz ne de nesneyiz. Biz doğrudan doğruya enerjiyiz. Çünkü bizler iş yapma kapasitesine (yetisine) sahibiz.”, dedim.

Öte yandan Sonsuzluk türleri başlıklı yazımda “benlik özne değil, nesneye dönüşmektedir”, dedim. Bu iki tanımın birbirleri ile çelişmediklerini şimdi açıklayacağım. Enerjinin birçok türleri olmasına rağmen yoğun madde (parçacık) halinde iken iki farklı enerji türünden söz edebiliriz. Bunlar potansiyel enerji ve kinetik enerjidir. Potansiyel enerji maddenin durumu ile ilgilidir. Yani iş yapma yetisi vardır ama bu yeti henüz ortaya çıkmış değildir. Bu durumu daha 10. yüzyılda Farabi (870-950) “bilkuvve” olarak tanımlamıştır. Bilkuvve sözündeki anlam “kuvvete dönüşebilen” şeklinde anlaşılmalıdır. İş yapan kuvvet olduğuna göre henüz kuvvet olmamış enerji türü olan potansiyel enerji ile özümüz eşdeğerdir.

Farabi’ye göre varlık önce düşünce boyutunda bilkuvve olarak hareketsiz (potansiyel) enerji şeklinde vardır, sonra bilfiil olarak hareketli (kinetik) enerji şeklinde belirgin hale geçer. “Kuvveden fiile geçmek” sözü günümüz Türkçe’sinde “düşünceden eyleme geçmek” anlamını taşır. İkinci adım bu bilkuvve durumda olan potansiyel enerjiyi aktif hale geçirip kinetik enerji haline dönüştürmektir. İşte, bu noktada sorulması gereken bilkuvve durumundaki enerji bilfiil hale kim tarafından geçiriliyor?

Genelde düşünce boyutunda olan “varlık” bizim benliğimiz tarafından harekete geçirilerek etken hale getirilir. Çünkü “benlik” nesneye dönüştüğünde diğer nesneleri etkiler ve kendi çıkarı doğrultusunda şekillendirir veya yönlendirir. Benlik etken olduğu sürece özne edilgen kalır. Emir veren benlik de kontrolü ele geçirip hayatımızı yönlendirir.

Tasavvuf düşüncesi bu tür emreden benlik boyutuna “Nefs-i Emmare” demiştir. Emmare, “emir eden” anlamını taşır. Batı psikolojisinde bu benlik boyutuna “ego” denmiştir. İnsan egosunu güçlendirerek kendini güvende hisseder. Ancak bu güven veren yapı yapay bir barınaktır. En ufak fırtınada yıkılmaya hazırdır. Bu bakımdan hayat fırtınası içinde, biz insanlar egomuz yıkılmasın diye, onu sürekli kuvvetlendirir, sağından solundan destekleriz.

Fakat amaç onu sürekli desteklemek değil yıkıp yepyeni, farklı malzemeden yeni bir yapı oluşturmaktır. Türlerin oluşumu başlıklı yazımda dedim ki: “İşte Karmaşa kuramındaki k parametresi kuantik bir sıçrama ile aniden Dk kadar değişikliğe uğrarsa bir çatallaşma (bifurcation) olur ve yeni bir tür belirir”. Bu ifadeyi benliğe uygularsak, Karmaşa kuramının öngördüğü şekilde benlik ani bir kuantik sıçrama ile değişikliğe uğrayabilir. Bu değişiklik de yönetimin karar veren egodan alınıp özneye devredilmesi şeklindedir.

Eğer bilkuvve durumunda olan özne bilfiil hale geçerse yaşamın kalitesi de amaçları da değişir. Artık önemli olan insanın kendi egosunun yerel faydası ve çıkarı olmak yerine, çevrenin ve bütünün faydası ve çıkarı olmaya başlar. “Bütün” kavramı holografik olarak tüm evren şekline dönüştüğünde özne-evren özdeşliği gerçekleşmiş olur. Bu ifadede “evren” sözünü maddesel, nesnel evren olarak anlamamak gerekir. Artık evren deyince metafizik (fizik üstü) bir gerçeklik kast edilmektedir.

Ancak, bu metafizik evrenin bütünlüğüne ulaşmak hiç de kolay değildir. Adım adım ve her durumda rıza ve tevekkülle, bulunduğu boyutun hakkını vererek, ilerleme sağlanır. Artık karar veren benlik ego olmadığına göre ne insanın kendisi ne de çevresi bir nesne olarak görülmez. İnsanın gerek kendisinin ve gerek çevresinin bir enerji yumağı olduğu bilinci içinde etkileşmeler yerelden genele doğru kaydırılır.

Bu boyuta yükselmiş insan için her nesne parçacık özelliğini kaybetmiş, dalga özelliğini kazanmıştır.

Noktasal sonsuzluk

Tarih: 16:51 on 22/2/2006

Bir önceki yazımda üçüncü tür bir sonsuzluktan söz ettim. Bu sonsuzluk türü hem geometrik hem de aritmetik olması bakımından doğrudan doğa ile ilgilidir. Yani doğada olması beklenen, fakat nedense bizim boyutumuzda belirmeyen bir sonsuzluk türüdür. Bu tür sonsuzluğa “singülarite” (tekliğin sonsuzluğu) da denmektedir.

Anafor adını verdiğimiz olaylara hem havada hortum olarak hem de suda yerel çekici bölgeler olarak rastlıyoruz. Fakat bu anaforlar sıfır noktasına (merkeze) yaklaşsalar da oraya varamazlar. Çünkü oraya varmaları için sonsuz hıza ve sonsuz enerjiye ulaşmaları gerekir ki bizim evrenimizde bu mümkün değildir.

Mantıksal olarak kendi üzerine dönüşümlü önermeler de aynı anaforlar gibi bizi içlerine çekerler. Onlardan kurtulmak mümkün değildir (Bakınız: Çelişkili önermeler başlıklı yazım). Mikro evreni açıklamak isteyen Kuantum kuramında da noktasal sonsuzluk sorunu vardır. Foton ile bir bütün oluşturan elektron ilerlerken bir foton saldığını ve yine aynı fotonu emdiğini düşünelim.

Richard Feynman (1918-1988) parçacıklar arası etkileşmeyi saçılma grafikleri ile gösterip elektronun öz enerjisini hesaplamak isteyince noktasal sonsuzlukla karşılaşmıştır. Bir elektron önce bir foton saçıyor ve bir süre sonra geri emiyor. Fakat fotonu geri emmesi için onun bir  karadelik olması gerekmez mi? Genel Görelilik kuramına göre ancak kardelikler evrende fotonu dahi salmayan bir çekici güce sahiptirler.

Bu mantıktan hareketle evrende hem mikro boyutta hem de makro boyutta sonsuz çekici güce sahip karadelikler vardır. Her iki boyutta da karadelik yapısı bir noktasal sonsuzluğa gider. Eğer maddenin sonsuz kere bölünmesi mümkün olsaydı gene aynı noktasal sonsuzluk karşımıza çıkacaktı. İşte bu duruma engel olan enerjinin ancak sonlu kuantumlar (birimler) halinde aktarılabileceği görüşüdür. Bu kabul sayesinde noktasal sonsuzluk sorunu çözülmüştür.

Fakat elektronun öz enerjisini hesaplarken sorun gene karşımıza çıkmaktadır. Bunun çaresi sonsuzluğu bir mertebe geriye iterek birinci mertebede hesap yapabilmeyi sağlamaktır. Bu mekanizmaya fizikte “renormalizasyon” adı verilir. Feynman’ın kendisi bu renormalizasyon mekanizmasını “pisliği halının altına süpürerek görmezden gelmek”  olarak tanımlamıştır.

Evren her boyutta kendine benzeyen yapılar üretiyor. Bu özellik evrenin bir Fraktal olduğuna işarettir. Üstteki resimde noktasal çekim gücünü resimleyen bir fraktal görüyoruz. Bu noktasal çekimi sağlayan noktanın sonsuz hıza ve sonsuz enerjiye sahip olması gerektiğini yukarıda belirttim. Sonsuz hız sahibi olan parçacıklar bizim evrenimizde bulunmasalar da Takiyon evrendeki parçacıklar (dalgalar) sonsuz hıza ulaşabilirler (Bakınız: Işıktan hızlı başlıklı yazım).

İşte bizim için çelişkili bir durum olan noktasal sonsuzluğu, merkezde bulunan Takiyonlar ile açıklayabiliriz. Onların düzen getirici özelliği sayesinde çevredeki yapılar (dalga paketleri) merkeze doğru çekilirler. Fraktalin çeper bölgesindeki siyah noktalara dikkatinizi çekerim. Bu resimde görülen spiraller uzam dediğimiz ortamın eğrilmesi olarak da yorumlanabilir. Çekici kuvvet uzamı (makro boyutta uzayı) bükmekte ve diğer nesneler (gök cisimleri) bu bükük geometride en kısa yolu izleyerek merkeze doğru çekilmektedirler.

Eğri uzayların geometrisini geliştirmiş olan iki matematikçi Georg Riemann (1826-1866) ve Nicholai Lobatchevski (1793-1856) sayesinde bugün karadeliklerin yapısı ve uzay bölgesi hakkında fikir yürütebiliyoruz. Fakat noktasal sonsuzluk sorununa halen bir çözüm bulunmuş değildir. Fiziksel olarak tutarlı açıklama Kuantum kuramı sayesinde değil, TE modeli sayesinde olduğu kanısındayım.

Sonsuzluk türleri

Tarih: 07:18 on 22/2/2006

Kısır bir döngü başlıklı yazımı şu cümle ile bitirmiştim: “Var olmak için insan düşünmek zorundadır ama düşünce yoluyla da varlığını anlaması mümkün değildir”. Ne kadar ilginçtir ki insan varlığını anlayamadığı halde kendine bir benlik üretmektedir. “Benlik” kendi varlığına anlam kazandıran bir kavramdır. Eğer “benlik” (ego) kavramı olmasa var olması da tehlikeye düşebilir. Diğer canlıların böyle bir yapay kavrama gereksinimleri yoktur. Çünkü onlar varlıklarını bedenleri sayesinde sürdürebilirler. Oysa ki insanın bedeni oldukça güçsüz olduğundan düşünce yoluyla kendine bir “varlık nedeni” yaratmalıdır. Bu durumda “benlik” özne değil, nesneye dönüşmektedir.

Özne insanın doğal var olan yapısı, benlik ise kendi ürettiği yapay bir kavramdır. İnsan kendini güvende hissetmesi için erken yaşta “benlik” kavramını üretir. Çocukta benlik bilinci 2-3 yaşında iyice belirgin olmaya başlar. Zaman geçtikçe bu benliği  güçlendirip süsleyerek, gerçek özünden gittikçe uzaklaşır. Benlik bir nesneye dönüştüğünde tanımlanabilen, şekli ve özellikleri bilinen, sonlu bir yapı olur. Özne ise gittikçe derinlere itilen, tanımsız ve belirsiz bir varlığa dönüşür. Batı psikologları özneye “id” adını vermişler, onu içgüdülerin ve hayvansal yaşam dürtülerinin toplamına indirgemişlerdir. Oysa ki özne, evrenin holografik bir özeti olarak evrenle aynı özellikleri içeren canlı varlığın özüdür.

İşte yukarda belirttiğim gibi, insan özünden uzaklaştığı için kendi varlığını anlamakta aciz kalıyor. Özünü sorgulayan insan kendi holografik yapısının farkına vardığı anda, evrenle ilgili sorular sormakta ve yanıtlar ararken sonsuzluk kavramıyla yüzleşmektedir.

Evren sonlu mudur? Sonsuz mu? Sorusu hepimizin merak ettiği bir sorudur. Evren sonlu fakat hudutsuzdur. Hudutsuzluğu tanımlamak için basit bir örnekten başlayayım. Tek boyutlu hudutsuzluğa örnek iki ucu birleşmiş olan kapalı bir eğri çizgidir. Bu eğri çizgi herhangi bir yüzey içinde var olabilir. Kapalı olduğu için sonlu fakat aynı zamanda tek boyut içinde ne başı ne de sonu tanımlanamadığından hudutsuzdur. Şu halde tek boyutlu hudutsuz nesne iki boyut içinde tanımlıdır.

İki boyutlu hudutsuz nesneye örnek ise bir kapalı yüzeydir. Böyle bir yüzeyin ne başlangıcı vardır ne de sonu. Kapalı olmasından dolayı sonlu fakat hudutsuzdur. Bu nesne de ancak 3-boyutlu uzam içinde tanımlıdır.

Üç boyutlu hudutsuz nesne ise dört boyutlu uzay-zaman içinde tanımlanmalıdır. Bu da bizim “evren” dediğimiz içinde bulunduğumuz yapıdır. Fakat nitelik olarak evren 3-boyutlu uzamdan farklıdır. Uzam-zaman deyince uzam + zaman anlaşılmamalıdır. Nasıl ki bir kapalı yüzey nitelik olarak bir eğri çizgiden farklı ise uzam-zaman da nitelik olarak 3-boyutlu uzamdan farklıdır.

Evrenin hudutsuzluğu onun niteliği, yani kendine has özelliğidir. Öznenin de bu tür farklı bir niteliği vardır. Bu bakımdan ne evren ne de özne tam olarak anlaşılamaz. Onları söze ve sayıya döküp bir model geliştirebiliriz. Fakat bu durumda onların niteliksel hudutsuzluğu niceliksel sonsuzluğa dönüşmüş olur. Bilim adamları evrenin matematik modelini yapmakla bir yandan niteliksel (geometrik) hudutsuzluğunu kabul etmekte diğer yandan niceliksel (aritmetik) sonsuzluğun içine düşmektedirler.

Üç tür aritmetik sonsuzluk vardır.

1. Sayılabilir sonsuzluk. Buna örnek tam sayılar kümesidir. Tam sayıların sonu yoktur. Herhangi bir tam sayıya 1 ekleyin yeni ve daha büyük bir tam sayı elde edersiniz.
2. Sayılamaz sonsuzluk. Sayılamaz sonsuz sayılara “irrasyonel” sayılar denir, zira herhangi iki tam sayının bölümü olarak ifade edilemezler. Bu tür sonsuzluğa örnek sıfır ile bir arasına düşen gerçel (reel) sayılardır. Bu tür sayıların kesirleri uzayıp gider. Doğadaki sabitler bu tür sayılamaz sonsuzluğa sahip sayılardır. Örneğin, p sayısı 3.141592654.... şeklinde uzar gider. Bugün bile, en güçlü bilgisayarlar kullanıldığı halde, pi sayısının sonu bulunmamıştır. Üstelik pi sayısında herhangi bir düzen, kendini tekrarlayan bir sayı dizisi, de yoktur. Bir diğer örnek e sayısıdır. Bu sayı da 2.718281828... şeklinde uzar gider. Doğa ve evren ile ilgili matematik modellerde sabit olan sayılar e ve pi sayılarını içerdiklerinden, evrende ve öznede sayılamaz bir sonsuzluk bulunduğunu kabullenmek zorundayız.

        Üçüncü tür sonsuzluktan bir sonraki yazımda söz edeceğim.

Neg-entropi kavramı

Tarih: 07:34 on 21/2/2006

Varlık hakkında bir hayli söz ettikten sonra biraz da “bilgi nedir?” sorusuna yönelelim. Çünkü varlık ile bilgi birlikte ele alınmaları gerekir. Eski düşünürlerden bu yana ontoloji (varlık bilimi) ile epistemoloji (bilgi bilimi) üzerine uzun uzun düşünülüp, yorumlar yapılmıştır. Örneğin, Eflatun (M.Ö 428-347) bilginin üretilmediğine, “idea” adını verdiği kavramların keşf edildiklerine inanırdı. Genelde bilginin varlıktan ayrı olduğu ve bilinç tarafından üretildiği iddia edilir. Oysa ki bilgi varlığın düzenlenmesi sonucu oluşur. Yani herhangi bir karmaşık yapı düzene girdiğinde bilgi sahibi olmuş olur. Bu ifadenin tersi de doğrudur. Bilgi sayesinde herhangi bir karmaşık yapı düzene girer. Fakat,  öncelikle bilgi nasıl oluşur? Sorusuna yanıt arayalım.

Bilgiyi bilinçle ilişkilendirmek onu varlıktan soyutlayıp koparmak anlamına gelir. Oysa ki cansız yapılarda da bilgi birikimi olur. Örneğin, bir kitaba yazılmış bilgi insan tarafından yazılmış olsa bile, artık insana ait değildir. O bilgi her isteyenin ulaşıp kullanabileceği bir tür enerjidir. Kitapta durduğu sürece pasif (edilgen), okunup kullanılmaya başlandığında ise aktif (etken) bir enerjiye dönüşür. “Kitaba dökülmüş bilgi insan bilgisinin kayıt altına alınmış şeklidir”, diyebilirsiniz. Ama, kayıt altına alındığı andan itibaren artık o insandan bağımsız, evrenin malı olmuştur.

Bilgi için “madde ile etkileşip onu düzenleyen bir tür enerji” diyebiliriz. İnsan zihninde, veya herhangi bir ortamda (kitap, bilgisayar belleği gibi) durduğu sürece edilgen (potansiyel), nesneleri değiştirdiği ve onları daha düzenli hale getirdiği andan itibaren etken (kinetik) bir enerjidir. Bildiğimiz madde de aynı özelliklere sahip olduğuna göre madde = enerji = bilgi olmaktadır. Şu halde madde (nesne) bilgi ile eşdeğerdir. Daha doğrusu her var olan nesneler topluluğu, canlı veya cansız, bilgi içerir. İnsanların yaptığı da bu bilgiyi kullanmasını öğrenmekten başka bir şey değildir.

Bilginin etken olduğunu varlığa getirdiği düzenli yapıdan anlarız. İnsanlar bilgi ile silah da üretirler. Bu silahlarla diğer insanlara ve çevreye zarar verip düzen yerine karmaşa da getirebilirler. Fakat hiçbir savaş sonsuz değildir. Bir süre sonra sona erdiğinde yeni bir düzenli sistem oluşur. Bu durum yağmurun ve fırtınanın ardından bitkilerin yeşermesine benzer. Düzenin oluşması için önce düzensiz bir durumun var olması gerekir.

TE modelinde bilgiyi getirip düzenli yapılar oluşturan Takiyonlar olduğundan söz ettim. Takiyonlar bu bilgiyi nerden getiriyorlar? Elbette ki kendi düzenli evrenlerinden. Peki ama bu düzenli evren nasıl oluştu? Bizim ışık-altı evrenin düzensizliğinden. Çünkü, düzensizlik olmasa düzen tanımlanamaz, düzen olmasa düzensizlik tanımlanamaz. Demek ki bizim evrenimiz Takiyon evrene muhtaçtır, Takiyon evren de bizimkine muhtaçtır. Bu iki evrenin iç-içe olduklarından söz ettim.

Haberleşme kuramına Enformasyon kuramı da denir. Bu sözcükte en-formasyon iç-oluşum veya iç-şekillendirme anlamı bulunur. Yani “haberleşme” denince düzenli bir dönüşümle içsel şekillendirme anlaşılmalıdır. Bu şekillendirilmiş yapıyı da ölçebilmek için Entropi kavramı, daha doğrusu tersi olan Neg-entropi kavramı kullanılır. Negentropi, Entropinin ters işaretlisi, Negatif Entropi demektir. Nasıl ki Entropi düzensizliğin ölçüsü ise, Negentropi de düzenin ölçüsüdür. Sistem dengeli bir yapıya dönüştüğünde Entropi ile Negentropi birbirlerine eşittir. Sistem hareket halinde iken biri azalırken diğeri artar. Yani, Negentropi ile Entropinin toplamı sabittir. Bu ifadenin bilinen şekli Enerji korunumu yasasıdır.

Fakat “sistem” sözü geçtiğine göre tek bir parçacıktan veya dalgadan söz etmiyorum. Bir parçacıklar küme’sinden veya bir dalga paketinden söz ediyorum. Demek ki bilginin oluşması için en az iki nesne olması gerekir. Çünkü haberleşme en az iki nesne olmasını gerektirir. İki nesnenin düzenli bir yapıya dönüşmesi için birbirlerine doğru yaklaşıp bir bütün oluşturmaları gerekir ki bu duruma biz “madde çekim yasası” diyoruz. Veya Genel Görelilik kuramına göre uzayın bükülmesi diyoruz. Ama bunun için de aralarında bir haberleşme bağının oluşması gerekir. İşte bu bağı oluşturan ışıktan hızlı hareket eden Takiyonlardır.

Bu haberleşme bağı kurulduğu andan itibaren bilgi alış-verişi oluşur. Demek ki bilgi içeren Takiyonlar sayesinde evrende daha düzenli yapılar ortaya çıkmaktadırlar.

Yerellik ve indirgeyicilik

Tarih: 09:35 on 20/2/2006

18 ve 19. yüzyıllarda gelişmiş olan klasik bilimin etkisi altında genel bir kanı olarak Yerellik ve İndirgeyicilik yaklaşımları yerleşmiştir. Bu yaklaşımlar birer ilke olmayıp sadece birer varsayımdırlar.

Yerellik: Etkileşimlerin sadece yerel nedenlere dayalı olduklarını varsayar. Böylece uzaktan ve anında etkilerin bulunamayacağını iddia eder. Isaac Newton (1643-1727) klasik mekanik kuramında yerellik varsayımını hem onaylamış hem de dışlamıştır. Kendi yasası olan “Her etkiye yerel olarak ters yönde eşit bir tepki oluşur” görüşü ile yerelliği onaylarken, maddelerin birbirlerini anında çektikleri görüşünü savunduğu çekim yasasında yerelliği dışlamıştır.

Bu çelişik durum Einstein tarafından giderilerek her etkinin en çok ışık hızı ile yayılacağını savunmuş ve anında, uzaktan etkileri yok saymıştır. Oysa ki Takiyon Evren modelinde ışıktan hızlı hareket eden Takiyonların en alt hızı ışık hızı olup hızlarının üst sınırı yoktur. Yani sonsuza yakın hızlarla anında etkide bulunabilirler. TE modelinde yerellik varsayımı geçerli değildir.

Sürekli zaman kavramı, hatta sürekli uzam kavramı da yerellik varsayımından türerler. Çünkü “süreklilik” ile “yerellik” el-ele giden kavramlardır. Bir etkinin yerel olması için “yer” adını verdiğimiz uzam-zaman yapısının sürekli olması şarttır. Eğer süreklilik yoksa bir noktada oluşan etkiler süreksiz bir sıçrayışla farklı bir noktada tepkiye neden olabilirler. Böyle bir durum ise klasik bilim görüşü tarafından ret edilir.

Oysa ki Kuantum kuramı ani sıçrayışları kabul eder ve sürekliliği ret eder. Örneğin, atom çekirdeği etrafında dönen bir elektron parçacık olmayıp bir dalga gibi hareket ettiğinden yeri belirsizdir. Bir yörüngeden diğerine ani bir sıçrama yapar ve tekrar kendi eski yörüngesine anında geri sıçrar. İki yörünge arasındaki enerji farkına eşit bir enerjiye sahip olan bir foton da bu arada elektron tarafından salınır.

Bu olayı ne yerellikle ne de indirgeyicilikle bağdaştıramayız. Çünkü indirgeyicilik varsayımına göre bir bütünü parçalarına ayırarak anlamak mümkündür. Oysa ki elektrondan fırlayan foton elektronun yapısına sahip değildir. Elektron maddesel bir parçacık iken foton maddesel bir parçacık değildir. Kuvvet ileten bir parçacıktır. Aslında ikisi de parçacık değillerdir. Her ikisi de uzayda yerel olarak tanımlanamayan yaygın dalgalardır.

Elektron-foton ikiliği indirgenemez. Çünkü ikisinin toplamı olan yapı hem biridir hem de diğeri. Kuantum kuramı parçacıkları sınıflayarak bir indirgeme yapsa da bu indirgeme nereye kadar sürecektir? Nötron ve protonların Kuark adı verilen parçacıklardan oluştukları varsayılıyor. Kuarklar ise bağımsız olarak gözlenmedikleri için onları birbirlerine bağlayan Glüon adlı parçacıklar varsayılıyor. Fakat değişik doğa kuvvetlerini bir bütün olarak açıklamak isteyen fizikçiler Sicim adını verdikleri birtakım çok küçük (Planck uzunluğunda) yapılar ileri sürüyorlar. Bu sicimler de yeteri kadar istenilen görevi yapmadıkları ortaya çıkınca Membrane adını verdikleri esnek yüzeyleri varsayıyorlar.

Tüm bu yaklaşımlar ve varsayımlar yerellik ve indirgeyicilik varsayımlarında ısrar etmekten ortaya çıkıyor. Eğer bu iki varsayım gevşetilse ve ışıktan hızlı etkileşimlerin olabileceği kabul edilse, pek çok sorun çözülür kanısındayım. Eğer süreklilik genel olarak yoksa, o zaman sürekli bir uazy-zaman kavramına ve dolayısıyla ne "yer" ne de "eter" kavramına gerek vardır.

TE modelinde yerellik olmadığı gibi indirgeyicilik de yoktur. Çünkü gerek Karmaşa kuramı gerekse Holografik yaklaşım bütünsel olarak davranan bir evrene işaret ediyor. TE modeli de hem Karmaşa kuramını hem de Holografik evren modelini içeren, onları dışlamayan, üstelik Kuantum sıçramalarını da bulunduran bir modeldir. Üstelik TE modelinde süreklilik de yoktur. Evrenin açılıp kapanması sürekli bir olay olarak tanımlanmıyor. Ani ve kuantum zamanı kadar kısa bir sürede evren bir durumdan diğer duruma geçmekte, bu geçiş de ani bir sıçrama şeklinde olmaktadır.

Türlerin oluşumu

Tarih: 07:04 on 20/2/2006

Yeryüzünde görülen çeşitli bitki ve hayvan türlerinin oluşumu hakkında bir kuram geliştiren Charles Darwin (1809-1882) doğal seçilim yoluyla evrimin gerçekleştiğini ileri sürmüştür. Bu görüşe göre doğaya ve çevre şartlarına uyum sağlayan türler doğal bir seçilim ile varlıklarını sürdürmekte ve evrimleşerek değişmektedirler.

Bu görüş genel bir çizgi içinde doğru olmakla birlikte ayrıntılarda birtakım zorluklarla karşılaşıyor. Örneğin, basit organizmalardan karmaşık yapılara geçiş yavaş ve sürekli olmamış yeni türler aniden, süreksiz bir sıçrama şeklinde belirmiştir. Yani, sürekli küçük değişimler doğada görülmüyor. Genlerin (mikro) değişimini bedensel (makro) değişimlerin izleyeceği görüşü de sorgulanabilir. Çünkü genlerde kendilerini tamir eden bir mekanizma var. Çevreye uyum sağlamak fikri bir totolojidir. Çünkü bizim çevremizde var olan türler otomatik olarak “uyum sağlamış” kabul edilip diğer (kaybolmuş) türler “uyum sağlayamamış” olarak tanımlanmaktadır. Günümüzde çevresi ile çok iyi bir uyum içinde olan türler yok oluyorlar. Fosil buluntular yeni türlerin çok kısa bir sürede ortaya çıktıklarını gösteriyor. Türler gelişmiyor, aniden oluşuyor.

Türlerin oluşumuna en temel açıklama getiren iki kuram vardır. Bunlar Karmaşa kuramı ve Kuantum kuramıdır. Karmaşa kuramında başlangıç şartlarının önemli olmadığını gördük. Herhangi bir t₁ anında P₁ fonksiyonu bilinirse t₂ anında k parametresine bağlı olarak P₂ fonksiyonu bilinebilir. Karmaşa kuramında k parametresi önemli rol oynar. Bu parametredeki ufak bir farklılaşma büyük değişikliklere yol açabilir.

Kuantum kuramı ise bir durumdan diğerine ani bir sıçrama ile geçileceğini söyler. Kuantum kuramında zaman sürekli olmadığından bir anda yeni bir durum ortaya çıkabilir. İşte Karmaşa kuramındaki k parametresi kuantik bir sıçrama ile aniden Dk kadar değişikliğe uğrarsa bir çatallaşma (bifurcation) olur ve yeni bir tür belirir.

Bu durumu en açık olarak virüslerde görmekteyiz. Örneğin, grip virüsü sürekli olarak ani sıçramalarla yeni türler oluşturuyor. Bu duruma “virüs uyum sağlıyor” şeklinde bir açıklama getirsek dahi “uyum” sözü yavaş bir değişime işaret ettiği için pek uygun bir kavram değildir. Benim tercih ettiğim ifade “virüs aniden farklılaşıyor ve yeni türler oluşuyor” şeklindedir.

Türlerin oluşumunda Kuantum kuramının etkisi sadece genetik değişimlerle açıklanamaz. Bu etki tüm evrenin küçük bir hacim içine sıkışması ve Takiyonlardan gelen düzen ile ilgilidir (Bakınız: Sorular yanıtlanıyor başlıklı yazım). Evren her küçüldüğünde Takiyonlar yeni türlerin oluşumuna etki etmekte ve bu oluşum bir kuantik sıçrama şeklinde aniden olmaktadır. Evren büyüdüğünde ise holografik olarak (temel yapı aynı kalsa da) birbirine benzeyen fakat yine de farklı olan türler oluşuyor.

Sadece yeni türlerin oluşumu değil, aynı tür içindeki farklılaşma da bu kuantik sıçrama şeklindedir. Örneğin binlerce karınca gurubu vardır. Hepsi de aynı karınca türüne ait olsalar da aralarında birçok özellikleri bakımından ayrılmaktadırlar.

Bir diğer örnek, kök bir ana dilden türeyen lehçeler ve ağızlar, ana dilin yan kollara ayrılışı, çok kısa bir zaman aralığı içinde, adeta ani bir oluşumdur. Bu olayda da Acayip Çekici etkisini ve çatallaşmayı görmekteyiz. Acayip çekici tek ise sistem o noktaya doğru yaklaşıp sabit ve dengeli olmaktadır. Bu durum hem yeni türlerin hem de yeni dillerin kalıcı olmalarını açıklar. Fakat acayip çekici birden fazla ise sistem kararsız denge durumunda olur ve çok küçük bir dış etki bile onun tümüyle karmaşaya sürükleyebilir.

Karmaşa içine giren sistemin davranışı ise belirsiz olur. Aniden dağılabileceği gibi iki çekici merkez arasında gidip gelerek, salınım hareketi içinde, varlığını sürdürebilir. Birçok toplumun tarih sahnesinden silinmiş olması ve birçok türün doğada yok olması bu etki ile açıklanabilir. Öte yandan iki çekici merkeze rağmen varlığını sürdüren toplumlar da vardır. Örneğin, Belcika, Kanada ve İsviçre birden fazla dilin konuşulduğu ve dış çekici güçlerin etkin olduğu ülkeler olmalarına rağmen denge içinde varlıklarını sürdürüyorlar.

Karmaşa ve düzen

Tarih: 15:34 on 19/2/2006

Son iki yazımda Karmaşa kuramının en temel denklemlerinden hareketle Fraktal ile Acayip Çekici kavramlarını açıklamaya çalıştım. Fakat acayip çekici denen merkezi nokta tek bir nokta olmayabilir. Eğer iki tane acayip çekici varsa sistem ikisi arasında salınım hareketleri yapar.  Yukarda görülen resim Lorenz Fraktalı olarak bilinir. İki merkez etrafında sistem sürekli gidip gelir ama her yörünge bir öncekinin aynı değil sadece benzeridir.

Bu yapıyı anlamak için basit bir denklemden hareket edelim. Altın Oran başlıklı yazımda verdiğim      x² = x + 1 denklemini biraz farklı yazıp bir de sabit parametre ekleyelim.

P_n+1(x) = k.P_n(x) – k.P_n(x)² denkleminde n+1 inci terim n’inci terim ile sabit bir k parametresinden elde edilir. Hem başlangıç değeri olan P(x) sayısına hem de k’nın değerine göre farklı sonuçlar ortaya çıkmaktadır. Örneğin, k = 3.1 ve P₁(x) = 0.5 seçilirse iki adet “tuhaf çekici” belirir. Bunlardan biri 0.558 ve diğeri 0.765 değerleridir. Sistemin denklemi sürekli bu iki sayı arasında gidip gelir.

Fakat aynı denklemde k =4 ve P₁(x) = 0.4 seçersek hiçbir çekici nokta belirmez ve değerler sürekli belirsiz bir şekilde sıçrar durur. Sistem karmaşık hale gelmiş olur ve düzen oluşmaz. Türbülans denen olayın nedeni budur.

Farklı k değerleri çok farklı sonuçlara yol açmaktadır. Fakat, dikkat edersek, hem k değerinde hem de başlangıç şartında çok küçük bir değişim yapmak sonuca çok büyük etkileri olabiliyor. Fraktal yapıda kendine benzeme özelliği bazı değerler için kaybolmazken diğer bazı yakın değerler için düzenden tümüyle düzensizliğe ulaşıyoruz. Fakat parametrelerin biraz değişmesi yeniden düzenin geri gelmesini sağlıyorlar.

Kayalardan akan suyun türbülansı, yükselen sigara dumanının hareketi, fırtınalı rüzgarlar, tayfunlar, borsa hareketleri, zarların yuvarlanışı, kalbin fibrilasyona girmesi gibi çok farklı olaylar karmaşa kuramı ile açıklanıyor. Bir ağacın yeni bir budak vererek dal oluşturması, hatta kan damarlarının oluşumu dahi Lorenz Fraktalindeki parametrenin belirli birtakım değerler arasında kaldığı durumlarda gerçekleşebiliyor. Bir coğrafi bölgede bazı tür hava akımlarının oluşumu (hortum, tayfun, muson rüzgarları gibi) belirgin bir sıcaklık aralığına bağlı olduğunu ve aynı olayın farklı sıcaklık aralıklarında neden oluşmadığını şimdi daha iyi anlıyoruz.

Eğer yukarıdaki denklemde P_n(x) = t₁ anı olarak düşünülürse, bir an sonrası olan t₂ anı sadece k parametresine bağlı olduğu görülüyor. t₁ anındaki evrenin durumu ile sabit k parametresi bilindiğinde t₂ anındaki durum bilinebilir. Eğer evren Holografik olarak iki merkez arasında salınıyorsa bir “an” bildiğimiz genişlemiş evren, hemen sonraki “an” daralmış ve küçülmüş evren olabilir. Bu hareketi de sadece kendine benzeyerek kendi üzerine dönüşümlü bir yapı ile sağlayabilir. Altın Oran başlıklı yazımda görülen resim çok büyük bir sistemin spiral hareketle nasıl da sıfıra doğru küçüldüğünü göstermektedir.

Elbette ki burada belirttiğim basit denklemler bizim evrenimizi açıklamaya yetmezler. Ancak bu basit örnekler sayesinde, Takiyon Evren modelinde sözünü ettiğim açılıp-kapanma olayının pekala mümkün olabileceğini ve bunun için sadece “an”daki bilginin yeterli olacağını anlamış bulunuyoruz.

Ayrıca, Acayip Çekici veya çekicilerin Fraktal olmalarından dolayı sistemde sürekli kendine benzeyen (fakat kopyası olmayan) yapılar ortaya çıkmaktadır. Bu benzerlik her boyutta görülmektedir. Ancak, Fraktaller kesirli boyutta olduklarından tam sayıdan oluşan “Klasik Boyut” kavramı da terk edilmelidir.

Karmaşa Kuramı ile birçok sistem açıklanabiliyor. Meteroloji, Biyoloji, Ekonomi, Tıp, Astronomi, Kozmoloji hatta Sosyoloji ve Psikoloji dahi bu kuramdan yararlanıyor.

Altın oran

Tarih: 09:26 on 19/2/2006

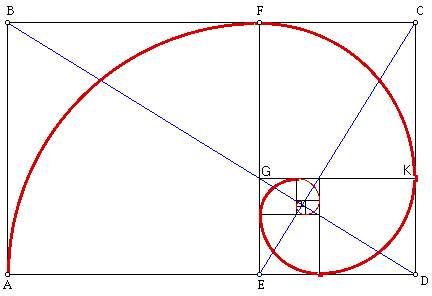
Yukarıda sözünü ettiğim “kendi üzerine dönüşümlü” sistemler ile Altın Oran arasında yakın bir ilişki vardır. Bu oran sadece matematik bir ilgi odağı olmayıp fizik ve dolayısıyla doğa ile de yakından ilgilidir. Altın oran çok eski dönemlerden beri bilinmektedir. Kadim Mısır kültürü ehramların yapısında bu oranı kullanmış, kadim Yunan filozof ve matematikle ilgilenen düşünürler de Altın Oranı onlardan öğrenmiştir.

 

Altın oran mantığı şudur. Bir doğru parçasını öyle bir noktasından bölün ki tüm uzunluğunun uzun parçaya oranı, uzun parçanın kısa parçaya oranına eşit olsun.

 

Yani  l-----------------l-------------l şeklinde bir doğru parçasında   A + B  =  A 

                 A                   B                                                         A         B

 

Kolaylık olsun diye A = x ve B = 1 seçelim. Bu durumda x² = x + 1 olur.

Bu denklemi x² - x – 1 = 0 şeklinde yazıp köklerini bulursak x(1) = 1.6180339887...ve x(2) = - 0.6180339887...buluruz. Bu iki kökten pozitif olan x(1)’e büyük T adını verelim.

 

T irrasyonel bir sayıdır. Yani iki tam sayının oranı olarak gösterilemez. Fakat iki tam sayının oranı kendi üstüne dönüşümlü bir kural dahilinde T sayısına yaklaşır. Bu kuralı Fibonacci dizisinden çıkarırız. Asıl adı Leonardo Pissano olan Fibonacci (1170-1250) İtalyada doğmuş fakat Mısırda büyümüştür. Matematik meraki da o dönemde çok ileri düzeye ulaşmış İslam matematiğinden kaynaklanmıştır.

Fibonacci 1,1 çiftinden başlayarak son iki sayının toplamından yeni bir sayı üretmiş ve bu kendi üstüne dönüşümlü kuralı tekrarlayarak şu diziyi elde etmiştir:

1,1,2, 3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,.............

Bu dizide ard arda olan iki sayıdan büyüğünü küçüğüne bölerseniz görürsünüz ki T sayısına doğru yakınsar. Örneğin, 233/144 = 1.618055 iken 6765/4181 = 1.618033 olup gittikçe T sayısına doğru yaklaştığımızı görürüz. Fibonacci sayılarına F(n) dersek herhangi peş-peşe bir çift için F(n)/F(n-1) => T sayısına doğru yakınsar fakat asla eşit olmaz.

Bu durumun birçok ilginç açılımı vardır:

1-     Kendi üstüne dönüşümlü önermeler belirsizliklere ulaşırlar. İki Fibonacci sayısının peş-peşe oranı da kendi üstüne dönüşümlü bir kural içerir. Bu bakımdan T sayısı sonlu bir sayı olmayıp sonsuza kadar kesirleri sürer gider. Bu “irrasyonel” olma özelliği tüm doğa sabitlerinin ortak özelliğidir.

2-     T sayısı “kuadratik” (kareli terim içeren) bir denklemin köküdür. Kareli terim ise kendi üstüne dönüşümlü olduğunda Kaos (karmaşa) yaratır. Bu durumu bir önceki Kelebek etkisi başlıklı yazımda açıkladım.

3-     Fibonacci dizisi iki tane “1” sayısından başlayarak ard-arda iki terimin toplamından oluşuyor. T sayısı ise ard-arda iki terimin bölümünden oluşuyor. Yani, hem diziyi oluşturmak için hem de T sayısına yaklaşmak için son iki sayıyı bilmek yetiyor. Dolayısıyla teklikten ikiliğe geçilirken yeniden tekliğe yaklaşılıyor.

Bu son noktanın önemli fiziksel ve felsefi sonuçları vardır. Bu noktayı daha iyi anlayabilmek için Altın Oranı iki boyutlu bir dikdörtgene uygulayalım. Öyle bir dikdörtgen bulalım ki uzun kenarı ile kısa kenarının toplamının uzun kenara oranı, uzun kenarın kısa kenara oranına eşit olsun. Gene oranın 1.6180339887... olduğunu görürüz. Eğer bu oranı tekrarlarsak şekildeki gibi bir noktaya doğru yakınsadığını görürüz. ABEF noktalarından geçen kare CFGK noktalarından geçen kareye göre kenarı T kadar daha büyüktür. Aynı oranı defalarca küçülterek tekrarlarsak şekil çok küçük bir kareye doğru yakınsar. BD ve CE köşegenlerinin kesim noktası şeklin odak noktasıdır. İki köşegenin oranı ise gene T sayısıdır. 

Bu şekilde bir kareden başlayarak kendine benzeyen ve kendi üzerine dönüşümlü karelerin bir odak noktasına doğru yakınsadıklarını görüyoruz. Bu noktaya “Acayip Çekici” nokta adı verilmiştir. Çünkü bu nokta sistemin denge noktası olup tüm kuvvetlerin bu noktadan kaynaklandığını düşünebiliriz. Ayrıca köşelerden geçen kırmızı çizgi bir spiral çizmekte sonsuzluğa yaklaşan girdap görünümü vermektedir.

Doğada da bu tür girdaplara oldukça sık rastlamaktayız.

Kelebek etkisi

Tarih: 22:48 on 18/2/2006

Fizikçiler uzun yıllar, hatta birkaç yüzyıldır matematik çözümü kolay olan “çizgisel” yapılarla ilgilendiler. Çizgisel yapılara örnek düzgün görünüşlü, kolay tanımlanan geometrik şekiller ve matematik fonksiyonlardır. Örneğin, bir doğru çizgiyi y = a.x + b denklemi tanımlar. a parametresi doğrunun x ekseni ile yaptığı açıyı ve b parametresi de doğrunun y eksenini kestiği noktayı belirler.

Bu doğru denklemi çözümü kolay olan çizgisel yapıları tanımlar. Fakat y = a. X² + b denklemi çizgisel olmayıp, bir x  sayısının karesini içerir. Kolay olsun diye a = 1 ve b = 0 alıp y = X² denklemini inceleyelim. Bu denklemi kendini tekrarlayan bir yapıya uygulayalım. Yani, y(n) = y(n-1).y(n-1) olsun. Bu ifade ile her yeni adımı hesaplamak için bir önceki adımda elde edilen değer kullanılacaktır. Aralarında çok az fark olan iki sayı ile başlayalım. Bunlardan biri x değeri için  1’den çok az büyük, örneğin x = 1.00005 ve diğeri, x değeri için 1’den çok az küçük, örneğin 0.99995 olsun. Bu iki sayıya yukarıda belirtilen tekrarlı dönüşümü uygulayalım. Her yeni adımın hesabı için bir önceki adımda elde edilen sayının karesi alınacaktır.

x = 1.00005, x.x = x² =1.0001,   x². x² = x⁴ = 1.0002,  x⁴. x⁴ = x⁸ =1.0004 .....şeklinde işleme devam edersek sayının büyüyüp birkaç adımda çok büyük sayılara doğru gideceğini kolayca görebiliriz. Öte yandan x = 0.99995 sayısına aynı işlemi uygulayalım.

x = 0.99995, x.x = x² =0.9999,   x². x² = x⁴ = 0.9998,  x⁴. x⁴ = x⁸ =0.9996.....şeklinde gittikçe 1 sayısına doğru yaklaşacağını görürüz. Aralarında 0.0001 (onbin’de bir) kadar küçük fark bulunan iki sayı çizgisel olmayan ve kendine benzeyen bir işlem sonucunda çok farklı sonuçlar verebiliyor.

Bu örnek basit bir şekilde iki önemli özelliğin etkilerini ortaya koyuyor.

1. Çizgisel olmayan ilişkilerin etkisini ve
2. Kendi üzerine dönüşümlü benzerliklerin etkisini.

Çizgisel (lineer) olmayan ilişkiler doğadaki pek çok yapıda karşımıza çıkıyor. Bu tür ilişkilerle oluşan şekillere Fraktal adı verilmiştir. Çünkü bu şekillerin boyutu tam sayı olmayıp kesirli bir sayı olmaktadır. Örneğin bir süngeri düşünün. Sünger 3-boyutta yer kaplar ve üç boyutlu gibi görünür. Fakat içindeki deliklerin çokluğundan dolayı kıvrımları çok olan 2-boyutlu bir yüzeye de benzer. Bu bakımdan sünger ne 2-boyutlu bir nesnedir, ne de 3-boyutlu. Süngerin boyutu kesirli olup 2 ile 3 arasındadır.

Fraktal yapılara doğada pek çok örnek vardır. Örnek olarak gökteki bulutları, ağaçların dal ve yapraklarını, hatta akciğerin iç yapısını dahi gösterebiliriz. Hepsinde de kendine benzeyen fakat aynen tekrarı olmayan “dönüşümlü” bir etkileşme buluyoruz. Çünkü resimde görülen yaprağı Fraktal yaklaşımla bir bilgisayar çizmiştir.

Çizgisel bir gelişme göstermeyen sistemlerde, çok yakın başlangıç şartları dahi çok farklı sonuçlar verebilirler. İşte Karmaşa kuramında “Kelebek etkisi” denen olay budur. Eğer gelişim ve etkileşim çizgisel olmayıp karmaşık ise bir kelebeğin kanat çırpışı kadar ufak bir fark dahi çok büyük farklara yol açabilir.

Kendi üzerine dönüşümlü sistemlerin çelişik sonuçlar verebileceğinden söz etmiştim (Bakınız: Çelişkili önermeler başlıklı yazım). “Çelişik” derken, çizgisel bir mantık yapısına ters düşen ve kararsız bir sonuca ulaşan önermeleri kast ediyorum. Bu tür önermelerin doğadaki karşıtları Fraktallardır. Çünkü onları da çizgisel bir denklemle açıklayamayız ve boyutları hakkında kesin bir karar veremeyiz.

Evrenin yapısı da karmaşık bir Fraktaldir. Modern kozmoloji kuramları evrenin 4 boyuttan çok daha fazla boyuta sahip olduğunu söylüyorlar. Kanımca, evrenin boyutu tam bir sayı olmayıp, örneğin 5,5 gibi, kesirli bir sayı olabilir. Ayrıca evren sürekli kapanıp açıldığı için kendi üzerine dönüşümlü bir özelliği vardır. Bu özelliğinden dolayı, birbirine benzeyen fakat aynen tekrarı (kopyası) olmayan cansız ve canlı yapıların oluşumuna yol açmıştır.

Cansız yapılara örnek mikro evrendeki atom ve molekül yapısından makro evrendeki güneş sistemine ve gök adalarına kadar benzer oluşumlardır. Canlı yapılara örnekler ise bitkiler ve hayvanlar aleminde ortaya çıkmış olan, birbirlerine çok benzeyen fakat asla birbirlerinin kopyası olmayan canlı türleridir.

Özgür irade

Tarih: 12:08 on 18/2/2006

Albert Einstein (1879-1955), Rabindranaz Tagore (1861-1941)’a bir mektubunda şöyle der: “Eğer ay’a neden dünya etrafında dönmekte ısrar ediyorsun? Diye sorulsaydı, şöyle bir yanıt verirdi: ‘Ben başlangıçta buna karar verdim ve kararımdan dönmem.” Bugün böyle bir yanıt karşısında sadece gülümseriz. Çünkü ay dünyanın çekim etkisi altındadır ve kendi iradesi dışında dünya etrafında dönmektedir. Özgür irade ile başlangıç şartları arasında bir ilişki vardır.

Eğer başlangıç şartları bir sistemin ilerde nasıl davranacağına karar veriyorsa özgür irade diye bir yeti olmaması gerekir. Kaderci görüş de her önemli olayın insana baştan itibaren “alın yazısı” olarak tespit edildiğine inanır. Büyük Patlama denen evrenin ilk oluşumu tek bir kere gerçekleşmiş ise, gerçekten de evrenin sonu bellidir. Çünkü ilk durumda başlangıç şartları nasıl iseler, doğa yasaları gereği evrenin gelişimi ve “ölümü” de başlangıç şartlarına bağlı olarak kesinlik kazanmış demektir. Determinist görüş her sistem için başlangıç şartlarının belirleyici olduğuna inanır.

Oysa ki Takiyon Evren modelinde tek bir başlangıç yoktur. Evren sürekli açılıp kapandığından her saniye içinde milyarlarca kere yeniden başlangıca dönüyor demektir. Bu bakımdan başlangıç şartları da sabit olmayıp evrenin sonu da belirsizdir. Bu açılıp kapanma olayından haberdar olmadığımızı söyledim (Bakınız: Sorular yanıtlanıyor başlıklı yazım). Fakat zaman kavramı bu akordeon hareketi ile yakından ilgilidir.

Evren genişlerken, ışıktan yavaş hareket eden parçacıklar düzenli yapıları düzensiz hale dönüştürürler. Bu durum bize zamanın geçmişten geleceğe doğru tek boyutlu bir hareketi gibi görünür. Oysa ki, Takiyonların etkisi ile düzensizlik bir süre sonra tekrar düzene dönüşür. İşte bu düzenli sisteme dönüşme süreci zamanın tersine hareketi olarak anlaşılmalıdır. Takiyonların zamanda ters yönde (gelecekten geçmişe doğru) ilerlediklerinden söz etmiştim.

Şu halde evrenin zamanı tek yönlü olmayıp, tersinir olarak iki yönlüdür. Zaten Kuantum kuramı sürekli bir zaman değişkeni kabul etmez. Onun için sadece “an” vardır. Belli bir anda sistemin seçtiği “yol” (seçenek, tercih) başlangıç şartlarından bağımsız olarak o andaki tüm etkenlerin sonucunda ortaya çıkan bütünsel bir birlikteliğin sonucudur. Bu duruma “bifurcation” (çatallaşma) denmektedir. Çatallaşma sadece iki dal gerektirmez. Sistemin karşısına birçok olanak çıkabilir ve sistem bunlardan birini seçer. Ancak bu seçim ne tümüyle özgür bir seçimdir ne de tümüyle belirlenmiş (determinist) bir seçimdir. Seçimde her ikisi de etken olmuştur. Yani, özgür irade hem vardır hem yoktur. Vardır, çünkü kaderci bir bakışla “alın yazısı” yoktur. Yoktur, çünkü o anda kararı veren kişi, farkında bile olmadan, kendi iradesini aşan yerel olmayan (ışıktan hızlı) etkilerle kararı vermektedir.

İnsanın özgür iradesi tek başına iken daha fazla, toplu halde iken daha azdır. Toplu halde iken birtakım kurallar devreye girmekte, bu kurallar da özgür irademizi kısıtlamaktadır. İşte aynı durum evren için de geçerlidir. Evren küçülüp dar bir hacim içine yoğunlaştığında Takiyonların da etkisiyle düzenli sistemler ve doğa yasaları oluşmaktadır. Evrenin sıkışık hali çatalın bir kolu, genişlemiş hali ise çatalın farklı bir koludur. Evren sıkışık durumda iken içindeki dalgacıkların hiçbir seçenekleri yoktur. Takiyonların etkisi üstün gelir. Evren genişlediğinde ise Takiyon etkisi zayıflar ve dalgacıklar bağımsız birer birim gibi davranırlar. Biz insanlar da bu birimleri bağımsız ve yalıtık görünüşlerine kanarak özgürlük üzerine yorumlar yaparız. 

Oysa ki, görmekteyiz ki, ne tam bağımlılık ne de tam bağımsızlık mümkündür. İki durum sürekli birbirleri ile karşılıklı etkileşerek denge oluştururlar. İnsan toplum içinde bağımlı olduğu gibi ülkeler de topluluklar haline geldiklerinde ortak kurallar ile bağlanırlar ve kısıtlanırlar.

Bilimde Karmaşa kuramı bu hem bağımlı hem bağımsız olmak durumunu matematik denklemlerle çok güzel bir şekilde açıklamıştır. Karmaşa kuramının denklemlerine göre evrende “non-lineer” (lineer olmayan, çizgisel bir süreç izlemeyen), süreksiz ve yerel olarak öngörülmesi mümkün olmayan bir yapı vardır.

Bu yapıyı daha yakından inceleyeceğim.

İnsan ve evren

Tarih: 07:33 on 18/2/2006

Takiyon Evren Modeli ile sadece evrenin oluşumu ve bugünkü durumu değil, aynı zamanda insan yetenekleri ve düşüncesi de açıklık kazanmaktadır. Evren bir holografik yapı ise ve Takiyonlar sayesinde evrenin her noktası ışıktan hızlı bir şekilde etkileşiyorsa, insan kendini tanımakla evreni de tanımış olur.

Kendini tanıyan insan bir yandan birlik duygusuna erişirken öte yandan sonsuzlukla da temasa geçmiş olur. Zira evrenin uzay-zaman sonsuzluğuna holografik olarak zamanda ‘şu AN’da’ ve mekanda ‘burada’ noktalarından sıçrama yapmak mümkündür.

İnsanla evren arasındaki bu yakın ilişkiye değinmiş olan fizikçi, (1930’lu yillarda Nobel fizik ödülünü de kazanmış olan) Paul Dirac’tir. Dirac (1902-1984)’ın ileri sürmüş olduğu Antropik Prensibine göre “Fizik biliminde bazı sabit sayılar az bir miktar farklı olsalardı evrenimiz bugünkü durumuna asla ulaşamazdı ve bu çok farklı oluşan evrende insan da ortaya çıkamazdı”. İnsan evrende tesadüf eseri oluşmuş bir varlık değildir ve evrenle bütünsel bir ilişki içindedir.

Antropik Prensibin ‘Insanı merkez yapan prensip’ olduğu sanılabilir. Oysa ki, bu yaklaşım ben-merkezci (egoist) bir bakış açısı olmayıp sadece insanı dışlamış olan nesnel fizik bilimine öznel insan yapısını katmak olarak algılanmalıdır. Zira evreni gözleyen ve evren hakkında fikir yürütüp model geliştiren insan ile evren ‘içiçe’dirler. Bu ilişki sadece yerel olmayıp zaman ve mekândan bağımsız, bütünsel bir ilişkidir.

Eğer insan varlığın bütünsel bir holografik kaydı ise bu kayıtta zaman ve mekandan bağımsız, çok eski dönemlerden kalma, bilgiler, tecrübeler, imgeler ve simgeler bulunabilir. Hatta Sigmund Freud (1856-1939) ile ayni dönemde yaşamış olan Carl Gustav Jung (1875-1961)’un iddia ettiği gibi ‘arketipler’ dahi bulunabilir. Arketipler en eski dönemlere ait modeller, imgeler ve simgelerdir. Örneğin, insan arketipini ‘Anima’ (dişi) ve ‘Animus’ (erkek) arketipi olarak iki temel motif veya kavram olarak düşünebiliriz.

Anima, doğuran ve koruyan dişi özelliği ile doğayı ve doğa güçlerini temsil eden bir Tanrıça motifi olarak insanlık tarihinde önemli bir rol oynamıştır. Eski toplumlarda Ana-Tanrıçalara büyük önem verilmesi, insan yaşamının doğaya bağlı olusu ve toprak ürünlerinden bolluk ve bereket beklentisi ile yakından ilişkilidir. Anadolu ve Mezopotamya Tanrıçaları hep bolluğu ve bereketi simgeliyorlardı. Animus ise, insanın bedensel (kas) gücünü ve uygulayıcı yönünü belirtir. Ayrıca, Anima her erkeğin hissi ve duygusal yanını, Animus ise her dişinin karar veren yönetici yanını temsil eder. Öyle anlaşılıyor ki, her insanda holografik olarak kayıt edilmiş olan hem erkeklik hem de dişilik özellikleri bulunmaktadir. Bu özellikler birbirleri içinde uyumlu bir girişim ve kaynaşım içinde oldukları sürece insan dengeli ve huzurlu olur. Birinin diğerine fazlaca üstün gelmesi halinde karşı cinsi etkileyip kontrol altına almak arzusundan doğan dengesiz bir karakter ortaya çıkar. Doğru olan Yin-Yang  simgesinde olduğu gibi, birleşmiş ve kaynaşmış, dengeli bir kişilik elde edebilmektir. Her insanda bulunan Anima-Animus ikiliği insanda teklik halinde birleşmesi sonucu “insan” varlığı oluşmuştur.

Evrendeki tüm varlıklarda görülen teklikte ikilik özelliği, ortak ve gizli holografik bağların varlığına işarettir. Bizim için önemli olan bu bağların farkına varmak ve sonsuzlukla iletişim içine girebilmektir. Medyumların, şamanların (kamların), şifacıların, Reiki enerjisi ile temas kuranların ve telepati gücüne sahip olanların pratikte yaptıkları, bu holografik yapıyı harekete geçirerek insanlığa faydalı olabilmektir.

Klasik bilim bu gibi öznel güçleri görmezden gelse de ilerde insan-evren ilişkisine önem verileceği kanısındayım. Çünkü insanın evrenle olan holografik ilişkisi bilimsel bir açıklama ile anlaşılıp uygulamaya konabilir. Burada insanın özel bir konumu olduğunu söylemek istemiyorum. Canlı veya cansız her varlıkta bu holografik kayıt, değişik seviyelerde olduğuna göre, her varlığın da insan kadar önemi ve evrende insana eşdeğer bir konumu vardır.

Yin ve Yang

Tarih: 07:57 on 17/2/2006

Evrenin tek bir foton gibi düşülebileceğinden söz ettim. Aslında gördük ki tek bir evren yok. İki adet evren var. Biri görünen, diğeri görünmeyen evren. Biri ışık-altı parçacıkların evreni, diğeri ışık-üstü parçacıkların evreni. Bu ikilik modern “sicim kuramında” ve “birleşik alan kuramında” ortaya çıkan bir diğer sorunu da çözüyor. O da “Magnetik Monopol” denen tek kutuplu mıknatıs sorunu.

Evrende tek kutuplu mıknatıs görülmüyor. Bir çubuk mıknatısı hangi noktasından ikiye bölseniz bölün derhal iki kutup oluşuyor. Bunlardan biri kuzey diğeri güney kutup oluyor. İki aynı kutup birbirini itiyor, iki farklı kutup birbirini çekiyor. Bu yapı bizim dünyamızda dahi var. Dünyamızın mağnetik alanı aynen bir mıknatıs gibidir. Coğrafi kuzey kutbuna yakın mağnetik kuzey kutbu, coğrafi güney kutbuna yakın mağnetik güney kutbu vardır. Bu durumun neden böyle olduğu bilinmiyor.

Elektrik ve mağnetik kuvvetler tek bir kuvvetin iki farklı görüntüsü olarak kabul edilir. Bu birleşik kuvvete elektromağnetik kuvvet adı verilir. Fakat elektrik ve mağnetik alanlar tam olarak simetrik değiller. Elektrik alan tek başına bir elektrik yükü oluştururken, mağnetik alan tek başına bir mağnetik yük oluşturmuyor. Oysa ki Sicim kuramı ve Birleşik Alan kuramı gibi modern kuramlar tek bir mağnetik yük (monopol) olması gerektiği görüşünü ileri sürüyorlar.

İşte bu sorun da Takiyon Evren modelinde çözülmüş durumdadır. Çünkü iki evren varsa bu evrenler küçük bir hacim içinde sıkıştığında tek bir karmaşık yapı halindeler. Ayrıldıklarında ise iki ayrı mağnetik kutup özelliği de ayrılmış oluyor. Yani genişlemiş ışık-altı evrenin tümünde tek bir mağnetik kutup (örneğin kuzey), diğerinde (Takiyon Evrende) ise gene tek bir kutup (güney) oluşuyor. Evrenin sıkışık vaziyette iken genişlemesine etki eden de bu tek kutuplu mağnetik özellik.

Fakat bu tek kutuplu mağnetik özellik genel olarak ve yaygın bir şekilde evrenimizde bulunduğundan biz tek kutuplu mağnetik birim görmüyoruz. Yani, göz önüne getirebilmek için şöyle bir benzetme yapayım. Işık-altı ve ışık-üstü evrenler bir mıknatıs gibi davranıyorlar. Boyları ister küçük, ister büyük olsun daima bir kuzey bir de güney mağnetik kutup oluşturuyorlar. Bu iki kutbun birbirlerini çekme özelliğinden dolayı evrenimizle Takiyon evren daima hem bitişik hem de iç-içe bulunuyor. İç-içe bulundukları için de tek kutuplu bir mıknatıs oluşmuyor. Yani çift kutuplu mıknatısları oluşturan da Takiyonların düzen sağlayıcı etkisidir.

Çünkü karşıtların birliği sayesinde varlık varlığını sürdürür. Etkenlik edilgenlik başlıklı yazımda bu durumu açıklamıştım. Resimdeki yin ve yang şekli birbiri içine karışmış fakat gene de ayrı duran iki yapıyı gösteriyor. Birinin merkezinde diğeri var. Bu bakımdan hem ayrılar hem değiller.

Çevremizde bulunan tüm canlılarda bu karşıt fakat birbirini çeken yin-yang özelliğini görüyoruz. Dişil ve eril yapı her hayvan türünde var. Eğer bir türün üyeleri bir araya buluşmakta zorluk çekiyorlarsa iki cinsiyetli hale dönüşüyorlar. Örneğin, salyangoz çok yavaş hareket ettiğinden bir ömrü boyunca karşıt cinsli bir diğer salyangoza rastlama olasılığı oldukça küçüktür. Bu bakımdan tüm salyangozlar hem eril hem dişil özelliği taşırlar. Karşıt cinse gerek duymadan yavrulayabilirler.

Diğer hayvanlar ve insanlar ise erkek veya dişi şeklinde iki ayrı cinsiyet halinde doğuyorlar. Fakat aradıkları karşı cinstir. Çünkü ancak o zaman “tam” olabilirler. İki kutup birleşmedikçe tamlık oluşmuyor. İşte doğanın dengesi bu. Varlık da varlığını ikiliği teklik haline getirerek sürdürüyor. Bu bakımdan tek bir evren yerine iki evren gerekiyor.

Mikro evrende de aynen makro evren gibi karşıtların birliğini görüyoruz. Artı yüklü proton ile eksi yüklü elektron en basit ve en temel atom olan hidrojen atomunu oluşturmuştur. Diğer tüm karmaşık atomlar bu temel yapıdan sonra oluşmuşlardır. Evren de varlığını sürdürmek için Takiyon Evrenle birleşmiş bir birleşik yapı oluşturmuştur.

Sorular yanıtlanıyor

Tarih: 10:02 on 16/2/2006

Evrenin küçülüp büyümesi olayı bizim gündelik gözlemlerimizle uyuşmuyor. Ne böyle bir durum gözlüyoruz ne de aletlerimiz ölçebiliyor. Bunun iki nedeni var.

1. Açılıp kapanma o kadar hızlı oluyor ki bunu fark etmek (ölçmek) mümkün değildir. Bu kısa süre “an” olarak tanımlanırsa, en kısa zaman süresi olarak AN Planck zamanına yakın bir süre olması gerekir. Planck zamanı ise T(p) = 1.33 x 10^-43 saniyedir. Şu halde 1 AN yaklaşık olarak 10^-40 sn alınabilir. Bu o kadar kısa bir süredir ki hiçbir mevcut alet bu süreyi ölçemez. İlerde dahi bu sürenin ölçülmesi mümkün olmayabilir.
2. İkinci neden ise bizim ölçmek istediğimiz evrenin hareketine uygun olarak hareket etmekte olmamızdır. Evren açılıp-kapanırken biz de birlikte açılıp-kapanıyoruz. Yani, olay bizim dışımızda cereyan etmiyor. Bu akordeon hareketinde biz gözlemci değil, katılımcıyız. Gözlem yapmak için bir gözleyen bir de gözlenen olmalıdır. Oysa ki bu harekette gözleyen ile gözlenen bir tek bütündür.

Evren tek bir dalga paketidir. Biz de, özne olarak, bu dalga paketini oluşturan daha küçük dalga paketçiklerinden biriyiz. Evren küçülürken, veya büyürken bizimle birlikte evreni oluşturan tüm dalga paketçikleri aynı hareket içinde olduklarından bizim için fark edilecek bir durum oluşmamaktadır. Nasıl ki Takiyonlar gözlenemiyorlarsa, aynı şekilde evrenin peryodik hareketi de gözlenemez.

Klasik Genel Görelilik ve Büyük Patlama modellerinde ortaya çıkan ikinci soru: . Neden evrenin her bir tarafına bakıldığında aynı kozmik ışıma görülüyor? Sorusudur. Şimdi biliyoruz ki, Takiyon evren ile bizim ışık-altı parçacıkları evreni etkileştikleri için, ışık hızından dahi büyük bir hızla “bilgi” evren içine yayılmakta ve her tarafta eşit bir yoğunluk yaratmaktadır. Kozmik ışımanın her yönde aynı oluşu da bu nedenledir.

Bu homojen madde yoğunluğuna neden olan evrenin sıkışma evresinde oluşan parçacıkların daha sonra (genişleme evresinde) her yöne doğru eşit bir olasılıkla yayılmalarıdır. Zaten Termodinamiğin ikinci ilkesi bunu gerektirir. Bu parçacıklar çeşitli maddesel parçacıklardır. En fazla olasılıkla oluşanlar da Nötrinolardır.

Nötrino adı verilen parçacık, küçük bir nötrona benzer. Kütlesi sıfır veya sıfıra çok yakındır ama spini ½ olduğundan nötron gibi kendi etrafında dönmektedir. Fakat bir Lepton olduğundan Baryonlarla zayıf bir etkileşme içindedir. Bu bakımdan, evrende belirgin bir etki yapmaz. Fakat deneysel olarak da ölçülmüştür.

Bir görüşe göre evrenin genişlemesine neden olan bu Nötrinolardır. Bu parçacıklara “karanlık madde” diyen fizikçiler de vardır. Şu halde “Karanlık Madde” evrende yaygın olarak bulunan fakat henüz bir araya gelmemiş olan maddesel parçacıklardır. Deniyor ki: “Fakat bu karanlık madde bizim evrenimizin maddesi olan nötron ve protonlar olamaz. Çünkü evrendeki nötron ve proton sayısı bu hızlı genişlemeyi açıklamaya yetmiyor”.

Doğrudur, çünkü genişlemiş evrene bakıyorlar da ondan. Baryonlar ve Leptonlar evrene daralmış durumda iken etki edip genişletiyorlar. Genişlemiş durumda fazlaca bir etkileri olmuyor. Genişleme ilk tepkimenin sonucudur. Fakat bu ilk tepkime, Büyük Patlama modelinde varsayıldığı gibi tek bir kere olup bitmiş bir olay değildir. Sürekli olan ve tekrarlanan bir olaydır.

Son olarak “singülarite” sorusuna yanıt getirmek gerekiyor. Evren her ne kadar açılıp kapansa da hiçbir zaman noktasal sonsuzluk durumuna ulaşmıyor. Noktasal sonsuzluğa engel olan ise enerjinin bölünmez bir kuanta oluşundandır. Eğer enerji sonsuza kadar bölünebilirse sıfır hacım içinde sıfır enerjiye ulaşılması gerekir. Oysa ki Kuantum kuramı göstermiştir ki en küçük enerji birimi ışık kuantasıdır ve bölünemeyen bu enerji birimini Planck E = h.f olarak belirtmiştir. h = 6.624x10^(-27) erg-saniye.

Evren küçüldüğünde tek bir foton gibi görülebilir. Bu fotonun da bölünmez bir özelliği vardır. Üstelik foton yer kaplamasa da içinde birçok dalga barındıran bir dalga paketidir.

Takiyon Evren modeli

Tarih: 07:13 on 16/2/2006

Takiyon evrenin varlığını kabul ederek birçok yanıtı olmayan soruya yanıt bulmaktayız. Önemli sorulardan biri: “Bu evrende gördüğümüz düzenli yapıların (gök cisimleri, kristaller, canlılar), evrenin içindeki homojen madde dağılımının ve doğa yasalarının nedeni nedir?” sorusudur.

Tüm bu düzenli yapıları ve homojen dağılımı sağlayan Takiyonların düzen sağlayıcı etkisidir. Çünkü, daha önce söylediğim gibi, onların Termodinamiği bizimkinin tersidir. Fakat hem-hem mantığı gereğince bizim evrenimiz hem ölçülen hem de ölçülemeyen iki evrenin bileşiminden oluşmaktadır. Ölçülen evrende gördüğümüz yapıların nedenini ölçülemeyen evrenin varlığı ile açıklamış oluyorum.

Diyebilirsiniz ki: “Sen metafizik kavramlarla fizik yapmak istiyorsun”. Hem evet hem hayır. Evet, çünkü ölçülemeyen, fizik ötesi, bir gerçeklikten söz ediyorum. Hayır, çünkü bu ölçülemeyen gerçeklikten hareketle ölçülen evreni açıklayabiliyorum.

 Diyebilirsiniz ki: “Tanrı varsayımı da aynı şeyi yapıyor”. Evet ama Tanrı varsayımı bir “Tanrı iradesi” gerektiriyor. Oysa ki Takiyonlar kendi doğaları icabı, hiç irade gerekmeden, düzen oluşturuyorlar. Dolayısıyla bu model (adına Takiyon Evren modeli veya kısaca TE diyelim) metafizik olmayıp, doğrudan matematik temeli olan fizik bir modeldir.

Modern fizik zaten baştanbaşa ölçülemeyen kavramlarla çalışıyor. Quarklar, Glüonlar, Sicimler ve en son “Membrane” denilen esnek yüzeyler, hep ölçümüzün dışında parçacıkların varlığını açıklamaya çalışan “metafizik” kavramlardır. Demek ki fizikçiler düşünce modelleri üreterek yeni ve ölçülemeyen birimlerden hareket etmek zorunda kalıyorlar. Bu keyfi bir seçim görülse de bir noktada modelin öngürdüğü birtakım sonuçlar, deney ve gözlemlerle doğrulanmak veya yanlışlanmak durumundadır. Eğer doğrulanırlarsa kabul görürler, yanlışlanırlarsa ret edilirler.

Şimdi gelelim Büyük Patlama başlığı altında yönelttiğim soruları yanıtlamaya. Birinci soruda evrenin neden düz olduğu, yani şimdiye kadar neden dağılmadığı ve neden tekrar büzülüp bir noktasal sonsuzluğa dönüşmüş olmadığı sorgulanıyor. Bunun nedeni, TE sayesinde evren bir termodinamik denge durumunu sürdürüyor olmasıdır. TE’nin etkisi ile, açılıp kapanan, dinamik ve hareketli, üstelik sürekli genişleyen bir evren oluşmuştur.

Önce evrendeki kapanma (bir küçük hacme doğru büzülme) olayına bakalım. Eğer evren holografik bir yapıda ise en küçük biriminde dahi tüm evrenin bilgisi bulunması gerekir (Bakınız: Holografik evren başlıklı yazım). Bu özelliği sayesinde tüm evren bir ufak hacım içine kodlanarak sığabilir. Bu küçük hacım ‘evrenin küçük bir hacmi’ olarak düşünülmesin. Bu küçük hacım, dalga paketinin büzülmesi olarak düşünülmelidir. Tek bir dalga paketi olan evrenimiz, yine tek bir dalga paketi olarak büzülürken içindeki dalgacık paketlerinin titreşimi (frekansı) artar. Dolayısıyla çok yüksek enerjili bir ışık-altı ve ışık-üstü parçacıkların karışımından oluşan bir mikro hacım oluşur.

Bu küçük hacımda Takiyonların düzen getirici etkisi ile bir yandan yeni parçacıklar oluşurken, diğer yandan var olan ışık-altı nesneler düzene girerler. Yeni parçacıklar evrenin Entropi’sini arttırırken, düzene giren yapılar yerel olarak evrenin Entropi’sini azaltırlar. Böylece evrenin toplam Entropi’si sabit kalır. Toplam Entropi sabit ise evren dengede demektir. Çünkü termodinamik dengeye ulaşmış her sistemde Entropi sabittir.

Böylece yok olmadan sonsuza kadar sürekli bir denge durumu sürebilir. Fakat evren genişliyor. Bunun nedeni oluşmuş olan yeni parçacıkların evrenin dalga fonksiyonuna yaptıkları baskıdır. Yeni oluşan parçacıklar ışık-altı parçacıklar olduklarından dar bir hacim içine sıkışmış evrene baskı yaparak onu genişletirler. Bu durum bir balon içine üflenen hava moleküllerinin balonu şişirmesine benzer. Maddesel parçacıklar birbirlerini dışladıklarından yeni bir hacim yaratmak zorundadırlar. Dolayısıyla evrenin genişlemesine neden olmaktadırlar. Fakat bu genişleme sonsuza kadar süremez.

Var olan evren, varlığını sürdürmek için yeniden büzülmek zorundadır. Bu durumu da Etkenlik edilgenlik başlığı altında açıklamıştım.

Takiyon etkisi

Tarih: 11:40 on 15/2/2006

Evrenimizde iki tür parçacık (dalga) görmekteyiz. Bunlar:

1. Maddesel parçacıklar olan Baryonlar ve Leptonlar
2. Maddesel parçacıkların etkileşmelerini sağlayan Bozonlar.

“Baryon” Nötron ve Protonlara verilen ortak isimdir. Leptonları ise Elektron, Müon, Tau ve Nötrinolar oluşturur. Bu parçacıkların tümü yarım spinli, yani bir eksen etrafında saat ibresi yönünde veya tersine dönerler. Bu parçacıklar döndüklerinden birbirlerini dışlarlar ve aynı hacımda bulunamazlar. Bildiğimiz “cisim” bu maddesel parçacıkların bir-araya gelmelerinden oluşur. 

Bozonlar ise farklı yapıda olup sıfır veya tam spin sahibidirler. Yani, ya dönmezler veya dönmeleri birbirlerini dışlamalarını gerektirmez. Bu bakımdan yer kaplamazlar. Diğer maddesel parçacıkların içinde veya üzerinde olduklarını varsayabiliriz. Çünkü varlıklarını ancak etkileşme sırasında ölçebilmekteyiz. Bozonlar çeşitli Mezonlar, Foton, Graviton ve Higgs parçacığı adları ile bilinirler.

Maddesel parçacıkların etkileşmeleri Bozon alış-verişi ile olur. Her etkileşme bir kuvvet içerdiğinden, Bozonlar kuvvet ileten parçacıklar olarak da bilinir. Şu anda pek ciddiye alınmayan Takiyonlar da bir tür Bozon olarak görülmelidir. Çünkü onlar evrende görülen düzeni ışıktan hızlı hareket ederek sağlamaktadırlar.

Evrende görülen gök cisimleri (yıldızlar ve galaksiler) ilk patlamadan sonra nasıl oluştular? Buna yanıt olmadığını daha önce belirtmiştim (Bakınız: Büyük Patlama başlıklı yazımda 3. soru). Başlangıçta hiçbir yoğunluk farkı yoktu. O zaman yerel yoğunluk farkını oluşturan nedir? Hangi kuvvettir. Kütle çekimi kuvveti bu durumu açıklamaya yetmez. Zira tüm parçacıklar bir araya gelip tek bir gök cismi oluşturmaları gerekirdi. Yani, evren yoğun tek bir kütle halinde katılaşıp kalması gerekirdi. Oysa ki pek çok farklı yoğunlukta gök cismi görmekteyiz.

Bu durumu açıklamak için şöyle diyeyim: “Evren hem tek bir nesnedir (dalgadır) hem değildir”. Tek bir dalgadır çünkü içindeki değişik nesnelerin (dalgaların) ortak bir bütünlüğü, onların etkileşiminden oluşan tek bir dalga paketidir. Öte yandan, tek bir nesne değildir çünkü içinde pek çok ayrılmış olarak duran dalga paketleri vardır. Evren bir dalga paketi olarak içindeki dalgalardan farklı bir yapıya ulaşmıştır. Kendi başına bir tür parçacık olarak da düşünülebilir. 

Fakat bu evren tek başına değildir. Dışında fakat bitişik durumda olan “Takiyon evren” ile etkileşmektedir. Takiyon evren ışıktan hızlı hareket eden bozon türü parçacıklardan oluşmuştur. Bozonlar yer kaplamadıkları için Takiyon evren de yer kaplamaz. Bu bakımdan bizim evrenimizin hem içinde hem dışındadır. İçindedir, çünkü sürekli “vakum titreşimleri” sayesinde bizim evrenimize düzen getirmektedir. Dışındadır, çünkü ışık hızı iki evrenin ara-kesiti durumundadır.

Bu iki evrenin ara sınırı olan ışık neden sabit hıza sahip olduğunu şimdi açıklamak mümkündür. Kolay anlaşılsın diye sıvılarla bir örnek vereyim. Bir şişenin yarısına kadar su ve üstüne diğer yarıyı dolduracak kadar zeytinyağı koyalım. Şişeyi çalkalarsak su ile zeytinyağı karışacak ve aralarındaki sınır kalkacaktır. Fakat bir süre sonra şişeyi dinlenmeye bırakırsak su ile zeytinyağı ayrılıp aralarında yeniden bir sınır oluşacaktır. Her çalkalamada sınır yok olacak, her dinlendirmede sınır oluşacaktır.

İşte şu anda bize görünen evren genişlemiş, dolayısıyla “dinlenmiş” durumdadır. Burada ‘dinlenmiş’ derken parçacıklar arası mesafe oldukça açılmış ve etkileşme azalmış demek istiyorum. Çünkü ölçülen boşluk enerjisi oldukça az olup sıfıra yakındır. Takiyonların etken oldukları durum, bu genişlemiş olan evren durumu değil, evrenin çok daha küçük bir hacimde sıkışmış olduğu durumdur. Takiyon etkisinin sürekli ve güçlü olabilmesi için de evrenin nefes alıp-verir gibi sürekli açılıp kapanması gerekir.

Evren her kapanıp sıkıştığı durumda Takiyonlar evrene düzen getirip hem yerel olarak yoğunluk farklarına neden oluyorlar, hem de “doğa yasaları” dediğimiz düzgün davranışların ve korunum yasalarının oluşumunu sağlıyorlar.

Işıktan hızlı

Tarih: 08:35 on 15/2/2006

“Dalga paketi” kavramı temel parçacıkları anlamak için önemlidir. Bu kavram sadece temel parçacıklar için değil, her türlü etkileşen sistemleri, hatta evreni dahi anlamamıza yardımcıdır.

Basit olsun diye iki dalganın etkileşimini inceleyelim. Her bir dalga bir “varlık” olarak düşünülebilir. Zira dedik ki dalga ile parçacık (dolayısıyla varlık) eşdeğerdir. Bu iki dalga girişime girdiğinde bir paket oluştururlar. O andan itibaren yeni bir yapı ortaya çıkmış demektir. Oluşan dalga paketi ne dalgalardan biridir ne de diğeri. İkisinden de bir miktar özellik bir araya gelerek dalga paketini oluşturmuştur. Bu iki dalga ayrılsalar dahi yerel olmayan bir şekilde birbirleri ile etkileşmeye devam ederler.

“Yerel olmayan” derken, ışık hızından daha hızlı bir şekilde, demek istiyorum. Fakat öte yandan biliyoruz ki ışık hızı sabittir ve bu hız aşılamaz. O zaman bu durum nasıl açıklanmalı?

Etkileşmeyi sağlayan başka bir parçacık olması gerek. Zira, Kuantum kuramına göre iki nesne arasındaki etkileşme daima bir ara parçacık (artık parçacık dediğimde dalga anlaşılmalıdır) gerektirmektedir. Bu parçacık da ışıktan hızlı hareket etmelidir. Acaba böyle parçacıklar var olabilir mi?

Özel Görelilik kuramına göre ışık hızından daha yüksek hızlarda hareket edebilen parçacıklar var olabilmektedirler. Özel Görelilik denklemlerinde v>c korsak, yani parçacığın hızını ışık hızından büyük kabul edersek, görürüz ki sanal kütleli ve zamanda geriye giden parçacıklar ortaya çıkmaktadır. Önceleri böyle parçacıkların varlığı ret edilirken günümüzde var olabilecekleri görüşünü savunan birçok fizikçi bulunmaktadır. Takiyon adı verilen bu parçacıklar sanal (imajiner ‘kök içinde eksi bir sayı’) kütleli olduklarından aletlerle gözlenmeleri mümkün değildir. Bir diğer zorluk da Takiyonların gelecekten geçmişe hareket etmelerinden dolayı bizim ölçüm aletlerimizle girişime girmelerinin olanaksız oluşudur. Biz neden-sonuç içinde geçmişten geleceğe gelişen olayları ölçeriz. Tersini ölçemeyiz zira evrenimizde nedensel olaylar hep geçmişten geleceğe doğru gelişirler.

Bu nedenselliğin bir diğer yansıması da Termodinamiğin ikinci ilkesinde belirir. Bu prensibe göre kendi haline bırakılan kapalı bir sistem içindeki parçacıklar hep düzenli bir dağılımdan en düzensiz dağılıma doğru hareket ederler. Bir kapalı kap içindeki hava molekülleri her tarafa eşit miktarda yayılırlar. Bir köşeye toplanıp diğer hacmı boş bıraktıkları görülmez. Yani doğada hep düzenden düzensizliğe ve tekrar düzene doğru bir değişim vardır. Bunun nedeni ise evrenimizin ışıktan yavaş hareket eden maddesel parçacıklardan oluşmuş olmasıdır. Bu nedenle de zaman geçmişten geleceğe doğru ilerler, gibi görünür bizlere.

Peki ama Takiyonlar nasıl davranırlar? Işıktan hızlı hareket ettiklerine göre onların termodinamiği bizimkinin tam tersi olacaktır. Düzensizlikten düzene ve tekrar düzensizliğe doğru hareket edeceklerdir. Işıktan hızlı hareket ettiklerinden onların en yavaş hızı da ışık hızı olacaktır.

Takiyonlar düzen sağlayıcı parçacıklardır ama bizim evrenimizle etkileşmeleri mümkün müdür? Evet, bunu da Kuantum kuramının belirsizlik prensibi sağlar. Nasıl ki radyoaktif bir çekirdek aniden bir gama ışını salarsa ve bu ışın ne zaman salınacağı bilinemezse, aynı şekilde hudut bölgede (ışık hızı bölgesinde) Takiyonlar bizim evrenimize geçip etkileşirler. Bu olaya ‘Tünel Olayı’ da denir. Bir tünelden geçer gibi bir başka alemden (evrenden) bizim evrenimize geçerler ve anlık bir etkileşme ile düzen sağlayıp tekrar kendi evrenlerine dönerler. Bu öylesine kısa bir süredir ki “an” içinde etkileşme sona erer. Ama olay sürekli bir tekrar içindedir. Bu kısa süreyi ölçecek hiçbir alet henüz yoktur, olacağı da şüphelidir. Zira belirsizlik ilkesi dolayısıyla ölçülen hakkında kesin bir bilgi de edinmek olanaksızdır.

İşte bir araya geldikten sonra ayrılan parçacıların (dalgaların) ışıktan hızlı haberleşmeleri Takiyonlar sayesinde olduğu görüşündeyim. Bu görüş bir varsayım olsa da evrenin bugünkü durumunu açıklamakta önemli bir etken olduğunu göstereceğim.

Belirsizlik ilkesi

Tarih: 23:49 on 14/2/2006

 

Dalga paketi kavramı üzerinde bir miktar durmak istiyorum. Zira bu kavramın hem ışığı hem de parçacıkları anlamakta büyük yararı var. Resimdeki görülen dalga paketi tek başına gibi görünse de aslında arkazemin boşluğunu oluşturan bir enerji ortamının içinde bulunmaktadır ve de ondan farklı değil. Dalga paketi ortamla aynı malzemeden oluşmuş. Burada görüntü basit olsun diye 2-boyutlu çizilmiş.

Dalga paketinin altında görülen kesikli iki çizgi aslında iki farklı titreşime (frekansa) sahip iki ayrı dalgayı betimliyor. Bu iki dalganın saniyedeki titreşim sayıları oldukça yakın. Üst-üste bindiklerinde bazı titreşimler toplanıp artarken bazı titreşimler birbirini zıt yönde etkileyerek toplam küçülüyor. Ne kadar fazla dalga üst üste binerse dalga paketi o kadar belirgin oluyor. Fakat hiçbir zaman tek bir noktada yoğunlaşmıyor. Dalga paketinin daima bir yaygınlığı var. İki ucu arasındaki uzaklık dalga paketinin dalga boyu oluyor. Bu mesafeye x diyelim.

Görüldüğü gibi dalga paketinin iki ucunda bir belirsizlik var. Dalga tam olarak nerde başlıyor ve tam olarak nerde bitiyor belli değil. Dalga paketinin yerini belirtmek istersek ortalama bir değer alıp yaklaşık bir olasılık değeri vermemiz gerekir. Çünkü dalga yaygın bir yapı olup parçacık gibi yeri kesinlikle bilinemez. Ayrıca uçlardaki dalgalar gittikçe küçülseler de asla tümüyle sıfır olamazlar. Yani, arkazemin tümüyle düz bir göl yüzeyine benzemez. Daima denizdeki küçük dalgacıklar gibi birtakım titreşimler olacaktır. Boşluğun enerjisi bu yüzden sıfır olamaz. Fizikte bu duruma “vakum titreşimi” denmektedir. Bu küçük dalgacıklar büyük dalga paketinin diğer dalga paketleri ile iletişimini de sağlar.

Sözünü ettiğim “uzamın bükülmesi” olayı bu uçtaki dalgacıkların rezonansa girmeleri sayesinde olur. “Rezonans” olayını birbirine uyumlu olma, aynı titreşimlere ulaşma, karşılıklı etkileşim içinde olma şeklinde açıklamak mümkündür. Bu durum insanlar için de geçerlidir. Karşılıklı anlaşanlar aynı dalga boyunda olduklarını, aynı titreşimleri hissettiklerini söylerler. Bunun da nedeni bizim (öznemizin) nesne olmayıp bir enerji paketi yapısında oluşumuzdan dolayıdır.

Şimdi size basit ve yaklaşık bir şekilde Heisenberg’in Belirsizlik ilkesi hakkında bilgi vermek istiyorum. Louıs De Broglie (1892-1987) maddesel parçacıkların dalga gibi davrandıklarını açıklayan eşitliği ileri sürdü. Bu ifade p = h / x şeklinde olup soldaki p parçacığın momentumu (hızı çarpı kütlesi), h Planck sabiti ve x dalga boyudur.

Eşitliğin sol tarafı parçacık, sağ tarafı dalga özelliği gösterir. Her dalganın hem momentumu hem de dalga boyu farklı olduğundan. Bir dalga paketini oluşturan dalgalar için p = n.Δp ve x = m.Δx yazabiliriz. Burada momentum ve yerin, her birinin belirsizliklerinin belirli bir katı olduğunu var sayıyoruz. m ve n birer tam sayı olup en azından 1 veya daha büyük birer tam sayı olmaları gerekir.

Bu durumda p = h / x eşitliği  n.Δp = h / m.Δx veya (n.m)Δp.Δx = h

olur. (n.m) çarpanı en az 1 veya daha büyük olması gerektiğinden denklem:

                                                Δp.Δx ³ h   olur.

Bu eşitsizliği Heisenberg (1901-1976) 1927 yılında ifade etmiş ve o günden beri Heisenberg’in belirsizlik ilkesi olarak kalmıştır. Parçacığın (dalganın) hızındaki belirsizlik ve yerindeki belirsizlik birlikte sıfır olamayacağını gösterir. Çünkü Planck sabiti her ne kadar küçük olsa da sıfırdan farklıdır. Bu denklemde parçacığın kütlesi m belirmemekte sadece momentum denen bir büyüklük görülmektedir.

Anlamı ise dalganın bir kütlesi olmasa da momentumu daima olduğudur. Momentum kavramını klasik anlamda gündelik hız kavramı olarak düşünebiliriz. Eğer parçacığın (dalganın) hızındaki belirsizliği azaltmak istersek yerindeki belirsizlik artmalıdır. Eğer yerini kesinlikle belirlemek istersek yeri ile ilgili belirsizliği azaltmalı dolayısıyla hızındaki belirsizlik artmalıdır.

Yokluk kavramı

Tarih: 08:55 on 14/2/2006

Madde ile boşluk (uzam) aynı enerjinin farklı yapısı (farklı yoğunluğu) olarak görülmelidir. Zira Kuantum kuramı göstermiştir ki “madde” dediğimiz nesneler hem dalga hem parçacıktırlar. Yani, parçacık veya parçacıklar küme’si olan madde türleri, ki bunlara gök cisimleri de dahildir, yerel olarak tanımlanamayan dalgasal yapılardır. Zira dalga bir tek noktada tanımlı değildir. Şu halde boşluk dediğimiz maddesiz ortam da tek bir noktada tanımlı olmadığına göre, Boşluk = Dalga = Uzam = Parçacık = Madde eşdeğer kavramlar olarak karşımıza çıkmaktadırlar.

Kavramsal olarak madde ile boşluk (vakum) ayrılmazlarsa mantıksal olarak çelişkiye düşmemek için Aristo mantığındaki ‘Özdeşlik İlkesi’ terk edilerek Hem-Hem mantığı devreye sokulmalıdır. Önermemiz: “Madde hem vardır hem yoktur”, veya eşdeğer olarak “Boşluk, yoğunluğu çok az olan maddedir”.

Burada önemli bir noktaya dikkat etmek gerekir. Boşluk tam olarak (100 de 100) boş olmadığına göre fiziksel yokluk mümkün değildir. Yokluk dendiğinde matematikteki “sıfır küme’si” akla gelmemelidir. Sıfır sayısı doğada bulunmaz. Sadece mantıksal olarak özdeşlik ilkesinden türer. Oysa ki yukarıda kullanıldığı şekilde “yokluk = Fiziksel yokluk” (doğadaki yokluk) şeklinde anlaşılmalıdır. Doğada ise mutlak “yokluk” yoktur.

Var olan bir A nesnesi düşünün. Özdeşlik ilkesine göre A ancak kendisine eşit olabilir. Yani, A = A dır. Eğer eşitliğin sağındaki A terimini sol tarafa aktarırsak A – A = 0 olur. Burada “0” küme’sini tanımlamış oluyoruz. Diyoruz ki, bir nesneden kendisini çıkarırsak geriye hiçbir şey kalmaz. Ama bir nesneden kendisini çıkarabilir miyiz? Bir nesneyi bir ortamdan veya bir kümeden çıkarabiliriz. Kendisinden çıkaramayız. Şu halde “sıfır” sayısı gerçek (fiziksel) bir kavram değildir. Sadece bizim mantık sistemimizin gerektirdiği bir kavramdır.

Oysa ki Hem-hem mantığında bir kavram hem kendisi hem de zıt kavramı pekala olabilir. Şu halde A = B olabilir. Klasik mantıkta A – B = 0 olmalıdır. Oysaki, Hem-hem mantığında A – B = C gibi sıfırdan farklı bir değer alabilir. C’nin sıfır olma zorunluluğu yoktur. Aynı şekilde “Madde hem vardır hem yoktur” derken, buradaki “yokluk” kavramı “sıfır küme’si” değildir. “Yokluk” kavramı fiziksel “vakum” olarak anlaşılmalıdır.

Klasik matematik doğa ile ilişkili önermeler üretmez. Soyut kavramlar ile çalışır ve onlar arasında, kendi mantık kuralları çerçevesinde, ilişkiler bulur. Oysa ki fizik düşüncesi doğrudan doğa ile ilişkili olmalıdır. Kullanacağı kavramlar doğadaki olaylara uygunluk göstermeli ve mantığı da doğa olaylarını açıklayacak kadar esnek olmalıdır. Katı Aristo mantığı doğadan kopuk, soyut ve ideal bir evrene uygun olabilir. Ama bizim fiziksel evrenimize uygun değildir. Zaten çelişkiler de bu yüzden belirmektedirler.

Aristo mantığına zaman içinde “formel mantık” denmiştir, çünkü bu mantık “formları” (şekilleri) incelemek için yaratılmıştır. Eski düşünürler ideal bir dünya hayali peşinde evreni geometri ile açıkladılar. Geometri formlarla, yani şekillerle, ilgilenir. İdeal şekiller de doğru, üçgen, kare, daire, beşgen...gibi tanımları kolay olan simetrik ve oldukça basit çizimlerdir. Oysa ki etrafımıza baktığımızda doğada ne ideal doğru buluyoruz, ne de ideal üçgen. Doğada var olanlar hep karmaşık, eğik-bükük, yamrı-yumru, ideal olmaktan uzak şekillerdir. Fiziğin konusu da bu yapıları araştırmak ve neden böyle göründüklerine mantıklı yorumlar getirmektir. Doğadaki yapıları ve ilişkileri de formel mantık ancak bazı basit durumlarda açıklayabilmektedir. Daha temel sorularda ise yetersiz kalmaktadır. Bu bakımdan Hem-hem mantığı bize daha geniş düşünce ufukları açtığı görüşündeyim.

Nesneyi “ancak fiziksel ortamdan çıkarabiliriz” dedik. Kendisinden çıkaramayız. Fakat fiziksel ortam kendisi ise o zaman nesneyi kendisinden çıkarabiliriz. Burada çıkarmak kavramını “yer değiştirmek” şeklinde algılamalıyız, tümüyle “yok etmek” şeklinde değil.

Ortam belli bir noktada bir “dalga paketi” oluşturarak yoğunlaşıyor. Daha sonra bu dalga paketi ortamda bir bükülme yaratıyor. Bu bükülme diğer bir dalga paketinin yarattığı bükülme ile karşılaştığında ikisi arasında bir ortak yol (bükük ortam) oluşuyor. Bu ortak yol boyunca ilerleyen dalga paketleri birbirlerine doğru yaklaşıyorlar. Böylece bizim evrende gözlediğimiz kütlelerin birbirlerini çekmesi olayı gerçekleşiyor.

Bu açıklama hem Genel Görelilik kuramına uygun olmakta hem de parçacık-dalga eşdeğerliği ile çelişmemektedir.

Büyük Patlama

Tarih: 06:07 on 14/2/2006

Einstein 1916 yılında Genel Görelilik kuramını yayınladığında uzamın madde tarafından büküldüğünü iddia ederek yerçekim kuvvetine tümüyle farklı bir yorum getirdi. Bu durumu göz önüne getirmek için şöyle bir benzetme yapabiliriz. Gerili bir çarşafın iki ucuna ağır iki adet bowling topu koyalım. Bu iki top çarşafı bükecekler ve ikisi arasında oluşan kıvrım boyunca birbirlerine doğru yaklaşacaklardır.

İşte benzer şekilde büyük gök cisimleri uzayı bükerek birbirlerine doğru yaklaşıyorlar. Böylece Newton’un kütle çekim yasası tümüyle geometrik olarak kuvvet kavramına gerek duyulmadan açıklanmış olmaktadır. Tek bir gök cismi yakın çevresindeki uzamı büker fakat kendinden uzakta duran uzam bükülmeden düz bir çarşafa benzer. Bu yaklaşımda madde ile uzam iki ayrı nesne olarak görülmekte, madde uzamdan bağımsız olarak uzamın içinde duran bir varlık olduğu kabul edilmektedir.

Oysa ki her ikisini aynı ve tek bir enerjinin iki farklı yoğunluğu olarak da düşünebiliriz. Uzamı çok az yoğunluklu madde, maddeyi de yoğun uzam olarak düşünebiliriz. Böylece biri diğeri içinde hareket etmesi gerekmiyor. Hareket eden ortamın kendisi olup yer yer sıkışarak yoğun madde türlerini oluşturuyor. Yoğunlaşmadığı bölgelerde ise maddenin bulunmadığı geniş boşluklar meydana geliyor.

Boşluk (vakum) dediğimiz maddesiz ortam tümüyle boş değildir. İçinde az miktarda da olsa enerji bulunuyor. Bu enerji “arkazemin ışıması” denen yaygın fakat oldukça zayıf bir enerji olarak ölçülmüştür. Arkazemin ışıması mutlak sıfır olan –273 dereceye oldukça yakın +3 K derecedir. Arkazemin ışıması, uzayın hangi boş noktasına bakarsak bakalım aynı değerde ölçülmektedir. Demek ki uzam her bölgede aynı özelliklere sahiptir, yani homojendir. Uzaydaki madde yoğunluğu (birim hacim içinde bulunan madde miktarı) oldukça sabit. Uzayın bir bölgesi ile diğer bölgesi aynı miktarda yıldız ve gök adaları barındırıyor. Bu durumu açıklamak için Büyük Patlama modeli ileri sürüldü.

Büyük patlama (Big Bang) modeline göre evren ilk önce bir noktada birikmiş bir enerji topu idi. Aniden ve kısa zamanda genişleyerek önce elektronları, protonları, sonra atomları ve en sonunda gök cisimlerini oluşturdu. Fakat bu modelde birçok açıklanmamış sorular hala yanıt beklemektedir. Bu sorulardan en önemli 5 tanesini kısaca sıralayayım.

1.      Şimdiki modele göre evrenin var olmakta devam etmesinin nedenini açıklamak çok zor. Çünkü şimdiye kadar (yaklaşık 11 milyar yıl) ya dağılıp yok olması gerekirdi veya tekrar büzülüp bir nokta sonsuzluğu içinde "büyük yok olma" (Big Crunch) haline noktasal sonsuzluğa dönüşmeliydi. Evren neden şimdiye kadar dağılıp yok olmadı?

Getirilen yanıta göre kozmolojik sabit öyle bir değerde ki ne sonsuz genişleme ile ve ne de sonsuz büzülme ile yok olmaya izin veriyor. Buna modelin "düz" oluşu deniyor. Fakat bu düz durumun nedeni bilinmiyor.

2. Neden evrenin her bir tarafına bakıldığında aynı kozmik ışıma görülüyor? Bu ışıma yaklaşık 3 K derecedir. Çünkü evrenin iki ayrı uzak bölgesi "kozal" (nedensel) olarak bağlı değiller. Işık hızı sabit olduğundan kozmik radyasyon da ancak ışık hızı ile erişebilir. Fakat evren ilk dönemlerde o derece hızlı genişledi ki ışık bir uçtan diğer uca bilgi ulaştırması mümkün değildi. Bu homojen yapının nedeni nedir?

Bu soruya yanıt yok.

3. İlk galaksileri ve yıldızları oluşturan bir neden olmalı. Eğer bir yoğunluk farkı varsa bu yoğunluk farkına sebep olan nedir?

Bu soruya yanıt yok.

4. Evrenin genişlediği kabul ediliyor fakat bu genişlemenin gittikçe daha hızlandığı saptanıyor. Oysa ki yavaşlaması normaldir. Bu hızlanarak genişlemeye neden olabilecek bir "karanlık madde" hipotezi var. Fakat bu karanlık madde bizim evrenimizin maddesi olan nötron ve protonlar olamaz. Çünkü evrendeki nötron ve proton sayısı bu hızlı genişlemeyi açıklamaya yetmiyor. Şu halde bu karanlık maddeyi oluşturan nedir? Karanlık maddenin yapısı nedir?

Bu soruya yanıt yok.

5. Singülarite (noktasal sonsuzluk) problemi. Eğer evren bir büyük patlama ile başlamış ise bu bir noktadan olması gerekir. Yani başta noktasal bir sonsuzluk vardı. Bu ise her türlü hesabı imkansız hale getirir. Yani Genel Görelilik baştan çökmektedir. Bu noktasal sonsuzluk sorunu nasıl çözülmelidir?

Bu soruya da yanıt yok.

Tüm bu sorular evrenin sürekli nefes alıp-verdiği bir modelde yanıt buluyorlar.

Etkenlik-edilgenlik

Tarih: 10:21 on 13/2/2006

Etkenlik ile edilgenlik bir madalyanın iki yüzü gibi birbirlerini tamamlar. Ne biri tek başına vardır ne de diğeri tek başına var olabilir. Etken olan özne, edilgen olan nesnedir, demiştim (bakınız: Bütünsel evren başlıklı yazım). Fakat evrenin kendisi hem etken hem edilgendir.

Evrende ve bizim çevremizde sürekli birtakım canlı veya cansız varlıkların, yapıların bir araya toplanarak organize sistemleri oluşturduklarına tanık oluyoruz. Evrenin derinliklerinde galaksiler, nebülalar, yıldız toplulukları ve daha birçok gök cisminin varlığından haberdar olmaktayız. Bu yıldızlar ve yıldız toplulukları evrenin geniş boşluklarında dağılıp yok olacakları yerde varlıklarını sürdürüyorlar.

Yani, karmaşadan organize (düzenli) sistemler oluşuyor. Dünyamızdaki çeşitli canlı varlık türleri de aynı şekilde insanı şaşırtan bir düzen sergiliyorlar. Nesneler edilgen durumda iken onları bir araya getiren birtakım etken kuvvetler var. Daha doğrusu, edilgen durumda olan nesneler bir-araya geldiklerinde etken hale dönüşüyorlar. Bir-araya gelmeleri ile birlikte gizli olan enerji bir anda aktif hale geçip birliğin sürmesi için etken olmaya başlıyor.

Çevremizde gördüğümüz şirketler, dernekler, vakıflar, politik partiler ve nihayet devletler hep bu mekanizmanın belirtileri, örnekleridir. Birkaç kişi bir-araya gelip bir şirket oluşturuyorlar. Sonra şirket güçlendikçe diğer ufak şirketleri satın alıyor. Daha da büyüyünce bulunduğu ülkenin sınırlarını aşıp uluslararası dev bir holding haline dönüşüyor.

Canlılık da aynı mekanizmanın başka bir görüntüsü. Önce mikro organizmalar oluşuyor. Sonra onların bir-araya gelişi ile daha büyük canlılar ortaya çıkıyor. Fakat bir gizli denge mekanizması da büyümenin sonsuza kadar sürüp gitmesine engel oluyor. Bir-araya gelmenin sonucunda oluşan sistem büyüdükçe yapının dengesi kararsız hale dönüşüyor. İçten titreşimler, yalpalamalar, sürtünmeler, huzursuzluklar artıyor ve eğer sistem kontrolden çıkarsa dağılıyor. Bu durum hem canlılar, hem cansızlar, hem de insan toplulukları için geçerli. Yani genel bir doğa yasası.

Demek ki, temelde iki kuvvet var. Ancak bu iki kuvvet birbirlerine muhtaç durumda. Biri olmadan diğeri de olamıyor. Bu iki kuvveti “Toplayan” ve “Dağıtan” kuvvetler olarak tanımlayalım. Birinin etken olmasıyla diğeri edilgen hale geçiyor. Dolayısıyla bir süre toplayan etken, dağıtan edilgen olurken bir süre sonra dağıtan etken, toplayan edilgen duruma geçiyor.

Her var olan varlığını bu iki kuvvetin dengesi sürdüğü sürece var olmakta devam ediyor. Fakat enerji aynı durumda kalmayıp dönüştüğü için de denge sonsuza kadar devam edemiyor. Özne Enerjisi başlığı altında dedim ki: “Enerji atıl kalamaz. Sürekli üretir, dönüştürür ve kendi de dönüşür”. Dönüşen enerji, kuvvetlerden dağıtıcı olanı etken hale geçirerek dengenin bozulmasına ve yapının dağılmasına neden olur.

Toplayan ve dağıtan kuvvetler mikro boyuttan (atom ve atom-altı) makro boyuta (gökcisimleri ve yıldız toplulukları) kadar benzer sistemlerin oluşumunu sağlıyor. Atom yapısında merkezde bir çekirdek ve çevresinde dolanan elektronlar olduğu gibi güneş sisteminde merkezde bir yıldız (güneş) ve etrafında dolanan gezegenler vardır. Daha büyük boyutta “galaksi” denen yıldız topluluklarını bir arada tutan, merkezde bulunan bir karadeliğin varlığından söz ediliyor. Tüm bu sistemlerde merkez etrafında dönüş hareketi var.

Yani, var olan sistemin varlığını sürdürmesi sürekli bir peryodik hareket ile olabiliyor. Peryodik hareket, kendini tekrarlayan, etken ile edilgen kuvvetlerin birbirini izlediği, fakat dengede kaldığı bir hareket türüdür. Varlık bu şekilde varlığını sürdürmektedir. Biz insanlar, hareket ederek etken oluyor ve enerji harcıyoruz. Fakat varlığımızı sürdürüp yaşamak için de beslenerek enerji depoluyoruz. Aynı şekilde nefes alıp-verme olayına bakalım. Nefes alarak havadaki oksiyenden enerji sağlıyoruz ama bu enerjiyi yenilemek için de nefes vermek zorunda kalıyoruz. Biri diğerini gerektiriyor ve izliyor.

Evren de aynı şekilde nefes alıp-vererek varlığını sürdürür.

Holografik Evren

Tarih: 07:01 on 13/2/2006

Konumuz “varlık” olduğuna göre varlık ile yokluk arasındaki ilişkiye değinmemiz gerekir. Fransız kimyacı Lavoisier (1743-1794) “Hiçbir şey yoktan var olmaz, var olan hiçbir şey yok olmaz” demiştir. Bu ifade maddeler için değil de enerji için geçerlidir. Çünkü enerjinin yok olmadığını, sadece şekil değiştirdiğini biliyoruz. Tüm nesneler, insan dahil, enerjidir. Ancak, daha önce de sözünü ettiğim gibi (Bakınız:Özne Enerjisi başlıklı yazımda), öznenin hem var hem de yok olma durumu vardır. Hem-hem mantığının bulunduğu bu durum sadece biz insanlara ait bir özel durum mudur, yoksa tüm var olanlar için geçerli midir?

Bir yandan enerjinin yok olamayacağı diğer yandan hem var hem yok olabileceği durumu nasıl açıklanabilir? Yanıtı gene aynı sözünü ettiğim yazıda bulunuyor. Dedim ki:  “Ne tam olarak varız ne de tam olarak yokuz”. Enerjimizi tam olarak devreye sokamadığımız için tam olarak var olamıyoruz. Bir görüşe göre beynimizin sadece % 10 kadarını kullanıyoruz. Yüzde doksan kadarı hala bizim kontrolümüz dışında. Bunun da başlıca nedeni şu anda yaşar olmayışımız. Ya geçmişin hayalleri veya geleceğin beklentileri içine dalarak enerjimizi odaklayamıyoruz. Tam olarak var olmak için enerjinin odaklanması gerekiyor. Ancak o zaman etkin olmak ve şeyleri değiştirmek mümkün.

Tam olarak yok olmayışımız sonucu hafıza (bellek) denen depo sayesinde bilginin bir andan diğerine aktarımını sağlıyoruz. Evet, bellek bir çeşit depodur. Fakat bildiğimiz türden nesnelerin üst üste veya yan yana yığıldığı bir depo değil. Bellekte enerji dalgalarının girişim motifleri depolanıyor. Açıklayayım.

İnsanın kendi iç elektriksel dalgaları var. Elektro-Encephalo-Gram (EEG) denen beyin dalgalarını ölçen alet bize açıkça bu dalgaların varlığını gösteriyor. Keza EKG de kalbin dalgalarını ölçen bir diğer alet. Bu doğal iç kaynaklı dalgalarla duyu organlarından gelen dış kaynaklı elektriksel-kimyasal dalgaların girişimi beyinde nöronların karmaşık bağlar kurup holografik olarak bellek dediğimiz bilgi deposunu oluşturmaktadırlar. Belleğin bir hologram olarak beyinde kayıt edildiğini iddia eden beyin cerrahı Karl Pribram 1969 yılında Holografik Model görüşünü ileri sürmüştür.

Holografik Modeli anlayabilmek için holografik kayıt sistemini anlamak gerekir. Hologram, monokromatik (tek renkten oluşmuş) ışık kullanarak yapılmış olan bir tür fotografa benzer. Ancak, ayrıntıya girildiğinde fotoğraftan da oldukça farklı olduğu görülür. Tek bir dalga boyu (renk) içeren ışık hüzmesi (demeti) ikiye bölünerek biri hologramı yapılacak olan cisme, diğeri ise doğrudan kayıt eden ortama (fotoğraf kağıdına) yöneltilir. Cisim üstünden yansıyıp kayıt ortamına ulaşan ışık demeti diğer (doğrudan gelen) demet ile girişime girer. Sonuçta bu iki ışık demetinin girişim çizgileri kayıt ortamında sabitleşir. Cisim kaldırıldıktan sonra, aynı tek renkli ışık demetlerinden biri kayıt ortamından yansıtılıp diğer hüzme ile havada girişime girdiğinde uzayda üç-boyutlu cismin görüntüsü belirir. Cismin üç-boyutlu görülmesinin nedeni bir mercek kullanılmamış olmasıdır. Fotoğraftan farklı olarak, cismin iki boyutlu tek bir görüntüsü yerine cismin çeşitli bölgelerinden yansıyan pek çok ışık dalgasının, yaygın bir şekilde, girişim çizgilerinin kaydı yapılmış olmaktadır. 

Hologramın ilginç bir özelliği da kayıt ortamının ufak bir parçasında dahi cismin 3-boyutlu görüntüsünü yeniden oluşturacak bilgilerin tümünün depolanmış olduğudur. Şu halde beynin herhangi bir ufak parçası dahi belleğin tümünü barındırabilecek özelliklere sahiptir. Demek ki kayıt eden ortamın her bir noktasında tüm bilgi kodlanmış durumdadır ve bu ortamın en küçük parçası dahi bütün hakkında tüm bilgileri barındırmaktadır.

Holografik kayıt bize çok büyük ve çok karmaşık bir yapının dahi çok küçük bir bölgeye kodlanarak sığabileceğini göstermektedir. Bu durum sadece insanlara ait olan özel bir durum değildir. Tüm evren bir hologram olarak görülebilir. Bu durumda evrende de aynı hologramda olan özellikler bulunabilir. Yani, evrenin en küçük parçası tüm evren hakkında bilgi barındırmaktadır. Ben, şahsen, evrenin bir hologram olduğuna kesinlikle inanıyorum. Çünkü bu modelin özelliklerinden yararlanarak daha ileride evrenin bugünkü durumunu dahi açıklamanın mümkün olduğunu göstereceğim. Dolayısıyla inancımı tutarlı ve anlaşılır bir evren modeli ile destekleyeceğim.

Hem-hem mantığı

Tarih: 18:25 on 12/2/2006

Kendi üzerine dönüşümlü önermeler karar verilmesi mümkün olmayan (doğruluğu veya yanlışlığı kanıtlanamayan) mantığa ters düşen önermelerdir. Bu önermeler kuyruğunu ısırmaya çalışan köpek gibi sürekli bir döngü içinde sonsuza kadar sürerler. Bu bakımdan bir sonsuzluk türü olarak tanımlanmaları gerekir. Bu tür sonsuzluğa “kendi üzerine dönüşümlü sonsuzluk” da diyebiliriz. 

Sonsuzluk türleri hakkında ilerde söz edeceğim. Şimdilik bu tür üzerinde biraz duralım. Bir anafor gibi kendi etrafında dönen bu sonsuzluktan kurtulmak için yapılacak tek şey mantık kurallarını değiştirmektir. Yani, bir önermede ileri sürülen kavram ile onun karşıt kavramının aynı anda doğru olmalarına izin vermek gerekir. Bu durum klasik Aristo mantığında mümkün değildir. Bir kavran hem kendi hem de aksi olamaz. Örneğin bir insan hem kısa boylu hem uzun boylu olamaz. Bir önerme hem doğru hem yanlış olamaz. Çünkü bu kabul özdeşlik ilkesine aykırıdır.

Özdeşlik ilkesine göre A, A’dır. A kendinden başka bir şey olamaz. Özellikle A = Anın aksi (zıddı) olamaz. Eğer bu kuralı kaldırırsak yeni bir mantık oluşturmuş oluruz. Bu mantığa “Hem-hem mantığı” diyelim. Modern fizik bilimlerinden Kuantum kuramında hem-hem mantığına uygun düşen önermeler bulunmaktadır.

Kuantum kuramının belirsizlik ilkesine göre bir cismin uzaydaki yerini kesin olarak bilmek istersek onun momentumu (hızı) hakkında kesin bilgiye ulaşamayız. Aynı durum zaman ve enerji çifti için de söz konusudur. Bu belirsizlik ilerde geliştireceğimiz daha hassas veya daha güçlü ölçüm aletlerinden bağımsız bir kısıtlamadır. Kuantum kuramına göre zaman sürekli ve ölçülebilen bir değişken değildir. Sadece süreksiz ve noktasal ‘an’ kavramı mevcuttur. İki an arasındaki süreyi doldurmak ve zamanın akış yönünü saptamak bize düşmektedir. Zaman yönü bize bırakılmış ise zamanın akış yönü geçmişten geleceğe doğru olabileceği gibi, tam aksi yönde gelecekten geçmişe doğru da olabilir. Geçmişten geleceğe doğru tek yönlü akan zaman kavramı yerine, her iki yönde akabilen tersinir zaman anlayışına varmak “Hem-hem mantığını” kabullenmemizi gerektirmektedir.

“Zaman hem geçmişten geleceğe hem de gelecekten geçmişe akar” önermesini çelişkisiz olarak kabullenmek için hem-hem mantığına gereksinim vardır. Bir olayın filmini çekip o filmi tersten oynattığımızı düşünelim. Bu durumda zaman gelecekten geçmişe akar. Eğer izlediğimiz olay bize mantıksız ve olanaksız gelmiyorsa zaman okunun yönü hakkında bir kesin karara da varamayız. İşte atom altı parçacıkların dünyasında durum budur. Zaman oku hakkında kesin bir yargıya varmak mümkün değildir.

Hem-hem mantığının geçerli olduğu bir diğer örnek, ışığın hem dalga hem de parçacık özelliklerini içermesi gösterilebilir. Bir deney sonucunda dalga yapısı ortaya çıkarken diğer bir deney sonucunda parçacık yapısı ortaya çıkabilir. Şu halde deney yaparak ışığın yapısını ve özelliklerini sorguladığımızda birbirlerinden farklı, hatta çelişik yanıtlar alabilmekteyiz. Sadece ışık değil, tüm nesneler hem dalga hem de parçacık özelliğine sahiptirler. Gerçek hem birinde hem de diğerindedir. Madde hem dalgadır hem de parçacık.

Modern bilimin ışığında yeni bir tür mantık ortaya çıkmakta ‘gerçek’ dediğimiz olgu mutlak olmak özelliğini yitirmektedir. Görüyoruz ki “gerçek” mutlak değil görelidir. Sadece maddenin değil, zamanın da göreli olduğunu ‘Görelilik kuramı’ (Rölativite) ileri sürmüş ve bu iddia deneysel olarak kanıtlanmıştır. Göreli gerçek ile başa çıkmanın yolu da alışıla gelmiş Aristo mantığındaki özdeşlik ilkesinden vazgeçmektir.

Çelişkili önermeler

Tarih: 10:56 on 12/2/2006

Düşüncenin, özellikle sistematik düşüncenin, kurallarına mantık diyoruz. Evet, “mantık” sadece bir kurallar dizisidir. Bu kuralları biz insanlar koyuyoruz ve koyduğumuz bu kurallar çerçevesinde önermeler ürettiğimizden dolayı da birbirimizle anlaşabiliyoruz. Bu kurallara uymadan ileri sürülen fikirlere de “mantıksız düşünce” deyip çıkıyoruz.

Mantık kuralları çerçevesinde düşünen insan çelişik önermelerden hoşlanmaz. Daima açık, seçik ve belirgin önermeler ister. Örnek olarak, “Ben hep yalan söylerim” önermesine A önermesi adını verelim. A önermesi mantıksal olarak mümkün müdür?  Eğer bir kişi hep yalan söylüyorsa bu söylediği A önermesi de yalandır. Demek ki hiç yalan söylemiyor. Hiç yalan söylemeyen kişinin ise “Ben hep yalan söylerim” dememesi gerekir. Şu halde, bu önerme bir çelişki içermektedir ve ya önermeyi “mantıksız” olarak ret etmeliyiz, veya kişinin aynı anda hem doğru hem de yalan söylediğini kabullenmek durumundayız. Fakat insan bazen yalan söyler, bazen de doğru söyler. Aynı anda hem doğru hem yalan söyleyebilir mi?

Bu türden önermelere birer kelime oyunu olarak bakmamak gerekir. Alfred Whitehead ile birlikte ‘Principia Mathematica’ adlı 3 ciltlik matematiksel mantık kitabını yazan İngiliz mantıkçı ve felsefeci Bertrand Russell (1872-1970), kümeler kuramında çelişki içeren bir önerme tanımlayarak matematikte bir bunalım yaratmıştır.

Russell’ın matematik mantıkla ilgili sorusu şu şekilde ifade edilebilir: “Eleman olarak kendini içermeyen bütün kümelerin kümesi kendini içerir mi, içermez mi?” Örnek olarak, kitap kümesini düşünelim. Yer yüzündeki tüm kitapları içeren küme bir kitap değildir. Şu halde ‘kitap küme-si’ kendini içermez. Bu türden düşünülebilecek tüm kümelerin toplamı olan küme kendini içermesi gerekir, zira eleman olarak kendini içermemektedir. Oysa ki kendini içermemesi gerektiğini baştan şart koşuyoruz. Şu halde ortada derin bir çelişki vardır. Çelişkiden çıkmanın yolu ise kümenin hem kendini içerdiğini hem de içermediğini kabul etmekten geçer. Çünkü klasik mantık yaklaşımı ile çelişkiden kurtulmamız mümkün değildir. Çelişkiyi yaratan, önermenin kendi üstüne dönüşümlü olması ve kendi hakkında yine kendinden hareketle bir yargıya varılmak istenmesidir. Aynı şekilde “Ben hep yalan söylerim” önermesi de ‘ben’ sözünü içerdiğinden, kendi üstüne dönüşümlüdür.

“Kendi üstüne dönüşümlü” derken kendi hakkında bir yargıya ulaşmak isteyen önermeleri kast ediyorum. İnsan, bir önceki yazımda belirttiğim gibi, kendi hakkında yargıya varmak istediğinde çelişkilerle karşılaşıyor. Çünkü, bir kavram ancak başka bir kavram ile anlam kazanıyor. Bu da tüm kavramların birbirlerine bağlı olduklarını gösteriyor. Tek başına (başka hiçbir tanıma dayanmayan) bir önerme anlamsız ve dayanaksız olup boşlukta kalıyor.

Örneğin, “kuğu kuşu beyazdır” önermesine bakalım. Bu önerme doğada tüm kuğu kuşlarının beyaz olduklarını onayladığımız sürece doğrudur. Eğer siyah renkli bir kuğu kuşu bulursak (ki bulunmuştur) önerme yanlış olur. Demek ki bir önerme doğa ile ilgili ise tek başına ne doğrudur ne de yanlış. Daha doğrusu anlam içermeyen bir “totolojidir”. Ancak kendi dışında (örneğin doğa ile) bir başka varlıkla karşılaştığında doğru veya yanlış olabilmektedir. Şu halde bilimsel önermeler söz konusu olduğunda “şimdiki bilgimiz dahilinde ......” demek durumundayız. Deney ve gözlemlerimiz bizim şimdiki bilgi durumumuzu belirlerler. Yeni deney ve gözlemler mevcut bilgimizin yanlış olduğunu her an ortaya koyabilirler. Bu duruma “bilimin yanlışlanabilir olması” ilkesi diyoruz. Çünkü bilim, nesneler arasındaki ilişkilerden söz eder. Onların iç yapısını açıklamaya çalışırken dahi yeni nesneler tanımlamak zorunluluğu duyar.

Aynı durum matematikte de vardır. Matematik mantıkta matematiksel ifadeleri sayılarla ifade edebiliriz. Bir sayısal ifadenin de doğru veya yanlış olduğunu belli kurallar çerçevesinde tespit edebiliriz. Kurt Gödel (1906-1978) “Bu sayısal ifade yanlıştır” önermesini sayısal olarak belirttikten sonra, kuralları uygulamış ve yanıtın ne doğru ne de yanlış olarak kesinlik kazanmadığını saptamıştır. Kendi hakkında yargıya varan bir önerme çelişkili olmaktadır. Sonuçta matematik dahil, tüm formel (Aristo kurallarına bağlı) mantık sistemlerinin karar verilemez önermeler içerdikleri ve dolayısıyla çelişkiler barındırdıkları gerçeği ortaya çıkmıştır.

Öyle anlaşılıyor ki, klasik formel mantığın yetersizliğini kabullenmek zorundayız. 

Kısır bir döngü

Tarih: 08:40 on 12/2/2006

Düşünce doğal ve zorunlu bir eylemdir, dedim. Ama, düşünme yetisi sadece insanlara ait bir özellik de değildir. “İnsan düşünen hayvandır” derler. Doğru değil. Her canlı varlık düşünebilir. Ama bu yetisini mecbur olmadıkça kullanmaz. İnsanın düşünme yetisi mecburiyetten, şartların zorlamasından dolayı, gelişmiştir.

İnsan dışında tüm canlılar yaşadıkları doğal ortamla tam bir uyum içindedirler. Bedensel yapıları dış ortama, doğal çevreye  ve iklim şartlarına göre şekillenmiştir. Eko-sistem dediğimiz çevre ile adeta bütünleşmişlerdir. Varlıklarını sürdürmek için doğal davranmaları ve içgüdülerine uymaları yeterlidir.

Oysa ki insan denen canlı hiçbir özel bedensel yapıya sahip değildir. Hızlı koşamaz, maymun gibi çevik değildir. Kuyruğu olmadığı için denge gücü oldukça zayıftır. Kürkü olmadığından soğuktan korunacak doğal bir örtüsü yoktur. Ne gözleri kartalınki kadar keskindir ne de burnu köpeğinki kadar hassastır. İnsan aslında, aciz bir mahluktur.

Varlığını sürdürmek için de tek kullanabileceği organ beynidir. Son iki milyon yıl içinde insandaki en önemli değişiklik beyninin yaklaşık 100 de 100 büyümüş olmasıdır. Buna karşılık ne bacaklarında, ne kollarında ne de ellerinde belirgin bir değişiklik olmuştur. İnsan düşünme yetisini kullanarak doğaya uyum sağlamakla kalmamış, üstelik doğayı da kendine uydurmayı başarmıştır.

Dış şartlar zorladığı vakit, hayvanların da pekala düşünebildikleri deneysel olarak kanıtlanmış bir gerçektir. İnsanlar ise, yeryüzünde daha ilk adımlarını attıkları anda dış şartların zorluklarıyla karşılaşmışlar, varlıklarını sürdürebilmenin telaşı içine düşmüşlerdir.

Şu halde “neden düşünüyorum?” sorusunun yanıtını bulduk sanırım. “Düşünüyorum, çünkü düşünmek benim için bir zorunluluktur”. Descartes’in dediği gibi, düşünmek benim varlık nedenimdir.

İnsanlar önceleri en temel yaşamsal gereksinimler için düşünmek zorunda olmuşlar, fakat yaşam tarzları düzenli olmaya başladıkça kendi varlık nedenlerini düşünmeye başlamışlardır. “Ben düşündüğüm için varım” diyecekleri yerde “Ben neden varım?” sorusuna kendi dışlarından yanıtlar aramışlardır. Eğer insan düşündüğü için varsa, düşünmediği sürece de yok demektir. Daha doğrusu, varlığı hakkında bir yorum yapmak gereğini duymaz. Hayvanlar düşünme zorunda olmadıklarından varlık nedenlerini asla sorgulamazlar. Onlar varlıklarını yaşarlar ama o konuda yorum yapmazlar.

İnsanların kendi varlıkları ile ilgili ilk yorumları mitler ve destanlardır. Bunlara “yaradılış destanları veya hikayeleri” de diyebiliriz. Varlıklarını açıklayacak ve onlara güven verecek bir düşünce ürünüdür bu destanlar. Belki bir miktar doğruluk payı olsa da çoğu kez büyük çapta hayal ürünüdürler.

Zaman geçtikçe ve insanlar sistemli düşünme yetisini geliştirdikçe bir yandan din diğer yandan bilim gelişmiş, her biri kendince yaradılış destanları üretmişlerdir. Düşünce, belli bir mantık yapısı içinde kavramlar ürettiği için insan da kendi ürettiği düşünce kaleleri içinde hapis olmuş kalmış durumdadır. Şimdiki insanlığın durumu bir kısır döngüdür. Var olmak için düşünmek zorundadır ama düşünce yoluyla da varlığını anlaması mümkün değildir.

Eskilerin dediği gibi aşağı tükürse sakal, yukarı tükürse bıyık.

Bütünsel evren

Tarih: 06:34 on 12/2/2006

Blog, bir kitap gibi sürekli okunmuyor. Ara-ara, vakit buldukça okunan bir yazı türü. Bu bakımdan, bir miktar yazı biriktiğinde toparlayıcı bir özet vermek yararlı olur kanısındayım.

Dedim ki, öznenin dışında kalan her-şey nesnedir. Özne ise “ben” dediğim, kendi özüme ait olan tözdür. Fakat her insanın tözü vardır. Her insan bir öznedir. Benim için diğer canlı veya cansız varlıklar birer nesne iseler, diğer insanlara ne demeli? Onlar da birer nesne olmaları gerekmez mi? Evet, onlar benim için ne kadar “nesne” iseler, ben de onlar için o kadar nesneyim. Çünkü o özneler için ben de bir şey’im.

Demek ki, insan hem bir öznedir hem de bir nesnedir. Öznedir, çünkü bir töz sahibidir. Enerjisi olan ve şeyleri harekete geçiren bir cevherdir. Öte yandan diğer özneler tarafından şekillendirilen, harekete geçirilen, yoğrulan, yontulan ve eğitilen bir şeydir. Bu iki durum el-ele gider ve biri olmadan diğeri var olamaz.

Benim varlığım diğer varlıkları gerektiriyor, onların varlığı da benim varlığımı gerektiriyor. Şu halde bağımsız nesne olabilir mi? Tek başına, bir taş gibi sonlu, yalıtık bir varlık mümkün mü? Hayır, mümkün değil. Yani varlıklar birbirlerine bağımlı oldukları gibi, üstelik de birbirlerini yaratıyorlar.

Burada “yaratma” eylemi üzerinde biraz durayım. Yaratırken insan yoktan var etmiyor. Yaratırken, yukarda ifade ettiğim gibi, şekillendiriyor, yoğuruyor ve eğitiyor. Eğitim bir eğip-bükme eylemidir. Her çocuk önce ailesi tarafından, daha sonra okul ve çevre tarafından eğitilir. Yani belli birtakım varsayımları ve toplum kurallarını öğrenir, şekle şemaile sokulur. Artık o insan kendisi değildir artık. Toplumun değer yargıları ile yoğrulup yeniden yaratılmıştır.

Ama bu arada birçok bilgi edinmiş, en azından düşünmeyi öğrenmiştir. Düşünme eylemi her ne kadar doğal ve bir bakıma zorunlu olsa da, düzgün ve sistemli düşünebilmek ayrı bir yetenektir. Bu yetenek doğuştan var olan bir özellik değildir. Sistemli düşünce öğrenilir. Okulların da en büyük faydası insanda sistemli düşünce yetisini geliştirmeleridir.

Ancak, bizim okullarımızda uygulanan eğitim sistemi bu yetiyi ne derece geliştiriyor? Sistematik düşünceyi mi öğretiyor, yoksa ezberci ve sorgulamayı engelleyen bir eğitim sistemi mi uyguluyor? Bu da ayrıca düşünülüp tartışılması gereken bir konu.

Bağımsız varlık olamayacağına göre, “evren bütünsel bir iletişim içindedir” de diyebiliriz. Her var olan, yakın çevresi ile güçlü, uzak çevresi ile zayıf bir bağ kurar. Bu bağ sayesinde bilgi, duygu ve düşünce alışverişinde bulunur. Ne sadece alır ve ne de sadece verir. Sürekli bir enerji akımı gidip gelir. Hareket halindeki bu soyut enerji de eylem başlatarak somut olgulara yol açar.

Artık günümüzde, klasik “bağımsız nesne” kavramını terk etmemiz gerekiyor. Her nesne çevresi ile tanımlanır ve çevresinden etkilenir. Çevre dediğimiz şey ise nesneler topluluğundan başka bir şey değildir. Bu durumu soğanın tabakalı yapısına benzetebiliriz. En içte soğanın cücüğü vardır. Bu soğanın cevheridir. Soğan o cücüğü sayesinde varlığını sürdürür. Toprağa gömüldüğünde sürgünü veren soğanın cücüğüdür. Ama o cücüğün var olmasını sağlayan, onu koruyup besleyen de etrafındaki tabakalardır.

İşte insan da, soğanın cücüğü gibi, bir cevher olup varlığını etrafındaki koruyucu çevre sayesinde sürdürür. İnsanı çevresinden soyutlarsanız kısa zamanda varlığını yitirir. Cevher yok olmaz ama şekil değiştirir. Yani, insanın özü olan enerji hiçbir zaman yok olmuyor. Fakat belli bir insan görünümünde kalabilmesi için de koruyucu bir çevreye gereksinim duyuyor.

Bu durum sadece insan için değil tüm var olan nesneler için de aynıdır.

Özne enerjisi

Tarih: 23:43 on 11/2/2006

Özne olmak zor, şey olmak kolaydır, dedim. Neden? Çünkü özne doğrudan doğruya enerjidir. Enerji de iş yapmak durumundadır. Enerji atıl kalamaz. Sürekli üretir, dönüştürür ve kendi de dönüşür. Enerji aynı durumda, eylemsiz, kalamaz. Sürekli eylem içinde olmak zorundadır. En temel eylem de düşünce eylemidir.

İşte bu bakımdan beynimiz sürekli faaldir. Çünkü her insan faildir de ondan. Ancak, anlamlı faaliyet (eylem) olduğu gibi, anlamsız eylem de vardır. Peki ama bu “anlam” konusuna kim karar verecek? Kimin eylemi anlamlı, kiminki anlamsız? Nasıl yapacağız bu ayırımı?

Yanıtı çok kolaydır. Her insanın eylemi kendisi için anlamlıdır. İnsan anlamsız bir eylem yapamaz. İstese de yapamaz. Ama, bana anlamlı gelen eylem size anlamsız gelebilir. Demek ki, “anlam” kişiseldir. Her insana göre farklıdır. Dolayısıyla “Anlam görelidir”.

Şu halde anlam içeren kavramlar da görelidir. Mutlak bir kavram var mıdır? Örneğin zaman ve mekan (uzam) kavramları. Bu iki kavram mutlak mıdırlar? Modern bilim (Görelilik ve Kuantum kuramları) göstermişlerdir ki ne uzam ne de zaman mutlak değillerdir. Uzam, değişmez bir yapıya sahip değildir. Daralıp genişleyebilir. Gözlemciye göre farklı boyutlar alabilir. Farklı görüntüler oluşturabilir.

Keza zaman da daralıp genişleyebilir. Geçmişten geleceğe uzanan mutlak bir zaman kavramı sadece bir varsayımdır. Bir ön yargıdır. Bize öğretilmiş olan “dün”, “bugün”, “yarın” kavramlarının bir uzantısıdır. Ya varlıklar ve nesneler? Onlar mutlak mıdır?

Her var olan bir süre sonra yok oluyor. Bu süre ise bazen çok kısa bazen de çok uzun olabiliyor. Neye ve kime göre uzun-kısa? Elbette ki bizim yaşamımıza göre. Ölçüt bizim yaşam süremiz. Ama bizim süremiz de mutlak değil. Bir süre için var olduğumuza inanıyoruz, bir süre sonra da yok olacağımıza inanıyoruz.  Fakat, aslında ikisi de tam olarak doğru değil. Ne tam olarak varız ne de tam olarak yokuz.

“Tam olarak” derken şunu ifade etmek istiyorum. Özne enerjidir, dedim. Biz de özneyiz, dedim. Biz = Enerjiyiz, sonucuna vardım. Ama, enerji tam olarak var mıdır? Enerji denilen kavram, ne tam olarak var ne de tam olarak yok. Daha doğrusu, hem var hem yok. Çünkü enerjinin kendisini doğrudan algılamıyoruz. Sadece onun etkilerini duyularımızla algılayabiliyoruz. Sıcaklık, örneğin, ısı enerjisinin göstergesidir. Hareket, mekanik enerjinin göstergesidir. Aynı şekilde, düşünce ve düşüncenin sonucu ortaya çıkan eylem öznenin bir göstergesi, bir tezahürüdür. Ama kesin bir kanıtı da değildir.

Duyularımız tarafından ancak dolaylı olarak algılanan bir kavramın “tam olarak var” olduğunu iddia edebilir miyiz? Öte yandan etkilerinden haberdar olduğumuz için de “tam olarak yok” da diyemiyoruz. Bizim “öznemiz”, varlığına inandığımız fakat açık seçik bir şekilde kanıtlayamadığımız bir enerji türüdür.

En azından, insanların büyük çoğunluğu için durum böyledir.

Düşünceyi düşünmek

Tarih: 21:42 on 11/2/2006

Düşünüyorum, ama nasıl düşünüyorum? ve daha da önemlisi, neden düşünüyorum?

Nasıl düşünüyorum? Sorusuna yanıt arayan pek çok insan şu sonuca varmış: “İnsanlar kavramlarla düşünür” Kavram olmasa düşünce de olmaz. Kavram ise bir soyutlamadır. Aklımızın bir konuyu veya olayı kavrayabilmesi için gerekli olan düşünce birimlerine kavram diyoruz. “Kavram” bir sözcük olsa da bir tasarımdır. Zihnin soyut bir yorumudur.

Demek ki, düşünürken hem soyut kavramlar üretiyoruz, bir de üstelik onlarla oynayıp yorumlar yapıyoruz. Daha da ilginci, bu yorumlara kendimiz de inandığımız gibi, yorumlarımızın doğruluğuna diğer insanları da ikna etmeye çalışıyoruz. İlginç doğrusu.

Kavramlarla bir mantıksal yapı oluşturmaya “bilimsel düşünce” veya “felsefi düşünce” diyoruz. Birinde doğa ile bir ilişki kurma çabası var, diğerinde (felsefede) bu çaba dahi yok. Bu iki tür düşünce yapıtı, tutarlı ve saygın bir yorum olarak ciddiye alınmalıdır. Çünkü bu düşünce türlerinde doğayı, insanlığı ve yaşamı sorgulayıp anlamlı ve tutarlı yanıtlar arama gayreti vardır. Üzerinde uzun uzadıya tartışılan düşünce ürünleri bu tür olanlardır.

Bir de kabuller ve varsayımlar üzerine kurulu, babadan gördüğünü tekrarlayan, derinliğine bir sorgulama içermeyen düşünceler vardır ki onlara ben sadece “düşünce kirliliği” demek durumundayım. Nasıl ki ses kirliliği, görüntü kirliliği varsa, düşünce kirliliği da vardır. Bunlar da bol miktarda sürekli olarak, her fırsatta karşımıza çıkmakta, anlamlı ve derin düşünmemize engel olmaktadırlar.

Fakat, bilimsel düşüncede ve felsefi düşüncede “ön yargılar”, “varsayımlar”, “geleneksel kabuller” yok mu? Elbette ki var. Onlar bizlere öylesine işlenmiş, öylesine sindirilmiş ki onlarsız düşünmeyi dahi beceremiyoruz. Onlar “biz” olmuşlar. Biz de “onlar” olmuşuz.

Nedir bu önyargılar, varsayımlar ve geleneksel kabuller? Saymakla bitmez. Ama başlayalım. Örneğin “nesnellik varsayımı” üzerinde biraz düşünelim. “Nesne” deyince ne anlıyoruz? Madde mi? Cisim mi? Ne-ise-ne mi? Evet, bu sonuncusu. Ne-ise-ne. Yani, tanımlanamayan, ne söze ne de sayıya sığmayan soyut bir kavram.

Nesneyi bir cansız varlık olarak düşünmek bizi canlı-cansız ayırımına ve bu kavramların tanımına götürür. Canlı varlık ne zaman cansız olur? Veya cansız varlık hangi şartlarda canlılık kazanır? Bu gibi derin konulara sonra gireceğiz. Şimdilik nesne için şöyle bir tanım yapabiliriz. Nesne: Öznenin dışında kalan her “şey”.

İyi de, bu tanım bize iki tane yeni tanım yapmamızı gerektiriyor. Özne nedir? ve Şey nedir?

Özne, cümle içinde iş yapan, yani fail. Fizikte ise iş yapma gücüne sahip olana “enerji” diyoruz. Şu halde “İş yapan enerji ise, özne = enerjidir”. Bir diğer ifadesi de bizim özümüz enerjidir. Biz (özne) ne maddeyiz ne de nesneyiz. Biz doğrudan doğruya enerjiyiz. Çünkü bizler iş yapma kapasitesine (yetisine) sahibiz. 

Bu tanımdan hareketle diyebiliriz ki: “Şey, iş yapma yetisine sahip olmayan varlıktır”. Şu halde “şey” enerji sahibi değildir. Veya en azından enerjisini ortaya koyabilme yeteneği yoktur. Enerjisi olsa da gizlidir. Onun enerjisini açığa çıkartabilmek için dıştan ona etki etmek ve onun tepkisini sağlamak gereklidir.

Fizik ve Metafizik

Tarih: 19:52 on 11/2/2006

Doğaya bakan eski insanlar iki ayrı alem (gerçeklik alanı) görmüşlerdir. Bunlardan biri dünya ve dünyada olan çeşitli değişimler, hareketler ve ilişkilerdir. Diğeri ise gökte gördükleri uzak nesneler ve onların hareketleridir. Böylece ay altı ve ay üstü evreni ayırmak fikri doğmuştur. Çünkü ay altındaki evreni yakından tanıyabiliyor ve bir miktar kontrol da edebiliyorlardı. Oysa ki ay üstü evren (güneş ve yıldızlar) tümüyle insanların kontrolü dışında, erişilmesi mümkün olmayan, uzak bir gerçeklik olarak varlığını sürdürmekte idi.

         Bu iki evreni ayırınca insanlar ay altı evreni inceleyen disipline “fizik”, ay üstü evreni inceleyen disipline de “metafizik” dediler. Metafizik, fizik-ötesi anlamını taşır. Günümüzde metafizik demek fiziksel olmayan, ruhsal alemle ilgili görüşler içeren disiplinler anlaşılmaktadır. Oysa ki metafizik sözü ay-üstü evreni inceleyen disiplin, yani astroloji için kullanılmıştır. Eski dönemde ay üstü evren ruhların evreni sayıldığından bu görüş yerleşmiştir. Çünkü, ölen insanın ruhu, özellikle yöneticilerin ruhu, yok olmadığına inanılıyordu ve göğe yükselip bir yıldız olarak varlığını sürdürdüğü inancı hakimdi. Gök cisimlerinin hareketlerini izleyerek geleceği tahmin etmenin mümkün olduğu inancı da vardı.

Eski insanlarda gök merakı geleceği tahmin etmek, yani bugünkü duruma bakarak yarını bilmek gereksiminden türemiştir. Burçlar ve yıldız falı ile eski Maya takvimi hep bu gereksinimin ürünüdürler. Güneşe de o dönem insanları, bir yaşam kaynağı olarak, kutsal bir varlık olarak, veya daha doğru bir ifade ile kutsal varlığın bir nesnel görüntüsü olarak bakmakta idiler.

Ama durum bugün dahi pek farklı değil. Hala birtakım verilerden hareketle, varsayımlar yürüterek, veya belli kabuller çerçevesinde yorumlar yapıp tahminler yürütüyoruz. Gök cisimleri birer "tanrısal varlık" değiller, ama gerçekten göründükleri gibi "var" olduklarını iddia edebilirmiyiz?

Işık bir noktadan diğerine sabit bir hızla ulaşıyor. Bu hız sonsuz değil. Saniyede 300.000 km. Evet, oldukça yüksek bir hız, ama gene de sonlu. Örneğin, güneşin ışığı bize 8 dakikada ulaşıyor. Bu arada (yani geçen 8 dakikalık süre içinde) güneş yer değiştirse veya tümden yok olsa bizim haberimiz olmayacak. Ancak 8 dakika sonra durumun farkına varacağız.

Ya daha uzak yıldızların ve galaksilerin ışığı? Onların ışığı bize binlerce, hatta milyonlarca yıl sonra ulaşıyor. Bu uzun sürede o yıldız, veya yıldız kümesi ne oldu? Hangi farklı duruma dönüştü? Acaba hala var mı? Yoksa tümden yok mu oldu? Hiç bilmiyoruz.

Kuramlar da bize pek yardımcı olamıyorlar. Varlık ne derece var? İşte bu soru binlerce yıldan beri insanları düşündürmüş. Bir de "varlık" deyince ne anlaşılmalı? Duyu organlarımızla algıladıklarımız gerçekten var olduklarından emin olabilir miyiz?

Duyu organlarımıza ne derece güvenebiliriz? Descartes (17. yüzyılda yaşamış Fransız düşünürü) "Duyularımıza güvenemeyiz. Tek güvencemiz düşüncemizdir. Düşünüyorum, şu halde var'ım" demiş.

Biz de onun yolunda düşünce kervanına katılalım.

 Alıntı:  http://bilgisev.blogcu.com/

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 - Turkiye / Denizli 

Ana Sayfa / index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy)/ Astronomy