"Le développement de la science occidentale a eu pour base deux grandes réalisations : l'invention du système logico-formel par les philosophes grecs, et la découverte qu'il est possible de trouver des relations causales par une expérimentation systématique (à la Renaissance).

La logique formelle est bien présente dans la géométrie euclidienne. Dans celle-ci, on détermine d'abord les axiomes et les définitions, ainsi que les postulats nécessaires aux constructions ; à partir de ces prémisses, la démonstration des théorèmes est ensuite abordée. En fait, au cours de l'histoire, des doutes concernant l'un des postulats ont abouti à la création d'un nouveau domaine des mathématiques : la géométrie non euclidienne.
Au siècle dernier, Riemann a remarqué que l'existence d'un groupe de déplacements n'est pas lié à une courbure totale nulle, mais plus généralement à une courbure totale constante : c'est pour cette remarque fondamentale que son nom est resté attaché à la géométrie sur la sphère, où la somme des angles d'un triangle est supérieure à deux droits.
 

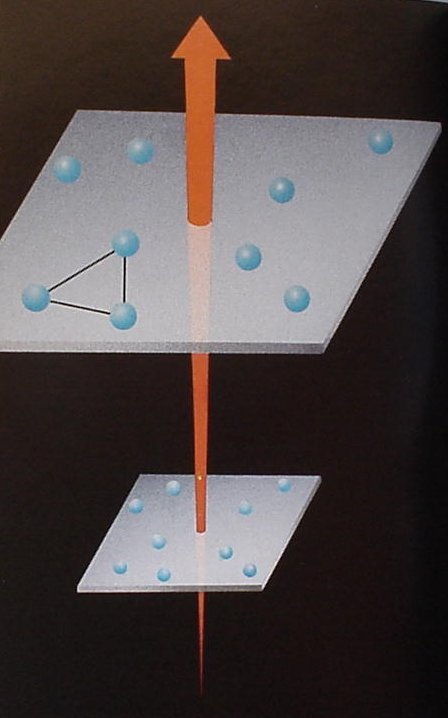
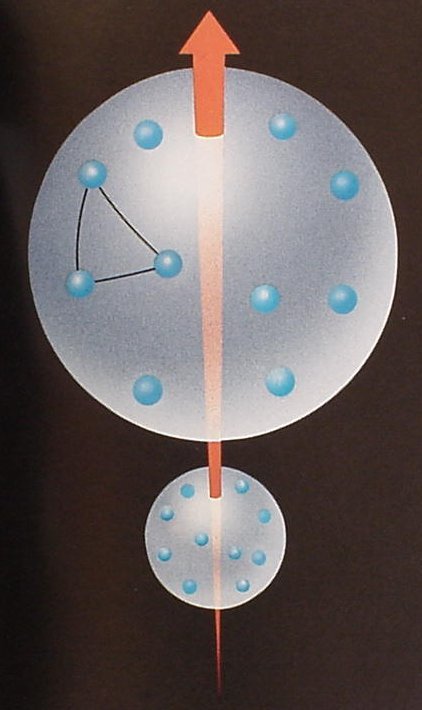
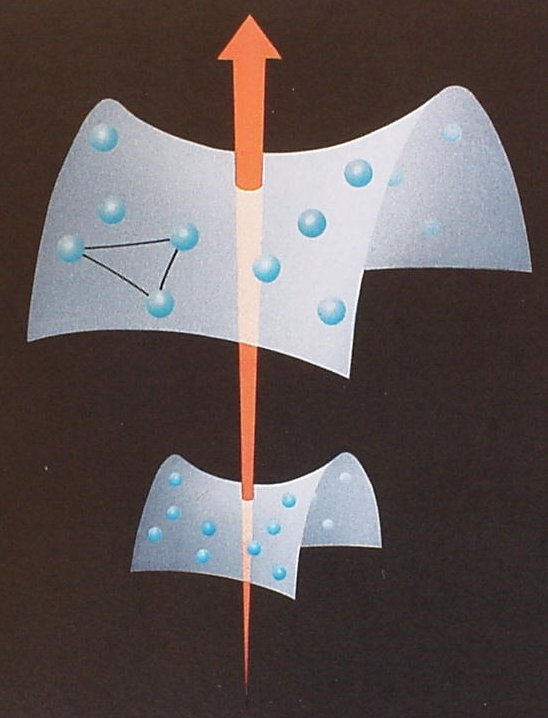
L’idée centrale de la relativité générale est de considérer les phénomènes gravitationnels comme une simple conséquence du fait que l’espace-temps possède une courbure. Le concept de courbure est issu de la théorie mathématique des espaces de Riemann ; on peut s’en faire une idée simple dans certains cas. La surface d’une sphère, par exemple, est un espace courbe à deux dimensions. Imaginons des êtres plats ne pouvant se déplacer qu’à la surface de cette sphère. Il leur est donc impossible de s’élever au-dessus de cette surface et de s’apercevoir qu’ils vivent sur une sphère. Leur monde n’aurait que deux dimensions. Pour ces êtres plats, le plus court chemin entre deux points n’est  plus la ligne droite, mais un grand cercle. Plus généralement, pour un espace courbe de dimension quelconque, on appelle géodésique le chemin le plus court entre deux points voisions. C'est la généralisation de la notion de ligne droite pour un espace courbe.
On se représente bien la courbure d'une surface sphérique parce qu'elle peut être observée de l'extérieur ; mais quand tout l'espace possède une courbure, c'est bien plus difficile. Dans la théorie d'Einstein, non seulement l'espace est courbe, mais l'espace-temps l'est également.

Dans sa théorie, Einstein distingue l'absolu (espace-temps) du relatif : cela correspond en géométrie à la distinction faite entre un objet géométrique (point, droite ...) et ses coordonnées (qui dépendent d'un repère). Après des siècles d'études, les mathématiciens on montré que la structure mathématique clé en géométrie est la structure de groupe. La géométrie euclidienne, par exemple, est fondée sur le groupe des déplacements : les propriétés géométriques euclidiennes sont caractérisées par leur invariance vis-à-vis de ce groupe. L'étude spatio-temporelle des phénomènes physiques est elle aussi caractérisée par un groupe de transformations, le groupe de Poincaré. Les référentiels privilégiés pour ce groupe sont les référentiels d'inertie.