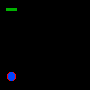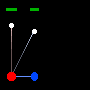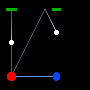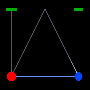Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey/Denizli
Time Dilation
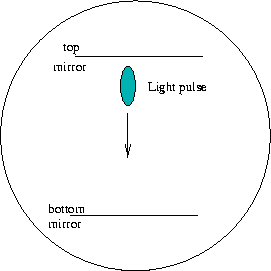
In order to attempt to prove this theory of time dilation, two very accurate atomic clocks were synchronized and one was taken on a high-speed trip on an airplane. When the plane returned, the clock that took the plane ride was slower by exactly the amount Einstein's equations predicted. Thus, a moving clock runs more slowly when viewed by a frame of reference that is not in motion with it. Keep in mind that when the clock returned, it had recorded less time than the ground clock. Once re-united with the ground clock, the slow clock will again record time at the same rate as the ground clock (obviously, it will remain behind by the amount of time it slowed on the trip unless re-synchronized). It is only when the clock is in motion with respect to the other clock that the time dilation occurs. Take a look at Fig 4 and Fig 5 below.
|
Let's assume that the object under the sun in Fig 4 is a light clock on wheels. A light clock measures time by sending a beam of light from the bottom plate to the top plate where it is then reflected back to the bottom plate. A light clock seems to be the best measure of time since its speed remains constant regardless of motion. So in Fig 4, we walk up to the light clock and find that it takes 1 sec for the light to travel from the bottom to the top and back to the bottom again. Now look at Fig 5. In this example, the light clock is rolling to the right, but we are standing still. If we could see the light beam as the clock rolled past us, we would see the beam travel at angles to the plates. If you are confused, look at Fig 4 and you'll see that both the sent beam and received beam occur under the sun, thus the clock is not moving. Now look at fig 5, the sent beam occurs under the sun, but the reflected beam returns when the clock is under the lightning bolt, thus the clock is rolling to the right. What is this telling us? We know that the clock standing still sends and receives at 1-second intervals. We also know that the speed of light is constant. Regardless of where we are, we would measure the light beam in fig 4 and fig 5 to be the exact same speed. But Fig 5 looks like the light traveled farther because the arrows are longer. And guess what, it did. It took the light longer to make one complete send and receive cycle, but the speed of the light was unchanged. Because the light traveled farther and the speed was unchanged, this could only mean that the time it took was longer. Remember speed is distance / time, so the only way for the speed to be unchanged when the distance increases is for the time to also increase.
We'll look at time intervals in the next section.
Time dilation
The fact that the speed of light is the same in all reference frames has the consequence that moving clocks run slow. This means that if two events occur at the same place, such as the ticks of a clock, a moving observer will measure the time between the events to be longer. The relation between a time measured by a stationary observer t0 to the time t measured by an observer moving with velocity v is:

The gamma factor appears often in relativity. It is always greater than unity, but very close to it for small velocities. (If the velocity were greater than c, gamma would be undefined; but that never happens, as we will see shortly.)
This result can be shown to result from the two fundamental postulates by considering a light clock. This imaginary clock would work by ticking every time a light pulse reflected back to the lower mirror as shown below.
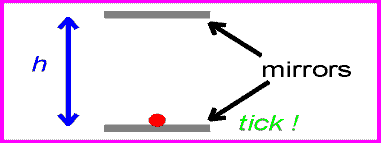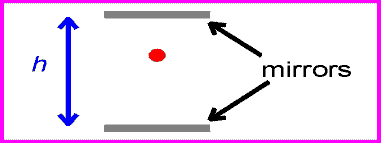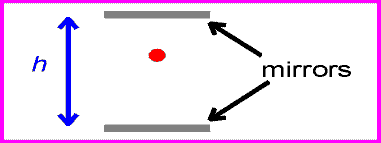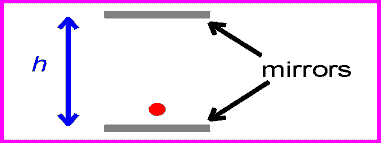
The time between ticks and tocks for the stationary clock is:
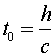
One can now view the same clock as it moves past with velocity v.
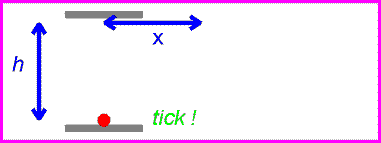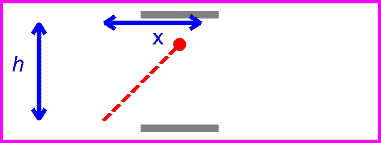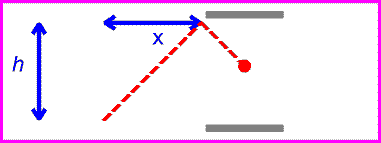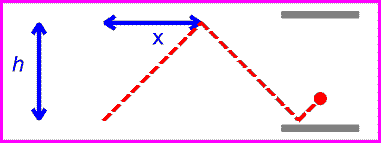
The time between ticks and tocks is again given by the distance traveled by the red pulse divided by c.
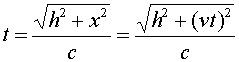
Solving the above equation for t in terms of h, v and c gives

Thus the moving observer sees a longer time by the factor g defined above.
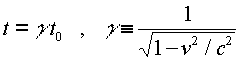
We derived the time dilation effect using a very simple clock; but the result applies equally to all clocks, including complex ones such as decaying radioactive particles or even biological systems. It is therefore better to think of the effect as an unexpected truth about space and time, rather than as a property of the clock. In any case, the effect is NOT caused by forces operating on the clock---since as you know, NO force is required to keep an object moving at constant velocity.
Time Dilation
The Galilean transformation laws 11.1-11.3 were derived by applying
common sense to simple thought experiments. We now need to abandon common
sense, to some extent, but retain the speed of light postulate.
Surprisingly, we are almost immediately forced to abandon the notion of
absolute time (i.e. Galilean transformation law 11.2). To see how this
comes about, imagine constructing a very simple clock that consists of
light pulses being bouncing back and forth between two vertical mirrors,
as shown in Fig. 11.4 below.
The distance d between the mirrors is 300 million meters, so that
it takes precisely one second for light to get from one mirror to another.
(Clearly this is another gedanken experiment: easy to imagine, but
hard to do in practice.) The clock therefore ticks one second everytime a
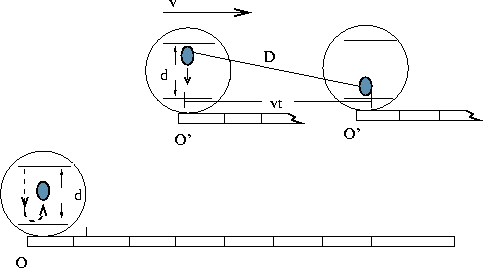
light pulse hits one of the mirrors. Suppose now that you have two
identical such clocks, one in frame of reference O, the other in
O', moving at relative speed v, as illustrated in
Fig.11.5 below.
Let us now synchronize the two clocks so that the light pulses in both
clocks leave the top mirror at precisely t = t' = 0. When
the light pulse in O'arrives at the bottom mirror this clock tick
once so that this time interval is one second, as measured by O'.
Now we wish to find out what is time does the clock in O read at
the instant that the clock in O' ticks once second? The intuitive
answer is that if one second passes in O' then one second must also
pass in O. However, we need to dispense with our intuition. By the
time the light pulse in O'arrives at the bottom mirror, the clock
in O' has moved forward a horizontal distance of v x
t relative to O, where t is the time that measured by
the clock in O. An observer in Otherefore sees this light
pulse move along the diagonal line shown in the Fig. 11.5. The total
distance D traveled by this light pulse, i.e. the length of the diagonal,
is necessarily greater than d, the distance between the mirrors.
We now invoke the speed of light postulate, which requires the light pulses in both clocks to move at precisely the same speed relative to O and hence travel the same distance in the given time interval. Hence, the light pulse in the clock attached to O also has traveled a distance D, and has already bounced off the bottom mirror by the time the clock in O' ticks one second. An observer in O therefore concludes that the clock attached to O' is running slow.
This is a very startling result. It says that two identical clocks that run at precisely the same rate when compared in the same reference frame will appear to disagree when viewed from different frames: time is not absolute, but depends on the frame of reference of the observer. This conclusion seems even more bizarre if one recalls that the relativity of motion postulate does not allow us to discern which of the two observers is actually in motion. If we repeat the above argument, but from the point of view of an observer moving with O' , we will be lead to precisely the same conclusion, only in reverse. An observer in O' sees the light pulse of the clock in O travels along a diagonal Dand is forced to conclude that the clock in O is running slowly. Each observer therefore thinks that it is the other clock that is running slowly, and there is no sense in which we can claim that one clock or the other is the culprit. Time itself is relative.
It is not difficult to get a quantitative expression relating the time elapsed on O's clock to that of O'. The distance between the mirrors, dis related to the time t' measure by O' according to d = ct', where c, as usual is the speed of light. (We are using the fact that displacement = (velocity x time).) Since the speed of light is precisely the same for both observers, the time t elapsed in that frame is related to the distance D traveled relative to O by a similar relation: D = ct. Using the Pythagorean theorem relating the sides of a right triangle, we know that D2 = d2 + (vt)2. When we substitute the expressions for D and d in terms of the corresponding times, we get the desired relationship:
With a little bit of algebra we can express t explicitly in terms of t'. What we find is that the time measured in O is proportional to the time as measured by in O':
| t =
|
(11.5) |
The constant of proportionality,
![]() is called the time dilation factor. It depends on the relative
velocity v and is given by the expression:
is called the time dilation factor. It depends on the relative
velocity v and is given by the expression:
There are several important things to notice about the time dilation
factor. First of all, no matter what the velocity is,
![]() is always greater than one, so the clocks always appears to run slower
when observed by someone in a different (uniformly moving frame.
is always greater than one, so the clocks always appears to run slower
when observed by someone in a different (uniformly moving frame.
Secondly,
![]() depends only on (v/c)2, the square of the ratio
of the relative velocity v to the speed of light c. Hence it
doesn't care about whether v is positive or negative (i.e. whether
the motion is to the right or to the left). Moreover, when v is
much less than c, the ratio v2/c2
is much less then one. In this case the denominator in 11.6 is very nearly
equal to one, and so is
depends only on (v/c)2, the square of the ratio
of the relative velocity v to the speed of light c. Hence it
doesn't care about whether v is positive or negative (i.e. whether
the motion is to the right or to the left). Moreover, when v is
much less than c, the ratio v2/c2
is much less then one. In this case the denominator in 11.6 is very nearly
equal to one, and so is
![]() .
This explains why the bizarre consequences of Special Relativity do not
affect our daily lives. We do not regularly experience relative velocities
anywhere near 300 million meters per second. At the more Earthly speed of
100 km/hr, or about 30 m/s, the ratio v/c is 30 divided by
30 million, or one millionth. The square of a very small number is smaller
still. In this case
v2/c2
= 10-12and consequently, the time dilation factor differs from
one by only one part in 1012. This is clearly too small to be
detectable. We can now understand why many of the predictions of special
relativity are counter-intuitive. Our intuition is based on low velocity
experiences. If there is a life form somewhere in the Universe that
regularly travels at near light speeds, its intuition would lead to very
different conclusions.
.
This explains why the bizarre consequences of Special Relativity do not
affect our daily lives. We do not regularly experience relative velocities
anywhere near 300 million meters per second. At the more Earthly speed of
100 km/hr, or about 30 m/s, the ratio v/c is 30 divided by
30 million, or one millionth. The square of a very small number is smaller
still. In this case
v2/c2
= 10-12and consequently, the time dilation factor differs from
one by only one part in 1012. This is clearly too small to be
detectable. We can now understand why many of the predictions of special
relativity are counter-intuitive. Our intuition is based on low velocity
experiences. If there is a life form somewhere in the Universe that
regularly travels at near light speeds, its intuition would lead to very
different conclusions.
The time dilation factor is only relevant when the relative velocity is
a significant fraction of the speed of light. For example, if v =
c/2 (i.e. one half the speed of light), the time dilation factor is
1/![]() or approximately 1.2. In this case an observer in O sees the clock
in O' run 20 % slower. Conversely, an observer moving with O'
will see the clock in O running 20% slower.
or approximately 1.2. In this case an observer in O sees the clock
in O' run 20 % slower. Conversely, an observer moving with O'
will see the clock in O running 20% slower.
One final important feature of the time dilation factor is that as the
relative velocity gets near the speed of light, the denominator nears zero,
and expression for
![]() blows up: dividing by zero gives infinity. This suggests that something
strange happens as velocities approach the speed of light. We will have
more to say about this a bit later.
blows up: dividing by zero gives infinity. This suggests that something
strange happens as velocities approach the speed of light. We will have
more to say about this a bit later.
To understand the true significance of all this, one must keep in mind that time dilation does not apply only to the special types of clocks I described above. In fact, all physical processes appear to slow down when view from a different uniformly moving frame. This effect has been verified experimentally in many contexts. One of these involves elementary particles called muons, which are created when high energy cosmic rays hit the upper atmosphere. These muons are unstable and normally decay into a different form of matter within about two microseconds (two millionths of a second). The muons created by cosmic rays plummet towards the Earth at very high speeds, typically of the order of 99% of the speed of light. At this speed they should be able to travel a distance of (300 million meters/second times .000002 seconds ) or 600 meters. Hence they should decay somewhere in the upper atmosphere. What is observed, however, is that the muons get significantly closer to the Earth's surface than the above argument suggests. In fact, some of them hit the Earth.
The explanation comes from Special Relativity. In accordance with the
time dilation effect, the physical process responsible for muon decay
appears to be running slowly when viewed from the Earth. If the muon is
moving at a velocity of .99c, the time dilation factor
![]() is about 7. Thus, to an observer on Earth, the muon appears to live seven
times longer (about 14 microseconds instead of just 2). It therefore can
travel seven times further (over 4 kilometers), and traverses most of the
atmosphere before decaying.
is about 7. Thus, to an observer on Earth, the muon appears to live seven
times longer (about 14 microseconds instead of just 2). It therefore can
travel seven times further (over 4 kilometers), and traverses most of the
atmosphere before decaying.
| Clocks
Vermilion and Cerulean construct identical clocks, consisting of a light beam which bounces off a mirror. Tick, the light beam hits the mirror, tock, the beam returns to its owner. As long as Vermilion and Cerulean remain at rest relative to each other, both agree that each other's clock tick-tocks at the same rate as their own. |
| Time dilation
But now suppose Cerulean goes off at velocity v relative to Vermilion, in a direction perpendicular to the direction of the mirror. A far as Cerulean is concerned, his clock tick-tocks at the same rate as before, a tick at the mirror, a tock on return. But from Vermilion's point of view, although the distance between Cerulean and his mirror at any instant remains the same as before, the light has further to go. And since the speed of light is constant, Vermilion thinks it takes longer for Cerulean's clock to tick-tock than her own. Thus Vermilion thinks Cerulean's clock runs slow relative to her own.
|
| Relativity Simplified |
This page uses |
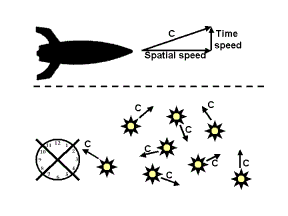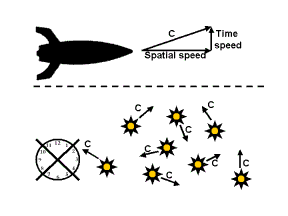
Relativity has always been taught using Minkowski's geometry, where the time dimension is markedly distinguished from spatial dimensions. It is possible though, to describe the effects of relativity using a pure Euclidean geometry where time and spatial dimensions are essentially identical in nature. Full articles on Euclidean relativity can be found on my homepage. Below is a laymen's version of such a description that provides simple and intuitive explanations for most relativistic phenomena.
First, the concept of speed in 2, 3 and 4 dimensions is explained,
meanwhile introducing the notion of speed in the time dimension. This is
then used to show the mechanisms behind relativistic time dilation and
length contraction. The last sections show why the speed of light remains
constant in all situations, followed by a brief overview of conclusions
from the main articles on Euclidean relativity.
1. Spatial dimensions and the time dimension
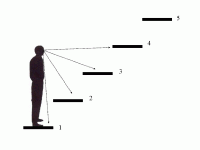 Imagine
a man standing on a staircase with steps of about one third of his own
height. He will be able to see the surface of the step he is standing on
as well as the next two that are in front of him. The fourth step is
harder to see, for his view on it is partly blocked (he may see it from
the bottom or the front side). The fifth is even harder to see, or perhaps
even invisible.
Imagine
a man standing on a staircase with steps of about one third of his own
height. He will be able to see the surface of the step he is standing on
as well as the next two that are in front of him. The fourth step is
harder to see, for his view on it is partly blocked (he may see it from
the bottom or the front side). The fifth is even harder to see, or perhaps
even invisible.
Suppose he eats something very nutritious and his body suddenly grows a full step in height. He is now able to see four steps but his view on the fifth step is partly blocked. That fifth step now looks exactly like the fourth step before he grew. The looks of the other four steps are not really different from the three steps he used to see before.
He grows older and, like older people do, he shrinks in size. He shrinks a full two steps and now he can clearly see two steps but the third is partly blocked. That third step now looks identical to the original fourth.
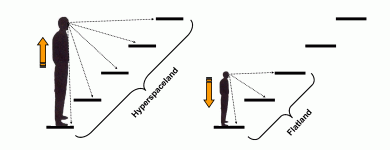 We
can translate this staircase into our space-time. The visible steps are
our spatial dimensions and the partly visible higher step is our time
dimension. The time step/dimension is actually just another spatial step/dimension
but that only becomes clear when you move up and down in the dimensions.
What you call a spatial dimension from your own "dimensional
viewpoint" may be a time dimension from another observer's
dimensional viewpoint. For the man who grew tall, our 4-dimensional
space-time is his 4-dimensional space, while he lives in 5-dimensional
space-time or "Hyperspaceland". For the man who shrunk, our 3-dimensional
space is his 3-dimensional space-time. He lives in "Flatland".
We
can translate this staircase into our space-time. The visible steps are
our spatial dimensions and the partly visible higher step is our time
dimension. The time step/dimension is actually just another spatial step/dimension
but that only becomes clear when you move up and down in the dimensions.
What you call a spatial dimension from your own "dimensional
viewpoint" may be a time dimension from another observer's
dimensional viewpoint. For the man who grew tall, our 4-dimensional
space-time is his 4-dimensional space, while he lives in 5-dimensional
space-time or "Hyperspaceland". For the man who shrunk, our 3-dimensional
space is his 3-dimensional space-time. He lives in "Flatland".
2. Spatial speed and speed-in-time
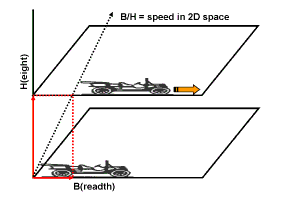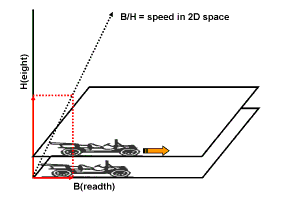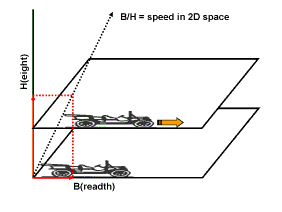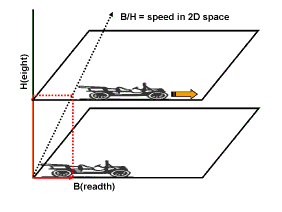 We
measure speed by dividing a covered distance by a time duration. Traveling
one meter per two seconds, our speed is 1/2 m/s.
We
measure speed by dividing a covered distance by a time duration. Traveling
one meter per two seconds, our speed is 1/2 m/s.
If we call the time duration, the seconds, a "length" in the dimension time we recognize that speed is just a division of a change of position in two different dimensions.
A division of a change of position in two spatial dimensions, let's say from dimension 1 (breadth) and dimension 3 (height), is for us merely a "dimensionless" and rather meaningless number. However, for the old man whose size shrunk this division does have a meaning: it represents a spatial speed in his 2-dimensional world because dimension 3 is his time dimension. This implies that the position of his whole 2-dimensional space in that third dimension must change, otherwise there would be nothing to compare the change of position in his spatial dimension nr. 1 with.
This change of position in the 3rd dimension looks to us as a normal spatial speed but for the man who shrunk it cannot be a spatial speed because he is simply not able to see this 3rd dimension as a spatial dimension. For him it intuitively feels like a change of position in his time dimension.
It may not be so hard to understand that our intuitively felt "motion in time" actually is similar. Our 3D space apparently moves in our time dimension too. But how should we calculate this speed-in-time in terms of a division? Seconds per second doesn't seem to make much sense.
Well, for the man who grew after eating the very nutritious food, this is very obvious. For him, the original time dimension changed into a normal spatial dimension and another, higher dimension became his new time dimension. If he now wants to express a spatial speed in his 4-dimensional space he simply divides his spatial distance traveled by his time duration in the fifth dimension. The 4-dimensional spatial speed he measures is the speed-in-time for us humble beings, lacking the very nutritious food. Our inability to "see" it as a real speed is due to our inability to measure lengths in the fifth dimension that is used to calculate it. Our speed-in-time turns into a regular spatial speed as soon as one is able to perceive an extra dimension, like the tall man does.
But how then do we calculate the speed-in-time (that will henceforth also be referred to as "timespeed") for the tall man? Obviously it must be a change of position in his 5th dimension divided by a change of position in yet another higher 6th dimension. And so on, and so on. It's a recursive, or fractal-like system.
3. Spatial speed and time speed
 Einstein's
theory of relativity predicts a limit in the speed that a thing can have
Einstein's
theory of relativity predicts a limit in the speed that a thing can have
The faster something moves, the slower time ticks away in that thing. If the speed of a rocket is for example 4/5th of c (about 240.000 km/s) then one second on a clock in the rocket takes as much as 1.67 seconds according to the watch of somebody who stands still on the ground. So the clock in the rocket runs slow according to the man on the ground. The man standing still thus has every right to think that the timespeed in the rocket is slower than his own.
Notice here that we quietly switched from a comparison of time durations to a comparison of time speeds. It's straightforward to compare the time durations on the clocks at the man and in the rocket and express these in seconds per second. But in this case we can also compare the timespeeds and express the result in seconds per second because in that comparison the common fifth dimension that is used to calculate both speeds cancels out in the division. To see that, divide e.g. 1/3 by 2/3. The result is 1/2 and the "3" has vanished.
We have seen that whenever spatial speed goes up, timespeed goes down and vice versa. When spatial speed is zero, the timespeed must therefore be at its maximum. On the other hand when spatial speed equals its maximum, which is the speed of light c, the timespeed actually has reduced to zero. For a clock in a rocket traveling at that speed it will take forever to tick away a second according to the man on the ground. Thus:
- Rule 1: zero spatial speed means maximum timespeed
- Rule 2: zero timespeed means maximum spatial speed
 There
is a very simple and familiar formula that can be used to express this
relation between spatial speed and timespeed. It is Pythagoras rule for
rectangular triangles: A2+B2=C2.
There
is a very simple and familiar formula that can be used to express this
relation between spatial speed and timespeed. It is Pythagoras rule for
rectangular triangles: A2+B2=C2.
If we call A the spatial speed and B the timespeed then it appears that
the sum of spatial speed and timespeed is always the same if we add them
with Pythagoras rule like in a triangle. So we can say:
(spatial speed)2+(timespeed)2=C2.
The letter C for the hypotenuse in this imaginary triangle was taken on purpose because the sum of the speeds is always equal to the speed of light c. This is clear from the two rules we saw above.
This allows us to enhance our rules:
- Rule 1: zero spatial speed means maximum timespeed c
- Rule 2: zero timespeed means maximum spatial speed c
- Rule 3: the Pythagorean sum of both is always c
4. Length in space and length in time
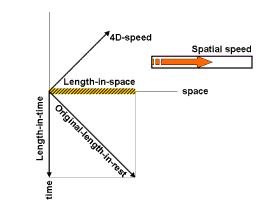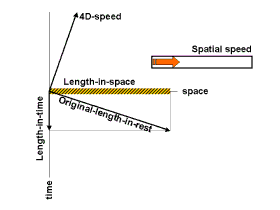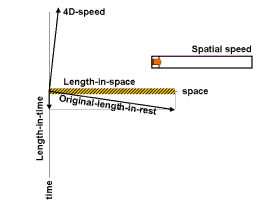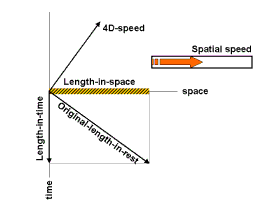 Whenever
something moves (fast) in space its length contracts in the direction of
its motion. Furthermore its time coordinate is no longer the same in all
points but has decreasing values in points along the direction of
its motion. We say that the points (formally the 4D "events") are non-simultaneous.
Note that this is not the same as its slower timespeed!
Whenever
something moves (fast) in space its length contracts in the direction of
its motion. Furthermore its time coordinate is no longer the same in all
points but has decreasing values in points along the direction of
its motion. We say that the points (formally the 4D "events") are non-simultaneous.
Note that this is not the same as its slower timespeed!
The contraction is a loss of length in the spatial dimension but the non-simualtaneity
is in fact a gain of "length" in the time dimension. The usual length-in-time
of an object in rest is zero, i.e. all its points then have the same time
coordinate. Its length-in-space is then at its maximum.
Similar to the relation we saw above between the speeds in space
and time, the lengths in space and time are also related according
to Pythagoras' rule:
(length-in-space)2+(length-in-time)2=(original-length-in-rest)2
What mechanism hides behind this? Let's look at things from the
perspective of the tall man again. Recall that the object's spatial speed
goes up and its timespeed goes down, so the direction of its speed
actually rotates in 4 dimensions according to the tall man.
Apparently the tall man sees that not only its speed rotates but along
with it also its orientation in 4D. The object's length rotates out of
our 3D space and gets a component in the fourth dimension, hence its
length in our time dimension. What's left for us to see is the component
of its 4D length in our 3D space, hence the contraction of its spatial
length.
Another very nice interactive visualization of this effect was made by
Adam Trepczynski on this page (you will need the Adobe Flash Player
browser addon to play it).
5. Speed of photons and speed of mass particles
Light rays travel at speed c and consist of millions and billions of tiny photons. These photons travel in all different directions in our breadth, length and height dimensions and every oblique direction inbetween.
The thing that all these photons have in common is that they all travel at exactly that same speed c, no matter what direction they take and no matter who looks at them. This reminds to rule number 3 that we just found out which will indeed appear to be the basis for this universal speed of the photons. The obvious question now is: "What is the timespeed of the photons?". Well, if they all travel at speed c in our space then their timespeed must be zero always. We say that the "distance between events" is zero for the photon. This means in regular words that the time stands still for all photons. Always and for every observer.
But if there is no timespeed in any photon at all we might just as well say that the whole time dimension does not exist for the photon. After all, if everything in the universe would never ever move a single inch in space and it all started at a single point in space then everything would still be sitting at that same single point and you might as well say that space does not exist.
 Its
a bit more complex in reality. Thats why this story is called the
laymen's version. In reality some properties of the photon that are
related to its wave-nature do actually exist in the time dimension but to
explain that here would make it all too confusing. So let's stick with the
photon's particle-nature that has no clock. That photon lacks dimension
number four so it is 3-dimensional and it always travels at speed c.
Its
a bit more complex in reality. Thats why this story is called the
laymen's version. In reality some properties of the photon that are
related to its wave-nature do actually exist in the time dimension but to
explain that here would make it all too confusing. So let's stick with the
photon's particle-nature that has no clock. That photon lacks dimension
number four so it is 3-dimensional and it always travels at speed c.
Going back again to the speed of the rocket we see there that its combined speed, i.e. the Pythagorean sum of its spatial and timespeed is also c. But now we remember that the timespeed was just a spatial speed for the man who ate the very nutritious food! That means that the rocket has a spatial speed c in four dimensions according to that tall man. Even stronger: any rocket, no matter what speed it has according to us, will have a spatial speed c in four dimensions according to the tall man (remember that this speed is rotated in four dimensions). If we now realize that this rocket actually consists of millions and billions of tiny mass particles then it is easy to see that any of these millions and billions of tiny mass particles travels at speed c in four dimensions according to the tall man. And they travel in all kinds of directions too because molecules, atoms, electrons, protons and so on travel criss-cross through each other.
6. Three-dimensional and four-dimensional worlds
Its a small step on the staircase to see the parallel between the photons and the tiny mass particles. The first apparently live in a 3-dimensional world while the latter live in a 4-dimensional world. Both travel at speed c in their dimensional environment. The three-dimensional speed of the photons is measured by us using our time in the fourth dimension. The four-dimensional speed of the mass particles is measured by the tall man using his time in the fifth dimension while we can only measure its spatial component using our fourth dimension.
We go a little further now and try to imagine what the old man who
shrunk sees of this all. He sees only two spatial dimensions and one time
dimension. But these three together are exactly the three dimensions that
the photons live in. How does that translate in his world?
Whatever speeds the photons have in whatever of these three dimensions, it
will always add up to c, using Pythagoras. Now we put the old man
on the back of one of these photons and imagine what he sees when another
photon travels parallel to his photon. The two spatial dimensions of the
old man actually form a plane and this world is sometimes called "Flatland"
in popular books. We choose a nice symmetrical situation and assume that
the flat space of the man stands rectangular to the direction in which his
photon travels.
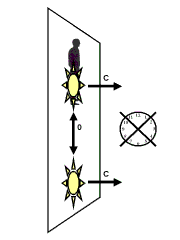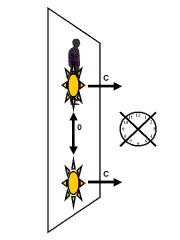 If
the second photon is in the same plane and travels parallel with the first
photon, the old man will think that the second photon stands still. On the
other hand, if the second photon travels at an angle rectangular to the
first photon, the old man on the back of the first photon will think that
the second photon travels at speed c away from him in his plane.
If
the second photon is in the same plane and travels parallel with the first
photon, the old man will think that the second photon stands still. On the
other hand, if the second photon travels at an angle rectangular to the
first photon, the old man on the back of the first photon will think that
the second photon travels at speed c away from him in his plane.
A clever reader will now say: "Hey, this does not make any sense because if the second photon does not travel parallel to the first, it will immediately vanish out of the flat world of the old man and become invisible". This sounds logic, but what about the tiny mass particles traveling at high speeds in our spatial dimensions? They should immediately vanish from our 3-dimensional space too. To be more precise: they should actually vanish "in the past", because their timespeed is slower than ours. Still, we keep seeing them, so Nature somehow makes sure that we can always keep an eye on everything, no matter in what time zone it has "vanished" (if you don't find this very satisfactory: think of the time dimension as being fully contracted, or "curled up" in our space). The same is true for the second photon that travels rectangular to the old man on the back of the first photon. Although it should "vanish" in the past of the old man (which we do see as a regular third spatial dimension!), Nature makes sure the old man keeps seeing it.
The bottom line is that the old man is able to see photons move at all speeds from zero to c in all kinds of directions in his flat world. So another parallel shows up with the way we see mass particles move in our space.
What does it mean?
To summarize what has been told up till now we can say that everything moves at speed c, but you need to be "tall" enough to see that in all worlds. Your speed in time is equal to c, because from your own point of view you yourself always stand still (your spatial speed with respect to yourself is zero). Furthermore, some particles, like the photons, obviously have one less dimension than others, like mass particles. Once you get this, a lot more of these symmetries can be found between the 3-dimensional and 4-dimensional worlds. It also enables you to draw conclusions and make suggestions beyond what is generally accepted yet. I will mention a few here to give you an idea but the justification of it requires a more thorough approach that does not fit in the context of this simplified story:
- A similar dimensional hierarchy we saw between the photons and mass particles can be found between the electromagnetic field and the gravity field. It turns out that the electromagnetic field is 4-dimensional while the gravity field is 5-dimensional.
- Like photons are the boson for the electromagnetic field, so are mass particles themselves the boson for the 5D gravity field (so forget about the illustrious graviton). Black holes obviously are its fermions.
- Bosons and fermions are one and the same thing. What looks like a fermion from "below" (e.g. a 3-dimensional viewpoint) looks like a boson from "above" (e.g. a 4-dimensional viewpoint).
- There may exist a very simple way to give something a speed forward without fiercely throwing away something backward, i.e. propulsion without the need for propellant. It would utilize the 4D nature of the photon's momentum vector.
Physics - Special Relativity

Light does not have mass, it is an electromagnetic wave. A change in an electric field causes a magnetic field and a change in an magnetic field causes a electric field this will continue as a photon. These fields were described by Faraday and Maxwell worked out the mathematics of this. The speed of the photon is determined by the electromagnetic properties of the material that it travels through.
So what about when the photon is traveling through a vacuum? In this case what will its velocity be relative to?
Do we need the concept of an either which the velocity of a photon will move relative to?
Can we use a photon to determine the absolute velocity of our frame-of-reference (thereby breaking the relativity principle)?
Einstein proposed that the velocity of a photon in a vacuum will be a constant known as 'c'. This velocity will be the same regardless of the velocity of the frame of reference of the observer. So several observers, all moving relative to each other, will nevertheless all see the photon traveling at the same speed.
Postulates:
- The laws of physics are the same for all observers independent of how any given observer may be moving through space, in other words, there is no experiment one can do that will distinguish one observers frame-of-reference as somehow 'preferred' (closer to being at rest with respect to the universe as a whole) over that of any other observer. (this applies to both Newtonian and Einstianian physics.
- The speed of light, through a vacuum, will always be the same regardless of the frame-of-reference of the observer.
Effect of velocity on time
We can construct a clock with two mirrors a fixed distance apart (say 1m) and then set a photon reflecting back and forward between the mirrors.

If we put this clock on a moving train we can measure the effect of velocity on time.
First measure time in the frame of reference of the train. If the mirrors are 1m apart then, the time taken for the photon to travel from one mirror to the other is:
t0= 1/c
where
- t0= time in frame of reference of train
- c = speed of light
The horizontal distance traveled by the train will be:
x = v tv = v/c
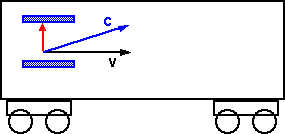
We now measure the time from the frame-of-reference of the ground. From this reference the photon appears to travel at an angle which is the sum of its vertical and horizontal components. This velocity of the photon will be c.
So the time in the frame of reference of the ground will be:
tv= distance / c
The distance is the vector sum of 1m in the vertical direction and v t0 in the horizontal direction (this horizontal distance traveled by the train will be the same as the above case because its perpendicular to the direction of the light).
So,
distance2 = 1 + (v/c)2
Therefore,
tv= distance / c = sqrt(1 + (v/c)2) /c
tv= t0 sqrt(1 + (v/c)2)
or
t0= tv / sqrt(1 + (v/c)2)
since this factor occurs frequently in special relativity we
often represent it by
![]() (gamma) so,
(gamma) so,
t0= tv
![]()
where:
- tv= time interval in the moving frame of reference relative to the observer.
- t0= time interval in the frame of reference of the observer.
-
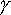 =
1 / sqrt(1 + (v/c)2)
=
1 / sqrt(1 + (v/c)2)
Therefore when the clock is moving relative to the observer the time interval is longer and therefore it appears to be running slow.
Effect of velocity on distance
This time we turn the mirrors round so that the light is traveling in the same direction as the train.

Again, in the frame of reference of the train, and assume mirrors are 1m apart then, the time taken for the photon to travel from one mirror to the other is:
tv= 1/c
where
- tv= time in frame of reference of train
- c = speed of light
The horizontal distance traveled by the train will be:
xv = v tv = v/c
Now we repeat in the frame of reference of the ground, the horizontal distance traveled by the train will be:
x0 = v t0
x0= v tv sqrt(1 + (v/c)2)
x0= xv sqrt(1 + (v/c)2)
so
xv= x0
![]()
So the apparent distance of a moving object appears to be shortened in the direction of the velocity, however distance perpendicular to the velocity does not change, we can prove this by using symmetry.

Imagine two rings A and B, approaching each other at high speed, if size did change perpendicular to the velocity then:
- In the frame of reference of A then B will reduce in size, therefore B will pass inside A.
- In the frame of reference of B then A will reduce in size, therefore A will pass inside B.
A cant be simultaneously inside and outside of B, so this type of perpendicular size reduction cant happen.
We can combine the time dilation, and distance change in the direction of the velocity but not perpendicular, can be combined to give the Lorentz transform here.
Invariant interval
Two events that are simultaneous for one observer are not generally simultaneous for another. If two events e1 and e2 are separated by length L and time T. These values will depend on the reference frame of the observer.
The invariant interval
![]() is:
is:
![]() 2=
T 2- (L/c) 2
2=
T 2- (L/c) 2
This is the separation between the two events in space-time. The invariant interval between any two events must be the same for all observers, no matter how they are moving relative to each other.
L' =
![]() (L
- v T)
(L
- v T)
T' =
![]() (T
- v L/c2)
(T
- v L/c2)
For special relativity the symmetry of the invariant interval replaces the symmetry of time for Galilean physics.
Mass-Energy
According tok Noethers theorem every Symmetry has a corresponding physical constant.
| Symmetry | Physical constant |
| The invariant interval
|
Energy-Momentum m2c4=E2 - p2c2 |
where:
-
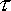 = invariant interval
= invariant interval - T = time
- L = length
- c = speed of light
- m = rest mass
- E = energy
- p = momentum
When the mass is stationary p=0 and the equation becomes;
Energy of stationary mass = m c2
If v is low compared to c the equation becomes:
E = m c2 + p2 /2m + ...
Which is roughly:
E = m c2 + 1/2 m v2
Energy = rest mass + kinetic energy
Kinetic Energy
The Kinetic Energy in the frame of reference of the mass = 0.5 m v2
Mass = gravitational charge
Potential Energy
Potential Energy is a form of energy that's stored in an object by virtue of the object being under the influence of some force.
Relativistic effects
General Relativity (GR) predicts that clocks in a stronger gravitational field will tick at a slower rate. Special Relativity (SR) predicts that moving clocks will appear to tick slower than non-moving ones. Remarkably, these two effects cancel each other for clocks located at sea level anywhere on Earth. So if a hypothetical clock at Earths north or south pole is used as a reference, a clock at Earths equator would tick slower because of its relative speed due to Earths spin, but faster because of its greater distance from Earths center of mass due to the flattening of the Earth. Because Earths spin rate determines its shape, these two effects are not independent, and it is therefore not entirely coincidental that the effects exactly cancel. The cancellation is not general, however. Clocks at any altitude above sea level do tick faster than clocks at sea level; and clocks on rocket sleds do tick slower than stationary clocks.
For GPS satellites, GR predicts that the atomic clocks at GPS orbital altitudes will tick faster by about 45,900 ns/day because they are in a weaker gravitational field than atomic clocks on Earth's surface. Special Relativity (SR) predicts that atomic clocks moving at GPS orbital speeds will tick slower by about 7,200 ns/day than stationary ground clocks.
The Twin Paradox
The twin paradox involves two identical clocks, one of which departs and the later returns, having traveled some distance in the intervening time at great speed. The clock which went on the voyage evidences less elapsed time. To make the problem more concrete, imagine two twins, Dick and Jane, each 20 years old. Dick departs on a space voyage, traveling at 0.8 c, to a star 20 light years away. When Dick returns, he is 50 years old, while Jane is 70 years old.
Exercise 1.12
Discuss this paradox.
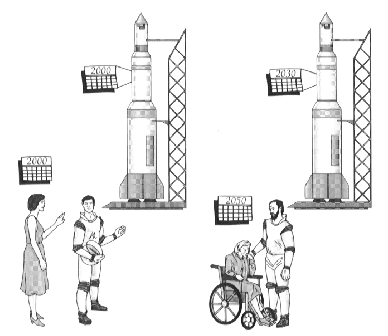
Figure 8: An astronaut who returns from space evidences the time dilation by his/her slower ageing.
- Time Dilation: We consider an experiment with a light clock
as viewed from two different inertial frames. A rocket ship flies by
at speed v from left to right, as shown in Figure 2 below (and
in a computer animation).
Figure 2: Time Dilation
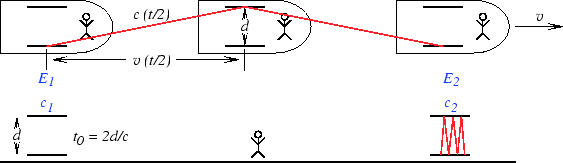
A ``light clock'' with one mirror a distance d above the other is in the rocket ship. In the rocket ship's frame the round trip time for light to go from the bottom mirror, bounce off the top mirror and return the bottom mirror is t0 = 2d /c. From the ground frame (shown in Figure 2) it takes longer for the light to make the round trip, because it has further to travel (certainly much further than 2d in Fig. 2). Thus, the person on the ground (who may have his own identical light clock) measures a longer time (than t0) for the round trip, and therefore determines that the rocket ship clock is running to slow. We conclude that moving clocks advance more slowly than stationary clocks.
This is somewhat paradoxical because, by a reciprocal argument, we would conclude that the person in the rocket ship determines that the clock on the earth is too slow! How can each person think that the other person's clock is too slow? (This question is related to the famous ``twin paradox'', which will be discussed later.) To answer this question, one needs to realize that the stationary observer (say the one one the ground) needs two synchronized clocks at separate places to compare time with the moving observer (a ground clock and the rocket clock have to be at the same place to be directly compared). The ``moving observer'' (rocket ship) will claim that the ground observer's two clocks are not properly synchronized (remember discussion of simultaneity). This is the moving observer's explanation as to why the ground observer ``thinks'' the moving observer's clock is too slow. It is ``really'' the ground clocks that are too slow (according to the moving observer). We'll discuss this more below when we discuss the famous ``twin paradox''.
Calculation of the time dilation effect:
Period of stationary light-clock: The distance the light travels is 2d for a round trip, and since the speed of light is c the time for a round trip is t0 = 2d /c.Period of moving light-clock: We compute the time t/2 for the moving clock. From the figure, we see that in time t/2 the rocket has moved a distance v(t/2), and the light pulse has moved a distance c(t/2). Using the Pythagorean Theorem, we can relate these distances to the distance d = ct0/2. We find:
c2 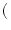 t/2
t/2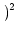 - v2
- v2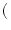 t/2
t/2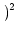
= d2 = c2 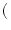 t0/2
t0/2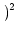
(t/2)2 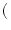 1
- (v/c)2
1
- (v/c)2![$\displaystyle \left.\vphantom{1-(v/c)^2}\right]$](../PU/t_img58.png)
= (t0/2)2 t 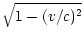
= t0 t = 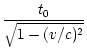 ,
,(1) This last equation relates time t for the moving clock to advance one period (round trip of light) to the time t0 for the stationary clock to advance one period. We see that t > t0, which means that the period of the moving clock is greater than the period of the stationary clock, or in other words, ``moving clocks advance more slowly''.
Concept of proper time: Another way to say that ``moving clocks advance more slowly'' is to note that the time interval between the two events:
 rocket
ship at left
rocket
ship at left and
and
 rocket
ship at right
rocket
ship at right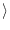 (events E1 and E2 in the figure)
is equal to
t0 = 2d /c as measured by the rocket clock,
and equal to
t = t0/
(events E1 and E2 in the figure)
is equal to
t0 = 2d /c as measured by the rocket clock,
and equal to
t = t0/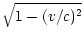 > t0 as measured by the clocks on the
ground. Note that for the rocket clock, these two events are in the
same place. The proper time between two events is the amount of
time between those events as measured by an inertial reference frame
in which those events occur at the same place. For the two events
in our example the proper time interval is t0. The
proper time interval between two events is always smaller than the
time interval as measured in a reference frame where the two events
are not at the same place.
> t0 as measured by the clocks on the
ground. Note that for the rocket clock, these two events are in the
same place. The proper time between two events is the amount of
time between those events as measured by an inertial reference frame
in which those events occur at the same place. For the two events
in our example the proper time interval is t0. The
proper time interval between two events is always smaller than the
time interval as measured in a reference frame where the two events
are not at the same place.
Time must be relative
If the speed of light is the same even if the light source itself is moving at some speed relative to the person doing the measuring, then how does this affect the way different observers measure time and space and combine them into spacetime?
Let's take the red and blue cars from the previous example, and let's
mount a laser on top of the blue car. We'll put a mirror on the blue car
as shown in the figures, and aim the laser at the mirror perpendicular
to the direction the blue car is travelling.
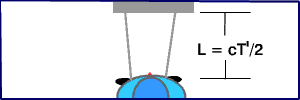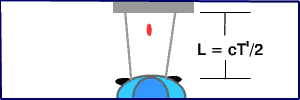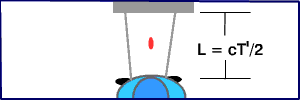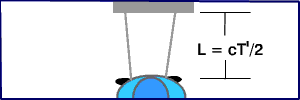 |
Here is the laser pulse viewed in the frame of reference of the blue car. |
Within the time interval T' measured by the driver of the blue car operating the laser, the laser light travels a distance 2 L from the laser to the mirror and back.
Meanwhile, the driver of the red car sees the blue car go whizzing by.
According to the red driver, the laser took a total time T to hit
the mirror and return. (She's willing to agree with the driver of the
blue car that the distance between the laser and the mirror is L,
since neither driver has any velocity in that direction.) She measures
the blue car to have travelled a distance X = U T and the laser
pulse to have travelled a total distance of 2 D = c T in time
T.
Here is the laser pulse viewed in the frame of reference of the red car. |
 |
Here is where the problem arises. Since we just deduced above that c T' = 2 L and c T = 2 D, the only way we could have T' = T would be if D = L.
Therefore, the red and blue drivers do not measure time equally..
Now how can we sort this out and find out how their measurements of time
should differ in order to account for the observed constancy of the
speed of light?
What both drivers agree on is the distance L perpendicular to the
motion of the cars. Using the Pythagorean Rule on the laser pulse's path
in space, we get
L2 + (X/2)2 = (c T/2)2 .
From the blue driver's point of view L2 = (c T'/2)2 , and putting these together and using X = U T we get: (c T')2 + (X)2 = (c T)2 or
T = T' / (1 - (U/c)2)1/2
This is stupendous! The drivers of the blue and red cars don't measure the same time for the laser to hit the mirror and come back! We are forced to conclude this if we want to be consistent with the observed constancy of the speed of light (so far) in Nature.
This has profound implications for the mathematical modelling of space and
time as observed in Nature. This means we have to expand the idea of
Euclidean analytic geometry to include the observer-dependent
relativity of measurements of time and space. This opens up a
gigantic can of mathematical worms, eventually bringing us to black
holes, wormholes and at least the abstract mathematical possibility of
time travel.
| What we've learned here is called Relativistic time dilation. The process that occurred in the blue driver's rest frame with in time T' was perceived by the red driver to have occurred in time T = T' / (1 - (U/c)2)1/2, which can be much much greater than T' if U is close to the speed of light c. |
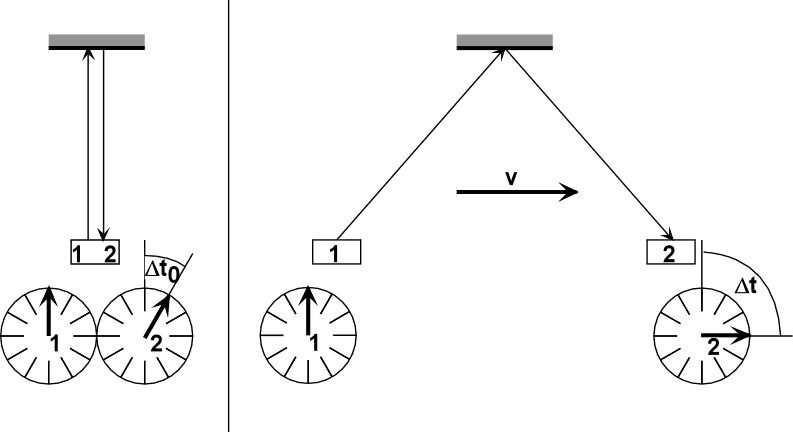
Time Dilation
Possibly the most unintuitive result
from Relativity is the idea of time dilation. In its most basic form, it
says that when an object speeds up relativistically, time will appear to
slow down for the object. Before the Special Theory, this idea had never
been considered. The idea that time was an absolute measure ruled the
thoughts of scientists until the early twentieth century. However,
Einstein proposed the idea that time was relative; it was different for
every body in the universe.
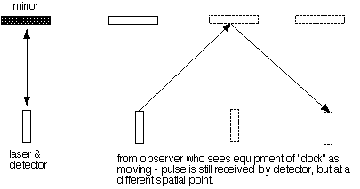
To understand why this happens, we can look at the picture to the left.
Let's say we are in a train and had a laser shining off of a mirror and
reflecting back. The light would travel a certain distance. Now, let's
say the train is moving fast compared to the ground. Someone looking
into the train from the ground would see the light travel similar to the
second diagram; however someone inside the train sees the light travel
similar to the first diagram. The distance the light travels in the
perspective of someone on the ground is greater than the distance it
travels from the perspective of someone in the train. Because we know
that light always travels at a constant speed, c, so the light cannot be
speeding up or slowing down. So how could the light travel two distances
in the same amount of time?
The answer is time dilation. When the train is moving fast, time slows
down for it relative to someone on the ground. Likewise, for the person
in the train, the ground is moving fast relative to the train. Therefore,
with respect to someone on the ground, time is moving slower for the
person in the train. This is what allows the light to appear to travel
two different distances in the same interval of time, relative to a
single reference point, of course.
To calculate how slow time is going for some other inertial frame, we
must make the calculation below. In the final equation below, To is the
"proper time" or the time that the moving body reads. This is multiplied
by gamma, which is defined as one over the square root of one minus the
square of the velocity another inertial reference frame is reading the
body divided by the speed of light squared.

Note that gamma can never reach zero. As the velocity of the body
approaches c, the time dilation grows very big; however, the velocity
can never be c! If v were equal to c, gamma would be equal to zero,
which is an undefined result.