"Understanding the Theory of Relativity"
by Ronald C. Pine

 Slow Time and Fast Time

When you're sitting in a room listening to a very boring speech or lecture, it seems to take forever, and time "drags"; when the lecture is so interesting that it all seems to take place in a matter of moments, time "flies". But we all "know" that this is only a subjective experience, that the real time measured by an objective instrument such as a clock clicks along at the same rate whether or not we are interested in what is happening.

But do we really know this? Our knowledge of the objective world must be pieced together on the basis of our subjective experiences. For all we know at the moment we become engrossed in some interesting activity, at that precise moment everything in the universe "speeds up", including the clock! Or perhaps at the precise instant that we become bored, the universe decides to "slow down" everything, including the clock. So when we look at the clock and see that an hour has passed, we conclude that an objective hour has passed, but how do we really know if it was a fast hour or a slow hour? If everything in the universe could speed up or slow down, then the clock would either speed up or slow down as well, and there would be no way to tell.

Preposterous you say. All that is needed is for two people to be in the room, one bored and the other not, and then have both see that based upon the objective clock time, one hour has passed. Case closed. As Socrates and Plato noted long ago, it is impossible for a single individual to be objective. The experiences of others and communication with others about what they experience are necessary conditions for understanding the world. Part of what we mean by "objective" knowledge is public knowledge, a knowledge established by a community of observers. Also implied is a definite state of existence independent of our observations. In the case of time, it is what it is independent of our emotional states.

But wait. Suppose someday we finally discover another intelligent form of life separated from us by a great distance. Suppose that just by chance one day their entire planet is bored and everyone on our planet is not. Where will we now look to find an objective clock? How would we know that the universe does not slow down for them and speed up for us? We could synchronize two clocks on Earth and then transport one to this distant planet. How would we know that the two clocks stay synchronized? We would assume that if nothing is physically wrong with the clocks, they would stay synchronized. But unless we have a way of directly comparing the time these clocks are measuring, we would not know whether they are still synchronized.

This example is far-fetched, but its possibility demonstrates that unless a universal standard of time measurement exists, we cannot say we know that time flows on uniformly as our common sense dictates and does not speed up or slow down. Instead we must admit that we are assuming that time behaves throughout the universe the way we experience it here on Earth. We are assuming that on some other planet "now" is the same as "now" here on Earth, that at any given moment there is a "slice of simultaneity" throughout the universe.

This assumption is, of course, rather safe and reasonable for most practical purposes on Earth. But is it true? The history of science has shown us repeatedly that we should be very careful in projecting those views of reality that are practical as real. Most of what human beings do on this Earth can be accomplished by assuming the same set of beliefs accepted in the Middle Ages. We see the Sun moving everyday and we do not feel the Earth moving. We have learned, however, that our experience on this planet encompasses but a small portion of all that exists and that the universe is not required to conform to our view of things.

Strange indeed. The fact that we have no way of knowing if the universe is slowing down or speeding up at any given moment, that we must "assume" that it is not, is a paradox. It is the kind of thinking that the average person would not take seriously. With problems like this, small wonder that few people major in philosophy at universities. History shows us, however, that great thinkers have always taken such paradoxes seriously, seeing them as nature's way of waking us up to some possible secret and revealing the fallibility of our "normal" thinking. In this chapter we will see that Albert Einstein's realization that Newtonian scientists assumed, like the rest of us, that time stays normal stimulated a great discovery.

Einstein and a Philosophical Discovery

An important assumption we make about our universe is that a clock measures time the same regardless of our perspective of it. Suppose we synchronize two clocks and separate them. Suppose one clock stays on Earth and another is taken to Mercury. How do we know that they stay synchronized? Again following Newton, we assume that time flows on objectively, everywhere being the same, and that assuming that the clocks are both working correctly, they will objectively measure this flow the same way. If the clock on Earth says 2:00, I assume that this is also the time on Mercury according to the other clock. If two full hours have passed on Earth since I last looked at the clock, I assume that exactly two full hours have passed on Mercury as well.

One of the great tasks of philosophy is to reveal the assumptions we make when we assert something to be true. Often this is very difficult precisely because it is so easy. Our assumptions are usually so obvious, so fundamentally embedded in our outlook, that we cannot recognize that we are making them. Philosophical analysis is a vital part of the scientific method. As we saw in "Philosophy and the Scientific Method", many ideas are involved in deducing possible results that can then be tested by experiment. Behind every experiment is a hypothesis set, consisting of the main hypothesis, many minor hypotheses and assumptions. This set, along with the conditions of the experiment, serves as a premise for inferring what should happen when nature is subjected to our probing. Logically, if the result of an experiment is negative, if what we expect to happen does not happen, then this proves only that at least one of the ideas of the hypothesis set must be false. Thus, it is important to identify as many as possible of the ideas that make up the premises for the predicted result.

Einstein recognized that to assume that two separated clocks stayed the same involved a philosophical bias. Why should they stay the same? If we are to be empirically honest and subject all our assumptions to tests, then we need some way to measure what time the clocks record. Because there is no big cosmic clock in the center of the universe for all to see simultaneously, the only way we can measure the time of our clocks and see if they stay synchronized is by directly comparing them, and at great distances this necessarily involves the speed of light. To be sure that a clock on Mercury is still keeping the same time as one on Earth, we must communicate with an observer by Mercury by sending an electromagnetic signal traveling at the speed of light. Also, because both planets are moving in relation to each other and because the speed of light is finite, we must take into account the speed of light and what effect, if any, the relative motion of the planets might have on this speed.

At the turn of the century when Einstein as a young man was thinking about such things, the speed of light had also become a paradox. It was known that the speed of light had a finite but very great velocity (186,000 miles per second), and it was assumed that the measurement of this velocity, like any other velocity, should change depending upon how fast the source of light is moving and in what direction. For instance, if we are on an object moving at a speed of 18 miles per second, the speed of our Earth around the Sun, and we send a signal to Mercury in the direction of the motion of the Earth around the Sun, then should not the speed of the electromagnetic signal be the regular speed of light plus the speed of our motion (total of 186,018 miles per second)?

If a train is moving at 60 miles per hour and a person on the train is walking at 3 miles per hour in the same direction as the train is moving, then that person's total speed, as measured by a stationary observer, is 63 miles per hour. The two velocities are added together. Should not light be the same?

By the turn of the century experiments showed that light did not behave the way our common sense says it should. No matter what speed or direction an object moved, a beam of light from that object was always the same--186,000 miles per second. Whether a beam of light was traveling in the direction of Earth's motion, at right angles to its motion, or in the opposite direction of its motion, the speed of the light beam was precisely the same.

The implications of this result were not easy to digest. If we could travel in a special vehicle, say at only 100 miles per second less than the speed of light (185,900 miles per second), and we turned on a flashlight and pointed it in the direction of our motion, the flashlight beam would move away from us at the regular speed of light. If we increased our speed to 185,999 miles per second, we would not gain on the beam of light. Finally, if our vehicle could reach the speed of light, the speed of our flashlight beam would still be the normal speed of light. It doesn't matter if we're holding the flashlight within the vehicle or we're watching someone holding the flashlight as they fly by, the beam travels at the speed of light in our reference frame! In the case of light the normal addition of velocities does not work; one plus one is one!

Einstein boldly accepted these paradoxes as axioms: Time must be "tested", and the speed of light is the same regardless of the speed of its source. Einstein then recognized that for science to establish universal laws of nature, laws that remain the same regardless of one's point of view, then a price had to be paid. We must accept the fact that when we test time, it will speed up or slow down relative to moving frames or reference. We must accept as commonplace that because Mercury and the Earth are moving in relation to each other, and any electromagnetic communication device will transmit a signal at the speed of light unaffected by the relative motion of the planets, the clocks on these planets will not be synchronized when they are compared.

Cosmic Trains

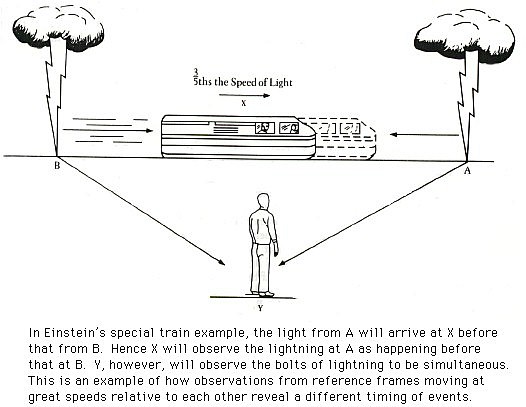
In the figure shown imagine a special train moving toward point A and away from point B. On the train is a person we will designate as X. As the train passes by, imagine a person, Y, midway between points A and B. Suppose as Y watches the train pass, at exactly the moment X is opposite Y, two bolts of lightning strike the ground from Y's point of view simultaneously at points A and B. How would X view the two bolts of lightning?

Let's imagine that the train is moving very fast, at about three-fifths the speed of light. Since X is moving toward point A at such a great speed, the light from A will be received significantly before the light from point B, which will have to catch up to the swiftly moving train. Thus, whereas from Y's point of view the two events were simultaneous (happening at the same time), from X's point of view they were not simultaneous at all. The bolt of lightning struck A before B. Who is right?

It is tempting to respond immediately that Y is right because X is moving. It is comfortable to think that Y's reference frame is the right place from which to view the "actual truth of the matter". Because X is moving so fast, it is easy to believe that his experience is an illusion due to his motion. If X got in the "right place", if he slowed down, then both observers would see the same thing, the bolts of lightning striking the ground at the same time. But wait. Y is also moving. Y is, in fact, moving many different ways, depending upon which reference frame is adopted. If Y is close to the equator of the Earth, he is moving at about 1,000 miles per hour. From the point of view of the Sun, Y is moving at approximately 66,600 miles per hour as the Earth orbits the Sun. And from the point of view of the center of our galaxy, he is moving at a speed of over 500,000 miles per hour as the Sun orbits the galactic center. Where is the right place? Why can't X assume that Y is the one who is moving?

A Newtonian might object that X could use simple mathematics to detect his motion relative to the lightning flashes, and on this basis he could calculate the simultaneity of the flashes. In other words, perhaps X could measure the incoming speed of light from A and find that it is approaching at a speed equal to the speed of light plus X's own speed, three-fifths the speed of light. The opposite, of course, is true when X looks at light coming from point B.

Unfortunately, in the case of light, nature does not cooperate. If X had the proper equipment to measure the speed of the incoming light signals from A and B, he would find that the speeds of each beam are the same, the normal speed of light. Similarly, if Y had the proper equipment, he would also find the beams coming from A and B to have the same speed. Thus, both observers are entitled to adopt the perspective that they are at rest and the other is moving.

Einstein's solution states that we must obey the facts. The speed of light, as a law of nature, is the same everywhere for every observer, and this is true no matter how each observer is moving relative to another. Furthermore, unless we are willing to make an unwarranted metaphysical assumption, time must be tested; that there is a "right" place where time is absolute is just an assumption for which there is no evidence.

Time is very much related to our relative place in space. Our time measurements (clocks, calendars) are actually spatially "local" things. On Earth when we measure one hour, we are really measuring a portion of our space, a portion of the rotation of the Earth (approximately 15 degrees). On Mercury this convention would be inconvenient, because that planet rotates once every 59 Earth days and revolves around the Sun in 88 Earth days. The combination of these rotation and revolution periods makes one Mercury day equal to two of its years!

Einstein's theory of relativity teaches us that when we are fairly close together and moving together - when, as on Earth, the speed of our relative motions is very small in comparison to the speed of light - then time will behave itself. In our train example, if the train is moving at a normal train speed, then X also measures the bolts of lightning as simultaneous. But when astronomical objects are widely separated and move at great speeds relative to each other, time does not obey Earthly standards.

Our assumption of an absolute time, the intuitive feeling that time clicks along at a steady rate throughout the universe, that "now" on Earth is the same as "now" at all locations, is due to the fact that we normally do not move at such great speeds relative to the speed of light. These relative measurements of time show up only when relative speeds are attained appreciably close to the speed of light. This is the essence of Einstein's great discovery: partly a philosophical discovery (time must be tested) and partly an empirical discovery (the speed of light is the same in all reference frames). For the most part, the rest was logic and mathematical deduction.

It is important to understand that the relativity of time measurements is necessary to preserve the laws of nature. Although two observers will measure the temporal occurrence of events differently, from their respective reference frames they will not notice anything unusual. The theory of relativity does not prove that everything is relative. Both observers in our train example will find that the laws of nature apply normally, regardless of what they might think or wish to be true. If observer X conducted experiments in a laboratory on the train, he would obtain the same results as Y would in a laboratory located in his reference frame.

Einstein took this thought logically to its limits in his Autobiographical Notes:

After ten years of reflection such a principle resulted from a paradox. If I pursue a beam of light with a velocity equal to the speed of light, I should observe such a beam at rest. However, there seems to be no such thing [light has always been measured with a speed equal to the speed of light, regardless of the reference frame]. From the very beginning it appeared to me intuitively clear that, judged from the standpoint of such an observer, everything would have to happen according to the same laws as for an observer who, relative to the Earth, was at rest.

Time Dilation

Einstein then realized that if the laws of nature are the same from every standpoint, then for physicists to be able to continue to do physics in a universe of relative moving objects, they will need to mathematically transform how time will be viewed from different reference frames. Einstein used a mathematical equation called the Lorentz-Fitzgerald transformation. It worked perfectly. The equation is a relatively simple algebraic relationship:

In this equation, T is the time of an event in a reference frame moving at a velocity v in relation to an observer is measured by the variable T'. The c is a constant, the speed of light. Let's see how it works.

Suppose in our train example that X and Y both possessed clocks that some time ago were synchronized when the train was stationary. Y then moved at a normal speed, very slowly compared to the speed of light, to a point between A and B. Suppose at a prearranged time X departs and that for the past 15 minutes by Y's reckoning the train has left the initial starting point and been moving to the point where Y is at an average speed of three-fifths the speed of light. Y would need to be 100,440,000 miles away, and it would have taken him a little over 191 years to travel to this point at 60 miles per hour. What time will the clock of X read according to the equation? If we plug in the data,

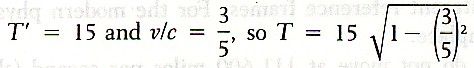
When X pases Y, X's clock will show that the train has been moving for only 12 minutes! From X's point of view, time has slowed down relative to Y. It would not just seem to slow down; real physical measurable effects would be seen when X and Y compare their clocks. If X and Y both lit cigars at the prearranged time, X would find that his cigar has burned less than Y's as they pass each other.

X will experience nothing unusual. The laws of nature are the same, including those for burning cigars. For X everything will appear normal including the movement of his clock. At no point will he see the clock suddenly slow down dramatically. It will appear normal. Likewise, Y will not suddenly see the last few minutes of his expected 15 minutes fly by like the clocks in bad aspirin commercials. It will also appear normal. Nor will either notice anything strange about the rate their cigars burn. Time slows down in reference frame X only in relation to reference frame Y. Within their respective reference frames, everything is normal.

This slowing down of time of a reference frame relative to another reference frame is called time dilation. As unbelievable as it may seem, it is one of the most accepted scientific facts of our time. It has been tested in numerous ways. Very precise atomic clocks have been synchronized and then compared again after one was flown around the world in a speeding jet. The clock on the speeding jet slowed down in relation to the clock that stayed on the ground. A similar test was conducted using one of the U. S. space shuttles with the same result.

Scientists now apply time dilation routinely in sophisticated laboratory situations. In the billion-dollar particle accelerator laboratories all over the world, physicists keep special particles of matter "alive" far longer than would normally be expected because of the time dilation effects that result by accelerating particles to speeds close to the speed of light. In this way special forms of energy can actually be stored for use in crucial experiments.

Trains, of course, do not move at three-fifths the speed of light (or 111,600 miles per second); hence, it is easy to see why time dilation effects were not noticed by common sense observations. Theoretically, spaceships could travel this fast. What kind of astronautical scenarios are possible? Suppose we know twins 20 years of age, one an astronaut who will take a space voyage that will take 20 years by Earth time. Suppose that the astronaut twin averages in his rocketship a speed of three-fifths the speed of light. How old will each twin be when they meet again 20 Earth years from now? Using the time dilation equation we have:

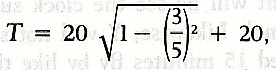
which would equal 36. The twin who stays on Earth will be, of course, 40 years of age. And yet his brother will now be 36!

This example is not science fiction. We believe, based on the best laboratory data available and other corroborating evidence, that this effect on an astronaut would indeed happen. If it is so hard to believe, it is because we have difficulty realizing that the things we take for granted on Earth do not necessarily apply throughout the cosmos. With Einstein, the cosmos is now our laboratory, and we must adjust to the conditions of this new laboratory.

Stranger still, consider this scenario. The star Vega, a star very much like our Sun and a possible candidate for a planetary system, is approximately 32 light years away. Suppose in the near future a 30-year-old mother, who has a 5-year-old son, went on a space voyage to explore this star, averaging the colossal speed of 99.5 percent the speed of light. At such a speed, it would take her about 64 years Earth time to make the trip. When she returns, her son, who remained on Earth, would be into his 69th year. Both would be in for a great shock. The 69-year-old son would embrace his long-awaited 36-year-old mother! Their personal histories would have seemed to be normal in all other respects, but it would now be clear that travelling at great speed slows our histories down from one point of view and allows us to speed to the future from another. If such a voyage were taken, the mother astronaut, if she left in the year 1990, could get to the year 2054 in a little over 6 years.

An event requiring only 6 years for the mother would require 64 years for the son. In our train example, an event that happened before another event for one observer (lightning striking point A before point B for the observer X on the train) happened at the same time for another observer (the stationary observer, Y). If would also be possible then for another observer moving in the opposite direction of reference frame X at a great speed to record the lightning striking at point B first. Thus, one person's past could be another's future. Would it then be possible for the mother to return at an age before her son was born?

Not according to Einstein's theory, not if the speed of light is a law of nature. Because the speed of light is an absolute that cannot be exceeded, causal connections, such as mothers' causing the birth of babies, are preserved in their normal sequences. According to Einstein's theory, the measurement of "before" and "after" may involve a wide latitude, but the order of events will not be changed. The time between the mother's "before" and "after" of her space voayge is much shorter than that experienced by her son, but both would experience her leaving before she came back.

If and only if the speed of light can be exceeded will the sequencing of causal events be changed, and it is a basic consequence of Einstein's theory that the speed of light cannot be exceeded. According to his theory, it would take an infinite amount of energy to accelerate any object (even an electron) up to the speed of light and thus require more than an infinite amount of energy to exceed the speed of light. Note, however, that the speed of light would only need to be exceeded by 0.004358 percent for the mother, if she left on the day of her 30th birthday, to return on the beginning of the second day after her 24th birthday, at least one year before her son was born and a few months before the conception! What would happen if she were then involved in a fatal car accident?

Epistemological Implications

The epistemological implications of relativity theory are very significant. The role of the observer is much different from that of Newtonian science. In Newtonian science the variety of perspectives of human observation, and the observer himself, could be ignored, excused as irrelevant to our descriptions of the real world. The different results of observation due to different reference frames were considered to be simply practical inconveniences that could be reconciled by Galilean transformations. But in relativity theory, the observer is intimately involved in scientific measurement, and what is measured can be different depending on one's reference frame. Our knowledge of the world must unfold from empirical measurement of it. In the destruction of absolute space and time, Einstein showed that an honest empiricism must involve the observer, and that to some extent what is real does depend on us.

However, Einstein did not think he had proved that each observer is involved in creating reality. Einstein did not doubt the existence of an independent physical reality, or whether there must be some absolutes. In fact, the intent of his theory was to preserve absolutes, the laws of nature. Einstein thought the secret structure of nature resembled the internal mechanism of a special, mysterious, cosmic clock. We are forever limited to seeing the outside motions of the hands and can only submit hypotheses about how the internalmechanism produces the movements of the hands. But limited as we are, we can judge which hypotheses are better on the basis of which ones predict best the motions that we observe.

Einstein's basic insight concerning space and time served as only the first premises in the development of the many marvels of 20th-century physics. From these insights, known as the Special Theory, Einstein later showed in his General Theory that if his ideas on space and time were true, many hard-to-believe things must be true of our cosmic laboratory, as one sees in the study of quantum mechanics, for example.

Although Einstein did not believe that his theory proved that human observers create reality, he did show that the observer beings to play a crucial role in what is real and that Copernicanism had gone too far, or in a sense not far enough. The completion of the Copernican revolution in Newtonianism fulfilled the dream of a unified science; the laws that governed terrestrial motion were the same that governed celestial motion. This enabled other ideas to get in through the back door: Our common-sense notions of space and time, which worked so well on Earth, were assumed to be true for the entire universe. This assumption was so pervasive that it was not recognized as an assumption, especially given the success of Newtonian physics. In revealing this assumption as a metaphysical postulate and not an empirical fact Einstein showed that what was masquerading as a removal of humankind and subjectivism from science was actually a projection of a subjective human point of view, which is close enough to the truth at a certain level to enable us to fail to recognize it as a human point of view.

Think about this last statement carefully. Think about it for a long time. It is crucial for understanding the paradox of 20th-century science. Our intuitive feeling that there must be an objective time and space is actually just a projection of a human point of view. We can accurately calculate the motions of the planets within our solar system using a perspective of uniform space and uniform time. We can send our robot spacecraft to the outer planets and beyond. Our equations work. But that they work in this domain does not prove that the concepts we assume in applying the equations are valid for other domains. As we will see in our discussion next of quantum physics, this realization is only the beginning. As in a long romantic relationship, one's partner may eventually reveal a totally unexpected set of personality traits. After Newton we thought we knew what the universe was like. Little did we suspect the unnerving surprises it had in store for us in the 20th century...

Concept Summary

Newtonianism forces us to assume that space and time are absolute--that each event has one spatial and temporal location. In this chapter we have seen that part of Einstein's discovery involved a philosophical insight, that Newtonianism involved this assumption, and that scientific knowledge of space and time would require empirical tests. It seems paradoxical that we cannot safely assume and know upon reflection alone that time flows on uniformly throughout the universe as our common sense dictates. It never occurs to me that if I leave my home at 8:00 and arrive at my office at 8:30 that I am assuming that it is not then 9:00 at home.

Einstein recognized that one could not assume that two widely separated, initially synchronized clocks kept the same time. He recognized that time must be tested by measuring and comparing what time each clock records. To compare such clocks, one must take into account the speed of light and the relative motions of the reference frames of each clock. Einstein showed that when this is actually done, because the speed of light had been discovered to be the same regardless of its direction and the speed of its source, our intuitive sense that time is something that just clicks along independently of moving objects will be violated when we compare initially synchronized clocks. Simultaneity is relative to a reference frame, and time dilation, the slowing of time relative to another reference frame, is a fact of life. If my home and office were separated by many light years, not only could I not assume the times to be the same, but my home (depending on the distance and the speed of my travel) could be many thousands of years in the future when I arrive at work.

Although the success of Einstein's theories does not imply that everything is relative or that scientists create reality, it does show that an honest empiricism, one that tests fundamental assumptions, has brought the observer into 20th century physics. To some extent what is real does depend on us. Einstein's theories also set the stage for the great paradox of 20th century science. We must be careful about what we assume is objective; what seems to be obviously an objective property of reality (say, what time it is) may be a subjective projection of a merely human point of view, one applicable to only a limited range of experience (to velocities far less than the speed of light). Nothing seems to me more certainly objective and independent of my wishes than the thought that it is the same time at my home now as at my office regardless of the distance between the two, but Einstein has shown that reality need not obey my sense of certainty or the workings of the human mind.

------------------------------------------------

The Theory of Relativity:

The photoelectric effect basically proves the duality of light:

Light is a Wave

Light is a Particle (a photon)

When light strikes a piece of metal, like the image above, the photon from the light are of a high enough energy to eject electrons on the surface of the metal.

Its easy to remember that nothing travels faster than light, but there are other things to conceder:

Light in a Vacuum travels at 299,792.458 m/s

Light travels slower than that depending on the medium - i.e. the refractive nature of the medium

Why is this? Because light is also a particle and like all other particles, they interact. The limit on the speed of light is because light is also a particle. This may not make sense, but Relativity helps to explain this.
 

The Theory of Relativity:

In 1905, Albert Einstein published his Special Theory of Relativity and in 1916, his General Theory of Relativity was released. While Einstein is best known for his theories, the ideas of Relativity really began with Galileo Galilei. This "Galilean Relativity" was called by Einstein as common sense (and not in the way as an insult, more like a base of understanding). An example of this "common sense" is the train and baby analogy:

A train is moving at 'x' velocity past a train station. On the train, a baby is crawling in the direction of the train. Observers in the train see the baby crawling at 'y' speed. As the train passes the train station, observers standing still see the baby moving at the speed of x + y.

The idea of Relativity is that to any observer, the speed of an object depends on their time frame. I may see my friend throw a football and I can see the ball move at a particular speed. A plane flying overhead either in the direction or against the direction of the moving football will witness a different speed. One is not more correct than another, just another frame of reference. This is the essence of Relativity.

What make Einstein's theory of Relativity special is that it addresses objects that are traveling at high speeds -  like the speed of light. Astronomers often use the term "relativistic" when describing or studying a certain phenomenon. This term that can have two meanings:

• The object or phenomenon is moving near or at the speed of light

• The speed of the phenomenon will change depending on the frame of reference

Discussing the Theory of Relativity will take far too many pages - and I am by no means an expert. Two very good books for additional reading are:

Einstein, Albert. Relativity. The Special and the General Theory. Crown Trade Paperbacks. New York, 1961.

Sartori, Leo. Understanding Relativity. A Simplified Approach to Einstein's Theories. University of California Press. Berkeley, 1996.

A basic summary of Einstein's works:

• The laws of physics are the same in any reference frame

• The speed  of light is the same for all observers

• "A moving clock runs slow" - in other words, time slows down to the outside observer

• The length of a reference object is shorter to the outside observer

Keep in mind that these changes in time and length are very minute, and any noticeable changes will only occur as that reference frame travels closer to the speed of light.
Our nearest star is Proxima Centauri Alpha (Alpha Centauri) at 4.3 light years away. That means if I had a light powerful enough to reach this star, it will take 4.3 light years to get there. If I were to get on a space ship and fly to Alpha Centauri, I am now in a different reference frame with my own clock - as I reach velocities near the speed of light, I notice that it does not take 4.3 years to reach my target, it is actually less.
 

The twin paradox is a famous example of Relativity in action:

There are two brothers that are twins. At the age of 30, one of the twins takes a cruise on a rocket that is traveling 99% the speed of light. He does this for a straight year, returning to Earth on his 31st birthday. To his surprise, his brother is 7 years older.

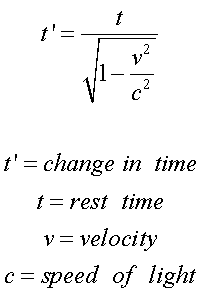
The formula above is the formula to use if you want to determine your own reference frame.

While all of this talk of slowing time sounds fantastic - and hypothesis' abound such as travel beyond the speed of  light for  time travel - but there are two boundaries to overcome also based on Relativity:

• Nothing can travel faster than the speed of light

• The mass of an object increases as the velocity towards the speed of light is reached

The second statement means  this: if I were traveling at the speed of light, or pretty close to it (i.e. 98 to 99%), my mass would become infinite. The energy required to move infinite mass would also be infinite.
Some rules of physics still apply regardless of the frame of reference.
To end this section, I will regale a joke/riddle I heard as a child:
If you are traveling in a car at the speed of light, and you turn on your headlights, do they work?
The answer to this question is yes - because the speed of light is the same for ALL observers, including those traveling at the speed of light.
 

Time

Consider the situation shown in figure  h. Aboard a rocket ship we have a tube with mirrors at the ends. If we let off a flash of light at the bottom of the tube, it will be reflected back and forth between the top and bottom. It can be used as a clock; by counting the number of times the light goes back and forth we get an indication of how much time has passed: up-down up-down, tick-tock tick-tock. (This may not seem very practical, but a real atomic clock does work on essentially the same principle.) Now imagine that the rocket is cruising at a significant fraction of the speed of light relative to the earth. Motion is relative, so for a person inside the rocket, h/1, there is no detectable change in the behavior of the clock, just as a person on a jet plane can toss a ball up and down without noticing anything unusual. But to an observer in the earth's frame of reference, the light appears to take a zigzag path through space, h/2, increasing the distance the light has to travel.

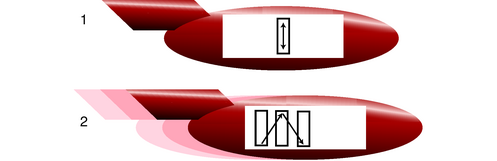
h / A light beam bounces between two mirrors in a spaceship.

If we didn't believe in the principle of relativity, we could say that the light just goes faster according to the earthbound observer. Indeed, this would be correct if the speeds were much less than the speed of light, and if the thing traveling back and forth was, say, a ping-pong ball. But according to the principle of relativity, the speed of light must be the same in both frames of reference. We are forced to conclude that time is distorted, and the light-clock appears to run more slowly than normal as seen by the earthbound observer. In general, a clock appears to run most quickly for observers who are in the same state of motion as the clock, and runs more slowly as perceived by observers who are moving relative to the clock.

We can easily calculate the size of this time-distortion effect. In the frame of reference shown in figure h/1, moving with the spaceship, let t be the time required for the beam of light to move from the bottom to the top. An observer on the earth, who sees the situation shown in figure h/2, disagrees, and says this motion took a longer time T (a bigger letter for the bigger time). Let v be the velocity of the spaceship relative to the earth. In frame 2, the light beam travels along the hypotenuse of a right triangle, figure i, whose base has length

Observers in the two frames of reference agree on the vertical distance traveled by the beam, i.e., the height of the triangle perceived in frame 2, and an observer in frame 1 says that this height is the distance covered by a light beam in time t, so the height is

where c is the speed of light. The hypotenuse of this triangle is the distance the light travels in frame 2,

Using the Pythagorean theorem, we can relate these three quantities,

and solving for T, we find

The amount of distortion is given by the factor , and this quantity appears so often that we give it a special name, γ (Greek letter gamma),

We are used to thinking of time as absolute and universal, so it is disturbing to find that it can flow at a different rate for observers in different frames of reference. But consider the behavior of the γ factor shown in figure j. The graph is extremely flat at low speeds, and even at 20% of the speed of light, it is difficult to see anything happening to γ. In everyday life, we never experience speeds that are more than a tiny fraction of the speed of light, so this strange strange relativistic effect involving time is extremely small. This makes sense: Newton's laws have already been thoroughly tested by experiments at such speeds, so a new theory like relativity must agree with the old one in their realm of common applicability. This requirement of backwards-compatibility is known as the correspondence principle.

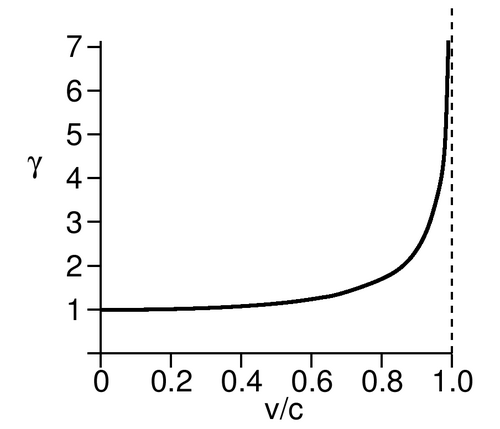
j / The behavior of the γ factor.

Space

The speed of light is supposed to be the same in all frames of reference, and a speed is a distance divided by a time. We can't change time without changing distance, since then the speed couldn't come out the same. If time is distorted by a factor of γ, then lengths must also be distorted according to the same ratio. An object in motion appears longest to someone who is at rest with respect to it, and is shortened along the direction of motion as seen by other observers.

No simultaneity

Part of the concept of absolute time was the assumption that it was valid to say things like, “I wonder what my uncle in Beijing is doing right now.” In the nonrelativistic world-view, clocks in Los Angeles and Beijing could be synchronized and stay synchronized, so we could unambiguously define the concept of things happening simultaneously in different places. It is easy to find examples, however, where events that seem to be simultaneous in one frame of reference are not simultaneous in another frame. In figure k, a flash of light is set off in the center of the rocket's cargo hold. According to a passenger on the rocket, the parts of the light traveling forward and backward have equal distances to travel to reach the front and back walls, so they get there simultaneously. But an outside observer who sees the rocket cruising by at high speed will see the flash hit the back wall first, because the wall is rushing up to meet it, and the forward-going part of the flash hit the front wall later, because the wall was running away from it.

k / Different observers don't agree that the flashes of light hit the front and back of the ship simultaneously.

We conclude that simultaneity is not a well-defined concept. This idea may be easier to accept if we compare time with space. Even in plain old Galilean relativity, points in space have no identity of their own: you may think that two events happened at the same point in space, but anyone else in a differently moving frame of reference says they happened at different points in space. For instance, suppose you tap your knuckles on your desk right now, count to five, and then do it again. In your frame of reference, the taps happened at the same location in space, but according to an observer on Mars, your desk was on the surface of a planet hurtling through space at high speed, and the second tap was hundreds of kilometers away from the first.

Relativity says that time is the same way --- both simultaneity and “simulplaceity” are meaningless concepts. Only when the relative velocity of two frames is small compared to the speed of light will observers in those frames agree on the simultaneity of events.

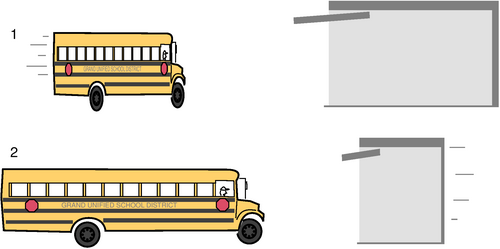
l / In the garage's frame of reference, 1, the bus is moving, and can fit in the garage. In the bus's frame of reference, the garage is moving, and can't hold the bus.

The garage paradox

One of the most famous of all the so-called relativity paradoxes has to do with our incorrect feeling that simultaneity is well defined. The idea is that one could take a schoolbus and drive it at relativistic speeds into a garage of ordinary size, in which it normally would not fit. Because of the length contraction, the bus would supposedly fit in the garage. The paradox arises when we shut the door and then quickly slam on the brakes of the bus. An observer in the garage's frame of reference will claim that the bus fit in the garage because of its contracted length. The driver, however, will perceive the garage as being contracted and thus even less able to contain the bus. The paradox is resolved when we recognize that the concept of fitting the bus in the garage “all at once” contains a hidden assumption, the assumption that it makes sense to ask whether the front and back of the bus can simultaneously be in the garage. Observers in different frames of reference moving at high relative speeds do not necessarily agree on whether things happen simultaneously. The person in the garage's frame can shut the door at an instant he perceives to be simultaneous with the front bumper's arrival at the back wall of the garage, but the driver would not agree about the simultaneity of these two events, and would perceive the door as having shut long after she plowed through the back wall.

Applications

Nothing can go faster than the speed of light.

What happens if we want to send a rocket ship off at, say, twice the speed of light, v=2c? Then γ will be . But your math teacher has always cautioned you about the severe penalties for taking the square root of a negative number. The result would be physically meaningless, so we conclude that no object can travel faster than the speed of light. Even travel exactly at the speed of light appears to be ruled out for material objects, since γ would then be infinite.

Einstein had therefore found a solution to his original paradox about riding on a motorcycle alongside a beam of light. The paradox is resolved because it is impossible for the motorcycle to travel at the speed of light.

Most people, when told that nothing can go faster than the speed of light, immediately begin to imagine methods of violating the rule. For instance, it would seem that by applying a constant force to an object for a long time, we could give it a constant acceleration, which would eventually make it go faster than the speed of light. We'll take up these issues in section 1.3.

Cosmic-ray muons

A classic experiment to demonstrate time distortion uses observations of cosmic rays. Cosmic rays are protons and other atomic nuclei from outer space. When a cosmic ray happens to come the way of our planet, the first earth-matter it encounters is an air molecule in the upper atmosphere. This collision then creates a shower of particles that cascade downward and can often be detected at the earth's surface. One of the more exotic particles created in these cosmic ray showers is the muon (named after the Greek letter mu, μ). The reason muons are not a normal part of our environment is that a muon is radioactive, lasting only 2.2 microseconds on the average before changing itself into an electron and two neutrinos. A muon can therefore be used as a sort of clock, albeit a self-destructing and somewhat random one! Figures m and n show the average rate at which a sample of muons decays, first for muons created at rest and then for high-velocity muons created in cosmic-ray showers. The second graph is found experimentally to be stretched out by a factor of about ten, which matches well with the prediction of relativity theory:

Since a muon takes many microseconds to pass through the atmosphere, the result is a marked increase in the number of muons that reach the surface.

Space and Time

We've arrived at a paradox. The rule that we've described for translating velocities in one reference frame to another frame, "common sense relativity", is not consistent with Einstein's second postulate that the speed of light is the same in all inertial reference frames. There are only two ways for this to be true. Either distances are different from one inertial frame to the next, time is different from one frame to the next.

In fact, both of these things are true. The first effect we call "length contraction" while we call the second effect "time dilation".

Length Contraction

Length contraction is sometimes referred to as Lorentz contraction, or Lorentz-FitzGerald contraction. The mathematical formula for describing it was arrived at by Lorentz and Fitzgerald before Einstein, but it took Einstein to fully understand its significance and embed it into a complete theory of relativity. The principle is this:

The length of an object in a frame in which it is moving is shorter than the length of the same object in a frame in which it's at rest.

An illustration may make this less confusing:

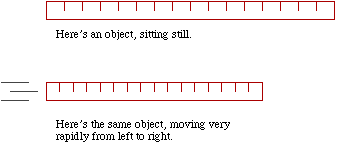
In the top illustration, we view the ruler in the reference frame in which it is at rest. The length of an object in its own rest frame is called its "proper length". The proper length of a yardstick is one yard. In the lower illustration, the ruler is moving. In longer, more complicated words, we view the ruler from a reference frame in which the ruler is moving. The principle of length contraction says that the ruler is shorter in this frame.

This contraction is not an illusion. Any accurate experiment we might devise to measure the length of this ruler as it moves past us will reveal a shorter length than the object has at rest. The ruler doesn't just look shorter when it's moving. It is shorter! However, it's only shorter along the direction it's moving. In the second illustration above, the ruler is moving horizontally, and it's shortened horizontally. You might notice that vertically, it's the same size in both illustrations.

Time Dilation

The effect called time dilation is similar to length contraction, and it works like this:

The time between two events, in a frame in which those events occur at different locations, is longer than the time between those same two events, in a frame in which those events occur at the same location.

This one's a bit more confusing. Again, I'll try to illustrate.

Either of these clocks can be used to measure the time it takes the first clock to travel from point A to point B. However, the two clocks will give different results. We can think of it this way. The two events we're talking about are the clock leaving point A, and the clock arriving at point B. In our frame, these events take place at different points (A and B). However, let's look at this from the reference frame of the upper clock. From this point of view, the upper clock is at rest (anything is at rest from its own point of view) and the bar containing the points A and B is rushing by from right to left. So the two events, the departure of point A and the arrival of point B both take place at the same point: the point where the clock sits! (The time measured by the upper clock is called the "proper time".) By the principle stated above, the lower clock will register a longer time than the upper clock as the upper clock moves from point A to point B.

A simpler, less precise way of stating this principle is:

A moving clock runs more slowly than a stationary clock.

The most famous hypothetical illustration of time dilation is usually called the twin paradox. Suppose there are twins named Harry and Mary. Mary takes off in a spaceship which travels very fast away from earth (it must travel close to the speed of light for the effect to be noticeable) and returns very fast. We can think of the human body as a clock which records the passage of time by aging. Since Mary is moving very fast, her clock runs slowly, compared to Harry's clock. As a result, when Mary arrives back at earth she has aged less than Harry has. How much less depends on how far she has traveled, and how fast.

Time dilation is not just a crazy idea. It has been verified experimentally. Perhaps the best example of this involves a subatomic particle called a muon. The muon is an unstable particle, which means that shortly after one is created, it decays into lighter particles. How long a muon takes to decay has been measured very precisely. Anyway, it's been observed that a muon moving close to the speed of light lives longer than a muon that's at rest or moving slowly. This is a relativistic effect. From the point of view of the moving muon it doesn't live any longer, because from its point of view, it's at rest. It's only in the frame of the laboratory through which the muon moves that the lifetime is lengthened, or "dilated".

I should add at this point that there are many, many other tests of the ideas we've seen so far, and of the other implications of relativity that we'll see later. My point is, even though it's still often referred to as the "theory" of relativity, don't think that this implies that special relativity is in doubt. It's very well established.

Relativity Before Einstein

Here we have a railroad car. 

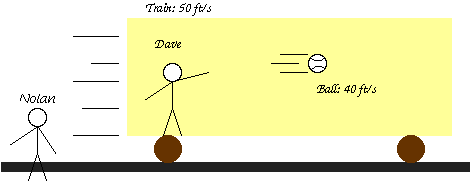
Let's suppose for the moment that the railroad car is not moving. Dave (on the train) throws a baseball to the right at 40 feet per second (ft/s). This means that after one second, the ball is 40 feet in front of him. (We'll ignore gravity, and assume the car is at least 41 feet long..)

Now we put the train in motion. The train is moving in a straight, level line at a steady 50 ft/s. Dave goes through the exact same motion that would produce a 40 ft/s throw in the stationary train. The moving train is an inertial frame of reference, so Einstein's first postulate says that life on the moving train is just like life on the train at rest. Specifically, if Dave goes through exactly the same motion, the ball will be 40 feet in front of him after one second, whether the train is moving or not.

Next, we'll consider the flight of the ball from Nolan's point of view. Suppose that at the instant Dave throws the ball, Dave and Nolan are side by side. Since the train is moving at 50 ft/s, after one second Dave is 50 feet ahead of Nolan. And of course, the ball is 40 feet in front of Dave. So after one second, the ball is 90 feet (40 + 50) ahead of Nolan.

In other words, from Nolan's point of view the ball is traveling 90 ft/s.

To summarize,

• The velocity of the ball relative to Dave is 40 ft/s.
• The velocity of Dave relative to Nolan is 50 ft/s.
• So the velocity of the ball relative to Nolan is 90 ft/s.

(Are you starting to see why this is called "relativity"?)

Mathematically, we write it this way:

The three relative velocities in this equation are just those listed immediately above. (You can match them up from the subscripts for "ball", "Dave", and "Nolan".) The basic idea is that to get the velocity of the ball in a second reference frame (Nolan's), we take the velocity of the ball in the first reference frame (Dave's) and we add or subtract (depending on the directions of things) the relative velocities of the two frames. This insight is often attributed to Galileo, and is sometimes referred to as "Galilean relativity". I sometimes refer to it as "common sense relativity", since we were able to sit down and reason it out just using common sense. (This is not to belittle the achievements of Galileo Galilei, who was one of the finest scientific minds ever seen.) In fact, the logic by which we arrived at this equation is so simple and so reasonable, that it's hard to imagine that it could be wrong.

The Train Revisited

To see the impact of Einstein's second postulate, let's go back and look at our train illustration again. This time, however, we'll take a much faster train, and instead of a baseball, our "thrown object" will be light. If thinking of light as an "object" bothers you, just remember that light travels in the form of small particles called "photons". (Maybe quantum physics will be my next project. :-) Anyway, Dave shines his flashlight forward in the train, hurling photons forward with a speed of about 300,000,000 meters per second (m/s) as predicted by Maxwell's equations and verified experimentally. The train moves at 100,000,000 m/s, as Nolan looks on.

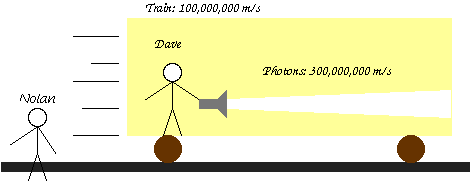
Now we've already been through this situation. The photons move at a speed of 300,000,000 m/s relative to Dave, while Dave moves at a speed of 100,000,000 m/s relative to Nolan. So to calculate the speed of the photons relative to Nolan, we have only to add these numbers. The speed of the photons relative to Nolan is 400,000,000 m/s.

And there lies the problem. This directly contradicts Einstein's second postulate, which says that the speed of light in Nolan's frame must be the same as in Dave's frame: 300,000,000 m/s. So which is wrong: the "common sense" (Galilean) relativity that we deduced a couple pages ago, or Einstein's postulates? Well, scientific experiments (many scientific experiments) back up Einstein, so let's assume he's right and let's try to figure out what could be wrong with common sense relativity.

Remember that the decision to add the velocities came fairly simply. After one second, a photon has moved 300,000,000 meters ahead of Dave, and Dave has moved 100,000,000 meters ahead of Nolan. So the photon must move 400,000,000 meters ahead of Nolan during that second. There are only two ways that this can possibly not be 400,000,000 m/s:

1. The 300,000,000 meters, relative to Dave, is not really 300,000,000 meters relative to Nolan.
2. One second for Dave is not one second for Nolan.

As strange as each of these possibilities may sound, they are, in fact, both correct.

Time Dilation and Length Contraction

 

Time Dilation

The most important and famous results in Special Relativity are that of time dilation and length contraction. Here we will proceed by deriving time dilation and then deducing length contraction from it. It is important to note that we could do it the other way: that is, by beginning with length contraction.

 

Figure 2.1: Time dilation on a moving train.

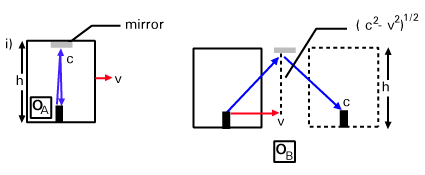
Consider the situations shown in the diagram. In i) we have the first observer O_A at rest with respect to a moving train, which has velocity v to the right with respect to the ground. The carriage has a height h and has a mirror on the roof. O_A designs a clock that measures the passage of time by firing a laser placed on the floor at the roof of the carriage and registering the time taken for it to hit the floor of the carriage again (after bouncing off the mirror on the roof). In O_A's frame the time taken for the laser light to reach is roof is just h/c and the roundtrip time is:

tA =

In the frame of an observer on the ground, call her O_B, the train is moving with speed v (see ii) in Figure 2.1). The light then follows a diagonal path as shown, but still with speed c. Let us calculate the length of the upward path: we can construct a right-triangle of velocity vectors since we know the horizontal speed as v and the diagonal speed as c. Using the Pythagorean Theorem we can conclude that the vertical component of the velocity is as shown on the diagram. Thus the ratio the diagonal (hypotenuse) to the vertical is . But we know that the vertical of the right-triangle of lengths is h, so the hypotenuse, must have length . This is the length of the upward path. Thus the overall length of the path taken by the light in O_B's frame is . It traverses this path at speed c, so the time taken is:

tB =  =

Clearly the times measured are different for the two observers. The ratio of the two times is defined as γ, which is a quantity that will become ubiquitous in Special Relativity.

= γ≡

All this might seem innocuous enough. So, you might say, take the laser away and what is the problem? But time dilation runs deeper than this. Imagine O_A waves to O_B every time the laser completes a cycle (up and down). Thus according to O_A's clock, he waves every t_A seconds. But this is not what O_B sees. He too must see O_A waving just as the laser completes a cycle, however he has measured a longer time for the cycle, so he sees O_A waving at him every t_B seconds. The only possible explanation is that time runs slowly for O_A; all his actions will appear to O_B to be in slow motion. Even if we take the laser away, this does not affect the physics of the situation, and the result must still hold. O_A's time appears dilated to O_B. This will only be true if O_A is stationary next to the laser (that is, with respect to the train); if he is not we run into problems with simultaneity and it would not be true that O_B would see the waves coincide with the completion of a cycle.

Unfortunately, the most confusing part is yet to come. What happens if we analyze the situation from O_A's point of view: he sees O_B flying past at v in the backwards direction (say O_B has a laser on the ground reflecting from a mirror suspended above the ground at height h). The relativity principle tells us that the same reasoning must apply and thus that O_A observes O_B's clock running slowly (note that γ does not depend on the sign of v). How could this possibly be right? How can OA's clock be running slower than OB's, but OB's be running slower than OA's? This at least makes sense from the point of view of the relativity principle: we would expect from the equivalence of all frames that they should see each other in identical ways. The solution to this mini-paradox lies in the caveat we put on the above description; namely, that for t_B = γt_A to hold, O_A must be at rest in her frame. Thus the opposite, t_A = γt_B, must only hold when O_B is at rest in her frame. This means that t_B = γt_A holds when events occur in the same place in O_A frame, and t_A = γt_B holds when events occur in the same place in O_B's frame. When v 0⇒γ 1 this can never be true in both frames at once, hence only one of the relations holds true. In the last example described (O_B flying backward in O_A's frame), the events (laser fired, laser returns) do not occur at the same place in O_A's frame so the first relation we derived (t_B = γt_A) fails; t_A = γt_B is true, however.

 

Length Contraction

We will now proceed to derive length contraction given what we know about time dilation. Once again observer O_A is on a train that is moving with velocity v to the right (with respect to the ground). O_A has measured her carriage to have length l_A in her reference frame. There is a laser light on the back wall of the carriage and a mirror on the front wall, as shown in Figure 2.2.

 

Figure 2.2: Length contraction in a moving train.

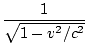O_A observes how long the laser light takes to make a roundtrip up-and-back through the carriage, bouncing back from the mirror. In O_A's frame this is simple:

tA =

Since the light traverses the length of the carriage twice at velocity c. We want to compare the length as observed by O_A to the length measured by an observer at rest on the ground (O_B). Let us call the length O_B measures for the carriage to be l_B (as far as we know so far l_B could equal l_A, but we will soon see that it does not). In O_B's frame as the light is moving towards the mirror the relative speed of the light and the train is c - v; after the light has been reflected and is moving back towards O_A, the relative speed is c + v. Thus we can calculate the total time taken for the light to go up and back as:

tB =  +  = ≡γ2

But from our analysis of time dilation above, we saw that when O_A is moving past O_B in this manner, O_A's time is dilated, that is: t_B = γt_B. Thus we can write:

γtA = γ = tB = γ2⇒ = γ⇒lB =

Note that γ is always greater than one; thus O_B measures the train to be shorter than O_A does. We say that the train is length contracted for an observer on the ground.

Once again the problem seems to be that is we turn the analysis around and view it from O_A's point of view: she sees O_B flying past to the left with speed v. We can put O_B in an identical (but motionless) train and apply the same reasoning (just as we did with time dilation) and conclude that O_A measures O_B's identical carriage to be short by a factor γ. Thus each observer measures their own train to be longer than the other's. Who is right? To resolve this mini-paradox we need to be very specific about what we call 'length.' There is only one meaningful definition of length: we take object we want to measure and write down the coordinates of its ends simultaneously and take the difference. What length contraction really means then, is that if O_A compares the simultaneous coordinates of his own train to the simultaneous coordinates of O_B's train, the difference between the former is greater than the difference between the latter. Similarly, if O_B writes down the simultaneous coordinates of his own train and O_A's, he will find the difference between his own to be greater. Recall from Section 1 that observers in different frames have different notions of simultaneous. Now the 'paradox' doesn't seem so surprising at all; the times at which O_A and O_B are writing down their coordinates are completely different. A simultaneous measurement for O_A is not a simultaneous measurement for O_B, and so we would expect a disagreement as to the observers concept of length. When the ends are measured simultaneously in O_B's frame l_B = , and when events are measured simultaneously in O_A's frame l_A = . No contradiction can arise because the criterion of simultaneity cannot be met in both frames at once.

 

Be careful to note that length contraction only occurs in the direction of motion. For example if the velocity of an object is given by  = (v_x, 0, 0), length contraction will occur in the direction only. The other dimensions of the object remain the same to any inertial observer.

Sayfa başına dön

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 - Turkiye / Denizli 

Ana Sayfa / index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy) /Astronomy