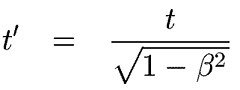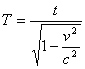- Debido a la velocidad relativa entre los relojes de la Tierra y los
que están en los satélites, los relojes de éstos irán levemente más lentos
que los de la Tierra (efecto previsto por la Relatividad Especial).
- En los satélites la gravedad es más tenue que en la superficie de la
Tierra, por lo que sus relojes irán levemente más rápido que los de la
Tierra (efecto previsto por la Relatividad General).
Ambos efectos se
compensarían si la órbita tuviera un radio 1,5 veces el radio terrestre,
pero como es de casi 4 veces, los relojes de los satélites van más rápido
que los terrestres. Si no se corrigiera ese efecto habría desfases de 38
microsegundos cada día, lo que provocaría un error en la posición de 11 Km.
La révolution Einstein
Entretien. Michel Paty évoque l’année 1905 au cours de laquelle un
physicien inconnu jette les bases de la nouvelle conception de la réalité.
Michel Paty est physicien et directeur de recherche émérite au CNRS,
actuellement professeur invité à l’université de São Paulo (Brésil). Il
est l’auteur de nombreux ouvrages de vulgarisation de la physique, de
philosophie et d’histoire des sciences (1).
« Année miraculeuse », dit-on pour évoquer cette
année 1905 au cours de laquelle Einstein entre dans l’histoire, à l’âge de
vingt-six ans. Il n’est alors pourtant qu’un employé de bureau, inconnu
des savants et a fortiori du grand public ?
Michel Paty. « Annus mirabilis » : il serait préférable de dire
année admirable plutôt qu’année miraculeuse. Einstein était rationaliste :
mieux vaut laïciser l’expression !
Lorsqu’il publie, en effet, dans l’une des meilleures revues scientifiques
de l’époque, les articles qui feront date, Einstein est employé à l’office
des patentes de Berne en Suisse. Mais il a la formation d’un chercheur,
acquise à l’École polytechnique de Zurich, et il soutient cette année-là
sa thèse de physique. Depuis quatre ans, il se heurte à l’impossibilité de
trouver un poste en université, peut-être (bien qu’il ne l’ait jamais dit)
en raison d’un numerus clausus imposé aux juifs dans les universités de
l’empire allemand.
Ses contemporains remarquent-ils tout de suite
l’importance de ces publications ?
 Michel
Paty. Michel
Paty. On y prête attention, mais pas de façon spectaculaire.
C’est beaucoup plus tard qu’Einstein deviendra aux yeux du grand public «
le plus grand savant de ce siècle », comme titreront les journaux. Au
lendemain de la séance fameuse du 6 novembre 1919 de l’Académie royale de
Londres, où Arthur Eddington, astronome britannique de renom (et pacifiste
comme lui), présente les résultats d’une observation effectuée lors d’une
éclipse totale du Soleil visible au Brésil et en Afrique.
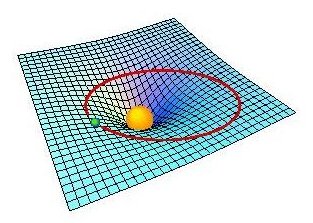
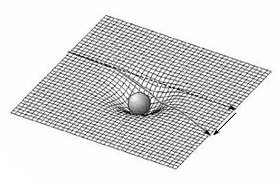
Cette observation confirme la théorie de la relativité générale
qu’Einstein a publiée à la fin de l’année 1915. Les position apparentes
des étoiles voisines du Soleil à cet endroit du ciel sont déplacées comme
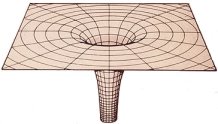
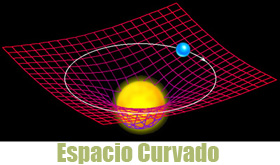
le prévoit la théorie : l’espace est « courbe » au voisinage du Soleil,
c’est-à-dire que la lumière ne suit pas un chemin rectiligne lorsqu’elle
se trouve à proximité d’une grande masse, que sa course est déviée. C’est
la première grande vérification de la relativité générale. Mais, quatorze
ans plus tôt, on n’en était pas là.
Pourtant les découvertes de l’année 1905 sont
exceptionnelles ?
 Michel
Paty. Michel
Paty. Tout à fait. Einstein intervient de façon décisive en apportant
des solutions originales à trois des problèmes les plus difficiles et les
plus discutés par les physiciens de cette époque.
En premier lieu, sur la thermodynamique (2) et la question de la
constitution atomique de la matière. Einstein reformule un aspect de la
théorie thermodynamique, celui qui s’occupe du lien entre les propriétés
d’un gaz et le mouvement de ses particules constitutives, exprimé à l’aide
de probabilités.
Il donne à la probabilité mathématique un sens physique et en tire une
relation de fluctuation entre des grandeurs. Il applique cette idée au
mouvement brownien (visible au microscope) provoqué par le mouvement
moléculaire sous-jacent (invisible), et cette relation de fluctuation est
peu de temps après vérifiée par le physicien français Jean Perrin : ce qui
démontre pour la première fois que la matière est effectivement constituée
d’atomes (on peut ainsi, en effet, les compter et les mesurer).
Deuxième grand problème : le rayonnement électromagnétique, la lumière. On
pensait à l’époque que ce rayonnement se propage comme une onde dont
l’énergie est distribuée de manière continue.
Einstein l’étudie au niveau atomique par la thermodynamique et montre que
cette énergie doit au contraire être discontinue.
C’est là le point de départ fondateur de la physique quantique qui
s’occupera des propriétés des atomes et des particules élémentaires. Enfin,
la troisième contribution, la théorie de la relativité restreinte.
L’expression est fort connue, mais son contenu
moins... Qu’entendre notamment par « relatif » et « restreint » ?
Michel Paty. D’abord, « restreint ». En 1905, Einstein démontre la
relativité des phénomènes électromagnétiques ou optiques par rapport au
mouvement uniforme (ce mouvement ne modifie pas les propriétés et les lois
de ces phénomènes). Dix ans plus tard, il formulera une théorie où l’on
considère de manière semblable tous les types de mouvements accélérés : la
relativité est généralisée à tous les mouvements. Ensuite, « relativité ».
On connaissait depuis Galilée la relativité du mouvement pour la mécanique
des corps (en particulier l’équivalence du mouvement uniforme et du repos).
Mais on ne pensait pas qu’elle puisse être également valable pour les
propriétés optiques et électromagnétiques des corps : la théorie
ondulatoire de la lumière (de Fresnel) et la théorie électromagnétique (de
Maxwell) faisaient appel à un milieu, l’éther, en repos absolu, ce qui
devrait privilégier le repos par rapport au mouvement.
Et pourtant on n’avait jamais pu mettre en évidence par l’observation une
différence entre le repos et le mouvement pour ces phénomènes. Einstein
eut l’idée que la - relativité est un principe d’invariance de la nature,
s’appliquant aussi aux lois de l’optique et de l’électromagnétisme.
Il transforma la théorie électromagnétique de façon qu’elle obéisse au
principe de relativité. Pour y parvenir, il fut conduit à modifier le
concept de vitesse, et donc les concepts d’espace et de temps. Au lieu de
considérer ces derniers comme des grandeurs seulement mathématiques, il
leur donna une signification physique : les rapports d’espace et de temps
dans les mouvements doivent obéir eux-mêmes au principe de relativité pour
que les lois physiques soient invariantes par rapport au mouvement.
Cela liait étroitement l’espace et le temps entre eux, dansne même
grandeur, l’« espace-temps ».
Quels ont été les effets de ces théories dans le
développement des connaissances et des techniques au cours du XXe siècle ?
Michel Paty. Hormis la mécanique des corps ordinaires qui reste en
accord avec la théorie newtonienne classique, les autres domaines de la
physique en ont été bouleversés : physique des milieux continus, solides,
élastiques ou fluides, physique atomique, et ensuite physique nucléaire et
subatomique, qui font appel à la théorie quantique et à la relativité
restreinte. La plupart des développements techniques modernes, qui ont
transformé notre cadre de vie, leur sont redevables.
Quant à la relativité générale, elle permet de comprendre les objets
célestes nouveaux que sont les quasars, les trous noirs, et d’autres,
découverts à partir des années soixante et soixante-dix. Avec elle, il
devient légitime de prendre l’univers entier pour objet de science : cette
dernière, la cosmologie, découvre ensuite que l’univers n’est pas statique
mais en expansion dans l’espace, et en évolution au cours du temps. Entretien réalisé par Lucien Degoy (l'Humanité du
17/01/2005)
(1) Notamment la Physique
du XXIe siècle, EDP Sciences 2001, et Einstein philosophe PUF, 1993.
(2) Étude des propriétés des corps en fonction de la température et de la
pression.
TEORIA DE LA RELATIVIDAD:
A finales del siglo XIX la
comunidad científica sabia que había mucho por crear e inventar, aplicando
los diversos principios físicos descubiertos, tales como la electricidad,
magnetismo y mecánica, pero estaban convencidos de que ya casi no quedaba
nada nuevo por explicar, la naturaleza había sido descubierta en su
totalidad y ahora solo tenia que comenzar a aplicarse esos conocimientos a
las actividades del ser humano para su propio beneficio y bienestar.
Hasta ese momento los
cimientos de la física eran dos grandes columnas construidas por dos de los
científicos más grandiosos de la ciencia. Una la teoría de la mecánica,
donde todos los conocimientos de cinemática y dinámica desde Aristóteles
hasta Galileo, fueron condensados en una sola teoría, conocida hoy como la
Mecánica Clásica, o Mecánica Newtoniana. La otra columna sustentaba la otra
mitad de la física, referente a los efectos magnéticos y eléctricos
conocidos desde los griegos hasta los últimos avances de Oersted, Faraday y
Lenz. Toda esta información técnica fue unificada en la Teoría del
Electromagnetismo del genial científico ingles James Maxwell.
Pero en
realidad algo andaba mal, pues fueron apareciendo
algunos nuevos cuestionamientos o efectos fisicos
desconocidos, y se pensó que “puliendo” un
poco los conceptos del momento podrían explicarlos fácilmente, así que casi,
fueron subestimados por gran parte de los investigadores de esa época.
Esos
nuevos fenómenos y cuestiones fueron:
a)
El efecto fotoeléctrico
b)
La formula de la radiación de un cuerpo caliente
c)
Las rayas en los espectros de emision del Hidrógeno
(Nota:
esos efectos los puedes estudiar en este sitio)
Amigo
sigamos con lo nuestro....
El concepto de relatividad
ya existía y se conocía como la Relatividad de
Galileo, y prácticamente consistía en la suma algebraica de velocidades
según sea el sistema de referencia que se adopte. Por ejemplo, suponte que
estés parado en el andén de una estación de trenes y en un instante pasa
moviéndose hacia la derecha un vagón de pasajeros a la velocidad de 60 km/h
con respecto a ti, que te encuentras detenido al costado de las vías. Para
un pasajero sentado adentro del mismo vagón dicho tren se mueve a 0 Km/h, es
decir, se encuentra detenido con respecto a ÉL,
pues ambos se mueven juntos. Ese pasajero con respecto a
TI, a que velocidad de desplaza?... no hay dudas, pasa a la misma
velocidad que el vagón, ósea a 60 km/h.
Supongamos ahora que un
segundo pasajero se levanta de su asiento y comienza a caminar hacia la
derecha a 10 km/h. respecto del vagón. A que velocidad se mueve este
respecto del pasajero sentado, creo que tampoco hay dudas, y es de 10 km./h.
pues vagón-pasajero sentado pertenecen al mismo sistema.
Bien, pero ahora ese
pasajero a que velocidad se desplaza respecto a TI
que te encuentras sobre el anden?. Para este caso,
la velocidad del pasajero será de 70 Km./h, es decir, que como ambos tienen
el mismo sentido de desplazamiento dichas velocidades se suman: 60+10=70.
Si otro pasajero se levanta
pero camina hacia la izquierda a 15 km/h, ahora la velocidad del mismo
respecto a tu posición, será de: 60-15=45, porque tienen sentidos contrarios.
Si se quiere determinar la
velocidad del primer pasajero que se paro, respecto del segundo, es de:
10+15=25 Km/h. Es como si se estarían alejando uno del otro a razón de 25
km/h adentro del mismo vagón. En el supuesto caso
que ambos ahora se acercan hacia sus asientos nuevamente a la misma
velocidad, también la velocidad de uno respecto del otro será de 10+15=25
Km./h., pero ahora acercándose uno al otro. Se puede usar el signo (-) para
indicar que se alejan y el signo (+) para indicar que se acercan, solo es
una convención.
Que pasa si uno de ellos,
mientras camina hacia la izquierda a 15 km./h, saca una pelotita y la lanza
hacia la derecha a razón de 50 km/h hacia la derecha. Cual será la velocidad
de la pelotita respecto a TI, que sigues detenido
en el anden?. Bien ahora será el cálculo es así: 60+50-15=95 Km./h.
60 del vagón hacia la
derecha + 50 de la pelota hacia la derecha – 15 del pasajero hacia la
izquierda=95
...
amigo me sigues el concepto?,...Estás
de acuerdo?.
Es tal como indicaba al
inicio, la relatividad de Galileo, solo consiste en sumar velocidades
usando el signo (+) o (-) según sea es sentido de las mismas. (en realidad
la suma es vectorial, pero para el alcance de esta explicación
alcanza con este definición)
Si se invierte la situación
y ahora el pasajero desea determinar tu velocidad (que estas sobre el anden)
respecto a su posición En este caso la situación es exactamente la misma,
para el pasajero, es el quien se encuentra detenido y es el anden quien
se mueve acercándose hacia el a la velocidad de 60 km./h es decir son
dos situaciones totalmente equivalente, cada observador tiene su propia
visión de la situación, y cada uno tomara los mismos valores antes
calculados.
Para comenzar a darle
propiedades a estos conceptos, en física se dice que cada objeto en
movimiento o detenido, tiene su propio marco de medición o de coordenadas,
es decir, que cada observador estudia y mensura la situación desde su
propio sistema de referencia. Se puede decir que cada pasajero tiene un
sistema de referencia, la pelotita tiene otro, y tú que te encuentras
detenido también tienes el tuyo. En el caso del pasajero sentado, el sistema
será el mismo que el del vagón, porque ambos se mueven simultáneamente. Cada
uno observa al resto desde su propia ubicación, y sumará
o restará las velocidades según sea el sentido del
movimiento de los diversos objetos estudiados. Cuando todos los sistemas de
referencia se mueven respecto de los demás a velocidades uniformes, se dice
que esos sistemas son inerciales.
Resumiendo todo lo
antedicho, significa que cada observador tiene su propio y único sistema de
referencia. Por ejemplo tu que estás en este
momento leyendo este apunte, te encuentras en reposo con respecto al sistema
de referencia tierra, es decir, que tu con respecto al piso estas a cero de
velocidad. Pero imagina ahora que alguien te esta mirando desde la Luna.
Este observador va a concluir que tu estas girando sobre un eje a la
velocidad de 1vuelta/día. Si seguimos alejándonos, y alguien se detiene en
el Sol, dirá que tienes dos movimientos uno sobre tu eje y otro alrededor
del sol, con una velocidad que tarda 365 días en recorrer toda la orbita.
Como puedes observar cada observador desde su propio marco de referencia
tiene sus propias conclusiones.
Unas líneas mas arriba
cuando hablábamos de los sistemas inerciales, es importante destacar, una de
sus principales características, y consiste en que cada uno de esos sistemas
las leyes de la física, como la conservación de la energía, de la cantidad
de movimiento lineal y angular, etc. se cumplen para cualquier observador
que este dentro o fuera del sistema de referencia en estudio. Por ejemplo si
adentro del vagón armo un laboratorio y realizo una serie de investigaciones
de principios físicos, TODOS ELLOS SE VERIFICARAN TAL COMO SI LOS ESTUVIESE
HACIENDO SOBRE LA TIERRA. Lo mismo ocurre con la pelotita, si armo sobre
ella otro laboratorio y realizo más experiencias, las mismas responderán a
los principios físicos conocidos. Y así sobre cualquier sistema de
referencia inercial que utilice, siempre en cada uno de ellos se verificaran
las leyes de la mecánica y del electromagnetismo. Si nos ponemos a pensar
esto no tiene nada raro, pues nuestro laboratorio de la Tierra, no es más
que otro laboratorio armado sobre una pelotita en movimiento en algún rincón
del universo. Seguramente si pasa alguna nave espacial cerca del planeta, y
nos observa y mide nuestros experimentos obtendrá otros valores numéricos
distintos a los nuestros, pero sus conclusiones físicas serán exactamente
igual a las nuestras. De todo lo antedicho, se puede concluir que no existe
ningún sistema de referencia ideal, que en física se llama sistema
absoluto. Es decir no existe un sistema que se encuentre totalmente en
reposo y podamos referenciar todas las mediciones a ese sistema especial. No
hay en el universo un sistema que sea dueño de la verdad absoluta de todas
las mediciones, pues todos están en movimiento y cada uno tiene su propia
realidad.
Volviendo ahora al inicio
de este apunte, por allá en los primeros años del siglo XX, los científicos
estaban muy concentrados tratando de determinar las diversas propiedades de
la luz, tales como su velocidad exacta, su naturaleza, su energía, su medio
de propagación, etc. En realidad nadie sabia como hacia para llegar de un
lugar a otro. Así como el sonido usa el aire para desplazarse, la luz que
medio usa para moverse. La primera respuesta fue que utiliza un medio que se
encuentra en todo el universo, que es transparente, de baja densidad e
inunda todos los huecos del espacio, este medio se llamo: ETER. Desde su
propuesta los físicos se pusieron a tratar de encontrarlo, porque seria
fantástico encontrar algo que se encuentre fijo en todo el universo para
tener una referencia fija. Los primeros encargados de buscar este medio
fueron dos grandes físicos experimentales, conocidos como Michelson-Morley,
y así se conoce hasta nuestros días al experimento realizado. Básicamente el
experimento consistía en emitir un rayo de luz en un sentido, por ejemplo,
en dirección al movimiento de la tierra, y otro en sentido contrario, de tal
manera que en un sentido la velocidad de la tierra se sume a la de la luz y
para el otro caso se reste. (el primer rayo es mas veloz que el segundo).
Esos haces de luz, luego de recorrer una misma distancia, se hacen reflejar
en unos espejos para que retornen al punto de partida. Como un rayo es más
rápido que otro, y deben recorrer la misma distancia, entonces llegaran al
punto de partida con un retardo de tiempo, pues uno demorara más que otro en
recorrer ese mismo espacio.
El experimento se hizo de
diversas formas, perfeccionando los métodos de medición del sistema. Se
efectuaron distintas mediciones durantes varios años, JAMAS SE PUDO MEDIR
UNA DIFERENCIA, los haces siempre llegaban al mismo tiempo, la velocidad de
la tierra no les influenciaba para nada.
Conclusión: EL ETER
NO EXISTIA, y entonces en que se apoyaba la luz para trasladarse?. (En este
sitio: El Fin de Eter)
Es aquí donde entra en
escena un jovencito alemán, estudiante avanzado de ciencias físicas en
Zurich, dotado de una genialidad especial, que le permitió dar una
explicación clara y correcta de lo que realmente pasaba con la luz, y los
objetos que se mueven a velocidad cercanas. Ese genial hombrecito, fue
Albert Einstein, que en los momentos libres que tenia en su trabajo en una
oficina de patentes, reformulo toda la física clásica de Newton conocida
hasta ese momento. De aquí en más la mecánica clásica seria solo un caso
particular de una mecánica más amplia y general, llamada mas tarde Física
Relativista, y que se aplica a las partículas que se mueven a grandes
velocidades. A partir de ese momento Albert Eisntein pasaría a ser el físico
más grande de la comunidad científica de todos los tiempos.
Einstein partió para su
teoría física desde dos postulados que parecen inofensivos pero tienen todo
el poder para explicar la naturaleza del universo. (los postulados son
afirmaciones sin demostración) Mas tarde dichos postulados fueron
demostrados con la experiencia.
Ellos son:
1-La luz se mueve siempre a
velocidad constante de 300.000 Km/seg, independiente de la velocidad de la
fuente emisor.
2-No existe ningún
experimento posible en una nave que nos permita saber si nos estamos
moviendo.
Observa que el primer
postulado ignora la relatividad de Galileo, donde se suman las velocidades.
Por ejemplo si sobre el tren un pasajero saca una linterna y envía un haz de
luz, cual será la velocidad del haz respecto a tu que estas detenido en el
anden. Según Galileo seria: 300000+ la velocidad del tren. Pues bien,
Albert , pidiendo perdón a Newton, niega toda esa teoría y propone una nueva
a partir de estos postulados. A partir de los postulados que Einstein había
formulado, la velocidad de la luz siempre seria constante de 300.000 Km/s
“salga a la velocidad que salga”, no interesa la velocidad de la fuente.
Además la luz no necesita de un medio material para transportarse, se mueve
a través del vacío.
Si la velocidad de la luz
dependiera de la velocidad del emisor, se tendría una forma de determinar el
movimiento uniforme, experiencia que negaría al segundo postulado. Por
ejemplo, si hacemos un ejercicio mental, que tanto le gustaba a Albert,
suponte que vas sobre una nave que va aumentando rápidamente su velocidad y
tú tienes un espejo en la mano donde te puedes ver reflejado. Resulta que
cuando viajes a una velocidad superior a la de la luz, tu cara desaparecerá
del espejo por que ya la luz que tu rostro irradia no lo alcanzara. Otra
situación similar para reflexionar es la siguiente: suponte parado al fondo
de una calle desde donde puedes observar la siguiente bocacalle a una cuadra
de distancia. Hacia ti viene un auto a gran velocidad y por la calle
perpendicular se le acerca una motocicleta en el mismo instante de cruzarse,
de tal manera que el auto debe hacer una “S” para evitar la colisión. En
este caso, si las velocidades se sumaran, la velocidad de la luz que emite
el auto te llegaría antes que la de la moto ya que este se dirige hacia ti.
Por lo tanto verías al automóvil hacer una “S en el aire” si saber porque,
ya que la luz de la moto aun no te ha llegado.
Esto ultimo ejemplos son
creaciones mentales, pero hay casos reales en el universo, como el moviendo
de estrellas, donde se ha determinado fehacientemente que los postulados
anteriores se cumplen y que la velocidad de una onda es siempre constante
independiente del centro emisor.
En 1905, Einstein, que años
mas tarde recordaría que paso por uno de los momentos mas duro y pesados de
su vida científica, tuvo que aceptar que cada sistema de referencia tiene su
propio espacio-tiempo, y que la idea de un tiempo absoluto como lo había
planteado dos siglos antes Newton estaba errado. Matemáticamente la
velocidad es igual al espacio recorrido sobre el tiempo empleado. Pero ahora
bien, si la velocidad de la luz siempre debía ser la misma, no quedaba duda
que el núcleo de la cuestión estaba en esos dos rígidos conceptos, y que el
sentido común no nos dejaba analizarlos, porque eran obvios. Como la hora
seria distinta, según la mida detenido en la vereda o subido a una carreta?.
No es eso ridículo, sin sentido.
Ahora bien apliquemos esos
nuevos conceptos nacidos de los postulados de Albert, a un otro ejercicio
mental. Nuevamente recurriremos a dos naves espaciales en el medio del
oscuro vacío en un rinconcito del universo, a miles de kilómetros de nuestra
querida Tierra. Suponte que una nave tiene un reloj de luz, una especie de
linterna que emite un rayo de luz hacia arriba y al llegar al techo se
refleja en un espejo, para volver al punto de partida. Supongamos que el
tiempo transcurrido desde la salida del rayo hasta su regreso es de 1
segundo. Para un astronauta adentro de esa nave observara que la luz sale
verticalmente hacia arriba llega al espejo y regresa al origen, es decir,
recorre dos veces la altura de la nave en un segundo. Ese astronauta puede
ser tu es este mismo momento, donde ves subir y bajar un rayo de luz, a
razón de 1 seg. por ciclo.
Ahora la segunda nave
también tiene instalado exactamente el mismo sistema de reloj, con igual
tiempo por ciclo y ella pasa a tu costado a una velocidad v de por ejemplo
10.000 km/h. Mi pregunta es la siguiente: como ves la trayectoria del rayo
de luz desde tu nave. No crees que así como ves subir o bajar al rayo,
también lo ves , simultáneamente, avanzar con la nave?. Que crees,… no tengo
razón?. Realmente es así, el rayo sube y se desplaza horizontalmente, de tal
forma que es movimiento compuesto es una línea inclinada hacia arriba que
nace en el reloj. Para el astronauta de la nave la luz solo sube y baja,
pero para ti “que estas fuera de su sistema de referencia” el rayo hace otro
recorrido. Por lo antedicho, el rayo recorre “para ti que estas afuera” una
distancia mayor que la doble altura que observa el astronauta interior a la
nave. Si ahora aplicas el primer postulado de Einstein, donde afirma que la
velocidad de la luz es siempre la misma, podrás concluir que el tiempo que
tarda la luz desde que sale del reloj hasta que regresa es mayor que el que
tu mides en tu propia nave que solo sube y baja verticalmente. Por lo tanto
cuando mides el tiempo en una nave que se mueve con respecto a ti podrás
observar que dicho tiempo se hace más lento, porque cuando en tu nave mides
un segundo en la otra pasa una fracción más. Resumiendo, el tiempo
trascurrido en un sistema (nave) que se mueve es siempre mas lento, es decir,
los relojes atrasan.
Si analizas la situación,
pero ahora invertida, notarás que el segundo
astronauta, el que se mueve en el caso anterior, observara exactamente lo
mismo que tu. El observará
que su rayo solo baja y sube en un segundo, y que es el de la otra nave el
que recorre mas distancia, por lo tanto concluirá que es su reloj el que
anda bien, pero el de la otra nave esta atrasando.
Algo parecido ocurre con
las toma de mediciones de distancias, que es consecuencia del atraso del
tiempo. Si el espacio recorrido es igual a la velocidad por el tiempo
empleado, notara fácilmente que cuando calculamos la distacia recorrida por
un móvil, el espacio será distinto según se tome el tiempo de un sistema de
referencia u otro. Si estoy detenido y observo
pasar la nave a cierta velocidad v, el espacio en mi sistema será igual a
dicha velocidad por el tiempo t. Pero resulta que ese tiempo t es menor en
el sistema en movimiento, por lo tanto la nave recorrerá menos distancia en
su sistema, que el calculado para el nuestro.
Resumiendo, se dice que las
distancias se acortan.
Explicacion Matemática
de la Teoría:
Es sólo una consideración intuítiva, en realidad Albert inició sus
deducciones apoyandosé en las transformaciones de Lorentz.
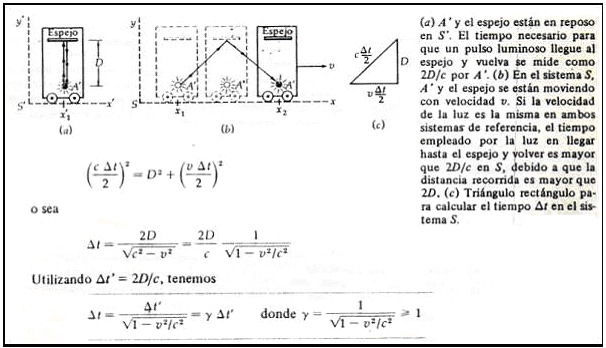
Sino
entiendes las fórmulas y deducciones enviame un mail que recibirás
mas explicaciones.
Nota que
el tiempo Delta_t es mayor a Delta_t' en un factor gamma.
Que
significa?.
Que cuando la luz en tu reloj, demore por ejemplo 1seg. entre subir y
bajar, tu observarás que la luz en la otra nave demorará más en recorrer esa
trayectoria triangular. Cuando haces los cálculos observarás que ese tiempo
se amplia en un factor gamma (que es mayor que 1) respecto a tu tiempo
propio.
Este factor
será cada vez mayor cuanto mayor sea la velocidad de la nave.
Suponiendo
que v=0.8c (80% de c), el tiempo en la otra nave se incrementará en un 66%,
respecto del tuyo, por lo tanto, mediras: 1.66 seg.
Cuando la
velocidad llegue a la velocidad de la luz, gamma será infinito.
Un Caso
Real:
En la atmósfera a unos
10.000 m. aproximadamente de altura aparecen partículas elementales llamada
muones que se desplazan a una velocidad muy cercana a la de luz, a unos
0.998 de c. Esa partículas son muy inestables y en reposo tienen un tiempo
de vida de 0,00000002 s. (2x10-8), es decir sumamente corto. Bien si se
calcula sin tener en cuenta la física relativista, se observara que al
multiplicar el tiempo de vida por su velocidad, los muones solo recorrerían
unos 600 metros, antes de desaparecer, por lo que ninguno podría llegar a
la superficie de la Tierra. Experiencias realizadas en tierra, han
confirmado la aparición de millones de ellos, contrariando a los cálculos
físicos aplicados. Justamente ahí surge el error, porque en el sistema del
muon a esa velocidad el tiempo en el sistema Tierra es de unos 15 veces
superior, y ese es el tiempo que hay tomar para efectuar los cálculos (15 x
2 microsegundos=30). Con ese nuevo tiempo los 600 m iniciales se
transformarían en 9000 m. y explicaría porque llegan a la superficie. Esos
9000 en el sistema Tierra, se reducen a 600 m. en el sistema muon, porque
ahora se debe usar el tiempo del muon.
Como se puede observar las
diferencias de tiempo y espacio están directamente relacionadas con la
velocidad del sistema. A mayor velocidad mayores diferencias, pero solo
notables cuando la velocidad se aproxima a la de la luz. Cuando la velocidad
es baja, inclusive, por ejemplo, la velocidad de un cohete al salir del
planeta, es de unos 40.000 km/h se la considera baja y los efectos
relativistas no pueden considerarse, porque prácticamente no existen. Para
estas velocidades la teoría de Newton se aplica con total eficacia, sin
dudar en que podamos caer en errores. Las formulas que mas abajo vamos a
determinar cuando se aplican para ejemplos con bajas velocidades se
transforman automáticamente en las formulas obtenidas de la Mecánica de
Newton, por lo que esta ultima pasa a ser un caso especial de un mas
general, conocida hoy como la Teoría Especial de la Relatividad.
Matemáticamente las
formulas de Tiempo y Espacio se pueden obtener de la usando el ejemplo
anterior de las naves en el espacio. Lógicamente Einstein no las obtuvo así,
para ello se valió de unas transformadas conocidas como de Lorentz, que fue
otro científico contemporáneo que estaba estudiando el tema. La matemática
utilizada por el científico no fue tan elemental, pero tampoco se apoyo en
la más avanzada matemática conocida en esa época. No fue así para la
resolución de las ecuaciones que explican la Teoría General de Relatividad,
cuando el movimiento es acelerado, donde tuvo que auxiliarse de herramientas
actualizadas del análisis matematico. Aplicar dichas ecuaciones a distintas
situaciones físicas genera más de un dolor de cabeza a los avanzados
estudiantes de ciencias exactas, cuando deben realizar sus prácticas.
Como
te he dicho, Einstein encontró que la teoría de Newton ``estaba mal'' y eso
no significó que las cosas comenzaran a caerse para arriba. Incluso si
decimos que la teoría de Newton es ``incorrecta'', da la impresión de que
entonces la teoría de Einstein es la ``correcta''.
Mañana
mismo o dentro de algunos años, un hipotético físico, por ejemplo Jacob
Newenstein, puede descubrir que la teoría de Einstein ``está mal'' en serio.
Pero aunque eso pase, las cosas no van a empezar a caerse contra el techo,
ni a moverse más rápido que la luz.
Einstein simplemente elaboró una descripción de la naturaleza más precisa
que la de Newton, y es posible que alguien halle una aún mejor. Pero la
naturaleza no va a modificar su comportamiento para satisfacer la teoría de
algún físico: es el científico quien deberá exprimir sus sesos para que su
teoría describa a la naturaleza mejor que todas las teorías anteriores.
Anotado por Carlos
Una de las grandes desgracias de la vida en la Tierra es el aislamiento. La
vida quiere expandirse y ocupar cualquier nicho que exista (quizá la Tierra
sea uno de
esos nichos) y los seres humanos tenemos también ese impulso de colonizar.
Pero ante nosotros, tenemos el inconveniente de la inmensidad del espacio.
El sistema estelar más próximo Alpha Centauri se encuentra a 4,36 años luz
de la tierra y el centro de la galaxia a 27.700 años luz. Estas distancias
parecen insalvables y más suponiendo, como propone la teoría de la
relatividad, que nada puede viajar más rápido que la luz.
Pero las cosas no son tan imposibles como las hemos pintado.
Según la teoría de la relatividad, el tiempo se relentiza cuando viajas a una
velocidad cercana a la de la luz. De esta forma, si nos movemos
suficientemente rápido, podemos ir a almorzar al centro de la galaxia. El
único inconveniente es que han pasado 27.700 años en la Tierra desde que
salimos.
Esto se puede ver
fácilmente en las ecuaciones
de transformación de Lorentz. Donde tenemos como relación entre el tiempo en
reposo y el tiempo en la nave que viaja a gran velocidad
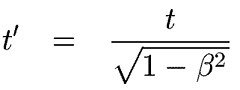
Esto significa que cuando este cociente tiende a 0, cuando beta=v / c=1, casi
un instante de tiempo en el sistema en movimiento es una eternidad en el
sistema en reposo. Esto, como os podéis imaginar es consistente con las
ideas básicas de la teoría de la relatividad,
la velocidad de la luz es constante
independientemente del observador. Para los más escépticos, y a
los que les guste comerse el coco, os puedo poner un breve ejemplo:
Imaginemos una increible
nave espacial que viaja desde la Tierra a Alpha Centauri prácticamente a
velocidad c (99,9%). Los astronautas, durante el viaje, deciden medir el
tiempo que tarda en ir y volver un rayo reflejado en un espejo. La línea que
une el espejo y la linterna está situada en la perpendicular al movimiento
de la nave. Claramente y como indica la figura el tiempo sería t=2d/c, muy
corto
Por otro lado, tenemos que ese mismo rayo para los observadores de la Tierra
tiene que recorrer mucha más distancia, pues la nave se está moviendo casi a
la velocidad de la luz y por lo tanto, tiene que recorrer mucha distancia en
la dirección horizontal (vt').

De esta forma, el tiempo que tarda el rayo en ir y volver de la linterna es
mucho mayor. En concreto, la distancia a recorrer por la luz es la dada por
los dos lados idénticos del triángulo de la figura. Contando que la
velocidad de la luz es c
y la nave se mueve a velocidad v
la distancia es d'^2=(2d)^2+(vt')^2,
con lo que como ct'=d'
y t=2d/c
despejando t'
obtenemos
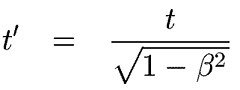
¡Qué casualidad! es el resultado de la transformación de Lorentz para el
tiempo.
De esta forma vemos que los sucesos de la nave transcurren más
lentamente para los observadores de la Tierra. Esto significa que el tiempo
transcurre mucho más lentamente dentro de la nave que en la Tierra, según
los observadores de la Tierra. Mientras que para los astronautas todas sus
experiencias cotidianas continúan siendo iguales que antes de iniciar el
viaje.
Midiendo longitudes y tiempos: paradojas relativistas
La constancia de la velocidad de la luz trae aparejadas consecuencias
sorprendentes sobre las nociones newtonianas de espacio y tiempo: estos
dejan de ser absolutos para pasar a depender del observador. Estas
consecuencias, que fueron descriptas por el propio Einstein,
son fáciles de deducir...
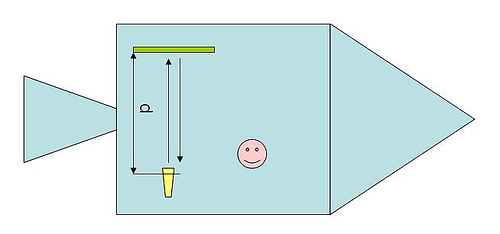
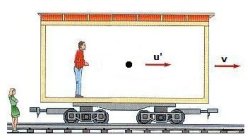
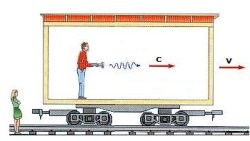
Dilatación del tiempo: consideremos un observador
situado en un vehículo, que apunta con una fuente de luz hacia el techo,
donde hay un espejo. Si denominamos con la letra c a la velocidad de la luz
y con h la altura del vagón, el tiempo transcurrido hasta que la luz retorna
al observador es t = 2h/c.
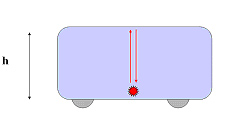
¿Cuál es el tiempo transcurrido entre esos dos eventos para observadores
en el andén, si el tren se desplaza a velocidad v? Desde el sistema
fijo al andén la luz recorre una distancia mayor.
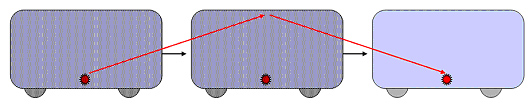
Como la velocidad es la misma, el tiempo T transcurrido debe ser mayor.
Usando el teorema de Pitágoras fácilmente se comprueba que
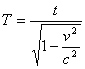
Contracción de longitudes: si en el ejemplo anterior
hacemos dos marcas en el andén en las posiciones donde el haz de luz sale y
llega al observador, esa distancia es igual a vT para los observadores del
andén. Sin embargo, para observadores en el tren la distancia es menor,
igual a vt. En otras palabras, si medimos la longitud de un objeto en reposo
y obtenemos un valor L0, al medir la longitud del mismo objeto en
movimiento obtenemos un valor menor por un factor
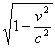
Los ejemplos anteriores muestran que las mediciones de intervalos
temporales y espaciales son relativas al observador. Se puede ver
sencillamente también que la simultaneidad es un concepto relativo.
Estos fenómenos no son observables cotidianamente porque son muy pequeños
para velocidades mucho menores que la de la luz. Pero se han comprobado
experimentalmente de distintas maneras. Por ejemplo, el tiempo de vida medio
de ciertas partículas elementales inestables depende de su velocidad. La
primera verificación experimental de la dilatación temporal fue realizada
observando muones producidos en la atmósfera. Se han realizado
comprobaciones más directas colocando relojes en aviones comerciales y
cohetes.
Estas propiedades no intuitivas del espacio y el tiempo dieron lugar a un
conjunto de paradojas, que resultan de aplicar incorrectamente los
resultados de la teoría de la relatividad.
Estas paradojas no sembraron dudas sobre la validez de la teoría. La
más célebre es la llamada paradoja de los gemelos, que
consiste en considerar dos gemelos que se separan viajando a velocidades
cercanas a la de la luz. Al reencontrarse, uno de los dos es más joven por
el fenómeno de dilatación del tiempo. Sin embargo, cada uno de ellos podría
argumentar que es el otro quien debería ser más joven. A pesar de que la
situación es aparentemente simétrica, en realidad no lo es, ya que, para
reencontrarse, uno de los mellizos debe haberse acelerado. Otros ejemplos
involucran velocidades aparentes mayores que la de la luz, con violaciones
aparentes al principio de causalidad.
La Teoria della Relatività Speciale
H içbir
yazý/ resim izinsiz olarak kullanýlamaz!! Telif haklarý uyarýnca
bu bir suçtur..! Tüm haklarý Çetin BAL' a aittir. Kaynak gösterilmek þartýyla siteden
alýntý yapýlabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa / Ýndex / Ziyaretçi
Defteri /  E-Mail / Kuantum Fiziði / Quantum Teleportation-2
E-Mail / Kuantum Fiziði / Quantum Teleportation-2
Time Travel Technology /
Kuantum Teleportation /
Duyuru
/ UFO Technology
Roket bilimi /
CetinBAL
/Astronomy
|
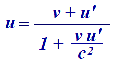
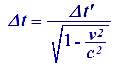

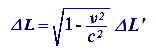




 Michel
Paty. On y prête attention, mais pas de façon spectaculaire.
Michel
Paty. On y prête attention, mais pas de façon spectaculaire.  Michel
Paty. Tout à fait. Einstein intervient de façon décisive en apportant
des solutions originales à trois des problèmes les plus difficiles et les
plus discutés par les physiciens de cette époque.
Michel
Paty. Tout à fait. Einstein intervient de façon décisive en apportant
des solutions originales à trois des problèmes les plus difficiles et les
plus discutés par les physiciens de cette époque.