Special Theory of Relativity

Lecture Notes by I. Bars

Einstein's Special Theory of Relativity describes the correct rules of physics for fast moving objects both in the macroscopic and subatomic world. It was developed by Einstein from two postulates which ended up being correct:

(1) (1) The laws of physics are the same in any inertial frame of reference (inertial means no external forces acting on the frame).

(2) (2) The speed of light in vacuum is always the same constant c irrespective of the speed of its source and irrespective of an observer static or moving.

The first postulate was assumed and used since Newton’s time. The second, more daring, postulate was motivated by Maxwell’s prediction that light has a definite speed c=300,000 km/s as given by the electromagnetic wave theory of light. There was no room in Maxwell’s theory for different observers to see different values. Also attempts to define an absolute reference frame (the Ether) became untenable in the face of negative experiments by Michelson and Morley. However, the later does not seem to be the motivating factor for Einstein’s postulate .

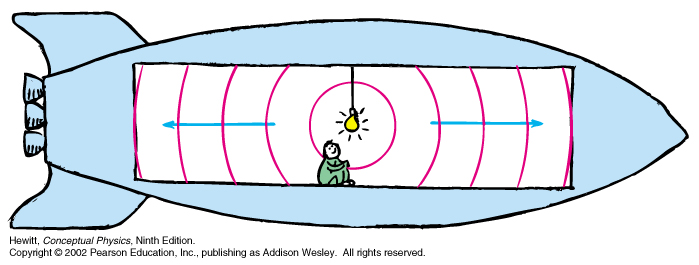
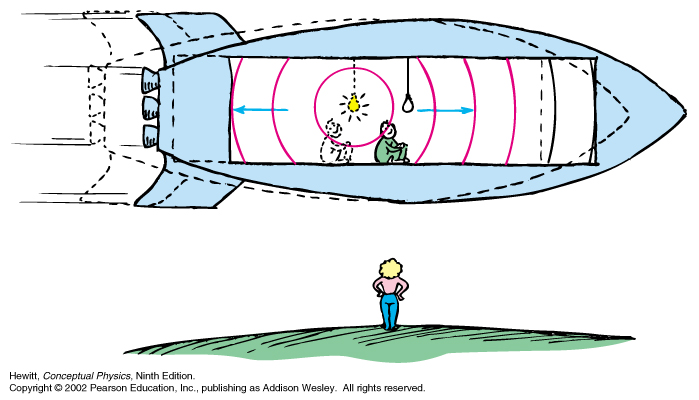
As consequences of the postulates, as seen by a static observer, the laws of physics in a fast moving frame may seem non-intuitive and surprizingly different than the ones in a static (or even a slow moving) frame, but all puzzles are explained by understanding the concepts of relative time and space, which undergo a revolution.

Relativistic addition of velocities.

It helps to see the correct relativistic formula for addition of velocities right at the beginning of the discussion, to remove the mystery of how the speed of light is always the same irrespective of observer or of source. This is counter-intuitive because it is unlike the relative motion of objects we observe in our everyday life (mainly slow moving objects).

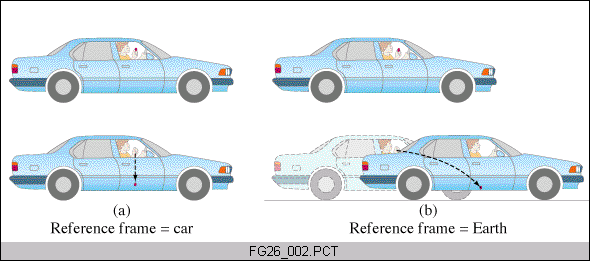
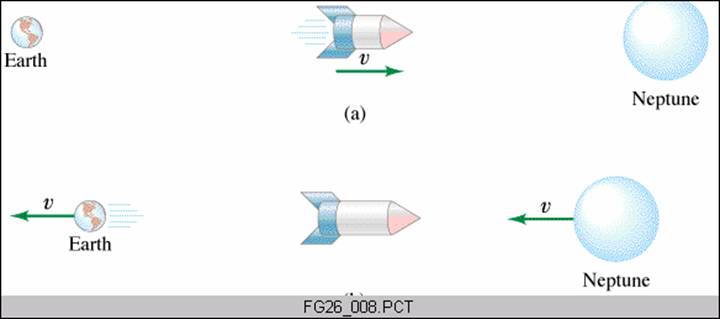
If you throw a particle with a speed v₁ from a spaceship moving at a speed v_2,the total speed V_total as observed outside of the spaceship in the static frame is given by the formula in the box. Here v₂ is the relative speed of the two observers. Positive or negative values for either v₁ or v₂ are taken depending on their directions.

Addition of velocities
parallel or antiparallel

to a line

V_total=(v₁+v₂)/(1+v₁v₂/c²)

If v₁v₂/c²<<1 then V_total ≈ v₁+v₂ (everyday life)

e.g. if v₁=0 then V_total = v₂(picture below)

e.g. if v₂=0 then V_total = v₁(no relative motion)

If v₁=c then V_total =c for any v₂(light from ANY moving source)

If v₂=c then V_total =c for any v₁(ship at speed of light)

The picture shows the case for v₁=0 (object has no horizontal velocity relative to the car in case (a)), and any v₂.

A static observer outside of the car sees object at V_total = v_2. This is like everyday life.

A fast moving rocket (#1) shoots a fast moving projectile (#2), what is the speed of #2 as measured by an observer on Earth?

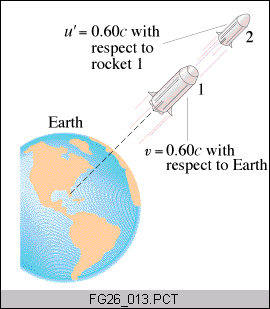
V_total=(v₁+v₂)/(1+v₁v₂/c²) = (0.60c+0.60c)/(1+0.60 x 0.60 ) = (1.20/1.36) c = 0.88 c

Simultaneity

What is a simultaneous event?

	Light signals reach simultaneously both ends of the chamber of the ship as seen by the traveling observer
	From the point of view of the static observer the signals do not reach simultaneously the ends of the chamber because the ship is moving while light moves at the same speed in either frame

The two observers do not agree on simultaneity. So simultaneity is not an absolute concept, and time measurements are not absolute or universal.

· · When you look out the window, the scene on your retina - the scene you see - is not all happening at the same moment.

· · The stars in a photo of the night sky were not all there looking as they do at the same moment, even though the light from them arrived on the film at the same instant.

· · If you see two stars explode at the same time, one of the events might have happened earlier to an observer from some other galaxy.

Time dilation

Now consider a beam of light as shown in the picture and observed from inside or outside the spaceship

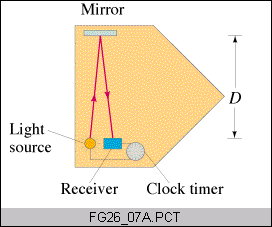
Light is observed at the same speed c in either frame. The observer in the ship and the static observer outside have identical clocks, but measure a DIFFERENT time lapse for the same event (emission - reception).

Observer on ship

Observer outside

Time = distance/ speed of light

Δt_ship=2D/c

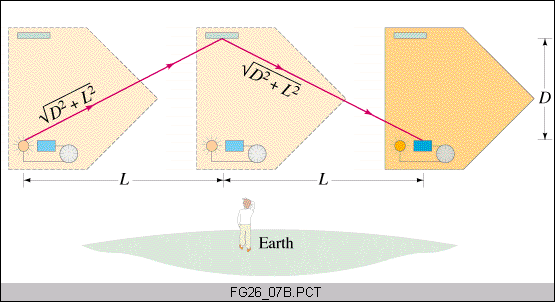
Δt_Earth =2(D²+L²)^1/2 / c

Δt_Earth = Δt_ship / (1-v²/c²)^1/2

A little algebra: The ship is moving at speed v, therefore 2L=vΔt_Earth while 2D=c Δt_ship . Replace these to get Δt_Earth = Δt_ship [1+(v Δt_Earth)² /(c Δt_ship)²]^1/2 , then square it, and solve as above. Or, use the right triagle up to midway (( c Δt_Earth /2 )²= ( v Δt_Earth /2 )² + ( c Δt_ship /2 )^2, and solve to obtain the same result.

Time Dilation: Δt_Earth is obviously larger since light travels a longer distance. It is what the observer outside measures on his static clock. Therefore as observed by the static observer, the static clock ticks FASTER as compared to the moving clock (or the moving clock ticks SLOWER as compared to the static clock).

So, an astronaut on Earth ages faster than an astronaut on a spaceship according to observers on Earth (biological clocks). The astronaut on the spaceship feels nothing different.

Twin paradox: Isn’t the role reversed for the twin on the spaceship, and he thinks he ages faster compared to twin on Earth? So when he returns to Earth, who is really older? No paradox, because the twin on the spaceship is not on an inertial frame. He must accelerate (forces acting) to start, to turn around, and to slow down.

If you sit inside a chamber that revolves at high speeds, and then get out, you see that your twin who was outside is older.
An elementary particle that decays, such as a muon or a neutron, lives longer when moving at high speeds in accelerators (an experimental fact!!)
As observed by us, light from the center of the Milky Way galaxy reaches the solar system in 25,000 years, but a traveler moving at the speed of light measures 0 seconds for the same trip.
You definitely age less rapidly when you go on a round trip to Japan at 500 km/hr. But alas…by a negligible amount!! For a 20 hr roundtrip you age 7.2 x 10^-9sec less (use (v/c)²=[(500/3600)/(300,000)]²=2 x 10^-13).

Space contraction

Question: How fast should you move to get to a far away galaxy in 5 years, while people on Earth measure 100 years. How far is that galaxy as seen from Earth, or as seen from the ship?

Answer: v/c=(1-( Δt_ship /Δt_Earth)²)^1/2=(1-(5/100)²)^1/2=0.99875; d_Earth=(100x365x24x3600 sec)x((0.99875)x(300,000) km/sec) = 9.5 ×10¹⁴km; d_ship==(5x365x24x3600 …..)=0.48 ×10¹⁴km. Space is contracted!!

According to measurement from Earth (comparing clocks to those on the ship) the distance between the two planets is d_Earth=v Δt_Earth, but according measurements on the spaceship the distance is d_ship=v Δt_ship. Therefore as seen from the ship the distance between the planets is smaller. Changing the frame of reference, the planets are passing by the ship, so the observer on the ship sees a smaller distance between the planets relative to an observer that is static relative to the planets.

d_ship= d_Earth (Δt_ship / Δt_Earth) à d_moving= d_static (1-v²/c²)^1/2

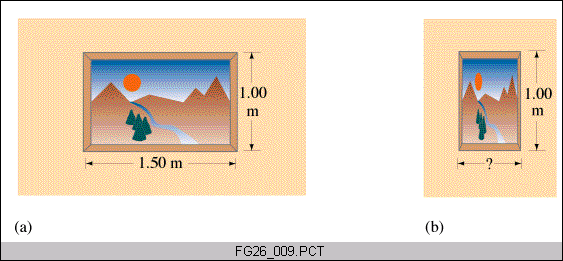
So as seen by a static observer, a moving meter stick (lying parallel to the direction of motion) appears shorter as compared to a static meter stick.

A moving tennis ball moving at high speeds looks like a pancake. At the speed of light the pancake looks like zero thickness.
To a traveller moving at the speed of light, the distance between our solar system and the center of the galaxy (or any other distance) looks like zero.
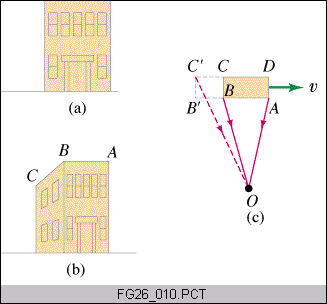
Passing by a painting or a house at high speeds they would look contracted horizontally.
One could see the side of the house at the moment facing it while passing by it, because light from the side emitted at a slightly earlier time (and traveling a longer distance at the same speed as other light) just reaches the observer when facing the house, and while the house is not blocking the ray.

Conclusion: Time, like space, is not absolute, but they are inter-related. They both depend on the observer. Events that appear simultaneous in one frame of reference are not simultaneous in moving frames of reference. Each observer has his own space-time.

Space contraction: L=L₀(1-v²/c²)^1/2. Time dilation : t = t₀/(1-v²/c²)^1/2.

T,L are as measured by static observer watching a moving clock or a moving stick

t_{0 ,}L₀ are as measured by observer that moves together with the clock or with the stick

Energy, momentum, mass and relation to velocity.

The mass of a particle at rest is called its rest mass m₀. When the particle moves it has momentum p and energy E=(p²c²+m₀²c⁴)^1/2. Think of a right triangle with hypotenuse E and perpendicular sides pc and m₀c². The speed of the particle v/c is given by the ratio of the side pc to the hypotenuse E. From the triangle we see what happens as one side gets much larger than the other, you approach the extreme relativistic (fast) or extreme non-relativistic (slow) limits

pc E=(p²c²+m₀²c⁴)^1/2( = mc² equivalent mass)

m₀c²rest energy

The particle at rest (p=0) has energy E=m₀c². The speed of the particle is given by v/c=(cp/E). Therefore (from the triangle) the maximum v is c, and it can be attained only by massless particles m₀=0. A massless particle cannot stop since v/c=1.

The maxium attainable speed is the speed of light. Light is described as a massless particle (the photon). Any particle that has zero mass cannot slow down and must move with the speed of light. The neutrino is another particle whose mass is zero or almost zero, hence it moves at (or almost at) the speed of light.
A particle that has non-zero rest mass m₀can never attain the speed of light although it can come closer and closer to it as its momentum is increased. Thus, macroscopic objects that have huge masses have a hard time attaining large enough energies, and therefore move at speeds much smaller than the speed of light.
A summary of the formulas

momentum p
p

=mv

= m₀v/ (1-v²/c²)^1/2

energy E

E=(p²c²+m₀²c⁴)^1/2(hypotenuse)

= mc²

= m₀c²/ ( 1-v²/c²)^1/2

speed v
v/c=cp/E (ratio)

v=p/m

fast (triangle tall and skinny)
m₀=small or p=large

fastest (m₀=0 or p=infinite, not practical)
E=pc (e.g. light, neutrino)

maximum speed
v_max=c (e.g. light)

slow (triangle short and fat)
m₀=large or p small

E=m₀c²+m₀v²/2 (second term like KE Newton)
static (p=0 or v=0)) E= m₀c²

v=p/m₀
(Newton)

The energy of a particle increases as its momentum increases E=(p²c²+m₀²c⁴)^1/2(equivalently when its velocity increases E = m₀c²/ ( 1-v²/c²)^1/2). The equivalent mass m satisfies E= mc² with m= m₀ / ( 1-v²/c²)^1/2 . As the velocity increases the equivalent mass increases as shown.

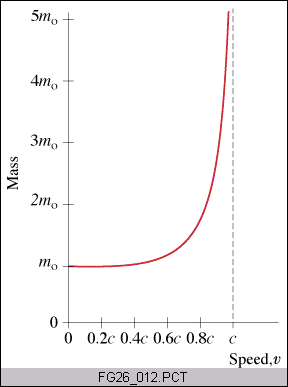
E=mc^{2 .} Energy and mass are two facets of the same thing.

Mass can be created from energy, e.g. high frequency photon near nucleus creates electron + positron out of the vacuum.

Mass dissapears to create energy, e.g. electron+positron beams at SLAC annihilate to give photons, those can convert to other matter.

Other examples are fission and fusion. Energy from the sun ! Energy from nuclear reactors.

Consequences of Einstein's Theory of Special Relativity

Suppose that Einstein is right: the speed of light is measured to be the same by observers in all inertial frames. What does that mean? Well, consider a few simple situations.

Blue Man stands in a room. He decides to measure the height of his room by bouncing a light beam off the ceiling, and measuring the time it takes to return.

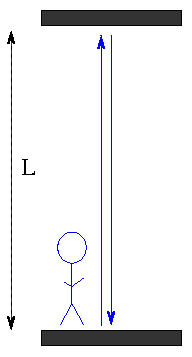
The height of the room is L, and the light beam travels at c, so the time it takes for the beam to go there and back is

                    2*L
       t(blue)  =  -----
                     c

So far, so good.

Now, consider another observer: Red Man. Blue Man is in a frame which zooms past Red Man at a constant velocity v. As Red Man watches the Blue Man and his room go by, he also measures the distance travelled by the light beam.

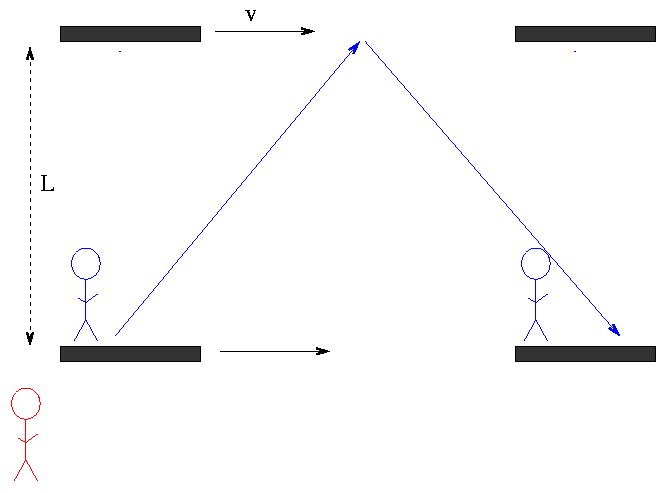
What distance does the light beam travel, according to Red Man?

Viewgraph 1

Now, if Red Man and Galileo were standing together and watching the beam, Galileo would say,

Behold! The room moves past us sideways at speed v, carrying the light with it. So the light beam travels faster than usual: it has a vertical component of 300,000,000 m/s, plus a horizontal component of v, and thus a total speed of

speed of light beam = sqrt ( 300,000,000*300,000,000 + v*v )

The time it takes to reach the ceiling of the room and bounce back is, naturally, the same

2 * L time to go and return = ------- c

that Mr. Blue Man measured.

But if Einstein were present, he would disagree:

Actually, the light beam travels at exactly the same speed,

speed of light beam = 300,000,000 m/s

from both our point of view, as we watch the room fly past us, or from Mr. Blue Man's point of view, inside the room. It is the time taken to make the trip which changes, not the speed of light.

So, according to Einstein, how long does the light beam take to make its trip, as seen from the ground with Red Man?

Viewgraph 2

Viewgraph 3

Viewgraph 4

Viewgraph 5

Tests of Time Dilation

Viewgraph 6

 Assume that planes fly at about 500 mph = 250 m/s
 relative to the ground.

      Q1:   How long does it take a plane to fly around
            the world?

      Q2:   According to the stationary observer floating
            above the North Pole,

               what is the gamma factor for Joe?

               what is the gamma factor for red plane?

               what is the gamma factor for blue plane?

      Q3:   What is the difference between Joe's watch 
            and the red plane's clock when they meet?

      Q4:   What is the difference between Joe's watch 
            and the blue plane's clock when they meet?

Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.

Ana Sayfa / index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy)/Astronomy