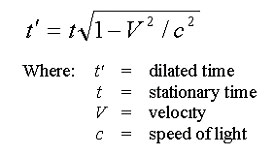| |
Time Travel Research Center
© 2005 Cetin BAL - GSM:+90
05366063183 - Turkey / Denizli
Special Relativity

Galilean and Newtonian Relativity
A -Frames of Reference: The place from which an event is being observed
2.Inertial Frame: A frame of reference that is not being accelerated
3.Invariant Quantities: Measurements that are the same for all observers in
inertial frames of reference
1. Mass
2. Time
3. Distance
4. Velocity Addition:
1- If observers in two different frames of reference (that are in motion
relative to each other) are observing motion of the same object, they will
both measure it to be traveling at different speeds.
2-Mathematically: v2 = v1 + v
a. v: the velocity of frame one with respect to frame two
2. v1: the velocity of the object measured by an observer in frame one.
3. v2: the velocity of the object measured by an observer in frame two.
Example:

a-Bart is in frame one and sees Homer moving at 25 mph (v1).
2-Nelson is in frame two and sees Bart moving at 5 mph (v).
3-Therefore Nelson will see Homer moving at 30 mph (v2).
2- Einstein's Relativity
A.Origins
1.James Clark Maxwell mathematically predicts the speed of light in a vacuum
(but in what frame?)
2.Michealson/Morely Experiment shows that the earth's motion through the
solar system does not appear to affect the speed of light we observe
3.Young Einstein contemplates what it would be like to ride with a light
beam.
2.Postulates (axioms that are to be taken for granted):
1.The laws of physics are the same in all inertial reference frames
2.The speed of light in a vacuum is the same for all observers (Speed of
light is invariant)
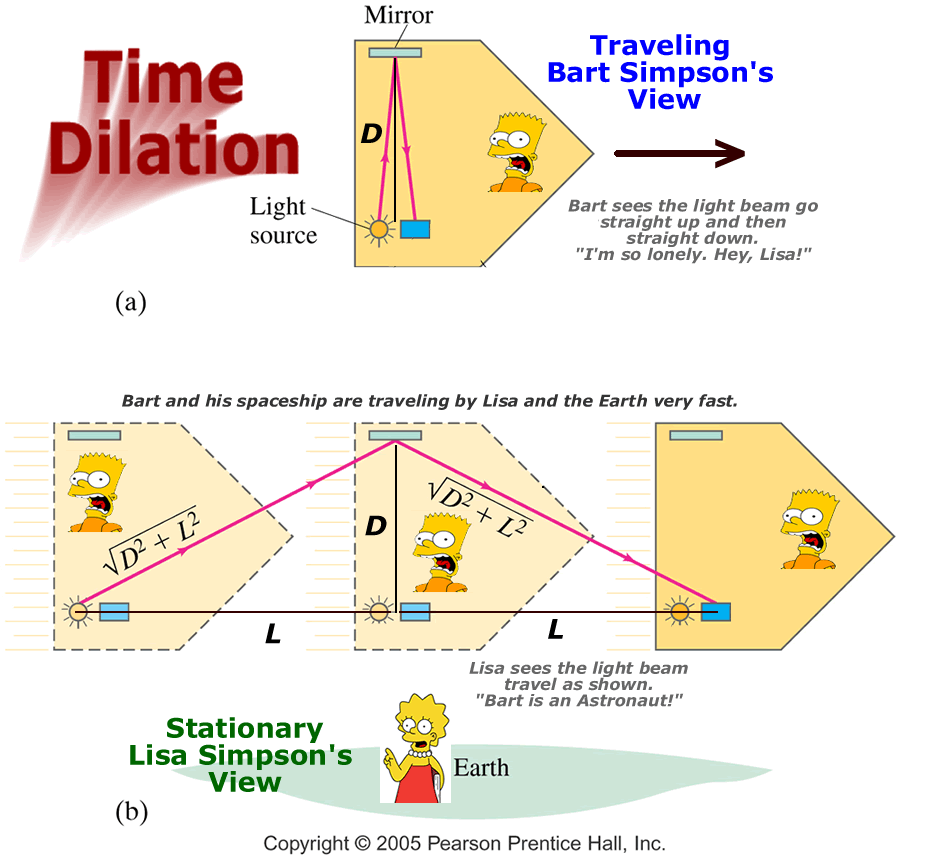
3.Consequence 1: Time Dilation
1.The time that passes while an event is taking place is different in
different frames of reference. Consider the situation depicted below. A beam
oflight is fired through a small hole in the floor of a space ship. The beam
travels to a mirror placed above the hole and bounces back down to the floor.
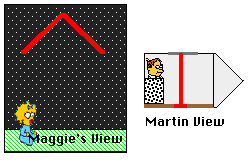
This event is viewed by two observers (one in the ship and one on earth).

2.It is clear that the two observers will see the light travel different
distances. Maggie will see it traveling both vertically and horizontally,
while Martin will see it traveling only vertically. If Einstein is correct
and they both measure the same speed, then they must measure different times
for the event to take place. Martin measures a shorter time because the
light travels a shorter distance.
Mathematically the two times are related by the following equations:
a.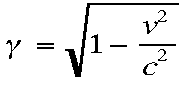
2.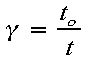
3.to is the time
that passes on the ship (Martin's time) and t is the time that passes on
earth (Maggie's time)
4.Consequence 2: Length Contraction
1.The distance between two points in space also is different in different
frames of reference. Consider the situation depicted below. An Astronaut is
traveling between two planets at a very high speed. This motion is observed
by the astronaut and by a person on one of the planets.
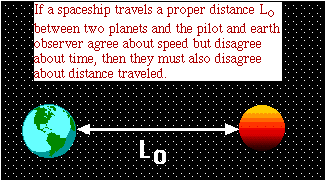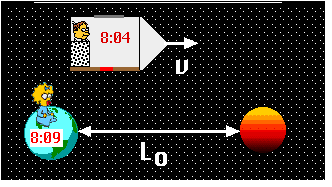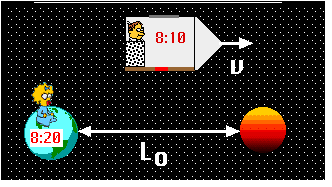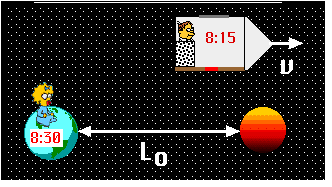
2.Since they agree upon the relative speed of the observer with respect to
the planets but disagree about the time that passes during the travel, they
must also disagree about the distance that is traveled.
3.Mathematically the two distances are related by the equation:
a.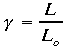
2.Gamma is the same as it is for time and L o is the proper length (the
length measured by the observer in the frame with the objects being measured)
5.Consequence 3: Mass Increase
1.When an object is traveling near the speed of light its mass increases if
measured in other frames.
2.Mathematically the two distances are related by the equation:
a.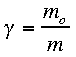
2.Gamma is the same as it is for time and m o is the proper mass (the mass
measured by the person in the frame with the object being measured)
A new exhibit on Albert Einstein dissects his slippery science
Peter Weiss
Science exhibits don't often come with a warning sign. But there's one at
the entrance to a sprawling, new exhibit on Albert Einstein's life and
science at the American Museum of Natural History in New York City. The sign
has no words. It's a video screen whose center is dominated by a dark blob.
Around the blob yawn strangely bloated, bowed, stretched, and sometimes
doubled images of museum visitors. That's how they might appear if light
from them were distorted by a black holean unimaginably dense package of
matter whose existence follows from Einstein's theories.
 |
|
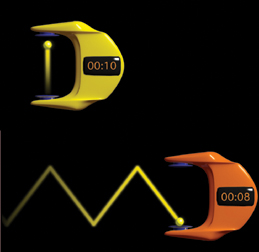
TIME TRAVEL. Animations of clocks that tick when a
light pulse hits a mirror demonstrate time's slowdown for a moving
object (bottom) relative to a stationary one. Because light's speed is
constant and a diagonal path is longer than a vertical one, the orange
clock ticks more slowly than the yellow clock.
American Museum of
Natural History |
What's the message of this cryptic warning? Astrophysicist Michael M.
Shara, curator of the exhibit, translates it this way: "From the minute you
step through the front door, we will twist your view of space and time and
what your entire vision of the universe is like."
The exhibit delivers just that. Using computer simulations of warped
space, time-manipulating soundscapes, and sparkling light sculptures, the
displays immerse visitors in Einstein's counterintuitive science. In the
exhibit's quieter, less flashy galleries, Einstein himself is minutely
scrutinized. With artifacts, film footage, handwritten letters, and other
documents, the exhibit probes Einstein's often-tumultuous lifehis
friendships, loves, and political pursuits. The museum bills the new
displays as "the most comprehensive exhibition ever on the life and theories
of one of the greatest scientists of all time."
Follow the light
Albert Einstein is best known for a handful of monumental achievements.
They include his iconic equation, E = mc2, which
led ultimately to nuclear weapons, nuclear power, and enhanced understanding
of the sun and other stars. Perhaps even more famous are his theories of
relativity, which radically changed notions of time, space, and gravity.
Although most people are aware that Einstein fomented a revolution in
physics, few are acquainted with the specific ideas behind that upheaval,
notes physics educator Gretchen Walker, who helped coordinate the exhibit
for the museum. In the new exhibit, about half the display space is devoted
to conveying the gist of Einstein's most renowned revelations about light,
time, energy, and gravity.
"It's the first attempt to explain the essence of Einstein's scientific
contribution in a museum exhibition," says physicist Hanoch Gutfreund of the
Hebrew University in Jerusalem at the recent launch of the exhibit.
The starting point for those explanations is the nature of light. Is it
just a waveas most turn-of-the-century physicists had viewed itor also a
stream of particlesas Einstein ultimately concluded? If it's a wave, then
what medium does it undulate through? Is it like an ocean wave advancing
through the water?
Einstein already had begun pondering such questions as a teenager in the
1890s. The exhibit includes a sheet from a six-page handwritten letterbilled
as Einstein's first scientific paperwhich the 16-year-old boy mailed to his
uncle. In it, the budding theorist imagines what it would be like to ride on
a light wave.
Scientists at that time considered light to be moving ripples in a
tenuous, uniform medium, called the aether. They presumed that the aether
filled all of space. To test for its presence, scientists observed light
beams propagating simultaneously in perpendicular directions and looked for
a speed difference. The idea was this: Because Earth plows through the
aether as it traces its orbit, light should appear to move slowest along the
direction in which the planet pushes into the aether, quickest along the
opposite direction, and at intermediate speeds along other directions. Yet
the experiments detected no deviation in light's speed, regardless of
direction.
This result deeply disturbed most physicists of the day.
Einstein took the findings at face value, rejected the idea that light
travels through an aether, and went on to explore other logical consequences
of light's apparently constant speed. One deduction is that nothing can move
faster than light.
His cogitations eventually led him to develop the so-called special
theory of relativity, which he first published in 1905. The theory's name
connotes that it is limited to bodies that are moving at a constant speed
rather than extending to objects in any type of motion. In his theory of
relativity, Einstein deduced that time and space themselves must fluctuate.
"He accepted a nonsensical universe," says Shara. With simple animations,
the exhibit demonstrates how Einstein came to that view.
Time rules
Numerous recent experiments, such as comparisons of clocks aboard planes
and on the ground, have demonstrated that moving clocks tick more slowly
than stationary ones. Einstein reached this conclusion theoretically from
the premise that the speed of light is constant. The exhibit illustrates
this logic. Adding eerie ambiance to those time-dilation displays, a
staccato soundtrack of ticking clockssome speeding up, others slowing downplays
in the background.
"It's a wonderful exhibit," comments Princeton University astrophysicist
J. Richard Gott III, author of Time Travel and Einstein's Universe
(2001, Houghton Mifflin). Says Gott: "They picked out a key itemmoving
clocks tick slowlyand explained it three different ways." If one
explanation doesn't get through to a museum visitor, he notes, then another
probably will.
On display also are six original sheetsneatly hand-written by Einstein
in Germanfrom a 72-page, 1912 manuscript on special relativity. Einstein's
relativity investigations included calculations describing what happens to a
body when it emits light. The results revealed that mass (m) would be
transformed into energy (E) by a conversion factor, the speed of
light (c) squared. One of the displayed pages includes the earliest
remaining inscription by Einstein of E = mc2.
To calculate just how subtly or dramatically time will slow down for a
given moving object, it's critical to know how fast the object is moving. To
illustrate that aspect of time dilation, a wall-sized bank of digital clocks
in the exhibit invites the visitor to suppose that Einstein had boarded a
space ship on the day of his birthMarch 14, 1879and zoomed off at various
speeds.
For a half-dozen speeds ranging from that of today's spaceshipsessentially
0 percent of light speedto 99.99999999 percent of light speed, the clocks
indicate today's date as it would be for the space-faring Einstein. For
example, in the slowest ship, Einstein would have aged 123 years, right
along with his friends and family on Earth. At the fastest speed, however,
nearly 20 hours of Earth time would have elapsed for each second that would
have ticked by for Einstein. That means that the baby Einstein who rocketed
away on the day he was born would now be only 1 day old.
Having found a cosmic speed limitthe speed of light, which is almost
300,000 kilometers per secondEinstein also exposed a profound flaw in the
theory of gravity handed down by Isaac Newton centuries before. Newton had
proposed that the force of gravity acts instantaneously to attract two
distant masses to each other. Einstein realized that this couldn't be. His
cosmic speed limit required that nothing, including gravity, could act
instantaneously over a distance.
Developing an alternative explanation for gravity took Einstein a decade.
He published that alternative, the general theory of relativity, in 1915.
The exhibit includes original pages of a hand-written draft of that seminal
report, which extends the unexpected consequences of motion to accelerating
objects.
Ultimately, Einstein showed that gravity's effects result not from
instantaneous action across distances but from a warping of space-time
itself. The sun's mass, for instance, distorts space-time in its own
vicinity. That warping confines Earth and other planets to their elliptical
orbits.
Even people's puny bodies bend space and time, albeit to a negligible
degree. To give exhibit visitors a feel for this usually unperceived fact of
their lives, a computer instantaneously calculates and amplifies their
bodies' gravitation effects on surrounding space. As people approach a wall-sized
monitor, it shows richly colored swells and dips in space-time. The biggest
people and those closest to the wall trigger the most elaborate images. The
display gives weight-consciousness a whole new meaning.
Unfinished business
 |
|
PERPETUAL PONDERER. After early theoretical triumphs,
Einstein tried unsuccessfully to explain within one, unifying theory the
fundamental forces then known: gravity and electromagnetism.
Lotte Jacobi Collection/Univ.
of New Hampshire |
Curiously, all these pursuits stem from work Einstein had done before
1920. Although he continued to work diligently in physics until his death in
1955 at the age of 76, he produced no further landmark theories.
That's partly because Einstein was caught up during his later decades
fighting a futile, rear-guard action against quantum physics, whose laws
govern the realm of the very small. In particular, he objected to the
randomness in particle behavior that the new approach predicted. Quantum
physics proved to be, like relativity theory, a great 20th-century
revolution in modern physics, but it left Einstein behind.
Ironically, Einstein initially helped build the foundations of quantum
physics. Indeed, he won the 1921 Nobel Prize in Physics for a 1905 advance
in which he established a theoretical grounding for the particle-like aspect
of light. The exhibit includes the medal and certificate that he received
with that award.
Also, by continuing to be an astute skeptic, Einstein prodded quantum
physics' developers to improve their theory.
In the latter part of his life, Einstein was also preoccupied with
another theoretical quest. Having already clarified the nature of
electromagnetism and reformulated gravity, the aging Einstein sought to
unite those two phenomena within a single, comprehensive theory.
Rather than considering the last 30 years of Einstein's life a waste,
Columbia University string theorist Brian R. Greene says that the period
"was really what launched the current generation of work in the physical
sciences." In one of the exhibit's galleries, Greene and other scientists
discuss Einstein's scientific legacy in continuously running video clips.
Einstein never stopped his search for a unified theory. The day before
his death on April 18, 1955, from a ruptured aortic aneurysm, Einstein asked
his secretary to bring to the hospital a pad of paper on which he had been
working. That very sheaf of papers, which Einstein smothered with
calculations, serves as send-off as visitors leave the exhibit.
The Human Equation
Taking a comprehensive look at Einstein, the man
Besides being a great scientist, Albert Einstein was a father of the
atomic age, a passionate defender of civil liberties, an ardent pacifist,
and a champion of Jewish causes. Many papers, photos, films, and other
artifacts that illustrate his multiple facets are on display in the new
exhibit at the American Museum of Natural History in New York.
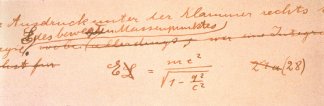 |
|
FORMULA E. Einstein wrote this version of his famous
equation in a 1912 special-relativity manuscriptthe oldest surviving
document with the equation in Einstein's hand. Whereas the simpler form
E=mc2
applies to an object at rest, the version shown here applies also to
moving objects.
Israel Museum,
Jerusalem |
Included is his final high school report card, which dispels the myth
that Einstein was a poor student. In fact, he received good-to-excellent
grades in all subjects, and the highest possible marksall 6sin math and
physics.
A letter from Einstein side-by-side with a response from Franklin Delano
Roosevelt Jr. illuminates Einstein's role in prompting the United States to
develop the first atomic bombs. In those letters, Einstein encourages
research into such weapons, and President Roosevelt confirms that he has set
in motion the machinery to pursue that goal.
Other memorabilia depict Einstein promoting socialism, fighting against
Sen. Joseph McCarthy's anti-Communist witch-hunt of the early 1950s, and
supporting the fledgling State of Israel.
From the collected mementos, a seamy side of Einstein also emerges. In a
letter, Einstein flirts with one of the many women with whom hea married
manhad romantic affairs.
"We don't want to whitewash him," says exhibit curator Michael M. Shara.
"Some of his family relationships were rocky, to say the least."
The Einstein exhibit, organized by the museum, the Hebrew University of
Jerusalem, and the Skirball Cultural Center in Los Angeles, runs in New York
until Aug. 10, 2003. It's scheduled to travel to Los Angeles in 2004 and
Jerusalem in 2005.
Letters:
In your article, you describe Einstein's negative
reaction to Newton's proposition that gravity acts instantaneously on two
objects. The notion of simultaneous (if not instantaneous) properties in
physics is one of the basic notions of quantum physics. I do not feel that
Einstein's "particle-like" description of light makes him (even "ironically")
"a builder of the foundations of quantum physics."
Elmer E. Smalling III
Plano, Texas
I was disappointed to observe in your article the
almost universal distortion of special relativity. What is mind-bending
about relativity is not time dilation. Einstein expanded our universe by
showing that not only will an observer on the yellow clock (in the article's
illustration) conclude that the orange clock is ticking slower, but an
observer on the orange clock will conclude that the yellow clock is ticking
slower, and both will be correct!
David M. Smith
Plano, Texas
Time Dilation
I. Inertial Bodies
In the Orientation page of this document, there is a fairly intuituve
explanation as to why time seems to slow down when observers are in relative
motion.. The following is a more physical description of what happens to
time when the obervers and observees travel at velocities near the speed of
light.
In order to supplement our understanding of the subject, we will use a
time keeping mechanism known as a clock--a light clock in this case. A light
clock, as shown in Figure 1 consists of a light bulb and two nearly parallel
mirrors. A beam of light is sent from the light bulb to the top mirror, then
reflected to the bottom, to the top, to the bottom, to the top, etc... Every
time the beam of light hits the bottom mirror, we say that a "tick" has
happened.
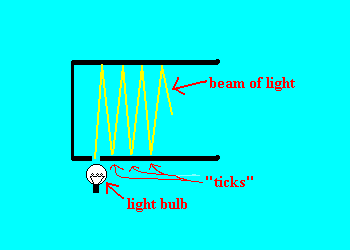
Figure 1: Light Clock
Suppose we take this light clock and accelerate it to to speeds close to
the speed of light. Now, instead of going straight up and down, a beam of
light travels the path shown in Figure 2. The lights starts at the bulb at t
= 1; by the time the light gets to the top mirror (t = 2), the whole clock
is shifted over; and by the time the light gets to the bottom mirror (t=3),
the whole clock is shifted far to the right. So we can see that if the clock
is moving fast enough, a tick will only occur when the light has traveled a
certain length as well as a certain height.
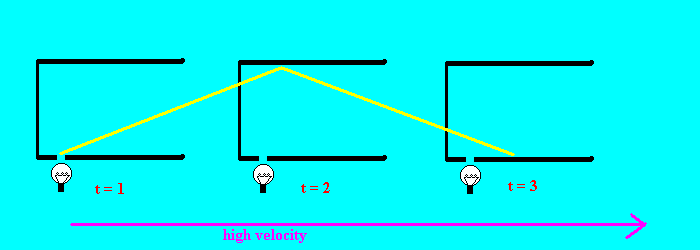
Figure 2: Sushi
Since the speed of light is constant in all frames of reference, and
light is travelling a longer distance, the time between ticks is longer. To
a person standing on top of the clock, time does not slow down; for in his
reference frame, the light is still going straight up and down (at the speed
of light). However, to an outside observer, time has slowed down on the
light clock.
II. Accelerating Bodies
When bodies undergo acceleration, wacky things happen. With inertial
bodies, time slows down mutually . But what if two bodies meet at point A,
accelerate at different speeds, and then meet at the same event (point B).
If time slowed down mutually, could they ever be at the same event again?
The answer is 'no'. In fact, if two bodies meet at point A, accelerate to
different speeds, and then meet at point B, they will notice that a
different amount of time has elapsed for the two of them. This is usually
phrased in term of the twin paradox: If one of two twins goes on a a wildly
acclerating, near speed-of-light escapade while the other twin stays at home
and plays bridge, they will find that (if they meet again) they have
different chronological ages.
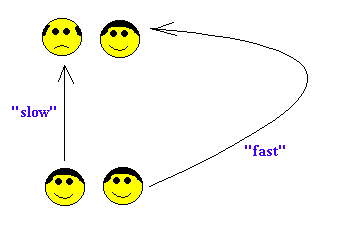
Figure 3: Minkowski Diagram of the Twin Paradox
References:
''A new exhibit on Albert Einstein dissects his slippery
science''
2002. Einstein, a groundbreaking exhibition on
the man and his science premieres at American Museum of Natural History.
American Museum of Natural History news release. Nov. 15.
2002. Einstein, a major new exhibition on the
man and his science, to open at American Museum of Natural History November
2002. American Museum of Natural History news release. July 23.
| |
-----------------------------------------------------------------------------------------------------------------------------------------------
Updated 4/15/03
See new Appendix C-- a critique of Einstein's original paper in
Annalen der Physik, 1905
Also an addition to Appendix A-- a critique of Richard Feynman's
explanation of the Michelson/Morley interferometer from Six Not-so-easy
Pieces.
And a re-running of my equations to show the influence of S0
upon the problem
An Algebraic Correction
to Special Relativity
Miles Mathis
Anyone predisposed to dismiss this paper out of hand should be warned
from the beginning that it is unlike any other critique of Relativity he
or she has read. It is not a philosophical or metaphysical treatise. It
is the discovery of the actual algebraic errors in Special Relativity. I
follow Einstein line by line, and show precisely where the mistakes are.
In this, I believe I may be the first. The most notorious critic of
Einstein, Herbert Dingle, said (Nature, 1967) "I have enough
mathematical insight to see that it is a waste of time to look for
mathematical flaws in the theory." Few, if any, have bothered to look at
the basic math in the years since, believing the equations to have been
already combed by the best minds of the century, and proved beyond a
reasonable doubt by field tests. In the last decade, field tests have
put the equations into question again, although nearly all, if not all,
of the mathematical and theoretical work has gone into making these new
tests fit the equations, rather than vice versa. This paper shows that
the fault lies in the transformation equations, and is easily
correctable.
I rush to add that in correcting the transformation equations of Special
Relativity, I am not thereby exploding Relativity in toto. I
accept time dilation and length contraction as a fact. I accept the
speed of light as a constant. My critique of Einstein's equations is an
effort to fine tune them, not to jettison them.
Specifically, this paper was written in response to the call by the Jet
Propulsion Lab for help in understanding why the equations of Relativity
were yielding wrong numbers in their calculations on space satellites.
To date, no explanation has been offered that explains the discrepancies,
despite many replies to the call for help, and many theories published
in Physical Review Letters and elsewhere. My paper is unique in
that it offers new transformation equations, with which I make
predictions about the numbers generated by JPL. That is, I have solved a
concrete problem of applied mathematics, and I have the numbers to prove
it.
I first discovered the central tenets of this paper in November of 2000,
although I had been working on and off (mostly off) on the problem ever
since my first reading of Einstein's book Relativity in high
school. The bulk of the paper was written before Thanksgiving of 2000,
and it was in final form before the end of that year. I have spent the
last two years trying in vain to get the paper published (in Physical
Review Letters, Annalen der Physik, et. al.). PRL refused on
length considerations-- they have a 4 page limit. AdP did not
comprehend my argument. I am not sure they read it, or made any attempt
to understand it. I have therefore resorted to self-publication on the
web, hoping that by so doing I will be able to make proper claim to the
ideas in it, should any argment arise to precedence.
I began working in earnest on the paper in late 1999, after reading an
article in Newsweek reporting that the Jet Propulsion Lab was
getting inaccurate numbers for its space satellites using Einstein's
equations. I saw immediately that here was a concrete problem, one that
went well beyond all the theoretical arguments about Relativity that I
had read. What seemed to me to be necessary was a mathematical, as
opposed to a theoretical, critique of Relativity-- a critique that
showed specifically where the math was wrong. Corrected equations would
then allow me to make real predictions about these space satellites.
That is precisely what I have done in this paper. What follows is the
paper almost exactly as it was presented to PRL in early 2001.
(Cover Letter)
This paper is a straightforward correction of the Lorentz equations
used by Einstein in Special Relativity. It is a correction that has
never been discovered or put forward since the publication of Einstein's
original paper in Annalen der Physik in 1905. The correction is
a simple algebraic critique of the primary equations Einstein presents
in that paper and in the book Relativity. This paper is not a
philosophical treatise, or a discussion of theory. It is the discovery
of the actual mathematical errors made in Special Relativity by
Einstein, and by Lorentz insofar as he influenced the math of
Einstein. Nearly all the math in this paper is high-school algebra,
and may be understood by any educated reader.
You may ask why a correction is necessary, considering the success
of Relativity in the 20th century and the currently unassailable status
of the equations. It is necessary for several reasons. First of all,
the equations are yielding unresolvable data from space satellites.
This has been known for several decades, and was reported on most widely
by Newsweek in 1999. In addition, data from Io (Jupiter's moon)
that has been an accepted part of the canon for centuries contradicts
the Lorentz equations: this has never been resolved. More recently, the
binary pulsar PSR 1913+16 has presented similar data, though its
significance has never been related to Special Relativity. Other
experiments and theories in the recent past have also been undermined by
the Lorentz equations (and their corresponding General Relativity field
equations) including calculations of redshifts, the Hubble constant, and
all theories dependent on these numbers. Likewise, data from particle
accelerators is dependent upon these equations to yield useful
information, and many unresolvable situations have occurred,
unexplainable with the current Lorentz transformations and the field
equations derived from them.
I think you will be shocked at the simplicity of the error made by
Einstein and the simplicity of the new equations. It is not that
Relativity is more difficult than we imagined. It is that Einstein and
Lorentz made it seem more complex than it really is. The new equations
and explanations are not more esoteric than those of Einstein. They are
vastly more accessible and understandable. And they mesh much more
easily with other accepted knowledge.
One other thing must be mentioned: despite the large cosmetic
changes in the equations (they look quite different-- they are much more
elegant, for one thing), they provide only a small change in the actual
predictions of science. As I show in the paper, Einstein's equations
have stood for so long because they mirror the correct equations in many
instances. At the speed and trajectory of a space satellite, for
instance, Einstein's equations fail by only the tiniest of fractions.
Not coincidentally, this tiny failure is precisely equivalent to the
observed failure. I think you can see how powerful this makes my
equations. They correct a standing theory without destroying it, and
make that theory infinitely more amenable to facts as well as to
commonsense. This at the same time that the mathematics of the theory
is clarified and simplified.
Physics has so far resisted any questioning of Special Relativity
for two reasons. One, because the specific mathematical errors could
not be pointed to, incontrovertibly. The "density" of the theory had
made it very difficult to unwind. Two, because so much of recent
science depends upon the continued strength of Relativity. Between them,
the math of Relativity and Quantum Mechanics support most of the
equations of contemporary physics. If Relativity should be thrown out,
where would that leave us? The corrections I offer below will, I
believe, revolutionize many areas of physics; but they do not threaten
to undermine the foundations of Relativity. The phenomena of time
dilation and length contraction, for instance, are made even more
certain. And the theoretical justification (or interpretation) of these
phenomena is made transparent even to the layperson-- which only serves
to make the theory stronger.
This all goes to say that institutions like the Jet Propulsion
Lab will breathe a great sigh of relief: they will get an answer to
their decades-old problems without having to bring the walls of science
down to do it.
P.S.(to Annalen der Physik) The Jet Propulsion Lab published a
request for assistance in Physical Review Letters several years
ago, on the problem of the satellites. They received many replies, but
no solution. None of the replies concerned Special Relativity. I have
previously sent this paper to Physical Review Letters, but they
have refused to publish it due to its length. I cannot make a suitable
critique of Special Relativity in just four pages. As your length
criteria are more lenient, and as the problem directly concerns a famous
theory first published in your journal, I thought it might be of
interest to you.
An Algebraic Correction
of the Transformation Equations
(the Lorentz Equations)
of Special Relativity
Abstract
In this paper I will show that the first equation of Special
Relativity, the famous x' = x - vt, is fatally flawed. I will do this
with simple high-school algebra.
I will then show that a basic substitution error by Einstein in the
derivation of the term gamma (caused, in part, by the error above
and in part by math borrowed from Lorentz) leads to transformation
equations that are subtly flawed. I will also show why Einstein's
equations are so nearly correct, despite being arrived at by faulty math.
Next, I will correct these errors and offer new transformation
equations. These new equations will be arrived at in a straightforward
way, again with simple math. Furthermore, I will show that Einstein's
transformation equation for velocity is in fact an equation for two
degrees of relativity, and that there is presently no equation for one
degree of relativity. I will offer a transformation equation for
velocity with one degree of relativity. I will derive this equation
using only simple algebra-- without the use of calculus.
I will then derive the corrected transformation equation for two
degrees of relativity, for velocity. Again, I will do this without
resorting to calculus.
Next, I will solve the specific problem of the Jet Propulsion Lab,
making a prediction for the exact amount of error in Special Relativity
that leads to the faulty numbers in General Relativity.
Next, I will show that the present interpretation of Special
Relativity-- as applying equally to objects in all relative trajectories--
is in direct conflict with other currently accepted facts, including
Roemer's calculations on Jupiter's moon Io and data from the binary
pulsar PSR 1913+16. I will show the simple and inevitable resolution
of this conflict.
Next I will prove that Lorentz made the same error as Einstein, and
that this error was caused by a faulty interpretation of the Michelson-Morley
interferometer. I will show that the diagram used to visualize the
interferometer by Lorentz, Michelson, and every physics textbook in the
20th century is conceptually flawed. And I will show precisely where
this flaw lies, mathematically, and how it led to the equations of
Special Relativity-- especially the Pythagorean component of gamma.
Finally, I will interpret the new equations, showing how they must
change our conception of the nature of Relativity, and of light, and of
measurement itself.
Introduction to the Problem
Only very recently has there begun to be a general acceptance, by the
status quo, that Special Relativity might be subtly flawed in some way.
For most of the 20th century, of course, it was sacrosanct. No one, in
the mainstream, would have thought to question it in any way. But now
there is beginning to be an accumulation of data that does not fit
Einstein's transformation equations precisely. The data that led me to
work seriously on the problem was supplied by the Jet Propulsion Lab.
For several decades, various space satellites have been found to be
acting a bit strangely. They are not where they are predicted to be,
according to relativistic calculations. The scientists who manage these
craft have dismissed any number of explanations for the discrepancy,
supplied to them by many of the best technicians in the field. But
still the problem is unresolved. It has proven to be such a thorn that
the JPL has even gone to the mainstream publications in the United
States, begging for help. Newsweek published a major article on
it in 1999.
Einstein published his paper on Special Relativity in Annalen der
Physik in 1905. The book Relativity was published for
general audiences in 1916. It has gone through many editions, but the
theory itself has not changed in the last 97 years. Einstein made
several predictions, which were confirmed by subsequent data, and the
theory quickly achieved a solidity and a fame that is perhaps unmatched
in history.
His intention was to reformulate Newton's equations for velocity to
conform to the latest facts. Light had recently been shown to have a
finite and constant speed, and Einstein saw that this would affect
calculations of position and velocity of measured objects. He saw that
the measurement of time would be likewise affected.
Light was proven to have a constant speed, regardless of the speed of
the observer, by the Michelson-Morley interferometer. The
interferometer (which is diagrammed in this paper) was designed to show
the velocity of the earth relative to the "ether." It was assumed
that light traveled either through, or relative to, this ether; and that
therefore the velocity of the earth would have to be added or subtracted
from the velocity of light. But the interferometer found that the
earth's velocity had no affect upon the measurement of the speed of
light, from any direction. This was one of the most mysterious outcomes
in the history of science. In trying to explain this null set, Heinrich
Lorentz proposed a set of contractions and expansions that would offset
the predicted measurements, bringing them into line with actual data.
His fudge-factor turned out to be a now famous term called gamma.
Not accidentally, Einstein's basic transformation term is also
gamma. Einstein was working independently of Lorentz, and on a
different problem. But they both used the same concepts, and the same
math, and so came to the same term.
Einstein began his derivation by postulating two co-ordinate
systems, S and S'. S is the co-ordinate system of the observer. S' is
the observed co-ordinate system. He then provides us with the basic
equation x' = x - vt, which he tells us is the Galilean transformation
equation from one system to the other. This also gave him x = x' + vt,
he assumed. He then produced the equations x = ct and x' = ct' to
show the distance light travels in the two coordinate systems. He
introduced gamma as the transformation term, as in the equation
x' = y(x - vt) where y is gamma. By
substituting values among these four equations, he achieved a value for
y in terms of his other variables.
Quite simple, really. Except that he never precisely defined his
terms. Not in the original paper. Not in the book. Not ever. And no
one has ever questioned these terms. What, for example, does v stand
for in the first equation? Is it the velocity in S or S'? One assumes
it is in S, since v is not prime. But we, the observer, are in S. If
we already know v, what are we looking for? What I mean is, v is how
the situation looks to us. Therefore, v is already a relative velocity.
If this is true, then what does the transformation equation tell us--
what is that value of v that we get at the end? On the other hand, if
the given v is really the v in S', it should be labelled v', to be
consistent. And that begs another question. How could we be given the
v' in S'? according to the current interpretation of relativity, we
cannot know what is going on in S' without a transformation equation.
We would then need a transformation equation in order to calculate one.
The mysteries of Special Relativity have been considered up to now
to be inherent in the problem. We have been told that it is not
comprehensible by ordinary mortals. It is subtle and complex, and all
one can do is accept the paradoxes. That is all part of the fun,
frankly. If it were transparent, it wouldn't be deep. This is the
current wisdom, anyway.
Unfortunately, it turns out that the confusion is Einstein's (and
Lorentz's) from the beginning. It is possible to define the terms
precisely enough that all the mystery disappears. We are then left with
distressingly simple equations that almost anyone can understand.
Over the last century there have been any number of lengthy
critiques of Special Relativity. All of these critiques, though, have
been no more than philosophical attacks upon the theoretical assumptions
and conclusions of Relativity as a whole. No one has yet been able to
point to the specific errors in the mathematics. Admittedly, Einstein's
explanations made this quite difficult to do. And the spectacular
successes of the theory acted as a sort of protective wall, keeping it
from being seriously questioned. Institutions like the Jet Propulsion
Lab could not publicly (or even privately) question such a fortified
theory, without direct mathematical evidence. I only hope the
following paper will begin the thaw.
The Equation
Einstein begins his book Relativity with a famous thought experiment.
It involves a railway embankment, a train, and a man on the train. The
train moves with a constant velocity v. Later, the man also moves, with
regard to the train. But for now we will limit ourselves to the train
and the embankment.
Let us start with an illustration.
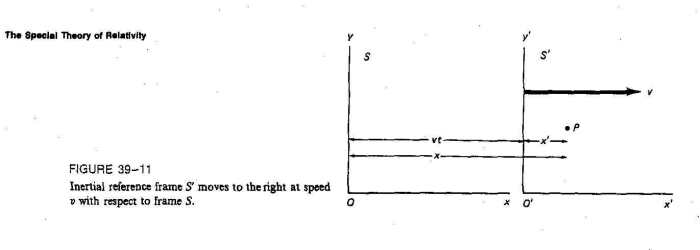
This illustration is very much like Einstein's train
illustration in the book Relativity, but here the artist has
tried to graph x', x, and vt. The man is at point P. We, the observers,
are understood to be watching from the embankment in S, the co-ordinate
system to the left
To go with this thought experiment, Einstein gives us this equation
(p.33, Rel.),
x' = x - vt
In his original paper of 1905 ["On the Thermodynamics of
Moving Bodies"], he gives the same equation. But neither there nor in
the book Relativity does he say where this equation comes from--
nor does he define any of the terms in the equation. In both instances
he simply pulls the equation from nowhere.
In the 1905 paper, the equation is completely mysterious; but
in the book he gives us a small clue. There Einstein says that this
equation is the Galilean transformation for the thought problem
illustrated above. Galilean simply means "classical" or pre-Einsteinian.
If you assume an infinite c, and equal t's, then the Lorentz
transformation for x reduces to this, he says.
But let's look closely at the illustration, and see what we
can find.
First of all, we are given that P is not moving in S'. The man should
not be moving with respect to the train at this point in the thought
experiment, as I said above. We know this for several reasons. One,
because Einstein in the book has given us v, the velocity of the train
relative to the embankment. But he has not given us a second v-- a v',
say-- as the velocity of the man relative to the train. There is only
one v in the equation above. Two, because Relativity is now used to
find the time dilation of a single observed object. Not an object
within an object (like a man moving in a train), but simply an object (the
train). Sub-atomic particles in quantum experiments are routinely found
to be time-dilated, for instance, but they cannot possibly be thought of
as an object within an object. The Lorentz equations for x and t (that
Einstein derives from this thought experiment) are-- or should be--
equations for only one degree of relativity. Meaning the train relative
to the observer, but not also the man relative to the train.
But if P is not moving in S', then x' is a meaningless
distance in this illustration. What I mean is that it would have been
simpler to place P on the y'- axis. If P does not move relative to the
x'-axis, then you just have a single velocity. It is easiest to graph a
single velocity by putting it at zero to start with.
In this case, its Galilean equation should be simply x = vt.
This is the equation we all learn in first-year physics.
But, of course, P may be placed anywhere in S' and we should
be able to write a transformation equation for it. Perhaps Einstein had
a reason for not putting P on the y'-axis. So, let's leave the man at P
and see if we can make sense of that.
If this is supposed to be an equation for a Galilean transformation,
what is x'? What I mean is, how can there be an x prime in a
Galilean transformation with one velocity? If there is only one t
and only one v, how can there be two x's? How could a train moving
with regard to a embankment, or a dot moving with regard to an eye, in a
Galilean system, have an x prime? x is its displacement with regard
to the eye. What is x' its displacement with regard to, in a Galilean
system?
The truth is, a Galilean system with one velocity allows
of no prime variables.
The equation x' = x - vt is a hybrid equation. It is part
Galilean and part Einsteinian, or relativistic. I contend that it is a
muddle.
Einstein's initial equation is supposed to be a classical equation. It
is supposed to be the classical reduction of a Relativistic equation.
But what he gives us is an equation that already assumes that every
moving object carries a co-ordinate system with it. As you can see,
the equation
x' = x - vt is neither classical nor relativistic. It does not
conform to any hypothetical reality in either theory. It is not a
true classical equation, since in Galilean space it is false, even
nonsensical. Nor is it a relavistic equation. As we know, the
relativistic equation includes the term gamma. Put simply,
Einstein has derived his equations from a non-working equation.
To prove this, let's go back to the illustration. Look closely. If P
does not move, x' is either 0, if it is understood to be the change in
x relative to S'; or it is the line marked vt, if it is the change in x
relative to S.
But let us consider the possibility that in the equation x' =
x - vt, Einstein means not x(prime) but x(initial), as in the
equation
vt = x(final) - x(initial)
This gives the equation the proper form, at any rate. Because
this form looks so familiar, every physicist in the 20th century has
accepted Einstein's first equation without question. At first glance,
it does seem to fit the situation. But Einstein's equation is subtly
different from this "change in x" equation.
This "change in x" equation is simply telling us that the man
starts out some distance x from the y'-axis. It is highly confusing for
Einstein to call it x' in this problem, as I will show. It would have
been better to label it xi -- for x(initial).
I have pursued this "detail" for a reason. Einstein derives the Lorentz
transformations from this equation. His derivation in appendix 1 in
Relativity is hard to follow, and I will not describe it here.
Physics textbooks now commonly derive it in this way:
Assume x' = x - vt
Assume that the transformation from Galilean equations to
Relativistic equations will be linear. Then
Step 1: x' = y(x - vt) where y is
the transformation term we seek.
and x = y(x' + vt')
[Notice the t' in the last
equation. Einstein did not label his t in
this equation t', but physics
textbooks have changed
the notation in order to make
the equations derivable.]
Now, says Einstein (following Lorentz), light travels in these
coordinate systems (S and S') in this way:
Step 2: x = ct and x' = ct'
Substituting the first equations into these equations gives us:
Step 3: ct = y(ct' + vt') = y(c
+ v)t' and
ct' = y(ct - vt) = y(c
- v)t
If we substitute t' from the second equation into the first, we find
that
Step 4: ct = y(c + v)y(c -
v)(t/c) = y2(c2 - v2)(t/c)
Cancel out the t on each side and solve for y:
Step 5: y = 1/(1 - v2/c2)1/2
This is the famous transformation term gamma.
But notice that x' in the equation x' = ct' cannot possibly be thought
of as xi or x(initial). It is obviously the change in x
during the period t'. However, the change in xi during any
t' will always be zero, because P is not moving in S'! The fact is, xi
is not a variable in S', at this point in the problem. It is a constant.
But x' in the light equation is a variable. It is the distance
light travels according to the clock on the train.
x' in the equation x' = ct' is not the same as xi
But Einstein substitutes one for the other. He and every
physics textbook in the 20th century have performed an illegal
substitution in Step 3.
Therefore gamma is arrived at by faulty math. It is
false.
~~~~~~~~
Another thing is strange here. Everyone knows that Einstein used the
Lorentz equations to find that time appeared to slow down and x appeared
to get shorter. But let's look for a moment at the two light equations
above. The light equations Lorentz and Einstein both used:
x = ct
x' = ct'
If these are true,
then c = x/t from the first of these equations
and x' = xt'/t by substitution
so x'/x = t'/t
This means that in these equations the apparent change in x
is proportional to the apparent change in t.
But when time slows down (in any system, or by any means of
measurement), the period gets larger. Time slowing down implies a
larger t, not a smaller t.
That is, t should appear to get larger as x appears
to get smaller.
Einstein even states this outright, in the book Relativity. He
says (p. 37) "As judged from K, the clock is moving with the velocity v;
as judged from this reference body, the time which elapses between two
strokes of the clock is not one second but gamma seconds, i.e. a
somewhat larger time. As a consequence, the clock goes more slowly than
when at rest." Again, he says "a somewhat larger time."
Physicists have focused on the sentence after that, up to now. But time
is not defined by the rate of the clock, not even by Einstein. Or stated
more precisely, time is not measured that way. Relativity is primarily a
theory of measurement, and so what is required is an operational
definition of time. Not what time is as an abstract concept, but what
time is as a measured quantity. Time is the length of the period, as
Einstein flatly states here. A second is not a stroke of the clock. A
second is the gap between strokes. It is a distance, by every
operational use of that word. Time is not the strokes of the clock, it
is the time between strokes of the clock. This is no semantic difference;
it is a matter of the definition of time. [To consider this question
further, see the links at the end of the paper-- a discussion of this
definition with several scientists and mathematicians, and a paper on
the operational definition of time.]
x and t should be in inverse proportion!
So, we should find that
x/x' = t'/t t = t'x'/x x = x't'/t
or xt = x't'
And, if x = ct
then c = x't'/t/t
and x' = ct 2/t'
Only if t = t' does t2/t' = t'
Einstein states that t does not equal t'
therefore x' does not equal ct'
Even the light equations were wrong!
~~~~~~~~
Let us go back for a moment to the first equation, x' = x - vt
Again, this is supposed to be the Galilean transformation equation
for x. Einstein says, (p. 33, Rel.)
"If in the place of law of the transmission of light we had taken as our
basis the tacit assumptions of the older mechanics as to the absolute
nature of times and lengths, then instead of the above we should have
obtained the following equations:
x' = x - vt
y' = y
z' = z
t' = t
"This system of equations is often termed the 'Galilei transformation.'
The Galilei transformation can be obtained from the Lorentz
transformation by substituting an infinitely large value for the
velocity of light c in the latter transformation."
But this is not the case. There is no such thing as a Galilei
transformation equation. For Galileo and Newton, no transformation was
necessary for a linear problem like this. x in S' would equal x in S.
The whole universe was a single co-ordinate system, and the train would
not have been given a system of its own. It is clear that the equation
for x in a Galilean system would have looked just like the other
equations (for y, z, and t). Meaning, x' = x. Or x = vt. But not,
x' = x - vt. This is one of the biggest mathematical blunders in history,
sitting in the open for a century. And until now unquestioned.
The equation cannot possibly give us a reasonable value in the situation
that Einstein diagrammed, with the train. Let us say we are with
Galileo, and we are looking at the train go by, and we want to calculate
a velocity for the train. How would we do this? I think you can see
that in the equation
x' = x - vt, x' is going to be zero, because x = vt.
And in the equation x = x' + vt x is always going to be 2x'.
As a Galilean equation, the equation makes no sense.
But even as a Lorentz equation, the equation makes no sense. Let us
look at Einstein's transformation equation for x.
x = x' + vt
(1 - v2/c2)1/2
At low values for v, x is greater than 2x'. You may say, But if v is
zero, then x = x'. Yes, but for any velocity greater than zero, no
matter how slow, x is greater than 2x'. I do not even understand how
one might go about plugging numbers into such an equation. What if our
train is going ten miles per hour? And what if we watch it for a hour?
Does Relativity want to tell us that the train is going to appear to
have gone more than twenty miles?
The truth is, the transformation equations don't even begin to make
any sense until they have been differentiated, in which case most of the
difficult terms drop out.
Those with a knowledge of Special Relativity will interrupt here to
point out that the transformation equation for x is only used to
generate a length contraction equation, in the form
L' = L[(1 - v2/c2)1/2]
This equation, at least, is in a sensible form. But I must point out
that length contraction along the x-axis implies a contraction of the
entire x-axis. Which is a contraction of distance. Which should have
been given us by the equation for x. [To get to the L equation from the
x equation requires more sleight of hand, which I pick apart in Appendix
B, if you are interested. Suffice it to say here that the x equation is
not used by scientists, since none of them can say how it might be used.]
I also must point out that relativistic equations are used on
quanta, which have no "length." And yet distance projections are made,
such as the distance a particle will travel before breaking up.
And the satellites of the Jet Propulsion Lab are slowing down in
ways that are subtly unpredictable by Relativity. This is obviously a
problem of distance, not of length. Nobody at JPL cares whether the
satellites are getting shorter. They care whether the total distance
traveled is getting shorter. So the transformation equations are being
misused, simply in order to make them work at all.
~~~~~~~~
Some physicists may now be shaking their heads, saying to themselves,
"no, no, no." They will say, Einstein's first equation describes a
completely different situation than the one I have plotted and critiqued
above. They will say that the equation x' = x - vt breaks down in a
wholly different way.
The equation may be thought of in this way, they will say:
Since, in general, x = vt, x' = x - vt may be thought of as
(some x) = (some x) - (some x)
It corresponds to the equation in the book that Einstein offers:
w = c - v
where w is the velocity of a light ray relative to the train,
c is the speed of light as measured from the embankment,
and v is the speed of the train
In fact, Einstein draws the analogy directly between the two equations.
Therefore we may think of the first "some x" as taking the place of w.
Therefore x' is the displacement of the man relative to the train,
vt is the displacement of the train relative to the
embankment,
so x must be the displacement of the man relative to the
embankment.
I say, this makes perfect sense except for one thing. The notation of
the variables is imprecise and confusing. x and vt appear (because
of the fact that they are both unprimed) to be in the same co-ordinate
system. But they are not. A much better notation would be the
following:
x" = x - v't'
This tells us that we have three co-ordinate systems-- the system of the
embankment, the train, and the man. And this notation stands to remind
us that the given velocity is v' : the local velocity of the train. It
is the velocity of the train as measured from the train, not as measured
from the embankment. Einstein never differentiates between the two. He
never gives us an equation to find the velocity of the train as measured
from the embankment-- which would be simply v. The v he derives in
Chapter XIII (on Fizeau) is the velocity of a moving man on the train,
but it is for two degrees of relativity. He gives us no equation (and
we still have no equation) for a single degree of relativity -- the
relative velocity of the train.
You may say, simply set the velocity of the man to zero and run the
equation. This will give the velocity of the train. But it won't, for
several reasons. One, because the current Lorentz equation for velocity
resolves to unity if you plug in zero for one of the given v's. It
tells you that your relative velocity is equal to your given velocity--
the local velocity of the train. This is no surprise, since Einstein
never differentiated between the two. This becomes crystal clear if
you set x" to zero in the last equation above. The equation then
becomes x = v't'. This tells us nothing. It also does not give us
an equation that can be manipulated by substitution in the way Einstein
manipulated his equation. What I mean is, x = v't' cannot yield the
term gamma.
~~~~~~~~
So far I have only done a critique of the algebra of Special Relativity.
But the math more commonly used in Special Relativity is calculus. It
has taken this form:
Let us say the man at point P in the illustration above is moving. The
velocity of the man as seen from the embankment is therefore
W = dx/dt = d[y(x' + vt')]/dt' where y is
gamma
Differentiation yields the equation
W = v' + v
1 + vv'/c2
But the form of this differentiation assumes that W = v' + v
where v' = the velocity of the man relative to the train, and
v = the velocity of the train
If v' = 0, then the equation resolves to W = v. v is a given quantity,
so the equation yields no information.
Einstein's equation for velocity tells us how fast the man appears to us
to be moving, if the man is moving in the train. But if the man
is not moving with regard to the train, the equation tells us nothing
about the apparent velocity of the both the train and the man relative
to the embankment. No one has seemed to notice that the train has a
relative velocity of its own. Or, if you take the given v as the
velocity of the train as seen from the embankment, then no one has
noticed that the train will have a local velocity that is different from
this observed velocity.
Look again at the beginning of this calculus problem as I have
stated it here. I have stated it as Einstein and the current textbooks
state it: "Let us say that the man... is moving." Notice that there
is no distinction in this sentence between 1) the man moving because he
is moving with regard to the train, or 2) the man moving simply because
he is seated in the train, and the train is moving.
By differentiating an equation of this form, Einstein has arrived
at a velocity that is in fact relative to two degrees. That is, the man
relative to the train, and the train relative to the embankment. The
current transformation equations do not derive a value for the relative
velocity of the train. Einstein and all the physicists of the 20th
century have not even noticed that this value is necessary-- that it is,
in fact, the value we were seeking in the first place. Nor have they
noticed that physics has ended up conflating, or substituting, one value
for the other. This confusion of terms has never even been noticed,
much less resolved.
~~~~~~~~
In glossing the calculus of Special Relativity in the section above, I
said that Einstein's equation for velocity gives us a number as long as
the man is moving with regard to the train. What I did not say is that
it gives the wrong number for that as well. It is wrong not only
for the substitution and conceptual mistakes I have already outlined,
but also for the following reason.
The main feature of the Lorentz equations is the term y, which I
have let stand for the Greek letter gamma (since this program
does not allow for Greek fonts). As I said above, Lorentz and Einstein
calculated gamma to be
y = 1/(1 - v2/c2)1/2
Where did they get this? Lorentz arrrived at gamma first, and
his thinking was not precisely the thinking of the substitution
equations I have listed the steps for above. It is obvious from its
form that gamma comes from applying the Pythagorean theorem to
something. But what? Lorentz intially came up with his equations to
answer the findings of the Michelson-Morley interferometer experiment.
This was before Einstein proposed the theory of Special Relativity. I
break down the interferometer experiment in appendix A, but a simpified
illustration here will show where the Pythagorean theorem comes from.
This illustration is directly from a college physics textbook, in the
chapter on Relativity.
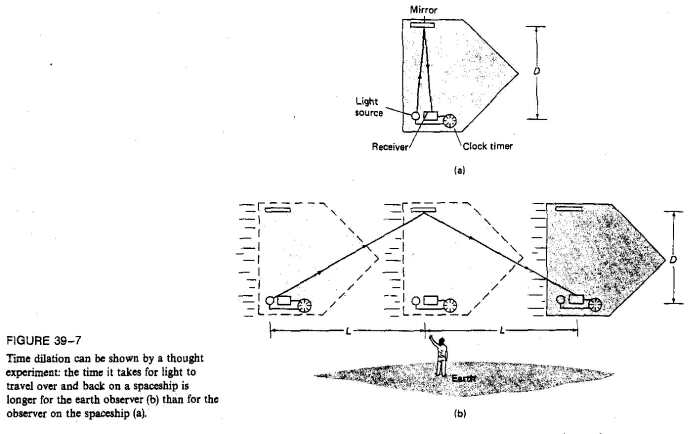
We have already seen two algebraic errors by Einstein in the invention
and derivation of the Lorentz equations. The third-- Lorentz' use of
the Pythagorean theorem in deriving his original equations-- arises from
the problem illustrated above.
What we find in the illustration is a spaceship with a light
projector inside. The spaceship at the top is the S' system, and it
illustrates the path of the lightray as seen from inside the spaceship
(a). Below is illustrated how the path of the lightray would look from
the outside (b), to a stationary observer on the earth. This is the S
system, obviously.
We are told that the observer on earth would observe the process
in (b) as it is illustrated. But notice that in (b) the lightray is
moving tangentially to the observer on earth. I hope is is obvious that
our observer cannot see this lightray. No one can see a tangential
lightray! We only see lightrays that come into our eyes. Every
lightray we see is coming directly toward us. We have no knowledge of
lightrays moving away from us or moving tangentially or even just
missing us. To have information about the situation on this spaceship,
we must be sent a signal from the ship directly toward us. In this
illustration, the editors of the book are performing equations on
imaginary light paths. Not observed paths, but abstractions. This is a
grievous conceptual error.
In the (a) part of the illustration, time is being measured by
observation. In the (b) part, time is measured by the imagination. Or,
to put it another way, in (a) the local observer is collecting real
data. Lightrays are entering the "receiver." In (b) the observer is
not basing his equations on collected data. He is not even collecting
any data. There are no lightrays coming toward him. In reality he
would not be seeing anything. The spaceship would pass him by, unknown.
He is making assumptions. He is assuming that if he could see
the same lightray (a) sees, it would be traveling in this manner. But
this is not observation, much less measurement. It is simply bad
methodology, and bad math.
The Michelson Morley interferometer was invented to to test the
situation described above. You can see how the Pythagorean theorem
would be used to calculate the distance light travelled in (b) given the
distances D and L. D and L are the sides of the triangle and the path
of the lightray in (b) is the hypotenuse. The Lorentz equations,
applied to the interferometer, work in exactly the same way. The
Lorentz transformations take us mathematically from (a) to (b).
This would be fine if the light ray appeared from the earth to
travel that path or that distance. But, as I said, the little man
waving does not observe that hypotenuse. It absolutely cannot be
part of his data!
One of the outcomes of Einstein's relativity is that all events are
local. That is, all measurements (of time, distance, etc.) are good
only for the measurer. Another measurer in another place will get
different measurements. And yet, by applying the Pythagorean theorem to
this situation, the authors of the textbook are attempting a non-local
measurement. They are taking information obtained in a local field [specifically,
the distance D, obtained by local measurement in (a)] and transferring
it into a non-local reference field [the field in (b)]. This is not
allowed, by the very theory they are trying to prove. In this way, the
argument is circular. In order to prove that all events are local, and
that time and distance are relative, they assume that quantities can be
transferred from one system to another, and that D and L in (a) are the
same as D and L in (b). But quantities like D are transferable only if
t and x are equivalent in both fields. Besides, D is a local
measurement of the co-ordinate system (a), while L is an observed
distance in (b), and yet they are treated exactly the same. No
transformation equations are done on either one before they are plugged
into the same right triangle!
I say "they," but it is not just the authors of this textbook or
the artists of this diagram. Lorentz and Einstein do the same thing.
Every illustration or conceptual analysis of this problem I have ever
seen makes this same error. The Lorentz equations came from precisely
this sort of diagram, and the Michelson-Morley experiment accepts it as
a given. It is the very reason that the Lorentz equations have the form
they do. If this diagram had not been the accepted view at the time of
the Michelson-Morley experiment, the Lorentz equations would not have
had the form of the Pythagorean theorem. As I will show, the true
equations for simple time dilation have no Pythagorean component at all.
[The equation for an object moving at an angle to an observer will use
plane triangle trigonometry, but not the Pythagorean theorem].*
*To read more about Michelson-Morley, or to see a diagram of the
interferometer-- and see its equivalence to the diagram above-- see
appendix A.
New Transformation Equations
Now let us derive new equations, correcting the mistakes we have
uncovered. Since the end result of the transformation equations has
always been the ability to derive a relative velocity from a local
velocity (or other known quantities), we should ask, what do these terms
mean? What is a local velocity and what is a relative velocity? It
turns out that these definitions are strictly practical. That is, these
velocities are determined by how we measure them. Historically we have
always measured velocity by one of two methods:
1) We measure our own velocity by using a clock and by
measuring our change in x relative to a known background. As an example,
if we were driving in a car (but did not have a built-in speedometer) we
would have to make use of mile markers. We would take note of the
markers as we passed them; and then, using our on-board clock, we would
calculate the velocity. Please notice that in this case we see the
markers from a negligible distance. The speed of light does not affect
our calculation, because we are at mile marker x when we see mile marker
x.
2) We measure the velocity of an object at some distance. This
measurement is arrived at in a completely different way than the first
one. Usually we are given x, as in the first problem. We know x
because we have already marked it off, or we have it as an accepted
number from previous experiments. But t is different. We use our own
clock, it is true. But, because the object is at a distance, and
because light has a finite speed, we do not see the object at the same
time that the object sees itself.
To make this clearer, imagine that the object is a blinking
light. In this case, there are actually two events. The object
blinking, and our receipt of the blink. These two events take place x
distance apart, and the gap in time is the time it takes for light to
travel x.
Let us make up our own thought problem to illustrate this.
Thought problem one:
Apparatus:
1) A blinker that blinks at a rate of one blink per second.
2) A tunnel marked off with lines, like a ruler, to indicate
distance.
3) An eye, with a clock that ticks at a rate of one per
second, at the beginning of the tunnel.
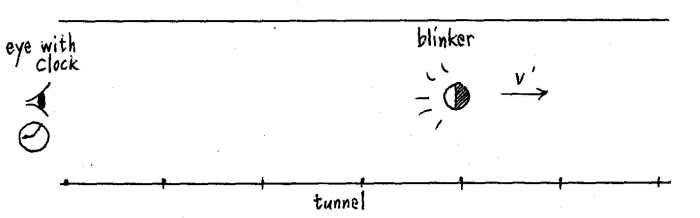
Experiment:
The blinker and the eye begin at rest, next to eachother.
Their blinks and ticks are exactly synchronous. The blinker then takes
off and goes through the tunnel at a constant velocity. It measures its
own velocity based on the number of marks it passes for each blink. It
reads the marks from a negligible distance. That is, it reads the marks
as it passes them .
The eye also measures the velocity of the blinker. It
measures the velocity of the blinker relative to its own clock. It
measures by seeing the blinks, which are blinks of visible light. The
eye is given x'. It has walked off the distance in a previous
experiment (or you may want assume the eye is the one who painted the
lines on the tunnel).
The blinker is set on a course directly away from the eye.
Assume that it reaches v' instantaneously.
Question:
Will the eye and the blinker measure the same velocity?
If not, how can the velocity measured by the eye be known
given the velocity as measured by the blinker itself (and vice versa)?
Answer:
Let t' = the period of each clock, from its own vicinity.
This is the period measured when the two clocks are side by side at the
beginning. Notice that the blinker is a clock. Each blink is a tick of
the clock.
x' = distance blinker has gone relative to tunnel marks,
according to its own visual measurements.
v '= velocity blinker is going, by it's own calculation.
Let t = period that the eye sees blinks from blinker. This gives
us the apparent period.
v = velocity eye calculates blinker to be going, based on
visual evidence.
This is the apparent velocity.
If you are with the blinker, then you will measure your own
velocity like this
v' = x'/t'
Let us say that your first blink is at the 1km mark. Your
second at the 2km mark, and so on.
Obviously, your v' = 1km/s
What then is v, the velocity of the blinker as measured by
the eye?
To discover this, we must first find T1. That
is, when does the eye receive the first blink, according to its clock?
t = period
T = time
Well, @ T1' = 1s,
x' = 1km, so the light must travel back to the eye 1km. It
takes the light 1km/c to do this. So we would expect the eye to
receive blink #1 at
T1 = T1' +
(x'/c) = 1.000003s
And
@ receipt of second blink, T2 = 2.000006.
@ receipt of third blink, T3 = 3.00001.
and so on.
So, for a simple blinker, the general equation would be
Tn = T n '
+ (xn' /c)
t = T2 - T1
t = t' + (change in x'/c)
A blinker with a period of 1s and a local velocity of 1km/s will appear
to have period of 1.000003s.
This period will be stable.
Now let us calculate the apparent velocity.
v = x'/t
= x'/[t' + (x'/c)]
= .999996km/s
You may say, "Wait, why did you use x' in that equation? And why did
you assume x' = 1km when you said that the light must go 1km to get
back to the eye, in the time equation? You can't assume these things!
Relativity tells us that the clock will slow down and that x will shrink.
x should be less than x'."
I am not assuming x' is the distance to use in the equation
for apparent velocity. I am given it. The velocity of an observed
object is either the given distance divided by the apparent time or the
apparent distance divided by the given time. These are the only
possible calculations for an observed velocity.
In the present case, v = x'/t or v = x/t' but
not v = x/t
The same goes for the light ray traveling back to the eye, in
the time equation. x' is simply a given here, just as c is a given.
Without them, any equations-- mine or Einstein's-- would be useless.
If I was not given x' (or v' and t', which is the same thing),
there is no way I could know it or calculate it. And there is no way I
could calculate v.
Think of it this way: A train passes at night. We don't
know the velocity, and we can't see the mile markers. All we can see is
a pulse clock on the train. Can we know its velocity relative to us?
No. The Lorentz transformations, as used up to now, can tell us nothing.
We must be given a local velocity v', or we must know x'. The apparent
velocity of the pulse clock is determined by its period and its speed.
That is, it could be ticking slowly and going slowly, or ticking faster
and going faster: in both cases it would look the same.
It is true, though, that x will look shorter to the observer,
as Einstein said. But this x is not x'. Nor is it the x used in the
apparent velocity equation, as I have shown. That x is given as x'.
What we are seeking for x here is the apparent distance.
It is calculated like this:
apparent x = (apparent v) X t'
If you are still unclear on why I used t' instead of t,
think of it this way. What we want is to multiply the apparent velocity
v by the time on our clock, right? We want to know what x is at T1
, and T2 , and so on, on our own clock. That is what it
means to measure by your own clock. If you know a runner's speed, and
want to calculate how far he runs in a time interval, you would not
check where he was as your watch ticked 1.000003, would you? You
calculate using your standard time interval, your own second hand.
You may say, "But you have defined t as the time for the eye,
and t' the time for the blinker. Now you want to switch." No. I
never defined t as the time for the eye. I calculated t to be the
apparent period of the blinker, as measured by the eye. This does not
mean that the eye's clock is ticking every 1.000003 seconds. It means,
of course, that the blinker's clock looks like it is ticking every
1.000003 seconds, from the eye. But the eye's clock is ticking at a
normal interval, for the eye; just as the blinker's clock is ticking at
a normal interval, for the blinker. This normal interval-- the rate a
clock goes as seen from its own vicinity-- I have defined as t'.
Notice that if the eye's clock had a period of t, then it would
not see the blinker's clock as slow. It see's the blinker's clock as
having a period of t, right? If the eye's clock also had a period of t,
there would be no difference. The blinker's clock is slow, relative to
the eye's clock, which therefore is not slow. Very simple.
So, @ T' = 1,
v = .999996km/s.
And x = .999996km/s = .999996km.
1s
This is just what we would expect.
t has apparently slowed down. And x has apparently shrunk.
That much is consistent with Einstein, at least.
But you can see that we have had to be very careful about
our t's and x's and v's. You cannot just substitute an x or a t into an
equation because it looks similar to another x or t. You must think
about what is really happening.
So, to sum up:
The blinker's period will appear to slow down, but the
period will remain stable (it will not continue to slow down further the
farther away it gets).
Therefore, the velocity will also appear to be slow. If the
blinker sends you a message telling you that its v' is 1km/s, then it
will have appeared to slow down relative to that.
If the blinker has a length along the x-axis, then the
blinker will be calculated to appear shorter, because there is an
apparent contraction along the x-axis. If you measured the blinker when
it was at rest next to you, then your calculation will be short relative
to that.
We have found that x = vt'
and v = x'/t
so, x/t' = x'/t
and xt = x't' just as Relativity predicted.
x and t are inversely proportional. As t appears to get larger, x
appears to get smaller
By substituting quantities we can now easily derive the direct
transformation equations, and calculate v from v' or x from x' and
v':
v = x'/t = x/t'
t = t' + (x'/c)
= t' + (v't'/c)
= t' (1 + v'/c)
v = x'/[t'(1 + v'/c)]
x' = v't'
v = v'
1 + (v'/c)
v' = v
1 - (v/c)
x = x'
1 + (v'/c)
Now that we have our new equations, I predict this complaint: "You are
assuming that t and x are absolute, before you even start. Your marked
off tunnel is an absolute system of coordinates, and your t's even
coincide. They may appear to be .000003s apart, but they are really the
same. Relativity does not rely on these assumptions. It transcends
them."
My answer is that I have done precisely what Einstein did. I
started with given quantities and derived unknowns from them by
discovering the proper equations. You are calling my givens "absolutes,"
but the terminology is meaningless. They are not absolutes, they are
accepted values. Einstein does not derive his relative velocities from
thin air. In his transformation equations, you must have certain
information to start with. I claim that my givens are no more absolute
than his. My givens are exactly the same as his. If my elucidation of
his process makes you think that these givens are absolutes, then I can
force you to admit that Einstein's givens are also absolutes.
In fact I will do so now. Einstein says (p.18, Rel.) that the
train has a given velocity v. The implication is that this velocity is
a local velocity. It must be the velocity of the train, as measured
from the train. He cannot mean the velocity of the train as measured
from the embankment. For if he meant as measured from the embankment,
then we would already be given a relative velocity, and we would not
need fancy transformation equations to find it.
Einstein then shows, correctly, that the train's clock will
look slow to the eye on the embankment and that the train's measuring
rods will look short. And he presents the Lorentz equations for t and
x. But then he never uses his relative x and t, that he derives by
these equations, to calculate a relative v. Isn't this strange? He
never concludes that there is a relative v that is different than the v
given in the problem. He derives two t's and two x's, but never derives
the second v, the relative v.
Later, he derives the Lorentz transformation for velocity,
using his t and x equations (Ch.8, on Fizeau). But this is for the
addition of velocities. It is for the situation in which the man on the
train is moving relative to the train and the train is moving relative
to the embankment (eye). You have two relative velocities and you want
to find the third. This equation gives us a velocity of two degrees of
relativity.
If Einstein had derived an apparent velocity for just the
train relative to the embankment, then it would have been clear that
something was wrong. Once you have two v's, a relative v and a given v
(the v in the illustration-- my v'), someone might ask, what was the
given v?
In other words, Einstein derived a Lorentz equation that gave
him a relative x. With this relative x, he can obviously calculate a
relative v. He has two t's and two x's. He will certainly have two v's.
The relative v from this transformation equation would be the v of train
relative to the embankment. What then was v'?
Or, to state it another way, What was the v in equation x' = x
- vt?
It is the v of the train relative to the tracks, as measured
from the train! Einstein must be given this velocity before he ever
starts: relative v is dependent on v'. So Einstein must have his
railroad track already marked off before he can calculate his relative x
and t!
He even admits this. At the top of the same page (p. 18) he
says, "Of course we must refer the process of the propagation of light (and
indeed every other process) to a rigid reference body (co-ordinate
system)." [his parentheses]
His problem implies the existence of a pre-existing system,
like my tunnel. But this system remains hidden throughout the problem.
Regardless, this system-- whether his or mine-- is not an "absolute."
It is not an absolute in the sense of contradicting the relativity of
measurement. It is a given, a postulate that allows for the calculation
of unknowns.
You may say, "Yes, but there are two co-ordinate systems (S and
S'). Distance in one will not be the same distance in the other. x
does not equal x'. You cannot just transfer x' into your equation-- as
you did when the blink was traveling from the blinker to the eye-- as if
you already knew the distance."
Einstein did.
S pecial Theory of Relativity
In 1905, Albert Einstein published his
Special Theory of Relativity. This work considered time not as a single
constantly flowing entity, but as part of a much more complex system,
linked with that of space itself. Because space and time are part of the
same entity, it is impossible to move in space without moving in time.
That is why it is called the space-time continuum. One of the most
amazing consequences of special relativity is that any moving clock
slows down relative to a stationary observer.
The faster we go, the more time slows
down; in other words, moving clocks run slowly. This is only noticeable
at speeds approaching the speed of light, 300,000 kilometers (km) per
second (186,300 miles per second). This is approximately seven times
around the Earth in a second.
This slowing down of clocks due to high
speeds is called time dilation and has a precise mathematical
relationship. The equation for time dilation is:
The units for these variables are still
the same. Time will be measured in seconds and velocity in meters per
second (m/s). To make the problems easier, velocity is usually given in
terms of c, where c is the speed of light in a vacuum. For example,
rather than the velocity being 1.5 x 108 m/s, we would write
0.5c. This is much easier to say and write, and it is a great hint as to
what type of problem you are solving. By doing this, v and c will always
have the same units, so that t and t will always have the same units.
Seconds are preferred, but other units of time can be used without long
conversions, thanks to this shortcut. To know which unit of time to use,
always keep the same units that you are given in the problem.
One of the strangest consequences of time
dilation is the so-called "twin paradox." In this "paradox," one
identical twin is sent at very high speed out into space. Because he or
she is traveling at a very high speed, all the clocks on board the
rocket, including the body clock of the twin, are slowed down in
accordance with the principle that "moving clocks run slow." Time does
go SLOWER for an astronaut in space than on Earth. Albert Einstein, some
80 years ago, called this the "twins paradox": if one of a pair of twin
sisters flies in space at great speed, at her return to Earth shell be
younger than her sister who stayed there. Einsteins theory of
relativity showed that time itself changes with the speed of motion of
the instrument that measures it.
For example, if one sister flies into
space for 5 years and reaches 99.5% of the speed of light (which is
185,400 miles per second or 298,500 kilometers per second) going out and
then again on the return leg, shell find her Earth-bound sister aged by
50 years while for her, just 5 years have gone by. In other words, they
are now 45 years apart in age!
During a Shuttle mission, the orbital
speed is only a tiny fraction of the speed of light (namely, 1/42857th).
So, the "time dilation," as the effect is called, is also tiny, but it
is there, nevertheless, as Shuttle experiments have proven. For example,
a highly precise atomic clock flying in an experiment called NAVEX on
STS-61A/Challenger in 1985 measured a slowdown of 0.000,000,000,295
seconds for each second of flight, almost exactly what Einsteins
formulas predicted. |
|
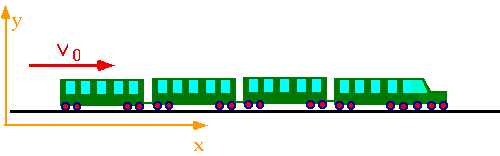
To find out how the time changes from one frame to another, consider
bouncing a light off a mirror as the train goes past.
In the train frame:
t = 2L/c
|
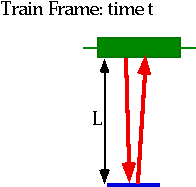 |
In the earth frame, the light has to travel further, since the train
has movedt' = 2D/c
and
D2 = L2 + (v0t'/2)
|
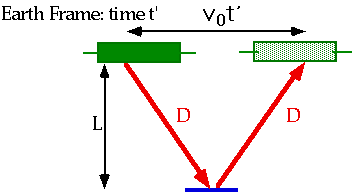 |
We have three equations
- D= ct'/2
- L = ct/2
- D2 = L2 + (v0t'/2)2
which can be combined
(ct')2 - (v0t')2 = (ct)2
so
t' = t (1-v02/c2)1/2
i.e. moving clocks run slow
e.g. Suppose you are in an OC Transpo bus (v0 = 10ms-1):
how slow will your watch appear to run compared to your clock at home?
e.g. A muon is a subatomic particle which lives 2x10-6 s. How
long will it appear to live if is travelling at .99c?
Note that (1-v02/c2)1/2
~ 1 for all cases we are familiar with (whihc is just as well!)
Since time is not the same in two frames, events which are simultaneous
in one frame are not in another.
Sayfa başına dön
Hiçbir
yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca
bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden
alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi
Defteri /UFO Technology/Duyuru
Kuantum Teleportation /Kuantum Fizigi
/Uçaklar(Aeroplane)
New World Order(Macro Philosophy)
/Astronomy
|
|




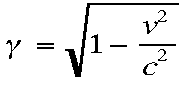
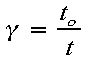

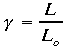
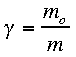


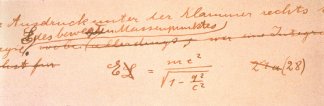







![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2