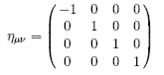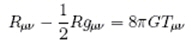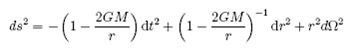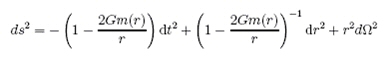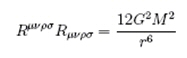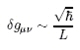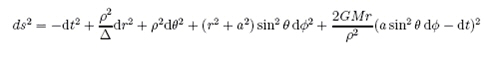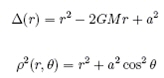|
Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey/Denizli |
Lumière sur les trous noirs
Lao Tseu (vers 600 av. J.C.)
 La
relativité générale nous décrit la gravitation comme une courbure de
l'espace-temps par la matière. Cela a d'ailleurs été vérifié par des
observations lors d'éclipses solaires : la lumière des étoiles occultées par
le soleil était courbée en passant à côté de la masse du soleil. Selon la
gravitation d'Einstein, une planète qui tourne autour d'une étoile ne fait
rien d'autre que rouler sur le bord de la courbure créée par l'étoile !
Etonnant, mais irréfutable....Voilà une chose qui a révolutionné la physique
au XX ème siècle et qui fait maintenant partie de nos certitudes
scientifiques de base.
La
relativité générale nous décrit la gravitation comme une courbure de
l'espace-temps par la matière. Cela a d'ailleurs été vérifié par des
observations lors d'éclipses solaires : la lumière des étoiles occultées par
le soleil était courbée en passant à côté de la masse du soleil. Selon la
gravitation d'Einstein, une planète qui tourne autour d'une étoile ne fait
rien d'autre que rouler sur le bord de la courbure créée par l'étoile !
Etonnant, mais irréfutable....Voilà une chose qui a révolutionné la physique
au XX ème siècle et qui fait maintenant partie de nos certitudes
scientifiques de base.
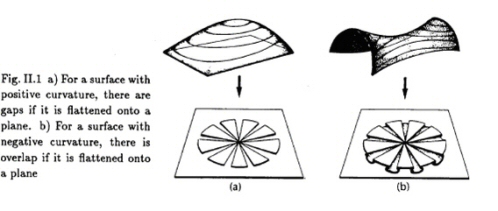
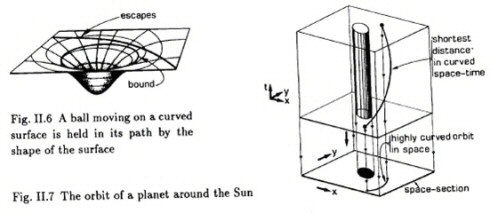
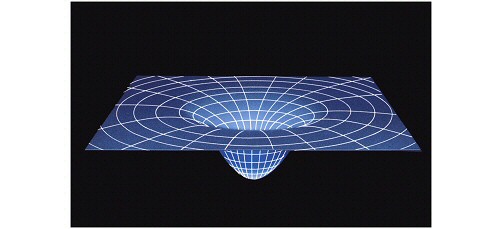
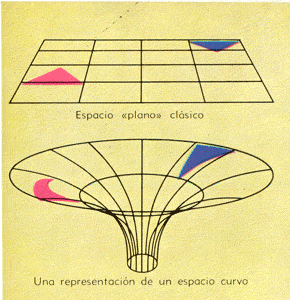
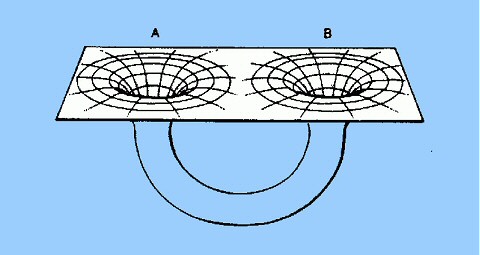
Il est certes très difficile de se représenter la déformation d'un espace
à 3 dimensions, mais on peut en avoir une idée assez juste en le projetant
sur une surface à 2 dimensions, une très mince feuille de caoutchouc par
exemple.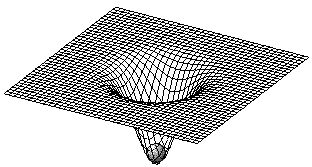 Une boule en bois va déformer la surface de la feuille souple en la creusant
un peu (figure de gauche). Une boule en fer va la déformer beaucoup plus,
creusant une sorte de cratère plus ou moins profond (figure de droite).
Une boule en bois va déformer la surface de la feuille souple en la creusant
un peu (figure de gauche). Une boule en fer va la déformer beaucoup plus,
creusant une sorte de cratère plus ou moins profond (figure de droite).
Que va-t-il se passer avec une boule en plomb ? On peut supposer qu'elle va
creuser un puits très profond, voire sans fond, ou alors qu'elle va crever
la fine membrane de caoutchouc....Notre boule de plomb, à l'échelle cosmique,
c'est ce qu'on appelle un trou noir.
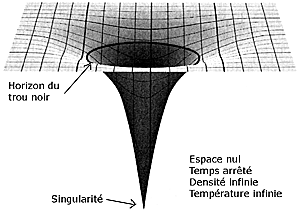
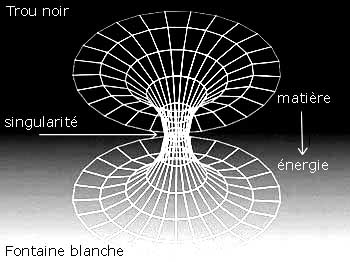
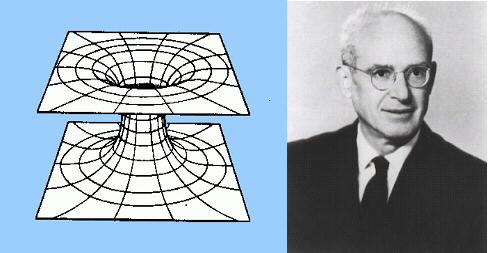
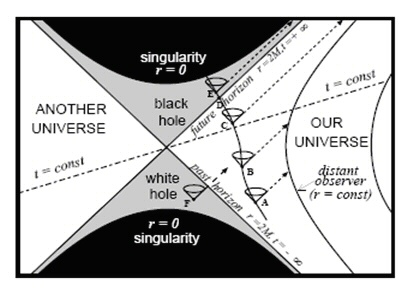
On a supposé que les trous noirs et les fontaines blanches pouvaient communiquer par des raccourcis de l'espace-temps nommés "trous de vers", appellation moins poétique ! Certains optimistes ont même avancé l'idée que cela nous permettrait de voyager à travers l'espace-temps. Malheureusement, un vaisseau spatial, même très solide, qui s'aventurerait à l'horizon d'un trou noir serait vite broyé avec ses imprudents passagers, par la gravitation infinie qui règne dans ce genre d'endroit !
On a déjà la quasi-certitude qu'il y a beaucoup de trous noirs dans l'univers. On en connaît trois types : les stellaires, les intermédiaires et les supermassifs. Il y en aurait même un au centre de notre galaxie ! Quant aux fontaines blanches, elles restent encore dans le domaine spéculatif, bien qu'elles ressemblent terriblement aux mystérieux quasars [1]....
Il est cependant assez tentant d'imaginer que trous noirs et fontaines blanches se rejoignent au point de leur "singularité". C'est comme si l'espace-temps se retournait sur lui-même...La matière engloutie par le trou noir ressortirait ailleurs dans l'univers sous forme d'énergie : une prodigieuse "réaction nucléaire"[2] transformant la matière en énergie ! Ce qui disparaît dans les trous noirs ne disparaît donc pas définitivement de l'univers observable, mais réapparaît ailleurs sous une autre forme.... La boucle est bouclée : paradoxalement, ce sont donc les trous noirs qui nous apportent la lumière !
[1] quasars (quasi stellar objects) : objets
mystérieux situés aux confins de l'univers observable, de la taille d'une
grosse étoile et rayonnant au moins 100 fois autant d'énergie qu'une grande
galaxie !
[2] "réaction nucléaire" n'est qu'une image, vu que la matière d'un
trou noir n'a plus d'atomes, donc plus de noyaux, plus de particules
élémentaires. L'état actuel de nos connaissances ne permet pas de dire ce
qui se passe dans des conditions aussi critiques. Pas question non plus de
reproduire cela en laboratoire...On peut juste imaginer que c'est une
réaction infiniment plus puissante que toutes les bombes H réunies !
Singularités, trou de ver et voyage spatio-temporel1°) Espace-temps de
Minkowski
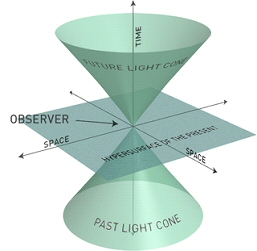
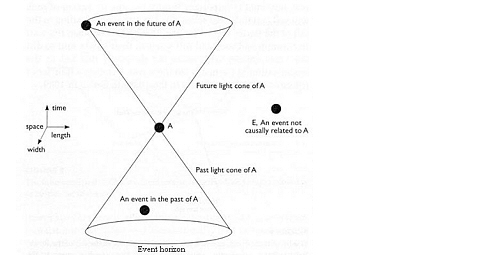
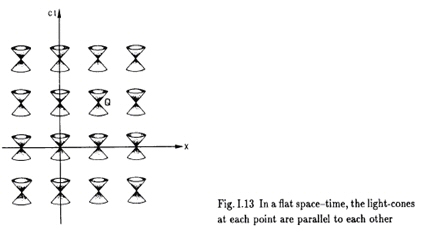
De manière générale, tous les quadrivecteurs ont un carré de norme possédant une valeur tombant dans les trois classes décrites précédemment. Ils seront respectivement dit de genre temps, nul (ou lumière), espace. Enfin les deux cônes définissent respectivement les régions passées et futures pouvant être en relations causales avec l’observateur.
On parlera de congruence de courbes aussi bien pour les lignes de courant que pour des trajectoires de photons dans l’espace-temps. La structure des événements dans l’espace–temps, ainsi que sa dynamique - car comme nous l’apprend la Relativité Générale, celui-ci est courbe et susceptible de changement - est traduite par la donnée de ces règles /horloges et d’un véritable champ de cône en chaque point de l’espace-temps. Quand l’espace-temps est plat et statique, les cônes sont tous ‘rigidement’ fixés. Ce ne sera plus le cas lorsque l’espace-temps sera courbe et dépendant du temps (cf. les schémas ci-dessus) En résumé la théorie de l’espace-temps de Minkowski repose sur : La conséquence la plus spectaculaire de cette géométrie de l’espace-temps est la dilatation du temps illustrée par le paradoxe des jumeaux de Langevin. C’est l’exemple bien connu de deux jumeaux dont l’un reste sur Terre alors que l’autre effectue un voyage aller-retour à une vitesse proche de la lumière entre la Terre et un point distant de 20 années lumière par exemple. A son retour, presque 40 années se seront écoulées sur Terre alors que lui pourra n’avoir vieilli que de quelques jours seulement. Ceci n’est pas de la science fiction ! Des horloges atomiques ultra précises ont été utilisées lors de voyages en avion ou en fusée autour du globe et on a invariablement vérifié non seulement ce phénomène mais aussi les prédictions exactes des équations de la relativité d’Einstein. Sans parler de la désintégration des muons dans les rayons cosmiques ou en accélérateurs qui vivent d’autant plus longtemps pour un observateur fixe sur Terre qu’ils se déplacent rapidement par rapport à lui. Encore une fois l’accord avec les prédictions des équations de la relativité est remarquable. Cette dilatation du temps est capitale pour qui veut comprendre comment un trou de ver peut être utilisé pour voyager dans le temps comme il a été proposé à la fin des années 80 par Kip Thorne. 2°) La Relativité générale
d’Einstein
Toujours comme annoncé, je vais faire quelques rappels sur la théorie de la relativité générale. Je conseille toutefois vivement au lecteur de se référer constamment au dossier suivant de Futura-Sciences pour des explications plus détaillées, voir même de le lire comme préambule indispensable avant de continuer pour qui n’a jamais rien lu sur la Relativité Générale (en abrégé RG). Einstein fut assez vite confronté au problème de la réconciliation entre la théorie de la gravitation de Newton et sa propre théorie de la relativité restreinte. Laplace avait montré que l’influence de la gravitation devait se propager au moins plusieurs millions de fois plus vite que la lumière pour correspondre aux orbites des planètes observées dans le système solaire. En outre, la théorie d’Einstein traite de la description des mouvements dans des référentiels sans accélérations. Miraculeusement ces deux problèmes sont liés et peuvent être surmontés par la remarque incroyablement simple suivante, les masses inertes et gravitationnelles des corps sont identiques. Qu’est-ce que cela signifie ? La masse inerte est le cœfficient qui intervient dans la loi de Newton liant l’accélération d’un corps à la force qu’il subit, celle dite gravitationnelle est liée à l’estimation de l’intensité de la force qu’un corps subit dans un champ de gravitation. Cela est d’autant plus troublant que dans le cas d’une force électrique ou magnétique c’est la charge qui apparaît, on soupçonne donc un lien entre lois de la mécanique et loi du champ de gravitation. Une application frappante de cette égalité c’est aujourd’hui les expériences dans des avions momentanément en chute libre. A l’intérieur tous les corps chutant à la même vitesse par rapport à la Terre, ils se mettent à flotter les uns par rapport aux autres. Localement on peut donc trouver un référentiel dans lequel les effets du champ de gravitation s’annulent ! Inversement on peut trouver un référentiel accéléré tel qu’un observateur puisse se croire immobile mais soumis à un champ de gravitation. Le pas fondamental suivant pour atteindre les fondements de la relativité générale consiste à regarder ce qui se passe lorsqu’on essaye d’appliquer la relativité restreinte à des corps accélérés. Généralement on considère le cas d’un disque en rotation uniforme. Chaque point le long d’un rayon est soumis à une vitesse v de plus en plus importante lorsqu’on s’éloigne du centre du disque. Une horloge en chacun de ceux-ci aura donc un décalage de plus en plus prononcé au fur et à mesure qu’on s’éloigne de ce centre. En outre la mesure de la circonférence du disque indique en raison de la contraction des longueurs que celle-ci n’apparaît pas comme vérifiant la relation C=2 La géométrie spatiale n’est donc plus euclidienne pour certains observateurs et ceci en relation avec le fait qu’on est en présence de mouvements accélérés. Or, on l’a vu, une accélération dans un référentiel est interprétable localement comme la présence d’un champ de gravitation. On vient donc de mettre en évidence un lien entre gravitation et géométrie de l’espace. Einstein en conclut que les phénomènes gravitationnels devaient être en toute généralité liés à une géométrie non euclidienne de l’espace-temps et pas seulement de l’espace, sans quoi on aurait une contradiction avec le concept même d’espace-temps en régime sans gravitation. C’est tout naturellement qu’il fut conduit à utiliser la théorie générale des espaces courbes à N dimensions introduite au 19 ième siècle par Riemann.
CERN yellow report 91-06 Ruth M. Williams
3°) Le Pont d’Einstein-Rosen et les trous de
vers de Wheeler-Misner
4°) L’Univers de Gödel et la solution de
Kerr
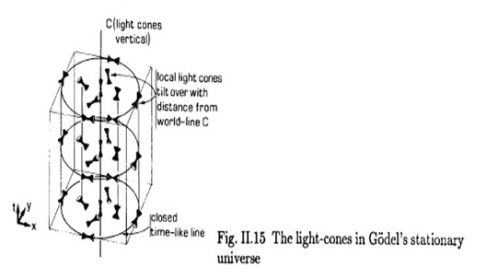
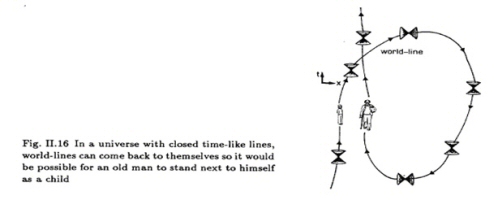
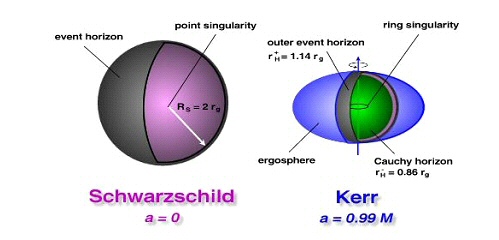
A - L’Univers de Gödel La généralisation dans le cadre de la RG de la solution newtonienne décrivant le champ de gravitation d’une étoile ne décrit avec celle de Schwarzschild qu’un corps dénué de rotation. Ce n’est pas très réaliste du point de vue de l’astronomie car les étoiles, tout comme les planètes , sont animées d’un mouvement de rotation. Une des premières solutions décrivant le champ généré par un corps en rotation fut celle de Van Stockum, (Stockum, W. J. van (1937). The gravitational field of a distribution of particles rotating around an axis of symmetry.. Proc. Roy. Soc. Edinburgh A 57: 135). L’histoire de son auteur vaut un roman à elle toute seule. C’est aussi le premier exemple où l’on voit une connexion entre le voyage dans le temps et l’existence d’une rotation associée à l’espace-temps. Probablement inspiré par cette découverte, par de nombreuses discussions avec Albert Einstein (dont il était le collègue et l’ami à Princeton) sur l’espace, le temps et leurs relations avec la physique et la philosophie le grand logicien Kurt Gödel stupéfia le monde en 1949 en exhibant une solution des équations d’Einstein décrivant un Univers en rotation. Ce qu’elle avait d’étrange était qu’il existait à l’intérieur de celle-ci des trajectoires permettant à un voyageur de remonter dans son propre passé !
5°) Les singularités en relativité générale
et le cylindre de Tipler
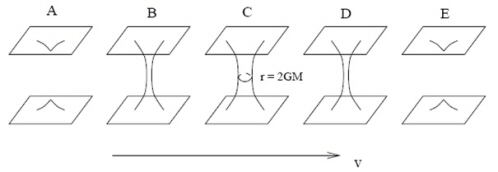
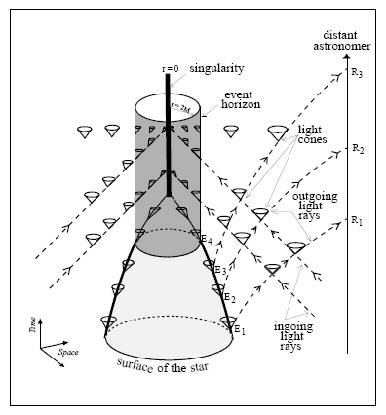
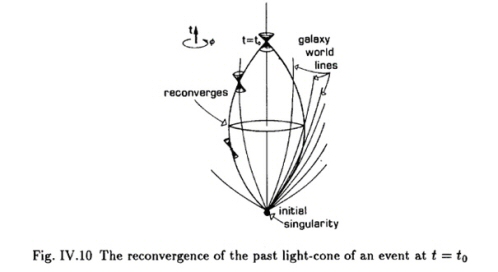
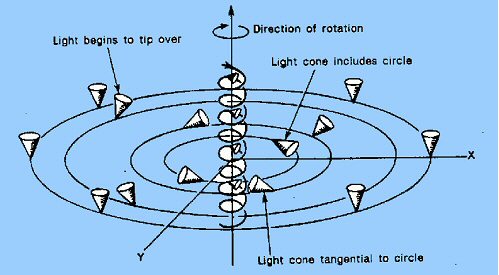
De manière similaire, l’apparition de singularités en cosmologie s’étudiera et s’établira à partir du comportement de basculement des cônes de lumière et de ‘focalisation’ des trajectoires des rayons lumineux au fur et à mesure que l’on remonte dans le temps. C’est ce que l’on voit sur le diagramme suivant :
|


Sur
ce diagramme on voit bien, à nouveau, le basculement des cônes au
fur et à mesure qu’on se rapproche du cylindre et l’apparition de
trajectoires possibles vers le passé.
Plus
tard il fut démontré qu’un cylindre de quelques milliers de km de
long et possédant la masse et la densité de quelques étoiles à
neutrons serait suffisant.
Il est important de bien voir
qu’une telle machine ne permet pas de remonter dans le passé plus
tôt que la date de sa propre création, ou d’aller plus loin dans le
futur que sa date de destruction ou d’arrêt.
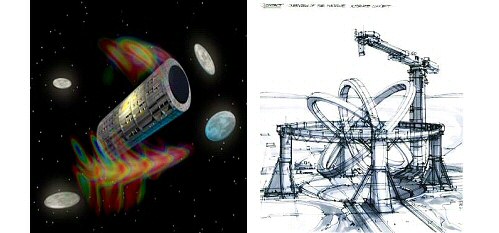
Cylindre de Tipler - La machine de ‘Contact’ de
Sagan
Dans le film’ Contact’, c’est une
idée similaire qui est reprise pour créer un trou de ver puisque
l’on voit d’imposants cerceaux en rotation ouvrant un passage vers
l’étoile Véga.

Jodie Foster dans ‘Contact’
6°) Le rayonnement de
Hawking

Hawking dans Star Trek rencontrant Einstein et
Newton à la suite d’une perturbation
spatio-temporelle
Parallèlement à Tipler,
Stephen Hawking s’était lancé dans l’analyse du comportement d’un
champ quantique en espace-temps courbe au voisinage d’un Trou noir
Le trou cosmique ultime formé lorsqu\'une étoile supergéante très massive explose en supernova à la fin de sa vie. L\'explosion crée un point superdense dans l\'espace dont rien ne peut échapper à l\'attraction gravitationnelle. Pour créer un trou noir, une étoile doit avoir une masse d\'au moins 60...');"
onmouseout=killlink()>trou noir. Alors que tout
semblait indiquer que rien ne pouvait en sortir il découvrit à sa
grande stupéfaction que ce n’était pas le cas et qu’on pouvait
associer un rayonnement à tout trou noir. Comment cela est-il
possible ?
C’est encore un tour de magie quantique. Le vide,
comme on le verra plus loin, ne l’est pas vraiment et est
continuellement agité par des paires de particules/antiparticules
émergeant fugacement avant de s’annihiler par recombinaison. On
parle de processus et de particules virtuels. Or si l’on considère
deux tels photons (qui sont leurs propres antiparticules) au
voisinage de l’horizon d’un trou noir, les forces de marée sont suffisantes pour que
l’un tombe dans le trou en traversant l’horizon. Le travail
fourni par les forces de marée pour séparer les particules ayant
alors fourni assez d’énergie pour que les particules deviennent
réelles et que l’une s’échappe vers l’infini, comme on peut le voir
sur les diagrammes ci-dessous.
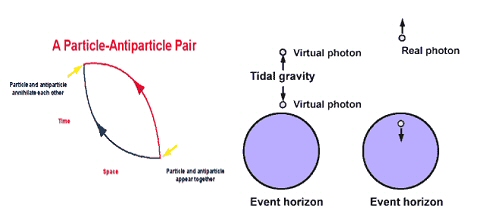
On peut calculer la probabilité pour que cela se
produise. Plus un trou noir est petit plus ses forces de marée sont
grandes et plus la probabilité de séparer des particules l’est
aussi.
Le bilan net est une décroissance de plus en plus
rapide de la masse d’un trou noir, car l’énergie emportée par la
particule s’échappant doit bien l’être au dépend de celle stockée
par celui-ci. En fait, il faut admettre qu’il y a comme une sorte de
courant d’énergie négative qui pénètre à l’intérieur du trou noir.
C’est loin d’être trivial, car depuis ses débuts la mécanique
quantique semble exiger le bannissement des énergies négatives comme
solutions physiques possibles de ses équations.
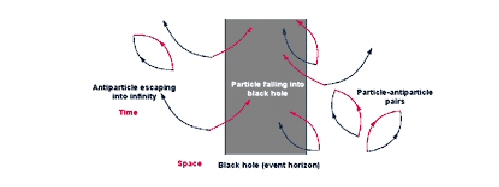
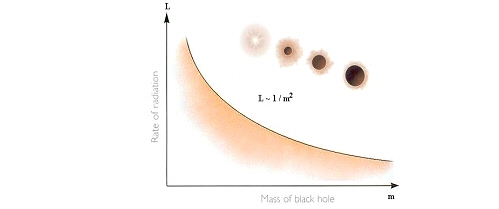
Ce
phénomène d’évaporation est fascinant et il faudrait lui consacrer
un dossier entier pour lui rendre justice, ce que malheureusement
nous ne ferons pas ici. Outre l’apparition problématique d’états
d’énergies négatives, capitale comme la suite de notre enquête sur
les trous de vers le montrera, il existe un autre phénomène digne
d’être noté.
On l’a appelé le ‘paradoxe de l’information.
Voyons ce que c’est.
Théoriquement un trou noir avale tout ce
qui traverse son horizon sans jamais le laisser ressortir. Il peut
être décrit uniquement et complètement par sa masse et son moment
cinétique (je néglige le cas chargé).Donc quoi que ce soit qui tombe
à l’intérieur, le trou noir ne retiendra que sa masse et rien
d’autre en l’absence de moment cinétique. De plus son évaporation se
produit avec un rayonnement dit thermique ou de corps noir qui est
le plus ‘désordonné’ possible.
L’information liée à
l’organisation des objets de même masse (par exemple) semble donc
être perdue à tout jamais lorsque qu’on les jette dans un trou noir
!
Ceci
est en contradiction avec les règles fondamentales de la mécanique
quantique qui pourtant sont essentielles pour arriver à ce résultat,
d’où l’emploi du mot ‘paradoxe de l’information.

David Gross (prix Nobel) - Gerard ‘t Hooft (prix
Nobel)
Hawking a fermement défendu, jusqu'à
récemment encore, que c’était bien ce qui se produisait. Par contre
‘t Hooft et Gross s’y sont toujours opposés. La question reste
ouverte en dépit de progrès récent issus de la théorie des cordes et
de Hawking lui-même indiquant qu’en fait l’information se
conserverait tout de même. Le rayonnement émit par le trou noir ne
serait pas complètement désordonné car pas totalement indépendant du
contenu interne de celui-ci.

Début de l'article de Hawking datant en fait de
1974
Dans les années 80 la théorie des trous de vers reçoit un nouveau souffle, surtout sous l’influence de Hawking.
En effet ils sont une possibilité logique pour expliquer le célèbre paradoxe de l’information avec les
On a vu aussi que selon Wheeler, la charge électrique et la masse des particules pourraient s’interpréter à partir de la topologie de l’espace-temps. Les paires de particules/antiparticules du vide étant alors des trous de vers de Misner apparaissant et disparaissant du fait des fluctuations quantiques de la métrique. De manière naturelle, toutes les constantes de masses et de charges pourraient ainsi être liées à des effets de ces trous de vers. Comme les questions de renormalisation des particules en théorie quantique des champs se posent pour les masses et les charges de celles-ci on comprend aisément tout le potentiel de la théorie des trous de vers pour la physique des particules.
En outre John Wheeler avait proposé, à la suite d’une estimation numérique simple, que cette structure fluctuante des trous de vers soit responsable de l’annulation, ou tout du moins de l’affaiblissement conséquent, de la constante cosmologique.
C’est
facile à comprendre, si la densité de trous de vers virtuels est
assez grande, ils possèdent une énergie gravitationnelle
d’interaction qui est susceptible de régulariser l’énergie du vide
et de lui donner une valeur comparable à celle que l’on observe. Des
calculs préliminaires plus approfondis par Hawking, et surtout
Sydney Coleman, ont montré que c’était effectivement une explication
possible. Bien qu’aucune démonstration solide n’ait vraiment pu être
apportée. Les wormholes étudiés étaient autant de type Misner
qu’Einstein Rosen. Dans ce dernier cas on avait des bébés Univers
bourgeonnant à partir du nôtre et étant de la taille de Planck.
C’était la fameuse théorie des ‘baby univers’.
Sydney Coleman à Harvard - ‘Baby univers’
bourgeonnant à partir de notre espace-temps connecté momentanément
par un trou de vers avec notre univers.

L’article est référencé en annexe.
Tout était maintenant en place pour que
Kip Thorne fasse sa découverte fracassante.
De façon
incroyable tout est parti de Carl Sagan. Celui-ci cherchait à rendre
crédible son livre Contact. Son héroïne Eleanor Arroway y traversait
initialement un trou noir pour rejoindre la planète d’une ancienne race
extraterrestre ayant envoyé un message radio dans l’Univers pour
manifester sa présence.

Carl Sagan, l’auteur de ‘Cosmos’ et ‘Contact’ fut
un remarquable planétologue et vulgarisateur.
On le connaît
surtout pour son engagement dans le programme SETI.
Celui-ci comportait les plans d’une
machine permettant de voyager d’une étoile à une autre en ouvrant un
passage spatio-temporel sous forme de trou noir entre
celles-ci.
Evidemment, c’est une impossibilité comme nous
l’avons vu précédemment. Sagan s’adressa donc à son ami Kip Thorne,
grand spécialiste de l’astrophysique relativiste et ancien élève de
Wheeler. Il ne tarda pas à trouver une solution, il suffisait de
violer les conditions d’énergie des théorèmes garantissant
l’apparition de singularité. Pour cela il aurait fallu trouver de
l’énergie sous forme négative mais existait-il une telle forme
d’énergie ‘exotique’ dans l’Univers ?
La réponse allait venir
de la mécanique quantique (en abrégé MQ).
A - Les
particules remontant dans le temps de Feynman.


Richard Feynman, prix Nobel
On savait déjà depuis Feynman que la
mécanique quantique pouvait avoir son mot à dire dans le problème du
voyage dans le temps. Dans ses travaux sur l’électrodynamique
quantique, et en reprenant une idée de Wheeler (encore lui),
celui-ci avait montré qu’on pouvait représenter une anti-particule,
par exemple un positron, comme un électron mais remontant le
temps.
Si l’on considérait une particule d’antimatière,
mais d’énergie négative, alors la fonction d’onde décrivant en MQ
cette particule est fonction du produit E*t. Donc si E<0 et
t<0, c’est bien la même chose qu’une particule d’énergie normale
E>0 se déplaçant normalement dans le temps.
On montre que
cela est possible si en même temps la charge électrique est changée,
d’où cette étonnante affirmation :
Les états d’énergie
négative des particules remontant dans le temps sont en fait des
états positifs allant normalement du passé vers le futur mais avec
une charge opposée.
Ce qui est bien la description d’une
antiparticule comme le positron ou l’antiproton.
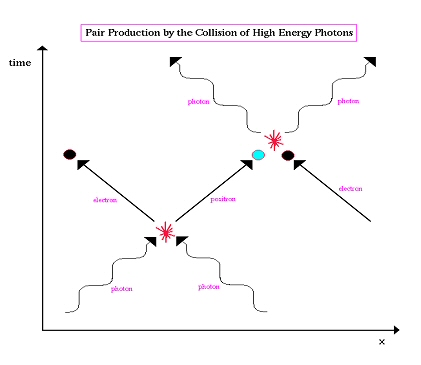
La matérialisation d’une paire
particule/antiparticule suivie de son annihilation est donc ré-
interprétable comme un seul électron mais zigzaguant dans l’espace
temps à la suite d’absorptions ou d’émissions de photons. Ce que
l’on voit dans les deux diagrammes donnés.
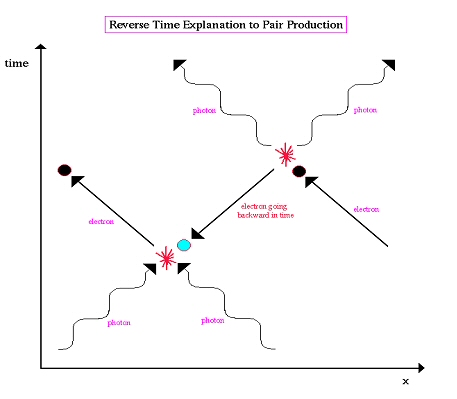
B
- Les fluctuations quantiques du vide.
Une conséquence
importante de la théorie quantique est celle de fluctuation du vide
quantique. Qu’est-ce à dire ?
En physique classique
les particules sont indestructibles et l’énergie se conserve sans
aucune exception à la règle.
Dans le monde magique de la
théorie quantique, surtout lorsqu’on se retrouve dans la théorie des
champs, ce n’est plus le cas. Si l’on considère la quatrième
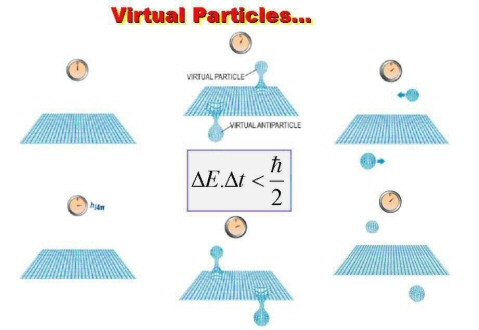
inégalité de Heisenberg on le comprend aisément.
Rappelons que
rien n’est parfaitement déterminé ni fixé en MQ où règne un flou et
une agitation gouvernés par des lois probabilistes.
A
l’instar des inégalités limitant la valeur précise simultanée de la
position et de la vitesse d’une particule, on ne peut pas non plus
lui associer précisément une énergie donnée à un instant précis sans
que l’incertitude delta E sur la valeur de cette énergie et celle
delta t sur l’instant auquel s’effectue une mesure de cette énergie
soit reliées par
![]()
On peut donc violer le principe de conservation de l’énergie
d’autant plus que cette violation reste courte. Comme Einstein
nous a appris que de l’énergie pouvait se transformer en particule
de masse M donnée, il en résulte que la MQ impose au vide de
bouillonner de paires de particules/antiparticules de toutes natures
et de toutes masses (électrons, quarks, photons, mini trous noirs,
etc.) apparaissant et disparaissant sans cesse. Comme ces
processus ne durent pas et qu’ils sont inobservables directement on
parle de processus virtuels.
D’après la RG, il doit non
seulement y avoir des gravitons (les ‘photons’ du champ de
gravitation) et des mini trous noirs mais le champ de gravitation
lui-même de ces particules virtuelles qui déforment et déchirent
sans cesse l’espace–temps à l’échelle microscopique. Ce n’est en
fait qu’une version alternative/complémentaire de l’image de Wheeler
de fluctuations quantiques de la métrique, les résultat étant
sensiblement les mêmes.
Il y a quand même un petit détail
désagréable. La MQ appliquée aux champs, qu’ils soient de particules
de matière ou d’interaction, introduit une densité d’énergie du vide
quantique qui est soit infinie soit très grande. On tombe sur le
fameux problème de l’énergie résiduelle du point zéro et de la
renormalisation en théorie quantique des champs impliquant une
constante cosmologique plus importante que la valeur
observée.
(Attention,
le signe de l’inégalité est bien > et non <)
C -
L’effet Casimir :
Ces fluctuations quantiques ne sont pas
des vues de l’esprit car elles se font sentir indirectement dans les
processus d’interactions matière-rayonnement. La valeur de la masse,
de la charge et du moment magnétique des électrons en porte
témoignage ainsi que ce qu’on appelle l’effet Lamb et surtout
l’effet Casimir. En effet l’apparition/disparition continuelle de
paires de particules virtuelles chargées décrit par les diagrammes
de Feynman ci-dessous se remarque dans la modification de la valeur
de la charge et de la masse d’un électron qu’on lui attribuerait en
l’absence de ces fluctuations.

Diagrammes de Feynman - Hendrik Casimir de
fluctuations de paires quantiques
C’est
en étudiant ces effets fins en physique atomique que H.Casimir fit
sa découverte la plus célèbre.
L’électromagnétisme étant
la force la plus intense à notre échelle, c’est dans son cadre que
les effets des fluctuations quantiques du vide sont le plus
facilement notables. Si l’on introduit deux plaques conductrices
faiblement séparées, les longueurs d’onde associées aux
particules

virtuelles
agitant le vide, comme les photons dans ce cas, sont plus courtes
entre les deux plaques de métal qu’à l’extérieur. Cela modifie la
valeur de l’énergie du vide qui se comporte alors comme si l’on
avait de l’énergie négative. C’est pourquoi on mesure une force
attirant les deux plaques et les forçant à se
rapprocher.
C’est le fameux effet que Casimir avait prévu
en 1948 !
Steve Lamoreaux du Los Alamos National
Laboratory a réussi en 1997 avec ses collègues à le mesurer
précisément. C’est l’exemple le plus simple, et surtout constaté
expérimentalement, où l’on peut voir que la mécanique quantique peut
produire des effets dits ‘exotiques’ en ce qui concerne
l’énergie.
Voila donc bien la clé recherchée par Thorne
!
Une telle énergie négative existe bel et bien dans
l’Univers et devrait donc permettre de maintenir le wormhole ouvert.
Il suffirait de ‘tapisser’ celui-ci avec de l’énergie négative,
produite par un mécanisme du genre de l’effet Casimir, pour violer
les conditions sur la positivité de l’énergie impliquant
l’apparition d’une singularité.

Il
est très important de comprendre d’une part que cet effet d’énergie
négative est justement ce qui intervient aussi dans l’évaporation
des trous noirs selon le mécanisme de la radiation Hawking, d’autre
part que cette énergie négative n’est pas de l’anti-matière. La
physique des champs quantiques en espace-temps courbes, juste sur
l’horizon, se traduit par un flux d’énergie négative à l’intérieur
de celui-ci compensant précisément le départ des particules
rayonnées à l’infini par le trou noir et provoquant la décroissance
de sa masse.
Restait donc à voir ce que diraient les
équations d’Einstein couplées avec une distribution de ‘matière
exotique’ possédant une énergie négative.
8°) L’article de Morris -Thorne -Yurtsever –
1988

En
1988 Thorne, Morris, et Yurtsever révélèrent le résultat de leurs
calculs avec l’énergie négative ainsi que l’incroyable implication
de ceux-ci.

Kip Thorne
Non seulement il
était théoriquement possible d’ouvrir un passage entre deux points
de l’espace et de le traverser sans encombre pour voyager entre les
étoiles de façon quasi instantanée
mais on devait aussi pouvoir voyager dans le temps
!
Regardons cela d’un peu plus près.
La
métrique solution des équations d’Einstein qu’ils trouvèrent est la
suivante :
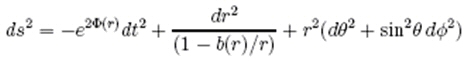
Elle
ressemble à celle de Schwarzschild pour l’intérieur d’une étoile et
elle doit satisfaire des conditions de décroissance à l’infini pour
se raccorder à un espace-temps plat de Minkowski.
Voilà
comment cela marche, c’est tout simple en fait.
Ayant
ouvert un trou de ver traversable, et en supposant celui-ci très
stable, on peut imaginer laisser une de ses bouches d’entrée sur
Terre alors que la seconde pourra être emportée à l’intérieur d’un
vaisseau spatial en vol relativiste effectuant un aller-retour de
disons 1000 ans pour un observateur resté sur Terre.
Si la
vitesse pendant le trajet est très proche de la lumière, il pourra
ne s’être écoulé que quelque heures ou quelques jours dans le
vaisseau. On est précisément dans le cas célèbre des jumeaux de
Langevin.
Il existera donc alors un décalage temporel
entre les deux bouches du trou permettant de remonter dans le passé
jusqu à mille ans avant le retour du vaisseau sur Terre ou dans le
futur jusqu'à 1000 ans après le départ du vaisseau pour quelqu’un
resté sur la planète.
C’est ce qu’on
voit sur le diagramme d’espace-temps ci- dessous repris des cours de
Thorne à Caltech (Methusalem restant sur Terre alors que Florence
effectue son voyage interstellaire).
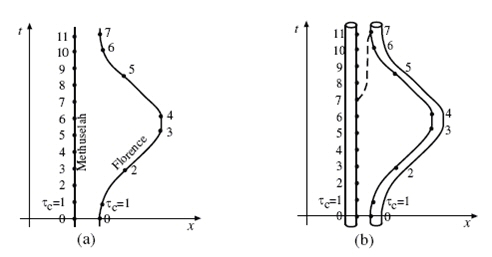
Il
y a quand même un ‘petit’ problème. Matt Visser, un physicien
spécialisé dans la théorie des trous de vers a fait les estimations
suivantes.
Si l’on devait construire un trou de ver stable de
1 m de diamètre il suffirait de ‘tapisser’ la bouche du trou de ver
de seulement 10-21 m d’énergie négative, soit moins d’un millionième
de la taille d’un proton. Là où cela coince c’est qu’il faudrait
disposer de l’énergie libérée par 10 MILLIARDS d’étoiles en une
année !
A - La conjoncture de la
protection chronologique de Hawking :
En 1992 Hawking a
fait toute une série de calculs pour essayer de prouver que l’on ne
peut pas modifier le passé car aucune boucle du genre temps ne
pourrait exister autrement que pour les particules élémentaires.
Sans en donner une démonstration complète les résultats qu’il a
obtenus sont nettement défavorables.

Sa
conclusion finale est célèbre ‘La meilleure preuve que les voyages
dans le temps sont impossibles est que nous ne sommes pas envahis
par des hordes de touristes venues du futur’. On peut mettre en
relation ses raisonnements avec le phénomène suivant.
B -
Un effet Larsen ? :
Le plus grave problème que pose la
possibilité de créer un trou de ver traversable est celui lié à un
effet bien connu que l’on appelle l’effet Larsen (du nom du
physicien danois Søren Larsen (1871-1957). Nous avons tous un jour
ou l’autre été confrontés au problème d’un coup de téléphone
amplifié de façon stridente par un haut-parleur. Le téléphone
enregistre le son émis par le haut-parleur qui est alors renvoyé au
correspondant pour être enregistré à son tour et réémis à l’aide du
haut-parleur etc.…
De manière similaire, des ondes
électromagnétiques (par ex) voyageant vers le passé dans le trou de
ver pourraient à nouveau l’emprunter dans le futur et ainsi de
suite. De l’énergie positive s’accumulera donc dans le trou de
ver ce qui finira par contrebalancer l’énergie négative responsable
du caractère traversable du trou de ver.
La question
centrale est ‘Ok mais en combien de temps ?’
Les calculs
faits jusqu'à présent montrent que c’est si rapide qu’un objet
‘macroscopique’ n’aurait pas le temps de traverser la bouche du trou
avant qu’il ne se ferme. Cependant la réponse ultime est enfouie
dans les lois de la gravitation quantique non perturbative, une
théorie encore à naître.
Des voyages supra-luminiques
seraient donc peut être encore possibles dans l’espace, mais dès
qu’on essayerait de voyager dans le temps les lois de l’Univers
conspireraient pour l’empêcher. C’est aussi la conclusion à laquelle
est arrivé Igor Novikov, l’ancien collaborateur principal du grand
Zeldovitch.
C - Le principe d’auto cohérence de Novikov
:

De gauche à droite Chandrasekhar, Novikov et
Zeldovitch
Le problème du grand-père est
une objection classique au voyage dans le temps. Si vous
remontez dans le temps pour tuer votre grand-père alors vous
n’existez pas donc vous ne remontez pas dans le temps et votre
grand-père est toujours vivant donc vous allez le tuer, etc.
Ne
pourrait-on pas cependant considérer des types de voyage dans le
temps possibles ?
C’est ce que Novikov et d’autres ont
voulu savoir. Les résultats que donnent les équations de la RG sont
illustrés par l’exemple suivant. On pourrait imaginer une bille
lancée vers la bouche d’un wormhole et émergeant dans son propre
passé pour se percuter et s’empêcher de rentrer dans la bouche de
celui-ci. C’est une version physiquement simple à traiter du
paradoxe du grand-père. Inversement on pourrait avoir une boule se
percutant pour se forcer à aller dans le wormhole. Tout calcul fait,
seule cette dernière solution est autorisée par la RG classique
semble- t-il.
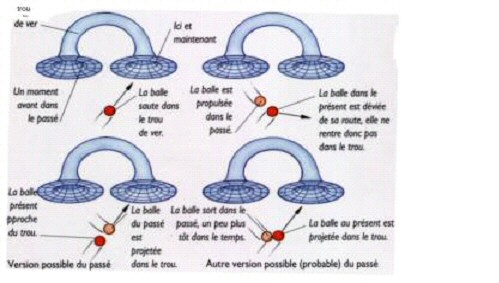
Pour
arriver à cette conclusion, Novikov et ses collaborateurs se sont
appuyés sur des calculs relativement élémentaires mais reposant sur
un des principes les plus fondamentaux de la physique, celui de
‘moindre action’.

Reconnaissez-vous ce que lit Igor Novikov ?
9°) Le LHC en 2007/2008 : des trous noirs et des wormholes en
laboratoire ?
Toutes ces spéculations sur les
trous de vers semblent bien loin de la réalité et ceux-ci à tout
jamais hors de portée de notre technologie.
Ne perdons pas
espoir si tôt !
La fin des années 90 et le début des
années 2000 seront peut être considérés par les historiens de
l’avenir comme l’aurore d’un changement profond dans l’histoire de
l’humanité. On a vu que la possibilité de créer et de maintenir
ouvert un wormhole dépendait en grande partie d’une compréhension de
la gravitation quantique et de son accessibilité
technologique.
Or, jusque vers 1998 environ, tout semblait
indiquer qu’il fallait construire un accélérateur grand comme la Galaxie
pour monter suffisamment en énergie afin que se manifeste directement la
gravitation quantique. Cette même année, des travaux indépendants mais
complémentaires de Nima Arkani-Hamed, Savas Dimopoulos et Gia Dvali d’une
part et Lisa Randall, Raman Sundrum d’autre part, ouvrirent la possibilité
qu’on se soit trompé.
De
manière inespérée, le futur accélérateur de 27 km de diamètre en
construction près de Genève au CERN pourrait bien
suffire.
Quelques années plus tard, en 2001/2002 précisément,
Steven Giddings et Savas Dimopoulos déposèrent sur ArXive deux
articles révolutionnaires considérant sérieusement la possibilité de
créer des mini trous noirs s’évaporant par effet Hawking au LHC, le
Large Hadron Collider, que l’on a mentionné précédemment.
De tout ce qui précède les liens entre trous noirs et
wormholes doivent maintenant être clairs.
http://xxx.soton.ac.uk/abs/hep-th/0205027
http://xxx.soton.ac.uk/abs/hep-ph/0106295
http://www-library.desy.de/preparch/desy/proc/proc02-02/Proceedings/pl.7/landsberg.pdf
Des
trous noirs au LHC peut être, mais alors pourquoi pas aussi des
wormholes lors des collisions entre protons ? Reste à trouver une
signature expérimentale.
La découverte de la fission
nucléaire avait elle aussi commencée par quelque chose de très ténu
alors peut-être peut-on rêver et attendre impatiemment
2007/2008.

Voici
la disposition des expériences avec leurs détecteurs associés le
long des 27 km de circonférence du LHC. L’expérience susceptible de
mettre en évidence des mini trous noirs s’évaporant est liée au
détecteur Atlas que l’on voit sur ce schéma de l’anneau du Large
Hadron Collider.
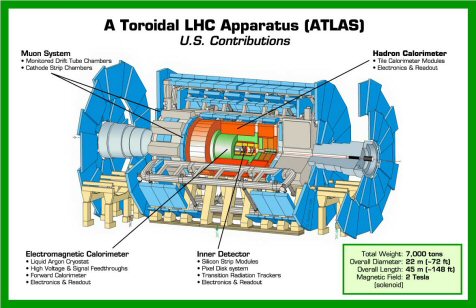
Ce
super détecteur Atlas est peut être l’une des machines les plus
complexes de toute l’histoire de l’humanité. Verra-t-il le Higgs,
les partenaires supersymétriques des quarks et des leptons et ce qui serait fabuleux
l’évaporation de mini trous noirs ? L’Avenir le dira bientôt
!
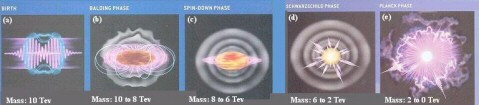
Possible formation et évaporation d’un mini trou noir
par collision entre quarks, contenus dans les protons, lors de la
collision des faisceaux proton-proton au
CERN.

Vue d’artiste du super collisionneur dans son
tunnel et l’extension de celui-ci près du lac Léman.
Remerciements
L'auteur du
dossier remercie chaleureusement toutes les personnes ayant
participées d'un façon ou d'un autre à ce travail,elles se
reconnaîtront.Une mention spéciale pour Loïc Villain et sa lecture
attentive du dossier,cependant s'il devait rester des erreurs elles
ne sauraient être attribuées qu'à moi.
La science-fiction fait grand
usage du voyage dans le temps ainsi que du concept de trous de vers,
des raccourcis dans l’espace-temps permettant de contourner la
limitation de la vitesse des trajets interstellaires imposée par les
lois de la relativité restreinte.
S’agit-il de quelque chose
de totalement impossible, sommes-nous condamnés à ne jamais voir des
machines temporelles ou des ‘portes des étoiles’ uniquement qu’au
cinéma ?
L’objet de ce dossier est d’examiner à partir des
données les plus récentes de la physique théorique moderne ce qui
est crédible et ce qui ne l’est pas.
La théorie de la
relativité, surtout celle traitant de la gravitation c'est-à-dire la
relativité générale d’Einstein, sera notre guide tout au long de
notre voyage vers la nature de l’espace et du temps.
C’est
pourquoi les deux dossiers de Futura-Sciences sur la théorie d’Einstein (relativité
restreinte et relativité générale) sont des lectures conseillées avant de
lire ce qui va suivre, ils sont indispensables pour quiconque n’a jamais
regardé quoi que ce soit sur la relativité.
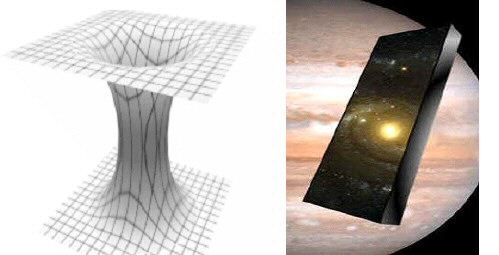
Nous
essayerons dans un premier temps de voir s’il est réaliste de
voyager dans le temps ou dans l’espace à partir d’un trou noir. Jusqu’ à récemment,
c’était souvent comme cela que la science fiction permettait à ses
personnages de s’affranchir des limites de
l’espace-temps.
Pour cela nous devrons explorer un peu la
partie de la relativité qui traite des singularités.
On verra
aussi que l’idée de voyager dans le temps à l’aide des effets
prédits par la relativité générale est ancienne, bien qu’il ait
fallu attendre le milieu des années 80 pour voir apparaître les
premières discussions vraiment sérieuses sur la façon de s’y prendre
pour voyager à l’aide de distorsions de la structure de l’espace et
du temps.
Les trous noirs
Sommaire
Espace-temps de Minkowski
La Relativité générale d’Einstein
Le Pont d’Einstein-Rosen et les trous de vers de Wheeler-Misner
L’Univers de Gödel et la solution de Kerr
Les singularités en relativité générale et le cylindre de Tipler
Le rayonnement de Hawking
Mécanique quantique et fluctuations du vide
L’article de Morris -Thorne -Yurtsever – 1988
Le LHC en 2007/2008 : des trous noirs et des wormholes en laboratoire ?
H
içbir yazý/ resim izinsiz olarak kullanýlamaz!! Telif haklarý uyarýnca bu bir suçtur..! Tüm haklarý Çetin BAL' a aittir. Kaynak gösterilmek þartýyla siteden alýntý yapýlabilir.The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa / Ýndex / Ziyaretçi
Defteri / ![]() E-Mail / Kuantum Fiziði / Quantum Teleportation-2
E-Mail / Kuantum Fiziði / Quantum Teleportation-2
Time Travel Technology / Kuantum Teleportation / Duyuru / UFO Technology