Spacetime and Energy:
  • relativity unifies space, time, mass and energy
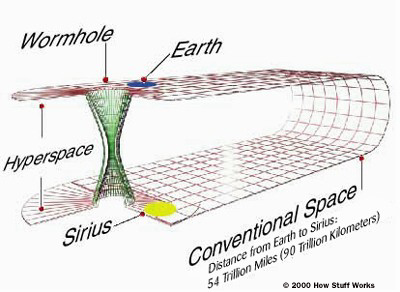
Special relativity and E=mc2 led to the most powerful unification of physical concepts since the time of Newton. The previously separate ideas of space, time, energy and mass were linked by special relativity, although without a clear understanding of how they were linked.

 

 

  • explanation provided by general relativity, where a complete theory of gravity is provided by using the geometry of spacetime
The how and why remained to the domain of what is called general relativity, a complete theory of gravity using the geometry of spacetime. The origin of general relativity lies in Einstein's attempt to apply special relativity in accelerated frames of reference. Remember that the conclusions of relativity were founded for inertial frames, i.e. ones that move only at a uniform velocity. Adding acceleration was a complication that took Einstein 10 years to formulate.

 

Equivalence Principle:

 

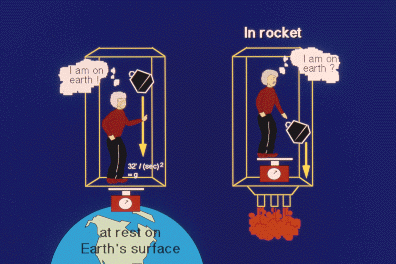
  • equivalence principle equates accelerating and gravity effects
The equivalence principle was Einstein's `Newton's apple' insight to gravitation. His thought experiment was the following, imagine two elevators, one at rest of the Earth's surface, one accelerating in space. To an observer inside the elevator (no windows) there is no physical experiment that he/she could perform to differentiate between the two scenarios.

The equivalence principle is a fundamental law of physics that states that gravitational and inertial forces are of a similar nature and often indistinguishable. In the Newtonian form it asserts, in effect, that, within a windowless laboratory freely falling in a uniform gravitational field, experimenters would be unaware that the laboratory is in a state of nonuniform motion. All dynamical experiments yield the same results as obtained in an inertial state of uniform motion unaffected by gravity.

Introduction

General relativity was the revolutionary theory proposed by Albert Einstein in 1915 that proposed a new way of explaining the nature of gravity. Previously, Einstein had said that distance and time are not fixed; they were based on the motion of the observer with his Theory on Special Relativity (It’s relative!). Now, with his new theory, gravity was established as being equal to acceleration, and, thus, gravity had the capability of warping space!

No one can distungish between an accelerated lift and gravitation.

History and Development

Introduced by Albert Einstein in 1915 after the last theory on the nature of gravity proposed by Isaac Newton about one hundred and fifty years earlier, the Theory of General Relativity has achieved colossal fame, even after Einstein won the Nobel Prize for work in another field – the photoelectric effect – in 1921. General Relativity is based on the Equivalence Principle, which states that gravitation and acceleration are two phenomena describing essentially the same underlying concept.

Einstein first explained this Equivalence Principle in 1907 when he said, “We shall therefore assume the complete physical equivalence of a gravitational field and the corresponding acceleration of the reference frame. This assumption extends the principle of relativity to the case of uniformly accelerated motion of the reference frame.” Basically, by incorporating what Einstein had said in this theory on Special Relativity and stating that gravity and acceleration are equivalent, then it can be said that motion affects gravity (like time and space), as well. The principles of General Relativity have been used to predict the bending of light emitted by stars and the precession of Mercury, and these two predictions have been confirmed experimentally. Unfortunately, the two most spectacular phenomena predicted by General Relativity – the validity of black holes and the power of gravity on the whole universe – are thought to not be confirmable.

  

  • although a simple and common sense assumption, the equivalence principle has strange consequences
  • such as, photons will be effected by gravity, even though they have zero mass
An immediate consequence of the equivalence  principle is that gravity bends light.To visualize why this is true imagine a photon crossing the elevator accelerating into space. As the photon crosses the elevator, the floor is accelerated upward and the photon appears to fall downward. The same must be true in a gravitational field by the equivalence principle.

The principle of equivalence renders the gravitational field fundamentally different from all other force fields encountered in nature. The new theory of gravitation, the general theory of relativity, adopts this characteristic of the gravitational field as its foundation.

 

 

Caption: The person in the spaceship has no experimental or intuitive means of distinguishing whether he is motionless on the surface of the Earth or in space accelerating at a rate equivalent to 1 Earth gravity. The implication of this is that the acceleration due to motion and that due to gravity are equivalent, which in turn implies that space is curved in the presence of a gravitational field.

 

General Relativity :

  • general relativity combines special relativity with the equivalence principle
  • general relativity first resolves the problem of the instantaneous transfer of gravity under Newton's theory by stating that gravity propagates at the speed of light
The second part of relativity is  the theory of general relativity and lies on two empirical findings that he elevated to the status of basic postulates. The first postulate is the relativity principle: local physics is governed by the theory of special relativity. The second postulate is the equivalence principle: there is no way for an observer to distinguish locally between gravity and acceleration.

The general theory of relativity derives its origin from the need to extend the new space and time concepts of the special theory of relativity from the domain of electric and magnetic phenomena to all of physics and, particularly, to the theory of gravitation. As space and time relations underlie all physical phenomena, it is conceptually intolerable to have to use mutually contradictory notions of space and time in dealing with different kinds of interactions, particularly in view of the fact that the same particles may interact with each other in several different ways--electromagnetically, gravitationally, and by way of so-called nuclear forces.

Newton's explanation of gravitational interactions must be considered one of the most successful physical theories of all time. It accounts for the motions of all the constituents of the solar system with uncanny accuracy, permitting, for instance, the prediction of eclipses hundreds of years ahead. But Newton's theory visualizes the gravitational pull that the Sun exerts on the planets and the pull that the planets in turn exert on their moons and on each other as taking place instantaneously over the vast distances of interplanetary space, whereas according to relativistic notions of space and time any and all interactions cannot spread faster than the speed of light. The difference may be unimportant, for practical reasons, as all of the members of the solar system move at relative speeds far less than 1/1,000 of the speed of light; nevertheless, relativistic space-time and Newton's instantaneous action at a distance are fundamentally incompatible. Hence Einstein set out to develop a theory of gravitation that would be consistent with relativity.

  • remembering that mass changes with motion, and that mass causes gravity, Einstein links mass, gravity and spacetime with the geometry of spacetime
Proceeding on the basis of the experience gained from Maxwell's theory of the electric field, Einstein postulated the existence of a gravitational field that propagates at the speed of light, c, and that will mediate an attraction as closely as possible equal to the attraction obtained from Newton's theory. From the outset it was clear that mathematically a field theory of gravitation would be more involved than that of electricity and magnetism. Whereas the sources of the electric field, the electric charges of particles, have values independent of the state of motion of the instruments by which these charges are measured, the source of the gravitational field, the mass of a particle, varies with the speed of the particle relative to the frame of reference in which it is determined and hence will have different values in different frames of reference. This complicating factor introduces into the task of constructing a relativistic theory of the gravitational field a measure of ambiguity, which Einstein resolved eventually by invoking the principle of equivalence.

Einstein discovered that there is a relationship between mass, gravity and spacetime. Mass distorts spacetime, causing it to curve. Gravity can be described as motion caused in curved spacetime .

 

 

  • gravity as geometry of spacetime returns physics to classic levels of the ancient Greeks
  • however, spacetime is not Euclidean
  • matter tells spacetime how to curve, and spacetime tells matter how to move (orbits)
Thus, the primary result from general relativity is that gravitation is a purely geometric consequence of the properties of spacetime. Special relativity destroyed classical physics view of absolute space and time, general relativity dismantles the idea that spacetime is described by Euclidean or plane geometry. In this sense, general relativity is a field theory, relating Newton's law of gravity to the field nature of spacetime, which can be curved.

Gravity in general relativity is described in terms of curved spacetime. The idea that spacetime is distorted by motion, as in special relativity, is extended to gravity by the equivalence principle. Gravity comes from matter, so the presence of matter causes distortions or warps in spacetime. Matter tells spacetime how to curve, and spacetime tells matter how to move (orbits).

  • two classical tests of general relativity:
  • the first is the deflection of starlight by the Sun's gravity as measured by the 1919 solar eclipse experiment
There were two classical test of general relativity, the first was that light should be deflected by passing close to a massive body. The first opportunity occurred during a total eclipse of the Sun in 1919.

Measurements of stellar positions near the darkened solar limb proved Einstein was right. Direct confirmation of gravitational lensing  was obtained by the Hubble Space Telescope last year.

  • the 2nd test was the prediction of time dilation in a gravitational field, first shown by atomic clocks in the mid-70's (note the need of advanced technology to test general relativity)
  • the effects of general relativity require sensitive instruments under the condition of weak fields, i.e. conditions where the acceleration due to gravity is much, much less than the speed of light
  • strong fields are found in extreme situations such as near neutron stars or black holes
The second test is that general relativity predicts a time dilation in a gravitational field, so that, relative to someone outside of the field, clocks (or atomic processes) go slowly. This was confirmed with atomic clocks flying airplanes in the mid-1970's.

The general theory of relativity is constructed so that its results are approximately the same as those of Newton's theories as long as the velocities of all bodies interacting with each other gravitationally are small compared with the speed of light--i.e., as long as the gravitational fields involved are weak. The latter requirement may be stated roughly in terms  of the escape velocity. A gravitational field is considered strong if the escape velocity approaches the speed of light, weak if it is much smaller. All gravitational fields encountered in the solar system are weak in this sense.

Notice that at low speeds and weak gravitational fields, general and special relativity reduce to Newtonian physics, i.e. everyday experience.

Black Holes:

 

  • as gravity increases the escape velocity increases
  • when escape velocity exceeds the speed of light a black hole forms
The fact that light is bent by a gravitational field brings up the following thought experiment. Imagine adding mass to a body. As the mass increases, so does the gravitational pull and objects require more energy to reach escape velocity. When the mass is sufficiently high enough that the velocity needed to escape is greater than the speed of light we say that a black hole has been created.

 

 

  • since photons have zero mass, a better definition of a black hole is given by curvature
  • a black hole is an object of infinite curvature, a hole in spacetime
  • the Schwarzschild radius defines the event horizon, the point of no return around the black hole
Another way of defining a black hole is that for a given mass, there is a radius where if all the mass is compress within this radius the curvature of spacetime becomes infinite and the object is surrounded by an event horizon. This radius called the Schwarzschild radius and varys with the mass of the object (large mass objects have large Schwarzschild radii, small mass objects have small Schwarzschild radii).

Schwarzschild radius is the radius below which the gravitational attraction between the particles of a body must cause it to undergo irreversible gravitational collapse. This phenomenon is thought to be the final fate of the more massive stars.

The gravitational radius (R) of an object of mass M is given by the following formula, in which G is the universal gravitational constant and c is the speed of light: R = 2GM/c2 . For a mass as small as a human being, the gravitational radius is of the order of 10-23 cm, much smaller than the nucleus of an atom; for a typical star such as the Sun, it is about 3 km (2 miles).

  • a black hole is still visible by its distortion on local spacetime and the deflection of starlight
The Schwarzschild radius marks the point where the event horizon forms, below this radius no light escapes. The visual image of a black hole is one of a dark spot in space with no radiation emitted. Any radiation falling on the black hole is not reflected but rather absorbed, and starlight from behind the black hole is lensed.

                                    

  • the structure of a black hole contains only an event horizon and a singularity
Even though a black hole is invisible, it has properties and structure. The boundary surrounding the black hole at the Schwarzschild radius is called the event horizon, events below this limit are not observed. Since the forces of matter can not overcome the force of gravity, all the mass of a black hole compresses to infinity at the very center, called the singularity.

                                             

  • the size of a black hole is set by its mass
A black hole can come in any size. Stellar mass black holes are thought to form from supernova events, and have radii of 5 km. Galactic black hole in the cores of some galaxies, millions of solar masses and the radius of a solar system, are built up over time by cannibalizing stars. Mini black holes formed in the early Universe (due to tremendous pressures) down to masses of asteroids with radii the size of a grain of sand.

 

  • spacetime is severely distorted near the event horizon, and extreme effects are seen
Note that a black hole is the ultimate entropy sink since all information or objects that enter a black hole never return. If an observer entered a black hole to look for the missing information, he/she would be unable to communicate their findings outside the event horizon.

                                  

Black Holes and Neutron Stars

Neutron stars and black holes are among the most exotic objects in the universe. A lump of neutron star matter the size of a sugar cube would weigh as much as all humanity, and the stars have magnetic fields a trillion times Earth's. Since we can't reproduce such conditions in laboratories, we have to observe neutron stars with telescopes to figure out their properties. Recently the Rossi Explorer, a new X-ray satellite, discovered a remarkable new phenomenon of neutron stars that strip matter from their companion stars: their brightness varies almost periodically more than a thousand times per second. I will describe how this phenomenon gives us a sensitive new tool to probe the properties of neutron stars, and how it may even help us search for black holes.

Intro to Black Holes

 

A black hole is a region of space in which the matter is so compact that nothing can escape from it, not even light; the "surface" of a black hole, inside of which nothing can escape, is called an event horizon. The matter that forms a black hole is crushed out of existence. Just as the Cheshire Cat disappeared and left only its smile behind, a black hole represents matter that leaves only its gravity behind.

Black holes are usually formed when an extremely massive star dies in a supernova. However, some people think small black holes were formed during the Big Bang, and that the resulting "mini black holes" may be in great abundance in our galaxy.

In principle, black holes can have any mass; black holes formed by stellar death have at least twice the mass of our Sun. Unlike ordinary things (e.g., rocks), which have a size roughly proportional to the cube root of their mass, black holes have radii proportional to their mass. The event horizon of a nonrotating black hole the mass of our Sun has a radius about 3~km. Thus, large black holes aren't very dense! A black hole a billion times as massive as our Sun, such as is thought to exist in the center of some galaxies, has an average density just twenty times the density of air.

Black holes, like any gravitating objects, exert a tidal force. If you approach a black hole feet first, the gravitational force at your feet is greater than the force at your head. The tidal force at the event horizon is smaller for larger black holes: you would get torn to shreds far outside a black hole the mass of our sun, but at the event horizon of a billion solar mass black hole the tidal force would only be a millionth of an ounce!

Strange Facts About Black Holes
  • Light bends so much near black holes that if you were near one and looking away from the hole, you would see multiple images of every star in the universe, and could actually see the back of your own head!
  • Inside a black hole the roles of time and radius reverse: just as now you can't avoid going into the future, inside a black hole you can't avoid going in to the central singularity.
  • If you stood a safe distance from a black hole and saw a friend fall in, he would appear to slow down and almost stop just outside the event horizon. His image would dim very rapidly. Unfortunately for him, from his point of view he would cross the event horizon just fine, and would meet his doom at the singularity.
  • Black holes are the simplest objects in the universe. You can describe one completely by just its mass, spin rate, and electric charge.

How Do We Detect Black Holes?

Black holes don't radiate light, and an object that falls inside a black hole doesn't emit light either, so detecting them can be challenging.

Just as with neutron stars, if a black hole is in a binary and it strips gas from its companion, we can detect X-rays from the resulting accretion disk . The light from accretion disks around black holes looks very similar to the light from disks around neutron stars, and it is not always possible to tell with certainty which object lurks at the center of the disk, although in six cases so far we're sure that the central object is a black hole.

You can also infer the presence of a black hole in the center of some galaxies. This is done by observing stars near the center of the galaxy. If the stars are moving very rapidly around some unseen object, Kepler's laws can be used to estimate the mass in the center. In some cases the mass must be at least a hundred million times our Sun's mass, in a region only a few light years across. Astronomers are virtually certain that the only explanation is a black hole, but we lack direct evidence.

The detection of black holes is very difficult and controversial, and it is being studied actively by many research groups.

Origin and Scale of Neutron Stars

A neutron star has roughly the mass of our Sun crammed in a ball ten kilometers in radius. Its density is therefore a hundred trillion times the density of water; at that density, all the people on Earth could be fit into a teaspoon! Neutron stars are born during supernova, and are held up by neutron degeneracy pressure. These stars are relatively rare: only about 10^8 in our galaxy, or one in a thousand stars, so the nearest one is probably at least 40 light years away.

Neutron Stars and Extreme Physics
  • Density at center can be several times the density of an atomic nucleus, so we can't explore this regime in laboratories. The properties of this matter are unknown, and may include such exotic things as enormous conglomerations of quarks.
  • Magnetic fields are a trillion times Earth's, and more than a million times as strong as can be achieved in laboratories.
  • Matter in the central parts of neutron stars is thought to be a superconductor, even at a hundred million degrees!

Neutron stars therefore have states of matter that cannot be duplicated in laboratories. Study of them helps us test our theories, and perhaps discover new physics. But how can we observe neutron stars?

Observing Neutron Stars

 

We see a normal star by the light it gives off during fusion. Neutron stars are very hot, more than 100,000 K for most of their lifetimes, so this sounds promising but most of the energy comes out as X-rays (not visible light). Also, neutron stars are so small that at typical distances they are ten billion times fainter than you can see with your naked eye, which is too faint for even the Hubble Space Telescope. We need some other way to see neutron stars.

One way is to see them as radio pulsars. Another way is if the neutron star is one member of a binary, in which case the gravity of the neutron star can strip gas off its companion. The gas from the companion falls onto the neutron star, and emits fantastic power in X-rays: as much as 50,000 times the luminosity the Sun produces. This is a tremendously efficient way to generate energy. Dropping a kilogram of matter onto the surface of a neutron star releases as much energy as a five megaton hydrogen bomb!

Since the neutron star is a very small target, astronomically speaking, gas can't fall onto it directly. Instead, gas spirals around the neutron star, and friction with itself releases huge amounts of energy in what is called an accretion disk. Studying the X-rays from accretion disks can give us hints about the star: for example, how does matter behave at extremely high densities?

 

The Equation of State

As mentioned above, we want to know the properties of the extremely dense matter in the center of neutron stars. One way to characterize the matter is by its equation of state.

The equation of state can be pictured as the relation between the density of matter and its pressure. Consider a glass of water. The shape of the water in the glass can be changed easily (e.g., by sloshing it around), but the volume, and hence the density, of the water is extremely difficult to change. Even if you apply a huge amount of pressure to the water, for example by a piston, the density changes hardly at all; this is the basis of hydraulic presses. Water may therefore be said to have a stiff equation of state. In contrast, the volume of air in an empty glass can be changed easily, with little pressure, so air may be said to have a soft equation of state. So, a knowledge of the equation of state tells us, essentially, how squeezable the matter is.

In the case of a neutron star, knowledge of both the mass and radius of a particular neutron star would tell us the equation of state. This is because gravity squeezes the star, and the more mass the star has the more gravity squeezes it. If the star has a large radius (meaning, say, 15~km!), it was relatively successful in resisting gravity and thus has a very stiff equation of state. If the star has a small radius (say, 8~km), it was not as successful in resisting gravity and it has a softer equation of state. We therefore need to estimate the mass and radius of neutron stars.

 

Estimating NS Masses and Radii

No easy task, this. Astronomical measurements are often challenging, because we can't go to a star and experiment on it. Neutron stars are especially tough, because they are relatively small and far away: even the closest one would appear to be the size of a bacterium on the Moon, so we have to find other ways to determine the mass or radius of a neutron star.

One way to do this is to use Kepler's laws. If we can figure out how far two stars in a binary are from each other, and the duration of their orbital period, we know something about their masses. Only for neutron stars in binaries do we have even a rough estimate of the mass, and in only a few of those cases do we know the mass accurately.

Estimating the radius is much more difficult than estimating the mass. Unlike the mass, the radius doesn't have any strong effects on what we can observe. From astronomical observations alone, neutron stars could have radii from 5~km to 30~km (although most of that range, all but about 7~km to 20~km, is ruled out by what we know of nuclear physics).

So, we need some kind of breakthrough in the evidence to allow us to further constrain the radii of neutron stars.

An Unexpected Discovery

We can only discover what our instruments can detect, so many times in astrophysics a breakthrough in our understanding has come from an improvement in instrumental capabilities.

Such was the case when the Rossi X-ray Timing Explorer was launched on December 30, 1995. Its many outstanding properties include an unprecedented sensitivity to very rapid variations of the X-ray intensity of accreting neutron stars, i.e., neutron stars stripping mass from their stellar companions. This led to the discovery of a completely unexpected phenomenon: fast intensity oscillations, sometimes more than a thousand times per second!

Kilohertz Intensity Oscillations

Figure 1 shows the X-ray brightness from one neutron star system, as a function of time. The intensity goes up and down nearly 1000 times per second. There are at least 10 known neutron stars that show this, and we have discovered that:

  • The intensity variations are fast, up to 1200 times per second
  • For a given neutron star, the frequency of the variations goes up and down with time: in one case, the variation can be anywhere from 500 per second to 1100 per second

The dramatic change in frequency means that it can't be something simple like the spin frequency of the neutron star, since the star can't easily be spun up or down. However, the common occurrence of this phenomenon and its other properties mean that it is telling us something fundamental about the flow of matter onto neutron stars.

Implications
  • The frequency with which the clump goes around the star is calculated by Kepler's laws: the higher the frequency, the closer the clump has to be to the star. This limits the radius of the star.
  • When the effects of Einstein's general relativity are included, it turns out that we also get an upper limit to the mass of the star.
  • The result is that the neutron stars in these systems must have masses less than 2.2 times our Sun's mass, and radii less than 17~km. This is the first convincing observational limit to the radius of neutron stars.

Key Points
  • The matter in the center of neutron stars is incredibly dense, and we can't reproduce it on Earth.
  • So, the study of neutron stars can tell us things about the universe that would otherwise remain forever undiscovered.
  • One way to find out about the dense matter of neutron stars is to determine the equation of state of neutron stars, which is the relation between their pressure and density.
  • The equation of state is known if we know both the mass and radius of a neutron star.
  • But, astronomical observations are indirect: we can't experiment on stars.
  • Neutron stars are particularly difficult, since they are relatively small and distant.
  • Luckily for us, the recently-discovered phenomenon of rapid X-ray intensity oscillations may allow us, for the first time, to estimate both the mass and radius of some neutron stars and thus know their equation of state.
  • As it turns out, if we knew the equation of state of neutron stars, we would also know their maximum mass. This ends up helping in the search for black holes in our galaxy.
  • This phenomenon is still new, and we continue to learn things about it at a rapid pace, both observationally and theoretically; these are exciting times!

 

Glossary
Accretion disk:
the pattern of flow of matter from a normal star to a neutron star or black hole, which is flattened and thus disk-like.
Degeneracy pressure:
a quantum-mechanical phenomenon; fermions, such as electrons or neutrons, obey Pauli's exclusion principle, so that no two fermions can occupy the same state. Thus, if fermions are squeezed together they resist even if there is no temperature and no energy generation. This resistance to squeezing is degeneracy pressure.
Equation of state:
the relation between the pressure and density of a given type of matter, which is an indication of how the matter resists squeezing. If the matter resists squeezing strongly (e.g., water), the equation of state is stiff; if it resists squeezing only weakly (e.g., air), the equation of state is soft.
Event horizon:
in a black hole, the point beyond which events cannot be detected. This is the point of no return; an object that falls inside the event horizon can't get out.
Kepler's laws:
rules for the orbital motion of planets or anything else bound by gravity. The law of most interest here is that the square of the orbital period is proportional to the cube of the orbital separation, and inversely proportional to the mass. Thus, if we see an orbital period, we can estimate the mass or orbital separation and therefore constrain the mass and radius of a neutron star.
Singularity:
in a black hole, the "center point", at which densities, tidal forces, and other physical quantities become infinite. Our current physical theories break down at this point.
Tidal force:
the force an object feels because of the differential pull of gravity at different distances.

 

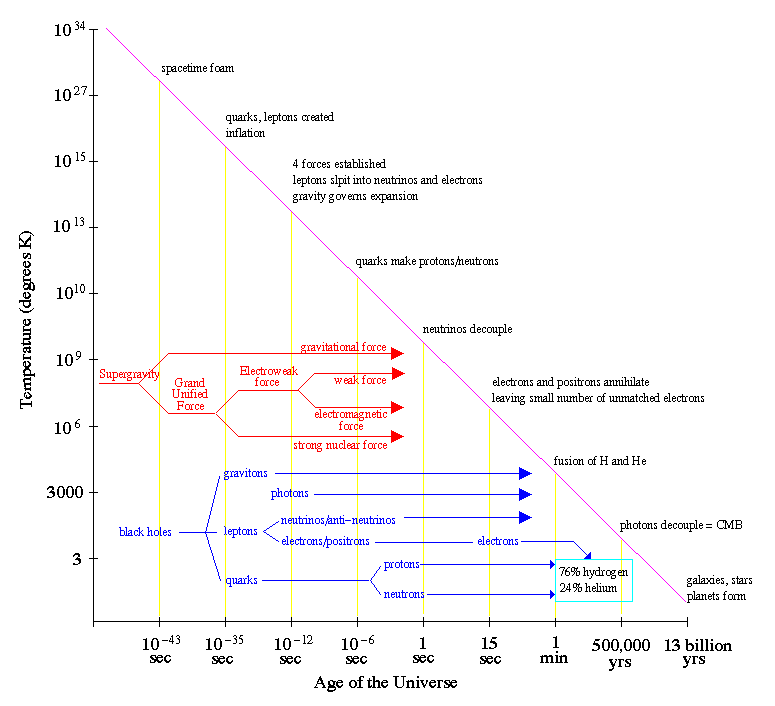
Birth of the Universe :

Physics of the early Universe is at the boundary of astronomy and philosophy since we do not currently have a complete theory that unifies all the fundamental forces of Nature at the moment of Creation. In addition, there is no possibility of linking observation or experimentation of early Universe physics to our theories (i.e. its not possible to `build' another Universe). Our theories are rejected or accepted based on simplicity and aesthetic grounds, plus there power of prediction to later times, rather than an appeal to empirical results. This is a very difference way of doing science from previous centuries of research.

 Our physics can explain most of the evolution of the Universe after the Planck time (approximately 10-43 seconds after the Big Bang).

     

However, events before this time are undefined in our current science and, in particular, we have no solid understanding of the origin of the Universe (i.e. what started or `caused' the Big Bang). At best, we can describe our efforts to date as probing around the `edges' of our understanding in order to define what we don't understand, much like a blind person would explore the edge of a deep hole, learning its diameter without knowing its depth.

 

Quantum Gravity:

Physicist frequently search for unifying principles that hopeful lead to deeper, more fundamental laws of Nature. The unification of the theory of electricity with the theory of magnetism led to an understanding of light as electromagnetic radiation. One obvious unification is between quantum mechanics and general relativity, the so-called theory of quantum gravity.

Quantum gravity is a type of quantum theory of elementary particles and their interactions that is based on the particle symmetry known as supersymmetry and that naturally includes gravity along with the other fundamental forces (the electromagnetic force, the weak nuclear force, and the strong nuclear force).

The electromagnetic and the weak forces are now understood to be different facets of a single underlying force that is described by the electroweak theory. Further unification of all four fundamental forces in a single quantum theory is a major goal of theoretical physics. Gravity, however, has proved difficult to treat with any quantum theory that describes the other forces in terms of messenger particles that are exchanged between interacting particles of matter. General relativity, which relates the gravitational force to the curvature of space-time, provides a respectable theory of gravity on a larger scale. To be consistent with general relativity, gravity at the quantum level must be carried by a particle, called the graviton.

 

Unifying theories usually begin by exploring new realms of experience. For example, particle theories (what are the fundamental particles that matter is made of) find deeper meaning by exploring high energies (i.e. high mass ranges) using large particle accelerators.

 

Quantum gravity asks the question, ``what is the behavior of gravity on extremely small scales?'' What are the properties of mini black holes and how does the force of gravity compared to other subatomic forces? These questions are particularly crucial to cosmology since the very early Universe was an environment dominated by extremely high pressures and temperatures, and the folding of spacetime on quantum scales.

           

There is currently no complete theory for combined quantum and gravity, as the process of unification proved to have many more mathematical difficulties than expected. Many believe that the problems indicate that a new, much deeper theory must exist out of which quantum mechanics and general relativity emerge. However, some partial elements of a working composite of quantum mechanics and general relativity have predicted gravitational waves and Hawking radiation.

 

 

Unification:

One of the reasons our physics is incomplete during the Planck era is a lack of understanding of the unification of the forces of Nature during this time. At high energies and temperatures, the forces of Nature become symmetric. This means the forces resemble each other and become similar in strength, i.e. they unify.

 

An example of unification is to consider the interaction of the weak and electromagnetic forces. At low energy, photons and W,Z particles are the force carriers for the electromagnetic and weak forces. The W and Z particles are very massive and, thus, require alot of energy (E=mc2). At high energies, photons take on similar energies to W and Z particles, and the forces become unified into the electroweak force.

There is the expectation that all the nuclear forces of matter (strong, weak and electromagnetic) unify at extremely high temperatures under a principle known as Grand Unified Theory, an extension of quantum physics using as yet undiscovered relationships between the strong and electroweak forces.

The final unification resolves the relationship between quantum forces and gravity (supergravity).

In the early Universe, the physics to predict the behavior of matter is determined by which forces are unified and the form that they take. The interactions just at the edge of the Planck era are ruled by supergravity, the quantum effects of mini-black holes. After the separation of gravity and nuclear forces, the spacetime of the Universe is distinct from matter and radiation.

 

 

Cosmic Singularity :

One thing is clear in our framing of questions such as `How did the Universe get started?' is that the Universe was self-creating. This is not a statement on a `cause' behind the origin of the Universe, nor is it a statement on a lack of purpose or destiny. It is simply a statement that the Universe was emergent, that the actual of the Universe probably derived from a indeterminate sea of potentiality that we call the quantum vacuum, whose properties may always remain beyond our understanding.

Extrapolation from the present to the moment of Creation implies an origin of infinite density and infinite temperature (all the Universe's mass and energy pushed to a point of zero volume). Such a point is called the cosmic singularity.

 

Infinites are unacceptable as physical descriptions, but our hypothetical observers back at the beggining of time are protected by the principle of cosmic censorship. What this means is that singularities exists only mathematically and not as a physical reality that we can observe or measure. Nature's solution to this problem are things like the event horizon around black holes. Barriers built by relativity to prevent observation of a singularity.

 

Planck Era :

The earliest moments of Creation are where our modern physics breakdown, where `breakdown' means that our theories and laws have no ability to describe or predict the behavior of the early Universe. Our everyday notions of space and time cease to be valid.

Although we have little knowledge of the Universe before the Planck time, only speculation, we can calculate when this era ends and when our physics begins. The hot Big Bang model, together with the ideas of modern particle physics, provides a sound framework for sensible speculation back to the Planck era. This occurs when the Universe is at the Planck scale in its expansion.

 

Remember, there is no `outside' to the Universe. So one can only measure the size of the Universe much like you measure the radius of the Earth. You don't dig a hole in the Earth and lower a tape measure, you measure the circumference (take an airplane ride) of the Earth and divide by 2π (i.e. C = 2π radius).

The Universe expands from the moment of the Big Bang, but until the Universe reaches the size of the Planck scale, there is no time or space. Time remains undefined, space is compactified.String theory  maintains that the Universe had 10 dimensions during the Planck era, which collapses into 4 at the end of the Planck era (think of those extra 6 dimensions as being very, very small hyperspheres inbetween the space between elementary particles, 4 big dimensions and 6 little tiny ones).

During the Planck era, the Universe can be best described as a quantum foam of 10 dimensions containing Planck length sized black holes continuously being created and annihilated with no cause or effect. In other words, try not to think about this era in normal terms.

Spacetime Foam :

The first moments after the Planck era are dominated by conditions were spacetime itself is twisted and distorted by the pressures of the extremely small and dense Universe.

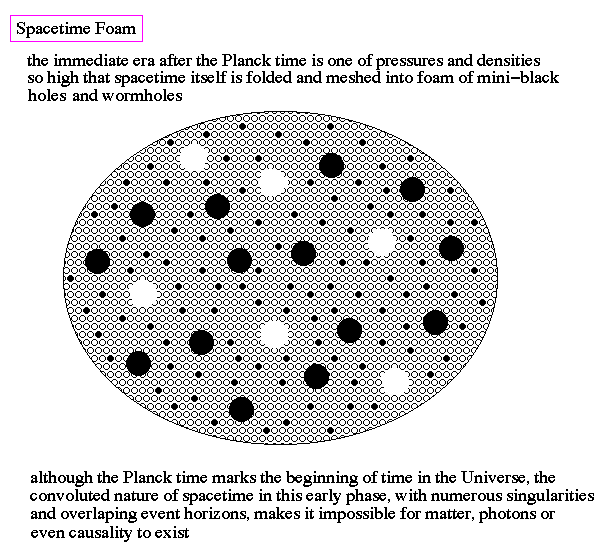
Most of these black holes and wormholes are leftover from the Planck era, remnants of the event horizon that protected the cosmic singularity. These conditions are hostile to any organization or structure not protected by an event horizon. Thus, at this early time, black holes are the only units that can survive intact under these conditions, and serve as the first building blocks of structure in the Universe, the first `things' that have individuality.

Matter arises at the end of the spacetime foam epoch as the result of strings, or loops in spacetime. The transformation is from ripping spacetime foam into black holes, which then transmute into elementary particles. Thus, there is a difference between something of matter and nothing of spacetime, but it is purely geometrical and there is nothing behind the geometry. Matter during this era is often called GUT matter to symbolize its difference from quarks and leptons and its existence under GUT forces.

Relativity meets the Planck scale

According to Special Relativity's time dilation and length contraction, two observers with relative motion are condemned to eternal disagreement about times and lengths. Or are they?

They will disagree over the arbitrary times measured in seconds and lengths measured in metres or whatever units. They would also disagree over clock ticks, atomic vibrations and light wavelengths. But what if there were some absolute times and lengths, determined by the very nature of the universe? And what if these quantities could be measured in different frames of reference. Wouldn't the observers have to agree on those having the same value, if they agree on the same laws of physics?

Well, there is an abolute length and an absolute time. It's possible that we'll never be able to measure them, so any threat posed to relativity is distant and perhaps even hypothetical. It is interesting to see whether and how these quantities might be included in relativity.

scales of length from metres to the Planck length The Planck length LP is defined by taking the constants of nature and combining them in such a way that their units combine to give a length. Planck's constant, h, has units of Joule seconds. Cavendish's constant G (the constant of gravitation) has units of N.m2kg-2. And the speed of light c has units of m.s-1. The combination that works is:

    LP = (hG/2pc3)1/2 .

The Planck length is 1.6 x 10-35 metres. (That's 0.000000000000000000000000000000000016 meters.) To give you an idea, let's compare it with the size of an atom, which is already about 100,000 times smaller than anything you can see with your unaided ey (an atom size is about 0.0000000001 meters). Suppose that you measured the diameter of an atom in Planck lengths, and that you counted off one Planck length per second. To measure the atomic diameter in Planck lengths would take you 10,000,000 times the current age of the universe. (After which time, for Joyce fans, the fires of hell may well have begun to begin to burn.)

 

Divide the minuscule Planck length by the speed of light (which is pretty big) and you get a really tiny unit of time, the Planck time, tP, which is:

    tP = (hG/2pc5)1/2 .

The Planck time is 5.4 x 10-44 seconds. (I'm wearing out the zero key on this keyboard, so I shan't write it out in full but you get the idea: it's brief.)

(There is also a Planck mass, which is (ch/2pG)1/2 = 22 mg. This doesn't sound very much, until you think of a fundamental particle with that mass. Or until you convert it into energy by multiplying by c2 to get 2.0 1012 joules or 1.2 x 1031 eV.)

Anyhow, these lengths and times are very small, but they are results solely of the values that appear naturally in our physical laws. So according to the principle of Special Relativity, it seems that different observers should observe them to be the same. So what about time dilation and length contraction? If these lengths and times are observable as physical lengths and intervals in moving frames, it appears that we shall need to modify Special Relativity to include them. One theory that does so is called Doubly Special Relativity, suggested in 2002 by Giovanni Amelino-Camelia.

Before we get too excited, we should point out just how far beyond current experimental technology these effects are. Particle accelerators are described by the energies that they can produce, and the latest generation produces energies of TeV, or 1012 eV. The Planck energy is 1.2 x 1031 eV. We are short by a factor of 1019. Which is a good thing.

Further, it's not clear (to this author, at least) what it would mean to measure these lengths and times in or from different frames of reference.

 

Quantum mechanics, gravity and relativity

So, where do these quantities come from? The speed of light c is the natural unit that relates time and space. G is the constant of gravity, and h is the constant of quantum mechanics. So the Planck scale defines the meeting point of gravity, quantum mechanics, time and space. Currently, we don't know much about this interaction, because gravity is so feeble that its influence on things as small as quantum systems is small.

Special Relativity and quantum mechanics work very well together. Relativistic quantum electrodynamic is a spectacularly accurate theory. Richard Feynman once described how accurate it was by saying: if you asked me how far it was to the moon and I said "do mean from my head or from my feet?" That accurate.

 

     

Quantum mechanics and gravity (whether Newton's theory of gravity or Einstein's theory of General Relativity) do not fit so neatly together. The problem can be put in several different ways, but I favour this one. From our discussion of virtual particles , we saw that virtual particles could be larger (ie more massive) if their lifetime and range were smaller.

Now both Newton's and Einstein's gravity predict that enough mass in a small enough space can produce a black hole: a region with a gravitational field so strong that its escape velocity is c. When we put the two ideas together, we find that there is a scale small enough for virtual black holes to exist. This is the Planck scale. On this scale, all of the weird, singular behaviour associated with black holes asserts itself. Space and time as continuous entities cease to have meanings over distances of 10-35 metres and times of 10-44 seconds. So relativity, a theory of space and time based on a continuum, must run into serious difficulties.

Which is perhaps not surprising: the Planck scale is a very, very long extrapolation from our current knowledge.

On this topic, we have so little direct knowledge that there are few hints to guide the development of theories, and even fewer constraints upon those theories. Consequently, there are several different families of theories that aim to produce a consistent theory of quantum gravity. Usually they include a larger number of spatial dimensions, not all of which are macroscopic*. At the moment, however interesting they be, these theories are speculative. Perhaps one of them will turn out to be a good, useful theory, and the others will fall. At the moment, we cannot put them to the test.

Today, we remember Democritus for speculating on the existence of atoms and Aristachos for proposing that the Earth went around the sun. The ancient Greek philosophers proposed so many ideas that it is perhaps not too surprising that some of them turned out to be consistent with facts discovered much later.

* How can we have more than three spatial dimensions? Surely Gauss' law (for electricity, magnetism and gravity) shows that we live in a locally flat geometry with three spatial dimensions?

Yes, experiments to test Gauss' law either directly or indirectly do show that our geometry is both pretty flat and three dimensional on the scale of the experiments conducted. If, however, the universe were closed in all but three of the spatial dimensions, and if in the closed dimensions the radius of the universe were much smaller than the size of measurements, then Gauss' law would apply only to the three large dimensions. Consequently electricity, magnetism and gravity would be inverse square laws on the scales that are experimentally accessible. The theories that use extra dimensions then have the possibility to use such things as standing waves on circumference of the universe in the closed dimensions.

 

THE EARLY UNIVERSE

 

We will not consider the detailed evolution of the Universe before ~ 10-6 seconds. This early epoch contains the Planck era, the GUTs era, and Electro-Weak era. Here, we will concentrate on the times when we believe we have a good understanding of what is going on.

A. Creation < t < 10-6 second

  • before about 10-6 second, T was greater than 1013 Kelvin and matter and radiation were in equilibrium, that is, the creation and annihilation of material

     

    was percolating along at a rate determined solely by the temperature of the Universe. The creation of matter via the annihilation of photons and the liberation of virtual pairs and the annihilation of matter and the production of photons were in balance, however, see below.

 

B. 10-6 s < t < 0.01 s, 1011 Kelvin < T < 1013 Kelvin

    Below T = 1013 K, proton and anti-proton and neutron and anti-neutron pair production stops. However, the annihilation continues. This causes most of the matter/anti-matter to convert into photons, however,...

     

C. 0.01 s < t < 0.1 s, 3 x 1010 Kelvin < T < 1011 Kelvin

    Density and T no longer high enough to maintain strong coupling between neutrinos and other forms of matter ===> the Universe becomes transparent to neutrinos (this de-coupling is in the same sense as the photons de-couple during the Epoch of Recombination). If we ever become technologically advanced enough to detect low energy neutrinos, then we, in principle, would be able to detect this Cosmic Neutrino Background (CNB) and so probe the Universe when it was less than ~ 1 second old!

D. Nucleosynthesis (Element Production) Era

    The era of Nucleosynthesis begins when T drops below ~ 109 Kelvin (and density ~ 1 gram per cubic centimeter) -- at higher temperatures, one cannot make complex nuclei; they would be broken apart as quickly as they were produced.

    An amusing note is that our understanding of nuclear reactions is much better for the conditions found in the Big Bang than for the conditions found in the interiors of stars!! The Big Bang is hotter than the interiors of stars. Terrestrial experimenters actually perform experiments at temperatures closer to Big Bang temperatures than to the low temperatures found in say the core of the Sun.

  • As is apparent, the Universe does not not make elements more massive than helium (the second simplest element0. This is due to the fact that the elements slightly more massive than helium are unstable. In particular, to make carbon, we must have the following events occur,

     

    • Helium + Helium ---> Berylium

       

    • Berylium + helium ---> Carbon

    The second step must occur very soon after step 1 is completed. Berylium is very unstable; it will decay back into the 2 helium nuclei with a half-life on the order of 10-16 seconds! In the early Universe, the density is too low for the Berylium to capture a the last helium nucleus before it decays and so the element production chain is halted. In stars, the densities are much higher and the capture rates are rapid enough to allow carbon to form before the Berylium decays.

General Relativity

Special relativity is generalised to accommodate non-inertial reference frames. This is done via the principle of relativity, illustrated in figure 15 and stated below.

 

It is not possible to distinguish (in a closed system) between the effects produced by a gravitational field and those produced by an acceleration of the closed system

 

Figure 15: Graphic depiction of the principle of equivalence.
 

This principle allows one to replace the effects of gravity by equivalent effects based on the geometry of space-time. Once gravity is ``abolished'' in this way, and there is no ``force of gravity'' then all (gravitating) objects will have motions described by Newton's First Law. That is, those in motion will continue in a straight line at constant velocity. However, ``straight line'' now means only locally straight (locally parallel to a co-ordinate axis in space). However, the geometry of space is now ``warped'' (no longer Euclidean) in such a way that the objects actual trajectory is ``similar'' to that calculated in the classical way. Einstein wrote down a Field Equation which allowed the warping of the geometry of space-time to be calculated given a certain mass distribution.

The trajectory of the moon around the earth is locally straight in a space-time region warped by the presence of the earth's mass. Such ``straight lines'' are called geodesics, defined as the shortest distance between two points in a curved space. This is illustrated in figure 16.

 

Figure 16: In General Relativity, the warping of the geometry of space-time due to mass distributions accounts for the effects of ``gravitational attraction''.
 

This is not simply an alternative but equivalent way of looking at gravity. It would not be such a disturbing idea if that were so ! It is easy to see that dramatic new ``gravitational'' effects may be predicted.

  • Because mass distributions warp space-time, a photon, which also has to travel along a geodesic (locally straight line in the warped space), will also be affected by the mass distribution. Thus General Relativity predicts that photons are subject to gravitational attraction ! Note that the classical theory
     
    (60)

     

    did not predict this for the photon ($m_0 = 0$).

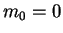  • Very dense matter can warp space so much that nothing, no particles (not even light) can ever escape, once they pass closer than a certain distance, known as the event horizon. Such objects are known as black holes. The density of nuclear matter, when aggregated in amounts equivalent to a large star, is sufficient to realise a black hole.

General Relativity is now widely accepted, following three major experimental verifications :

  • The perihelion precession of mercury is beyond that expected by classical theories, but exactly that predicated by General Relativity.
  • The gravitational red-shift of light (ie loss of energy ( 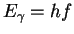$E_{\gamma} = hf$) by light as it escapes a gravitating body), as predicted by General Relativity has been quantitatively verified.
  • The bending of light in a gravitational field has been verified spectacularly during a lunar eclipse of the sun, and more recently by gravitational lensing.

Black holes have not yet been definitely verified, although there are many strong candidates in the cosmos, and further compelling theoretical evidences.

                            

The violent deaths of large stars (supernovas) and the collisions of extremely dense stars such as neutron stars with each other can cause spacetime disturbances to happen and to spread out in a wavelike manner. These waves are called gravity waves or gravitational radiation. Within the next five years gravitational radiation should be seen for the first time.

 

 
The Einstein Gravitational Field Equation is shown below. This equation states that the spacetime curvature of anyplace in the universe (left-hand side of the equation) must be equal to the distribution of matter and energy in that part of the universe (right-hand side of the equation).
 

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

Ana Sayfa / index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy) /Astronomy