Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
Spacetime Curvature
The observations and analysis that lead to the conclusion that the Expansion of the Universe is accelerating provide an elegant solution to a long-standing cosmological puzzle -- is the universe open or closed?. Two groups of astronomers -- the High-Z Supernova Search Team and the Supernova Cosmology Project have been working for years to obtain these results. The actual observations and analysis are not trivial, so the following is only an overview of the results and their meaning.
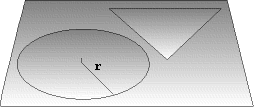
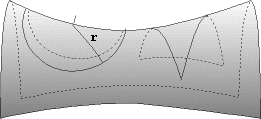
One of the primary questions of cosmology is, "Precisely what is the overall geometry of spacetime?" Is it flat with the universe finely balanced between expansion and contraction? Or is it positively curved with sufficient mass to eventually stop its own expansion? Such a "closed" universe must at some future epoch collapse again under its own gravity. Or is it negatively curved with insufficient mass to halt and reverse its own expansion? Such an "open" universe would expand forever perhaps eventually fading away as it thinned out.
Why is the curvature of spacetime related to the mass of the universe and therefore its fate? Because according to GR matter curves spacetime and consequently the amount of matter in the universe (its mass) will determine both its future and its structure. Curvature of 4 dimensional spacetime can be understood by analogy to 2 dimensional surfaces as follows.
|
|
|
|
|
|
Supernova can been seen over vast distances due to their remarkable brightness. Astronomers believe that they have come to a good understanding of one type of supernova (called Type Ia). In addition from a supernova's change in brightness over time they can determine its type. And for Type Ia supernovas theory allows astronomers to determine their absolute brightness. Comparing the observed brightness with its absolute brightness they can determine its distance. In this way supernova's can be used as a "standard candle" to determine the distance to galaxies in which they occur. Let's call this the "luminosity distance".
Astronomers have several means of determining distances in the universe and an important part of the ongoing work in this age is to cross-check as many of these as they can to refine the measurements overall. Another method of determining distance is redshift since the more distant a galaxy the greater its redshift. When luminosity distances to supernovas were compared to redshift distances to the galaxies in which they appeared astronomers found a discrepancy. The luminosity distances were greater. And the greater the redshift distance the greater the discrepancy. Clearly something is making the supernovas appear dimmer than they should in a consistent way -- the greater the distance the dimmer the supernova.
The light from a supernova (or any other light source for that matter) expands outward from the source in an ever expanding sphere at the Speed of Light. As the distance from the source increases the light dims because it must be spread over an ever growing spherical surface. The area of the surface of a sphere is given by the formula:
A = 4pr2
where r is the radius of the sphere. So if the distance to the source doubles the intensity of its light is reduced to 1/4th what it was at the closer distance. At least in Euclidean (i.e., flat) space this is true.
So, ruling out all other possible explanations (which has been done), if distant supernovae appear dimmer than they should it indicates that the surface of their expanding sphere of light is greater than that given by the above Euclidean formula. In real spacetime it would seem that the following is true:
A > 4pr2
This is just what we would expect if spacetime has an overall negative curvature.
Relativity and Black Holes Curvature and Geometry
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa / index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru