Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey/Denizli
SpaceTime Continuum in Special and General Relativity
Section Twenty-Six and Twenty-Seven
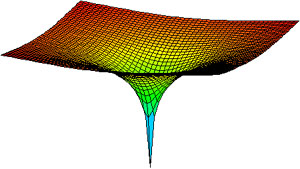
Albert Einstein's general theory of relativity describes gravity as a distortion in the four dimensions of space and time. Visualizing this is difficult, but a two-dimensional analogy makes it clearer.
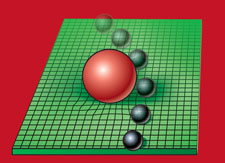
Imagine a sheet of rubber with a bowling ball at its centre. The ball is a planet, and deformation of the rubber surface it creates is equivalent to the way that real planets distort space. Objects travelling along the sheet will roll down the slope towards the bowl (see right), just as gravity would draw a passing comet towards the Earth. In Einstein's theory, the Earth attracts objects because it distorts nearby space, just as the bowl distorts the rubber sheet.
Now imagine two bowling balls spiralling around each other. This would create ripples on the rubber sheet, equivalent to the gravity waves produced when two stars orbit each other. By studying the ripples, observers can learn about the stars' movements.
Einstein's
Theory of Relativity
Special Theory of Relativity (Space, Time, and Motion)
- Principle of relativity: All observers not acted on by forces experience the same laws (an assumption, and we also assume that they move with constant velocity).
- Constancy of speed of light: All observers measure the same speed for light (a fact!).
- Consequences: Time dilation and length contraction; Increase of effective mass with speed, E = mc2; Mixing of space and time, replaced by spacetime.
- What does this have to do with black holes? Special relativity works well as long as gravity can be considered as a very weak force, and if we only observe what happens in relatively small regions; But otherwise, you have to add spacetime curvature...
General Theory of Relativity (Gravity)
- Equivalence Principle: Gravity affects all objects in the same way; it cannot be distinguished from what you feel when you are just accelerating. It is a fictitious force like the centrifugal one, why is why it affects everything the same way.
- Thought experiment: In a closed elevator, could you distinguish acceleration from gravity?
- What does this tell us? Spacetime is curved and objects in free fall don't follow straight line paths, this is the fictitious gravity; The real forces are the ones that make us deviate from free fall; Curvature of spacetime tells matter how to move.
- What causes the curvature? The global shape of spacetime may force it to be curved, plus matter/energy tells spacetime how to curve locally.
Light Bending
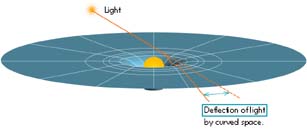
- The main idea: If gravity is caused by spacetime curvature and affects all objects the same way, it must affect light too (no matter what Newton's theory may say!).
- Have we seen this? Yes, from apparent shifts in the positions of stars when their light passes near a massive object, from images of distant galaxies seen through gravitational lenses, and from gravitational redshift of light from stars (the mass of Sirius B was measured this way!).
- How this is related to black holes: Curvature is what causes light to be bent so much that it is trapped, and produces regions from which not even light can escape.
- Other effects: If spacetime can be curved, we should be able to see other effects too...
Gravitational Waves
- What are gravitational waves? Ripples in the fabric of spacetime.
- Do we know they are out there? Yes, we have indirect evidence from the fact that the binary pulsar is gradually losing energy.
- How can we detect them? Several interferometer detectors, such as LIGO and VIRGO, are now operational; (Also search by monitoring spacecraft such as Cassini); other detectors are being planned
Other Predictions
- On Earth: Gravity makes time slow down, and the GPS would not work if general relativity was not taken into account.
- Near Earth: The fabric of spacetime twists like a vortex around a rotating body, making both orbits and spins of objects wobble (by tiny amounts!). [Astronomers are seeing evidence for this in the flickering of X-rays coming from near massive black holes.]
- In the Solar System: Since gravity affects lengths and times, orbits don't have exactly the shape that Kepler and Newton predicted.
- Wormholes? If the shape of spacetime can change, there is the theoretical possibility of shortcuts to remote places, as well as time travel...
- Can the whole universe be curved? This is also a fact! It is also possible that there are small extra dimensions! See what we know about cosmology...
These two sections are rather hard to understand, without suitable preparations; you have to review Einstein's Hole Argument, and his solution of that. First, Einstein illustrates the special character of the (Lorentz) metric in Minkowski space. This is rather straightforward, but this metric should be understood with the general Gaussian coordinates in view. When Einstein speaks of the "Euclidean" character of Minkowski space-time, he means that it is easy to give a physical meaning to coordinate values.
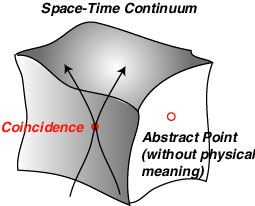
However, the same does not seem to hold in the space-time continuum of general relativity, since coordinates there do not have any direct physical meaning, unlike the case of the classical and special-relativistic picture. Thus Einstein wants to assert that we've got to reconsider the manner how we give a physical meaning to a point in a mathematical (abstract) continuum characterized by a set of coordinate values in the Gaussian manner. Recall that Gaussian coordinates may be arbitrarily chosen, and the space-time continuum is considered relative to that choice.
In section 27, Einstein is trying to say this (judging from his statements in other papers, from his solution of the Hole Argument): If you want to talk about physical space-time point, you need more than abstract coordinate values for that point. Any physical space-time points must be identified by encounters (coincidences) of two physical events, e.g., an encounter of two trajectories of material objects. Mere points in a space-time (4-dimensional) continuum do not signify physical events, unless they are matched with such encounters (coincidences). Here, he comes close to Leibniz's poisition that two physically indiscernible points are identical and that any points without such physical means of identification are merely "ideal", not "physically real". And if we realize this, Einstein is saying, it is now easy to see that the physical significance of Euclidean coordinates comes from the same factor, i.e., physical encounters or coincidences.
(This continuum is considered relative to an arbitrarily chosen coordinate system)
Although a coordinate system may be arbitrarily chosen, there are certain invariant quantities independent of that choice. The condition of general covariance (often confused with general principle of relativity by Einstein) assures that such invariants are preserved in any system.
Last modified, May 23, 2002. (c) Soshichi Uchii
Curvature and Riemann Tensor
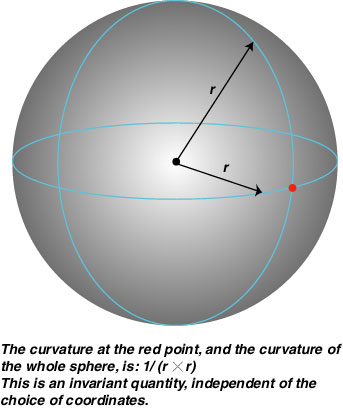
As Eddington nicely explained, Einstein's field equations can be constructed from components of Riemann curvature tensor. In a nutshell, the tensor G Eddington mentioned (sometimes called "Einstein tensor") is a sort of average of the Riemann curvature over all directions. Thus Riemann curvature is the basic notion for expressing gravitational fields; and although the expression of Riemann curvature tensor is different depending on our choice of a coordinate system, this curvature is an invariant quantity. A sphere has a definite (positive) curvature, and it is the same whatever coordinate system you may choose, and likewise an Euclidean plane is flat (zero curvature), independent of any coordinate system. Thus although metric is different in different coordinate systems, the curvature characterized in terms of metric is an invariant quantity.
Here is a brief illustration of this important notion of Riemann curvature, without getting into the mathematical definition of tensor (which may be quite tedious for ordinary people, including philosophers). First let us see a familiar example of two-dimensional curved surface, a sphere. (Any two geodesics on the sphere cross. Why? Because of its curvature. This is quite analogous to "attracting force". See Curvature within the Earth.)
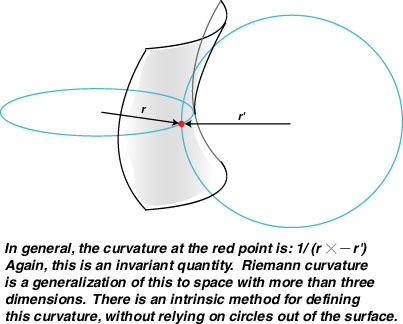
For any point on a two-dimensional surface, there are two circles that fit best at that point; if these two circles are on the opposite side of the surface, the curvature is negative.
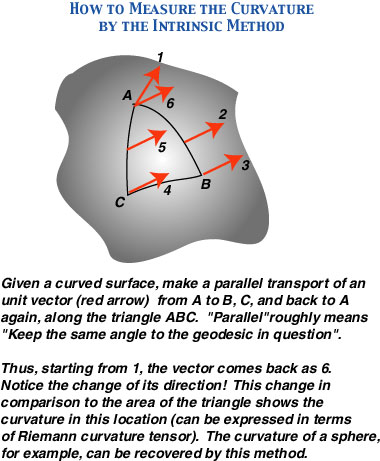
So far, we defined curvature using circles outside of the surface itself. But this is not essential; there is an intrinsic method for defining curvature.
Last modified, July 23, 2002. (c) Soshichi Uchii
Einstein's geometric gravity
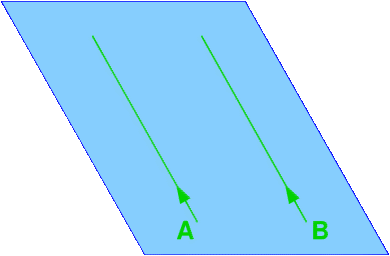
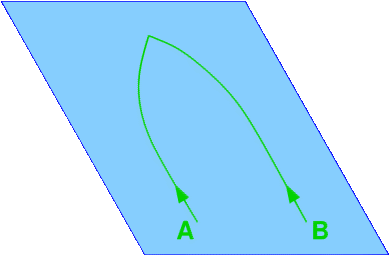
The key idea of Einstein's theory of general relativity is that gravity is not an ordinary force, but rather a property of space-time geometry. The following simplified analogy, which substitutes a two-dimensional surface for four-dimensional space-time, serves to illustrate this idea. Imagine empty space - in our case, a two-dimensional plane - with no forces acting between the bodies floating around. If there are no forces, then classical mechanics and Einstein's mechanics of special relativity are in agreement: Under these circumstances, bodies move along the straightest possible lines (which in this case are just straight lines in space) with a constant velocity. In the following image, this is symbolized by the straight paths of two particles A and B:
In particular, particles that start to move along parallel trajectories (as in the above image) will never meet, but are fated to remain forever at a constant distance from one another.
In the world of classical physics, if particles diverge from this behavior, it must be because there is a force acting on them. Forces accelerate particles, causing them to leave the straightest possible paths and follow curved trajectories instead. In our two-dimensional example, look at the following picture,
in which the particles A and B start out in parallel, but are then accelerated towards one another. In Newton's theory of gravity, gravitation is a force which could cause such an effect. For instance, the reason that the two particles in the above picture accelerate toward each other and then meet could be that they are both attracted gravitationally by a massive body located at the point of their meeting.
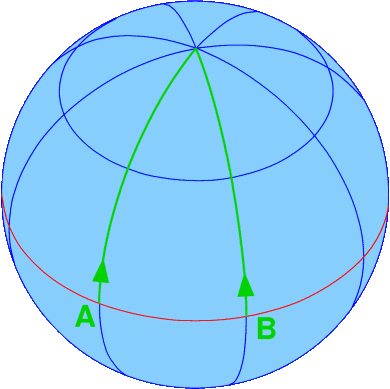
However, there is another possibility in which the same situation (where two particles that start out in parallel converge and finally meet) could arise. The two particles could still be moving on the straightest possible lines - not in the plane, but on a curved surface! The following image shows an example:
In that situation, there is no force making the particles deviate from the straightest possible lines; the mere fact that the particles are moving on a sphere means that, even if they still move as straight as possible, their paths will converge.
Einstein's theory is exactly analogous to this. In Newton's theory, gravity makes particles leave their straight paths. In Einstein's theory of general relativity, gravity is a distortion of space-time. Particles still follow the straightest possible paths in that space-time. But because space-time is now distorted, even on those straightest paths, particles accelerate as if they were under the influence of what Newton called the gravitational force.
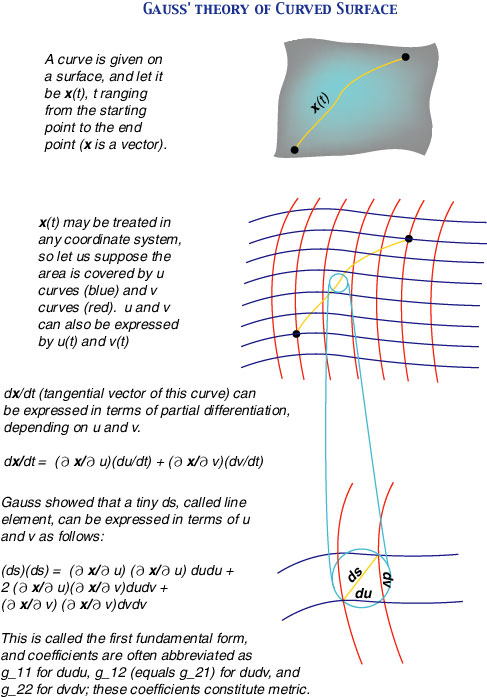
Gauss' Theory of Curved Surface
Einstein, in his theory of general relativity, used Riemannian geometry which is a generalization of Gauss' theory of curved surface. So if you can understand Gauss' theory, it will help your understanding of tensor and metric. The following figure shows essentials of this. Recall that not only the length of a curve, but also the whole geometry of the curved surface is determined if we know the formula for the line element ds; and this in turn is determined by metric.
Last modified November 27, 2001. (c) Soshichi Uchii
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa / index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru