9. The Riemann Curvature Tensor

First, we need to know how to translate a vector along a curve C. Let X_j be a vector field. We have seen that a parallel vector field of constant length on M must satisfy

DXj dt

=

0

......     (I)

for any path C in M.

If X^j is parallel along C, which has parametrization with domain [a, b] and corresponding points and on M, then, since

dXj dt

=

-ijh Xi

dxh dt

.........     (I)

we can integrate to obtain

Xj()

=

Xj()

-

b a

ijh Xi

dxh dt

.........     (II)

Question Given a fixed vector X^j() at the point M, and a curve C originating at , it is possible to define a vector field along C by transporting the vector along C in a parallel fashion?
Answer Yes. Notice that the formula (II) is no good for this, since the integral already requires X^j to be defined along the curve before we start. But we can go back to (I), which is a system of first order linear differential equations. Such a system always has a unique solution with given initial conditions specified by X^j(). Note however that it gives X^j as a function of the parameter t, and not necessarily as a well-defined function of position on M. If it does, then we have a parallelizable manifold.

Definition 9.2 If Xj() is any vector at the point M, and if C is any path from to in M, then the parallel transport of Xj() along C is the vector Xj() given by the solution to the system (I) with initial conditions given by Xj().

Examples 9.3
(a) If C is a geodesic in M given by xⁱ = xⁱ(s), where we are using arc-length s as the parameter (see Exercise Set 8 #1) then the vector field dxⁱ/ds is parallel along C. (Note that this field is only defined along C, but (I) still makes sense.) Why? because

D(dxj/ds) Ds

=

d2xj ds2

+

ijh

dxi ds

dxh ds

,

which must be zero for a geodesic.

(b) Proper Coordinates in Relativity Along Geodesics
According to relativity, we live in a Riemannian 4-manifold M, but not necessarily the flat Minkowski space. Further, the metric in M has signature (1, 1, 1, -1). Suppose C is a geodesic in M given by xⁱ = xⁱ(t), satisfying the property

dxi dt

,

dxi dt

<

0.

We call such a geodesic timelike. Looking at the discussion before Definition 6.1, we see that this corresponds, in Minkowski space, to a particle traveling at sub-light speed. It follows that we can choose an orthonormal basis of vectors {V(1), V(2), V(3), V(4)} of the tangent space at m with the property given in the proof of 8.2, with V(4) parallel to the vector dxⁱ/dt. We think of V(4) as the unit vector in the direction of time, and V(1), V(2) and V(3) as the spatial basis vectors. Using parallel translation, we obtain a similar set of vectors at each point along the path. (The fact that the curve is a geodesic guarantees that parallel translation of the time axis will remain parallel to the curve.) Finally, we can use the construction in 8.2 to flesh these frames out to full coordinate systems defined along the path. (Just having a set of orthogonal vectors in a manifold does not give a unique coordinate system, so we choose the unique local inertial one there, because in the eyes of the observer, spacetime should be flat.)

Question Does parallel transport preserve the relationship of these vectors to the curve. That is, does the vector V(4) remain parallel, and do the vectors {V(1), V(2), V(3), V(4)} remain orthogonal in the sense of 8.2?
Answer If X and Y are vector fields, then

d dt

X, Y

=

DX dt

,

Y

+

X ,

DY dt

,

where the big D's denote covariant differentiation. (Exercise Set 7 #7). But, since the terms on the right vanish for fields that have been parallel transported, we see that X, Y is independent of t, which means that orthogonal vectors remain orthogonal and that all the directions and magnitudes are preserved, as claimed.

Note At each point on the curve, we have a different coordinate system! All this means is that we have a huge collection of charts in our atlas; one corresponding to each point on the path.

Question Under what conditions is parallel transport independent of the path? If this were the case, then we could use formula (I) to create a whole parallel vector field of constant length on M, since then DX^j/dt = 0.
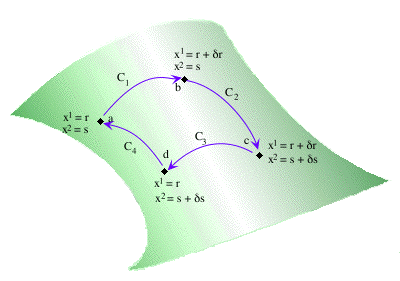
Answer To answer this question, let us experiment a little with our fixed vector V = X^j() by translating it around a little rectangle consisting of four little paths. To simplify notation, let the first two coordinates of the starting point of the path (in some coordinates) be given by

x¹() = r, x²() = s.

Then, choose r and s so small that the following paths are within the coordinate neighborhood in question:

C1: xj(t)	=		xi() if i 1 or 2 r+tr if i = 1 s if i = 2
C2: xj(t)	=		xi() if i 1 or 2 r+r if i = 1 s+ts if i = 2
C3: xj(t)	=		xi() if i 1 or 2 r+(1-t)r if i = 1 s+s if i = 2
C4: xj(t)	=		xi() if i 1 or 2 r if i = 1 s+(1-t)s if i = 2

These paths are shown in the following diagram.

Now, if we parallel transport X^j() along C₁, we must have, by (II),

Xj(b)	=	Xj(a) - 1 0 ijh Xi dxh dt dt	(since t goes from 0 to 1 in the path C1)
	=	Xj(a) - 1 0 ij1 Xi r dt	(see the definition of C1 above; only x1 changes...)

Warning:   The integrand term _i^j₁ Xⁱ is not constant, and must be evaluated as a function of t using the path C₁. However, if the path is a small one, then the integrand is approximately equal to its value at the midpoint of the path segment:

Xj(b)		Xj(a) - ij1 Xi(midpoint of C1)r
		Xj(a) - ij1 Xi(a) + 0.5 x1 (ij1 Xi)r r

where the partial derivative is evaluated at the point . Similarly,

Xj(c)	=	Xj(b) - 1 0 ij2 Xi s dt
		Xj(b) - ij2 Xi(midpoint of C2)s
		Xj(b) - ij2 Xi(a) + x1 (ij2 Xi)r + 0.5 x2 (ij2 Xi)s s

where all partial derivatives are evaluated at the point a. (This makes sense because the field is defined where we need it.)

Xj(d)	=	Xj(c) + 1 0 ij1 Xi r dt
		Xj(c) + ij1 Xi(midpoint of C3)r
		Xj(c) + ij1 Xi(a) + 0.5 x1 (ij1 Xi)r + x2 (ij1 Xi)s r

and the vector arrives back at the point a according to

X*j(a)	=	Xj(d) + 1 0 ij2 Xi s dt     (X*j(a) is the new vector at the point a)
		Xj(d) + ij2 Xi(midpoint of C4)r
		Xj(d) + ij2 Xi(a) + 0.5 x2 (ij2 Xi)s s

To get the total change in the vector, you substitute back a few times and cancel lots of terms (including the ones with 0.5 in front), being left with



X*j(a) - Xj(a)	=	Xj			x2	(ij1 Xi)
-	x1	(ij2 Xi)		rs

To analyze the partial derivatives in there, we first use the product rule, getting

Xj

Xi

x2

ij1

+

ij1

x2

Xi

-

Xi

x1

ij2

-

ij2

x1

Xi

rs

.........   (III)

Next, we recall the "chain rule" formula

DXj dt

=

Xj|h

dxh dt

in the homework. Since the term on the right must be zero along each of the path segments we see that (I) is equivalent to saying that the partial derivatives

X^j_|h = 0

for every index p and k (and along the relevant path segment; notice that we are taking partial derivatives in the direction of the path, so that they do make sense for this curious field that is only defined along the square path!) since the terms dx^h/dt are non-zero. By definition of the partial derivatives, this means that

Xj xh

+

ijhXi

=

0,

so that

Xj xh

=

- ijhXi.

We now substitute these expressions in (III) to obtain

Xj

Xi

x2

ij1

-

ij1pi2Xp

-

Xi

x1

ij2

+

ij2pi1Xp

rs

Now change the dummy indices in the first and third terms and obtain

Xj

x2

pj1

-

ij1pi2

-

x1

pj2

+

ij2pi1

Xprs

This formula has the form

Xj

Rpj12Xp rs

............     (IV)

(indices borrowed from the Christoffel symbol in the first term, with the extra index from the x in the denominator) where the quantity R_p^j₁₂ is known as the curvature tensor.

The terms are rearranged (and the Christoffel symbols switched) so you can see the index pattern, and also that the curvature is antisymmetric in the last two covariant indices.

R_b^a_cd = - R_b^a_dc

The fact that it is a tensor follows from the homework.

It now follows from a grid argument, that if C is any (possibly) large planar closed path within a coordinate neighborhood, then, if X is parallel transported around the loop, it arrives back to the starting point with change given by

�Xj

=

S

Rpj12Xp dS,

where S is the surface enclosed by the loop. If the loop is not planar, we choose a coordinate system that makes it planar, and if the loop is too large for a single coordinate chart, then we can break it into a grid so that each piece falls within a coordinate neighborhood. Thus we see the following.

Properties of the Curvature Tensor

We first obtain a more explicit description of R_b^a_cd in terms of the partial derivatives of the g_ij. First, we have the notation

gij,k

=

gij xk

for partial derivatives, and remember that these are not tensors. Then, the Christoffel symbols and curvature tensor are given in the convenient form

 

bac = 1 2 gak(gck,b + gkb,c - gbc,k) Rbacd = [biciad - bidiac + bac,d - bad,c]     (Notice that the indices c and d are switched in the negative terms.)

We can lower the index by defining

R_abcd = g_biR_aⁱ_cd

Substituting the first of the above (boxed) formulas into the second, and using symmetry of the second derivatives and the metric tensor, we find (exercise set)

(We can remember this by breaking the indices k, b, c, d into pairs (we can do this two ways) the pairs with b and d together are positive, the others negative.)

Notes
1. The "new kinds" of Christoffel symbols _ijk are given by

_ijk = g_pji^p_k.

2. Some symmetry properties: R_abcd = -R_abdc = -R_bacd

3. We can raise the index again by noting that

g^biR_aicd = g^big_ijR_a^j_cd = ^b_jR_a^j_cd = R_a^b_cb.

Now, let us evaluate some partial derivatives in an inertial frame (so that we can ignore the Christoffel symbols) cyclically permuting the last three indices as we go:

Rabcd,e + Rabec,d + Rabde,c	=	1 2	(gad,bce - gac,bde + gbc,ade - gbd,ace     + gac,bed - gae,bcd + gbe,acd - gbc,aed       + gae,bdc - gad,bec + gbd,aec - gbe,adc)
	=	0.

Now, I claim this is also true for the covariant partial derivatives:

Indeed, let us evaluate the left-hand side at any point m M. Choose an inertial frame at m. Then the left-hand side coincides with R_abcd,e + R_abec,d + R_abde,c, which we have shown to be zero. Now, since a tensor which is zero is sone frame is zero in all frames, we get the result!

In the exercise set, you will show that it is symmetric, and also (up to sign) is the only non-zero contraction of the curvature tensor.

We also define the Ricci scalar by

R = g^abR_ab = g^abg^cdR_acbd

The last thing we will do in this section is play around with the Bianchi identities. Multiplying them by g^bc:

g^bc[R_abcd|e + R_abec|d + R_abde|c] = 0

Since g^ij_|k = 0 (see Exercise Set 8), we can slip the g^bc into the derivative, getting

-R_ad|e + R_ae|d + R_a^c_de|c = 0.

Contracting again gives

g^ad[-R_ad|e + R_ae|d + R_a^c_de|c] = 0,

or

-R_|e + R^d_e|d + R^dc_de|c = 0,

or

-R_|e + R^d_e|d + R^c_e|c = 0.

Combining terms and switching the order now gives

Rbe|b

-

1 2

R|e

=

0,

or

Rbe|b

-

1 2

be R|b

=

0.

Multiplying this by g^ae, we now get

Rab|b

-

1 2

gabR|b

=

0,

or

G^ab_|b = 0,

where we make the following definition:

Einstein's field equation for a vacuum states that

G^ab = 0

(as we shall see later...).

Example 9.7
Take the 2-sphere of radius r with polar coordinates, where we saw that

g**

=

r2sin2 0 0 r2

.

The coordinates of the covariant curvature tensor are given by

Rabcd

=

1 2

(gbc,ad - gbd,ac + gad,bc - gac,bd) + ajdbjc - ajcbjd

.

Let us calculate R. (Note: when we use Greek letters, we are referring to specific terms, so there is no summation when the indices repeat!) So, a = c = , and b = d = . (Incidentally, this is the same as R by the last exercise below.)

The only non-vanishing second derivative of g_** is

g_, = 2r²(cos² - sin²),

giving

_a^j_cjbd = ^j_j = 0,

since b = d = eliminates the second term (two of these indices need to be in order for the term not to vanish.)

ajdjbc	=	jj	=
1 4		2 cos sin		(-2r2sin cos )	=	-r2cos2.

Combining all these terms gives

R = r²(sin² - cos²) + r²cos² = r²sin².

We now calculate

R_ab = g^cdR_acbd R = gR = sin²

and

R	=	gR
	=	sin2 sin2	=	1.

All other terms vanish, since g is diagonal and R_**** is assymetric. Click here to see an instance of this! This gives

R	=	gabRab = gR + gR
	=	1 r2sin2 (sin2) + 1 r2 = 2 r2  .

Exercise Set 9

1. Derive the formula for curvature in terms of the g_ij.

2. (a) Show that the curvature tensor is antisymmetric in the last pair of variables:

R_b^a_cd = - R_b^a_dc

(b) Use part (a) to show that the Ricci tensor is, up to sign, the only non-zero contraction of the curvature tensor.
(c) Prove that the Ricci tensor is symmetric.

3. (cf. Rund, pp. 82-83)
(a) Show that

Xj|h|k	=	xk (Xj|h) + mjk(Xm|h) - hlk(Xj| l)
	=	2Xj xhxk + Xl xk ljh + ljh xk)Xl + mjk xh)Xm + mjklmhXl - hlk(Xj| l)

(b) Deduce that

X^j_|h|k - X^j_|k|h = R_l^j_hkX^l - S_h^l_kX^j_{| l} = R_l^j_hkX^l

where

S_h^l_k = _h^l_k - _k^l_h = 0.

(c) Now deduce that the curvature tensor is indeed a type (1, 3) tensor.

4. Show that R_abcd is antisymmetric on the pairs (a, b) and (c, d).

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli 

Ana Sayfa / index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2   

Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru

Kuantum Teleportation /Kuantum Fizigi /Uçaklar(Aeroplane)

New World Order(Macro Philosophy)/Astronomy