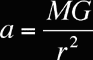Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
General Relativity and Special Relativity Files (Genel Rölativite ve Özel Rölativite Dosyası)

1- SpaceTime Continuum in Special and General Relativity
2- Singularités, trou de ver et voyage spatio-temporel
Evrensel Kütle Çekim
Newton, kütleçekim kuvvetini
![]()
olarak bulmuştur.
Burada;
M1, 2
cisimlerin kütlesi,
R
aralarındaki uzaklık,
G
ise 6,6710 − 11Nm2kg
− 2
değerinde olan kütleçekim sabitidir.
Kütle,
bir cisimdeki madde miktarının ölçüsüdür. Kütle her yerde aynı değere
sahiptir.
Kütlenin SI birim sistemindeki birimi kilogram'dır. Bu kg. olarak
kısaltılır. Kullanılan diğer birimler gram, ton ve pound'dur. Görelilik
teorisine göre duran kütle m ile enerji E arasında
E = mc2
bağlantısı olduğundan enerji birimi olan elektronVolt (eV) da kütle için
kullanılabilir. Özellikle kütle ve enerjinin birbirine dönüşebildiği
parçacık fiziğinde eV sık kullanılmaktadır. (yaklaşık
1 eV=1.783 × 10-36 kg).
Einstein teorisine göre uzay zaman eğridir.Uzay zamanın eğriliği kütle çekimi, yani gravitasyona eşittir. Bunu anlatacak bir örnek: Bir portakalın üstüne üç toplu iğne batıralım ve bu toplu iğnelere göre bir bıçakla portakalı keselim.Ortaya portakal kabuğundan yapılmış bir üçgen çıkacaktır.O üçgeni alıp masaya koyarsanız üçgenin kenarlarının düz olmadığını görürsününüz. Düz bıçakla kestiğimiz kenarlar eğridir. Şimdi aynı şekilde diyelim ki siz dünyadan bir uyduya bir sinyal gönderdiniz. O da bu sinyali başka bir uyduya gönderdi ve ikinci uydudan sinyal tekrar dünyaya aksettirildi. Işığın yörüngesi en kısa mesafelerden oluşan bir jeodezik üçgendir. Eğer güneş bu üçgenin içinde ise o zaman ortaya çıkan kenarları dışa doğru eğri bir üçgendir, tıpkı portakal kabuğu gibi. Çünkü güneşin kütlesinden dolayı ışık eğri bir yörünge takip ediyor. Bunu güneş tutulması esnasında arka plandaki yıldızlarının yerlerinin kaymasından görmüştük. Şimdi Einstein gibi şöyle düşünebilirsiniz : Ben güneşi ortadan kaldırayım ama uzay zamanı o üçgeni verecek şekilde eğri yapayım, tıpkı portakalın üstünde olduğu gibi.Bir bakış açısına göre güneşin kütle çekimi ışığın yörüngesini saptırıyor düz olmaktan. Öteki görüşte güneş hiç ortada yok, uzay zamanın eğriliği ışığın yörüngesinin düz olmamasını sağlıyor.


Einstein'in
uzay zamanı bükük olarak nitelendirmesinde ilk olarak ivme ile çekim alanı
arasında güçlü bir ilişki olduğunun farkına varması yatar. Asansör gibi,
kapalı bir kutu içerisindeki bir kişi, kutunun dünyanın çekim alanında
durağan mı olduğunu, yoksa serbest uzayda bir roketle ivme mi kazandığını
ayırt edemez. Eğer dünya düz olsaydı, elmanın Newton'un başına yerçekimi
nedeniyle veya Newton ve dünya yüzeyi yukarı doğru ivme kazandığı için
düştüğüne eşit biçimde inanılabilirdi. Gene de, ivme ile yerçekimi
arasındaki sözkonusu eşitlik, yuvarlak bir dünya için geçerliymiş gibi
görünmüyordu. Çünkü, dünyanın zıt taraflarındaki kişilerin zıt yönlerde ivme
kazanmaları ancak birbirlerinden sabit bir uzaklıkta kalmalarıyla mümkündü.
İvme ve yerçekimi ancak, büyük bir kütle; uzay-zamanı bükerek, yakın
çevresindeki nesnelerin yollarını eğerse denk olabilirdi!!!
Einstein kütle ve enerjinin, uzay-zamanı belirlenmesi gereken bir şekilde
bükeceğini düşünüyordu. Gezegen gibi nesneler uzay-zaman boyunca düz
doğrularla ilerlemeye çalışacak ancak uzay-zaman eğri olduğu için yolları,
bir çekim alanı tarafından bükülmüş gibi görünecekti.
Evren madde ile doludur, ve madde uzay-zamanı kütleler birbiri üzerine
düşecek şekilde büker. Einstein eşitliklerin zaman içerisinde değişmeyen,
durağan bir evreni tanımlayan bir çözüme sahip olmadığını buldu. Kendisinin
ve diğer birçok kişinin de inandığı sonsuz evrenden vazgeçmek yerine,
kozmolojik sabit adı verilen bir terim ekleyerek eşitlikleri düzeltti. Bu
sabit uzay-zamanı aksi anlamda büküyordu. Bunun sonucunda da kütleler
birbirlerinden uzaklaşıyordu. Evrensel sabitin itici etkisi, maddenin çekici
etkisini dengeleyerek evren için durağan bir çözüm sağlayabilecekti. Ancak
bu 1920lerde yapılan gözlemlere kadar ciddiye alınmadı. Bu gözlemlerde diğer
galaksilerin bizden ne kadar uzakta iseler o kadar hızla uzaklaşacakları
ortaya çıkarıldı...
Genelde hep klasik bir örnek verilir, kocaman gerilmiş
bir bez düşünün, üzerine de ağır küreler atın. Tabi kürenin durduğu yer
çukur olacak. Büyük kütle büyük çukurluk yaratır, ve bez üzerinde bir top
yuvarladığınız zaman yolları bu çukurlar tarafından bükülür. Yerçekiminin
uzayı bükmesi bu benzetmeyle anlatılır.
Ancak işler bu örnekteki gibi de basit değil her zaman. Einstein'in teorisi
de sonuçta matematiksel modellere dayanıyor ve bunlar tamamen soyut. Bu
oluşan bükülmeler de bizim bildiğimiz anlamdaki bükülmelerden değil, yani üç
boyutlu bir cismin yamulması şeklinde olmuyor.
Einstein'in teorisinde evren 4 boyutlu
bir manifold (Türkçe'si katman olabilir, emin değilim) şeklinde
tasarlanıyor, tabi uzaydaki hareketlerin vs de karşılık gelecek şekilde
modellemeleri var. Kütle çekimi denen şey de manifoldun yapısı üzerindeki
bir takım özelliklere karşılık geliyor.
Manifold teorisi ve rölativitenin salt denklem takımları üzerinde formel
anlamda derinlemesine çalışmadığım için ayrıntı veremeyeceğim, ama
olaya bu model çerçevesinde bakılınca olayların karışıklığa yer vermeden
anlaşılacağını düşünüyorum. Bazen üst düzey birşeyi ögrenciler yada
meraklılar anlasın diye basit modellerle anlatmaya kalkınca olay kafa
karıştırıcı bir hal alabiliyor. Matematik forumlarında bugüne kadar
yazılanlardan edindiğim izlenim bu. Lise matematiğinde bazı şeyler ispatsız
verilir, ya da muglak tanımlarla verilir, ögrenciye o tanımlarla (ki
adamakıllı teorik bilgi ister bunlar) zaman kaybettirmemek için. Tabi biraz
düşünen ögrenciler sonunda bazı terslikleri gözlemliyorlar ya da kendilerine
sunulanı kesin doğru diye kabul edip bazı yanlış düşünceler geliştiriyorlar.
Matematikte olduğu gibi fizikte de olayı tam manasıyla kavramak için, olayın
içine bizzat girmek gerekiyor bence.
Genel rölativite teorisine ait yerçekimsel alanı niteleyen denklem: Einstein General Field Equation:
gμ&nu =
the Riemann tensor describing the scale factor (metric) of spacetime. This
is essentially a determination of the distance between adjacent points in
spacetime.
Rμ&nu = the Ricci tensor, and is essentially derivatives
of the Riemann tensor.
R = the "trace" of the Ricci tensor describing the radius of
spacetime's curvature
Tμ&nu
= the stress-energy tensor describing the density
of mass-energy in spacetime
Bükülme olarak nitelendirdiğimiz bir ipin bükülmesi gibi birşey değil. Uzay ve Zaman'i iki ayrı boyut olarak düşünürsek oluşturdukları bir alan olacaktır. O alanın bükülmesinden bahsediyoruz. Aslında bu teorik fiziği Einstein'dan beri gayet net ve anlaşılır açıklayan pek insan olmadı. Düz olarak hareket eden bir nesne düşünelim mesela bir uçak gökyüzünde aynı rotada ilerlesin. Yeryüzünden uçağa bakınca düz görürüz ama dağlar ve yüzeydeki engebeler üzerinde uçak sanki kıvrılarak gidiyormuş gibi görünür. Uzay zamanın bükülmesi de böyle birşey. Gezegenler uzay-zaman içinde düz ilerlemeye çalışacak ancak uzay-zamanın bükülmesiyle çekim alanıyla bükülmüş gibi görünecektir.
Soru: Kütle çekimini bir bez üzerindeki küre gibi düşündük.Ve tabi bu bezin bir esnekliği olacak.Sormak istediğim şey tıpkı bezin kendi türüne göre farklı bir şekilde esnemesi gibi bir olay gerçekte de iki kütlenin bulunduğu ortama bağlı mı?Yani boşlukta iki kütlenin birbirini çekmesiyle suda veya başka bir ortamda iki kütlenin birbirini çekmesi aynı şeymi.Toparlarsak Newton Evrensel Çekim yasasına göre; F=G.m.M/d2 de ki kütle ve uzaklık ortama göre değişmediğine göre G sabiti ortama göre değişir mi?
Çekim kuvveti kütle fazlalaştıkca artar. Güneşin kütlesi dünyadan 330000 kat
fazladır. Bu durumda dünyada 60 kg olan bir kişi güneşte 20000 ton
olacaktır. Çekim kuvvetini etkileyen ikinci özellik uzaklıktır. Cisimlerin
merkezine doğru yaklaştıkca çekim kuvveti de artar. Yıldızların yakıtını
tüketip çöküşü sırasında yarıçapı azaldığı için çekim kuvvetleri aşırı
derecede artar. Bunlar pekçok insan için bilinen bilgiler ancak iyice
oturması için tekrar vurgulamak istedim.
İki cisim arasındaki yerçekimi kuvveti, bu iki cismin merkezleri arasındaki
uzaklık azaldıkca büyür. Yani uzaklığın karesi ile ters orantılı olarak
artar. Yeryüzünden belli bir uzaklıkta olan birisi bu uzaklığın yarısına
geldiğinde dünyanın o insan üzerindeki yerçekimi kuvveti dört kez artar.
Yerçekimin en fazla olduğu yer yerkabuğunun üzerindedir. Zira dünyanın
merkezine yaklaştıkca yerçekiminin etkisi de azalır! Yerçekiminin uzaklığa
bağlı oluşu sadece çekiminde bulunan cismin dışında bulunma halinde
geçerlidir. Ancak, o zaman cismin tüm kütlesinin merkezde toplanmış olduğu
düşünülebilir. Dünyanın içine girildikçe, ancak dünyanın merkeze daha yakın
olan kısmı çekecektir, üst tarafta kalan kısmın yerçekimine bir katkısı
olmayacaktır ve sonunda dünyanın tam merkezine gelindiğinde ise hiçbir çekim
kuvveti kalmayacaktır..
Ortamlara göre çekim kuvveti değişmez. Sadece ek kuvvetler girer araya.
Suyun içinde ve aynı seviyedeki karada çekim kuvveti aynıdır ama sudaki
kaldırma kuvveti çekim kuvvetine zıt yönde etkiler. Kütle ve çekim merkezine
uzaklık aynı kaldığı sürece yerçekimi kuvveti değişmez. Örneğin dünyadan
uzakta bir uzay gemisindeki insana göre dünya kütlesini kaybetmeden şimdiki
yarıçapının yarısına büzüldüğü takdirde, o insan üzerinde etkiyen yerçekimi
kuvveti değişmeyecektir. Çünkü insanın kütlesi dünyanın kütlesi ve insanın
dünyanın merkezine uzaklığı hep aynı kalmaktadır. Ancak dünya üzerinde
bulunan bir insan için bu farklı olacaktır. Dünyanın yarıçapının yarısına
büzülmesi dünya yüzeyindeki insan üzerindeki çekimi 4 kat arttıracaktır..
Soru: Öğrendiğim kadarıyla ışık bir karadeliğin yakınından geçerken bir sapmaya uğruyor. Bize öğretilene göre ise ışık madde değil. Madde olmayan birşeyin kütle çekimden etkilenmesi mümkün mü? Eğer kütle çekimden dolayı sapmaya uğruyorsa zamanda yolculuk yapması da gerekmez miydi?
Cevap: Bu soruyu daha önce de yanıtlamıştık. Kütle uzay-zamanda
bükülmeye yol açar. Karadelikler de çok büyük bir kütleyi çok küçük bir
hacimde toplamış cisimler. Dolayısıyla uzay/zamanın bükülmesi sonsuz
eğrilikte oluyor (dipsiz bir kuyu gibi). Böyle olunca da kendisi kütlesiz
olmasına karşın ve dolayısıyla kütleçekimini duymayan fotonlar da (ışık
parçacıkları) bu bükülmüş uzay/zaman dokusunu izleyerek yol aldıklarından
hareketlerinde bir sapma görülüyor. Eğer karadeliğin yakınlarından geçmekte
olan bir foton, karadeliğin olay ufku (yani uzayın dipsiz kuyu gibi
büküldüğü alan) içine düşerse, bu eğriliği sonsuza kadar izlediği için bir
daha dışarı çıkamıyor ve bu yüzden de karadelikler (adları üzerinde)
gözlemlenemiyor, varlıkları ancak dolaylı yollardan belirleniyor.
Acaba kütle merkezinden
dışarı doğru yayılan bu kuvvet engellenebilir mi?
Bunlar fotonlar gibi yansıtılabilir mi yada absorbe edilebilir mi ?
 |
|
|||
|
|
4- Special and General Relativity: A Very Brief Overview
5- Relativite Generale: La matiere courbe I'espace
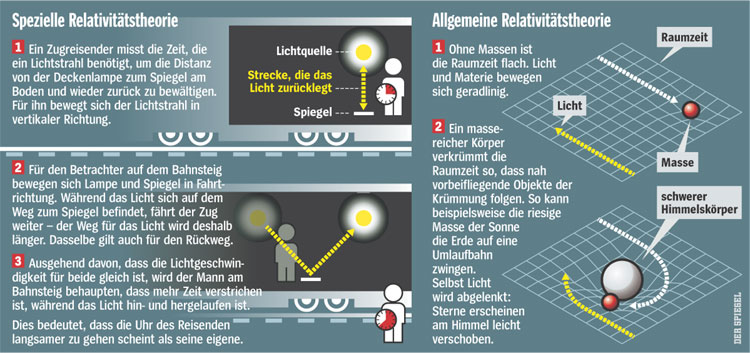
Spezielle Relativitatstheorie... Allgemeine Relativitatstheorie
8- 1905, la theoria d'Einstein: la causalite s'inscrit dans l'espace-temp
9- What is Relativity? an Introduction
10- 双生子佯谬 twin paradox - General Physics
11- The General Theory of Relativity (GR)
12 - General Relativity by Christian Magnan

13 - Special Relativity and Time Dilation
14 - Einstein's Theory of Special Relativity
- Special Relativity Theory (Pdf)
 |
Çetin BAL: Einstein'ın özel görelilik (Special Relativity) kuramına göre hızlanan cisimlerde ( tren, roket, uçak, araba... vb gibi) zaman yavaşlar. Daha teknik bir ifade ile yerde duran bir gözlemci için zaman belli bir hızla akarken bu gözlemciye göre hareket eden bir uçak yada tren içindeki bir saatin tik takları arasındaki zaman dıştaki gözlemcinin saatine göre daha da genişler. Dolayısıyla zaman yerdeki gözlemciye göre daha hızlı geçerken gözlenen hareket halindeki araç içinde zaman daha yavaş geçmektedir.Dolayısıyla dıştaki gözlemciye göre farklı algılanan tek şey zamanın geçişi değildir. Hareket halindeki bir nesnenin boyutlarıda dıştaki gözlemciye göre hareket yönüne doğru kısalmaya uğrar. Bu kısalma ''hızla'' doğru orantılı bir şekilde artar. Hareket halindeki gözlenen araçlardaki zaman genişlemeside buna yani hareketin hızına paralel olarak artar.
15- Understanding the Theory of Relativity - by Ronald C. Pine
16 - Special Relativity Theory - Joseph F. Alward, PhD
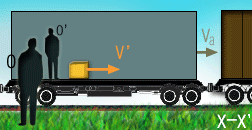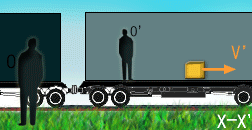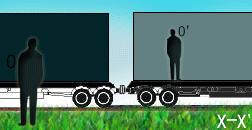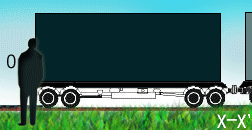
En la imagen
vemos una caja amarilla que se mueve en el interior de un tren.
El movimiento de este objeto es estudiado por dos observadores: Uno de ellos,
O, está en reposo junto a la vía. Mientras que otro se mueve con el tren,
aunque esté quieto en su interior.
Cada observador tiene su propio sistema de coordenadas y su reloj para
estudiar el movimiento de la caja. Tratamos con dos sistemas de referencia
en movimiento relativo.
Por otro lado, recordemos el primero de los principios de la Dinámica de
Newton , el principio de inercia, que podemos enunciar así: Para que un
cuerpo posea aceleración debe actuar una fuerza exterior sobre él.

Si desde un sistema de referencia se cumple este principio, el sistema se considera inercial. ¿Son todos los sistemas de referencia inerciales?. Para responder esta pregunta es mejor que nos introduzcamos en el siguiente apartado, el Principio de Relatividad.
17 - Einstein's theory of relativity...
18- TEORÍA DE LA RELATIVIDAD ESPECIAL O RESTRINGIDA
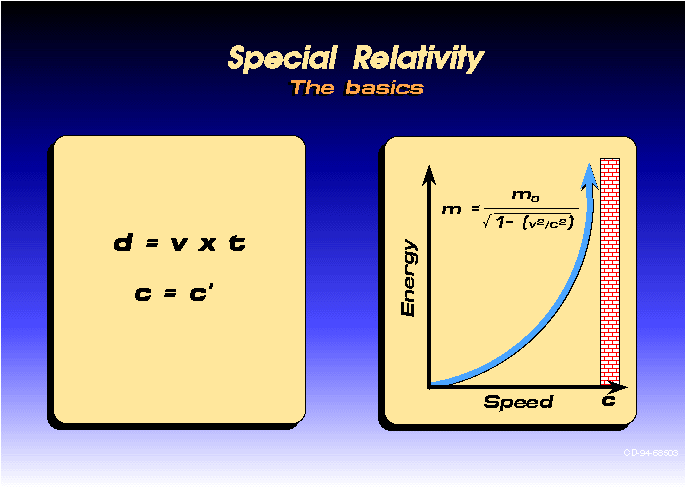
20- Time Dilation: Special Relativity
 |
|
 |
21-The Special Theory of Relativity
22 - 第二章 空间和时间
 |
 |
Evrenin geometrisinin ( uzay/zamanın düz çizgilerinin) kapalı bir evreni tasvir edip etmemesine bağlı olarak eğrilen uzay-zamanın geçmişe yada gelecek zaman/uzay noktalarına geçit verecek şekilde bükülüp bitişmesi ve topolojik geometri kaynaşmaları (tüp geçitleri) söz konusu edilebilir. Matematik ve fiziğin alan geometrisi denklemleri içinde nokta ve çizgilerin bu şekilde bitiştirilip kaynaştırılması ile salt denklemler içinde zaman yolculuğuna olanak sağlayan solucan deliği tünelleri oluşturulabilir. Evren geometrisi içinde bu çeşit tünellere en yakın oluşumlar karadeliklerdir.

23- Special Relativity...(Pdf)



26 - Albert Einstein - Relativitästheorie
27 - Time dilation

28- The Light Clock A Theoretical Proof of Time
29- Relativite Kuramı - Special Relativity
30 - Time dilation and length contraction in Special Relativity
31- A First Primer on Relativity
32 - Einstein: Special Relativity
33 - Special and General Relativity
34 - Derivation of the Time Dilation Formula
| Dünya, kütlesi ile içine girdiği uzay/zamanı bükerek eğriltir. Bu düz uzay ve zaman çizgilerinin eğrilmesini bizler kütleçekimi kuvveti olarak ölçümler ve duyumsarız. |
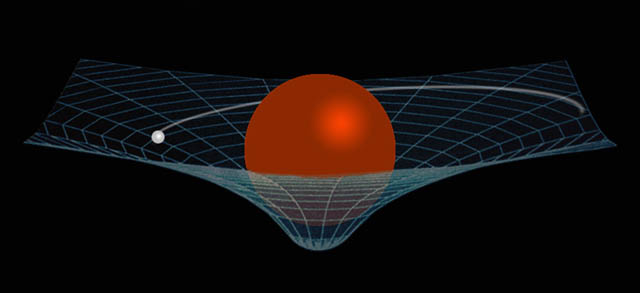
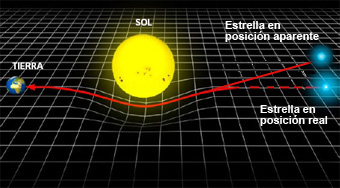
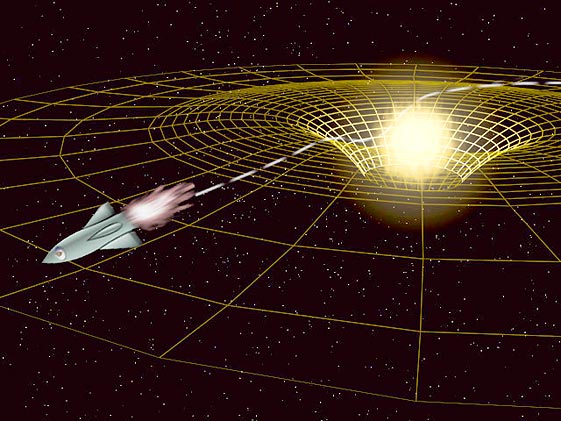
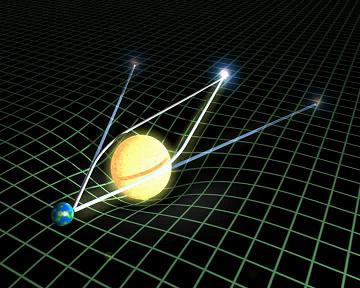
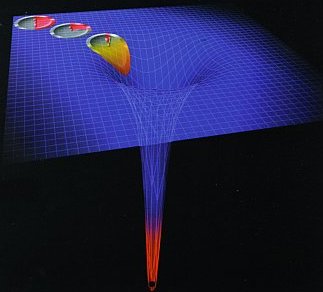
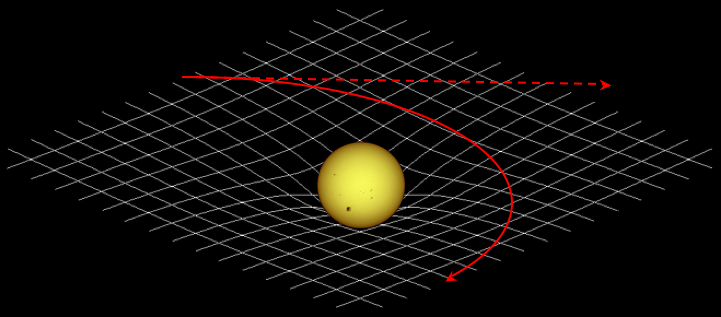
How the sun bends space,time and light

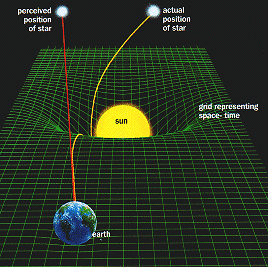
Although our sun is an ordinary star, and not a massive black hole, it distorts space-time into a "gravity well". As the sun moves against the background of fixed stars, their positions seem to move slightly. The effect is tiny - less than a thousandth of a degree - and is caused by gravity bending light. Light from the sun appears to be coming from a slightly different direction. It is bent because it follows a curving path across the sun's space-time "dimple", instead of the straight line it would follow in gravitationally undistorted space.
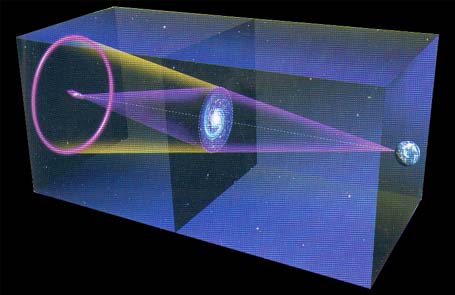
Extreme conditions at the Large Hadron Collider may produce wormholes in space-time. An advanced civilisation might be able to manipulate one of these to create a tunnel back to the point in time when the wormhole was first created. Colliding gravitational wavea from accelerated proton rip a wormhole in space-time ( 14 TeV concentrated into the space of 10 ^ -15 m ) The wormhole helps form a closed timelike curve, which allows particles to flow into the past, or from the future to the present. Dark energy might keep wormhole open, and could even make it wide enough for a person.
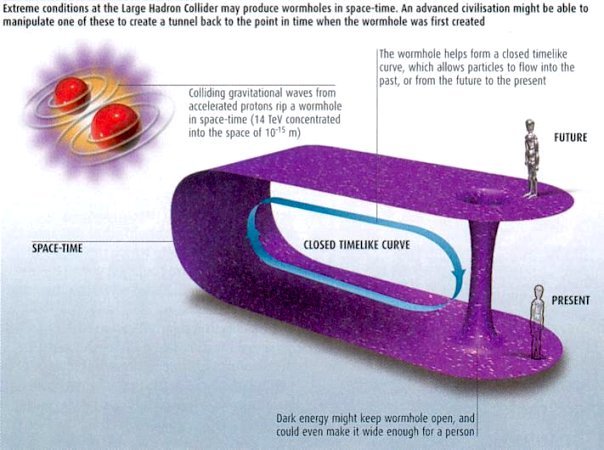
Closed Timelike Curve
wormhole
Physics. A theoretical distortion of space-time in a region of the universe
that would link one location or time with another, through a path that is
shorter in distance or duration than would otherwise be expected.
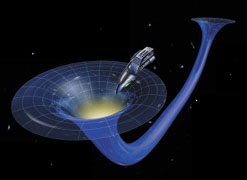
Analogy to a wormhole in a curved 2D space
Artist's impression of a wormhole as seen by an observer crossing the event
horizon of a Schwarzschild wormhole, which is similar to a Schwarzschild
black hole but with the singularity replaced by an unstable path to a white
hole in another universe. The observer originates from the right, and
another universe becomes visible in the center of the wormhole shadow once
the horizon is crossed. This new region is, however, unreachable in the case
of a Schwarzschild wormhole, as the bridge between the black hole and white
hole will always collapse before the observer has time to cross it. See
White Holes and Wormholes for a more technical discussion and an animation
of what an observer sees when falling into a Schwarzschild wormhole.
In physics, a wormhole is a hypothetical topological feature of spacetime
that is essentially a 'shortcut' through space and time. A wormhole has at
least two mouths which are connected to a single throat. If the wormhole is
traversable, matter can 'travel' from one mouth to the other by passing
through the throat. While there is no observational evidence for wormholes,
spacetimes containing wormholes are known to be valid solutions in general
relativity.
The term wormhole was coined by the American theoretical physicist John
Wheeler in 1957. However, the idea of wormholes was invented already in 1921
by the German mathematician Hermann Weyl in connection with his analysis of
mass in terms of electromagnetic field energy.[1]
This analysis forces one to consider situations...where there is a net flux
of lines of force through what topologists would call a handle of the
multiply-connected space and what physicists might perhaps be excused for
more vividly terming a wormhole.
John Wheeler in Annals of Physics
The name "wormhole" comes from an analogy used to explain the phenomenon. If
a worm is travelling over the skin of an apple, then the worm could take a
shortcut to the opposite side of the apple's skin by burrowing through its
center, rather than travelling the entire distance around, just as a
wormhole traveler could take a shortcut to the opposite side of the universe
through a hole in higher-dimensional space.
Definition
The basic notion of an intra-universe wormhole is that it is a compact
region of spacetime whose boundary is topologically trivial but whose
interior is not simply connected. Formalizing this idea leads to definitions
such as the following, taken from Matt Visser's
Lorentzian Wormholes:
If a Lorentzian spacetime contains a compact region Ω, and if the topology
of Ω is of the form Ω ~ R x Σ, where Σ is a three-manifold of nontrivial
topology, whose boundary has topology of the form dΣ ~ S², and if,
furthermore, the hypersurfaces Σ are all spacelike, then the region Ω
contains a quasipermanent intra-universe wormhole.
Characterizing inter-universe wormholes is more difficult. For example, one
can imagine a 'baby' universe connected to its 'parent' by a narrow 'umbilicus'.
One might like to regard the umbilicus as the throat of a wormhole, but the
spacetime is simply connected.
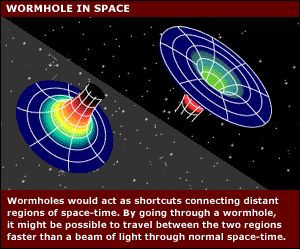
Wormhole types
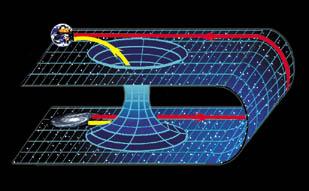
 Intra-universe
wormholes connect one location of a universe to another location of the same
universe (in the same present time or unpresent). A wormhole should be able
to connect distant locations in the universe by creating a shortcut through
spacetime, allowing travel between them that is faster than it would take
light to make the journey through normal space. See the image above. Inter-universe
wormholes connect one universe with another [1], [2]. This gives rise to the
speculation that such wormholes could be used to travel from one parallel
universe to another. A wormhole which connects (usually closed) universes is
often called a Schwarzschild wormhole. Another application of a wormhole
might be time travel. In that case, it is a shortcut from one point in space
and time to another. In string theory, a wormhole has been envisioned to
connect two D-branes, where the mouths are attached to the branes and are
connected by a flux tube [3]. Finally, wormholes are believed to be a part
of spacetime foam [4]. There are two main types of wormholes: Lorentzian
wormholes and Euclidean wormholes. Lorentzian wormholes are mainly studied
in general relativity and semiclassical gravity, while Euclidean wormholes
are studied in particle physics. Traversable wormholes are a special kind of
Lorentzian wormholes which would allow a human to travel from one side of
the wormhole to the other. Serguei Krasnikov suggested the term spacetime
shortcut as a more general term for (traversable) wormholes and propulsion
systems like the Alcubierre drive and the Krasnikov tube to indicate
hyperfast interstellar travel.
Intra-universe
wormholes connect one location of a universe to another location of the same
universe (in the same present time or unpresent). A wormhole should be able
to connect distant locations in the universe by creating a shortcut through
spacetime, allowing travel between them that is faster than it would take
light to make the journey through normal space. See the image above. Inter-universe
wormholes connect one universe with another [1], [2]. This gives rise to the
speculation that such wormholes could be used to travel from one parallel
universe to another. A wormhole which connects (usually closed) universes is
often called a Schwarzschild wormhole. Another application of a wormhole
might be time travel. In that case, it is a shortcut from one point in space
and time to another. In string theory, a wormhole has been envisioned to
connect two D-branes, where the mouths are attached to the branes and are
connected by a flux tube [3]. Finally, wormholes are believed to be a part
of spacetime foam [4]. There are two main types of wormholes: Lorentzian
wormholes and Euclidean wormholes. Lorentzian wormholes are mainly studied
in general relativity and semiclassical gravity, while Euclidean wormholes
are studied in particle physics. Traversable wormholes are a special kind of
Lorentzian wormholes which would allow a human to travel from one side of
the wormhole to the other. Serguei Krasnikov suggested the term spacetime
shortcut as a more general term for (traversable) wormholes and propulsion
systems like the Alcubierre drive and the Krasnikov tube to indicate
hyperfast interstellar travel.
Theoretical basis
It is known that (Lorentzian) wormholes are not excluded within the
framework of general relativity, but the physical plausibility of these
solutions is uncertain. It is also unknown whether a theory of quantum
gravity, merging general relativity with quantum mechanics, would still
allow them. Most known solutions of general relativity which allow for
traversable wormholes require the existence of exotic matter, a theoretical
substance which has negative energy density. However, it has not been
mathematically proven that this is an absolute requirement for traversable
wormholes, nor has it been established that exotic matter cannot exist.
In March 2005, Amos Ori envisioned a wormhole which allows time travel, does
not require any exotic matter and satisfies the weak, dominant, and strong
energy conditions [5]. The stability of this solution is uncertain, so it is
unclear whether infinite precision would be required for it to form in a way
that allows time travel and also whether quantum effects would uphold
chronology protection in this case, as analyses using semiclassical gravity
have suggested they might do in the case of traversable wormholes.
Schwarzschild wormholes
Lorentzian wormholes known as Schwarzschild wormholes or Einstein-Rosen
bridges are bridges between areas of space that can be modeled as vacuum
solutions to the Einstein field equations by sticking a model of a black
hole and a model of a white hole together. This solution was discovered by
Albert Einstein and his colleague Nathan Rosen, who first published the
result in 1935. However, in 1962 John A. Wheeler and Robert W. Fuller
published a paper showing that this type of wormhole is unstable, and that
it will pinch off instantly as soon as it forms, preventing even light from
making it through.Before the stability problems of Schwarzschild wormholes
were apparent, it was proposed that quasars were white holes forming the
ends of wormholes of this type.

While Schwarzschild wormholes are not traversable, their existence inspired
Kip Thorne to imagine traversable wormholes created by holding the 'throat'
of a Schwarzschild wormhole open with exotic matter (material that has
negative mass/energy).
Traversable wormholes
Lorentzian traversable wormholes would allow travel from one part of the
universe to another part of that same universe very quickly or would allow
travel from one universe to another. The possibility of traversable
wormholes in general relativity was first demonstrated by Kip Thorne and his
graduate student Mike Morris in a 1988 paper; for this reason, the type of
traversable wormhole they proposed, held open by a spherical shell of exotic
matter, is referred to as a Morris-Thorne wormhole. Later, other types of
traversable wormholes were discovered as allowable solutions to the
equations of general relativity, including a variety analyzed in a 1989
paper by Matt Visser, in which a path through the wormhole can be made in
which the traversing path does not pass through a region of exotic matter. A
type held open by negative mass cosmic strings was put forth by Visser in
collaboration with Cramer et al., [2], in which it was proposed that such
wormholes could have been naturally created in the early universe.

Wormholes connect two points in spacetime, which means that they would in
principle allow travel in time as well as in space. In a 1988 paper, Morris,
Thorne and Yurtsever[3] worked out explicitly how to convert a wormhole
traversing space into one traversing time.
Wormholes and faster-than-light travel
Special relativity only applies locally. Wormholes allow superluminal (faster-than-light)
travel by ensuring that the speed of light is not exceeded locally at any
time. While traveling through a wormhole, subluminal (slower-than-light)
speeds are used. If two points are connected by a wormhole, the time taken
to traverse it would be less than the time it would take a light beam to
make the journey if it took a path through the space outside the wormhole.
However, a light beam traveling through the wormhole would always beat the
traveler. As an analogy, running around to the opposite side of a mountain
at maximum speed may take longer than walking through a tunnel crossing it.
You can walk slowly while reaching your destination more quickly because the
length of your path is shorter.
Wormholes and time travel
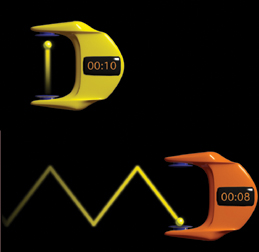
 A
wormhole could allow time travel. This could be accomplished by accelerating
one end of the wormhole to a high velocity relative to the other, and then
sometime later bringing it back; relativistic time dilation would result in
the accelerated wormhole mouth aging less than the stationary one as seen by
an external observer, similar to what is seen in the twin paradox. However,
time connects differently through the wormhole than outside it, so that
synchronized clocks at each mouth will remain synchronized to someone
traveling through the wormhole itself, no matter how the mouths move around.
This means that anything which entered the accelerated wormhole mouth would
exit the stationary one at a point in time prior to its entry. For example,
if clocks at both mouths both showed the date as 2000 before one mouth was
accelerated, and after being taken on a trip at relativistic velocities the
accelerated mouth was brought back to the same region as the stationary
mouth with the accelerated mouth's clock reading 2005 while the stationary
mouth's clock read 2010, then a traveler who entered the accelerated mouth
at this moment would exit the stationary mouth when its clock also read
2005, in the same region but now five years in the past. Such a
configuration of wormholes would allow for a particle's world line to form a
closed loop in spacetime, known as a closed timelike curve.
A
wormhole could allow time travel. This could be accomplished by accelerating
one end of the wormhole to a high velocity relative to the other, and then
sometime later bringing it back; relativistic time dilation would result in
the accelerated wormhole mouth aging less than the stationary one as seen by
an external observer, similar to what is seen in the twin paradox. However,
time connects differently through the wormhole than outside it, so that
synchronized clocks at each mouth will remain synchronized to someone
traveling through the wormhole itself, no matter how the mouths move around.
This means that anything which entered the accelerated wormhole mouth would
exit the stationary one at a point in time prior to its entry. For example,
if clocks at both mouths both showed the date as 2000 before one mouth was
accelerated, and after being taken on a trip at relativistic velocities the
accelerated mouth was brought back to the same region as the stationary
mouth with the accelerated mouth's clock reading 2005 while the stationary
mouth's clock read 2010, then a traveler who entered the accelerated mouth
at this moment would exit the stationary mouth when its clock also read
2005, in the same region but now five years in the past. Such a
configuration of wormholes would allow for a particle's world line to form a
closed loop in spacetime, known as a closed timelike curve.
It is thought that it may not be possible to convert a wormhole into a time
machine in this manner: some analyses using the semiclassical approach to
incorporating quantum effects into general relativity indicate that a
feedback loop of virtual particles would circulate through the wormhole with
ever-increasing intensity, destroying it before any information could be
passed through it, in keeping with the chronology protection conjecture.
This has been called into question by the suggestion that radiation would
disperse after traveling through the wormhole, therefore preventing infinite
accumulation. The debate on this matter is described by Kip S. Thorne in the
book Black Holes and Time Warps. There is also the Roman ring, which is a
configuration of more than one wormhole. This ring seems to allow a closed
time loop with stable wormholes when analyzed using semiclassical gravity,
although without a full theory of quantum gravity it is uncertain whether
the semiclassical approach is reliable in this case.
Wormhole
metrics
Theories of wormhole metrics describe the spacetime geometry of a wormhole
and serve as theoretical models for time travel. An example of a (traversable)
wormhole metric is the following:
One type of non-traversable wormhole metric is the Schwarzschild solution:
General Theory of Relativity - Curved Space-Time
An Introduction to Black Holes
Gravity Wave - Gravitasyonel dalgalar - daralıp sıkışan uzay /zaman dokusu

In Einsteins Universum haben Raum und Zeit eine übersichtliche Ordnung. Massereiche Körper krümmen die Raumzeit - in schöner Regelmäßigkeit
36 - World lines in special relativity
37 - Strings erzeugen eine universelle Symphonie - Relativitätstheorie
38- The General Theory of Relativity
39 - Zamanın Göreliliği
40 - Special Relativity
TIME DILATION
At this stage one may probably be thinking "Oh man, so length contracts...what
happens to time?" So, let's do another thought experiment, a rather
classical one at that... Consider the following situation, you are
sitting in a train carriage which is travelling near the speed of light
to some unknown destination (yes it is the train again - not very
imaginative, but saves me time when making the graphics...). In front of
you is a light hanging from the roof and there's a mirror on the floor
which reflects the light back up. You have a large clock with which to
time how long it takes for the light to reach the mirror and be
reflected back to the top. Your good old buddy Einstein is standing
outside, watching you and the train ride past. He too has a large clock,
and is timing how long it takes for the light to travel down to the
mirror and back.
As you can see in diagram 1, within your reference frame, the light only
has to travel up and down. But in diagram 2, from Einstein's perspective,
the light has to travel not only up and down but horizontally as well.
Since the light has a longer distance to travel, more time is taken (remember
that the speed of light is always constant!). Hence, the dilation of
time.
Now for the mathematical part. The time
interval between two events as seen by an observer (in this case, you)
in the same reference frame where the events are taking place, is called
proper time (to).The proper length (lo) of an
object is the length of the object measured in the frame where it is at
rest. Let's simplify the above diagrams to the following two below.
Diagram one is from your point of view in the carriage, and diagram 2 is
from Einstein's perspective outside the train.
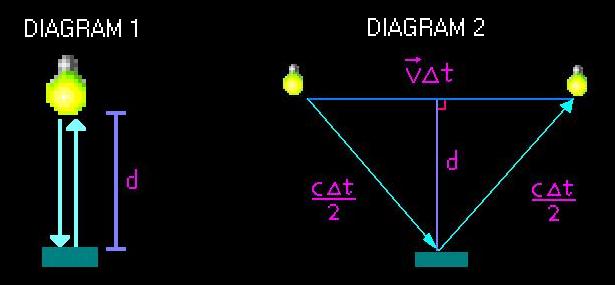
From diagram 1, to = 2d / c
From diagram 2 using Pythagoras' Theorem:
(c Δ t / 2)2 = (v Δ t / 2)2 + d 2
Solving for Δ t gives:
Δ t = 2d / (c2 - v2)1/2
Δ t = 2d/c x [1/ (1 - v2/c2)1/2 ]
Since Δ t0 = 2d/c, sub this into the equation:
Δ t = to / (1 - v2/c2)1/2
41- Einsteins spezielle Relativitätstheorie
42 - Beschleunigerphysik für Anfänger
43 - Relativistische Raumkonzepte
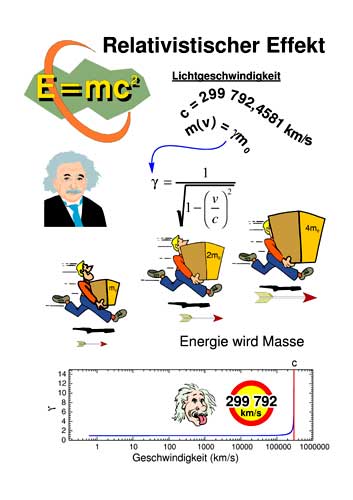


45- The warped universe of relativity theory
47 - Space-Time- Energy continuum
|
Einstein's Theory of
Gravitation -Spacetime curving around a star-
Einstein realized that those observers in the presence of a gravitational field, and those in accelerating reference frames would not be able to determine their situation. He in turn, found that acceleration and gravity were equivalent. But in order to prove his idea, he needed to come up with a theoretical framework that would account for this. Einstein knew that a framework explaining gravity could also resolve the conflict in his theory of special relativity, and so he began working on a new theory of gravitation. Einstein's theory of gravitation says that space will curve in the presence of matter, and this curvature will cause effects that we know as gravity. While Einstein was developing his equations, he quickly realized that standard mathematics (including calculus) would not be able to handle the situations described by his theory. He began researching the branch of mathematics called tensor analysis, which would allow him to develop equations to describe curved four-dimensional spaces. |
Gravitational time dilation
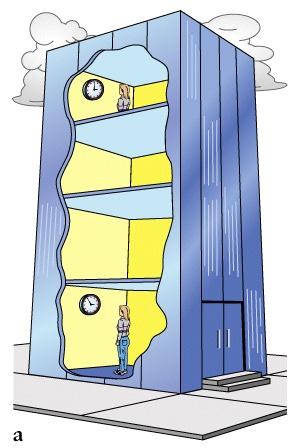

48 -Space and Time, Gravity - Equivalence Priciple
49- General Theory of Relativity
50 - Fisica Relatività Einstein
52- Einsteinın Gravitasyon Kuramının Önümüzdeki On Yılı(pdf)
53- Einstein Train and Special Relativity: Time Dilation
54- Special Theory of Relativity
Gravitational Time Dilation
A clock in a gravitational field runs more slowly according to the gravitational time dilation relationship from general relativity
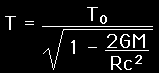 |
This is distinct from the time dilation from relative motion |
where T is the time interval measured by a clock far away from the mass. For a clock on the surface of the Earth, this expression becomes
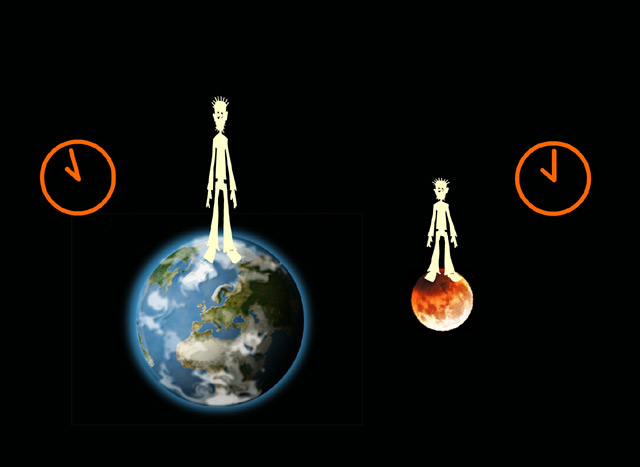

The violent deaths of large stars (supernovas) and the collisions of extremely dense stars such as neutron stars with each other can cause spacetime disturbances to happen and to spread out in a wavelike manner. These waves are called gravity waves or gravitational radiation. Within the next five years gravitational radiation should be seen for the first time.

When we talk about black hole, you may think of concepts like "wormhole" or "time tunnel" which give you a heavy flavour of sci-fi. In science fictions or movies, spaceship may enter a black hole, travel through spacetime via "wormhole" and finally emerge from somewhere in the Universe. However, most of the present astronomers will not take the concepts like spacetime travel seriously for reasons that they can neither find any mechanism leading to the formation of "wormhole", nor can they prove the existence of "wormhole" by way of astronomical observations. Moreover, recent studies on the topics demonstrate that even if "wormhole" does exist, it will be very unstable. An extremely small amount of matter passing through it will suffice to make it collapse. Up to now, the concept of spacetime travel by way of black hole can only be regarded as subjects of sci-fi and not a serious science.
 |
Other than some improvable guesses, interests in black hole studies in recent years are on the rise. What new discoveries have pushed astronomers into such relentless researches in everything connected with the black hole? How does the study of black hole help to the understanding of the evolution of the Universe?
Back in the 18th century, scientists like Laplace has already pointed out that highly compact objects might prevent their nearby light from escaping. Soon after Einstein published his General Theory of Relativity in the beginning of 20th century, Karl Schwarzschild found a mathematical solution of the theory to describe the spacetime structure of such object with spherical symmetry. That was the prelude to the study of black holes. Later on, Oppenheimer and others through calculation proved that supermassive stars under gravitational force could really collapse to form black holes. By the 70's, astronomers started to carry out systematic observations to look for evidence of black holes in binary system. The flush of observational evidence from the Hubble Space Telescope launched at the end of the 20th century further convinces us that black holes really exist. To the surprise of astronomers, black holes come in various sizes and origins, and are far more complicated than we can think of. For example, the sizes of black holes can vary immensely from a few to a few billions of solar masses! What is more important, the existence of these different kinds of black holes and the respective astronomical phenomena associated with them always brings far-reaching revelation to our understanding of the evolution of stars, galaxies and at last the whole Universe.

In the early days, man turned their eyes to the binary systems to look for black holes. From the spectral analysis of the orbit, if the invisible companion of a star in a binary system is 3.5 times heavier than that of the Sun, this dark celestial object is most probably a black hole. We take 3.5 solar masses as the benchmark for judging whether something is a black hole because we know we know that theoretically the mass of other compact objects (like neutron star) cannot exceed that maximum threshold. Otherwise those bodies will collapse under their own gravitational force into black holes. However, it is never an easy task to determine the mass of companion stars in binary systems just by way of spectral analysis. Miscalculations did always happen, as it is difficult to accurately measure factors like the luminosity of the visible stars in the pairs and the tilting of the orbits. Accretion disks formed when compact objects suck in matters of companion stars may also betray the existence of black holes. For neutron stars and black holes, accretion disk will emit high-energy X-rays when matters are spiraling in the compact objects, since immense gravitational force can cause substantial heat up of the matters. Searching for X-ray sources in the sky becomes the most important ways to locate neutron stars and black holes among binary system.

In recent years, with the help of X-ray satellites, astronomers make remarkable progress in the search of the Holy Grail. The main difference between neutron stars and black holes lies in the fact that neutron star has a solid surface whereas the black hole does not. Studies show that, in a binary system, huge energy is released when matter of companion star fall onto the surface of neutron star. On the contrary, when matter falls into black hole, it together with the energy generated will disappear behind the event horizon. For that reason, X rays emitted by neutron star binaries are stronger and their spectra exhibit special characteristics. For the total energy generated during the accretion process, the part confiscated by a black hole could be 100 times higher than the radiation that can narrowly escape from the formidable gravitational force. Astronomers are almost sure that the dark companions of many X-ray binaries are black holes and not neutron stars. V404 Cygni is one of the most well-known examples.
|
|
For
a long time, black hole's event horizon and its association bizarre
behaviours are only mathematical game. But observation by the Hubble Space
Telescope in recent years provided convincing evidence for the existence of
the event horizon. Researchers analysed a huge amount of ultra-violet
radiation data coming from a compact object called Cygnus XR-1. They found
two events showing the shortening of pulsating cycle and decaying of
radiations intensity. The signatures matched theories of what scientists
would predict to see. When matter is falling so close to the event horizon,
it will be circling the black hole with increasing speed and its light will
rapidly dim as it is stretched by gravity to ever-longer wavelengths.
However, it is impossible for astronomers to see the even horizon directly
due to the current technical limitation. Therefore what scientists
discovered so far is only an indirect evidence of the gravitational redshift
or similar phenomenon caused by black holes. But those results undoubtedly
become an important bridge for linking black hole theory with actual
observation.
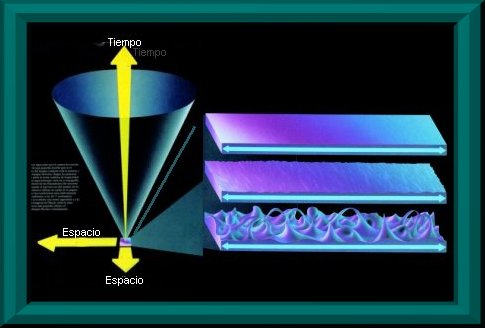
| Los físicos especulan que el cosmos ha crecido a desde una «nada» primigenia que al nacer comenzó el principio del tiempo y que, en ese parto, contenía toda la materia y toda la energía (arriba, izquierda). Según los primeros trabajos sobre la teoría cuántica de la gravedad, el propio espaciotiempo varió en su topografía, dependiendo de las dimensiones del universo guagua (bebé). Cuando el universo era del tamaño de un núcleo atómico (dibujo de arriba, a la derecha), las condiciones eran relativamente lisas y uniformes; a los 10-30 cm (centro) es evidente una cierta granulidad; y a la llamada longitud de Planck, todavía unas 1.000 veces más pequeño (abajo), el espacio tiempo fluctúa violentamente. |

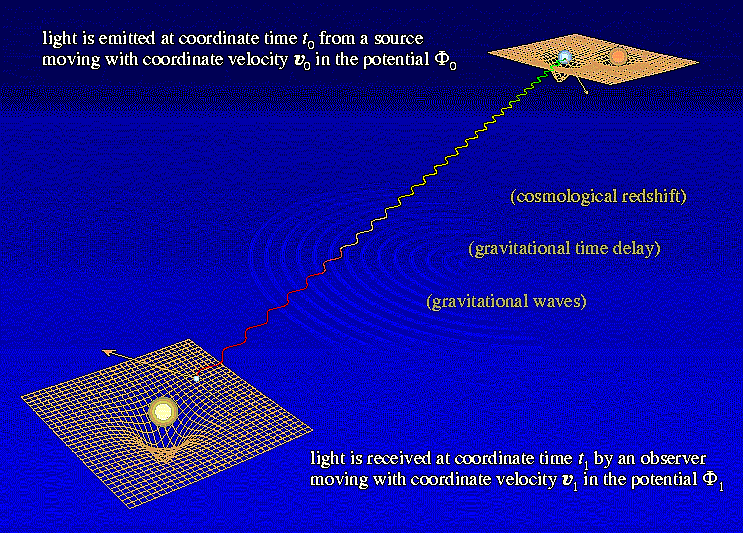


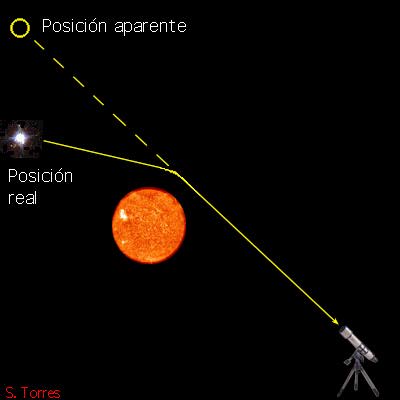
Lo spazio-tempo curvo e la luce
Il principio di relatività generale permette anche di superare il secondo assioma della relatività ristretta
se si considera la traiettoria della luce in un sistema accelerato, questa non risulta più rettilinea, ma curva :
|
Sistema inerziale Ü |
 |
Sistema accelerato Û |
Gli studi di Einstein lo portarono a ritenere che la luce possa essere deviata anche dalla curvatura dello spazio-tempo, quindi da una massa.
Ragioni alla base della teoria:
-
Secondo il principio di equivalenza l'effetto di un sistema di riferimento accelerato è indistinguibile da quello di un campo gravitazionale.
-
La luce trasporta energia: secondo la relatività ristretta non c'è differenza tra una quantità di energia E ed una massa m=E / C2.
è plausibile ritenere che la curvatura dello spazio-tempo abbia effetti
anche sulla propagazione della luce.
Una verifica sperimentale della teoria era impossibile sulla Terra, che ha massa troppo piccola.
Einstein cercò tale conferma mediante l'osservazione della deviazione dello spazio-tempo causata dalla massa del Sole.
Ebbe successo nel 1919, in occasione di un'eclissi solare totale.
La relativité générale et les trous noirs
I] Introduction à la relativité générale (1915)
Pour bien comprendre comment fonctionne un trou noir, il nous faut introduire la théorie de la Relativité Générale. Einstein a élaboré celle ci car la théorie de Newton posait deux principaux problèmes à ses yeux:
- Le premier est une énigme qui date depuis Newton: Lorsqu' on considère le mouvement d' un corps dans un champs de gravité, on écrit les équations suivantes (lois de Newton):
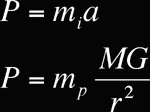
Avec
le poids,
la masse inertielle (ou inerte),
l' accélération,
la masse pesante,
la masse de l' astre,
la constante de gravitation,
la distance entre l' astre et le corps considéré.
Cependant, de nombreuses expériences sur la chute des corps lourds (comme celle de Roland Von Eötvös en 1890) montre que:
Cela a pour conséquence:
C' est a dire que la chute d' un corps est indépendant de sa masse, puisque l' accélération n' est pas fonction de la masse. Cette coïncidence (les deux masses n' ont absolument rien a voir) montre des faiblesses dans la théorie de Newton puisque elle n' est pas prévue, on se contente juste de l' observer.
- Elle est incompatible avec la relativité restreinte (1905) qui stipule que rien ne peut aller plus vite que la lumière. En effet, cela exclue les forces qui agissent instantanément à distance comme la gravité en mécanique classique.
Pour résoudre ces problèmes, Einstein part du principe d' équivalence: on ne peut distinguer un champs de forces d' inertie dans un mouvement uniformément accéléré d' un champs de gravitation. Par exemple, une personne dans un vaisseau en accélération constante de 9,8 m.s-2 ressentira exactement la même chose que si elle était sur terre. Maintenant, faisons une petite expérience de pensée: Soit une personne A immobile et une une personne B dans un vaisseau transparent en très forte accélération. Un photon est émis perpendiculairement au vaisseau depuis l' extérieur et traverse celui ci. Prenons d' abord le point de vue de A, voici ce qu' il observe:

Maintenant, le point de vue de B, voici ce qu' il observe:

On voit que le trajet de la lumière est courbé par l' accélération. Or d' après le principe d' équivalence, la gravité est identique à l' accélération, on peut donc en déduire que la gravité courbe les rayons lumineux. De plus, la lumière emprunte toujours le chemin le plus court entre deux points (géodésique), l' espace est donc courbé par la gravité. Grâce à des expériences de pensée similaire, nous pouvons montrer que le temps est ralenti à proximité d' une masse. En fait, la relativité générale montre que la gravitation n' est pas une force, mais une propriété géométrique de l' espace-temps. En effet, celui ci est courbé par la masse (et l' énergie, via E=mc^2). Ceci peut être résumé par la formule suivante: "L 'espace-temps agit sur la matière et lui indique comment elle doit se déplacer. Réciproquement, la matière agit sur l' espace-temps et lui indique comment il doit se courber". Dans un espace-temps à quatre dimensions, les planètes ne ressentent aucune force au voisinage du soleil, cependant, nous ne pouvons percevoir que la projection en trois dimension de cet espace-temps, et dans celle ci, les planètes sembles être "attirées" par le soleil par une force. La conséquence de tout ceci est que le temps et l' espace perdent totalement leur caractère absolu, puisque ces deux grandeurs dépendent maintenant de l' endroit où on se trouve (d' ou le nom de relativité).
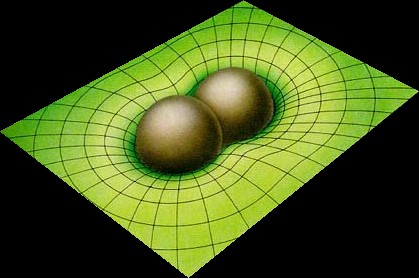
Bien sur, il est impossible de s' imaginer un espace-temps courbé à quatre dimensions, mais on peut par exemple le représenter en deux dimensions de la manière suivante:

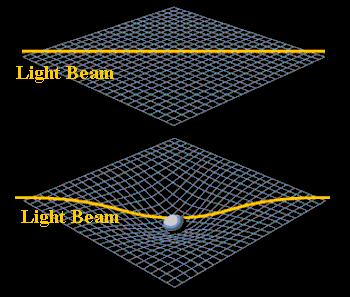
En l' absence de masse (schémas a), l' espace temps est plat (espace-temps de Minkowski), et la trajectoire de la lumière est rectiligne. Lorsqu' une masse est présente (schémas b), l' espace se courbe, et il en va de même pour la trajectoire des rayons lumineux.
Pour élaborer sa théorie quantitativement, Einstein a dû utiliser des outils mathématiques plus compliqués qu' auparavant. En effet, lorsque l' on parle de d' espace courbe, la géométrie Euclidienne ne s' applique plus et il faut utiliser une nouvelle géométrie développée par Riemann au XIXème siècle. Dans celle ci, la courbure peut être négative (comme la surface d' une selle de cheval), dans ce cas la, la somme des angle d' un triangle est inférieure à 180°. Elle peut être aussi positive (surface d' une sphère), la somme valant cette fois plus que 180°. Nous ne pouvons malheureusement pas approfondir la partie mathématique de la relativité générale car ceci demande demande un niveau bien trop élevé, cependant, des liens on été ajoutés dans la section bibliographie.
II]
Application aux trous noirs:
Nous avons vus que les
trous noirs pouvaient être abordés grâce à la mécanique classique dans la
première partie. Après cette première approche de la relativité, nous allons
voir à quoi cela correspond avec cette nouvelle théorie. Considérons une
étoile massive en effondrement gravitationnel représentée par le schémas
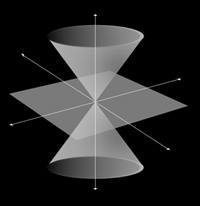
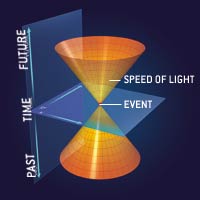
suivant:
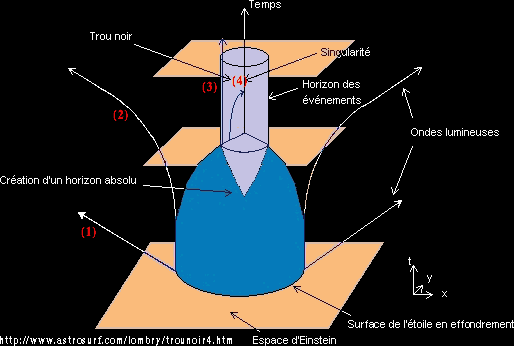
Avant que l' étoile ne commence à s' effondrer, les rayons ne sont que très peu courbés (1), et ils s' échappent en ligne droite. Au fur et a mesure que l' étoile s' effondre, les rayons émis ont de plus en plus de mal à s' échapper de l' étoile (2). Lorsque le rayon de l' étoile atteint Rs, si un photon est émis a ce moment, il restera à tout jamais au niveau de l' horizon du trou noir (3). Maintenant, si photon est émis après cette limite, il tombera irrémédiablement vers la singularité (4).
Si l' on veut représenter l' espace-temps aux alentours d' un trou noir, cela donne ceci:

Les cônes rouge représentent les trajets possibles pour un photon venant du passé, les cônes vert ceux du futur. On peut remarquer que plus on s' approche de l' horizon, plus les cônes sont déformés vers l' intérieur du trou noir. Cela signifie que la seul trajectoire possible pour un photon (et pour les autres particules) est de plonger vers la singularité.
Lorsqu' une masse se déplace, elle produit des sortes de rides dans l' espace temps, celles ci sont appelées ondes gravitationnelles. On peut faire l' analogie entre ces ondes dû a un mouvement de matière et un champs magnétique, qui lui est dû a un déplacement de charges. Pour produire ces ondes, la masse doit perdre de l' énergie cinétique (principe de la conservation d' énergie). Cela signifie que si deux trous noirs tournent l' un autour de l' autre, ils vont spiraler pour enfin fusionner entre eux. Pour produire ces ondes, il faut des quantités phénoménale d' énergie, c' est pourquoi on ne peut les rencontrer que lors d'évenements violents comme les supernovae et le mouvement de trou noir, lorsqu' il est extrêmement rapide. La terre crée bien des ondes gravitationnelles, mais en tellement faible quantité, qu 'elle ne se rapproche du soleil que de moins d' un atome par ans.
Il faut ajouter que lorsqu' un trou noir est en rotation (trou noir de Kerr), il entraîne avec lui l' espace-temps. Ceci a pour effet de réduire le rayon de l' horizon (en rouge), comme le montre l' animation suivante:
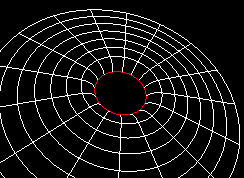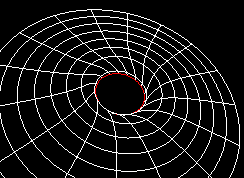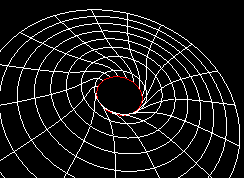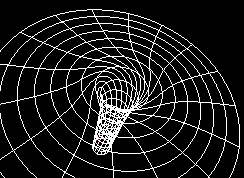
De plus, les rayons rayons lumineux sont déviés d' une manière différente suivant la rotation, en effet, celle les entraîne avec elle:
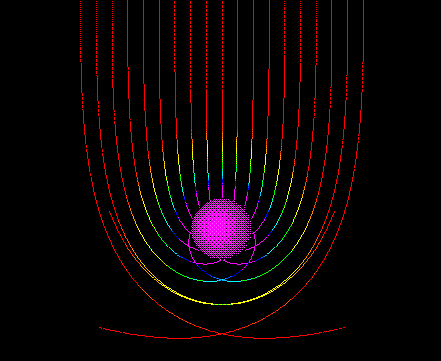
Rotation nulle.
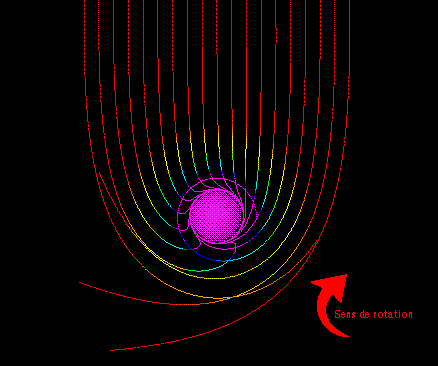
Rotation moyenne.
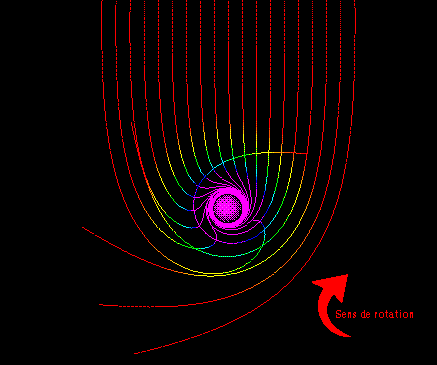
Forte rotation: on peut observer que cette rotation va jusqu'a faire "revenir en arrière" les photon: leur sens de rotation est inversé lorsqu 'ils s' approchent de l' horizon. Nous verrons en détail plus tard pourquoi les rayons sont de plus en plus décalés vert le violet.

General relativity (GR) or general relativity theory (GRT) is the theory of gravitation published by Albert Einstein in 1915. The conceptual core of general relativity, from which its other consequences largely follow, is the Principle of Equivalence, which describes gravitation and acceleration as different perspectives of the same thing, and which was originally stated by Einstein in 1907 as:
We shall therefore assume the complete physical equivalence of a
gravitational field and the corresponding acceleration of the reference
frame. This assumption extends the principle of relativity to the case of
uniformly accelerated motion of the reference frame.
In other words, he postulated that no experiment can locally distinguish
between a uniform gravitational field and a uniform acceleration.
Introduction
This principle explains the experimental observation that inertial and
gravitational mass are equivalent. Moreover, the principle implies that some
frames of reference must obey a non-Euclidean geometry: that spacetime is
curved (by matter and energy), and gravity can be seen purely as a result of
this geometry. This then yields many predictions such as gravitational
redshifts and light bent around stars, black holes, time slowed by
gravitational fields, and slightly modified laws of gravitation even in weak
gravitational fields. However, it should be noted that the equivalence
principle does not uniquely determine the field equations of curved
spacetime, and there is a parameter known as the cosmological constant which
can be adjusted.
The modifications to Isaac Newton's law of universal gravitation produced
the first great theoretical success of general relativity: the correct
prediction of the precession of the perihelion of Mercury's orbit. Many
other quantitative predictions of general relativity have since been
confirmed by astronomical observations. However because of the difficulty in
making these observations, theories which are similar but not identical to
general relativity, such as the Brans-Dicke theory and the Rosen bi-metric
theory cannot be ruled out completely, and current experimental tests can be
viewed at reducing the deviation from GR which is allowable. There are no
known experimental results that suggest that a theory of gravity radically
different from general relativity is necessary. (For example, the Allais
effect was initially speculated to demonstrate "gravitational shielding,"
but was subsequently explained by conventional phenomena.)
However, there are good theoretical reasons for considering general relativity to be incomplete. General relativity does not include quantum mechanics, and this causes the theory to break down at sufficiently high energies. A continuing unsolved challenge of modern physics is the question of how to correctly combine general relativity with quantum mechanics, thus applying it also to the smallest scales of time and space.
The "curvature" of spacetime
Mathematicians use the term "curved" to refer to any space whose geometry is
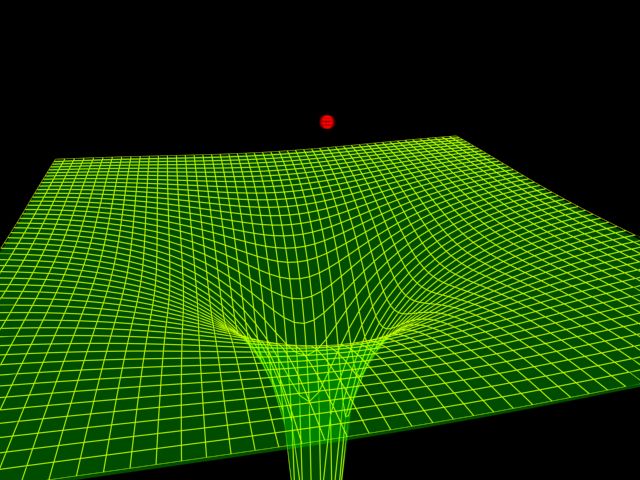
non-Euclidean. Frequently, this curvature is illustrated by an image
something like the following:

This graphic shows spacetime as a higher-dimensional flat space, with the "weight"
of a massive object "stretching" the trampoline-like spacetime "fabric",
which would result in trajectories around this "dent" being curved due to
the "slope" and the pull of gravity in some higher dimension . This image,
however, is only suggestive of the reality. It is important to remember that
spacetime is curved, not merely space, and that space is three-dimensional,
not two-dimensional as shown.
Another approach used to understand spacetime as a curved surface in three-dimensional space is to instead begin by imagining a universe of one-dimensional beings living in one dimension of space and one dimension of time. Each bit of matter is not a point on whatever curved surface you imagine, but a line showing where that point moves as it goes from the past to the future. These lines are called world lines.
While it can be helpful for visualization to imagine a curved surface
sitting in space of a higher dimension, that model is not thought to be true
in any meaningful sense for the real universe. Curvature can be measured
entirely within a surface, and similarly within a higher-dimensional
manifold such as space or spacetime. On earth, if you start at the North
Pole, walk south for about 10,000 km (to the Equator), turn left by 90
degrees, walk for 10,000 more km, and then do the same again, you will be
back where you started. Such a triangle with three right angles is only
possible because the surface of the earth is curved. The curvature of
spacetime can be evaluated, and indeed given meaning, in essentially the
same way.
Relationship to special relativity
The special theory of relativity (1905) modified the equations used in
comparing the measurements made by differently moving bodies, in view of the
constant value of the speed of light, i.e. its observed invariance in
reference frames moving uniformly relative to each other. This had the
consequence that physics could no longer treat space and time separately,
but only as a single four-dimensional system, "space-time," which was
divided into "time-like" and "space-like" directions differently depending
on the observer's motion. The general theory added to this that the presence
of matter "warped" the local space-time environment, so that apparently "straight"
lines through space and time have the properties we think of "curved" lines
as having.
On May 29, 1919, observations by Arthur Eddington of shifted star positions
during a solar eclipse confirmed the theory.
Foundations
General relativity's mathematical foundations go back to the axioms of
Euclidean geometry and the many attempts over the centuries to prove
Euclid's fifth postulate, that parallel lines remain always equidistant,
culminating with the realisation by Lobachevsky, Bolyai and Gauss that this
axiom need not be true. The general mathematics of non-Euclidean geometries
was developed by Gauss' student, Riemann, but these were thought to be
wholly inapplicable to the real world until Einstein developed his theory of
relativity.
Gauss had realised that there is no a priori reason that the geometry of
space should be Euclidean. What this means is that if a physicist holds up a
stick, and a cartographer stands some distance away and measures its length
by a triangulation technique based on Euclidean geometry, then he is not
guaranteed to get the same answer as if the physicist brings the stick to
him and he measures its length directly. Of course for a stick he could not
in practice measure the difference between the two measurements, but there
are equivalent measurements which do detect the non-Euclidean geometry of
space-time directly; for example the Pound-Rebka experiment (1959) detected
the change in wavelength of light from a cobalt source rising 22.5 meters
against gravity in a shaft in the Jefferson Physical Laboratory at Harvard,
and the rate of atomic clocks in GPS satellites orbiting the Earth has to be
corrected for the effect of gravity.
Newton's theory of gravity had assumed that objects did in fact have
absolute velocities: that some things really were at rest while others
really were in motion. He realized, and made clear, that there was no way
these absolutes could be measured. All the measurements one can make provide
only velocities relative to one's own velocity (positions relative to one's
own position, and so forth), and all the laws of mechanics would appear to
operate identically no matter how one was moving. Newton believed, however,
that the theory could not be made sense of without presupposing that there
are absolute values, even if they cannot be determined. In fact, Newtonian
mechanics can be made to work without this assumption: the outcome is rather
innocuous, and should not be confused with Einstein's relativity which
further requires the constancy of the speed of light.
In the nineteenth century Maxwell formulated a set of equationsMaxwell's
field equationsthat demonstrated that light should behave as a wave emitted
by electromagnetic fields which would travel at a fixed velocity through
space. This appeared to provide a way around Newton's relativity: by
comparing one's own speed with the speed of light in one's vicinity, one
should be able to measure one's absolute speed--or, what is practically the
same, one's speed relative to a frame of reference that would be the same
for all observers.
The assumption was whatever medium light was travelling throughwhatever it
was waves ofcould be treated as a background against which to make other
measurements. This inspired a search to determine the earth's velocity
through this cosmic backdrop or "aether"the "aether drift." The speed of
light measured from the surface of the earth should appear to be greater
when the earth was moving against the aether, slower when they were moving
in the same direction. (Since the earth was hurtling through space and
spinning, there should be at least some regularly changing measurements here.)
A test made by Michelson and Morley toward the end of the century had the
astonishing result that the speed of light appeared to be the same in every
direction.
In his 1905 paper "On the Electrodynamics of Moving Bodies", Einstein
explained these results in his theory of special relativity.
Outline of the theory
The fundamental idea in relativity is that we cannot talk of the physical
quantities of velocity or acceleration without first defining a reference
frame, and that a reference frame is defined by choosing particular matter
as the basis for its definition. Thus all motion is defined and quantified
relative to other matter. In the special theory of relativity it is assumed
that reference frames can be extended indefinitely in all directions in
space and time. The theory of special relativity concerns itself with
inertial (non-accelerating) frames while general relativity deals with all
frames of reference. In the general theory it is recognised that we can only
define local frames to given accuracy for finite time periods and finite
regions of space (similarly we can draw flat maps of regions of the surface
of the earth but we cannot extend them to cover the whole surface without
distortion). In general relativity Newton's laws are assumed to hold in
local reference frames. In particular free particles travel in straight
lines in local inertial (Lorentz) frames. When these lines are extended they
do not appear straight, and are known as geodesics. Thus Newton's first law
is replaced by the law of geodesic motion.
We distinguish inertial reference frames, in which bodies maintain a uniform state of motion unless acted upon by another body, from non-inertial frames in which freely moving bodies have an acceleration deriving from the reference frame itself. In non-inertial frames there is a perceived force which is accounted for by the acceleration of the frame, not by the direct influence of other matter. Thus we feel acceleration when cornering on the roads when we use a car as the physical base of our reference frame. Similarly there are coriolis and centrifugal forces when we define reference frames based on rotating matter (such as the Earth or a child's roundabout). The principle of equivalence in general relativity states that there is no local experiment to distinguish non-rotating free fall in a gravitational field from uniform motion in the absence of a gravitational field. In short there is no gravity in a reference frame in free fall. From this perspective the observed gravity at the surface of the Earth is the force observed in a reference frame defined from matter at the surface which is not free, but is acted on from below by the matter within the Earth, and is analogous to the acceleration felt in a car.
Mathematically, Einstein models space-time by a four-dimensional pseudo-Riemannian
manifold, and his field equation states that the manifold's curvature at a
point is directly related to the stress energy tensor at that point; the
latter tensor being a measure of the density of matter and energy. Curvature
tells matter how to move, and matter tells space how to curve.
The field equation is not uniquely proven, and there is room for other
models, provided that they do not contradict observation. General relativity
is distinguished from other theories of gravity by the simplicity of the
coupling between matter and curvature, although we still await the
unification of general relativity and quantum mechanics and the replacement
of the field equation with a deeper quantum law. Few physicists doubt that
such a theory of everything will give general relativity in the appropriate
limit, just as general relativity predicts Newton's law of gravity in the
non-relativistic limit.
Einstein's field equation contains a parameter called the "cosmological
constant" Λ which was originally introduced by Einstein to allow for a
static universe (i.e., one that is not expanding or contracting). This
effort was unsuccessful for two reasons: the static universe described by
this theory was unstable, and observations by Hubble a decade later
confirmed that our universe is in fact not static but expanding. So Λ was
abandoned, with Einstein calling it the "biggest blunder [I] ever made".
However, quite recently, improved astronomical techniques have found that a
non-zero value of Λ is needed to explain some observations.
Einstein field equation
The field equation reads as follows:
where Rik is the Ricci curvature tensor, R is the scalar curvature, gik is the metric tensor, Λ is the cosmological constant, Tik is the stress-energy tensor describing the non-gravitational matter, energy and forces at any given point in space-time, π is pi, c is the speed of light in a vacuum and G is the gravitational constant which also occurs in Newton's law of gravity.
The Ricci tensor and scalar curvature are themselves derivable from the gik. gik describes the metric of the manifold and is a symmetric 4 x 4 tensor, so it has 10 independent components. Given the freedom of choice of the four spacetime coordinates, the independent equations that make up the Einstein field equation reduce to 6.
Einstein thought of the cosmological constant as an independent parameter, but its term in the field equation can also be moved algebraically to the other side, written as part of the stress-energy tensor, and then interpreted as a form of dark energy whose density is constant in space-time.
The study of the solutions of this equation is one of the activities of a branch of astronomy named cosmology. It leads to the prediction of black holes and to the different models of evolution of the universe.
The vierbein formulation of general
relativity
This is an alternative equivalent formulation
of general relativity using four reference vector fields, called a vierbein
or tetrad. We have ea, a = 0, 1, 2, 3 such
that g(ea, eb) = ηab
where
.
See sign convention. One thing to note is that we can perform an independent
proper, orthochronous Lorentz transformation at each point (subject to
smoothness, of course) and still get a valid tetrad. So, the tetrad
formulation of GR is a gauge theory, but with a noncompact gauge group SO(3,1).
It is also invariant under diffeomorphisms.
See vierbein and Palatini action for more details. See Einstein-Cartan
theory for an extension of general relativity to include torsion. See
teleparallelism for another theory which predicts the same results as
general relativity but with FLAT spacetime with no curvature.
What Relativity Is
Relativity is a catch-all phrase for both the theory of special relativity and the theory of general relativity. Albert Einstein is the father of both theories, even though special relativity has it's roots in earlier work.
Contrary to popular belief, the theory of relativity does not say that everything is relative. It does say that the speed of light is constant. Since light is constant, special relativity reasons, things that we once thought were constant, namely length, mass, and time, are not constant.
What do we mean by constant? Think of it this way: in the newtonian model, no velocity was constant. For example, if you see someone riding their bike, you might say that they are going 15 miles per hour in relation to you. However, if you then started jogging along side of the bike, you might say that the bikes velocity is only 5 miles per hour, because you are running 10 miles per hour. Velocities are relative. In relativity theory, this is still for the most part true, with the exception of light. If you are not moving and light is riding a bicycle (for discussion's sake) toward you at the speed of light, you would measure it's speed as the speed of light. However, if you then started jogging along side of the bike, you would still measure it's velocity as the speed of light, even though you are now going 10 miles per hour. In fact, you could be going a million miles per hour in relation to your original position, but you would still measure the speed of light the same.
That's not all relativity tells us. Relativity also tells us that
![]() and that gravity is the
net effect of the curvature of space-time as a result of mass.
and that gravity is the
net effect of the curvature of space-time as a result of mass.
What is Special Relativity?
Special relativity is the theory published by Einstein in 1905. Specifically, special relativity says that light is constant, and as velocity increases length decreases, mass increases, and time slows down.

|
What is General Relativity?
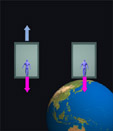
General Relativity is a "generalized" and enhanced version of special relativity. General relativity describes the same odd behavior at high velocities as special relativity, but adds a twist. General relativity throws in gravity. Einstein realized that there was no difference in the force of gravity and the force of acceleration. For example, someone in a rocket ship without windows cannot tell whether the ship is a rest on Earth or is accelerating through outer-space. The net effect (the person's feet pushing against the floor of the spaceship) is identical. If gravity has characteristics of motion, then strong gravitational feilds must make matter behave similar to high velocities. The "general" comes from the way the theory explains the phenomena. General relativity can theoretically explain any scenario in space-time. What is meant by "the curvature of space-time"? To know that, we must first learn what space-time is. |
Just about everything you can see is made out of atoms. Those atoms combine to form molecules, etc. Air is made out of atoms, water is made out of atoms, just about everything around us is made out of atoms. Imagine if we could see down to the atomic level. We could see all the atoms that make up everything. But what is in between the atoms? Nothing?
The answer is space-time. Time is an important part of it, because the theories of relativity tell us that as you move through space you also move through time. Einstein thought of space-time having four dimensions: up-down, east-west, north-south, and a fourth dimension that is time multiplied by i ( i is defined as the square root of -1). Thus, you have all the dimensions of space and one time-like dimension that makes up space-time. How does it curve?
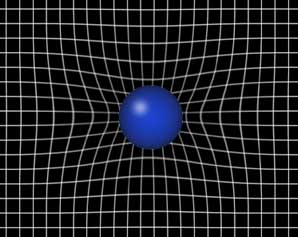
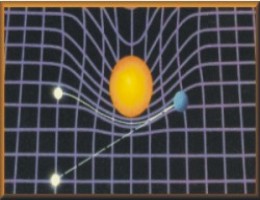
On the right you can see an illustration of this concept. Imagine space-time is the grid, and the blue sphere is something that is massive, like a star. The mass of the star causes space-time to curve. The greater the curve, the greater the attractive force of gravity. Notice that space-time is more curved closer to the object.
In the lower illustration, imagine that you are walking on the top straight line of the grid. You can measure the strength of the force pulling you closer to the ball by measuring the distance from the top straight line you are standing on to the bottom curved line. As you walk toward the ball, the distance between the line and the curve increases, thus the strength of the force increases.
This, of course, is not a perfect illustration, as it is a 3 dimensional representation of a 4 dimensional concept.
Jetzt können wir auf den Feuerknopf drücken und unseren Astronauten ins All schießen. Er dreht erst ein "paar Runden" um Geschwindigkeit aufzunehmen, und fliegt dann mit relativistischer Geschwindigkeit (in deutlichen Bruchteilen der Lichtgeschwindigkeit) auf einem solchen Kurs, dass wir bequem seine Uhr beobachten können. Was werden wir sehen?

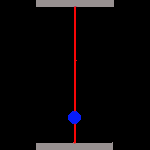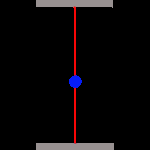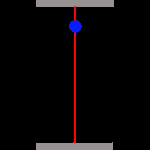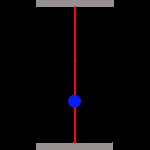
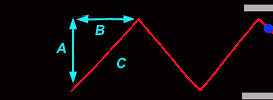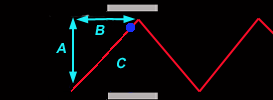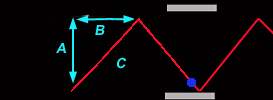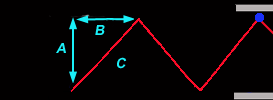 |
Während unsere (rechte) Uhr völlig normal weiterläuft, sieht die des Astronauten total anders aus! Wir sehen das Photon unten links starten, doch in der Zeit, die es für den Weg zum oberen Spiegel benötigt, haben sich die Spiegel durch die schnelle Bewegung des Raumschiffs verschoben und zwar mit der Geschwindigkeit des Raumschiffs v. Aus unserer Sicht muss das Photon damit scheinbar eine Diagonale (C) durchlaufen, und die ist natürlich länger als der direkte Weg (A) zwischen den Spiegeln unserer Uhr. Denn zusätzlich zur Strecke A durchläuft das Photon auch die Verschiebung beider Spiegel um die Distanz B. Allem Anschein nach wird die Zeit gedehnt, und wir bezeichnen diese Zeit als T'. Wir betrachten dies genauer, indem wir das rechtwinklige Dreieck aus den Strecken A, B und C untersuchen. |
 |
Minkowski, Einsteins ehemaliger Professor (der seinen Studenten Einstein noch als "faulen Hund" bezeichnete), erkannte in dessen Gleichungen die Bedeutung des Satzes des Pythagoras, der die Seitenverhältnisse eines rechtwinkligen Dreiecks beschreibt: A2 + B2 = C2. Das Photon durcheilt nun alle Strecken mit der Lichtgeschwindigkeit c, also A und auch C. Somit können wir sagen, dass sich die Strecken A zu C verhalten wie die Zeiten T zu T':
A/C = T/T'
Während das Photon C durchläuft, verschieben sich die Spiegel mit der Geschwindigkeit v um den Betrag B, daher gilt auch
B/C = v/c
Nun wollen wir untersuchen, wie sich die Laufzeiten zueinander verhalten. Wir beginnen damit, den Satz des Pythagoras durch C2 zu dividieren:
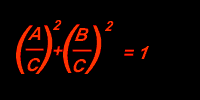
Wir bringen B/C auf die andere Seite:
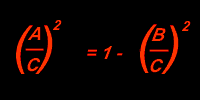
Um A/C berechnen zu können, müssen wir auf beiden Seiten die Wurzel ziehen:
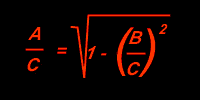
Jetzt können wir die Verhältnisse A/C und B/C durch die anderen physikalischen Größen ersetzen, da sie ja einander proportional sind. Die Strecke A ersetzen wir also durch T, die Zeit, die das Photon für einen Weg auf unserer Erduhr benötigt und C durch T', die verlängerte Zeit in der Raumschiffuhr. Wie wir oben gesehen haben, verhalten sich B/C = v/c, und wir ersetzen daher auch diesen Ausdruck:
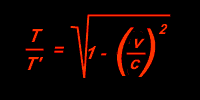
Wir bilden noch den Kehrwert und erhalten eine damit eine bequeme Möglichkeit, die Größe der Zeitdehnung zu berechnen:
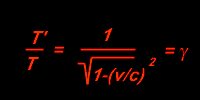
Why Relativity Works
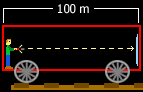 Jim
is in a train car without any windows. Because the car has no windows it
is dark, so Jim decides to turn on his flashlight. From the end of his
flashlight to the wall is 100 meters. Because Jim always measures the
speed of light to be constant at 3.00 x 10^8 m/sec and because Jim knows
that the wall is 100 meters away, Jim discovers that the light took only
1/3 x 10^-8 seconds to go from his flashlight to the wall.
Jim
is in a train car without any windows. Because the car has no windows it
is dark, so Jim decides to turn on his flashlight. From the end of his
flashlight to the wall is 100 meters. Because Jim always measures the
speed of light to be constant at 3.00 x 10^8 m/sec and because Jim knows
that the wall is 100 meters away, Jim discovers that the light took only
1/3 x 10^-8 seconds to go from his flashlight to the wall.
What Jim
doesn't know (because there are no windows) is that the train car he is
in is traveling along a track at 98% of the speed of light in relation
to Bob. Bob knows this because Bob is on the side of the track. In fact,
Bob can actually see inside the train car and knows that Jim has a
flashlight (trust me). Bob sees when Jim turns his flashlight on, and
notices when the light reaches the far wall of the traincar.

He measures the distance the train traveled from the time Jim turned on
the flashlight till the time the light hit the wall and discoveres that
the light traveled 994.98 meters. Bob, knowing that the speed of light
is constant at 3.00 x 10^-8 m/sec, calculates the time it took the light
to go from Jim's flashlight to the wall of the car to be 3.317 x 10^-6
seconds.
When Jim and Bob meet back up again, they decide to compare notes. They noticed that:
- both of them measured the speed of light to be the same, even though Jim was moving in relation to Bob.
- both of them measured the time it took the light to go from the flashlight to the wall.
- since Jim measured the time it took the light to go from the flashlight to the wall to be shorter than Bob's time, Jim must have experienced the event faster than Bob; Jim's clock must have measured fewer clock ticks and so run slower than Bob's.
- Bob knew that he could find out the distance Jim's flashlight was to the wall by subtracting how far Jim's train car traveled from how far the light traveled (which he already measured to be 994.98 meters). Since Bob know's Jim was going 98% of the speed of light, or 2.940 x 10^8 m/sec, and the light traveled for 3.317 x 10^-6 seconds, the car must have traveled 975.20 meters. 994.98 - 975.20 = 19.78 meters long. Jim's length actually decreased as observed by Bob!
At this point Jim rose up in frustration, exclaiming that he's quite sure the distance was at least 5 times that measured by Bob. But what Jim failed to realize was that Bob did not observe the light hit the end of the wall at the same time Jim did. Bob noticed the light hit the wall before Jim did, thus Bob measured the car's length as shorter. Thinking quickly, Bob tried to explain this to Jim, but Jim soon became tired of playing around with train cars and got into his spaceship to explore the galaxies, thus demonstrating the Twin Paradox.
Before we derive any equations, we must understand the concept of a light clock. A light clock looks like this:

We can use it to measure time because we know that time = distance / rate. (If you went 10 miles at 20 miles per hour, it took you 0.5 hours, right?) The distance the light travels is twice the length of the clock (this clock is on end, so it's the height here) and the rate at which it travels is the speed of light. So with a light clock, time = 2Length / c (remember that c is always the speed of light, or 3 x 10^8 m/sec).
The Lorentz Time Dilation Equation

Jim is in a train car. He's looking at his light clock.

Bob can see Jim's light clock too. This is what Bob sees. Bob has his
own light clock, which disagrees with Jim's.
Let's say:
- L is the height of the light clocks
- c is the speed of light
- t is Jim's time, the time it takes for one tick of his light clock, or t = 2L/c.
- t' (read "t prime") is Bob's time, the time is takes for one tick of Bob's clock.
- v is Jim's velocity.
Let's figure out the distance the light traveled, (according to Bob), using the Pythagorean Theorem (remember a2 + b2 = c2):
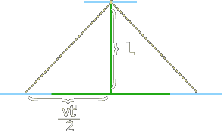
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]()
Since we can also say distance = rate x time (2 hours driving 60 miles per hour takes you 120 miles), we can say distance = ct'.
They are two
different ways of saying the same thing: ct' =
![]() . Let's work it out.
. Let's work it out.
Square both
sides: c2t´2 = 4L2 + v2t´2
Move term to the other side: c2t´2 - v2t´2
= 4L2
Factor out: t´2(c2 - v2) = 4L2
Bring term
to the other side: t´2 =
![]()
Factor out
a term on the bottom: t´2 =
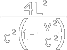
Get rid of
Squares: t´ =
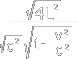
Simplify: t´
= 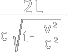
Since we know that, on a time clock, 2L/c is the time for each tick, we can replace 2L/c with t.
![]()
For each tick, t, on Jim's clock, Bob observes t' ticks on his own clock.
The Lorentz Length Contraction Equation
There are methods that use reasoning similar to the proof for the Lorentz Time Dilation Equation to prove the Length Contraction Equation. We won't look at them, but merely reason through discussion to come up with the equation for length contraction.

[ Man mano che la velocità del moto di Einstein si approssima alla velocità della luce, un osservatore fermo misura un accorciamento della lunghezza di Eistein nella direzione del moto. Questo effetto, della contrazione delle lunghezze è tanto maggiore quanto più relativistica è la velocità del moto.]
![]()
If you look at the time dilation equation (shown to the right) you can see that the bottom term (the part under the square root) approaches zero as the velocity approaches c. This means that when you divide t by that number the result gets larger and larger. What would you do if, instead of getting larger and larger, you wanted the result to get smaller and smaller? You, of course, would multiply by the term that goes to zero. The closer to zero it is, the smaller the result.
Since you know that length decreases to zero as velocity increases to c, you can reason that it decreases at the same rate the flow of time increases. This rate is what physicists call gamma. In the time dilation equation, you multiply t by gamma to get t', so t' = t(gamma). In the length contraction equation, you divide the length by gamma, so L' = L/(gamma). The equation looks like this:
![]()
Why Mass Increases with Velocity
Because it can? Not quite. Suppose Jim takes off in a spaceship leaving Bob behind. Jim has his spaceship set on constant thrust mode, so that the force of the engines pushing his spaceship forward is always the same. This makes Jim accelerate; he is always going faster and faster. But as we all know, the fastest Jim can ever go is the speed of light. So how can he always be going faster and faster?
Jim approaches the speed of light asymptotically, meaning he always is moving toward it, but never quite reaches it. His acceleration decreases the faster he goes, even though he is always accelerating. His acceleration will eventually be very small, but it will never be zero.
"But", says you, "physics tells us the Force = Mass x Acceleration, and you said Jim's spaceship's engines were always exerting the same force on the spaceship." And you are correct to point this out. Since f = ma, and f stays the same while a decreases, m, Mass, must increase. And it does. Look at the following graph:
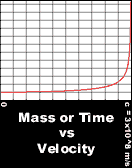 Since
Mass approaches infinity, and Jim's thrust is constant, his acceleration
will approach zero. If Jim wanted his acceleration to be constant, he
would have to increase his thrust at the same rate at which his mass was
increasing. This is very hard, since the thrust required to accelerate
him would also approach infinity.
Since
Mass approaches infinity, and Jim's thrust is constant, his acceleration
will approach zero. If Jim wanted his acceleration to be constant, he
would have to increase his thrust at the same rate at which his mass was
increasing. This is very hard, since the thrust required to accelerate
him would also approach infinity.
Adding Velocities in Relativity
In netwonian physics, you just added velocities.
For example, let's say Jim is on a train and Bob is on the side of the track. The train is going 50 miles per hour. Jim walks forward inside the train at 3 miles per hours relative to the train. In Newton's model of the universe, Bob would observe Jim moving at 53 miles per hour, because 50 + 3 = 53.
Newtonian physics breaks down at very high velocities, because if one simply added velocities, the result might very well exceed the speed of light. If the train in the previous example we moving at 75% the speed of light, and Jim walks forward at 50% the speed of light (a very rare feat indeed), Newtonian physics says he's going 125% the speed of light.
The trick is to realize that Bob see's Jim in slow motion. When Jim thinks he's running along the inside of the train at 50% the speed of light, Bob sees him as moving much slower.
Let's call
- w the velocity observed by Bob.
- u the velocity of the train.
- v the velocity of Jim walking inside the train.
- c, of course, the velocity of light.
Here's the
formula: w =
![]()
If you plug in all the numbers, you calculate that Bob sees Jim moving at 90.91% the speed of light. Of course, the difference between Newtonian physics and relativistic physics is only significant at very high velocities.
Where e=mc2 Comes From
Everyone knows the equation, but few know why it comes from relativity or how to derive it. Let's take a look at the equation for mass:
![]()
We can re-write this equation like this (replacing M' for Observed Mass and M for the mass of the object at rest):
![]()
We can expand
![]() using the binomial theorem just like we can expand (a+b)2
into a2 + 2ab + b2. As it turns out, when you
expand
using the binomial theorem just like we can expand (a+b)2
into a2 + 2ab + b2. As it turns out, when you
expand
![]() you end up with an infinite series. But the infinite series is such that
each term is less significant than the term before it. So we just need
to look at the significant parts to get an aproximation: the first two
terms. We end up with something like this:
you end up with an infinite series. But the infinite series is such that
each term is less significant than the term before it. So we just need
to look at the significant parts to get an aproximation: the first two
terms. We end up with something like this:
![]() =
= ![]()
We can put the expanded version back into our mass equation:
![]()
Distribute the
M: ![]()
A really cool
thing happened, (maybe you noticed). In physics, we use
![]() all the
time to represent the energy of a moving body. So, e =
all the
time to represent the energy of a moving body. So, e =
![]() . (Piece
of cake.) Now we can substitute it in our equation.
. (Piece
of cake.) Now we can substitute it in our equation.
![]()
You can
express the difference between something's rest mass and its observed
mass with (M' - M). We'll call this difference in mass m. The rest of
the derivation becomes obvious, and you have no other choice than to
come up with
![]() .
.
The Math Behind General Relativity
The math behind general relativity is called Einstein Field Equations. They are equations of the coupled hyperbolic-elliptic nonlinear partial differential type, which, in plain English, means that they are really, really hard. Einstein himself recognized the mathematical difficulties of general relativity as "very serious." He predicted it as being the primary hindrance of general relativity's development. The equation can be stated in a "symbolic form" that isn't very useful. Here it is:
![]()
It doesn't mean much to us, but you can see on the left of the equal sign the stuff that describes the curvature of space-time. On the right is the matter within space-time, and how it behaves.
Einstein'ın Görelilik İlkesi
Yıl 1905'e geldiğinde hiç beklenmeyen biri
fiziğin temellerini sarsamaya başladı. Bu kişi Albert Einstein'dı. İlk önce
"Hareketli Cisimlerin Elektrodinamiği Üzerine" ve daha sonra da "Özel ve
Genel Görelilik Teorisi" ile bilim tarihinde bir devrim gerçekleştirdi.
Klasik fiziğin mutlak uzay ve mutlak zaman fikri artık tarihe karıştı.
Çünkü Einstein, mutlak zaman ve mutlak uzay olamayacağını açıkça
gösterdi. Cismin hızına bağlı olarak bir mekan ve zaman yaşadığı
düşüncesini ortaya koydu. Buna göre; evrende hiçbir ayrıcalıklı hareket
yoktur, her cisim kendi hızına bağlı bir mekanda ve zamanda hayat
sürmektedir. Bunların bir sonucu olarak da mutlak referans çerçevesi,
mutlak durağanlık ve mutlak hareket kavramlarının yersiz olduğunu
belirtti. Ayrıca esir kavramının da lüzumsuz olduğunu söyledi. Esir
yoktur demiyordu. Sadece tespit edilebilir hiç bir sonucu olmayan esirin
gereksizliğini vurguluyordu.
Einstein ile değişen zaman ve mekan anlayışı, esire
duyulan gereksinimi ortadan kaldırdı. Çünkü Einstein'ın sisteminde böyle
bir hipoteze gerek yoktur. Zaten yapılan deneyler de bunu doğrulamıştır.
Einstein genel görelilik kuramının iki postulatı vardır. Bunlar:
1-) Tüm fizik yasaları tüm eylemsiz gözlem çerçevelerinde aynıdır,
değişmez.
2-) Işığın vakum (boşluk) ortamındaki hızı tüm eyelemsiz referans
sistemlerinde aynı değere sabittir. (C = 2,997 924 58x108m/s)
Birinci postulat; Newton görelilik ilkesinde bir genellenemesidir.
İkinci postulat ise gözlemcinin ışık hızını hep aynı bulacağını ışığın
cismin hareketinden bağımsız olduğunu söyler. Bu ise Galile toplama
ilkesini yanlışlar.
BÜZÜLEN UZAY-ZAMAN VE IŞIK
Genel rölativite teorisine göre ışık uzay-zamanda dosdoğru gidemez. Yıldızlar uzay-zamanı büzdüklerinden ve çok hızlı döndüklerinden çevrelerinde bir çekim alanı, elektromanyetik alan oluştururlar. Bu yıldızların yanlarından geçen başka bir yıldızın ışıkları da bu çekim arasında yollarını değiştirir, sapmalara uğrar. Bu sebeple uzayda belirli bir yerde gördüğümüz yıldızlar aslında farklı yerdedir. Çünkü biz yıldızları gözümüze gelen sapmış ışınların doğrultusunda görürüz.
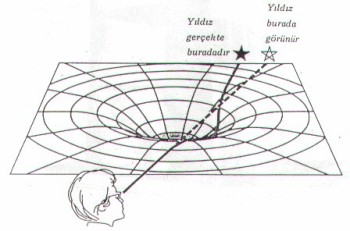
BÜZÜLEN UZAY-ZAMAN
Çekim gök cisimlerin hangi hareketinden ileri
gelmekteydi? Bu sorunun cevabı ise uzay-zamanın yapısıyla alakalıdır.
Einstein'a göre uzay, her tarafı aynı düzlemsel öklid geometrisine sahip
olmayıp tepe, çukur diyebileceğimiz mekanlar mevcuttur. Einstein'la
birleşen uzay ne zaman yine onunla katı değişmez yapısını yerine
büzüşen, çukurlaşan ve tepeleşen bir elastiki yapıya bürünmüştür. Tabi
bu Einstein dediği için değil uzay zamanın yapısının böyle olduğu
içindir. (Daha iyi bir açıklama yapılana kadar.)
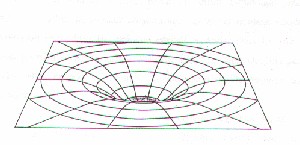
Einstein teorisine göre uzay-zamandaki bu
çukurlukların kaynağı ise gök cisimleridir. Güneş gibi büyük kütleli
cisimleri uzay-zamanı büker. Bunu açıklamak için basit bir örmek
verelim. Bir çarşafın üzerine bir bilye bıraktığımızda çarşaf üzerinde
bir büzülme olur. Buna benzer şekilde gök cisimleri sahip oldukları
kütle-enerji ve hareketlerinden dolayı uzay-zamanı büzerler. Bu sebeple
Einstein'a göre çekimi açıklamak için kuvvete gerek yoktur.
Bu teorinin savunduğu başka bir olayda büzülen mekandaki saatlerin
yavaşlamasıdır. Çok büyük kütleye sahip bir cisim bulunduğu uzay-zamanı
çukurlaştırıp bir çekim adanı alanı oluşturacağı için bu çekim alana
yakalanmış bir ışıkta yolundan sapacaktır. Bu mekanın eğriliği ne kadar
fazla ise ışık ışının bu mekandan geçmesi o ölçüde zaman alacaktır. Işık
hızı sabit aldığına göre zaman uzayacaktır. Hatta bu çekim alanının
merkezine olan uzaklıkla saatlerin yavaşlaması farklı olmalıdır.
O halde zaman büyük kütleli gök cisimleri üzerinde küçük kütleli bir
gezegene göre daha yavaş geçecektir. Örneğin güneş üzerinde zaman
dünyadakinden daha yavaş işleyecektir. Dünya yüzeyindeki saatte dünyadan
uzaklaştıkça hızlanacaktır.
RÖLATİVİTE ( GÖRELİLİK )
Kuantum kuramıyla atomun yapısı aydınlatılmaya çalışılırken, 1905 te yeni bir teori ortaya atıldı. I. Newton tarafından kurulan klasik fiziğin mikro boyutlarda yetersizliği anlaşılmıştı. Bunun yanında, cisimlerin ışık hızı mertebesindeki hareketinde de Newton fiziği bekleneni veremedi. Newton, hareketin evrende mutlak olduğunu; bulunulan yere ve zamana göre değişmediğini kabul ediyordu. Ancak, A. Einstein bunun mümkün olamayacağını; bir cismin uzaydaki durumuna göre zaman ve mekan özelliklerinin değişkenlik göstereceğini öne sürdü. Teori, farklı zamanlarda; Özel görecelik ve Genel görecelik adı altında oluşturulmuştur.
* Özel Görecelik:
Özel görecelik teorisi, 1887 yılında A. Michelson ve E. Morley tarafından gerçekleştirilen bir deneyin sonucunun yorumlanmasıyla elde edilmiştir. Deney; temelde uzay boşluğunu doldurduğu düşünülen ve J. C. Maxwell in, elektromanyetik dalgaların içinde hareket ettiğini öne sürdüğü esir maddesinin varolup olmadığını sınamak üzere gerçekleştirildi. Deneyde; Dünya nın, Güneş çevresinde döndüğü yöne gönderilen bir ışık dalgası ile bu yöne dik gönderilen ışık dalgası arasındaki faz kaymasının gözlenmesi esas alınıyordu. Herhangi bir kaymanın bulunması durumunda esirin haretinden dolayı ışık dalgalarının hızının azaldığı sonucuna varılacaktı. Fakat deney bekleneni vermemişti. Yüzlerce deneme sonunda, ışık hızının her zaman, her yerde sabit olduğu sonucuna varıldı.
A. Einstein, bu sonuçları anlamlandıran ve doğru olarak açıklayan ilk kişi oldu. Aslında asırlar önce Türk- İslam filozofu Kindi; zaman, mekan ve hareketin göreli; her cisme ve gözlemciye göre değişen yapıda olduğunu vurgulamıştı. Einstein bu düşüncelere deneysel kanıtları da katarak şu ilkeleri ortaya koydu:
* Tüm fizik yasaları, birbirine göre değişmeyen harekete sahip bütün eylemsiz gözlem çerçevelerinde ayni yazılmalıdır.
* Işığın boşluktaki hızı, kaynak ile gözlemci arasındaki göreli hareketten bağımsız olup daima sabittir.
Bu ilkeler; ışık dalgalarının hareketi için herhangi bir ortamın gerekmediğini, dolayısıyla esirin varlığına ilişkin bir varsayımın gereksiz olduğunu ortaya koydu. Böylece yüksek hızlardaki hareket ele alınırken bir tek referans noktası göz önüne alınacaktır. O da evrendeki tek sabit olan ışık hızıdır. Çünkü zaman, uzunluk ve kütle bu niceliğe göre değişmektedir. Sonuç olarak; göreli bir evrende;
1) Işık hızına yakın hareket eden nesnelerin hareket yönündeki kısalır ve kütleleri artar. Işık hızına, bir cismin ulaşması durumunda ise, bu cismin kütlesi sonsuz, uzunluğu da sıfır olur. Bu sonuçtan hareketle şu söylenebilir: Hiçbir cisim ışık ışık hızına ulaştırılamaz.
2) Işık hızına yakın bir hızla hareket eden sistemde zaman yavaş işler. Tam ışık hızına sahip bir cisim için ise zaman geçmez. Hareketli sistemdeki saat, duran saate göre;
oranında
daha yavaş çalışır.
3) Maddenin, hızlandırıldıkça kütlesinin artması; kütle ile enerji arasında yeni bir bağıntının doğmasına yol açmıştır.
E=mc2
İle verilen denklem, maddenin enerjiyle eşdeğer olduğunu ve çok küçük bir kütleden fazlasıyla enerji elde edilebileceğini göstermiştir. Atom bombalarının yapımı ve nükleer reaktörlerin çalışması bu sayede açıklanabilir.
* Genel Görelilik:
Özel görelilik, birbirine göre ivmesiz bulunan sistemler için geçerlidir. Ancak evrende ivmesiz hareket eden pek az şey vardır. Bu yüzden, A. Einstein daha genel bir teori olarak genel göreliliği 1916 da oluşturmuştur. Bu yaklaşımda da Einstein, klasik fizikte Newton tarafından kurulan yerçekimi ifadesinin yetersizliğine dikkat çekmiştir.
Fiziksel olarak, bir cismin uzayda ivmelenmesiyle onun üzerine bir yerçekimi ivmesinin etki etmesi birbirinden ayırdedilemez durumdur. Einstein; bu durumda, eğer bunları birbirinden ayıramıyorsak o halde bu etkiler birbirinin ayni olmalıdır şeklinde düşünerek bir cismin eylemsizlik kütlesiyle yerçekimi kütlesinin birbirine eşit olduğunu öne sürmüştür. Bu durumda genel göreliliğin ilkelerini şöyle belirlemiştir:
1- Fizik yasaları, eylemsiz yada ivmeli bir gözlem çerçevesinde aynıdır.
2- Sabit bir yerçekimi alanında eylemsiz referanz çerçevesi ile ivmeli bir referans çerçevesini birbirinden ayırmak imkansızdır.
Einstein, bu ilkelerden hareketle, evrenin uzay - zaman boyutunun her ikisiyle incelenmesi gerektiğini belirtmiştir. Böyle bir evren, Öklit geometrisinden uzak olup ancak Riemann geometrisiyle açıklanabilir. Uzay, içine boylu boyunca gerilmiş ağ gibi bir yapıya sahiptir ve Güneş gibi büyük kütleli cisimler bu ağda eğrilikler meydana getirir. İşte gezegenler de, bu eğriliğin etkisiyle yıldızların çevresinde dolanırlar. Bu eğri alan yalnızca fiziksel bir çukur olmaktan uzak olup eğriliğin miktarı arttıkça oradaki zamanın da daha yavaş işlemesine neden olur. Hatta bu eğrilikler ışığı da bükecek niteliktedir. Güneşin yakınından geçecek şekilde, çok uzak yıldızlardan gelen ışınların Güneşimiz tarafından eğriltildiği gözlenmiştir. Yine, Merkür gezegeninin günberi noktasının değişkenlik göstermesi ancak bu kuramla açıklanabilmiştir.
UZUNLUĞUN GÖRELİLİĞİ
Mutlak olmayan zaman ve mekanda uzunluklarda mutlak değildir. Uzunlukta
bulunduğu sisteme bağlıdır. Farklı referans sistemindeki gözlemciler
uzunluk için farklı değerler tespit ederler.
Bir nesnenin durgun bir çerçeveye göre ölçülen uzunluğuna has uzunluk
denir. Durgun sisteme göre değişmeyen bir hızla hareket eden sistemden
bakan gözlemci ölçümü has uzunluktan daha kısa olacaktır.
Uzunluktaki büzülelmeye aşağıdaki örnekleri verebiliriz.
%50 ışık hızıyla giderse %14,
%90 ışık hızıyla giderse %45,
%99 ışık hızıyla giderse %86 kısalacaktır.
Rölativistik olmayan hızlarda da bir kısalma olur fakat bu ihmal
edilebilecek kadar azdır. Örneğin saatte 80km hızla giden bir otomobil
tampondan tampona bir atom çekirdeği çapı kadar küçülür. Saatte 1000km
hızla giden bir jet uçağı ise bir atomun çapı kadar boyundan küçülür. Bu
nedenle ki bunları gözlemleyebilmek imkansızdır.
KÜTLENİN GÖRELİLİĞİ
Rölativite Teorisi'ne göre bir cismin hızı arttıkça kütlesi de
1/ ( 1 -V2/c2
)1/2
çarpanı kadar artar.
Klasik fiziğe göre cisimlerin kütlesi değişmez. Oysa rölativiteye göre
kütle hıza bağlıdır. Hız arttıkça kütlede artar. Uzunluk kısalmasında
olduğu gibi kütle artışı da rölativistik hızlarda geçerlidir.
Durgun haldeki bir cismin kütlesine durgun kütle denir. Durgun kütle
hızına bağlı olarak artar. Örneğin bir uzay gemisiyle ışık hızının %80'i
kadar hız yapan bir astronotun durgun kütlesi 70 kilogram ise
rölativistik kütlesi ; 116 kg olarak ölçecekti.
Durgun bir sistemdeki bir gözlemci astronotun yolculuk sırasındaki
kütlesini ölçebilseydi 116kg hesaplayacaktı. Fakat astronotumuz kendi
kütlesini ölçseydi yine 70 kg hesaplardı. Yani hareketli çerçevedeki
ölçümlerde kütle durgun kütleye eşit olur.
KÜTLE VE ENERJİNİN
EŞDEĞERLİĞİ
Klasik mekanikte iki cevher vardır. Kütle ve enerji. Yine klasik fizikte
iki korunum yasası mevcuttur. Maddenin korunumu kanunu ve enerjinin
korunumu kanunu. Fakat Einsten'in Rölativite teorisine göre kütle
enerjinin yoğunlaşmış bir halidir
(E=mc2)
. Buna göre klasik fizikteki görüşün aksine enerjinin de bir kütlesi
vardır. Modern fizikte iki yasasının yerine yalnız bir korunum yasası
vardır. Madde-Enerjinin korunumu. Bu deneylerle de ispatlanmıştır.

Burada önemli bir noktada çok az bir kütlenin çok yüksek miktarda
enerjiye eşdeğer olmasıdır. Bir maddenin tüm kütlesi enerjiye
dönüştürülebilirse elde edilen enerji
E=mc2
ile bulunur. Bu formüle göre 1 gram kütledeki enerji 1000watt'lık ampulü
2850 yıl yakar. Bu aynı zamanda 2000 ton yakılmasından elde edilecek
enerjiye denk gelir.
Normalde kömür, odun, gaz yakıtların yanması basit kimyasal olaylardan
ibarettir. Maddenin büyük bir kısmı enerjiye dönüşmeyip kısa dönüşümler
neticesinde enerji açığa çıkar.
İkinci Dünya Savaşı'nda Japonya'nın Hiroşima ve Nagazaki şehirlerini
yerle bir eden atom bombaları E=mc2 bağıntısının doğruluğunu çok acı bir
şekilde göstermiştir.
IŞIK HIZINA NİÇİN ULAŞILAMAZ ?
Bilindiği üzere cisimlerin boyu L =Lo ( 1 -V2/c2 )1/2 formülü ile kısalmaktadır. Eğer V=c olursa L = 0 olur. L'nin sıfır olması demek cismin kaybolması demektir. Ayrıca cisimlerin kütleleri m= mo / ( 1 -V2/c2 )1/2 formülüne göre artmaktadır. Hız arttıkça kütle artmaktadır. Hızlanma ile kütle artışı ters orantılıdır. Yani küçük hızlardan hızlanmaya başlayan bir cismin kütle artışı azdır. Cisim hızlandıkça hızlanma hızı yavaşlar, kütle artış hızı artar. Çünkü kütle arttıkça bu kütleyi hızlandırmak zorlaşır. Hız 299.000 km/s yükseldiğinde artık bundan sonra yapılacak itmelerin cisme vereceği enerjinin hemen hemen tümü kütleye pek az bir kısmı da hızda artışa neden olur. Bu rölativistik olmayan hızlardaki sürecin tam tersidir.
Hızını 299.792,5 km/sn yaklaştığında verilen kuvvet enerjisinin tümünden sağlanan enerji kütle artışına aktarılır. Hızı arttırmaya bir şey kalmaz. 299.792,5 km/s lik hıza ulaşabilseydik başlangıçta V=0 da belirli bir kütleye sahip olan bir cisim bu hızda hareket ederken kütlesi sonsuz olurdu. Bundan sonra hangi kuvveti uygularsak, hangi itmeyi verirsek verelim sonsuz kütleli bir cismin hızını değiştiremeyiz. Bu sebepledir ki rölativite teorisine göre belirli bir kütlesi olan herhangi bir cismin ışık hızına eşit veya daha büyük bir hıza kadar hızlanması imkansızdır.
İKİZLER PARADOKSU
Bir düşünce deneyi yapalım. 25 yaşında olan bir
astronotumuzu ışığın %95'ine erişen bir rokete bindirerek 25 ışık yılı
uzakta olan bir yıldıza gitsin. Giderken dünyada 25 yaşında ikiz
kardeşini 22 yaşında karısını ve 2 yaşında çocuğunu bıraksın. Acaba 20
ışık yılı uzaktaki yıldızdan geldiğinde evinde neyle karşılaşır?
Astronotumuz 95/100 c lik bir hızla yolculuk
yaptığı için zamanı yavaşlayacaktır. Fakat o bunu hissetmeyecektir. Bu
yavaşlamanın ise yaklaşık 15 yıla karşılık gelmektedir.
Yani normalde dünyada 50 yıl geçerken astronotumuz için 15 yıl
geçmiştir. Yani 40 yaşında olacaktır. İkizi ise 75, eşi 72 ve 52 yaşında
olur. Çocuk babasından tez yaşlanmıştır.
Burada şu soru sorulabilir; "İkizlerimizden hangisi ışık hızına yakın
bir hızla yolculuk yapmış ve neden yaşlanmayan kişi olmuştur." Buradaki
problem ikizlerimizin bağıl hareketinde yatmaktadır. Evde kalan
ikizimize göre kardeşi çok hızlı bir şekilde dünyadan uzaklaşmaktadır.
Roket içindeki astronotumuzu referans noktası olarak alırsak kendisi
durgundur , ailesi ve kardeşi ondan uzaklaşmaktadır. Bu durumda hangi
ikizimizin yaşlandığı çelişkisi ortay çıkar. Bu çelişki ikizler
paradoksu olarak bilinir.
Paradoksun çözümü ile hareketlerin aynı olmadığını anlamakta yatar.
Astronot olan ikizimiz uzaydaki yolculuğu boyunca hızlanma ve yavaşlama
hareketi yapmış olmalıdır. Bu sebeple eylemsiz bir sistem olamaz. Bu
sebeple de (eylemsiz olduğu için) özel göreliliğe dayanan düşüncelerimiz
onun sisteminde geçerli olmazlar. Dünyada kalan ikizimiz eylemsiz bir
sistemde bulunduğu için görelilik hakkında doğru tespitler yapabilir.
Buna göre astronotumuz yolculuğunu bitirip evine döndüğünde normale göre
aha genç olacaktır.
GRAVİTASON VE İVME
Einstein'ın ikinci devrimi genel göreliliktir.
Özel görelilikten bahsederken hep sabit hızlı eylemsiz hareketten
bahsettik. Hareket olayının özel bir durumunu inceledik. Bu yüzden
eylemsiz sistemlerdeki rölativitistik incelememize özel görelilik
teorisi adı verilir. Halbuki etrafımızda olan olayların hemen hemen
hepsinde ivme vardır. İvme, taşın düşmesinde, arabanın hızlanmasında,
dünyanın güneş etrafında dönmesi vb. her yerde vardır. Einstein özel
görelilikten sonra 1905'ten 1915'e kadar uğraşarak daha genel bir kuram
oluşturdu. Bu bölümde genel görelilik teorisine değineceğiz.
Düzgün olmayan hareketi incelemek sabit hızlı
hareketi incelemekten her zaman zordur. İşin içine ivme girince işler
biraz karışır. Sabit hızlı hareket eden sistemlerde dışarıda konumu
değişmeyen bir noktaya bakmadan hareket hissedilmez. Newton hareket
yasalarında ivmeli durumları da incelenmiştir ama ivme üzerinde
gerektiği ölçüde durmamıştır. Buda kütle ile ivme arasındaki küçük bir
paradokstan iler gelir.
Newton kendi sistemini kurarken kendisine bırakılan geometrik mirası
kullandı. Buda Öklid geometrisidir. Maddeler arasındaki etkileşmeler hep
öklid geometrisine sahip olduğu düşünülen bir yüzey içinde düşünülmüş ve
formüle edilmeye çalışıldı. Bunda da başarılı olundu. Sonuçta karşımıza
Newton mekaniği çıktı. Newton mekaniği fiziksel olayları açıklamada çok
başarılı oldu. Ufak gibi görünen sorunlar yok değildi, ama bunlarda
muhakkak bir yöntem ile bir gün açıklanabilecekti.
Newton'un eksikliklerinden biride ivmeye gereken önemi vermeyip çekim
üzerinde yoğunlaşmasıdır. Newton'a göre serbest bırakılan taşın yere
düşmesi, dünyamızın ve diğer gezegenlerin güneş etrafında dolanmalarının
sebebi maddesel çekim, gravitasyon kuvvetidir. Bu kuvvet bilindiği üzere
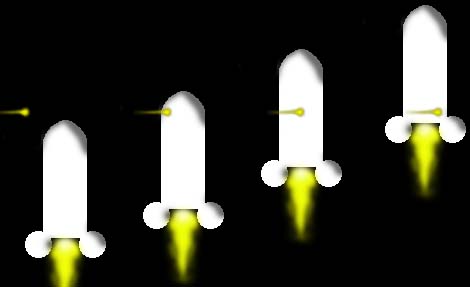
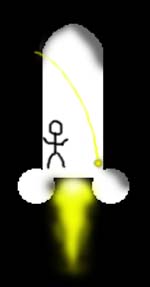
Einstein'a göre bizim gravitasyon adını verdiğimiz şey kaynağı gök
cisimlerin içinde saklı olan bir güç olmayıp, maddelerin hareketinden
ileri gelmektedir. Bu durumda özel bir asansör ile açıklanmaktadır.
Şimdi Einstein'ın bu örneğine değinelim.
* Uzay boşluğunda kalın bir ip ile yukarı doğru ölçülen bir asansör
düşünelim.
*Asansörün içindekiler ne asansörün içinde olduklarını ve ne de
yukarı doğru çekildiklerini bilmesinler. Dışarıyı da görmesinler.
* Asansör hızla yukarı doğru çekildiği için içindekiler asansörün
tabanına doğru çekiliyormuş hissine sahip olacaktırlar. İçlerinden biri
cebinden bir kalem çıkartıp serbest bıraksın. Kalem ivmeli hareket eden
asansörün etkisi yüzünden yere düştüğünde olay taban tarafından çekilme
şeklinde yorumlanacaktır.
* Şimdi ise dışarıdan birinin bu asansöre ateş ettiğini düşünelim.
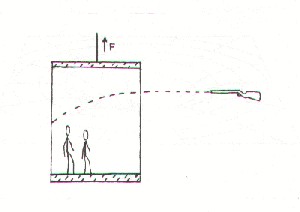
* Tüfekten çıkan kurşun asansör
yukarı doğru çekildiği için bir eğri çizerek şekildeki gibi karşıdaki
duvara saplansın. (Asansör içindeki gözlemcilerimizin boyu yeterli kadar
kısadır.)
* Asansörün içindekiler merminin giriş deliği ile karşı duvarda
saplandığı yerin yüksekliklerinin aynı olmadıklarını gördüklerinde, bunu
da çekime yoracaklardır. Merminin bu çekimden dolayı eğri çizdiğini
söyleyeceklerdir.
İşte Einstein'a göre çekim, gravitasyon dediğimiz şeyin kaynağı
harekettir. Einstein'a göre gök cisimlerinde çekim adına verdiğimiz şey
yine gök cisimlerin hareketinden ileri gelmektedir.
E
Ş ZAMANLILIK Klasik mekanikte bütün fiziksel olaylar tüm gözlem
çerçeveleri için aynı olan mutlak bir zaman vardır. Yani zaman herkes ve
her şey için değişmez hızda akar. Olayın cereyan ettiği konum, hız ne
olursa olsun zaman akışı değişmez. 1snlik zaman aralığı herkes için
aynıdır. Buna fizikte eşzamanlılık denir. Newton postulatlarından biride
budur. Lakin Einstein özel rölativite kuramında bunun yanlış olduğunu
gösterdi. Eintein'a göre zamanın akışı ölçümün yapıldığı referans
sistemine bağlıdır. Referans sisteminin konumu ve hızından etkilenir.
Bunu daha iyi anlamak Einstein'ın tasarladığı
düşünce deneyine değinelim.
* A noktasından B noktasına doğru hızla hareket eden bir tren
düşünelim.
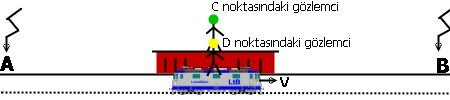
*Trenin üstünde tam
orta noktada bir gözlemcimiz olsun. Bu gözlemciA ve B noktalarında
meydana gelen olayları aynı anda görebilir nitelikte olduğunu kabul
edelim.
* A ve B noktalarının tam ortasındaki bir C noktasındaki bir istasyon
ve bu istasyonda da bir gözlemci olsun. Bu gözlemcide aynı şekilde A ve
B noktalarındaki olayları aynı anda gözlemleyebilsin.
* Trenimiz A noktasından B noktasına giderken saat tam 13.00 de C
istasyonundan geçiyor olsun.
* Tam saat 13.00 tren C istasyonundan geçerken A ve B noktalarına aynı
anda birer yıldırım düşsün.
* C istasyonundaki gözlemci sorumuza şu cevabı verir: "Saat tam 13.00
da A ve B noktalarına birer yıldırım düştü."
* Şimdi trenin tam ortasında bulunan C noktasındaki gözlemcinin
sorumuza verdiği cevaba bakalım.
* Saat tam 13.00 trenin gidiş yönü olan B noktasına bir yıldırım
düştü. Bundan biraz sonra ise trenin geliş noktası olan A noktasına bir
yıldırım düştü.
* Bu cevap bizi şaşırtmamalıdır. Çünkü tren A noktasından hızla
uzaklaşmaktadır. A noktasına düşen yıldırımın ışığı tren A noktasından
hızla uzaklaştığı için trenin üstündeki gözlemciye B noktasından gelen
yıldırımın ışığından biraz geç gelecektir. Bu sebeple trenin üzerindeki
gözlemci önce B noktasına düşen yıldırımı ondan bir iki salise sonra A
noktasına düşen yıldırımı görecektir.
* Acaba trenimiz ışık hızıyla yol alsaydı. Tren üzerindeki gözlemcimiz
bu yeni soruya nasıl cevap verirdi.
* Trenimiz ışık hızıyla yol alırken aynı olay vuku bulduğunda A
noktasına düşen yıldırımın ışık ışınlarını ışık hızıyla ilerlediği halde
ışık hızıyla hareket eden trenimize yetişemez. Bu durumda tren üstündeki
gözlemci şu cevabı verir.
" Saat tam 13.00 da B noktasına bir yıldırım düştü. A noktasına ise
hiç yıldırım düşmedi."
Aslında A ve B noktalarına yıldırım düşmüştür. Lakin gözlemcinin
konumu, hızından dolayı olayları farklı değerlendirebilmektedirler. Her
iki gözlemci de kendi referans sisteminde haklıdır. Çünkü görelilik
ilkesi tercihli bir eylemsizlik referans sisteminin bulunmadığını
söyler.
Ortaokul velisede okuduğumuz fizik derslerinde EINSTEIN'in Rölative(izafiyet) teorisini bir türlü anlayamamışızdır. İçimizde hep "Yav bu adam neyi bulmuş, bu kadar büyütülecek ne var" dediğimizi halen duyar gibiyim. Şimdi ben size bu teoriyi basite indirgenmiş örneklerle anlatmaya çalışacağım.
Neyse, şimdi bir uçakla saatte 800 km hızla uçtuğunuzu düşünün. Başka bir uçakta size doğru yine 800 km hızla yaklaşmakta olsun. Sizce ne kadar zaman içinde birbirinize yaklaşırsınız? Diğer bir deyimle rölatif hızınız nedir? Mantığınıza göre cevap 1600 dur.
Şimdi de bir uzay gemisinde, ışık hızının 4 te 3 u kadar bir hızla uzak bir yıldıza seyehat ettiğinizi düşünün. Sizce bu yıldızdan ışık size ne kadar hızla geliyor? Yine mantığınız size 4 te 3 ışık hızıyla geldiğini söyler, fakat ölçecek olursanız, size o uzak yıldızdan gelen ışık, yine saatte 300.000 km dir. Buna göre ışık hızı, kaynağı ve yönü ne olursa olsun değişmez. Buda seyehat hızı arttıkca zamanın geçişinin yavaşladığını açıklar.
Bu uzay gemisinde dünyaya dönüşünüzde, hızınız ışık hızına yaklaştıkca, uzay geminizde saatiniz sadece birkaç ayın geçtiğini gösterdiği halde, dünya zamanı ile yılların geçtiğini görürsünüz. Çocuklarınızdan da genç dünyaya dönersiniz.
Şimdi size rölative teorisinin insanlığa neler kazandırdığını yüzeysel olarak anlatmaya çalışacağım.
Bu görüşün özelliği 4 boyutlu olmasıdır. Bu 4.boyut zaman boyutudur (Einstein bu boyuta uzay-zaman boyutu adını vermiştir).Uzay-zaman boyutu, çekim kuvvetiyle ilgili teorileri değiştirdi. Bu teori, yerçekiminin okullarda öğrendiğimiz gibi iki madde arasında çekim kuvveti olduğu inancını yıktı.Yerçekimi yeni keşfedilen 4.boyutun uzay zamanı ile mekan-zaman boyutunun kavramı içindedir. Tabii siz bu şekilde anlamadınız. Size basit bir örnekle yardımcı olayım.
Yatay kaucuk bir yatak düşünün.Yatağın üzerine değişik ağırlıklarda ve boyutlarda toplar koyun.Toplar büyüklük ve ağırlıklarına göre kaucuk yatağa gömüleceklerdir.Yatağın kenarından küçük bir top yuvarlayın.Top diğer toplara doğru çekilecektir. İşte bu çekim rölative teorisinin temelidir. Madde, uzay zamanı kaymasına neden olur, uzay zamanı da maddenin hareketini tayin eder.
Genellikle uzay zamanı düzdür, fakat büyük kütlelere yaklaştıkça eğim kazanır.Bu eğim, sadece küçük kütlelerin hareketini etkilemekle kalmaz zamana da etki eder. Diğer bir deyimle çekim kuvvetti zamanı yavaşlatır.
Bir örnek daha:
Tamamıyla birbirine eş ayarlanmış çok hassas iki saat alın. Birini, çok yüksek bir binanın en alt katına,diğerini en üst katına koyun. Üst kattaki saatin biraz yavaşladığını göreceksiniz.Çünkü,üst kattaki uzay zamanı, çekimden dolayı daha eğimlidir.
ÖZEL RÖLATİVİTEYİ DOĞRULAMALAR
a)
Hızlandırılmış yüklü taneciklerin kütlesi
m(V)= mo / ( 1 -V2/c2
)1/2
formülü gereğince artacağından elektrik ve magnetik alandaki sapmaları
daha az olacaktır. Macken 1935 yılında voltajı 200.000'e varan bir tüpte
daha öncekilerden daha hassas bir deneme yaptı. Bu durumda elektronlar
210.000 km/s lik bir hıza eriştiklerinden kütleleri %40 arttı. Deney
sonuçları kütlenin göreliliğini açık bir şekilde destekliyordu.
b)
Çok eski çağlardan beri
temel toz cevher arandı. Kimya biliminin doğmasıyla bu cevherin Hidrojen
olduğu düşünüldü. Çünkü cisimlerin en hafifi hidrojenden 1gr alalım.
Diğer maddeler karbon 12gr,azot 14gr,oksijen 16gr,kükürt 32gr bunlar
hidrojenin tam katlarıydı. O halde bir cismin her bir atomu hidrojen
atomlarının birleşimi olduğu düşünüldü. Böylece yüzyıllardır aranan,
bütün evrenin temel harcı hidrojendi.
Bu hipotez daha sonra yapılan hassas deneylerle bazı cins maddelerin
atom ağırlıklarının hidrojeninkinin tam katı olmadığı ortaya çıktı. (Cl=35.5gr.
Mg=24.3gr.) Bunun üzerine savunulan hipotezden vazgeçildi. Daha sonra
yapılan daha hassas çalışmalar hidrojenin atom ağırlığı 1gr alındığında
hiç bir cismin atom ağırlığının tam olamayacağını gösterdi. Örneğin
oksijen için 16 ve karbon için 12 lik değeri %1 den çok daha
yaklaşıktır. Eğer oksijen birim alırsam ve oksijen=6 seçersek
hidrojen=1.008g olmak zorundadır. Böylece maddenin birliği fikri tamamen
ortadan kalkmış oluyordu.
Rölativistik hesaplar maddelerin birliğinin tekrar kurdu. Buna göre
hidrojen atomlarının yoğunlaşması sırasında bir ışınım yayınlanır. Faklı
cisimlerinin atom ağırlıklarındaki fark buradan ileri gelmektedir. On
altı atom hidrojen, bir atom oksijen oluşturmak için birleşirken toplam
kütlenin 8/1000'ini kaybetmektedir. Yani tekrar hidrojen yığınlarını
oluşturmak için bu kayıp enerjiyi vermemiz gerekir. Atom çekirdeklerinin
çok sağlam olmasının bir sebebi de budur.
c)
Rölativitenin açıklık getirdiği diğer bir olay güneşin ışınım kaynağının
tespitidir. O zaman ne kadar karbon-oksijen ne de radyoaktif kaynaklı
bir güneş bizi milyonlarca sene ısıtabilir. Peki neydi bizi neydi bizi
besleyen bu esrarlı kaynak ?
Einstein'ın maddenin enerjiden başka bir şey olmadığını söylemesi ile bu
soruda kabaca aydınlığa kavuştu. Maddenin tek bir gramının bile enerjiye
dönüşmesi korkunç bir enerjiye sebep oluyordu. Güneş'te her saniyede 4
milyon ton hidrojen 2 milyon ton helyuma dönüşüyor. Aradaki enerji farkı
ise bizim yeryüzünde yaşamamızı sağlıyor. Güneşte bir yıldız olduğu için
bu dediklerimiz bütün yıldızlar için geçerlidir. Kütlerinden sürekli
kaybederek etrafı aydınlatırlar. Deminde dediğimiz gibi bu kütlenin yok
olmasıyla değil dönüşümü sırasındaki enerji atımından kaynaklanmaktadır.
Şimdiki bilgimizle maddenin tamamen enerjiye dönüşebildiğini sanmak
saflık olur.
d)
20. Yüzyılda fizikteki
ikinci devrim kuantum teorisidir. Kuantum ve Rölativite hep birbirini
destekler mahiyettedir. Zaten kuantumların dünyasında düşük hızla
dolayısıyla klasik mekaniğin yaslarına yer yoktur. Burada biz sadece
pozitron ve müonlardan bahsetmekle yetineceğiz.
e )
Rölativite teorisine göre bir elektronun durgun kütle enerjisi:
E= moc2
/ ( 1 -V2/c2 )1/2
Bilindiği üzere bir kare kök için + ve - değerler alınabilir. Yani
elektronun durgun kütle enerjisi :
E= moc2
/ ( 1 -V2/c2 )1/2 ve E= - moc2
/ ( 1 -V2/c2 )1/2
yani
iki çözüm mevcuttur.
Pozitif işaretli enerji elektron içindi. Peki ya negatif enerji ne
demekti ? Bunun bir mana ifade edebileceğini düşünen İngiliz fizikçi
Dirac oldu. Bu negatif enerjili halleri araştırmaya başladı. Dirac 1929
yılında bu negatif enerjili elektronun (anti-elektron) teorik keşfini
gerçekleştirdi. Pozitron olarak da adlandırılan bu parçacıklar varlık
sahnesine 1933'te çıktı. Anderson kozmik ışınlar sayesinde pozitronların
gerçek olduğunu ispatladı. Bu ise teorilerimizi deneye uydurmaktan çok
öte bir şeydir. Bu rölativitenin evreni açıklamasındaki büyük
başarılarından biridir.
f)
Zamanın göreli olduğu
deneylerle gösterilmiştir. Örneğin müonlar uzaydan gelen kozmik
ışınların atmosferin yukarı katmanlarında soğurulması sonucu
oluşabilirler. Müonların kendisine yani durgun bir sisteme göre ömürleri
2,2.10-6 saniyedir. Müonlar kararsız yapılarından dolayı hemen
bozunurlar. Bozunmadan kendi sistemlerine göre c ışık hızıyla 600m'lik
yol gidebilirler. Bu sebeple de yere ulaşamazlar. Fakat deneylerde çok
sayıda müonun yere ulaştığını göstermiştir. Bu durum ise rölativitenin
zaman genişlemesi ile açıklanır. Yerdeki bir gözlemciye göre müonların
ömrü T/ ( 1 -V2/c2
)1/2 sn dir. T 2,2.10-6 sn
olduğuna göre ve
müonların hızı da yaklaşık V=0,99c olduğu için yerdeki bir gözlemciye
göre müonların ömrü yaklaşık 16.10-6 s dir. Bu sebeple yerdeki
gözlemciye göre müonların aldıkları yol 4800m'dir.
1976 da İsviçre'nin Genova şehrinde CERN Laboratuvarında müonlarla
ilgili deneyler yapıldı. Müonlar 0,994C'lik hızlara ulaştırılarak
toroide gönderildi. Müonların bozunmasıyla oluşan elektronlar toroid
etrafındaki detektörlerle incelendi. Bu inceleme sonucunda % 2'lik hata
ile hareketli müonların ömrü durgun müonlarınkinden 30 kez daha uzun
olarak ölçüldü(Hareketli müonlar daha geç yaşlandı ve daha geç öldü.
Aynı ışık hızına yakın bir hızda uzayda seyahat yapan ikizimiz gibi ).
Bu da rölativite ile tam bir uyum içindedir.
g)
Maxwell - Lorentz'in elektromagnetik teorisini destekleyen bütün
deneylerde rölativiteyi destekler. Zaten rölativite Maxwell - Lorentz
kuramlarından doğmuştur.
h)
Rölativitenin sonuçlarının en acı veren kanıtı ise atom bombasıdır.
Einstein ünlü
E=mc2
formülüne, enerjinin
kütleye kütlenin enerjiye dönüşümü ilkesine dayanan biri uranyum-235
diğeri plütonyumdan olan iki atom bombası Japonya'nın iki şehrini yerle
bir ederken 120.000 kişinin ölümüne sebep olmuştur.
GENEL RÖLATİVİTENİN DENEYLERLE DOĞRULANMASI
Einstein teorilerinin doğru olup olmadığını
sınayacak deneyler önerdi. Kendisinin düşüncelerinin doğruluğundan bir
şüphesi yoktu. Ama insanların haklı şüphelerini izole etmek şarttı. Buda
en iyi teorilerin deneyle doğrulanması ile olabilirdi.
Bu aynı zamanda bilimin metodunda bir yenilik arz ediyordu. Çünkü
bilim adamları deneyler yapar bu deney sonuçlarına göre olguları
açıklayacak kuramlar oluştururlar. Einstein ise matematiksel ve felsefi
çalışmaları sonucu oluşturduğu teorilerini sunuyor ve düşünceleri
yanlışsa, bunu kesin olarak yanlışlayacak deneyler öneriyordu.
Einstein'ın teorileri için normal tümevarım yerine tümdengelim metodu
işliyordu. Bu fikirler bilim felsefesine Popper'in yanlışlamacılık
metodu olarak geçecekti.
Genel görelilik kuramının doğru olup olmadığını anlamak için yapılan
deneylerde hep Einstein haklı çıktı. Şimdi Einstein'ı haklı çıkaran
olaylara değinelim.
2 - Einstein'ın önerdiği deneylerden biride, güneşin yakınından geçen bir yıldız ışıklarının sapmalarının güneş tutulmasında tespit edilmesiydi. Einstein genel görelilik kuramından güneş bu sapmayı 1,75 saniyelik bir açı olarak hesaplamıştı. 1919 yılındaki güneş tutulmasını tam olarak gözlemlemek için Güney Amerika'ya ve Afrika'nın batısındaki Principle adalarına gidildi. Arthur Edington ve Crommlin tarafından tam güneş tutulması sırasında yapılan gözlemlerde yıldızın 1,64 saniyelik açı farkı ile belirtilen yerde gözlemlendi. Daha sonraki güneş tutulmalarında Einstein'ın hesaplarına daha yaklaşık sonuçlar tespit edildi.
3 - Işık ışınlarının eğrilmesi ve yavaşlamasıyla Mariner 6 ve 7 serbest uzay araçlarıyla yapılan bir deneylerle de kanıtlanmıştır. Uzay araçları Mars dönüşünde güneşin etrafını dolanırken Dünya'dan araçlara gönderilen radyo sinyallerinin gidiş ve geliş süresi 200 mikro saniye uzamıştır. Bu sonuçlarda rölativite teorisini destekler mahiyettedir.

4 -
Çekim alanın zamanı akışını etkilemesini doğrulayan diğer bir deney 1960
yılında gerçekleştirildi. Deney çok yüksek bir binada yapıldı. Genel
rölativite teorisine göre binanın zemin katındaki saat en üst kattaki
saate göre daha yavaş çalışır. Zemin yeryüzünün merkezine (yani
uzay-zaman eğriliğinin çok olduğu noktaya) daha yakın olduğundan zaman
çok az bile olsa zaman daha yavaş akmaktadır. Hassas aletlerle yapılan
deneyde bu fark tespit edilmiştir.
Rölativite teorisini yanlışlama deneyleri %1'den daha küçük hata
oranına sahiptir. Buda rölativite teorisini büyük oranlarda
desteklemektedir. Rölativite teorisi mana ve matematiksel olarak
basitliği ve yalınlığı ile bilimin doğasına daha yakın daha anlamlıdır.
Rölativite astrofizikte, evren anlayışımız yeni bir kapı aştı. Uzay
hakkındaki düşüncelerimizin baştan sona değişmesine neden oldu.
Günümüzde rölativite kozmolojisinin bir ürünü olan kara delikler
popülaritesini sürekli artırmaktadır.
Special Relativity - SWF Animation Files - SWF Flash Dosyası
1- Einstein Train -Time Dilation and light clock
2- Gözlemcilere göre
hareket eden trendeki saatlerin göreli hızları

3- İkizler paradoksu - Twins Paradox

4- Gravitasyon ve ivmenin eşdeğerliliği
5- Light Clock
Unified Field Theory
 |
 |
1- Unified Field Theory (1 Dec 2002)
2- Deducing a Unified Field Theory from Electromagnetism
3- Unified Theory: All the major forces from gravity to magnetism, from weak to strong force are explained in such a way as to show they are really extensions of the same phenomenon.
H
içbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana
Sayfa / İndex
/ Ziyaretçi
Defteri / ![]() E-Mail / Kuantum
Fiziği / Quantum
Teleportation-2
E-Mail / Kuantum
Fiziği / Quantum
Teleportation-2
Time Travel Technology / Kuantum Teleportation / Duyuru / UFO Technology