Relativity :
|
Einstein's theory of relativity deals with Newtonian physics when energies or velocities are near the speed of light. Relativity is usually thought of as modern physics since it was developed at the start of the 20th century and could only be tested in the realm available to scientists by high technology. However, relativity primarily completes the revolution that Newton started and is also highly deterministic as is much of classical physics. |
Relativity :
Relativity, in physics, the problem of whether and how physical laws and measurements change when considered by observers in various states of motion. Specifically the term appears in the work of the German physicist Albert Einstein, whose special theory of relativity (1905) and general theory of relativity (1916) are major milestones in the history of modern physics.
|
In the holistic viewpoint of
relativity theory, concepts such as length, mass and time take on a much
more nebulous aspect than they do in the apparently rigid reality of our
everyday world. However, what relativity takes away with one hand, it
gives back in the form of new and truly fundamental constants and
concepts.
The theory of relativity is traditionally broken into two parts, special and general relativity. Special relativity provides a framework for translating physical events and laws into forms appropriate for any inertial frame of reference. General relativity addresses the problem of accelerated motion and gravity. |
Special Theory of Relativity :
|
By the late 1800's, it was becoming
obvious that there were some serious problems for Newtonian physics
concerning the need for absolute space and time when referring to events
or interactions (frames of reference). In particular, the newly
formulated theory of electromagnetic waves required that light
propagation occur in a medium.
In a Newtonian Universe, there should be no difference in space or time regardless of where you are or how fast you are moving. In all places, a meter is a meter and a second is a second. And you should be able to travel as fast as you want, with enough acceleration. In the 1890's, two physicists (Michelson and Morley) were attempting to measure the Earth's velocity around the Sun with respect to Newtonian Absolute space and time. This would also test how light waves propagated since all waves must move through a medium. For light, this medium was called the aether. The results of the Michelson-Morley experiment was that the velocity of light was constant regardless of how the experiment was tilted with respect to the Earth's motion. This implied that there was no aether and, thus, no absolute space. Thus, objects, or coordinate systems, moving with constant velocity (called inertial frames) were relative only to themselves. In Newtonian mechanics, quantities such as speed and distance may be transformed from one frame of reference to another, provided that the frames are in uniform motion (i.e. not accelerating). |
|
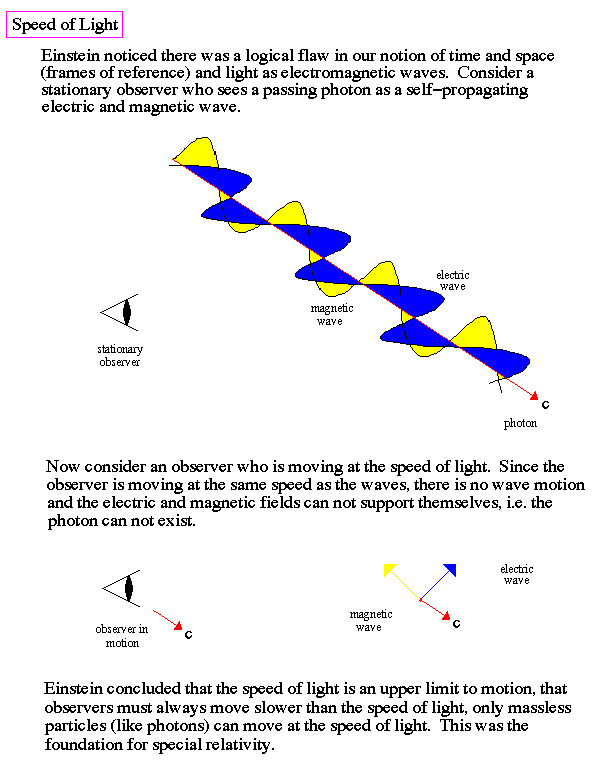
Considering the results of the Michelson-Morley experiment led Einstein to develop the theory of special relativity.The key premise to special relativity is that the speed of light (called c = 186,000 miles per sec) is constant in all frames of reference, regardless of their motion. What this means can be best demonstrated by the following scenario: |
Einstein put forward the idea that there were no absolute speeds in the universe. He stated that whether we are moving at a constant speed relative to something else, or that the something else is moving at a constant speed relative to us, is not relevant. Either point of view must be acceptable.
Being in a state of constant speed causes no forces to be acting on you. Hence you feel nothing even though you are zipping through the Milky Way at 900,000 km/hr. You only feel something when you accelerate or decelerate to another speed. Just as the free-float frames of reference were special in General Relativity, the frames of reference where one travels at constant speeds are special in Special Relativity.
Einstein put forward two postulates that are encapsulated
in what is called
The Special Theory of Relativity.
Light is special, in that all observers in constant motion relative to somebody else will see exactly the same speed for light in vacuum.
This postulate screws up space and time totally. If everyone is to see light as going 1 billion km/hr then everyone has to be measuring different space lengths and different time durations to get the velocity of light to come out so that everyone gets the the same 1 billion km/hr value.
Nobody can perform any experiment to show any differences in physical phenomena when they are traveling at constant speed relative to somebody else.
The laws of physics stay exactly the same when the observer is in constant motion, no matter how fast that motion is. If something blows up in a constantly moving frame of reference then all constantly moving frames of references will see the same thing blow up.
These two postulates essentially imply that whenever you move relative to someone else you enter into a distinct temporal universe. You will measure time differently from the other person and you will measure lengths differently from the other person. Things, however, will conspire in such a way that everybody will measure exactly the same value for the speed of light. Things will also conspire to never allow causes to precede effects. Special relativity preserves the causality of all situations.
The speed of light is a physically unattainable speed for
any object that has a mass. To accelerate a mass closer and closer to the speed
of light you need more and more energy. This can be interpreted as the mass of
the object getting larger and larger with speed.
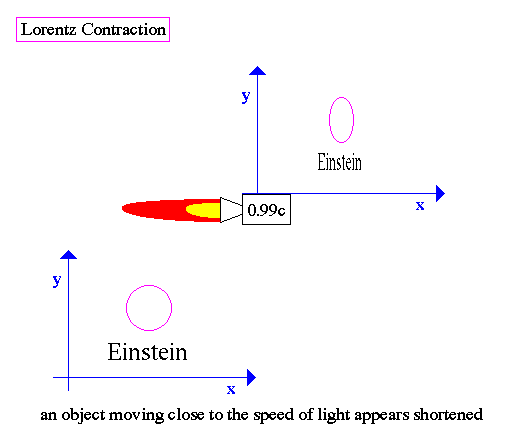
Two distinct events are said to be simultaneous if they occur at the same time.
If observers exist in distinct temporal universes they will disagree about
simultaneity. If they disagree about simultaneity, then since you must measure
the length of any moving object by using the idea of simultaneity, lengths will
not be the same in the different temporal universe.
Why then do we not notice these funny things every time we drive a car or ride a
bus? The answer is that these weird relativistic phenomena only happen when
movements are close to one billion kilometers per hour. No humans have ever gone
this fast. However little particles moving through the upper atmosphere do move
this fast. Particles being accelerated around rings such as those at the large
particle accelerator labs (Fermilab , CERN, etc) do move at these speeds. Jets
of charged particles coming from black holes and other exotic astrophysical
phenomena do travel at these speeds.
EXAMPLES
Galileo's Perspective
The animated picture below shows a train moving
past an observer who is stationary relative to us. There is a person on the
train throwing a ball at constant speed. The person standing sees the ball move
at a constant speed equal to the train's speed plus the speed that the person on
the train actually throws it.
|
|
special relativity theory
We calculate an object's momentum by multiplying its mass by how fast (and in what direction) it moves. Momentum cannot be created or destroyed, whether for a single object or a system of objects that interact with one another, unless another force comes into play. We can apply this tenet equally well to understanding the physics of billiards, collisions between asteroids, or the motions of a hundred billion stars in our Milky Way. Without force the total momentum of any system never goes up or down. Once begun, motion continues forever. This is the reason constant motion is the natural state of anything in the universe. This is the reason everything moves.
But is everything in the universe really moving? The newspaper on your coffee table, the tree in your yard, or the building you live in--don't they all stand still around you as you sit reading this book? In fact, they are still--to you. It's all relative.
Galileo and Newton both realized that the measurement of motion depends completely on your frame of reference. Suppose you see a unicyclist ride past at a certain speed. To him you move backward at that same speed, even though you think you're standing still on the sidewalk. If he is juggling at the same time, he sees the balls bob straight up and down from his hands. However, you see the balls move along forward arcs in space as he pedals past. Both viewpoints, or "frames of reference," are equally valid.
Similarly, let's say two cars approach each other on the road, each moving 50 miles per hour. If you stand on the sidewalk, in Earth's frame of reference, you see each car doing 50. But the driver of each vehicle sees the other car zoom toward him at 100 miles per hour. Velocities simply add together in the world of classical relativity as elucidated by Galileo and Newton. That's all well and good unless the cars somehow accelerate to millions of miles per hour. Then, this kind of relativity would fail. When we deal with the realm of superhigh speed, relativity takes on a special form.
In the late nineteenth century, Newton's laws of motion began to break down for objects that move very fast. The American physicists Albert Michelson and Edward Morley tried to add the speed of Earth's revolution around the Sun to the speed of a light beam using a sensitive light-measuring device called an interferometer. They were searching for signs of the "ether," an invisible and unmoving substance believed by physicists of the day to pervade the universe and carry waves of light. To their great surprise, the combined speed of Earth's motion and the ray of light was always exactly the same as that of light alone. Light did not seem to follow the known rules of Newtonian motion.
This puzzle lasted for nearly two decades. Then, in 1905 a theory that explained the startling result arose from the mind of 26-year-old Albert Einstein, a German physicist who worked by day as a patent officer in Switzerland. His mathematical treatise, innocently titled "On the Electrodynamics of Moving Bodies," presented a revolutionary idea that would become known as the special theory of relativity. Einstein asserted that the speed of light--186,282 miles per second--remains constant and can never be exceeded. Further, he said, speed is independent of how quickly an observer might move. Passengers on a spaceship traveling at 186,281 miles per second would still measure their headlight beams streaming away at the full speed of light. Observers on the ground would see the beams moving at exactly the same speed.
|
This theory has peculiar consequences. For example, if that unicyclist could pedal past you at 87 percent the speed of light, you would see him and his unicycle shrink to half their usual lengths. You would see his clock run at half the speed as your own. Further, his mass would be twice as large as when he stands still next to you. These bizarre relativistic effects are important in particle colliders, where physicists boost electrons and protons near the speed of light. They also dictate the behaviors of quasars and other superenergetic objects in the universe, which can expel matter at extremely high speeds. On Earth special relativity rarely comes into play. Newton's laws suffice for most of our day-to-day activities. Among the exceptions are satellites that use exquisitely accurate clocks, such as those in the Global Positioning System. These satellites orbit the planet at thousands of miles per hour. Their clocks slow down a tiny bit relative to those on the ground, just enough to ruin the precision of their measurements if we ignore the effect. The constant speed of light has another profound implication for our studies of the universe. On Earth we don't notice a delay as light travels from an object to our eyes. After all, a light beam can dash around the globe nearly eight times a second. But light's fixed speed begins to matter away from our planet. Light from the Sun takes about eight minutes to get here. We never see the Sun as it is now, only as it was eight minutes ago. Similarly, we see the next nearest star, Proxima Centauri, as it was 4.1 years ago--the amount of time its light takes to reach us. We see the nearest big galaxy, Andromeda, as it existed more than 2 million years ago. The light from ever more distant galaxies takes billions of years to reach us, from a time when the universe itself was still young. Indeed, our giant telescopes are the time machines into the past that Jules Verne dreamed about--with the disappointing exception that we cannot physically travel through those portals. Newton's laws also cease to operate reliably at submicroscopic scales. In the world of Galileo and Newton, one object orbiting another behaves much like a cat on a ramp. It can walk up or down the ramp, pausing at any level it likes. |
||
The Relativity of Time, Mass, and Length Most aspects of the physical world can be described in terms of three quantities that we would normally consider easily measured: time, distance, and mass. According to Einstein's relativity theory, however, most measurements are not absolute. Contrary to ordinary experience, they depend on the frame of reference of whoever is doing the measuring--that is, on the location and motions of the observer. This is especially true at speeds approaching the speed of light. The first assumption of special relativity theory is that observers inside a uniformly moving frame of reference will perceive physical events within their frame to be unaffected by its motion. But when observers look outside their own frame, its motion will affect what they see. This is the direct result of the theory's second assumption: that the speed of light is constant for all observers in uniform motion. Observers moving at different speeds relative to a light source thus will receive the light at different times and will be unable to agree that given events occur simultaneously. Without simultaneity we can make no comparison against a standard, such as determining the accuracy of clocks or matching both ends of a train to a length of track. |
||
|
||
|
|
||
But when physicists early in this century scrutinized the behaviors of atoms, they realized that only certain motions and energies are allowed. All others are forbidden. In this world, an electron orbiting the nucleus of an atom behaves more like a kangaroo on a tall, uneven staircase. It can hop one step or many steps at a time, going either up or down. However, it cannot stop in midair between two steps. That's one of the odd rules that physicists discovered for electrons in energized atoms. They can orbit only at certain "levels" around the atom, and at no others. Even stranger, we can never know exactly where the electron-kangaroo is or how much energy it contains. The more precisely we try to measure it, the more uncertain it becomes. This inability to measure the exact speeds and positions of subatomic particles at the same time is called the Heisenberg Uncertainty Principle, named for the German physicist Werner Heisenberg. It means that electrons are not bits that we can pinpoint in space, like motes of dust; rather, they are statistical blurs. Electrons and the tiny units of light energy called photons act like particles in some circumstances and like waves in others, a final oddity that defies rational explanation. To account for all of this, scientists developed a theory called quantum mechanics. It sounds like science fiction, but one experiment after another has confirmed the ability of quantum mechanics to predict the behavior of matter. Despite its impressive string of successes, Einstein found quantum mechanics so intellectually unpleasant that he spent the last decades of his life trying to disprove it. Even today, this subatomic world could not be more alien to our senses. Nevertheless, we depend on quantum mechanics to learn the properties of objects halfway across the universe. Much of our modern technology, from photocopiers to laser pointers to supercomputers, relies on quantum mechanics. But what are the exact speeds and locations of the electrons and photons in these devices? Heisenberg knew the answer: We can never know. |
Special Relativity :
Classical physics owes its definitive formulation to the British scientist Sir Isaac Newton. According to Newton, when one physical body influences another body, this influence results in a change of that body's state of motion, its velocity; that is to say, the force exerted by one particle on another results in the latter's changing the direction of its motion, the magnitude of its speed, or both. Conversely, in the absence of such external influences, a particle will continue to move in one unchanging direction and at a constant rate of speed. This statement, Newton's first law of motion, is known as the law of inertia.
As motion of a particle can be described only in relation to some agreed frame of reference, Newton's law of inertia may also be stated as the assertion that there exist frames of reference (so-called inertial frames of reference) with respect to which particles not subject to external forces move at constant speed in an unvarying direction. Ordinarily, all laws of classical mechanics are understood to hold with respect to such inertial frames of reference. Each frame of reference may be thought of as realized by a grid of surveyor's rods permitting the spatial fixation of any event, along with a clock describing the time of its occurrence.
According to Newton, any two inertial frames of reference are related to each other in that the two respective grids of rods move relative to each other only linearly and uniformly (with constant direction and speed) and without rotation, whereas the respective clocks differ from each other at most by a constant amount (as do the clocks adjusted to two different time zones on Earth) but go at the same rate. Except for the arbitrary choice of such a constant time difference, the time appropriate to various inertial frames of reference then is the same: If a certain physical process takes, say, one hour as determined in one inertial frame of reference, it will take precisely one hour with respect to any other inertial frame; and if two events are observed to take place simultaneously by an observer attached to one inertial frame, they will appear simultaneous to all other inertial observers. This universality of time and time determinations is usually referred to as the absolute character of time. The idea that a universal time can be used indiscriminately by all, irrespective of their varying states of motion--that is, by a person at rest at his home, by the driver of an automobile, and by the passenger aboard an airplane--is so deeply ingrained in most people that they do not even conceive of alternatives. It was only at the turn of the 20th century that the absolute character of time was called into question as the result of a number of ingenious experiments described below.
As long as the building blocks of the physical universe were thought to be particles and systems of particles that interacted with each other across empty space in accordance with the principles enunciated by Newton, there was no reason to doubt the validity of the space-time notions just sketched. This view of nature was first placed in doubt in the 19th century by the discoveries of a Danish physicist, Hans Christian Orsted, the English scientist Michael Faraday, and the theoretical work of the Scottish-born physicist James Clerk Maxwell, all concerned with electric and magnetic phenomena. Electrically charged bodies and magnets do not affect each other directly over large distances, but they do affect one another by way of the so-called electromagnetic field, a state of tension spreading throughout space at a high but finite rate, which amounts to a speed of propagation of approximately 186,000 miles (300,000 kilometres) per second. As this value is the same as the known speed of light in empty space, Maxwell hypothesized that light itself is a species of electromagnetic disturbance; his guess has been confirmed experimentally, first by the production of lightlike waves by entirely electric and magnetic means in the laboratory by a German physicist, Heinrich Hertz, in the late 19th century.
Both Maxwell and Hertz were puzzled and profoundly disturbed by the question of what might be the carrier of the electric and magnetic fields in regions free of any known matter. Up to their time, the only fields and waves known to spread at a finite rate had been elastic waves, which appear to the senses as sound and which occur at low frequencies as the shocks of earthquakes, and surface waves, such as water waves on lakes and seas. Maxwell called the mysterious carrier of electromagnetic waves the aether, thereby reviving notions going back to antiquity. He attempted to endow his aether with properties that would account for the known properties of electromagnetic waves, but he was never entirely successful. The aether hypothesis, however, led two U.S. scientists, Albert Abraham Michelson and Edward Williams Morley, to conceive of an experiment (1887) intended to measure the motion of the aether on the surface of the Earth in their laboratory. On the reasonable hypothesis that the Earth is not the pivot of the whole universe, they argued that the motion of the Earth relative to the aether should result in slight variations in the observed speed of light (relative to the Earth and to the instruments of a laboratory) travelling in different directions. The measurement of the speed of light requires but one clock, if, by use of a mirror, a pencil of light is made to travel back and forth so that its speed is measured by clocking the total time elapsed in a round trip at one site; such an arrangement obviates the need for synchronizing two clocks at the ends of a one-way trip. Finally, if one is concerned with variations in the speed of light, rather than with an absolute determination of that speed itself, then it suffices to compare with each other round-trip-travel times along two tracks at right angles to each other, and that is essentially what Michelson and Morley did. To avoid the use of a clock altogether, they compared travel times in terms of the numbers of wavelengths travelled, by making the beams travelling on the two distinct tracks interfere optically with each other. (If the waves meet at a point when both are in the same phase--e.g., both at their peak--the result is visible as the sum of the two in amplitude; if the peak of one coincides with the trough of the other, they cancel each other and no light is visible. Since the wavelengths are known, the relative positions of the peaks give an exact measure of how far one wave has advanced with respect to the other.) This highly precise experiment, repeated many times with ever-improved instrumental techniques, has consistently led to the result that the speed of light relative to the laboratory is the same in all directions, regardless of the time of the day, the time of the year, and the elevation of the laboratory above sea level.
The special theory of relativity resulted from the acceptance of this experimental finding. If an Earth-bound observer could not detect the motion of the Earth through the aether, then, it was felt, probably any observer, regardless of his state of motion, would find the speed of light the same in all directions.
|
This eliminates the paradox with respect
to Newtonian physics and electromagnetism of what does a light ray `look
like' when the observer is moving at the speed of light. The solution is
that only massless photons can move at the speed of light, and that
matter must remain below the speed of light regardless of how much
acceleration is applied.
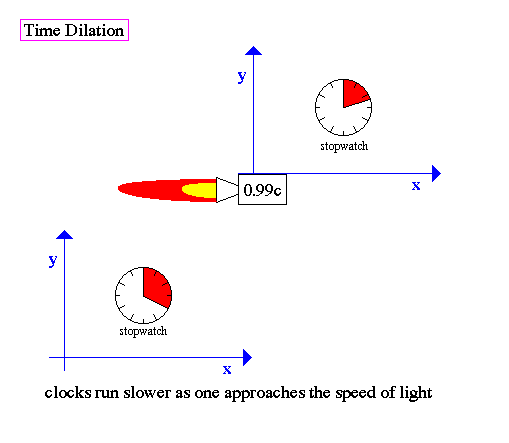
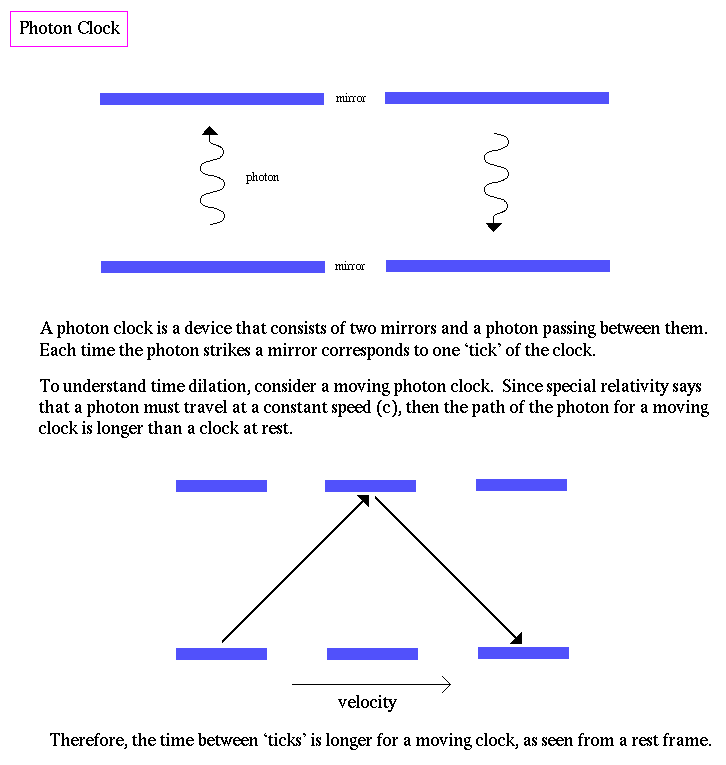
In special relativity, there is a natural upper limit to velocity, the speed of light. And the speed of light the same in all directions with respect to any frame. A surprising result to the speed of light limit is that clocks can run at different rates, simply when they are traveling a different velocities. |
|
This means that time (and space) vary
for frames of reference moving at different velocities with respect to
each other. The change in time is called time dilation, where frames
moving near the speed of light have slow clocks.
|
|
|
|
Time dilation leads to the famous Twins
Paradox, which is not a paradox but rather a simple fact of special
relativity. Since clocks run slower in frames of reference at high
velocity, then one can imagine a scenario were twins age at different
rates when separated at birth due to a trip to the stars.
It is important to note that all the predictions of special relativity, length contraction, time dilation and the twin paradox, have been confirmed by direct experiments, mostly using sub-atomic particles in high energy accelerators. The effects of relativity are dramatic, but only when speeds approach the speed of light. At normal velocities, the changes to clocks and rulers are too small to be measured. |
Twins Paradox:
From P. Davies, 'About Time':
Betty is going to leave Earth in the year 2000 and travel by rocket ship to a star eight light-years away (as measured in Earth's frame of reference) at a speed of 240,000 kilometers per second. To keep the sums simple, I shall neglect the periods the ship spends accelerating and braking (i.e., treat these periods as instantaneous), and also assume Betty doesn't spend any time sightseeing when she reaches the star. To achieve 80 percent of the speed of light in a negligible time implies an enormous acceleration, which would be fatal to a real human, but this is incidental to the argument. I could easily include a more realistic treatment of the acceleration, but at the price of making the arithmetic more complicated; the overall conclusions would be unaffected.
First let me compute the total duration of the journey as predicted by Einstein for each twin. At 80 percent of the speed of light. it takes ten years to travel eight light-years, so Ann, on Earth, will find that Betty returns in Earth year 2020. Betty, on return, agrees that it is Earth year 2020, but insists that only twelve years have elapsed for her, and her rocket clock - a standard atomic clock carefully synchronized before takeoff with Betty's identical clock on Earth - confirms this assertion: it reads 2012.
Now suppose we equip our twins with powerful telescopes so that they can watch each other's clocks throughout the journey and see for themselves what is going on. Ann's Earth clock ticks steadily on, and Betty looks back at it through her telescope as she speeds away into space. According to Einstein, Betty should see Ann's clock running at 60 percent of the rate of her own clock. In other words, during one hour of rocket time, Betty is supposed to see the Earth clock advance only thirty-six minutes. In fact, she sees it going even slower than this. The reason concerns an extra effect, not directly connected with relativity, that is usually left out of discussions of the
twins paradox. It is vital to include the extra effect if you want to make sense of what the twins actually see.Let me explain what causes this extra slowing. When Betty looks back I at Earth, she does not see it as it is at that instant, but as it was when the light left Earth some time before. The time taken for light to travel from Earth to the rocket will steadily increase as the rocket gets farther out in space. Thus Betty will see events on Earth progressively more delayed, because of the need for the light to traverse an ever-widening gap between Earth and rocket. For example, after one hour's flight as measured from Earth, Betty is 0.8 light-hours (48 light-minutes) away, so she sees what was happening on Earth forty-eight minutes earlier, for the light, which conveys the images of Earth to Betty, to reach her at that point in the journey. In particular, Ann's clock would appear to Betty-I'm referring to its actual visual appearance-to be slow anyway, irrespective of the theory of relativity. After two hours' flight, the Earth clock would appear to Betty to lag even more behind. This "ordinary" slowing down of clocks. and events generally, as seen by a moving observer, is called the "Doppler effect," named for a Swedish physicist who first used it to describe a property of sound waves. By adding the Doppler effect to the time-dilation effect, you get the combined slowdown factor.
Ann will also see Betty's rocket clock slowed by the Doppler effect, because light from the rocket takes longer and longer to get back to Earth. She will in addition see Betty's clock slowed by the time-dilation effect. By symmetry, the combined slowdown factor of the other clock should be the same for both of them.
Let me now compute the combined slowdown factor, first from Ann's point of view, then Betty's. To do so, I shall focus on the great event of Betty's arrival at the star. The outward journey takes ten years as measured on Earth. However, Ann will not actually see the rocket reach the star in the year 2010, because by this stage Betty is eight light-years away. Since it will take light a further eight years to get back to Earth, it will not be until the year 2018 that Ann gets to witness visually Betty's arrival at the star.
What is the time of the arrival event as registered on Betty's clock? Einstein's formula tells us that Betty's clock runs at 0.6 the rate of the clock on Earth, so ten years of Earth time implies six years in the rocket. The rocket clock therefore stands at six years on Betty's arrival at the star. So, when Ann gets to witness this arrival in 2018, the rocket clock says 2006. Thus, as far as the visual appearance of the rocket clock is concerned, Ann sees only six years having elapsed in her eighteen years-i.e., Betty's rocket clock has been running at one-third the rate of Ann's Earth clock. Now, Ann is perfectly capable of untangling the time-dilation and Doppler effects, and computing the "actual" rate of Betty's clock, having factored out the effect of the light delay. She will find the answer to be 0.6, in accordance with Einstein's formula. Thus Ann deduces (but does not actually see) that throughout Betty's outward journey Betty's clock was running at thirty-six minutes to Ann's hour.
From Betty's perspective, things are the other way about. She agrees, of course, that her rocket clock stands at 2006 when she arrives at the star, but what does she see the Earth clock registering at that moment? We know that in the Earth's frame of reference the arrival event occurs at 2010, but, because the star is eight light-years away, the light that actually reaches the rocket at that moment will be from eight years previously-i.e., 2002. So Betty will look back at Earth, on arrival at the star, and see the Earth clock registering 2002. Her clock says 2006. Therefore as far as the actual appearance of the Earth clock is concerned, it records two years having elapsed for Betty's six years. Thus Betty concludes that the Earth clock has been running at one-third the rate of her own rocket clock for the outward part of the journey. This is the same factor that Ann perceived Betty's clock to be slowed by, so the situation is indeed perfectly symmetric. Again, Betty can untangle the Doppler effect from the time-dilation effect and deduce that Ann's clock has "really" been running at 0.6 the rate of her own.
Without delay, Betty embarks on the return journey. Because Betty is approaching rather than receding from Earth the light-delay (i.e., Doppler) effect now works in opposition to the time-dilation effect. The former causes events to appear speeded, although time dilation still works to tell slow them down. Let's put the numbers in. First, what does Ann see as Betty speeds back towards Earth? Since we are agreed that Betty returns to Earth in the year 2020, and Ann actually sees Betty reach the star in 2018, the return part of the journey will appear to Ann, viewing the approach of the rocket from Earth, to be compressed into just two years of Earth time. We have already determined that, when, in 2018, Ann sees Betty's clock at the halfway point, it registers 2006, and that when Betty returns to Earth it will register 2012. So, for the two Earth years during which Ann sees the rocket traveling back, she will witness the rocket clock progress through the remaining six years. In other words, on the return leg of the journey Ann sees Betty's clock running three times faster than her own, Earthbound, clock. This is a key point: during the return journey the rocket clock appears from Earth to be speeded up, not slowed down. The Doppler effect beats the time-dilation effect. Again, Ann can untangle the time-dilation and light-delay effects and deduce that the rocket clock is "really" running at 0.6 the rate of her clock-i.e., although the rocket clock looks to Ann to be speeded up, she deduces that it is "really" running slow at exactly the same reduced rate (0.6) as it was on the outward journey. So, although the visual appearance of the rocket clock is quite different for the two legs of the journey, the time-dilation factor of 0.6 remains the same throughout.
Finally, let me examine the return journey as observed by Betty, in the rocket. She has experienced six years for the outward trip, and she experiences another six years for the return, reaching Earth in 2012 as registered on her own clock. During the return journey, however, Betty also observes the clock on Earth. She saw it (actually, visually) standing at 2002 at the moment she reached the star. We know she will get home I in 2020, so Betty will see the Earth clock progress through eighteen years during the six years aboard the rocket. Thus the Earth clock appears to the same factor as that by which Ann saw Betty's clock speeded up- there is complete symmetry on the return part of the journey too. Betty can again factor out the light-delay effect and deduce that the Earth clock is "really" running slow-at 0.6 of the rate of her rocket clock.
The crucial point to be extracted from all this is that during the periods when the rocket is traveling at a fixed speed Ann deduces that Betty's clock is running slow and Betty deduces that Ann's clock is running slow. On the outward part of the journey, each actually sees the other's clock running (even more) slowly, but on the return part of the journey each sees the other's clock speeded up. The deductions and experiences all fit together consistently, and refute the claim that there is any paradox attached to the statement that "each clock runs slow relative to the other.
For those readers who have waded through this arithmetic, it contains a hidden conclusion about distances. If you use the fact that in Betty's frame of reference Earth recedes at 0.8 of the speed of light, and the journey to the star takes just six rocket years, then the distance to the star as measured by Betty must be 0.8 x 6 = 4.8 light-years. Thus, although Ann measures the star to be eight light-years away, Betty measures the distance to the star to be only 4.8 light-years. The distance is shrunk by the same factor (0.6) as that by which time is dilated.
Spacetime:
|
Special relativity demonstrated that
there is a relationship between spatial coordinates and temporal
coordinates. That we can no longer reference where without some
reference to when. Although time remains physically distinct from space,
time and the three dimensional space coordinates are so intimately bound
together in their properties that it only makes sense to describe them
jointly as a four dimensional continuum.
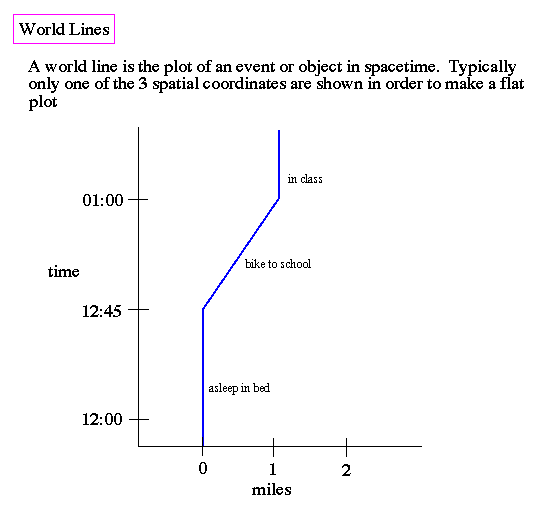
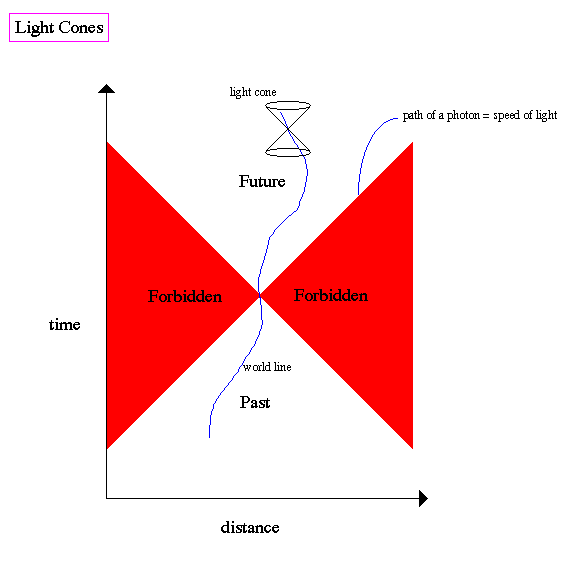
Einstein introduced a new concept, that there is an inherent connection between geometry of the Universe and its temporal properties. The result is a four dimensional (three of space, one of time) continuum called spacetime which can best be demonstrated through the use of Minkowski diagrams and world lines. |
what is the Time?
Einstein wrote when his friend Besso died, "For us believing physicists, the distinction between past, present, and future is illusion, however persistent."
Here is another spacetime diagram, this time from D. Postle, Fabric of the Universe, pg. 106:
 |
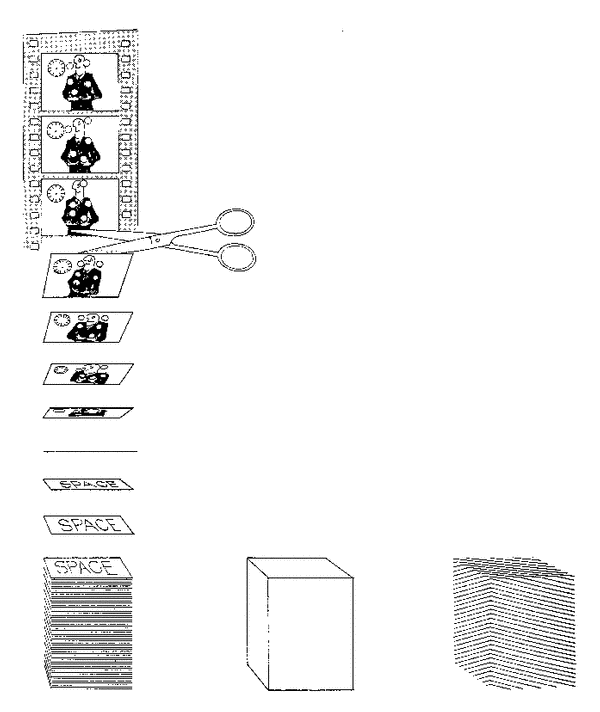We imagine our worldline in this spacetime diagram. Then, as David Park wrote, "our consciousness crawls along our worldline as a spark burns along a fuse" (in J.T. Fraser et al., eds., The Study of Time, pg. 113). As it crawls up our worldline we discover new slices of spacetime.
Postle included a continuous block of spacetime between the two different ways of slicing it. Quantum Mechanics calls into question whether such a concept is valid.
Imagine we take one of the piles of frames of the movie and shuffle it. The correlation between our consciousness and what it perceives remains the same. So -- would we notice any difference? I don't have any good way to approach a discussion of this question, but it is one that has fascinated me for years.
To avoid the two
logical problems given above, it is mandatory to allow for the existence of
multiple worlds. It turns out that the theory of physics, called quantum
mechanics, that governs all physical phenomena on the smallest scales can be
interpreted literally as a theory of parallel universes. Hence, quantum
theory is quite consistent with the idea that time travel can exist without
logical difficulties.
How is time viewed in a parallel universe scenario? Each moment of time is
seen as a distinct universe recreated from the previous universe such that
the rules of existence (the laws of thermodynamics) are obeyed. Below is a
diagram of a stack of 2-D universes. Time proceeds from the bottom of the
stack to the top of the stack. Time is then seen as just a universe label:
Time 1 = Universe 1, Time 2 = Universe 2, Time 3 = Universe 3, etc.
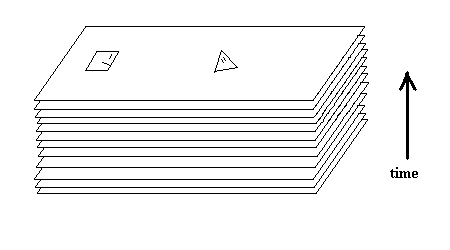
Louis de Broglie wrote a famous commentary on the worldview of the theory of relativity:
"In space-time, everything which for each of us constitutes the past, the present, and the future is given in block, and the entire collection of events, successive for us, which form the existence of a material particle is represented by a line, the world-line of the particle .... Each observer, as his time passes, discovers, so to speak, new slices of space-time which appear to him as successive aspects of the material world, though in reality this ensemble of events constituting space-time exist prior to his knowledge of them." -- in Albert Einstein: Philosopher-Scientist, pg. 114.
Dogen Zenji seemed to have a similar view 800 years ago. "It is believed by most that time passes; in actual fact it stays where it is. This idea of passing may be called time, but it is an incorrect idea, for since one only sees it as passing, one cannot understand that it stays just where it is. In a word, every being in the entire world is a separate time in one continuum." -- Shobogenzo.
Spacetime :
Spacetime, in physical science, single concept that recognizes the union of space and time, posited by Albert Einstein in the theories of relativity (1905, 1915).
Common intuition previously supposed no connection between space and time. Physical space was held to be a flat, three-dimensional continuum--i.e., an arrangement of all possible point locations--to which Euclidean postulates would apply. To such a spatial manifold, Cartesian coordinates seemed most naturally adapted, and straight lines could be conveniently accommodated. Time was viewed independent of space--as a separate, one-dimensional continuum, completely homogeneous along its infinite extent. Any "now" in time could be regarded as an origin from which to take duration past or future to any other time instant. Within a separately conceived space and time, from the possible states of motion one could not find an absolute state of rest. Uniformly moving spatial coordinate systems attached to uniform time continua represented all unaccelerated motions, the special class of so-called inertial reference frames. The universe according to this convention was called Newtonian.
By use of a four-dimensional space-time continuum, another well-defined flat geometry, the Minkowski universe (after Hermann Minkowski), can be constructed. In that universe, the time coordinate of one coordinate system depends on both the time and space coordinates of another relatively moving system, forming the essential alteration required for Einstein's special theory of relativity. The Minkowski universe, like its predecessor, contains a distinct class of inertial reference frames and is likewise not affected by the presence of matter (masses) within it. Every set of coordinates, or particular space-time event, in such a universe is described as a "here-now" or a world point. Apparent space and time intervals between events depend upon the velocity of the observer, which cannot, in any case, exceed the velocity of light. In every inertial reference frame, all physical laws remain unchanged.
A further alteration of this geometry, locally resembling the Minkowski universe, derives from the use of a four-dimensional continuum containing mass points. This continuum is also non-Euclidean, but it allows for the elimination of gravitation as a dynamical force and is used in Einstein's general theory of relativity (1915). In this general theory, the continuum still consists of world points that may be identified, though non-uniquely, by coordinates. Corresponding to each world point is a coordinate system such that, within the small, local region containing it, the time of special relativity will be approximated. Any succession of these world points, denoting a particle trajectory or light ray path, is known as a world line, or geodesic. Maximum velocities relative to an observer are still defined as the world lines of light flashes, at the constant velocity c.
Whereas the geodesics of a Minkowski continuum (without mass-point accelerations) are straight lines, those of a general relativistic, or Riemannian, universe containing local concentrations of mass are curved; and gravitational fields can be interpreted as manifestations of the space-time curvature. However, one can always find coordinate systems in which, locally, the gravitational field strength is nonexistent. Such a reference frame, affixed to a selected world point, would naturally be in free-fall acceleration near a concentrated mass. Only in this region is the concept well defined--i.e., in the neighbourhood of the world point, in a limited region of space, for a limited duration. Its free-fall toward the mass is due either to an externally produced gravitational field or to the equivalent, an intrinsic property of inertial reference frames. Mathematically, gravitational potentials in the Riemannian space can be evaluated by the procedures of tensor analysis to yield a solution of the Einstein gravitational field equations outside the mass points themselves, for any particular distribution of matter.
The first rigorous solution, for a single spherical mass, was carried out by a German astronomer, Karl Schwarzschild (1916). For so-called small masses, the solution does not differ appreciably from that afforded by Newton's gravitational law; but for "large" masses the radius of space-time curvature may approach or exceed that of the physical object, and the Schwarzschild solution predicts unusual properties. Astronomical observations of dwarf stars eventually led U.S. astrophysicists J.R. Oppenheimer and H. Snyder (1939) to postulate super-dense states of matter. These, and other hypothetical conditions of gravitational collapse, were borne out in later discoveries of pulsars and neutron stars. They also have a bearing on black holes thought to exist in interstellar space. Other implications of space-time are important cosmologically and to unified field theory.
|
Spacetime makes sense from special relativity since it was shown that spatial coordinates (Lorentz contraction) and temporal coordinates (time dilation) vary between frames of reference. Notice that under spacetime, time does not `happen' as perceived by humans, but rather all time exists, stretched out like space in its entirety. Time is simply `there'. |
Mass-Energy Equivalence:
|
Since special relativity demonstrates
that space and time are variable concepts, then velocity (which is space
divided by time) becomes a variable as well. If velocity changes from
reference frame to reference frame, then concepts that involve velocity
must also be relative. One such concept is momentum, motion energy.
Momentum, as defined by Newtonian, can not be conserved from frame to frame under special relativity. A new parameter had to be defined, called relativistic momentum, which is conserved, but only if the mass of the object is added to the momentum equation. This has a big impact on classical physics because it means there is an equivalence between mass and energy, summarized by the famous Einstein equation: |
|
The implications of this was not
realized for many years. For example, the production of energy in
nuclear reactions (i.e. fission and fusion) was shown to be the
conversion of a small amount of atomic mass into energy. This led to the
develop of nuclear power and weapons.
As an object is accelerated close to the speed of light, relativistic effects begin to dominate. In particular, adding more energy to an object will not make it go faster since the speed of light is the limit. The energy has to go somewhere, so it is added to the mass of the object, as observed from the rest frame. Thus, we say that the observed mass of the object goes up with increased velocity. So a spaceship would appear to gain the mass of a city, then a planet, than a star, as its velocity increased. Likewise, the equivalence of mass and energy allowed Einstein to predict that the photon has momentum, even though its mass is zero. This allows the development of light sails and photoelectric detectors. |
Einstein's theory of general
relativity and curved space-time
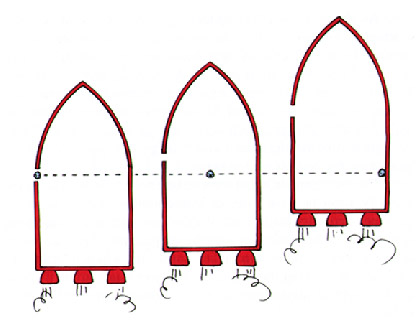
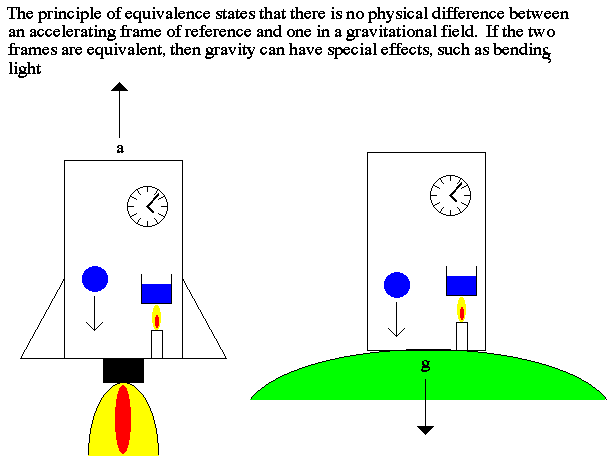
A dramatic example of non-inertial frames can been seen in accelerating rockets.
When a rocket accelerates, an occupant feels "gravity".
Consider a rocket with a small "window" in one side and a major league pitcher with amazing accuracy.
An outside observer sees a horizontally thrown ball travel in a straight line. Since the ship is moving upward while the ball travels horizontally, the ball strikes the wall somewhat below a point opposite the window.
To an inside observer, the path of the ball bends as if in a gravitational field.
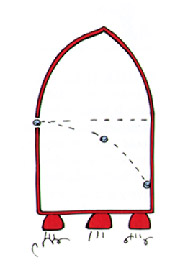
From this thought experiment we realize that we cannot tell the difference between an accelerating frame and one that is at rest and has a gravitational pull. This is the "equivalence principle" and is the corrnerstone to Einstein's theory.
Now replace the ball with a light beam. Again, to the observer in the rocket it will apear to have it's path "bent."
This tells us that gravity "bends" light
beams. Stars, including our sun are massive enough to bend light from
distant stars.
But, wait a minute... doesn't light travel
in a stright line? How can this be?
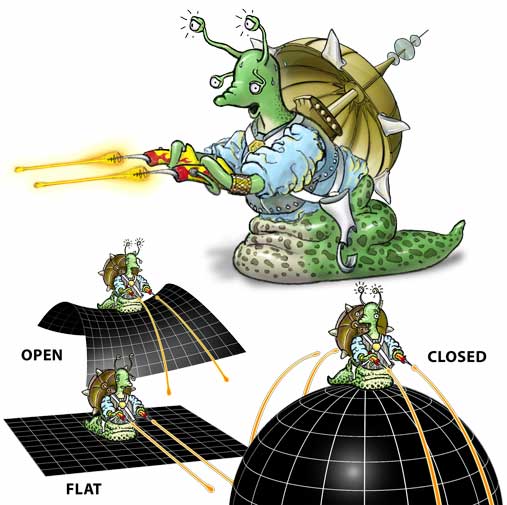
Perhaps space is somehow "curved" If this is the case then light still travels in a stright line, but now the idea of "striaght" has to change since our surface is no longer flat. Think about how we define parallel lines on a flat surface and one a sphere.
 |
 |
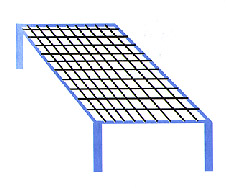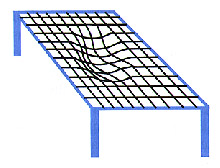Einstein's theory of special relativity talks about how space and time are connected. This theory deals with objects and reference frames moving at constant speeds. His theory of general relativity deals with accelerating objects (which includes gravity). The mathematics of special relativity isn't too bad, but the mathematics of general realtivity is a matter for a graduate level course. Both theories are well establish experimentally.
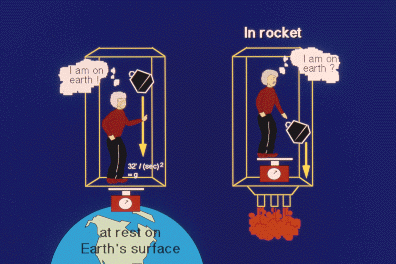
Principle of Equivalence
The idea that a free fall frame is possible for any object leads to one of
the strongest predictions of Einstein's theory. If all objects feel no force
when they achieve a free float state then the composition of materials will
never be important for gravitation. If something is in free fall, and it has
no weight, then it can do nothing else but float. A zero weight of gold is
just the same as a zero weight of feathers. They both should float
weightless at exactly the same height in a free fall frame. The principle
that says that all objects, no matter what their compositions, fall or float
in exactly the same way is called the Principle of Equivalence. This
principle also has another form that equates acceleration with gravity. It
is not possible to distinguish, in a small region of spacetime, the
difference between the acceleration of an object and the existence of
traditionally postulated gravitational force.
Mathematical aspects of relativity
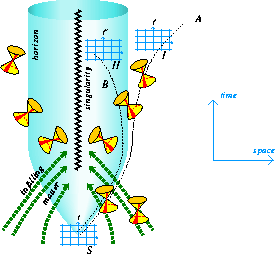
Einstein's theory of general relativity describes the gravitational field in terms of the curvature of spacetime. The precise form of the curvature is determined through Einstein's equations which form a set of 12 coupled hyperbolic partial differential equations. Because of the complexity of these equations exact solutions can only be found by looking for spacetimes with a high degree of symmetry. An example of such a spacetime is the Schwarzschild solution which describes a spherically symmetric black hole with a gravitational singularity at its heart. However when the Schwarzschild solution was first discovered most physicists believed that the existence of the singularity was the result of the high degree of symmetry. By using methods from differential geometry and topology Roger Penrose showed that singularities are general features of gravitational collapse and do not require spherical symmetry. This work was then extended by Hawking and Penrose to establish a number of singularity theorems which showed that gravitational singularities occur in many situations.
A feature of the singularity theorems is that they do not directly show the existence of black holes. Instead they show that spacetime is geodesically incomplete so that the worldline of an observer comes to an end and cannot be extended. The obstruction to extending the worldline is some kind of singularity, but this might be rather mild and need not correspond to a black hole. Research at Southampton is trying to improve on the singularity theorems to show that they predict the existence of genuine gravitational singularities. This work involves studying the structure and geometry of weak singularities. One can then apply Einstein's equations to a larger class of spacetimes so that points that were previously regarded as weak singularities can now be regarded as interior points of a more general spacetime. This work allows one to develop a new definition of gravitational singularity in which singularities are regarded as obstructions to the evolution of Einstein's equations rather than obstructions to extending geodesics. Mathematically this involves developing a new mathematical theory of non-linear generalised functions, which is essentail due to the inherent non-linearity of the gravitational field equations.
The main references on this research topic are
- Steinbauer, R. and Vickers, J.A. (2006) - The use of generalised functions and distributions in general relativity. Classical and Quantum Gravity, 23, (10), R91-R114. (doi:10.1088/0264-9381/23/10/R01)
- Vickers, J.A. (2006) Weak singularities in general relativity. International Journal of Modern Physics A. Particles and Fields, Gravitation, Cosmology, Nuclear Physics, 17, (20), 2779. (doi:10.1142/S0217751X02012065)
- Grosser, M., Kunzinger, M., Steinbauer, R. and Vickers, J. A. (2002) A global theory of algebras of generalised functions. Advances in Mathematics, 166, (1), 50-72. ((doi:10.1006/aima.2001.2018)
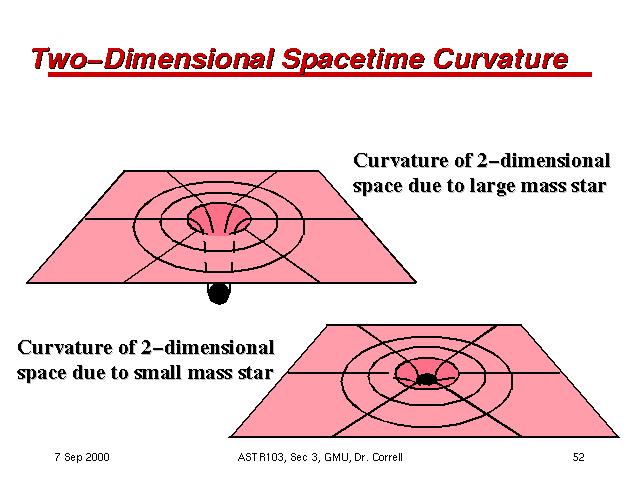
Space
and Time Warps Cont...
General Relativity was a major intellectual revolution that has transformed
the way we think about the universe. It is a theory not only of curved space,
but of curved or warped time as well. Einstein had realized in 1905, that
space and time, are intimately connected with each other. One can describe
the location of an event by four numbers. Three numbers describe the
position of the event. They could be miles north and east of Oxford circus,
and height above sea level. On a larger scale, they could be galactic
latitude and longitude, and distance from the center of the galaxy. The
fourth number, is the time of the event. Thus one can think of space and
time together, as a four-dimensional entity, called space-time. Each point
of space-time is labeled by four numbers, that specify its position in space,
and in time. Combining space and time into space-time in this way would be
rather trivial, if one could disentangle them in a unique way. That is to
say, if there was a unique way of defining the time and position of each
event. However, in a remarkable paper written in 1905, when he was a clerk
in the Swiss patent office, Einstein showed that the time and position at
which one thought an event occurred, depended on how one was moving. This
meant that time and space, were inextricably bound up with each other. The
times that different observers would assign to events would agree if the
observers were not moving relative to each other. But they would disagree
more, the faster their relative speed. So one can ask, how fast does one
need to go, in order that the time for one observer, should go backwards
relative to the time of another observer. The answer is given in the
following Limerick.
There was a young lady of Wight,
Who traveled much faster than light,
She departed one day,
In a relative way,
And arrived on the previous night.
So all we need for time travel, is a space ship that will go faster than
light. Unfortunately, in the same paper, Einstein showed that the rocket
power needed to accelerate a space ship, got greater and greater, the nearer
it got to the speed of light. So it would take an infinite amount of power,
to accelerate past the speed of light.
Einstein's paper of 1905 seemed to rule out time travel into the past. It
also indicated that space travel to other stars, was going to be a very slow
and tedious business. If one couldn't go faster than light, the round trip
to the nearest star, would take at least eight years, and to the center of
the galaxy, at least eighty thousand years. If the space ship went very near
the speed of light, it might seem to the people on board, that the trip to
the galactic center had taken only a few years. But that wouldn't be much
consolation, if everyone you had known was dead and forgotten thousands of
years ago, when you got back. That wouldn't be much good for space Westerns.
So writers of science fiction, had to look for ways to get round this
difficulty.
In his 1915 paper, Einstein showed that the effects of gravity could be
described, by supposing that space-time was warped or distorted, by the
matter and energy in it. We can actually observe this warping of space-time,
produced by the mass of the Sun, in the slight bending of light or radio
waves, passing close to the Sun.
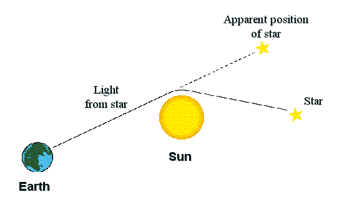This causes the apparent position of the star or radio source, to shift
slightly, when the Sun is between the Earth and the source. The shift is
very small, about a thousandth of a degree, equivalent to a movement of an
inch, at a distance of a mile. Nevertheless, it can be measured with great
accuracy, and it agrees with the predictions of General Relativity. We have
experimental evidence, that space and time are warped.
The amount of warping in our neighbourhood, is very small, because all the
gravitational fields in the solar system, are weak. However, we know that
very strong fields can occur, for example in the Big Bang, or in black holes.
So, can space and time be warped enough, to meet the demands from science
fiction, for things like hyper space drives, wormholes, or time travel. At
first sight, all these seem possible. For example, in 1948, Kurt Goedel
found a solution of the field equations of General Relativity, which
represents a universe in which all the matter was rotating. In this universe,
it would be possible to go off in a space ship, and come back before you set
out. Goedel was at the Institute of Advanced Study, in Princeton, where
Einstein also spent his last years. He was more famous for proving you
couldn't prove everything that is true, even in such an apparently simple
subject as arithmetic. But what he proved about General Relativity allowing
time travel really upset Einstein, who had thought it wouldn't be possible.
We now know that Goedel's solution couldn't represent the universe in which
we live, because it was not expanding. It also had a fairly large value for
a quantity called the cosmological constant, which is generally believed to
be zero. However, other apparently more reasonable solutions that allow time
travel, have since been found. A particularly interesting one contains two
cosmic strings, moving past each other at a speed very near to, but slightly
less than, the speed of light.
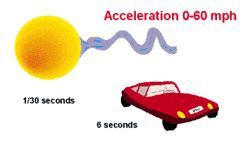Cosmic
strings are a remarkable idea of theoretical physics, which science fiction
writers don't really seem to have caught on to. As their name suggests, they
are like string, in that they have length, but a tiny cross section.
Actually, they are more like rubber bands, because they are under enormous
tension, something like a hundred billion billion billion tons. A cosmic
string attached to the Sun would accelerate it naught to sixty, in a
thirtieth of a second.
Cosmic strings may sound far-fetched, and pure science fiction, but there
are good scientific reasons to believed they could have formed in the very
early universe, shortly after the Big Bang. Because they are under such
great tension, one might have expected them to accelerate to almost the
speed of light.
What both the Goedel universe, and the fast moving cosmic string space-time
have in common, is that they start out so distorted and curved, that travel
into the past, was always possible. God might have created such a warped
universe, but we have no reason to think that He did. All the evidence is,
that the universe started out in the Big Bang, without the kind of warping
needed, to allow travel into the past. Since we can't change the way the
universe began, the question of whether time travel is possible, is one of
whether we can subsequently make space-time so warped, that one can go back
to the past. I think this is an important subject for research, but one has
to be careful not to be labeled a crank. If one made a research grant
application to work on time travel, it would be dismissed immediately. No
government agency could afford to be seen to be spending public money, on
anything as way out as time travel. Instead, one has to use technical terms,
like closed time like curves, which are code for time travel. Although this
lecture is partly about time travel, I felt I had to give it the
scientifically more respectable title, Space and Time warps. Yet, it is a
very serious question. Since General Relativity can permit time travel, does
it allow it in our universe? And if not, why not.
Closely related to time travel, is the ability to travel rapidly from one
position in space, to another. As I said earlier, Einstein showed that it
would take an infinite amount of rocket power, to accelerate a space ship to
beyond the speed of light. So the only way to get from one side of the
galaxy to the other, in a reasonable time, would seem to be if we could warp
space-time so much, that we created a little tube or wormhole.
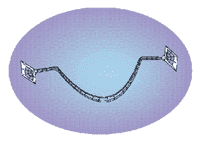This could connect the two sides of the galaxy, and act as a short cut, to
get from one to the other and back while your friends were still alive. Such
wormholes have been seriously suggested, as being within the capabilities of
a future civilization. But if you can travel from one side of the galaxy, to
the other, in a week or two, you could go back through another wormhole, and
arrive back before you set out. You could even manage to travel back in time
with a single wormhole, if its two ends were moving relative to each other.
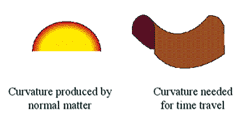One
can show that to create a wormhole, one needs to warp space-time in the
opposite way, to that in which normal matter warps it. Ordinary matter
curves space-time back on itself, like the surface of the Earth.
However, to create a wormhole, one needs matter that warps space-time in the
opposite way, like the surface of a saddle. The same is true of any other
way of warping space-time to allow travel to the past, if the universe
didn't begin so warped, that it allowed time travel. What one would need,
would be matter with negative mass, and negative energy density, to make
space-time warp in the way required.
Energy is rather like money. If you have a positive bank balance, you can
distribute it in various ways. But according to the classical laws that were
believed until quite recently, you weren't allowed to have an energy
overdraft. So these classical laws would have ruled out us being able to
warp the universe, in the way required to allow time travel. However, the
classical laws were overthrown by Quantum Theory, which is the other great
revolution in our picture of the universe, apart from General Relativity.
Quantum Theory is more relaxed, and allows you to have an overdraft on one
or two accounts. If only the banks were as accommodating. In other words,
Quantum Theory allows the energy density to be negative in some places,
provided it is positive in others.
The Geometry and Content of the Universe |
|||
|
|||
What does geometry mean to you?
|
H
içbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 - Turkiye / Denizli
Ana Sayfa /
index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru