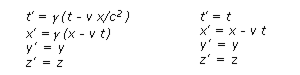Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
The Michelson-Morley Experiment
|
In 1887, Albert A. Michelson and Edward
W. Morley tried to measure the speed of the ether. The concept
of the ether was made in analogy with other types of media in
which different types of waves are able to propagate; sound waves can,
for example, propagate in air or other materials. The result of the
Michelson-Morley experiment was that the speed of the Earth
through the ether (or the speed of the ether wind) was zero.
Therefore, this experiment also showed that there is no need for any
ether at all, and it appeared that the speed of light in vacuum
was independent of the speed of the observer! Michelson and Morley
repeated their experiment many times up until 1929, but always with
the same results and conclusions. Michelson won the Nobel Prize in
Physics in 1907.
The Postulates of Special Relativity
On June 30, 1905 Einstein formulated the two postulates of special relativity: 1. The Principle of Relativity 2. The Constancy of Speed of Light in Vacuum
The speed of light in vacuum c (299792458 m/s) is so enormous that we do not notice a delay between the transmission and reception of electromagnetic waves under normal circumstances. The speed of light in vacuum is actually the only speed that is absolute and the same for all observers as was stated in the second postulate. |
-rays,
...) would propagate.
The Postulates of Special Relativity
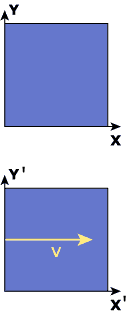
Inertial Coordinate Systems
.gif) |
 |
|
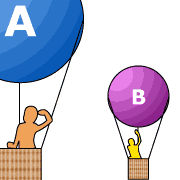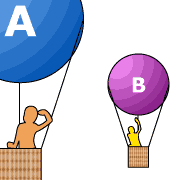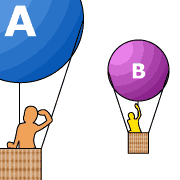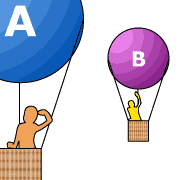
From the first postulate, it follows that there is no coordinate system which is in absolute rest. All motion with constant speed is relative and any coordinate system moving with constant speed (relative to the "fixed stars") is called an inertial coordinate system (or inertial frame [of reference]).
Two inertial frames A and B are moving with constant speed
relative
to each other. An observer at rest in A will say that objects at rest
in B are moving with respect to A. On the other hand, an
observer at rest in B will say that it is the objects at rest in A
that are moving with respect to B. Motion is relative!
The Postulates of Special Relativity
Simultaneity
|
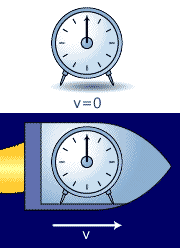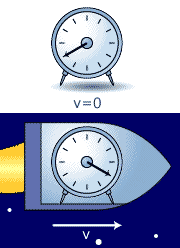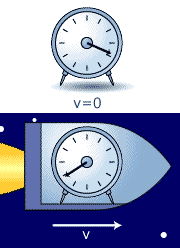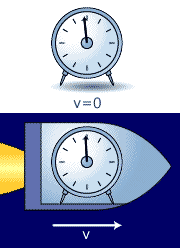
One of the most important concepts in
special relativity is the one of simultaneity. Two physical
events that occur simultaneously in one inertial frame are only
simultaneous in any other inertial frame if they occur at the
same time and at the same place. Time is relative! The two figures to the left, seen from two different inertial frames, help clarify the concept of simultaneity: Top figure: Bottom figure: |
|
|||||||||||
.gif){kind=small}
is
the Lorentz factor. Note that the spatial coordinates (y
and z) perpendicular to the direction of motion (x) are
unchanged. In the classical limit
, which
means that
,
special relativity is equivalent with classical Newtonian mechanics.
Furthermore, note that
, i.e.
time is relative in special relativity.Lorentz Transformations
Length Contraction (or Lorentz Contraction)
 |
 |
Suppose that a ruler of rest length
is moving with
constant speed v in the direction of its own length with respect to
an observer. The observer, however, will observe the length to be
This formula is the so-called length contraction formula. Note
that 
for all speeds
,
which means that the ruler is contracted according to the observer. Moving
rulers are shorter! Note also, that the spatial dimensions perpendicular to
the direction of motion, are not affected by the length contraction.
Einstein's Theory of Special Relativity
One of the peculiar aspects of Einstein's theory of special relativity is that the length of objects moving at relativistic speeds undergo a contraction along the dimension of motion. An observer at rest (relative to the moving object) would observe the moving object to be shorter in length.
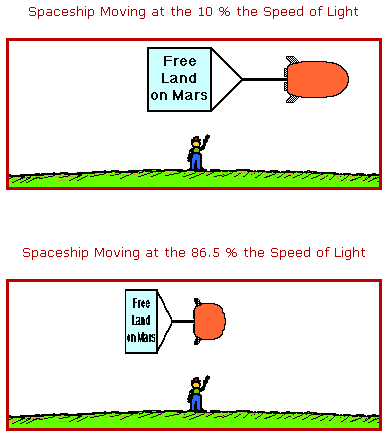
Lorentz Transformations
Length Contraction
the Car that Does or Does Not Fit into the Garage
 |
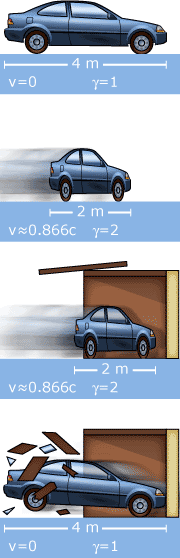The length contraction is no "illusion"; it
is real in every way. Consider the "unrealistic" situation of a man
driving a car of rest length 4 m wanting to get it into a 2 m garage.
He will drive at approximately 0.866 c in order to make
When the car stops in the inertial frame of the garage, it is, in fact, "rotated in space-time" and will tend to obtain, if it can, its original length relative to the garage. Thus, if it survived, it must now either bend or burst the door. At this moment a "paradox" might occur to the reader: What about the symmetry of this problem? Relative to the driver, will not the garage be only 1 m long? Yes, of course! How can a 4 m long car get into a 1 m long garage? Let us consider the situation in the inertial frame of the car. The open garage now comes towards the car. Because of the concrete wall, the garage will keep on going even after the crash with the car, taking the front of the car with it. But the back of the car is still at rest; it cannot yet "know" that the front has crashed, because of the finite speed of propagation of information. Even if the "signal" (in this case the elastic shock wave) propagates along the car with the speed of light, that signal has 4 m to propagate against the garage front's 3 m, before reaching the back of the car. This race would be a dead heat if v were 0.75 c, but now v is approximately 0.866 c. Thus, the car more than just gets into the garage! |
= 2, so
that his car contracts to 2 m. (It will be good to have a massive block
of concrete at the end of the garage in order to ensure that there is no
question that the car finally stops in the inertial frame of the garage,
or vice versa.) Thus, the man drives his (now contracted) car into the
garage and his gentle wife quickly closes the door!Lorentz Transformations
Time Dilation
|
Moving clocks record their own proper time.
(The proper time is the time recorded by a clock, which moves along with
the considered object.) The proper time interval
recorded by a clock moving with constant speed v relative to an
inertial frame A is given by
where
Hence Muons are elementary particles that can be produced when primary
cosmic rays hit the atmosphere of the Earth. The muons are created at an
altitude of around 15 km and the lifetime of the muons (i.e., the time
which the muons live in their own rest frame) is approximately
How can this be explained? Well, this can be explained in principle in two ways - by either using length contraction or time dilation. Assume that the muons move with a speed v close to that of light, e.g., v = 0.999 c. Time dilation: In the frame of the Earth, the lifetime of the muons
will be Length contraction: In the rest frame of a muon, the thickness of the
atmosphere is about 10 km/22 = 450 m. But during the lifetime of the
muon, the Earth will move the distance v |
,
is
the coordinate time interval recorded by clocks at rest in A,
i.e.,
.
for all
0 = 2.2
10-6
s. In classical Newtonian mechanics, this would mean that the muons
could in average move approximately cLorentz Transformations
Relativistic Doppler Effect
|
The Doppler effect: Motion towards or away
from a source will cause a change in the observed frequency (or
wavelength) as compared to the emitted frequency. All wave phenomena
(e.g., water, sound, and light) behave in this way. We will discuss below the Doppler effect and the concepts related to it as well as some formulas when relativistic effects are considered. Suppose a source (for example a lamp or even better, a laser) emits
light of frequency
This formula is usually called the relativistic Doppler formula. Note
that |
=
650 nm) at a speed of approximately v = 0.17 c, then the
light from the traffic light will actually appear to be green (
.Lorentz Transformations
Relativistic Addition of Velocities
|
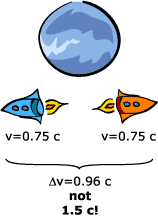
In classical Newtonian mechanics, two
different velocities
and
 are
added together by the formula
where
This formula is called the relativistic addition of velocities. Note that if |
,
is the
sum of the two velocities. However, in special relativity, the
velocities are added together as
.Lorentz Transformations
Space-Time and Minkowski Space
In classical Newtonian mechanics space the three-dimensional "world" is a place where all the events occur and time is absolute and the same for everybody. Space and time are separate and independent of each other and they cannot be mixed in any way.
In special relativity, however, space and time are just different coordinates of the so-called space-time, i.e., space and time merge together into a four-dimensional "world". The space coordinates and the time coordinate are mixed up together by the so-called Lorentz transformations. Every event corresponds to a point in space-time. In the words of Minkowski: "Henceforth space by itself, and time by itself are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."
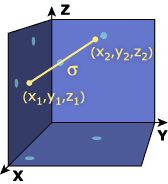
In classical Newtonian mechanics, we measure distances between two points by the formula
2 = (x1
- x2)2 + (y1 - y2)2 +
(z1 - z2)2,
where (x1, y1, z1) and (x2, y2, z2) are the coordinates of the two points. This is possible, since we have an absolute concept of simultaneity. In special relativity, however, the interval between two events is defined by
s2 = c2 (t1 - t2)2 - (x1 - x2)2 - (y1 - y2)2 - (z1 - z2)2,
where (t1, x1, y1, z1) and (t2, x2, y2, z2) are the coordinates of the two events. Note that s2 can in fact be negative! If we consider two events separated infinitesimally, (t, x, y, z) and (t + dt, x + dx, y + dy, z + dz), then the interval becomes
ds2 = c2 dt2 - dx2 - dy2 - dz2.
This "distance" formula is called the Minkowski metric and the corresponding four-dimensional "world" is called the Minkowski space-time or just the Minkowski space.
The Twin Paradox
 |
We should state from the
very beginning that the twin paradox is actually no paradox at all. The
"paradox" can be clarified as follows: A pair of twins, Adam and Eve,
are thinking of what will happen to their ages if one of them will go
away from Earth on a space journey. Will Eve for example be younger,
older, or have the same age as her brother if she leaves Earth with a
space-ship and then returns after some time? Actually, Eve will be younger than her brother when she returns to Earth. The reason is that Eve is not in the same inertial frame all the time. Assume that Adam and Eve are equipped with two watches (one each)
that are synchronized before Eve leaves on her space journey. When Eve
returns to Earth and Adam, the time
However, can you not turn the discussion around and say that Eve has been at rest in her space-ship while Adam has been on a "space journey" with planet Earth? In that case, Adam must be younger than Eve at the reunion! If these discussions were both correct, then Adam should be both older and younger than Eve at the same time. But both these discussions are not correct. Adam is at rest all the time on Earth, i.e., he is in the same inertial frame all the time, but Eve is not (as was stated above). Eve will feel forces when her space-ship accelerates and retards, and Adam will not feel such forces. P.S. Eve's space-ship has to consume fuel, which means that it costs to keep yourself young! |
according to Eve's watch. Thus, Eve is younger than Adam, when the two
twins meet again after Eve's space journey.
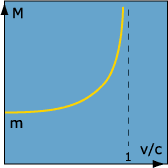
Energy is Equivalent to Mass
Energy and mass are related to each other by the well-known formula E0= mc2, where E0 is the rest energy, m is the mass, and c is the speed of light in vacuum. This means that mass and energy are equivalent.
The 'effective' mass M of an object moving relative to an observer at rest is given by
where E is the energy of the object and m is the mass of the object. This formula is called the relativistic mass formula.
Special Relativity as a Tool
At speeds close to the speed of light in vacuum c relativistic effects become important to consider. Such speeds are normally not encountered in everyday life. However, special relativity is used by scientists when doing calculations in, e.g., particle kinematics, since the particles often have speeds close to the speed of light in vacuum. Also in space physics, special relativity is an important tool.
In 1928, the brilliant English physicist P.A.M. Dirac unified the quantum theory of W. Heisenberg with special relativity in two papers named "The Quantum Theory of the Electron." He received the Nobel Prize in Physics for his contribution as early as 1933. He shared the prize with the Austrian physicist E. Schrödringer, who played a major role in the development of quantum mechanics. At a conference dedicated to the one-hundredth anniversary of Einstein's birth, Dirac said: "Right from the beginning of quantum mechanics, I was very much concerned with the problem of fitting it in with relativity. This turned out to be very difficult, except in the case of a single particle, where it was possible to make some progress. One could find equations for describing a single particle in accordance with quantum mechanics, in agreement with the principle of special relativity. It turned out that this provided an explanation of the spin of the electron." The equation that Dirac was talking about is today known as the Dirac equation and this is the equation describing the dynamics of particles with spin 1/2. Furthermore, Dirac said: " Also, one could develop the theory a little further and get to the idea of antimatter. The idea of antimatter really follows directly from Einstein's special theory of relativity when it is combined with the quantum mechanics of Heisenberg. There is no escape from it."
History of Special Relativity
Einstein was far from being the only person who contributed to the development of the theory of special relativity. However, he was the one who put everything together. Some important years:
 |
|
| 1687 Sir Isaac Newton published his book Philosophiae naturalis principia mathematica (or just Principia). In classical Newtonian mechanics, time was universal and absolute. |
|
| 1873 James Clerk Maxwell completed his theory of electromagnetism. This theory turned out to be compatible with special relativity, even though special relativity was not known at that time. |
|
| 1887 The famous Michelson-Morley experiment was performed by Albert Abraham Michelson and Edward Williams Morley. In the same year, during studies of the Doppler effect, Woldemar Voigt wrote down what were later to be known as the Lorentz transformations. The Lorentz transformations were also written down in 1898 by Joseph Larmor and in 1899 by Hendrik Antoon Lorentz. |
|
| 1898 Jules Henri Poincaré said that "... we have no direct intuition about the equality of two time intervals." |
|
| 1904 Poincaré came very close to special relativity: "... as demanded by the relativity principle the observer cannot know whether he is at rest or in absolute motion." |
|
| 1905 On June 5, Poincaré finished an article in which he stated that there seems to be a general law of Nature, that it is impossible to demonstrate absolute motion. On June 30, Einstein finished his famous article On the Electrodynamics of Moving Bodies, where he formulated the two postulates of special relativity. Furthermore, in September, Einstein published the short article Does the Inertia of a Body Depend upon Its Energy-Content? In which he derived the formula E0=mc2. |
|
| 1908 Max Planck wrote an article on special relativity. He was the second person after Einstein who wrote an article about this theory. In the same year, Hermann Minkowski also published an important article about special relativity. |
|
| 1915 On November 25, nearly ten years after the foundation of special relativity, Einstein submitted his paper The Field Equations of Gravitation for publication, which gave the correct field equations for the theory of general relativity (or general relativity for short). Actually, the German mathematician David Hilbert submitted an article containing the correct field equations for general relativity five days before Einstein. Hilbert never claimed priority for this theory. |
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru