Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
Relativistische Raumkonzepte
|
Wie viele Dimensionen hat die Welt?
Die Frage der Dimensionen der Raumzeit wurde seit der Entdeckung des
Minkowskiraums akut. Man kann die Gleichung für den Kegelschnitt (siehe
Abbildung 6) auf folgende Weise herleiten:
Zuerst nennen wir die allgemeine Formel für die Metrik, die sich aus der
Anwendung des Satz des Pythagoras (1) für drei Dimensionen ergibt:
ds2 = dx12+dx22+dx32 (6).
Unter der Voraussetzung, dass das Licht in der Zeit dt die Strecke ds mit der konstanten Geschwindigkeit c zurücklegt, gilt für den Weg mit ds=vdt:
ds2 = c2 dt2 (7).
Wir können nun (6) und (7) gleichsetzen, umstellen und erhalten dann
dx12 + dx22 + dx32 - (cdt)2 = 0 (8).
Die unterschiedliche Qualität der räumlichen und der zeitlichen
Koordinate bleibt hier durch das unterschiedliche Vorzeichen sichtbar.
Wenn wir jedoch die bekannte Eigenschaft der imaginären Zahl i als
i2= - 1 (9) verwenden,
können wir (8) umformen zu:
dx12 + dx22 + dx32 + (icdt)2 = 0 (10).
Damit bekommt die zeitliche Koordinate formal ((icdt)2 = dx42)
die gleiche Qualität wie die Raumkoordinaten.
Die Schreibweisen (8) oder (10) implizieren unterschiedliche Vorstellungen
über die Raumzeit, speziell ihre Dimensionalität. (8) impliziert ein
zeitlich dynamisches Verhalten in einem weiterhin dreidimensionalen Raum;
(10) geht von 4 Dimensionen in einer statischen, rein räumlichen,
geometrischen Vorstellung aus. 1920 verwendet Einstein die Darstellung (10)
(Einstein 1920a: 82f.), geht jedoch in einer Schrift von 1936 zur Form von
(8) über (Einstein 1936: 331).
Die neuen Ideen aus der Physik fanden eine rasche Aufnahme bei vielen
Künstlern. Ich möchte für beide raumzeitlichen Vorstellungswelten ein
Beispiel vorstellen:
| dx12 + dx22
+ dx32 - (cdt)2 = 0 Hier werden dreidimensionale Objekte so dargestellt, dass sie den Eindruck erwecken, sie würden sich bewegen; die Bewegungskomponente ist qualitativ von der Raumdimensionalität unterschieden: Abbildung 7: |
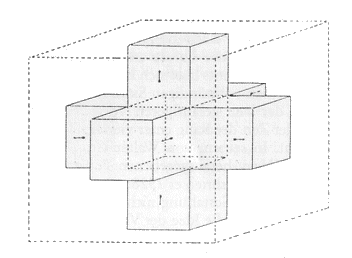
dx12 + dx22
+ dx32 + (icdt)2 = 0 Die Raumzeit wird als vierdimensionaler Raum dargestellt, in dem auf den Trick zurück gegriffen wird, dass z.B. dreidimensionale Objekte in den zweidimensionalen Raum hinein gefaltet werden können. Die 4. Dimension kann man derart in aufgefalteter Form im dreidimensionalen Raum andeuten - es entsteht ein sog. Hyperkubus (vgl. Banchoff 1991: 105ff.).
Abbildung 8: |
Gegen die Gleichstellung der 4 Dimensionen wie in (10) sprechen allerdings einige physikalische Argumente [1], wie die Inkongruenz der linken und der rechten Hand sowie das Auftreten von Dunkelheit nach dem Löschen eines Lichts (vgl. Kanitscheider 1991: 426).
Zur Interpretation der Einsteinschen Feldgleichung der allgemeinen Relativitätstheorie
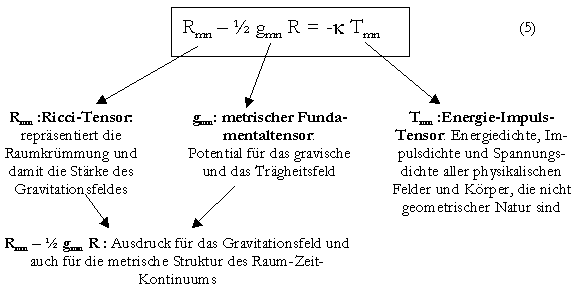
Die Einsteinsche Feldgleichung der allgemeinen Relativitätstheorie ((5),
mit k: Konstante) erfasst komplexe Zusammenhänge:
I. Das Gravitationsfeld und die metrische Struktur des
Raumzeitkontinuums sind miteinander unauflösbar verbunden (linke Seite der
Gleichung).
II. Die Krümmung/Gravitationswirkung (linke Seite) ist der Wirkung
der nichtgeometrischen Materiefaktoren (rechte Seite) äquivalent.
Die mathematische Äquivalenz in II. sagt erst einmal nichts über eine kausale Verursachung. Die Form der Gleichung wurde aber bewusst in Anlehnung an die Poissonsche Feldgleichung der klassischen Physik[2] gewählt. Die Energie-Impulsdichte gilt dabei als Quelle der Erregung eines Gravitationsfeldes (Gleichheitszeichen), das in unserem Fall eng mit der metrischen Struktur der Raumzeit verbunden ist (linke Seite). Das Feld bestimmt dann wiederum die Bewegungsmöglichkeiten von Objekten.

|
Der Zusammenhang von nichtgeometrisierter Materie (rechte
Seite) und Gravitation und Metrik (linke Seite) ist nichtlinear: Raum
und Zeit werden "durch das Schwerefeld bestimmt, während das Schwerefeld
seinerseits von der Verteilung der Massen im Universum abhängt." (Renn
2006: 200)
Abbildung 9: Abhängigkeit des Schwerefelds und der Raumzeitmetrik von der Masseverteilung(Quelle: Bublath 1999: 39) |
Das Raumzeitkontinuum ist eng verknüpft mit den Eigenschaften der Materie - einerseits (auf der linken Seite der Gleichung) mit der gravitativen Wirkung, andererseits auch mit den anderen Materieformen (den nicht gravitativen, nicht geometrisierten auf der rechten Seite der Gleichung). Einstein fasste zusammen:
Trägheit, Gravitation und metrisches Verhalten der Körper und Uhren wurden auf eine einheitliche Feldqualität zurückgeführt, dies Feld selbst wieder als von den Körpern abhängig gesetzt [...]. Damit waren Raum und Zeit zwar nicht ihrer Realität entkleidet, wohl aber ihrer kausalen Absolutheit (beeinflussend, aber nicht beeinflußt). (Einstein 1953: 206)
Einstein selbst war bis zuletzt nicht zufrieden mit der Uneinheitlichkeit von gravitativer (linke Seite) und nicht geometrisierter Materie (rechte Seite). Die möglichen Materie-Energie-Tensoren sind nicht theoretisch bestimmbar; als physikalisch sinnvoll erwiesen sich nur wenige der theoretisch möglichen. Einstein verglich seine Formel deshalb mit einem "Gebäude, dessen einer Flügel aus vorzüglichem Marmor (linke Seite der Gleichung), dessen anderer Flügel aus minderwertigem Holz gebaut ist (rechte Seite der Gleichung)" (Einstein 1936: 335). Einstein versuchte bis zuletzt, aus dem Holz ebenfalls Marmor zu machen, d.h. die gravitative und die elektromagnetische Wechselwirkung zu vereinen - mit der Quantentheorie konnte er in dieser Beziehung wenig anfangen (vgl. ebd.: 336).
Die Raummolluske
In der allgemeinen Relativitätstheorie gilt, dass der Raum[3] nicht mehr ein "starrer Bezugskörper" ist, sondern seine Metrik vom lokalen Gravitationsfeld abhängt. Diese Folge des allgemeinen Relativitätsprinzips beschreibt Einstein auch mit dem Wort "Bezugsmolluske" (Einstein 1920a: 67). Bloch paraphrasiert dies später:
Ein vierdimensionaler Riemannscher Raum liegt der allgemeinen Relativitätstheorie zugrunde, der nirgends mehr metrische Starre zeigt, sondern, nach Einsteins Ausdruck, "nachgiebig ist wie ein Mollusk". (Bloch EM: 110)
Trotzdem bleibt hier zu berücksichtigen, dass die Metrik der Raumzeit nicht völlig äquivalent mit den Materiewirkungen geworden ist. Es bleibt ein "Rest" übrig:
Die Metrik ist zur Beschreibung der Materie notwendig und deswegen durch die Materie selbst nicht festlegbar." (Kiefer 2003: 103)
Das bedeutet, dass die oben genannte Äquivalenz in II. nicht ganz
eineindeutig ist. Zwar kann man aus der Raum-Zeit-Metrik die
Materieverteilung im Kosmos ermitteln, aber die Materieverteilung bestimmt
die Weltmetrik nicht eindeutig (vgl. Treder 1998: 31). So wie für jeden
gewölbten Körper innerhalb des dreidimensionalen Raumes an jedem Punkt eine
Tangentialebene konstruiert werden kann, deren Menge den Körper "einhüllt",
so kann die "Raummolluske" durch jeweils entsprechend der Stärke des
Gravitationsfeldes geneigte Minkowskische Lichtkegel vorgestellt werden.
In schwachen Gravitationsfeldern und in lokalen Bereichen kann der
pseudoeuklidische Minkowskiraum als Näherung verwendet werden (vgl. Treder
1968: 7).
Die Messbarkeit im Riemannschen Raum
Es stellt sich heraus, dass auch in der allgemeinen Relativitätstheorie
die Raumzeit nicht vollständig in der materiellen Dynamik aufgehoben ist,
sondern es eine Dualität von raumzeitlicher Metrik, die auch als
Gravitationsfeld darstellbar ist (dem "Gravitationsäther"[4])
und nicht geometrisierbarer Materie gibt.
Eine weitere Fragestellung ergibt sich, wenn wir bedenken, dass wir nicht
über irgend welche abstrakten Materieformen bzw. Raumzeiten sprechen,
sondern dass wir Physik betreiben, also "eine Theorie, die auch zutreffen
muß." (Treder 1999: 49) Es geht also darum, die physikalischen
Bewegungsformen, die wir untersuchen, nicht nur spekulativ in einer
mathematischen Form darzustellen - sondern diese Darstellung muss auf ihren
Wahrheitsgehalt hin überprüfbar sein. Soweit es um raumzeitliche Bewegung
geht, muss in Raum und Zeit gemessen werden können.
In der speziellen Relativitätstheorie ist die Definition der
Gleichzeitigkeit immer nur für ein Inertialsystem möglich. Trotzdem, so
hatten wir bereits gesehen, lassen sich Raum- und Zeitkoordinaten noch
unmittelbar messen.
Diese unmittelbare Interpretation der Raum- und Zeitkoordinaten durch
Maßstäbe und Uhren geht in der allgemeinen Relativitätstheorie verloren.
Aber die Messbarkeit war für Einstein so wichtig, dass er den
korrespondenzmäßigen Anschluss an die Messbarkeit im euklidischen Raum zur
Richtschnur bei der Entwicklung der allgemeinen Relativitätstheorie
verwendet hatte (vgl. Renn 2006: 271).
Jene Verallgemeinerung der Metrik [...] beruht im Wesentlichen darauf, daß die Metrik der speziellen Relativitätstheorie für kleine Gebiete auch im allgemeinen Fall noch Gültigkeit beanspruchen kann." (Einstein 1953: 175; vgl. auch Einstein 1920d: 276)
Peter Mittelstaedt behauptet, Einsteins Forderung nach Messbarkeit sei eine "Konsequenz der von Einstein vertretenen methodischen Forderung, daß eine physikalische Theorie nur beobachtbare Größen enthalten darf" (Mittelstaedt 1989: 76). Heisenberg berichtet jedoch, dass das in dieser Form nicht stimmt:
"Aber Sie glauben doch nicht im Ernst", entgegnete Einstein, "daß man in eine physikalische Theorie nur beobachtbare Größen aufnehmen kann."
"Ich dachte", fragte ich erstaunt, "daß gerade Sie diesen Gedanken zur Grundlage Ihrer Relativitätstheorie gemacht hätten? Sie hatten doch betont, daß man nicht von absoluter Zeit reden dürfe, da man diese absolute Zeit nicht beobachten kann."[...]
"Vielleicht habe ich diese Art von Philosophie benützt", antwortete Einstein, "aber sie ist trotzdem Unsinn [...]. Vom prinzipiellen Standpunkt aus ist es ganz falsch eine Theorie nur auf beobachtbare Größen gründen zu wollen. Denn es ist ja in Wirklichkeit ganz genau umgekehrt. Erst die Theorie entscheidet darüber, was man beobachten kann.[...]
Nur die Theorie, das heißt die Kenntnis der Naturgesetze, erlaubt uns also, aus dem sinnlichen Eindruck auf den zugrunde liegenden Vorgang zu schließen" (Heisenberg 1988: 79-80).
Der Zusammenhang zwischen Messbarkeit und Darstellung objektiver raumzeitlicher Strukturen ist also komplizierter.
"Wie bestimmt man die Gleichförmigkeit der Bewegung eines Körpers? Wir benötigen dazu Inertialmaßstäbe und Inertialuhren. Woher haben wir solche? Aus diesen aufgeworfenen Fragen wird eine Grundsatz-Problematik der modernen Physik deutlich, nämlich die Problematik des Meßprozesses [...]
Das Messen kann nicht mehr so einfach wie im vorigen Jahrhundert als bloßes Vergleichen des Meßobjekts mit einem Maßstab gesehen werden, sondern es müssen darüber hinaus noch genau die Bedingungen des Messens fixiert werden. Dazu bedarf es aber einer eigenen Theorie des Meßprozesses [...]
Man setzt die Existenz von Inertialmaßstäben und Inertialuhren als Standard-Basis in unendlicher Entfernung von den gravitierenden Massen voraus und operiert mit diesen Meßmitteln. (Schmutzer 1981: 28f.)
Die Wahl der für die Theorie angemessenen Raumzeitstruktur hat einerseits das konstruktive Element, dass z.B. die Riemannsche Geometrie nicht unmittelbar aus den Tatsachen geschlossen werden kann, andererseits muss die gewählte Geometrie physikalische Erfahrung, also raumzeitliche Messungen, ermöglichen. Der "Dualismus" zwischen Raumzeit und materieller Dynamik ist kein trennender, sondern ein die Unterschiede bewahrender, verbindender.
Hermann Weyl hatte versucht, diesem Dualismus zu entkommen, indem er auch den Längenmaßstab selbst mit veränderte (vgl. Weyl 1921: 224). Dem wiedersprach jedoch Einstein. In der Rezension eines Buches von Weyl schrieb er:
Ferner möchte ich im Interesse der Vollkommenheit der Darstellung vom Standpunkte des Physikers wünschen, daß die physikalische Bedeutung des Abstandes (als unmittelbares Ergebnis der mit Maßstäben und Uhren zu gewinnenden Messungen) in der zweiten Auflage etwas mehr in den Vordergrund gestellt werde. (Einstein 1918c: 373).
Oder noch deutlicher:
Die zeit-räumlichen Abstände sind mit Hilfe von Maßstäben und Uhren physikalisch definiert. Betrachte ich zwei Gebilde (Maßstäbe bzw. Uhren), so ist ihre Gleichheit erfahrungsgemäß unabhängig von ihrer Vorgeschichte. Hierauf beruht die Möglichkeit, zwei benachbarten Weltpunkten eine Zahl ds zuzuordnen, welche physikalische Bedeutung besitzt. Indem die Weylsche Theorie auf diese empirisch begründete Zuordnung verzichtet, beraubt sie die Theorie einer ihrer solidesten Stützen und Prüfungsmöglichkeiten. (Einstein 1920c: 351: vgl. Weyl 1918: 40))
Dass diese messtheoretische Zuordnung eines starren Maßstabes nicht lediglich subjektive Willkür ist, sondern der raumzeitlichen Struktur der objektiven Realität auch entspricht, zeigt Einstein daran, dass es in allen Lichtbotschaften aus dem All scharfe Spektrallinien gibt. Das bedeutet, dass die Eigenfrequenzen desselben chemischen Elements überall gleich sind und als Standard für zeitliche Abstände gelten können (Einstein 1953: 163). Das lässt sich dann über die Lichtausbreitung auch auf die räumlichen Koordinaten übertragen.
Mit diesem Zustand des Dualismus von Raumzeit und Materiedynamik war Einstein letztlich nicht zufrieden:
Es ist eine logische Schwäche der Relativitätstheorie in ihrem heutigen Zustande, daß sie Maßstäbe und Uhren gesondert einführen muß, statt sie als Lösungen von Differentialgleichungen konstruieren zu können. (Einstein 1920c: 353)
Was ist real?
Bisher wurde meist angenommen, so etwas wie physikalische Teilchen,
Kräfte oder Felder könne man als real existierend annehmen, beim Raum gab es
Streitigkeiten, ob es ihn real gibt oder ob er lediglich eine ideelle
Denkvoraussetzung sei. Jetzt erweist sich ein Teil der Wirklichkeit, das
Gravitationsfeld und die Metrik als ineinander umwandelbar, als wesensgleich.
Wenn wir als "real" das definieren, was invariant ist, so würde das
Gravitationsfeld bzw. die Metrik diese Zuschreibung durch die Allgemeine
Relativitätstheorie verlieren. Wir erwähnten bereits das mentale Modell des
Menschen in einem frei fallenden Kasten ("Aufzug"), bei dem durch die
Fallbewegung die Wirkung des Gravitationsfeldes gerade aufgehoben wird. Wenn
wir also ein mitbewegtes Bezugssystem wählen, haben wir das Gravitationsfeld
"wegtransformiert", es ist nicht invariant, also nicht "real" (vgl.
Kanitscheider 1991: 175). Bei dieser Sichtweise bleibt ein anderes Moment
der Gravitation real: die Gravitationsgezeitenkraft.

|
In einem homogenen Gravitationsfeld besagt das
Äquivalenzprinzip, dass es für einen Menschen in einem geschlossenen
Kasten ("Aufzug") nicht möglich ist zu unterscheiden, ob er
Trägheitskräften oder der Gravitation unterliegt. Als mentales Modell
hierfür dient auch die Vorstellung, dass in einem frei fallenden Aufzug
die Gravitationskraft durch die Trägheitskraft aufgehoben wird. Insofern
kann die Trägheitsbewegung in eine Gravitationsbewegung umtransformiert
werden (bzw. umgekehrt). In einem nicht homogenen Gravitationsfeld (wie in Abbildung (10)) fallen die Massenpunkte nicht entlang paralleler Geodäten, sondern die Bahnen konvergieren. Diese Bewegung "aufeinander zu" kann in keinem Bezugssystem wegtransformiert werden. und ist Ausdruck der durch die Gravitation veränderten Geometrie der Raumzeit.
Abbildung 10: Gravitations-Gezeitenkräfte(aus Bublath 1999: 91) |
Legen wir jedoch eine andere Bestimmung von "Realität" zugrunde, nämlich diejenige, nach der real ist, was wirkt, so erhalten wir eine andere Sichtweise. Ian Hacking sagte über die Realität von Quarks: "If you can spray them, then they are real" (Hacking 1994: 22). In diesem Sinne wäre der sog. "Gravitationsäther", also die Einheit Gravitationsfeld/Metrik durchaus real, denn er bestimmt das physikalische Geschehen mit (vgl. Einstein 1920b: 317).
Kosmologie
Die Feldgleichung der allgemeinen Relativitätstheorie macht lediglich
lokale Aussagen. Sie hat auch nicht nur eine Lösung, sondern als System von
zehn nichtlinearen Differentialgleichungen zweiter Ordnung für gmn
können sehr viele verschiedene Lösungen berechnet werden, von denen nicht
alle physikalisch sinnvoll interpretierbar sind. Wie diese Grundgleichung
sich im realen, globalen Weltraum auswirkt, ist eine zusätzliche
Fragestellung (vgl. Einstein 1951/1979: 109). Weil die Feldgleichungen
allein keine Aussagen über das großräumige Universum machen, lassen sich
durch die Einbeziehung unterschiedlicher zusätzlicher Annahmen (z.B. über
die Homogenität und Isotropie der Materieverteilung) verschiedene Lösungen
errechnen, die dann mit der Wirklichkeit verglichen werden müssen. Einstein
hatte zuerst eine Lösung gefunden, die für ein statisches Weltall sprach,
wie er es auch erwartete. Jedoch fand der sowjetische Physiker Alexander
Friedmann 1922 eine andere Lösung für einen nichtstationären Kosmos. Später
wurde die Expansion des Weltalls auch experimentell bestätigt. Dabei gilt
weiterhin, dass es 1. keine eineindeutige Beziehung zwischen dem Materie-Energie-Tensor
und der Raummetrik gibt und 2. die globalen Eigenschaften sowie die
Topologie des Raums sich daraus auch nicht ergeben. Durch die Einbeziehung
von weiteren Zusatzannahmen ergeben sich vielfältige Lösungen der
Einsteinschen Feldgleichungen.
Hans Jürgen Treder entwickelte in den 90er Jahren eine Kritik an diesem
Vorgehen. Er folgte darin Ernst Mach, für den es keine Trennung zwischen
Grundgleichungen und kontingenten Anfangs- und Randbedingungen geben darf.
Das Weltsystem ist uns nur einmal gegeben mit allen seinen allein bestimmbaren Relativbewegungen. (Mach, zit. bei Treder 1998: 23, vgl. Mach 1983/1921: 222)
Das Ziel bestand also für Treder darin, eine Physik zu finden, in der es nur eine einzige exakte Lösung aller physikalischen Gleichungen gibt.
Die Aufhebung des Raumes im Machschen Prinzip
In einer historischen Darstellung der Entwicklung der Relativitätstheorie
ist dem sog. Machschen Prinzip eine große Bedeutung zuzuschreiben. Es war
ein wichtiges heuristisches Prinzip für Einstein, obwohl es in seiner
Theorie letztlich nicht gänzlich verwirklicht werden konnte. Die Debatte um
das Machsche Prinzip beinhaltet gerade die Frage nach dem Verhältnis von
physikalischer Materie und Raumzeit.
Ernst Mach hatte sich, wie viele andere, am absoluten Raum von Newton
gestört. Er meinte: "Bleibt man auf dem Boden der Tatsachen, so weiß man
bloß von relativen Räumen und Bewegungen." (Mach 1883/1921: 226). Er
versuchte das Newtonsche Eimerexperiment (siehe Abbildung 3) auf eine
alternative Weise zu erklären. Newton sah darin die Wirkung des absoluten
Raumes realisiert. Mach wollte diese aus seiner Sicht abstrakte Konstruktion
unnötig machen und verwies auf die Möglichkeit, die Trägheitsbewegung des
Wassers im Eimer durch die Wirkung von Kräften aus dem gesamten Universum zu
erklären. Die Trägheitskräfte sollen nicht durch Beschleunigung gegenüber
dem absoluten Raum, sondern gegenüber den Hintergrundmassen im Universum
zustande kommen. "Wenn wir daher sagen, daß ein Körper seine Richtung und
Geschwindigkeit im Raum beibehält, so liegt darin nur eine kurze
Anweisung auf die Beachtung der ganzen Welt." (ebd.: 227) Einstein
reihte das "Machsche Prinzip" als dritten Hauptgesichtspunkt seiner Theorie
neben dem Relativitäts- und dem Äquivalenzprinzip ein (Einstein 1918b: 241).
Dieses Prinzip bedeutet, "daß das G-Feld[5]
durch den Energietensor der Materie bedingt und bestimmt sei (ebd.: 242),
d.h. auch: "Das wahre metrische Feld gmn muß ganz durch die
Materie der Welt bestimmt sein" (Einstein 1922/1979: 66), d.h. d.h. die
Metrik muss in eindeutiger Weise aus Energie und Impuls der Materie im
Universum hervorgehen. Der Dualismus von Raumzeit und Dynamik wäre dann
aufgehoben. Nach Kanitscheider (1991: 170) kann das für die Feldgleichung
Verschiedenes bedeuten:
- in Abwesenheit von Materie (Tmn -> 0) ist kein Gravitationsfeld möglich (d.h. die Metrik degeneriert gmn -> 0)[6],
- in Abwesenheit von Materie wird die Metrik minkowskisch (gmn -> hmn)[7],
- in Abwesenheit der Materie verschwindet die Krümmung (Rabgd -> 0) oder
- es gibt keine Vakuumgleichungen.
Keine dieser verschiedenen Varianten ist in der allgemeinen
Relativitätstheorie erfüllt. [8]Die Metrik wird
nicht eindeutig von der Materie bestimmt, aber beeinflusst. Das Machsche
Prinzip gilt nur unter Einbeziehung zusätzlicher Randbedingungen.
Bis ca. 1920 meinte Einstein noch, seine 1915 gefundene Feldgleichung würde
der Machschen Forderung entsprechen. Seine 1917 veröffentlichte erste
kosmologische Lösung stimmt noch mit Machs Grundannahme überein, dass alle
Trägheitseigenschaften der Raumzeit durch die Masseverteilung bestimmt sind
(Einstein 1917). Unter Verwendung einer Gleichung mit dem kosmologischen
Glied l konnte Einstein einen geschlossenen, statischen Kosmos mit
gleichmäßiger Materieverteilung ableiten. Sogar als de Sitter zeigte, dass
auch die um l ergänzte Feldgleichung eine weitere Lösung besitzt, in
der es zwar keine Materie, aber Trägheitseigenschaften gibt - was dem
Machschen Prinzip widerspricht - widersprach Einstein.
Bestände die de Sittersche Lösung überall zu Recht, so würde damit gezeigt sein, daß der durch die Einführung des "l-Gliedes" von mir beabsichtigte Zweck nicht erreicht wäre. Nach meiner Meinung bildet die allgemeine Relativitätstheorie nämlich nur dann ein befriedigendes System, wenn nach ihr die physikalischen Qualitäten des Raumes allein durch die Materie vollständig bestimmt werden. (Einstein 1918a: 271)
Im Jahr 1919 begründet Einstein seine Skepsis gegen weitere kosmologische
Modelle immer noch mit dem Machschen Prinzip - aber für ihn wird die
Fragestellung der Besonderheit des elektromagnetischen Felds gegenüber dem
Gravitationsfeld bedeutsamer (Einstein 1919b). Im September 1920 verwendet
Einstein in einer Diskussion die Machsche Argumentation, nach welcher das
Gravitationsfeld durch ferne Massen induziert wird (Einstein 1920c: 354),
obwohl er im Mai bereits gegen Mach argumentiert hatte weil dessen Erregung
der Trägheitswirkung durch kosmische Massen eine neue Art Fernwirkung
voraussetzen würde (Einstein 1920b: 316). In diesem Zusammenhang spricht
Einstein nun sogar von einem physikalisch wirksamen Raum und gibt ihm den
Namen "Äther", der von der Materie mitbedingt wird.
Ungeachtet dieser Divergenz spricht er 1921 in London wieder davon, dass er
von einer räumlich geschlossenen Welt ausgeht, weil in seiner Theorie "die
physikalischen Eigenschaften des Raumes durch die ponderable Materie
beeinflußt sind." (Einstein 1921: 433) Das Insistieren auf der
Geschlossenheit scheint für eine weitere Verteidigung seines Standpunkts von
1917 zu stehen, obgleich die Wortwahl vorsichtiger geworden ist. Er spricht
davon, dass die Raumeigenschaften von der Materie "beeinflußt" sind, nicht
mehr "allein" oder "vollständig" wie früher. Im Manuskript der Leidener Rede
(1920b) fällt eine nachträgliche Änderung auf: Zuerst stand dort: "Nach
dieser Theorie [der allgemeinen Relativitätstheorie, A.S.] sind die
metrischen Eigenschaften des Raum-Zeit-Kontinuums in der Umgebung der
einzelnen Raum-Zeitpunkte verschieden und bedingt durch die außerhalb des
betrachteten Gebietes vorhandene Materie", wobei das hier hervorgehobene
Wort "bedingt" verändert wurde in "mitbedingt" (ebd.: 317, siehe Anmerkung
20 auf S. 322).
Noch 1922 verteidigte er seinen statischen Kosmos, indem er meinte, in der
Lösung von Alexander Friedmann, die einen dynamischen Kosmos bedeutet,
Fehler nachweisen zu können. Er sah schnell ein, dass er sich irrte (siehe
Einstein 1954 -Anhang 4). 1929 schließlich konnte Hubble nachweisen, dass
das Weltall tatsächlich expandiert. Einstein erfuhr 1931 von diesem Ergebnis
und es wurde klar, dass damit das Machsche Prinzip nicht mehr aufrecht zu
erhalten war.
1930 hat Einstein sogar den ursprünglichen Inhalt des Machschen Prinzips
umgekehrt. Während bei Mach der Raum auf rein (physisch) materielle
Körpereigenschaften zurückgeführt werden sollte, nahm Einstein jetzt an,
dass die physische Materie nur eine Folge räumlicher Eigenschaften sei.
Der Raum, ans Licht gebracht durch das körperliche Objekt, zur physikalischen Realität erhoben durch Newton, hat in den letzten Jahrzehnten den Äther und die Zeit verschlungen und scheint im Begriffe zu sein, auch das Feld und die Korpuskeln zu verschlingen, so daß er als alleiniger Träger der Realität übrig bleibt. (Einstein1930: 180)
Dass er sich auch später durchaus eindeutig gegen ein Festhalten am Machschen Prinzip ausgesprochen hat, zeigen zwei weitere Belege: In einem Brief an Felix Pirani im Jahr 1954 erklärte Einstein, "daß er es inzwischen nicht mehr einleuchtend finde, daß das Gravitationsfeld durch den Energieimpulstensor der Materie vollständig bestimmt sein solle, wie es das Machsche Prinzip fordert." (zit in Renn 2006: 298)
Denn eine solche Bestimmung ist ja nur dann möglich, wenn zuvor die Verteilung der Materie in der Raumzeit gegeben ist. Dies aber setzt bereits Wissen über eine gegebene Raumzeit voraus, was wiederum die Kenntnis der Metrik verlangt, die doch durch die Feldgleichung erst bestimmt werden soll. (ebd.)
Auch in seinen autobiographischen Notizen bekräftigt er diese Abwendung vom Machschen Prinzip mit dem Argument: "In eine konsequente Feldtheorie passt ein solcher Lösungsversuch nicht hinein..." (zit. in Renn 2006: 299). Trotzdem ist es auch eins der Ziele dieser weiter entwickelten Feldtheorie bei Einstein, die Forderung der Messbarkeit in einer letztlich vollständigen Theorie nicht mehr zu benötigen (Einstein 1949: 509)
Geometrodynamik - alles ist Raum
Wie schon erwähnt, war Einstein unzufrieden mit der Dualität der linken
und der rechten Seite seiner Feldgleichung (5). Der weitere Weg wurde von
ihm und auch nach seinem Tod von anderen Wissenschaftlern in weiteren
Vereinigungsversuchen gesehen. Eins dieser Programme war die Geometrodynamik
nach Wheeler in den 60er Jahren (Wheeler 1962). Das Machsche Prinzip hatte
die Vereinheitlichung von Raumzeit und dynamischer Materie durch die
Abschaffung der Raumzeit versucht - in der Geometrodynamik sollte die
Materie auf die Geometrie zurückgeführt werden. Es wurde vermutet, dass alle
nichtgeometrischen Materieformen aus der Krümmung einer geeigneten Geometrie
abgeleitet werden können. Dies war der Versuch, die "materielle Welt aus
leerem gekrümmten Raum aufzubauen" (Kanitscheider 1991: 429). Da
Vereinheitlichungen in der physikalischen Theorie bedeuten, in vorher
getrennten Bereichen ein gemeinsames Wesen aufzufinden, wurde bereits
spekuliert, dass "in den geometrischen Strukturen [...] das Wesen
physikalischer Prozesse zutage [tritt]." (Griese 1966: 76) Innerhalb der
Geometrie ergäbe sich jedoch auch hier eine Art Dualismus, und zwar jener
zwischen Metrik und Topologie (Von Borzeszkowski, Wahsner 1979: 215).
In den 70er Jahren erwies sich dieses Projekt in dieser Weise als nicht
realisierbar. Neue Theorien wie die String- und die Looptheorie entstanden,
wobei sich neue Ideen und Begriffe entwickelten, die nicht mehr einfach in
das alte Konzept einzuordnen waren. Die Loop-Theorie ist dabei eine Art "Erbe"
der Geometrodynamik.
String- und Looptheorien
Stringtheorie
Die derzeit aktuellsten Kandidaten für eine neue Theorie, die alle
bekannten physikalischen Wechselwirkungen vereinigt, sind die String- und
die Looptheorie. In der Stringtheorie wird angenommen, dass die kleinsten
Objekte, aus denen sich die Elementarteilchen aufbauen, nicht punktförmige
Objekte, sondern Wellen auf linienförmigen Objekten, nämlich den "strings" (auf
dt.: Schnur, Saite) sind. Diese Theorie erfordert nicht nur die bekannten 4
Dimensionen, sondern 10 und in ihrer weiter entwickelten Form als M-Theorie
11 Dimensionen. Genau so, wie die Anzahl der prognostizierten
Elementarteilchen immer weiter zunahm, so entstehen auch in der Stringwelt
immer neue Konzepte von Objekten, so z.B. auch zweidimensionale "Brane" (von
"Membrane"). Obwohl wir selbst nur auf einer Membran leben und auch Licht
und alle physikalischen Wechselwirkungen außer der Gravitation für uns auf
diese eine Membran beschränkt sind, könnte die Gravitation zwischen den
Branen wirken. Daraus lassen sich Experimente mit Messungen ableiten, die
aber noch nicht genau genug durchgeführt werden können, um diesen
eventuellen Einfluss zu messen. Um Effekte der zusätzlichen Dimensionen
entdecken zu können, wird auf Teilchenbeschleunigerentdeckungen gesetzt.
Die Strings und Brane bewegen sich nach wie vor in einer voraus zu setzenden
Raumzeit, auch wenn diese nun 11-dimensional ist. Lediglich eine von Hawking
entwickelte Variante könnte auf einen "Außenraum" verzichten (Hawking 2003:
207).
Prägeometrische Looptheorie
Seit Ende der 80er Jahre wurden alte Gedanken von Wheeler und Penrose
aufgegriffen und ein anderes Konzept einer erweiterten Theorie
vorangetrieben. Es ist die Theorie der Quantengeometrie, auch Loop Quantum
Gravity (Loop: Schleife) genannt. John Wheeler hatte in den 60er Jahren
bereits vorgeschlagen, die Raumzeit in den kleinsten Bereichen als "schaumförmig"
anzusehen, d.h. den Raum als ebenso gequantelt wie die Materie zu betrachten.
Roger Penrose entwickelte in den 70ern sog. "Spin-Netze", die als Grundlage
für eine Art "Raumzeit-Staub" zu verstehen waren. Raum und Zeit gelten dabei
nicht mehr als vorauszusetzendes Medium, sondern sie werden als Folge des
Aufeinanderwirkens der Elemente in "Spin-Netzwerken" erklärt (vgl.
Zimmermann 1991: 46ff.). Raum und Zeit entstehen aus quantenphysikalischen
Überlagerungen aller möglichen Zustände im Geflecht des Spin-Netzwerks.
Solch ein Netzwerk kann es schon "vor" dem Urknall gegeben haben und aus ihm
heraus entstand "beim" Urknall erst unser raumzeitliches Universum ("Initialemergenz").
Mittlerweile wurden bereits die mathematischen Voraussetzungen weit
entwickelt, um Bewegungen und Kräfte zu beschreiben, ohne eine
Hintergrundmetrik zu benötigen (basierend auf der mathematischen
Knotentheorie).
Demnach besteht die tiefste Fundierung unserer Welt auf einem nicht
raumzeitlichen Netzwerk von bestimmten Größen, die auch als "Twistoren"[9]
bezeichnet werden; daraus entsteht eine raumzeitliche Geometrie. Als
physikalische Materie bilden sich Anregungen in dieser Geometrie heraus (vgl.
Geometrodynamik). Da Geometrie und auch Materie quantisiert sind, können
sich Geometrie- und Materiequanten auch ineinander umwandeln, was für
Schwarze Löcher angenommen wird. In diesen Konzepten werden ebenfalls
Aussagen über beobachtbare Folgen der diskreten Raumzeit gemacht, vor allem
bei der Beobachtung von Gammastrahlen-Ausbrüchen (Smolin 2004: 62).
Rainer E. Zimmermann geht - die philosophischen Konzepte von Spinoza und Schelling sowie die physikalischen Ideen von Wheeler und Penrose präzisierend - davon aus, dass nur die mit Massen, Längen und Zeiten bestimmbaren Objekte als "Welt" zu verstehen sind Das bedeutet, dass die Überlegungen zur Grundlegung von Raum und Zeit keine Themen innerhalb der Welt darstellen, sondern zu ihrem Grund, den er mit Spinoza und Schelling Substanz nennt. (Zimmermann 2004: 447, 476) Die Vereinigung von allgemeiner Relativitätstheorie und Quantentheorie erfolgt also nicht innerhalb der Welt, sondern außerhalb, wobei der Grund selbst raum- und zeitlos ist (ebd.: 266ff.). Es geht also hier um eine "Prä-Geometrie" (ebd.: 310), die diskontinuierlich und ohne Metrik ist. "Der Kosmos wird dabei beschreiben als eine bloße lokale Verwerfung des globalen Netzwerks, an der Initialsingularität auftauchend, in der Zeit seiend, und - möglicherweise - in einer Endsingularität wieder in die Raum-Zeitlosigkeit verschwindend." (Eisenhardt, Kurth 1993: 24) Aus den prägeometrischen Strukturen heraus entstand unsere Welt aus einer "Initialemergenz", die als "Brechung der Zusammenhangsstruktur eines Vorzustands" (Kurth 1997: 270) beim Übergang in die raumzeitliche Existenz unseres Universums zu verstehen ist. Dabei sind mathematische Strukturen und Operationen in der Diskussion, die diesen Prozess nachzeichnen sollen, und es wird durchaus nach der "ontischen Referenz" dieser mathematischen Größen gefragt (Eisenhardt, Kurth 1993: 38), aber in dem Sinne, dass uns bewusst ist dass wir sie nicht wahrnehmen oder messen können (Zimmermann 2004: 494, 497).
Wir Menschen sind in diesem Konzept Teil der Welt, aber nicht ihres Grundes, der Substanz. Wir erleben die Welt in Raum und Zeit, innerhalb dieser betreiben wir die empirische Physik, die unserer experimentellen Erfahrung zugänglich ist. Darüber hinaus erfordert jedoch die tiefere Begründung von weltlicher Materie, Raum und Zeit eine andere Art Physik, eine fundamentale Physik, die gleichzeitig als spekulative Philosophie (im Sinne Schellings) zu verstehen ist. (ebd.: 518). Trotzdem gibt es keine absolute Trennung zwischen Welt und Grund, empirischer Physik und fundamentaler Physik bzw. spekulativer Philosophie. Worin besteht der Zusammenhang? Spin-Netzwerke gehören noch zur welthaften Physik, sie sind quasi ihr "Rand". Der Zusammenhang zu ihrem nicht mehr welthaften, d.h. nicht mehr physikalisch erkennbaren substantiellen Grund ist eben in dieser Begründung zu sehen: Die den Grund erfassende spekulative Phantasie muss Bezug auf das nehmen, was über die Welt mindestens bereits gewusst wird (ebd.: 483).
Fußnoten:
[1] Einstein betont, dass die
Gleichwertigkeit der Zeitkoordinate eine formale, aber keine physikalische
ist (Einstein 1920d: 263f.)
[2] Die Poissonsche Gleichung besagt für die
klassische Physik, "daß das Gravitationsfeld durch die Dichte r der
ponderablen Materie erregt wird." (Einstein 1922/1979: 81)
[3]Der "Raum" meint auch im Weiteren immer die
"Raumzeit".
[4] Zum Unterschied dieses Begriffes "Äther",
das auch Einstein (1920b) verwendet, siehe Weyl (1922: 324).
[5]Als G-Feld bezeichnet Einstein den durch den
Fundamentaltensor (der die metrischen Eigenschaften des Raumes sowie die
Gravitationswirkungen bestimmt) Raumzustand (Einstein 1918b: 141).
[6] So formuliert es Einstein: Es darf "kein G-Feld
möglich sein ohne Materie" (ebd.: 142).
[7] vgl. Schmutzer 1981: 106.
[8] Nur wenn das kosmologische Glied
hinzugefügt wird, gilt die erste Variante (ebd.).
[9] Twistoren berücksichtigen im Unterschied zu
Spinoren weitere "realistische" Parameter wie Bahndrehimpuls und Translation
sowie die Relativistik der Bewegungen (vgl. Zimmermann 1991: 49).
Hiçbir yazý/ resim izinsiz olarak kullanýlamaz!! Telif haklarý uyarýnca bu bir suçtur..! Tüm haklarý Çetin BAL' a aittir. Kaynak gösterilmek þartýyla siteden alýntý yapýlabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru