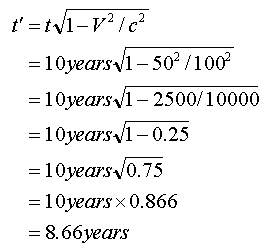|
Time Travel Research Center
© 2005 Cetin BAL - GSM:+90
05366063183 - Turkey / Denizli
Special Relativity in under 15 minutes!
The Special Theory of Relativity was proposed in 1905 by
Albert Einstein (1879-1955). The reason it is "special" is because it is
part of, or a "special case" of, the more comprehensive and complex General
Theory of Relativity. The latter, General Theory, was proposed by Einstein
in 1915.
 |
| Albert Einstein (1879 - 1955) |
Space and Time.
In an everyday co-ordinate system, such as a map, you can
specify a location using just dimensional distances. For example, to someone
looking for buried treasure we could say "go east for 20 miles, north for 5
miles, then dig down 30 feet". We have just specified a three dimensional co-ordinate
system. To this, Einstein added another factor, that of time. This still
makes sense in our everyday world: "go east for 20 miles, north for 5 miles,
dig down 30 feet, and then wait until 3 o'clock when I will meet you to
share the treasure!". However, if we go at very high speeds, speeds close to
the speed of light, things begin to change in a very strange way. The faster
we go the more our clock slows down relative to someone standing
still; time, for anything moving, changes! Instead of space and
time being separate things they are the same thing, called space-time.
In short: "moving clocks run slow".
 |
| Moving clocks run slow |
Einstein's Two Postulates.
The theory is based on two principles (postulates):
- Physical laws are the same in all frames of reference. That
is; any event within a portion of space (a frame) can be specified by
three spatial dimensions (east-west, north-south, up-down) and one
temporal dimension (time). Also, the laws that apply to us in everyday
circumstances (Newton's laws) also apply within each frame of reference.
- The speed of light is constant. By this it is meant that in a
vacuum, such as in space, the speed of light is always
the same, regardless of the speed of someone observing it.
The first postulate is seemingly simple and trivial. If I
sit and wait an hour in New York, an hour passes. If I sit and wait an hour
in Edinburgh then an hour also passes. I am, almost exactly, in the same bit
of space (frame of reference), moving around the Sun at the same speed
wherever I sit on the Earth. The way time passes in all frames of reference
is governed by the same laws.
While the first postulate is pretty much what one might
expect the second requires a little more explanation. The speed of light is
very close to 300,000 kilometres per second (around 186,300 miles per second).
Everyday experience tells us that if a bus is moving north at 30 miles per
hour and we are also walking north at 5 miles per hour then the bus is
moving away from us at 25 miles per hour.
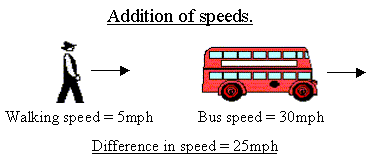
But what if we move in the same direction as a light beam?
Let's say we produce a pulse of light into space by quickly flashing a torch
(flashlight) on and off. We then follow the beam of light in a very fast
rocket moving at 100,000 km per second. How fast is the light beam moving
away from us? Common sense tells us that it is moving away from us 300,000
km minus 100,000 km per second, in other words, the light beam is 200,000 km
per second faster than us. Wrong! Remember that the speed of light is
always the same regardless of our own speed. From our
rocket we would see that the beam of light is still moving away
from us at 300,000 km per second! Likewise, if we were moving towards the
beam at a very high speed we would still see the light coming at us
at 300,000 km per second! This has enormous implications!

Time dilation.
If the speed of light stays the same then what is going on? Something
else has to change. That "something" is time.
As odd as it seems time is not constant. More accurately,
space-time is not constant. It can be changed, bent and twisted. The faster
we go the more time slows down ("moving clocks run slow"). This is only
noticeable, normally, at very high speeds such as those approaching the
speed of light, 300,000 km per second, which is approximately 7 times around
the Earth in a second.
What does all this mean? One of the most dramatic
consequences of this is that time itself will run at different speeds for
two people moving at different speeds relative to each other (hence "relativity").
Let's have an example. Mary, a 30 year old NASA astronaut, blasts off from
Cape Canaveral in her very high speed rocket in the year 2010 on a 10 year
mission to a nearby star. After a short time she is travelling at 270,000 km
per second, that is, 90% of the speed of light. To Mary everything looks
normal in her rocket; the clock seems normal and time passes for her the way
it did back on Earth. Her identical twin sister, Susan, is a NASA ground
controller for the mission. Ten years pass on Earth before the rocket
returns and when it does something is immediately apparent; while the Earth-bound
Susan has aged 10 years, her high-flying "twin" sister has only aged 5 years!
How can this be? Well, again we are back to "moving clocks run slow". At 90%
of the speed of light time slows down to about half of that relative to
someone who is stationary. So while 10 years have passed for Susan only 5
years have passed for Mary because her "clock" was running at half the speed
of those on Earth. This is called the twin paradox.
Remember that while Mary has only aged 5 years she still felt that time was
passing normally; this is not a way of living longer! Not only was her clock
running slow as far as a ground based observer is concerned, but her
time was running slow.

How fast can I go?
Some other consequences of the special theory of relativity are that:
- Distances shrink in the direction of motion.
- Mass (appears to) increase with speed.
- Nothing can travel faster than light.
For reasons of brevity the first point will not be covered here and the
latter two only very briefly.
Under the "rules" of special relativity the mass of any
object appears (to a stationary observer) to increase as the speed of the
object increases. At 90% of the speed of light mass will approximately
double, but at 99% of the speed of light the mass will increases by about 7
fold. As we get closer to the speed of light the mass increases very
dramatically until at the speed of light it would be infinite. The more
something weighs the more energy is required to move it, as we know from
everyday experience. To move something of infinite mass would require
infinite energy and this is clearly not possible, hence nothing can travel
faster than light. We live in a universe dominated by the Special Theory of
Relativity where faster than light travel is not possible. There are,
however, ways of breaking out of the constraints of the special theory and
travelling at speeds far in excess of that of light, at least for tiny
particles. As well as being very unusual and beyond the scope of the special
theory, the conditions for this are, as far as is yet known, of no practical
consequence.

Is it real?
This is all well and good, but what evidence is there?
After all it's just a "theory"! Well, there have been very many experiments
carried out on special relativity and all of them have shown it to be
correct. These range from experiments involving sub-atomic particles in high
speed accelerators to the slight, but expected, different clock rates of
some space exploration vehicles (such as the Voyager inter-planetary probes)
as compared with those on Earth.
One of the "proofs" is a much simpler experiment that was
first carried out in 1971 and has been repeated many times since then.
Atomic clocks have been carried on aircraft making long flights such as over
the Atlantic ocean. An aircraft, even the fastest, goes at a tiny fraction
of the speed of light, but at any speed "moving clocks run slow".
With an atomic clock on the ground and one in the aircraft it is possible to
measure the tiny differences in time produced by moving the clock. At the
speed an aircraft travels these differences are measured in millionths of a
second, but they are real and in exact agreement with what special
relativity says they should be. If Albert Einstein could have seen these
experiments he would be quietly and politely pleased, but not surprised.
The Light Clock A Theoretical Proof of Time
A Theoretical Proof.
In other pages in this series we have seen that there is
direct and measurable evidence for time dilation. One example from the many
available, that of atomic clocks carried on aircraft, has shown that moving
clocks do indeed run more slowly than stationary ones, just as predicted by
Einstein.
The distinction between scientific "proof" and "evidence"
is a complex one and will be dealt with in another page. For the moment
though it is sufficient to say that scientific proof is only available in
models, and never in reality. The primary laboratory of the theoretical
physicist is his or her own mind and so it is there that any initial
experiments must take place. These experiments are often called "thought
experiments". Of course, as Einstein was happy to admit, the only real way
to test a theory is by carrying out experiments in reality. However, the
germ of any physical experiment must start in the mind, and this page looks
at one of the best examples of a such a thought experiment; namely that of
the theoretical light clock.
A Light Clock.
Clocks exist in many forms. Among the many types of
clocks that have been made there are:
- Water wheel clocks that collect water in buckets marked with time
scales.
- Candles with marks on them to show how long they have been burning.
- Sundials that project the Sun's shadow onto graduated clock faces.
- Clockwork clocks that gradually release the energy stored in wound
springs.
- Clocks that measure the vibrational frequency of crystals such as
quartz, or even atoms.
Most clocks measure how many times a repetitive action is
carried out. For example, in a quartz watch the quartz crystal usually
vibrates at 32,768 times a second. These vibrations are counted by
electronic circuits. After 32,768 "ticks" have been counted a second is
added to the watch's display.
We can also use light to make a clock, at least in theory.
To do this we need to bounce a pulse of light between two mirrors that are a
known distance apart. Light travels at 186,300 miles per second, so if we
separate the mirrors by a distance of 93,150 miles (i.e. half 186,300) each
individual mirror will be struck by the pulse of light once a second. In
other words, the round trip from one mirror to the other and back again will
take the light pulse one second. We now have a clock:
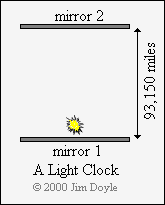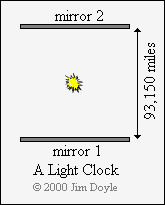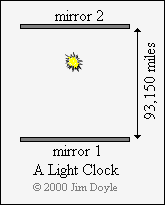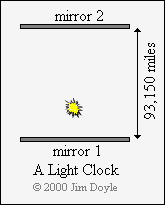
There are a number of practical problems with such a
clock. Probably the most obvious one is the separation distance of the
mirrors, but in reality we could put them very close together. The large
separation used here is just to demonstrate the principle and make the
mathematics easy. In reality the mirrors would absorb some of the light each
time they were struck by the pulse and after a time the light pulse would
dissipate completely. Also, the fact that we can see the light at all means
that at least some of it is being scattered thereby further weakening the
pulse. None of this really matters however, because we are dealing with a
theoretical proof and not an experimental one.
As an aside, there are systems that use the principle of
a light clock in order to perform important tasks. Radar is probably the
best known example. In a radar system pulses of "light" (i.e.
electromagnetic radiation) are beamed out at very close to the speed of
light. If the beam hits an object some of it will be reflected back (as if
from a mirror) and can then be detected by the radar receiver equipment. The
time taken between the beam being emitted and re-absorbed can be used to
calculate the distance of the reflecting object, usually an aircraft.
A Moving Light Clock and Pythagoras.
There is nothing really that extraordinary about a
stationary light clock. In fact there is nothing really that extraordinary
about a moving light clock if we are on the same moving platform as it.
Imagine being on a rocket moving at half the speed of light and that on this
rocket we have a light clock. As we travel through space we can see the
clock ticking away quite happily and there wouldn't be anything odd about it
(okay, we have to use our imagination here because the clock, as we have
seen, would be either enormous or so small that we can't actually see the
pulses, but we must remember that this is a thought experiment!).
Now let's imagine that we are being watched by an
external, and stationary, observer. We whiz past the observer holding the
light clock to the window. Will we both see the light clock doing the same
thing? No! To us on our rocket the pulses of light just go up and down the
way we would expect them to, but to the observer they will follow a
different path, one that maps out a series of triangles. The diagram below
shows the track of the light pulse as it moves past the observer:
At first this may not seem so strange. After all we could
do the same experiment with anything that went up and down in a transparent
box, but this is light and light has some very strange properties.
From the other pages in this series we know that light has a constant
speed. This is where things start to become interesting!
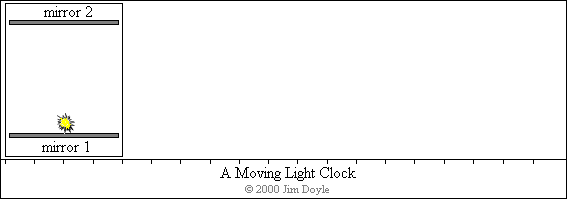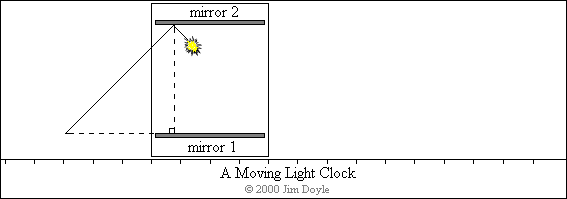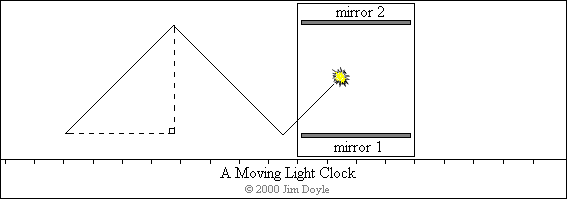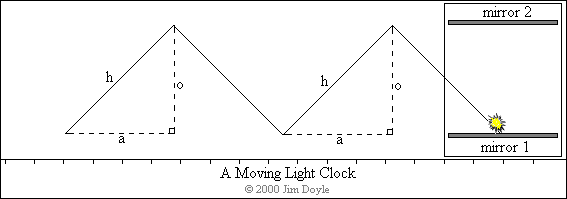
As we have seen the light moves in such a way, as viewed
by the external observer, that it traces out a series of triangles. We know
the mirrors are separated by the distance that light travels in half a
second (i.e. 93,150 miles) and that the spaceship is travelling at half the
speed of light, i.e. covering the same distance in the same time. We have
the opposite and adjacent measurements of a right-angled triangle and all we
need is a little help from Pythagoras to work out the length of the
hypotenuse:

The mathematics are correct but the actual result is
wrong! If it was correct it would mean that the pulse of light was
travelling a total distance of 2 times 131,734 miles = 263,468 miles every
second. It is a pulse of light however and can't travel faster than
186,300 miles in a single second, nothing can!
What's going on?
The external observer knows that the distance tracked out
by the pulse of light in a single second can't be more than 186,300 miles.
He also knows that the speed of light is constant. If the speed of light
can't change is there anything else that can? Einstein pondered this problem
and came to a breathtaking conclusion; if the speed of light is constant it
must be space and time that change.
Einstein realised that what the external observer would
really see would be a light clock that appears to be slowed down. The clock
has to behave like this otherwise it would break the universal speed limit.
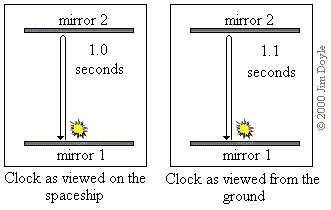
The "ticks" of the clock would now appear to be slower as viewed by the
external observer than as viewed by the person on the rocket. The rocket is
moving at 50% of the speed of light so according to the external observer
the time the pulse takes to get to the top mirror and back again would be
about 1.1 seconds. As viewed from an external stationary position the rocket
and everything on it would be running in slow motion. Time on the rocket
has, according to an external observer, slowed down by about 10%. To the
person on the rocket however, time would still seem to be passing normally.
Not only that but the spaceship and all its contents,
including the light clock, would appear squashed in the direction of motion
according to the external observer, but normal for the person on the
spaceship. Again, this is a consequence of the speed of light being constant
and so forcing space (more accurately space-time) to shrink. If the
space traveller takes a ruler and measures something the results will appear
normal because the ruler has shrunk as well.
The two observers would be experiencing space and time in
different ways relative to each other. Note that in each
individual's frame of reference everything seems normal; they would both
feel time passing normally and the laws of physics would still be the same
(as the first postulate states). It is only when observing each other's
frame of reference that they notice anything strange. As the speed of light
is approached these effects become even more apparent:

Moving Clocks.
We have seen that due to the constant speed of light a
moving light clock will appear to run slowly according to an external
observer. It was stated at the start of the page that the light clock was a
thought experiment and so it is. However, not only is the light clock
experiment expected to work in reality but every clock that has ever been
observed at high speeds slows down in just the way that the special theory
of relativity says it should. It is not just light clocks that run slowly at
high speeds, all clocks, including our own body clocks, slow down
at high speeds. Time for anything moving changes.
Time Dilation Worked Examples
The Time Dilation Equation.
Of all the major advances in physics from about 1900
onwards special relativity is the only one that can be understood in its
entirety without recourse to mathematics beyond that of high school
level. However, like all physics special relativity has at its base a
precise set of mathematical formulas from which predictions can be made
and tested against experimental results. It will come as no surprise
then that time dilation has a precise mathematical formula. This is it:
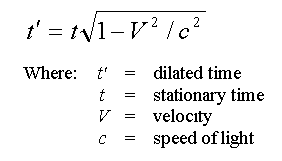
Example 1: Solving the Equation as a Factor of 1.
The effects of time dilation don't become really
noticeable until very high speeds are reached so for this worked example
I will use a speed of 90% of that of light, that is 270,000 km per
second (the speed of light is very close to 300,000 km per second). The
first thing we must do is to write down the equation:
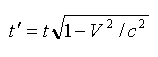
We now need to "plug in the numbers". Because V2/c2
is a ratio we can either use the exact values or just the percentages of
each value. It is easier to do the latter. Because we are only
interested in the dilated time factor we can set the stationary time to
be 1. Note that we can drop the percentage symbols and that c
is equal to 100% of the speed of light. Plugging in the numbers we get:
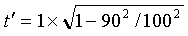
We can now begin to solve the equation. The first
thing we can do is remove the leading number 1 (anything multiplied by 1
is itself), then square the last two terms:
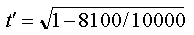
We can now reduce the equation by carrying out the
division:
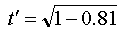
We then carry out the subtraction:
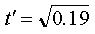
And finally we take the square root (and round the
answer to a workable value):
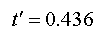
This result means that at 90% of the speed of light
local time has slowed down to 43.6% of that relative to an external
observer. Put another way, if a rocket is sent out into space on a 10 (Earth)
year mission at 90% of the speed of light the rocket and its occupants
will have only aged by about four and a half years when they return,
while everyone and everything on Earth will have aged 10 years.
Example 2: Solving the Equation as a Measure of Time.
The first example solved the equation as a factor of
one. This example puts a real time scale into the equation. In this
example we will look at how time changes over 10 years travelling at a
speed of 50% of that of light.
Instead of the step-by-step approach of the last
example I will just carry out the equation:
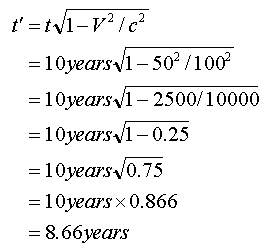
So for a rocket travelling at 50% of the speed of
light 8.66 years will pass in the same time as 10 years pass for a
stationary observer. Note that while the unit of time used was years it
could have been any other unit of time, such as seconds or millennia, as
long as the result is in the same units as the units used in the
equation.
Hiçbir
yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca
bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden
alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 - Turkiye / Denizli
Ana Sayfa /
index /Roket bilimi / E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi
Defteri /UFO Technology/Duyuru
Kuantum Teleportation /Kuantum Fizigi
/Uçaklar(Aeroplane)
New World Order(Macro Philosophy)
/Astronomy
|
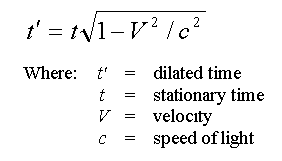
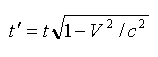
![]()
![]()
![]()
![]()
![]()