Alcuni fatti, di quanto detto, che ci riguardano
Inizio con una domanda
apparentemente banale. Qual è il tragitto più breve tra Milano e Parigi?
Credo che ognuno penserà ad una retta che unisce le due città. Beh,
facendo l’approssimazione di Terra è perfettamente sferica, il tragitto
più breve per noi che ci trasciniamo sulle superfici è un arco di
circonferenza, una geodetica. In linea puramente teorica si otterrebbe il
tragitto più breve bucando il suolo con un tunnel che unisce le due città.

Se poi
togliamo l’approssimazione precedente di perfetta sfericità della Terra,
dovendo recarci da L’Aquila a Teramo dovremmo fare un lungo tragitto
attraverso gli Appennini. Qui, fortunatamente, quel tunnel esistente ci
fornisce la nostra comoda geodetica.

Nello
spazio libero, salvo complicazioni che vedremo più oltre, la geodetica è
sempre una retta.

Naturalmente quel ragazzo non può percorrere tale geodetica: sarebbe
necessaria una teleferica. Ma, è bene chiarire, questo cammino rettilineo
è un qualcosa che solo raramente si incontra in natura. Gli esempi che
abbiamo fatto già mostrano quanto ora detto e si possono anche aggiungere
altre questioni. Quando si parla di cammino più breve, si sottintende:”quello
che si percorre nel minor tempo”. Ebbene fu uno scienziato francese,
Fermat, che scoprì che la luce si muove sempre su tragitti che richiedono
il minor tempo e, tali tragitti, non coincidono sempre con la linea retta.
Un esempio a tutti noto è quello della rifrazione, del bastone che, in
corrispondenza della supeficie di separazione acqua-aria, vediamo “spezzato”.
La luce, infatti, nel passare da una sostanza ad un’altra, cambia
direzione e questo ci fa vedere quel fenomeno che dicevo.
E tale
fenomeno, quello del tragitto che richiede minor tempo, fa anche parte
dell’esperienza ordinaria: il bagnino che tenta di salvare una persona in
difficoltà farà il massimo possibile di tragitto sulla sabbia perché qui
può camminare con minore resistenza di quanta non ne incontri in acqua.

Insomma, credo si sia capito che la geometria
di Euclide è solo una prima approssimazione nella descrizione del mondo.
Arriviamo a discutere di Relatività Ristretta con Einstein
I concetti di spazio e
di tempo, ad esso connesso, cambiano radicalmente all’inizio del secolo
scorso con alcune conseguenze che Einstein trasse da certe premesse.
Durante gli ultimi anni dell’Ottocento, a lato di vari interventi di
filosofi, la stessa fisica stava faticosamente tentando di mettere ordine
in una serie di fenomeni non riconducibili al quadro interpretativo di
Newton. Dagli inizi del Settecento, epoca dove situare i lavori di Newton,
erano state scoperte montagne di cose. Particolarmente l’elettricità, il
magnetismo e le osservazioni astronomiche. L’elettromagnetismo poneva dei
problemi. Era restìo ad una interpretazione euristica, che vedesse cioè le
sue leggi risultare le stesse per qualunque osservatore dei fenomeni in
gioco. Se due cariche elettriche si attraggono per chi le guarda stando
fermo, sembrerebbe straordinario si respingessero per uno che le osserva
camminando. In meccanica le cose erano ben chiare e sistemate da Galileo –
Newton con il principio di relatività. Secondo tale principio le
leggi della meccanica sono le stesse per tutti gli osservatori che sono
immobili o in moto rettilineo a velocità costante tra loro. Vi sono delle
semplici regole per poter descrivere un fenomeno da diversi punti di
riferimento. Ne fornisco in breve una. Se camminiamo nel corridoio di un
treno nel senso di marcia, la nostra velocità sarà quella che noi abbiamo
nel camminare, se la cosa è osservata da un passeggero che se ne sta
tranquillamente seduto. Ma se il nostro camminare nel corridoio del treno
è osservato da un signore che si trova ad un passaggio a livello, la
nostra velocità sarà quella del nostro camminare PIU’ quella del treno. E’
una semplice regola di somma di velocità (sottrazione nel caso noi si
cammini in verso opposto a quello di marcia del treno). Ebbene, il voler
applicare questo semplice principio all’elettromagnetismo portava a
descrizioni diverse per stessi fenomeni, a seconda dello stato di quiete o
di moto dell’osservatore.
Per mettere a posto tali cose si “inventarono” moltissime
ipotesi “tirate per i capelli”. Si introdussero strani concetti nella
fisica che non si capiva bene che significato avessero. Il fatto è che
venivano tirati in ballo di volta in volta, quando qualcosa non andava.
Non si trattava di un principio generale da cui far discendere delle
conseguenze, sempre in accordo con il dato principio. Sembravano tante
ipotesi ad hoc. Così, ad esempio si introdussero: il tempo locale (diverso
dal tempo assoluto), le lunghezze che si contraggono quando si è in moto a
velocità gigantesche, le masse longitudinali e trasversali per gli
elettroni, …. Insomma, se si fa caso, si toccavano, ogni volta, i concetti
alla base della meccanica, per mettere ordine nell’elettromagnetismo.
Einstein, nel 1905, fece la rivoluzione copernicana; invece di
continuare a mantenere la meccanica di Newton come tabù, invece di usare
di infinite ipotesi per piegare l’elettromagnetismo ai voleri di quella
meccanica, egli toccò proprio la meccanica. Era da lì, secondo Einstein,
che occorreva partire perché le cose tornassero anche
nell’elettromagnetismo.
Da varie osservazioni astronomiche, da varie equazioni che da
Maxwell si elaboravano, egli affermò come postulato una cosa che veniva
fuori da tutte le parti ma che nessuno osava sostenere con chiarezza
traendone tutte le conseguenze. In tutte le equazioni compariva una
costante che era di carattere elettromagnetico ma che riguardava anche la
meccanica. Questa costante coincideva con la velocità della luce nel vuoto
(i 300.000 Km al secondo di cui abbiamo parlato), che da ora indicheremo
con c. Inoltre tutte le esperienze note, a cui occorre aggiungere le
osservazioni astronomiche da poco realizzate (michelson, De Sitter),
mostravano sempre velocità che non superavano mai quelle della luce.
Sembrava cioè che la luce non sommasse la sua velocità con nulla e che
quella fosse una velocità limite, insuperabile. E qui si aveva una
violazione intollerabile proprio di quel principio di relatività che
abbiamo esemplificato con la somma o sottrazione di velocità per
osservatori diversi.
Einstein, che aveva ben presente tutto ciò, partì con due
postulati (leggi generali non completamente dimostrate ma che, a 100 anni
di distanza, non hanno mostrato cedimenti).
1)
TUTTE le leggi della fisica, non solo quelle della meccanica ma
anche quelle dell’elettromagnetismo, ubbidiscono al principio di
relatività.
2)
La velocità della luce nel vuoto ha sempre lo stesso valore da
dovunque e comunque la si misuri. Essa non si somma o sottrae ad altre
velocità e risulta una velocità limite.
Come si
vede, sembra che questi due postulati siano innocui. Sembrano petizioni di
principio che in realtà modificano poco o nulla. Invece hanno
rivoluzionato radicalmente la fisica e la concezione del mondo. Ma prima
di proseguire occorre avvertire che nella nostra vita ordinaria noi non ci
imbattiamo né con la relatività né con l’altra fisica che ha cambiato il
modo di concepire il mondo, quella dei quanti. Queste due fisiche
riguardano da un lato, relatività, oggetti in moto con velocità
dell’ordine di grandezza di quella della luce; dall’altro, quanti, oggetti
di dimensioni dell’ordine di grandezza atomica. Ma, nonostante quanto ora
detto, ambedue queste fisiche sono indispensabili per capire, almeno un
poco, della struttura dell’universo. Tralasciando i quanti, tenterò ora un
elementare approccio alla relatività di Einstein, quella del 1905, che si
occupa solo di oggetti in moto relativo a velocità costante e per questo
detta ristretta. Più avanti diremo delle cose sull’altra relatività di
Einstein (che venne sviluppata dal 1917 in poi), quella generale, che
mette in gioco anche accelerazioni tra sistemi di riferimento e che, in
senso più lato si occupa di cosmologia, di gravitazione.
Per quel che ci interessa dobbiamo concentrare la nostra
attenzione su quella velocità della luce che non può essere superata e che
non si somma a nient’altro. Cosa comporta ciò per la meccanica? Come la
modifica? Vediamo due disegnini che rappresentano un signore che cammina
su di un treno. Il primo di essi è relativo ad una situazione di
relatività Galileo – Newton: quel
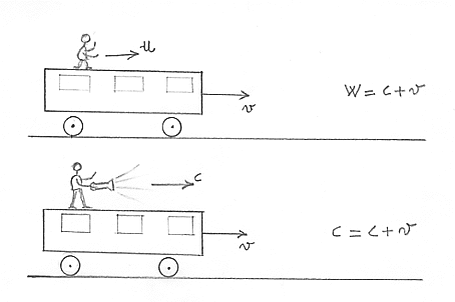
signore
che cammina con una velocità u sul treno che va ad una velocità v, viene
visto da un osservatore che è fermo ad un passaggio a livello andare ad
una velocità w = u + v. Nel secondo caso siamo in una situazione
einsteniana: dallo stesso osservatore al passaggio a livello, la velocità
c della luce della torcia che ha l’omino sul treno, che viaggia a velocità
v, non si somma con la velocità del treno. Si ha una situazione in cui c +
v = c. E’ un qualcosa che inizia ad urtare con il buon senso, qualità che
occorre accantonare se si vuole capire cosa accade. Una chiara evidenza
sperimentale di quanto sostenuto nelle esmplificazioni con i treni si ebbe
con le stelle doppie scoperte e studiate da De Sitter. Queste stelle hanno
la proprietà di ruotare vorticosamente, rincorrendosi ad una velocità v.
Ebbene, se osserviamo alcune di queste stelle, secondo il principio di
relatività galileiana, la luce proveniente da esse dovrebbe avere velocità
c + v, per la stella in avvicinamento alla Terra, e velocità c – v, per la
stella in allontanamento dalla Terra. Le misure fatte danno invece la
situazione della figura a destra: la luce arriva sulla Terra, sempre con
velocità c, non sommandosi (né sottraendosi) a quella delle stelle.

Stabilita questa proprietà della luce, cosa
essa comporta?
La simultaneità
Per quanto diremo occorrerà riferirsi ad oggetti fantastici,
non esistenti in natura. Avverto però che quanto qui raccontato e riferito
a tali oggetti fantastici, avviene davvero in mondi microscopici (dove si
ha a che fare con particelle portate a velocità prossime a quelle della
luce, con i raggi cosmici) o in fenomeni cosmologici. L’uso di oggetti
fantastici permette di avvicinare di più la nostra mente meccanicista ai
fenomeni che tento di descrivere.
L’oggetto fantastico di cui parlo è un treno alto 2.400 metri,
che viaggia a 180.000 Km al secondo (o, che è lo stesso, a 180 metri al
milionesimo di secondo o microsecondo; con la stessa unità, la luce
viaggia a 300 metri al microsecondo) e che ha pareti di vetro per poter
osservare cosa avviene al suo interno. Su un vagone di tale treno, al suo
centro, sistemiamo un osservatore T proprio sotto una lampada L che è al
centro del tetto del vagone. Sistemiamo poi un osservatore T ’ ad
osservare dal marciapiede cosa avviene nel treno.

Nel
vagone in alto, quando parte la luce da L, essa è osservata da T arrivare
simultaneamente sulle due pareti equidistanti 1 e 2 del vagone. Nel vagone
in basso, l’osservatore T ‘ al suolo vede scorrergli il vagone davanti. Se
nell’istante in cui il centro del vagone passa al traguardo di T ‘ si
accende L, allora T’ vedrà illuminarsi la parete 1 prima della 2 a
causa del fatto che mentre la parete 1 corre verso la luce che gli va
incontro da L, la parete 2 scappa da tale luce proveniente dalla stessa L.
Ciò ci deve far concludere che la simultaneità, concetto che non abbiamo
mai discusso nella nostra vita quotidiana, è ora discutibile. Si ma a che
serve la simultaneità ? Supponiamo di voler misurare il nostro gatto.
Mettiamo il centimetro in corrispondenza del muso simultaneamente a
quando tale centimetro va a sistemarsi dove comincia la coda. Se non
facciamo questa ipotesi, sempre implicita, rischiamo di avere non un gatto
ma una tigre! Insomma ci sparisce un concetto fondamentale e non è che
l’inizio.
Il tempo
L’osservatore T che sta sul vagone sa che esso è alto ( s = LT
=) 2.400 metri e sa che la luce viaggia a 300 metri al microsecondo (300
m/μs). Vuole calcolare il tempo t che la luce impiega per arrivare dalla
lampada L a lui, cioè a T. Con un facile conto di cinematica trova:
t = s/v -> t = LT/c
-> t = 2.400/300 μs = 8 μs.
Il tempo
quindi che l’osservatore immobile rispetto al fenomeno (luce che viaggia
dalla lampada a lui) misura è 8 μs.
Vediamo ora quanto tempo misura per lo stesso fenomeno
(luce che va da L a T) l’osservatore sul marciapiede T ‘.

La situazione è rappresentata nella figura qui sopra. Poiché la velocità della luce e quella del treno sono dello stesso ordine di grandezza, mentre la luce viaggia da L a T, il treno si sarà spostato di un tratto che porta T da T1 a T2. Quindi il treno avrà percorso un tragitto T1 T2, alla velocità di 180 m/μs mentre la luce percorre il tragitto LT2 alla velocità di 300 m/ μs. L’osservatore T ’ vedrà allora la luce arrivare sulla testa del signore che è sul treno quando questi occupa la posizione T2. L’osservatore T ‘ dovrà in definitiva misurare il tempo impiegato dalla luce per percorrere il tragitto LT2. Qui ci aiuta il teorema di Pitagora. Abbiamo il triangolo LT1T2 . Conosciamo il lato LT1 che è lungo 2.400m; sappiamo che il lato T1T2 è lungo 180 t (la velocità del treno per il tempo t durante il quale il treno va a quella velocità); sappiamo che il tratto LT2 è lungo 300 t (la velocità della luce per il tempo, lo stesso del treno, che la luce impiega per andare da L a T2); non resta che impostare la relazione pitagorica per ricavarci la cosa che vogliamo, cioè t:

(300 t)2 – (180 t)2 = (2.400)2
è t = 10 μs.
E siamo
arrivati al risultato: il tempo passa più velocemente per chi,
dall’esterno, vede passare il treno. Ed il risultato è generale: ogni
volta che lavoriamo con velocità vicine a c, il tempo passa più lentamente
per chi viaggia a velocità dello stesso ordine di grandezza di quella
della luce. E’ da osservare una cosa estremamente importante che in futuro
chiamerò semplicemente reciprocità. Il viaggiatore, colui che sta sul
treno, in base al principio di relatività, può essere considerato immobile
e dal suo punto di vista vedere colui che sta sul marciapiede muoversi ad
una velocità di 180 m/μs in verso opposto. Dal punto di vista del
viaggiatore, il tempo passa più velocemente per chi, dal treno, vede
passare una persona su di un marciapiede. Cosa accade in realtà ? Non lo
sappiamo, perché per saperlo occorrerebbe fermare il treno e confrontare
gli orologi. Ma per far ciò occorrerebbe mettere in ballo delle
accelerazioni negative ed usciremo fuori dalla relatività ristretta. Il
problema resta quindi quello di una misura e di un confronto di misure. Ed
ora ci troviamo con una clamorosa novità rispetto alla fisica di Galileo e
Newton: per costoro (ma per chiunque) il numero degli osservatori poteva
essere grande a piacere, ma i tempi per ciascuno erano sempre gli stessi,
cioè: t = t1 = t2 = … Ora invece si ha una
relazione come la seguente:
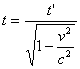
Cerchiamo di capire questa formula che a vista spaventa ma che è davvero
semplicissima. Supponiamo di vedere una di quelle orrende macchine oggi
molto in uso, un cacciabombardiere che sfreccia a 3.600 Km/h, cioè ad 1
Km/s, il tempo che misura il pilota è diverso da quello che misuriamo noi
? Tutto dipende da quel v2/c2 che compare sotto
radice quadrata al denominatore dell’espressione precedente. Questo
rapporto può essere molto piccolo ed allora si trascura con la conseguenza
che sotto la radice resta un uno, con l’ulteriore conseguenza che t = t’.
In tal caso è inutile parlare di relatività, i tempi vanno come per me a
Roma e per Chirac a Parigi. Può accadere che questo rapporto sia grande (ma
sempre inferiore ad uno). In tal caso entra in gioco la relatività. Non
può invece accadere che quel rapporto sia maggiore di uno (in realtà non
può neanche accadere che sia uguale ad uno). In tal caso, sotto la radice
verrebbe fuori un numero negativo. La radice darebbe origine ad un numero
immaginario. A tutt’oggi noi non sappiamo che significato dare a tempi
immaginari.
Allora, quanto vale quel rapporto nel caso del caccia?
![]()
Vale
zero! Il che vuol dire che anche per una delle macchine più veloci che
conosciamo la relatività non ha senso, basta ed avanza la fisica di
Galileo – Newton (applicare la relatività al moto di un caccia corrisponde
ad uccidere un moscerino con un missile intercontinentale a testata
nucleare). Ma quanto vale quel rapporto nel caso del nostro treno
fantastico?
![]()
quindi:
t = t’/0,8 -> 8t = 10t’ ,
che è
esattamente quello che avevamo trovato discutendo la cosa con numeretti
semplici ed utilizzando il teorema di Pitagora.
Le lunghezze
Poiché il tempo passa in modo diverso in condizioni di
osservazioni diverse, cosa accade degli spazi percorsi, delle distanze,
delle lunghezze? Qui il tutto è semplicemente conseguenza di quanto fin
qui detto.
L’osservatore che si trova sul treno sa che la sua velocità è
di 180 m/μs. Sa che la luce da L alla sua testa impiega 8 μs. Calcola con
facilità il tragitto che il treno ha percorso in questo tempo:
s = vt -> s
= 180 . 8 = 1.440 m.
Stesso
ragionamento e conto fa l’osservatore che sta sul marciapiede, solo che
tale signore ha visto passare un tempo diverso:
s = vt -> s =
180 . 10 = 1.800 m
Risulta
quindi una conseguenza evidente: le lunghezze di oggetti in moto si
contraggono, nel verso del moto (anche qui, per il principio di
relatività vale la reciprocità).
Questo
disegnino mostra schematicamente quanto dicevo: un osservatore fermo vede
come vediamo ordinariamente noi; un osservatore in moto a velocità
dell’ordine di grandezza di c vede un paesaggio deformato.
Che succede per la somma delle velocità ?
Avevo già detto che nel mondo relativistico risulta c + v = c
e, peggio che c + c = c. Come è possibile trovare una qualche relazione,
una formula che consenta questo? Nei suoi sviluppi Einstein la trova in
modo estremamente consequenziale e semplice.
Supponiamo di avere due oggetti con velocità rispettive u e v.
La soma di queste velocità può essere al massimo c. La formula einsteniana
per questa somma W è:
 ;
;
supponiamo ora che u sia uguale a c. Si ha:
 .
.
Ed ecco
che la somma di due velocità ci fornisce al massimo c. Per confermare ciò
nel caso limite di c + c, vediamo cosa accade:
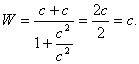
Occorre
ammettere che Einstein è proprio bravo, eh?
L’ultima questioncina, appena enunciata.
Einstein è noto per una sua formula tanto semplice quanto
rivoluzionaria:
E = mc2
Provo a
dire la grande novità che essa rappresenta rispetto al passato newtoniano.
Noi sapevamo che in una relazione in cui compare energia, massa e velocità
al quadrato, avevamo a che fare con le due variabili energia e velocità e
con una costante: la massa. Ricordiamo ad esempio l’espressione che ci
fornisce in fisica classica l’energia totale di un sistema: essa è:
E = mv2
Si può
vedere che si tratta apparentemente della stessa cosa: nella prima
relazione compare la velocità c della luce, nella seconda una velocità v
qualunque. Ho detto apparentemente perché qui vi è una differenza
sostanziale. Nella relazione classica, come detto, le variabili sono E e
v. Mentre nella relazione einsteniana le variabili sono E ed m (ricordo
che c è una costante). Si ha quindi:
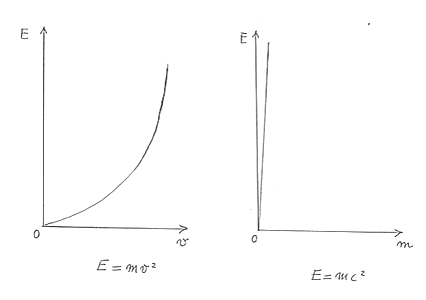
e si può
vedere che la relazione di Einstein introduce il concetto di massa
variabile, di massa che è la stessa cosa dell’energia, di una piccolissima
massa che equivale ad una infinitamente grande quantità di energia. In
modo un poco estemporaneo si può pensare alla massa come ad un concentrato
di energia ed all’energia come massa sfumata, diffusa nello spazio. Ma vi
è un qualcosa nelle considerazioni che abbiamo fatto che ci porta a
pensare a massa che debba variare? Sembrerebbe di no, a meno che non si
faccia attenzione. Il tutto nasce sempre da lì: dalla velocità c che non
può essere superata. Vediamo.
Supponiamo un oggetto in caduta in uno spazio enorme. Esso è
soggetto, supponiamo, ad una gravità come quella terrestre. La sua
velocità, cadendo, aumenta di circa 10 metri al secondo ogni secondo. Con
questa accelerazione di gravità l’oggetto, dopo circa una caduta di un
anno e mezzo solare, raggiungerebbe la velocità della luce. Ma l’oggetto
continua a cadere pur non potendo aumentare la sua velocità. Vedete che
siamo in difficoltà? Qual è l’altra grandezza che compare nella formula
che ci dà la caduta di un oggetto? Proprio la massa! A velocità che non
può aumentare, inizia a cambiare il valore della massa. E’ un modo solo
intuitivo, ma mostra alcune conseguenze della relatività che,
drammaticamente, abbiamo conosciuto su Hiroshima e Nagasaki. La
trasformazione di circa 50 chilogrammi di materia nell’ energia che
distrusse quelle città fu la prima tremenda dimostrazione della validità
di quanto Einstein aveva scoperto (e su cui non aveva mai voluto lavorare
per la produzione della bomba).
Una vignetta illustra in modo simpatico la scoperta di
Einstein:

Torniamo all’Universo
Avevamo iniziato con il
parlare di caratteristiche da assegnare all’universo. Abbiamo fatto un
lungo excursus e ritorniamo alla stessa domanda. Possiamo precisare le
questioni, per iniziare, così: finito, infinito, limitato, illimitato. Ed
allora vediamo cosa significano questi termini associandoli a dimensioni
spaziali. Con Coleman, prendo in considerazione un insetto in varie
situazioni.
Nella
figura (a), a sinistra, un segmento su cui un insetto “unidimensionale”
può solo andare avanti ed indietro, ha davanti a sé un mondo finito (il
segmento) e limitato (dagli estremi del segmento). A destra ci è una linea
che descrive una circonferenza. L’insetto può seguire questa linea finita
che però non ha limiti. Nella figura (b) siamo in un mondo bidimensionale.
A sinistra un piano che risulta essere per l’insetto finito e limitato. A
destra una superficie sferica che è altrettanto finita e, come la
circonferenza precedente, illimitata. Nella figura (c) siamo in un mondo a
tre dimensioni (non il nostro, si ricordi, perché il nostro ha almeno 4
dimensioni (facendo bene i conti se ne troverebbero undici). A sinistra,
dentro una sfera, una famiglia di insetti ha accesso a movimenti non solo
su piani ma anche nella terza dimensione: questo mondo continua ad essere
finito (la sfera) e limitato (un insetto non può continuare in linea retta
senza urtare sulla superficie della sfera). A destra gli insetti non hanno
il vincolo della superficie, hanno la possibilità di accedere alle tre
dimensioni spaziali e quindi questo universo è illimitato. Per pensare
alla sua finitezza occorre introdurre la gravità (una intensissima gravità
tale che impedisce anche ai raggi luminosi di allontanarsi dall’ammasso di
insetti). Tale forza li tiene uniti in un luogo da cui non riescono a
staccarsi. Ciò comporta che (Coleman): “anche se uno di questi scrutasse
nello spazio al di fuori dell’ammasso, i raggi luminosi giunti ai suoi
occhi risulterebbero incurvati e provenienti dall’ammasso stesso,
facendogli vedere insetti dovunque, cosicché non potrebbe mai avvertire la
presenza di alcuna cosa situata fuori dal proprio mondo”. Tali insetti si
potranno muovere in ogni direzione ma non si renderanno conto di girare
intorno a se stessi. In tal senso il loro mondo è illimitato. “Il loro
mondo è finito poiché le dimensioni del gruppo considerato nel suo insieme
sono finite ed il gruppo costituisce il loro mondo”. Il mondo potrebbe
diventare infinito ed illimitato solo se vi fosse un solo insetto che non
gravitasse con qualcun altro, oppure se vi fossero tanti insetti ma senza
gravitazione.
Questa vicenda delle dimensioni, degli spazi, dei limiti, … è
tanto importante che qualche fisico ha giocato in modo quasi divertente.
E’ il caso di Gamow che indicava il modo non corretto di riportare un
corpo tridimensionale a due dimensioni e quello corretto:

Fin qui, al di là dell’ultimo scherzo, abbiamo
solo dato delle definizioni ma ancora non ci siamo avvicinati a quale
dovrebbe essere il nostro universo. Qui, come fisici, urtiamo contro
qualcosa che non può diventare galileiana in senso stretto. I fenomeni
astronomici non li possiamo riportare in laboratorio e ricrearli per
“provare e riprovare”. Su di essi non si sperimenta cambiando le
condizioni e tentando di ricavare una legge. Per capirli occorre mantenere
“gli occhi” puntati al cielo ed osservare, istante dopo istante, eventi
che, messi insieme, ci diano le informazioni che cerchiamo. In tal senso
oggi abbiamo teorie non definitive, ma solo indizi. Da quel che sappiamo,
l’universo, oggi può ammettere solo tre differenti geometrie per
l’universo, quella euclidea, quella sferica o quella iperbolica. Dipende
da quante galassie vi sono in funzione della distanza da noi: se il numero
delle galassie aumenta come la distanza tra noi ed esse (r) elevata al
quadrato, allora l’universo è euclideo; un aumento minore indica che esso
è sferico; uno maggiore indica che esso è iperbolico. Questa verifica non
è semplice per un motivo, ancora non discusso, ma clamoroso. La luce che
oggi ci proviene da una data galassia è quella che tale galassia
aveva emesso in numero degli anni che la luce ha impiegato a giungere fino
a noi (se una galassia è a 1.000 anni luce, noi vediamo, oggi, la
luce che tale galassia ci ha inviato 1.000 anni fa. Se poi questa galassia
è a 100 milioni di anni luce, allora siamo proprio al di là del fossile,
vediamo luce fossile, vediamo cose che potrebbero già non esistere da
migliaia o milioni di anni!!! Se, oggi, vedessimo una stella che
dista da noi 1.000 anni luce esplodere, vedremmo un evento di 1.000 anni
fa!!! Ecco qui risiede la difficoltà del capire che tipo di universo
abbiamo, non disponiamo di dati “simultanei dello stato delle varie
galassie che “vediamo”. Comunque si può procedere a distinguere le tre
differenti possibilità ed il tutto può, a tutt’oggi, rappresentare con il
disegno seguente:

Iniziamo dal punto interrogativo che compare
nel disegno. E’ l’eventuale inizio dell’universo in un dato istante
(quello noto come big bang). Da questo supposto istante (c’è mai
stato?), sarebbero passati intorno ai 10 o 15 miliardi di anni ed ora ci
troviamo là dove, nel disegno, è scritto presente. Da qui in poi
possiamo, in base ai dati scientifici raccolti in vari modi, tentare
ipotesi che saranno o meno verificate con successivi dati sperimentali.
La curva più in basso rappresenta l’universo sferico (chiuso e
finito) che continuerebbe ad espandersi fino ad un suo massimo (effetti
dell’esplosione iniziale che ancora “scaglia pezzi a distanza”). Appena
giunto a questo massimo, dato che le forze gravitazionali iniziano pian
piano a prendere il sopravvento su quelle del moto inerziale dei “pezzi”
iniziali, l’universo inizia una contrazione su se stesso fino a che il
processo diventerà rapidamente implosivi, fino al punto in cui tutta la
massa dell’universo la si ritroverà di nuovo in un “punto” in modo da
originare un “big crunch”, un big bang alla rovescia. Di nuovo tutto
finisce, ma di nuovo tutto riproduce l’esplosione di pezzi che sono
implosi. Il processo, in linea teorica, è riproducibile fino a situazioni
analoghe (non uguali!) a quelle che conosciamo. Il tutto proseguirebbe
indefinitamente in un universo che chiameremo oscillante che, così
ipotizzato, né sappiamo possa realizzarsi, né dove possa andare a finire
(né da dove possa aver avuto origine).
La curva intermedia è quella che si avrebbe per un universo di
tipo euclideo. Esso risulterebbe aperto, infinito che aumenterà sempre la
distanza relativa tra galassie.
La curva più in alto rappresenta un universo tipo il
precedente, ma originato da un big bang più violento che origina una
geometria di tipo iperbolico.
Ciò che decide tra queste tre ipotesi è la densità di materia
dell’universo, tutta la materia “oscura” che esso contiene e che solo
molto indirettamente siamo in grado di conoscere. Possiamo dire con
ragionevole certezza che un universo chiuso ed infinito può esistere
solo se la densità di materia ha un certo valore minimo. A tutt’oggi
siamo alla ricerca di tale materia oscura attraverso la radiazione che
l’universo invia ai nostri strumenti.
Big bang?
Non aiuterebbe nessuno
una affermazione di principio sul punto-tempo in cui vi sarebbe stato il
big bang. Vi sono molti dubbie, ultimamente, sembrerebbe addirittura che
tale teoria sia da scartare. Ma piuttosto che dire quale teoria sarebbe
eventualmente da accettare, con complicazioni al di fuori di queste cose
molto discorsive, vorrei tentare di dire alcune parole su tale “inizio”.
Naturalmente i creazionisti vi pongono Dio. A loro non so cosa rispondere.
La fisica non risponde alla metafisica e non perché non voglia, ma perché
la cosa sarebbe una contraddizione in termini. Altri pensano, e qui non ho
mai capito il perché, ad un solo ammasso di materia costituente l’universo
ad un dato istante; tale ammasso sarebbe esploso (grande esplosione) e
tutta la materia, man mano che si allontanava, andava raffreddandosi
progressivamente con conseguente origine di sistemi planetari, stelle, e
pianeti. Resta la semplice domanda del perché ad un dato istante vi doveva
essere una gigantesca sfera in un dato punto-tempo dello spazio a quattro
dimensioni. Non vedo né ragioni logiche né ontologiche. Qui possono
iniziare montagne di disquisizioni su questa sfera primordiale, sul suo
perché, sul suo percome … Il miglior lavoro in tal senso lo ha fatto
Weinberg nel suo famoso I primi tre minuti dell’universo. Peccato
che a questi tre minuti manchi il primo istante. Ritorniamo sempre lì. Vi
sono invece fatti che sono iniziati a venire alla luce nel 1933 che
potrebbero raccontarci qualcosa di nuovo. In quell’anno fu scoperta
l’antimateria, la materia che ha caratteristiche fisiche “opposte” (non
posso ora dire di più) all’ordinaria materia. Da allora ad oggi si produce
ordinariamente antimateria nei laboratori di fisica avanzati. Qual è la
proprietà dell’antimateria che può interessarci? Se si incontra della
materia con dell’antimateria, vi è la sparizione di entrambe con la
comparsa di una enorme quantità di energia. Viceversa, in uno spazio “vuoto”,
con dell’energia diffusa, è possibile che “dal nulla” fuoriesca materia ed

antimateria. Sembrerebbe che questa è la strada migliore per cercare di
capire la comparsa di qualcosa che ha per noi le proprietà di materia,
comunque sia definita. Il fatto è che dovrebbe esservi nell’universo
all’incirca un 50% di materia ed altro 50% di antimateria. Alle nostre
osservazioni ciò non risulta. Noi “vediamo” solo materia e pochissima
antimateria. Alcuni astrofisica parlano di una sorta di arrangiamento tra
i due tipi di materia per cui si evitano reciprocamente. Vi sarebbero da
qualche parte intere galassie di antimateria che con cura evitano quelle
di materia … Ipotesi, certamente interessanti ma, per ora, al di fuori di
ogni conferma o negazione sperimentale.
Ma, al di là di queste speculazioni, resta il problema di un
punto dello spazio in cui in un dato tempo è nato o potrebbe nascere
qualcosa. Naturalmente non terrò conto delle fantasie creazioniste di un
preteso Dio, argomento di Platone, Aristotele, di San Tommaso, di Leibniz
e di Clarke, secondo il quale ogni evento ha una causa e, facendo una
catena di cause, dobbiamo fermarci ad un certo punto, punto che sarebbe
Dio. Tal cosa fu aspramente criticata da Kant e duramente attaccata da
Russel. Oggi mi pare priva di senso, non meritevole neppure di un
dibattito: oggi sappiamo una cosa fondamentale che non si conosceva appena
100 anni fa: è possibile creare materia ed antimateria dal NULLA. D’altra
parte, rimanendo in tema strettamente fisico, sembrerebbe che almeno una
legge della fisica sia violata dal sorgere di ordine da un primitivo caos:
il secondo principio della termodinamica (nessun ordine si crea
spontaneamente da una situazione disordinata). Mi permetto qui di
osservare che la nostra conoscenza riguarda comunque una ampia fetta di
universo ma, … ampia quanto? Voglio dire che il secondo principio parla
del bilancio complessivo di un processo. Ad esempio, se considerassi
l’uomo un sistema isolato, esso sarebbe negato dal secondo principio. Ma
l’uomo torna presente se solo si tiene conto che il bilancio dell’ordine
che la sua struttura rappresenta con il disordine che la sua vita comporta,
è tutto a favore del secondo principio. Penso a qualcosa del genere per
l’universo. Resta allora quel possibile punto dello spazio tempo. Un tal
punto, come quello dell’ipotetico big bang è conosciuto in fisica ed in
matematica come una singolarità. Si tratta di particolari
situazioni di confine con proprietà molto peculiari dovute a possibili
agenti esterni (vedremo tra un poco) come la gravità. E’ ad esempio
singolare l’eventuale confine dell’universo, ogni singolarità è ciò che è
al confine tra fisica e metafisica. E’ una cosa che fa un poco paura, un
buco nero, ad esempio (come vedremo).
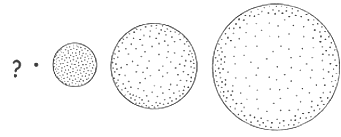
Si
tratta quindi del punto spaziotemporale inconosciuto ed al di fuori (almeno
per ora) dalla nostra portata esplicativa. Secondo la teoria del Big Bang
o anche da altre teorie che prevedono l’origine dell’universo da una
singolarità, da questa singolarità, sarebbe nato e “cresciuto” l’universo.
Questo processo sarebbe avvenuto in modo che nessuno da nessun punto sa
individuare l’altro punto, quello da cui sarebbe iniziato l’accrescimento.
La cosa che sembra complicata è meccanicisticamente visibile in modo
elementare. Se abbiamo un palloncino di gomma gonfiabile, se su questo
palloncino disegniamo tanti pallini, al gonfiare sempre più il palloncino
i pallini resteranno, aumenteranno le loro distanze reciproche e l’intero
universo crescerà. Ogni punto vedrà l’altro allontanarsi: nessuno di tali
punti risulterà privilegiato.
Ma, a
questo punto sorgono dei problemi che esemplifico in modo semplice: se
viene fuori un puntino in più? E se viene a mancare un puntino? Dietro
queste domande si nascondono le infinite domande della cosmologia.
L’universo Mantiene sempre la stessa quantità di materia? Ne crea? Ne
distrugge? … Insomma io voglio solo dire che non vi sono approcci
semplificati a queste questioni. Vi sono le questioni e queste tento di
presentare.
Un mondo speciale lo presentò John Wheeler nel 1979. In
particolari condizioni è possibile che un osservatore di oggi possa essere
responsabile di un qualcosa accaduto in un passato remotissimo. Se ciò
avesse un senso (e Wheeler dava senso alle sue affermazioni) noi staremmo
oggi osservando il nostro passato che acquista una realtà concreta
proprio grazie alle nostre osservazioni, come rappresentato nella figura
seguente nella quale la “codina” rappresenta l’origine del nostro universo.

In altro
modo e con altre argomentazioni, una cosa analoga la aveva detta Coleman
nel 1954. In un universo costituito da una ipersfera spaziotemporale (geometria
di Riemann), un osservatore osservando abbastanza a lungo osserverebbe
lungo la “retta-circonferenza” di tale geometria se stesso.

Ovvero:

Un
approccio più serio: cenni alla relatività generale di Einstein (1916)
Le cose dette in modo abbastanza semplificato in
questo ultimo paragrafo, tenterò di riportarle al lavoro che ha aperto
la strada a queste problematiche: l’altra relatività di Einstein, quella
del 1916, quella Generale.
La Relatività ristretta, alla quale abbiamo accennato, si
applica solo nel caso in cui non sia presente alcun campo gravitazionale.
E’ quindi veramente ristretta. E’ un qualcosa che riguarda geometrie e
spazi infiniti in senso euclideo. I moti inerziali prevedono questo. Per
questo Einstein si prefisse lo scopo di mostrare che l’equivalenza tra
sistemi di osservatori non deve riguardare i soli inerziali. Almeno per
un certo tipo di equivalenza deve essere possibile estendere tale
proprietà ad osservatori accelerati.
Se ci muoviamo con una data accelerazione vediamo gli altri
corpi che si muovono rispetto a noi con una accelerazione opposta.
Poiché abbiamo familiarità con la meccanica di Newton, attribuiremo
l’accelerazione di questi corpi a forze proporzionali alle loro masse
(Seconda legge di Newton). Le accelerazioni però insorgono solo
quando siamo su sistemi non inerziali. Esiste però una forza che ha lo
stesso tipo di comportamento: quella gravitazionale. Essa ha una
proprietà peculiare: imprime a tutti i corpi la stessa
accelerazione. E questa forza risulta proporzionale alla massa del corpo.
Se parliamo di altre forze ci accorgiamo che ognuna è diversa dall’altra
e che ciascuna agisce in modo diverso.
Ma torniamo ad un sistema inerziale. Esso risulta tale
quando abbiamo eliminato tutte le forze. Ma, disgraziatamente, non ci
possiamo liberare della gravitazione. Einstein iniziò allora con il
pensare che inerzia e gravitazione sono la stessa cosa:
entrambe agiscono sui corpi allo stesso modo e le forze che ne risultano
sono, per entrambe, proporzionali alle masse dei corpi stessi. Vi è
allora qualcosa che non va nel principio d’inerzia che occorrerà
riformulare.
Antica versione: “Esiste per i
corpi uno stato di moto standard, tale che un corpo che si trovi in
questo stato di moto non è sottoposto ad alcuna forza. Questo moto
standard è il moto rettilineo uniforme”.
Nuova versione: “Esiste per i
corpi uno stato di moto standard, tale che un corpo che si trovi in
questo stato di moto non è sottoposto ad alcuna forza. Questo stato di
moto segue l’inerzia e la gravitazione”.
Solo
se un corpo dovesse deviare da un tale stato di caduta libera diremo che
su di esso agisce una forza.
Una forza è dunque qualcosa che tende ad allontanare i corpi
dalle loro traiettorie standard, ciò che non vale per la gravitazione.
Arriviamo così a questa nuovissima affermazione: la gravitazione non è
da considerarsi come forza ma come inerzia. In termini più tecnici
questa cosa la si può dire così: la gravitazione non è una forza ma una
distorsione dello spazio-tempo. Se si è in uno stato di caduta libera,
la gravitazione intorno a noi sparisce (ecco la ragione dell’assenza di
peso nelle astronavi). Con ciò non si riesce però ad eliminare la non-uniformità
della gravitazione (la gravitazione è uniforme in una stanza ma non lo è
sull’Europa) e ciò vuol dire che vi sarà sempre una accelerazione
relativa ai corpi vicini.
In definitiva, l’impossibilità di eliminare completamente il
campo gravitazionale è causa permanente di un’accelerazione relativa tra
corpi e per costruire una teoria della gravitazione, l’effetto
intrinseco fondamentale che occorre descrivere è proprio l’accelerazione
relativa tra corpi vicini. In questo nuovo modo di vedere le cose,
occorre dire che la Relatività Ristretta continua a valere su piccola
scala, quando le distanze tra osservatori sono piccole; la Gravitazione
universale continua a valere su grandi distanze e deboli campi
gravitazionali.
Ma ritorniamo alla gravitazione come distorsione dello
spazio-tempo (sia dello spazio che del tempo) di cui parlavo poco fa.
Questo è uno dei risultati che la complessa elaborazione matematica
della Relatività Generale ci ha fornito. Naturalmente vi sono state
ulteriori elaborazioni (che ancora oggi continuano) dopo quella di
Einstein. Ma su questo punto specifico, tutte le teorie convergono: lo
spazio è deformato dal campo gravitazionale ed il tempo scorre in modo
differente a seconda dell’intensità del campo. Oggi, ad esempio,
abbiamo una verifica sperimentale di questa ultima affermazione: sulle
basi spaziali orbitanti intorno alla Terra, a causa della maggiore
debolezza del campo gravitazionale, si misura un tempo che passa più
velocemente rispetto alla Terra. Più forte è il campo gravitazionale,
più il tempo trascorre piano. Vi sono delle stelle così grandi da avere
una gravità che rallenta enormemente il tempo. E, come vedremo, poiché
la gravità alle soglie di un buco nero è immensa, in questa zona il
tempo inizierebbe a non scorrere più! Una tal situazione vista
dalla Terra sarebbe una immagine congelata nell’immobilità. Ma una tal
situazione non è visibile proprio perché la luce non può venirne
fuori a causa di quella immensa gravità. Per questo quello è un buco
nero: è uno di quei mostri di cui ho discusso in breve, una
singolarità spazio-temporale. Questa distorsione dello spazio-tempo
comporta che in un tempo che praticamente si va fermando, un oggetto che
stia entrandovi si stirerebbe sempre più fino a ridursi ad uno spago. Un
astronauta che vi entrasse per i piedi vedrebbe il suo corpo
assottigliarsi sempre più a partire dai piedi verso la testa. Tutto ciò
avverrebbe in un tempo lunghissimo; tutto tenderebbe
rapidamente all’eternità. Lo sfortunato astronauta troverebbe la
singolarità che rappresenta il confine del tempo e lì sparirebbe. La
singolarità segnala la fine di un viaggio senza possibile ritorno verso
nessuna parte ed in nessun momento. In un non luogo
dove l’universo sparisce.
In definitiva, una massa modifica la supposta omogeneità
ed isotropia dello spazio-tempo. Come illustrerò tra un poco, la prima
verifica di ciò fu realizzata dal fisico britannico A. Eddington durante
un’eclisse di Sole in Guinea nel 1919. E, data la presenza di masse nel
nostro universo, si può dire che l’universo non esiste fuori dal tempo
ma che, anzi, ne subordina la marcia.
Vediamo alcuni disegni. Il primo ci mostra un orologio su
una torre che cammina più in fretta di un orologio al suolo (ricordo che,
in base alla legge di gravitazione universale, più ci allontaniamo dal
centro della Terra e più la gravità diminuisce).

Riguardo alle accelerazioni relative tra corpi vicini per
formulare una teoria della gravitazione, possono aiutarci i disegni
seguenti.
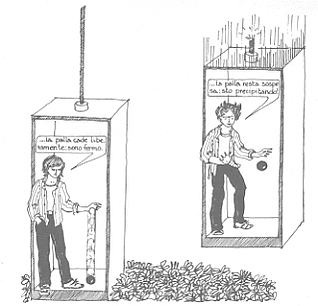
Se un
ascensore è al suolo, un oggetto, lasciato andare dentro di esso, cade
liberamente; in un ascensore in caduta, un oggetto lasciato andare,
resta dove è e non cade rispetto a chi lo lascia andare. Si deve notare
che, trovandoci noi in una stanza chiusa, possiamo accorgerci del suo
trovarsi o meno in un campo gravitazionale, proprio con confronti del
genere. Se invece un

ascensore è nello spazio, lontano da un qualunque campo gravitazionale,
un oggetto lasciato andare non cade. Se invece l’ascensore subisce una
accelerazione verso l’alto dovuta ad un campo gravitazionale, allora gli
oggetti fermi (rispetto ad un osservatore) cadono rispetto all’ascensore.
La deformazione dello spazio-tempo si può rendere bene con
l’immagine seguente:

Nella
figura a, lo “spazio”, rappresentato da una striscia di gomma elastica,
non è deformato da nessun campo gravitazionale; in b, agisce un piccolo
campo che deforma la striscia di gomma; in c questo campo è grandissimo
e provoca una grandissima deformazione della gomma-spazio. Più in
generale, la presenza di una massa dello spazio genera intorno a sé una
deformazione dello spazio (e per ciò che abbiamo già detto, del tempo),
che può essere rappresentata come una buca:
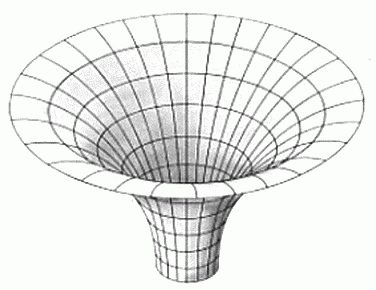
Se
insistiamo con la nostra rappresentazione di spazio con una striscia di
gomma, questa volta molto estesa, possiamo pensare di lanciare su tale
striscia una pallina di massa trascurabile. Tale pallina seguirà le
leggi della fisica che già conosciamo, continuerà in linea retta all’infinito.
Ma se tale pallina camminasse in uno spazio con varie masse disposte su
(dentro) di esso, allora essa rischia di deviare in vicinanza di una
massa perché ivi incontra l’avallamento che la massa provoca nello
spazio. Se poi la sua traiettoria è tale da puntare verso una data
massa, e quindi verso il centro della buca, tale pallina cadrà dentro la
buca, sarà cioè catturata dal campo gravitazionale di tale massa ed in
definitiva cadrà su di essa.
Nello spazio abbiamo a che fare con masse enormi e dobbiamo
quindi aspettarci campi gravitazionali giganteschi, tanto grandi da
attrarre o far deviare anche la luce (ricordo che, secondo la relazione
di Einstein E = mc2, la materia e l’energia sono in pratica
la stessa cosa e quindi anche la luce che è solo energia sente i campi
gravitazionali). Questo prevedeva la teoria di Einstein del 1916. Una
esperienza per verificare ciò la fece, come già accennato, Eddington.


Il
ragionamento fatto da Eddington è tanto semplice quanto geniale. La luce
proveniente da una stella arriva a noi senza sentire campi e quindi
senza deviazioni apparenti se la osserviamo di notte. Ma, se lungo il
cammino che la luce fa da quella stella alla Terra, interponessimo il
Sole, allora, l’enorme massa del Sole dovrebbe deviare la luce di questa
stella. Ecco un buon modo per verificare la bontà degli inizi della
teoria. Ma vi sono delle difficoltà. Anche se potessimo spostare il Sole,
la sua luce è così intensa che non ci permetterebbe di vedere le stelle.
Come superarle? Allora: il Sole è sempre tra noi e qualche stella e
quindi non abbiamo necessità di spostarlo. Il fatto che quando c’è lui
non vi sono stelle sembra insormontabile. Eddington pensò di spegnere il
Sole, di usare cioè un interruttore naturale che chiudesse la sua luce.
Una eclissi. Le cose stanno allora così. Di notte, da un certo luogo, ad
una data ora, il cielo mostra una data stella in una determinata
posizione (determinate distanze da altre stelle). Se è vero che il Sole
devia la luce di tale stella quando lo interponiamo nel tragitto di essa
fino alla Terra, la stella la dovremmo vedere in un’altra posizione, in
una sua posizione apparente. E tutto questo fece Eddington recandosi in
Guinea perché era lì che si aveva nel 1919 un’eclisse totale di Sole. La
cosa è ben descritta dalla prima delle due figure riportate più in alto
ed anche nella seconda, più schematica, in cui è mostrato l’angolo di
deviazione del raggio di luce che dipenderà dal campo gravitazionale del
Sole. Quindi nessun ulteriore dubbio: lo spazio è deformato dalla
presenza di masse. Più tali masse sono grandi e più la deformazione
spazio-temporale è grande. Una bella rappresentazione in due dimensioni
della deformazione dello spazio a seguito di qualche massa è mostrata
nelle figure seguenti dove le ascisse rappresentano lo spazio e le
ordinate il tempo. In i niente campi gravitazionali che invece sono
presenti in ii.

Questo
spazio è in definitiva “elastico” e deformabile come mostrato nella
figura seguente:
e
questa figura che mostra la deformazione dovuta a masse via via più
grandi ci dà anche l’opportunità di spingerci ad un qualche confine
della ricerca fisica. Se la deformazione spazio-temporale è piccola la
massa è ancora dentro l’universo che conosciamo. Ma se tale
deformazione cresce e diventa grande, molto grande, la massa che ha
creato tale deformazione può andarsene fuori dal nostro universo, come
mostrato in figura seguente:
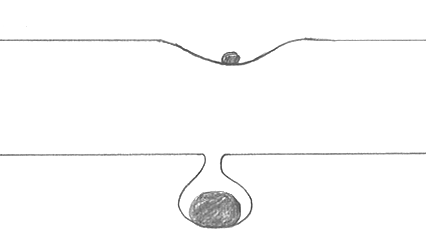
Ecco,
nel primo dei due disegni corrispondente ad una piccola massa, l’oggetto
è ancora visibile da un osservatore del nostro universo. Nel secondo
disegno (grande massa), la deformazione è tale che l’oggetto è sparito
dalla visibilità del nostro universo.
Ricapitoliamo un poco. Un corpo che si muove nello spazio in
assenza di forze seguirà la traiettoria geodetica sulla “striscia
elastica” dello spazio-tempo. Se in questo non vi sono masse, la lamina
sarà piatta ed il cammino geodetico del corpo sarà una linea retta. Se
però il corpo passa vicino alla depressione nella lamina originata da
una grande massa, il cammino geodetico sarà una linea curva, proprio
come il fiume che segue un percorso geodetico quando scende dalla
montagna. L’effetto della depressione nello spazio è quello di far
muovere il corpo in direzione della massa, ma esso lo fa solo seguendo
localmente il cammino geodetico, non a causa di una forza a lungo
raggio d’azione che emana da una massa lontana. Si deve osservare che
queste brevi osservazioni ci sbarazzano della legge newtoniana di
gravitazione universale. Così, invece di forze gravitazionali di ampia
portata, abbiamo corpi che ricevono istruzioni di rotta dalla topografia
locale dello spazio-tempo, topografia determinata dalla presenza
di masse. Cito un esempio, la precessione dell’orbita del pianeta
Mercurio (che dovrebbe essere noto), ma lo dico con il linguaggio della
relatività generale. L’orbita di Mercurio è curvata dallo spazio-tempo.
Che ne dite? Insomma, le anse ed i cambiamenti di direzione lungo il
cammino del fiume sono dettati dalla pendenza locale del terreno che
esso attraversa.
“Lo
spazio dice alla materia come muoversi. La materia dice allo spazio come
curvarsi” (J. A. Wheeler).
Ed in
definitiva, massa ed energia non sono nient’altro che deformazioni dello
spazio-tempo.
Ed ora dovremmo passare a rappresentazioni dello spazio-tempo
più precise. Ma prima diamo un occhiata alla macchina del tempo.
La macchina del tempo
Dal bel racconto di H. G. Wells che sembrava parlare di cose straordinarie, un poco come quelli di J. Verne, la scienza, almeno dal 1973, ha iniziato a parlare di viaggi nel tempo. Particolarissimi viaggi, ma certamente nel tempo. La "macchina" che realizzerebbe (il condizionale è d'obbligo, anche se non parliamo di fantascienza ma di alcune elaborazioni teoriche fatte da fisici famosi, ad iniziare da Einstein e Rosen) questa cosa potrebbe essere proprio un "buco nero". Ma prima di proseguire dimensioniamo un poco questo buco nero, questa singolarità, servendoci delle figure seguenti:

| AGGIORNAMENTO |
|
20.07.2004 Hawking cambia idea sui buchi neri Il fisico dà ragione al collega teorico John Preskill
Il celebre fisico Stephen Hawking ha ammesso che, dopo tutto, c'è
la possibilità che dai buchi neri possa sfuggire qualche tipo di
informazione. Da qualche tempo l'idea si era fatta strada fra gli
astrofisici, ma il fatto che sia stata accettata anche da uno dei
pionieri della teoria dei buchi neri negli anni settanta
costituisce una svolta importante. "Per molti potrà sembrare una
sorpresa, - ha commentato Gary Gibbons dell'Università di
Cambridge, collega di Hawking - ma il suo modo di fare scienza è
proprio questo: proporre una tesi e difenderla ad oltranza, fino a
quando non viene superata da un ragionamento migliore". © 1999 - 2004 Le Scienze S.p.A. |
E' impressionante vero? Il buco nero è un qualcosa di estremamente piccolo (stiamo comunque sempre all'interno di ordini di grandezza cosmici). Bene, quel buco nero, come dicevamo potrebbe riservare sorprese inaspettate. Quel disgraziato astronauta che vi era entrato, se potesse rimettere il naso fuori, avrebbe la sensazione che tutti gli eventi esterni sono accelerati e compirebbe quindi un viaggio verso il futuro. Una tal "macchina" è stata "pensata" dal fisico statunitense F. Tipler. Leggiamo la descrizione della macchina che ne dà lo stesso Tipler:
"Un cilindro con una enorme massa in rotazione trascinerà attorno a sé lo spazio-tempo. Questo cilindro dovrebbe essere alto 100 Km ed avere un diametro di 20 Km. Dentro dovrebbe esservi almeno la massa del Sole che avrebbe quindi la densità di una stella di neutroni. Questo cilindro dovrebbe ruotare su se stesso 2 volte ogni millesimo di secondo. Così, al centro, si formerebbe una singolarità (punto in cui la curvatura dello spazio-tempo diventa infinita, come vedremo più oltre) intorno alla quale sarebbe possibile il viaggio nel tempo: una nave spaziale potrebbe viaggiare lungo una traiettoria a spirale, attorno all'asse verticale, e ritornare indietro nel tempo. Ad ogni giro la nave tornerebbe nello stesso luogo ma in tempi sempre più remoti."
Due astrofisici dell'osservatorio astronomico di Roma, L. Stella e M. Vietri, hanno annunciato nel settembre del 1997 di aver individuato tre stelle di neutroni che, ruotando velocissime su se stesse, risucchiano e trascinano in un vortice lo spazio-tempo intorno a loro. Studiando i raggi X emessi da queste stelle, i due ricercatori si sono accorti che l'emissione non era costante ma variava nel tempo, come se la materia, risucchiata dalle stelle, ogni tanto cambiasse traiettoria. Dopo estenuanti calcoli, hanno concluso che l'effetto ha una sola possibile spiegazione: nella loro rotazione le stelle di neutroni non trascinano solo la materia circostante ma anche lo spazio ed il tempo ed è questa cosa che fa barcollare la materia lungo la sua traiettoria. Il fenomeno non è una scoperta assoluta. E' solo il ritrovare sperimentalmente un fenomeno previsto nel 1918 da due fisici austriaci, J. Lense ed H. Thirring, che lo avevano ricavato dalla Relativirà Generale di Einstein. A novembre del 1997, poi, alcuni fisici statunitensi del MIT hanno riscontrato lo stesso fenomeno nelle vicinanze di alcuni buchi neri appartenenti alla nostra galassia.
Vediamo, aiutandoci con un disegno, come sia possibile viaggiare nel tempo nel nostro spazio. Tale spazio è curvo nel senso più volte detto. Inoltre vi sono delle masse che lo deformano. Tanto più tali masse sono grandi (e non si confonda mai massa con volume: allo scopo si riveda l'ultima figura riportata) quanto più si addensano in volumi piccoli. Tali masse possono quindi essere enormi in volumi piccolissimi. E', come già detto, il caso di un buco nero, di una singolarità. Un buco nero che si "aprisse" da un lato (come fino ad ora visto) potrebbe "sfociare" in un altro lato, in un altro punto dello spazio-tempo, originando quello che si chiama cunicolo (o, in alcune condizioni, verme). Un cunicolo elementare è quello mostrato di seguito:
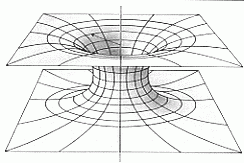
Rappresentiamo ora lo spazio attraversato da un cunicolo (la "striscia" rappresenta lo spazio ordinario quello che, ad esempio, percorrerebbe la luce in un suo normale tragitto):
Supponiamo ora che, camminando lungo la striscia, la luce vada da A a B. Ciò rappresenterebbe un normale avanzare del tempo come ordinariamente lo conosciamo che va dal presente A al futuro B. Pensiamo ora a della luce che parte da A. Essa viene catturata dal cunicolo in C e va a finire prima in D (fuori dal cunicolo) e quindi in B. Alla fine la luce è andata da A a B ma attraverso il cunicolo, tagliando tutto il tempo necessario a percorrere lo spazio ordinario. Questo rappresenterebbe un viaggio nel futuro. Supponiamo ora che la luce, sempre partita da A, entri in C per andare in D e, da D, ritorni lungo lo spazio ordinario (la striscia) verso A. Questo rappresenterebbe un viaggio nel passato (prima andiamo nel futuro, D, e poi torniamo indietro verso A).
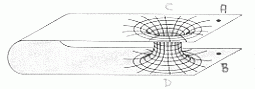
I cunicoli nello spazio tempo possono essere di vario tipo. Come esemplificazione mostro il "ponte di Einstein Rosen" chiamato verme:

Una "rete di mondi" allacciati tra loro da cunicoli e vermi potrebbe essere quella di figura seguente:

Concludo questa parte solo con il ricordare che questi fenomeni hanno luogo su scale non umane. Qui l'uomo è ancora distante da poter sopportare le violente alterazioni che fenomeni del genere gli procurerebbero: certamente ne uscirebbe triturato.
Visione euristica del mondo (per avvicinarci ad altre rappresentazioni di esso)
Fare fisica è come ricercare il bello. La perfezione delle forme e delle idee. E' scrivere musica, comporre sonetti, ballate e poesie. Vi è un linguaggio che ha dentro di sé capacità così coinvolgenti da lasciarti in un angolo a sognare. E' il mondo, l'universo con i suoi misteri tutti da indagare che è l'oggetto dello stupore, della meraviglia e della continua ricerca che asintoticamente porta l'uomo a conoscere. Molti tra i più grandi fisici hanno solo operato nel senso della "bellezza", dell'armonia, della semplicità, delle simmetrie, delle parità, ... Altri ne hanno anche parlato con linguaggi che commuovono perché toccano l'intimo del problema: il rapporto dell'uomo con la natura non solo contemplativo, ma esplicativo. Purtroppo molti si perdono questa meraviglia che a volte è nascosta dietro dei simboli che sembrano per iniziati, quando basterebbe un serio studio a livello di liceo scientifico per diventare perone in grado di capire e comunque di iniziare a capire. Superati i primi momenti di sconcerto, che si corrispondono al profano davanti ad una partitura di Ravel da "leggere". Quel pentagramma, quei pallini, quelle chiavi di violino, quegli stani simboli non potranno mai comunicare il "Bolero". Eppure c'è chi lo sa leggere lì! Ed io assicuro che la stessa cosa è con il libro della natura che, come diceva Galileo, è scritto in linguaggio matematico. Sono le note dell'armonia o dello sconfinato mistero popolato di mostri e di abissi infiniti che è lo sconosciuto e pur affascinante universo.
Già Newton utilizzava una immagine che è evocativa di pensieri e meditazioni che possono ben confrontarsi con L'Infinito del buon Leopardi. La propongo questa immagine, invitando a sentirla come un uomo della fine del Seicento poteva fare:

Vi è la Terra con un monte la cui vetta è V. Se si lanciano con "spinte" successive sempre maggiori degli oggetti da quella montagna, gli oggetti "cadranno" sempre sulla Terra finché .... Finché la spinta non sarà sufficiente a far camminare l'oggetto parallelamente alla superficie della Terra. In quest'ultimo caso l'oggetto cadrà indefinitamente di modo ché, alla fine, avremo un satellite terrestre. Siamo a 350 anni dal primo satellite terrestre, lo Sputnik sovietico, ed abbiamo una descrizione di tale operazione (la messa in orbita di un oggetto) così chiara, vicina, da commuovere chi davvero presti attenzione.
Molti grandi fisici hanno avuto questo senso del bello, questa visione euristica delle teorie che elaboravano. Molti di loro addirittura buttavano elaborazioni faticosissime perché, alla fine, non vi erano proprietà speciali ricercate a priori. Il pregiudizio ha sempre giocato un ruolo non esattamente raccontabile nel lavoro di moltissimi ricercatori. Solo Popper, che da buon filosofo, proveniente dalla sociologia, poteva dare una visione così asettica ed angusta della scienza. Si sente, come si sente!, se uno ha lavorato da scienziato o se ha fatto solo sociologia della scienza! E purtroppo, nel nostro mondo dai successi facili, è più gratificante fare i sociologi che non applicarsi davvero in estenuanti lavori scientifici. E così abbiamo la disgrazia di avere presunti epistemologi che neppure lo sono per aver lavorato in diretta, ma addirittura in ultima battuta, come l'ignoto Presidente del nostro Senato, tal Pera.
Provo a riportare qualche passo di noti scienziati per mostrare quanto, dietro ogni loro lavoro, fosse sempre presente la ricerca del bello.
"La natura è semplice e possiede pertanto una grande bellezza" (R. Feynman)
"Sono più importanti alcune equazioni belle che altre che si adattino ai dati sperimentali ... poiché le discrepanze possono essere dovute a dettagli secondari che non si sono tenuti in conto nel modo corretto e che saranno chiariti in ulteriori sviluppi della teoria ... Sembra che se si lavora con il fine di trovare bellezza nelle equazioni e se realmente si tiene una idea che abbia un senso, ci si trova nel cammino certo per il progresso." (P. Dirac)
"La fisica è una forma di introspezione e, come tale, è un arte" (D. Böhm)
"Tutti questi lavori sono basati nella fede di un mondo che abbia una struttura completamente armonica. Oggigiorno abbiamo più solide ragioni che mai per non lasciarci distogliere da questo meraviglioso credo. Equazioni di tale complessità come quelle del campo gravitazionale si possono trovare solo attraverso la scoperta di una condizione matematica logicamente semplice." (A. Einstein)
"La bellezza delle leggi della fisica si trova nella fantastica semplicità che adottano ... Qual è il meccanismo matematico definitivo dietro di esse? Deve essere sicuramente il più bello che si possa immaginare." (J. Wheeler)
Si potrebbe continuare e scoprire meraviglie di grandi poesie scritte da grandi scienziati. Ma..., purtroppo c'è un ma. Kant aveva detto, alla fine del Settecento, che quei rami della conoscenza che non si servono degli strumenti della fisica-matematica non possono ritenersi vera scienza. Si può anche tornare a Leonardo da Vinci (metà del Quattrocento) per dire la stessa cosa: "Nessuna ricerca dell'uomo può essere chiamata veramente scienza se non può essere dimostrata matematicamente". Ecco il problema risiede qui. Risiede cioè nel fatto che, per una completa e vera comprensione della bellezza di cui si parla occorre muoversi con agilità nel mondo della matematica. E tutti voi sapete quanto di rifiuto A PRIORI vi sia nell'apprendere tale affascinante disciplina. Dico qui una cosa semplice che ho misurato varie volte in conversazioni con persone di estrazione sociale la più diversa. In ogni salotto ogni astante si vergognerebbe di dire che non conosce Dante o Manzoni o Michelangelo o (più difficile) Prevert ... Nello stesso salotto ci si vanta di NON AVER MAI CAPITO LA MATEMATICA! E così, come con quelli che disertano la politica e ti lasciano solo, ad esempio, con la coltivazione di banane avanzatissima nel nostro Paese, allo stesso modo si è soli a godere delle meraviglie di cui prima, ma non solo! Se la vicenda si chiudesse solo sulle soddisfazioni personali, perché disturbare le categorie della conoscenza e dello spirito? Il fatto è che questa non conoscenza generalizzata della matematica impedisce di conoscere, ad esempio, la fisica nucleare, la microbiologia, la genetica, ... E chi decide per noi? Abbiamo noi gli strumenti per potere, CON COSCIENZA, scegliere per il bene del prossimo? Io credo, ed il referendum del 1987 sul nucleare in Italia ne è una chiara dimostrazione, che i miei concittadini decidano sulle emozioni e non sui fatti. Credo anche, e qui mi fermo, che la conoscenza sia la porta alla libertà.
Tutto questo discorso l' ho fatto per far intravedere come questa idea guida della bellezza abbia influenzato gli scienziati nel passato e continui a farlo oggi, in particolare relativamente a quel "mostro" che è la singolarità. Inizio da un esempio che risale alla metà del Settecento.
Secondo la fisica di Newton la materia deve essere intesa come rigida ed assolutamente impenetrabile. Supponiamo ora di lanciare due palle da biliardo l'una contro l'altra. Ad un dato istante vi sarà un urto. Se ci costruiamo un grafico di come varia la forza F al variare della distanza d, scopriamo una cosa che già sappiamo: al momento dell'urto deve esservi una discontinuità, cioè deve nascere istantaneamente una forza repulsiva infinita (è quel punto angoloso in basso nel disegno che è, ritroviamo il mostro, una discontinuità in fisica ed in matematica).

Questa rigidità, ed in particolare quella discontinuità, non piaceva al fisico dalmata J. J. Boscovich (1711 - 1787). La discontinuità si elimina pensando la materia almeno parzialmente penetrabile (pensate che, per quanto non appaia ai nostri occhi, due palle da biliardo si comportano come due palle di gomma: nell'urto l'una schiaccia - entra - un poco l'altra ed è proprio l'elasticità del sistema che fa rinculare le palle). Questa concezione, che nasce solo da considerazioni euristiche, comporta un grafico che elimina la discontinuità:

E noi oggi sappiamo essere questa una curva di forza per un urto o per il legame tra molecole o ... L'intuizione di Boscovich, eminentemente teorica e dettata, apparentemente, solo da motivi euristici, si è affermata.
Un procedimento analogo è stato seguito dal contemporaneo S. W. Hawking, uno dei più famosi studiosi mondiali (insieme a R. Penrose) di buchi neri, cioè di quelle mostruose singolarità.
Il "pregiudizio" porta a ritenere che nell'universo non vi debbano essere discontinuità. Ed una buca di potenziale, come quella di figura è una discontinuità:
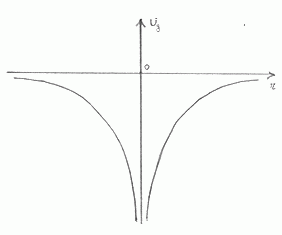
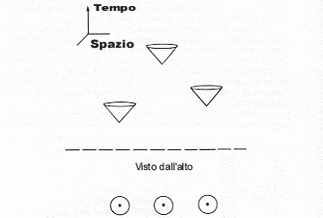
Infatti, si vede facilmente che il "potenziale gravitazionale" Ug varia con la distanza r secondo la relazione:
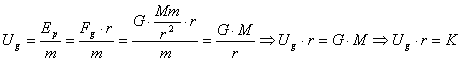
ed alla fine abbiamo un'iperbole equilatera, cioè il prodotto di due variabili uguale ad una costante (intendendo il tutto esteso allo spazio di modo che un ramo di iperbole si deve avere per ogni direzione r dello spazio: in tal modo io ho solo disegnato una sezione del disegno complessivo che in realtà, disegnato nello spazio, sarebbe come una coppa senza fondo). Si vede subito che se r diventa uguale a zero, ci troviamo di fronte ad una espressione non definita, una singolarità, appunto. Questa singolarità, in matematica si descrive così: per r che si avvicina allo zero, Ug tende ad andare verso l'infinito. In fisica la descrizione è diversa nelle conclusioni: per r che si avvicina allo zero, Ug tende a diventare molto grande. Proprio il pregiudizio che ha portato a studiare queste singolarità ha ipotizzato e poi trovato sperimentalmente dei buchi neri: non più qualcosa di non definito ma una realtà fisica da studiare e da tentare di conoscere.
Lo spazio-tempo
Abbiamo già visto che per dare un "punto" (o un "evento") nello spazio-tempo servono quattro coordinate: tre spaziali ed una temporale. Tanto per esemplificare la differenza tra tempo e spazio-tempo, consideriamo due aerei in uno spazio ordinario, euclideo. Se i due aerei avessero le stesse tre coordinate la cosa sarebbe semplicemente assurda. E' impossibile che due corpi occupino simultaneamente lo stesso luogo. La stessa cosa, nello spazio-tempo, sarebbe un disastro aereo.
Tentiamo ora una rappresentazione, dapprima semplificata al massimo. La semplificazione consiste nel rappresentare con un solo asse lo spazio che, in realtà, ha le tre dimensioni che conosciamo. In una tale rappresentazione, un punto spazio-temporale o "evento", sarà un punto ordinario:

Ogni punto di questo spazio-tempo rappresenta un avvenimento istantaneo (un fatto ordinario che avviene in un luogo definito ad un istante preciso, ad esempio, l'accensione di una torcia elettrica). Vediamo invece cosa rappresenta una linea come quella di figura seguente in tale rappresentazione. La linea rappresenta una "traiettoria" di un qualunque oggetto, ad esempio, il lanciare una pallina in aria per lasciarsela ricadere sulla mano. E' chiamata linea di universo
che è appunto la traiettoria di un oggetto nel mondo a quattro dimensioni dello spazio-tempo. Un esempio visivamente chiaro è quello di Francesca che ad un dato istante (le 12:00) sta studiando; quindi si alza, si allaccia una scarpa e si avvia per incontrare un amico.

Qui sotto, invece, vediamo tre eventi diversi tratti dalla quotidianità: A è un osservatore in riposo; egli incontra prima un signore in motorino B e dopo, in direzione opposta, un automobile C. Alla destra vi è la rappresentazione spazio-temporale di queste semplici cose.

Altro esempio di rappresentazione spazio temporale è quello della rotazione di un pianeta intorno al Sole. Poiché il sole si sposta velocissimamente verso Andromeda, un pianeta nello spazio-tempo non chiude l'orbita che risulta invece essere una spirale:

Da ultimo possiamo vedere nello spazio-tempo l'esemplificazione di un'onda provocata in uno stagno da un sasso lasciato cadere: il piano più in basso è quello che rappresenta il sasso che tocca la superficie dell'acqua, gli altri, al passare del tempo, rappresentano le onde che si dipartono da quel primo punto.

La figura seguente rappresenta ancora tre traiettorie differenti di tre differenti oggetti (A, B, e C); naturalmente ora ci riferiamo a cose qualunque.

La linea tratteggiata rappresenta invece la traiettoria di un segnale luminoso che l'oggetto A lancia verso l'oggetto B (tale linea ha sempre una inclinazione di 45° rispetto agli assi dello spazio e del tempo, se misuriamo il tempo in secondi e lo spazio in secondi luce. Supponiamo, per capire meglio, che l'inizio di A rappresenti Francesca a Roma che si alza dal tavolo e che l'inizio di B rappresenti un evento che avviene allo stesso tempo, come una persona che compra un giornale a Parigi. Se quella linea tratteggiata potesse essere orizzontale vorrebbe dire che, istantaneamente, Francesca saprebbe di quella persona che compra il giornale. E ciò non è possibile perché per conoscere quell'evento occorre almeno un segnale luminoso che informi di cosa è accaduto e tale segnale, come sappiamo, non ha velocità infinita.
La figura che segue, oltre a quanto riportato nella precedente, aggiunge una linea orizzontale che E' il presente per un dato osservatore, ed una linea obliqua (naturalmente con una inclinazione inferiore a 45° rispetto all'asse dello spazio, per quanto detto prima) che è il presente per un altro osservatore che si muova con una certa velocità rispetto al primo. Per "conoscere" il mondo in tutte le sue articolazioni, servirebbe un suo "spaccato", cioè una sezione verticale del grafico ora visto.

Tale sezione (che sarebbe il presente per un osservatore in moto a velocità infinita) è però impossibile perché per ottenerla occorrerebbe appunto disporre di una velocità infinita.

Supponiamo ora di avere un oggetto immobile nello spazio-tempo. Ad un dato istante, in un certo punto E, tale

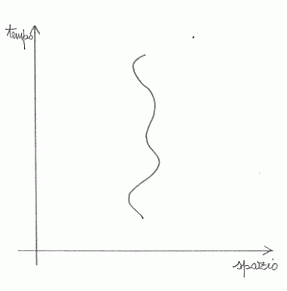
oggetto emetta un lampo di luce verso destra ed un altro verso sinistra.. La luce emessa da E sarà rappresentata da due

rette inclinate di 45° e 135° rispetto all'asse dello spazio. Poiché tutto ciò che in E può accadere ha sempre una velocità inferiore a quella c della luce, allora tutto il futuro di E sta nel triangolo tratteggiato. Mentre il punto E rappresenta

l'unico possibile presente per un osservatore che si trova in E. Allo stesso modo, tutti gli eventi che ci precedono stanno dentro un triangolo compreso tra due rette rappresentanti due lampi di luce inclinati di 225° e 315°
rispettivamente rispetto all'asse dello spazio e tutto il nostro possibile passato si trova dentro il triangolo tratteggiato (mentre E rappresenta sempre l'unico possibile presente.
Assegniamo ora due dimensioni allo spazio. Tutto ciò che abbiamo visto, in un unico disegno diventa (i triangoli si trasformano in coni e le linee diventano dei piani):

Il punto centrale è il presente per un dato osservatore. Il cono in alto è tutto il possibile futuro per questo osservatore, allo stesso modo che il cono in basso rappresenta tutti i possibili passati per lo stesso osservatore (insomma, per arrivare a quel punto si possono esser seguite infinite traiettorie comprese nel cono in basso e, da quel punto, il futuro può essere fatto di tutte le possibili traiettorie comprese nel cono in alto. Il piano orizzontale corrisponde alla retta orizzontale di un osservatore immobile, mentre il piano obliquo rappresenta la situazione di un osservatore in moto rispetto al precedente osservatore. Ciò che non è compreso tra i due coni è al di fuori dell'esperienza possibile dell'osservatore che sta nel punto di unione tra i due coni. Si può semplificare il disegno precedente riducendolo all'essenziale, per renderlo più leggibile: si vedono i coni "passato" e "futuro" con il nostro presente e l'ordine causale

degli eventi: Ad esempio::
- E'' non può influire su E e viceversa;
- E può influire su E';
- E' non può influire su E;
- E''' può aver influito su E e potrà influire su E';
- E non può influire su E'''.
Perse queste
relazioni causali potremmo anche uccidere nostra madre provocando la
morte del suo feto prima che nasca. Resta comunque da capire cosa vuol
dire quel "prima". Sembrerebbe infatti che, così stando le cose,
sarebbe impossibile un viaggio nel passato proprio per i motivi
suddetti. E' invece di interesse notare che la cosa è teoricamente
possibile [si veda D. Deutsch ed M. Lockwood: La fisica quantistica
del viaggio nel tempo, Le Scienze n° 309 del maggio 1994].
Il fisico Fernando de Felice, che insegna Relatività all'Università di
Padova, aggiunge questo commento all'articolo citato:
"Viaggi nel tempo e
consistenza causale
II radicarsi di
convinzioni preconcette che siano prive di evidenze sperimentali o del
supporto logico di una teoria può inibire in modo sensibile lo
sviluppo della conoscenza. Una di queste convinzioni è che i viaggi
nel passato siano impossibili perché permettono di creare situazioni
causalmente inconsistenti. L'esempio più diffuso è quello di un
esploratore che si porti nel suo passato fino a incontrare uno dei
propri nonni ancora nella sua infanzia e
Può accadere infatti
che, in presenza di condizioni così estreme, l'esploratore sia
nell'impossibilità di compiere azioni che creino paradossi insolubili
come quelli che si ottengono troncando la sequenza causale degli
eventi. Un risultato in questa direzione, che emerge non come mera
congettura, ma come implicazione di un'analisi matematica rigorosa, è
stato recentemente ottenuto da Igor Novikov e dai suoi collaboratori
presso il Centro di astronomia
Mettiamo allora un poco in gioco i coni di luce e diciamo che ogni osservatore dispone di uno di essi.


Naturalmente lasciamo il passato ed il cono che abbiamo di fronte comprende il presente ed il futuro.

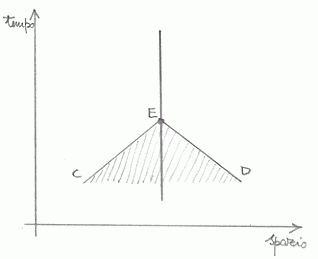
Poiché ogni osservatore ha un suo cono di luce, la situazione di tre osservatori, in assenza di gravità è quella mostrata qui sotto:
Se compare la gravità, una massa A (ad esempio una stella) i coni si "inchinano" verso tale massa, poiché la luce è attratta da tale massa (si ricordi l'esperienza di Eddington):

Se la gravità è molto intensa i coni di luce si inchinano ulteriormente fino a che, da un certo punto (raggio di

Schwarzschild), uno dei bordi del cono risulta inclinato secondo la verticale. Dall'interno di tale raggio risulta impossibile comunicare con l'esterno. La luce è ora tirata verso la grande massa che ha a sinistra. Non può uscirne.

E la situazione, vista dall'alto, è quella della figura precedente. In tal caso, quella stella è un buco nero. In quel luogo, di relativamente piccolo volume ma di enorme massa, vi è la singolarità, quel "mostro" che abbiamo già incontrato.
Prima di chiudere con questa chiacchierata assolutamente divulgativa, è utile chiedersi se la deformazione dello spazio è osservabile. La risposta è SI! Vediamone due esempi. Nel primo disegno, a sinistra, vi è un signore dentro un ascensore che lascia cadere due masse. Queste cadono verso il centro della Terra e, nel farlo, si avvicinano tra loro. Analoga situazione nello spazio in cui non agisca la gravità (figurina a destra), prevede una caduta delle due masse parallelamente tra loro, in senso euclideo.

Allo stesso modo si può seguire la deformazione di quattro masse che, dentro un ascensore in caduta, deformano la loro

posizione iniziale a rombo in una figura sempre più schiacciata. Il motivo è evidentemente lo stesso che accennavo prima: durante la caduta verso l'origine della gravità, le masse si attraggono anche tra loro e non seguono quindi traiettorie di tipo euclideo. Non si deforma quindi solo il parallelismo o il rombo, ma l'intera geometria.
Hiçbir yazý/ resim izinsiz olarak kullanýlamaz!! Telif haklarý uyarýnca bu bir suçtur..! Tüm haklarý Çetin BAL' a aittir. Kaynak gösterilmek þartýyla siteden alýntý yapýlabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru