Time Travel Research Center © 2005 Cetin BAL - GSM:+90  05366063183 - Turkey / Denizli 

Students learn to:

outline the features of the aether model for the transmission of light

In the past people believed that motion could only be carried by contact from one material to another. And since all the planets were in motion, there must be an invisible substance that carried this motion. Also, since all forms of known waves at that time needed a medium in order to be carried through, it was also assumed that light had to be travelling through some form of medium. This strange, all-pervasive medium was the "luminiferous aether". Since the Earth orbited the Sun, it was also reasoned that an 'aether wind' should be blowing past the Earth - just like air passing by when you are riding your bike. Just as the speed of sound in air depends on the air's properties, it was reasoned that this aether wind would also cause the speed of light to vary.

describe and evaluate the Michelson-Morley attempt to measure the relative velocity of the Earth through the aether

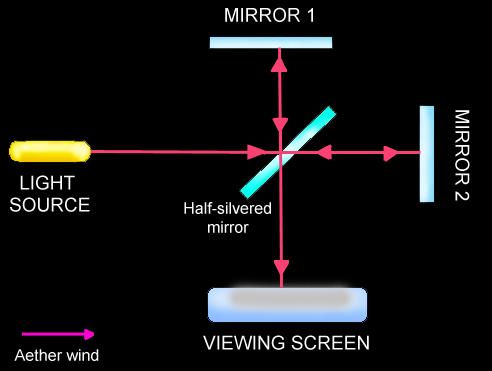
In 1887, using the properties of the Aether, Albert Michelson and Edward Morley made an attempt to measure the motion of the Earth through the aether. Light was sent from a source and split into two perpendicular beams by a half-silvered mirror. Two more mirrors then reflected the two light beams back, recombining them onto a viewing screen. As a result, an inference pattern would be displayed on the screen - relying on the wave properties of light to detect minute differences in arrival times of the waves. If the speed of light of the two beams and the distances they traveled were identical, then the waves would return in phase, adding constructively. A change in velocity due to the aether would cause the waves to be slightly out of phase and hence there would be a reduction in intensity of the wave, and the inference pattern would be slightly different.
 
Since the direction of this aether wind was unknown, the experiment was then rotated though 90^o and repeated. A change in the aether would be detected by a slight shift in the inference pattern produced by the light waves. But change or shift in the inference pattern was observed.
This result meant that only two conclusions could be drawn:
- the aether does not exist
- the speed of light is constant
[For more information, see the subheading below titled "More on the aether..."]

discuss the role of critical experiments in science, such as Michelson-Morley’s, in making determinations about competing theories

Critical experiments in science are carried out to test the many hypothesis put forward by the scientists. Not all theories can be right - even if they are backed up by the greatest thinkers of that time! (Remember Aristotle, who said that the Earth was the centre of the Universe?) Ideas that were previously established are questioned through critical experiments. One cannot just assume that just because something is so for one situation, that in another similar situation, the same will hold true. In order to be truly objective, one cannot just accept something as it is, one must question why? and perform critical experiments to gain appropriate results. Einstein once said "When the world ceases to be the scene of our personal hopes and wishes, where we face it as free beings, admiring, asking and observing, there we enter the realm of art and science." (Nice quote, not quite relevant to the dot point...but hey, it sounded good so I decided it was worth sticking in...)

outline the nature of inertial frames of reference

A reference frame is just a 'co-ordinate system' (one could call it a set of objects...) from which we take our measurements and make observations. Let's take the common train example. Two trains pull up on the same platform on opposite sides from opposite directions. One of these trains starts to move. For those people that catch the train everyday, remember sitting in one of the two trains and looking out the window? It's quite hard to tell which train is moving just by looking at the opposite train. But when we look at that bench on the platform which appears to remain fixed, one realizes that it is the opposite train that is moving. In this case, the reference frame would be the platform, the ground and the surrounding objects.

So what is an inertial reference frame? It is basically just a frame of reference in which Newton's 1st Law of motion applies. Newton's Law of Inertia states that "A body remains at rest or continues to move at a constant velocity unless acted on by an external force." Let's take an example of a starfighter streaking through space at a constant speed. Here, the starfighter's motion is constant relative to the background stars and therefore can be called an inertial reference frame. But once this starfighter decelerates and turns around, its motion is no longer constant relative to the background stars, and hence its frame of reference is non-inertial ie. it is accelerating.

discuss the principle of relativity

The entire concept of relativity depends greatly on the perspective (frame of reference) of the observer. To make things a little easier, let's 'break relativity down' and start with some history...

"GALILEAN RELATIVITY"
Believe it or not, the concept of relativity is much older than Einstein! It goes all the way back to Galileo and his study of motion. Let's look at some of the experiments he conducted. In these, an object was dropped from the mast of a moving ship. (For convenience sake, the picture below is of a modern sailing ship and a ball...)
 
The above picture is from the ship's reference frame. From this perspective, the ship is 'stationary', and the water moves by as do the clouds and the ball moves away and drops down.
[You'll have to excuse the stuffy graphics here, the program I used didn't convert them terribly well]
 
The picture above is from an observer's perspective some distance away from the boat. From this reference frame, the ball appears to fall straight down, everything else is 'stationary', it is the ship that is moving.

These experiments verified Galileo's belief that the motion of the ship had no effect on the motion of the ball, but the way the ball fell depended on the reference frame of the observer. Together with other 'thought experiments', Galileo came to a conclusion, today known as The Principle of Galilean Relativity which states that: the laws of mechanics are the same for a body at rest and a body moving with a constant velocity.

"NEWTONIAN RELATIVITY"
Isaac Newton took Galilean Relativity one step further saying that two observers travelling at the same relative velocity would see the same acceleration. Both observers will therefore agree on the mass being the same and so F = ma is equivalent in both frames. In his postulate Principia Mathematica, Newton defined 'absolute motion' as "the translation of a bod from one absolute place to another..." But what does he mean by "absolute place"? He also defined 'absolute time' as "absolute true and mathematical time, of itself, and from its own nature flows equally without regard to anything external".... Which just means that time is independent of space (after all that eloquent language...).
Although aware that motion is relative, Newton believed that there was some fixed frame of reference to which all other motions could be compared - the aether. But as we have seen previously, the search of the aether has ended in vain.

MORE ON THE AETHER...
Scientists at that time were extremely reluctant to drop the idea of the aether as an absolute reference frame. The following two proposals were put forward to account for the Michelson-Morley Experiment's negative/null result:
1) Someone suggested that the Earth 'carried the aether along' as it rotated so there would be no relative motion. But, other observations such as light aberration proved this theory to be rather absurd.
2) After studying Maxwell's equations of electromagnetism, Hendrik Lorentz and George FitzGerald proposed that the length of the apparatus used in the Michelson Morley experiment contracted in the direction of its motion! Sound ridiculous? But in fact they were on the right track! Unfortunately, even though it explained the null result it was just an ad hoc assumption. Lorentz's investigations were restricted mainly to electromagnetism and it was a daring step to extend this idea to ordinary dynamics. But then Henry Ponicaré introduced the 'Principle of Relativity' stating: "The laws of physics are the same for a 'fixed' observer as for an observer who has a uniform motion of translation relative to him". But all this was soon to be resolved with the coming of ... EINSTEIN person of the 21st Century ...

"EINSTEINIAN RELATIVITY"
Although Newton's Laws of mechanics are successful in describing motions that occur in everyday life, but when dealing with speeds close to the speed of light, inconsistencys appear and the laws seem to break down. In 1905 Albert Einstein proposed his theory of Special Relativity, which rocked the best of minds at that time and changed the whole notion of relativity and scientific thought...
At a science conference after Special Relativity was first postulated, one physicist stuck his head out of the crowd and asked "Is it true that out of everyone present here, only three people understand this concept of relativity? Wait a minute - I forgot who the third person was..."
The theory of Special Relativity is based on two main assumptions:
- that the laws of physics are the same in all inertial reference frames
- the speed of light in a vacuum is constant in all inertial frames of reference: c = 2.9979 x 10⁸ ms^-1
The implications of this appear to be impossible at first and seem to defy 'common sense'. Lengths appear to get shorter, masses increase and even time appears to slow down! All these effects, of course, depend on one's frame of reference. Those long held beliefs of space, time and classical mechanics are relative, not absolute, with Einstein described 'common sense' as a "deposit of prejudice laid down in the mind prior the age of eighteen..."

Note though, that Special Relativity does not include gravity, that idea was postulated later in General Relativity.

identify the significance of Einstein’s assumption of the constancy of the speed of light

Einstein postulated that the speed of light is constant and independent of the speed of the observer or its source. This conclusion was based on James Maxwell's field equations. Whilst analyzing electromagnetic fields, Maxwell discovered that the velocity of light was an intrinsic property of all electromagnetic radiation. If you were moving rapidly towards a source of light, you would not see the speed of the light coming towards you increase. If you were moving away from the source of light, the speed of light would not decrease either - it is constant regardless of your motion.
This theory showed the the concept of the aether was not needed, and that there is no such thing as an absolute frame of reference. All inertial frames of reference are equivalent - all motion is relative.

recognise that if c is constant then space and time become relative

To explain the concept of a relative space/time, let's do a little 'thought experiment'... Suppose you are driving a spaceship moving at half the speed of light towards Earth. You then pull out one of your high-tech laser beams and flash it to Earth in the direction of your motion. Now, what will this speed of light be? Before Einstein came, one would look at the situation and say, okay, the speed of light is c and the spacecraft which you are travelling on is c/2, therefore the speed of the laser beam would be c + c/2 = 1.5c . But! - according to our genius Einstein, the speed of light always remains at c! So, what's going on?! Well, let's look at the formula c = d / t. We know that the speed of light is c and must always remain at c, therefore, the extra 1.5 we calculated earlier must be shifted over to the d / t side of the equation. This means that if c remains constant, distance and time must change to account for this. Space and time are only relative concepts!!
[Hmm, from all this and more - as you will see later - the only thing that appears to be non-changeable is the speed of light... - note the extra emphasis on "appears"...]

discuss the concept that length standards are defined in terms of time with reference to the original meter

In order to understand relativity, let's look again at what is meant when we use the word "measurement". Measurement is "the process of comparing some quantity to a selected standard, and expressing the measured quantity as some factor of that standard". All measured quantities are relative. The SI unit for length is the metre, originally defined to be one ten-millionth of the distance between the North Pole and the Equator via Paris. This distance, was then engraved on a platinum-iridium bar which became the standard metre. All distances were compared to this standard. But as technology improved, the definition of the metre was changed to one defined in terms of the wavelength of a specific band of light emitted from an element called Krypton-86 when it was placed in a gas discharge tube and excited. Now the defination of the metre is: "the distance travelled by light in a vacuum in the fraction 1 / 299 792 458 of a second" (what a nice number!) But, strange as the defination may appear to be, our current standard of length is defined in terms of time!
Note that if one were to look further into areas such as Quantum Mechanics, one would discover that reality is what we measure it to be... (Just had to add that note! =P )

identify the usefulness of discussing space-time, rather than simple space

One would notice that in order to describe an event fully, one needs to know not only the location of the event, but the time at which it took place. On top of the coordinates x,y,z used to describe a location in 3D space, a fourth dimension time has to be described. And since both space and time are relative, they can easily be bundled together into a four-dimensional space-time continuum [sound familiar?]. This space-time continuum is further elaborated on in Einstein's theory of General Relativity which concern's gravity. Gravity here is just caused by mass and can be likened as to making a dent in the fabric of the space-time continuum, causing objects to 'roll' towards the mass and light to bend...[but you don't need to know all that yet!]

account for the need, when considering space-time, to define events using four dimensions

explain qualitatively and quantitatively the consequence of special relativity in relation to:
- the relativity of simultaneity
- the equivalence between mass and energy
- length contraction
- time dilation

THE RELATIVITY OF SIMULTANEITY...
Apart from the fact that this dot-point was made to sound good, the main idea of this is, that two events that are simultaneous (occurring at the same time) in one reference frame, may not be simultaneous in another. So, let's do what is called a 'thought experiment'! [if you're not keen on 'thought experiments' you'll probably be sick of them by the end of this module, so erase that and think; 'I love thought experiments!'] Anyway, suppose you are a Commander sitting in the middle of a mini-Space Station moving at a constant speed when suddenly, BANG! BANG! An enemy craft appears out of nowhere and starts shooting at you, luckily the pilot is a terrible shot, and only manages to scrape the front and back of your Station! At the same time, a pilot who has a bad engine is about half way down the Space Station observes the proceedings. Now the stationary pilot sees the two strikes simultaneously, deducing that they occurred at the same time since he was halfway in between the two events. On the other hand, since you are moving forwards towards the laser beam that scratch the front of your Station, even though light is independent of its obsever, the light from that laser beam will reach you first, hence you will conclude that this laser beam struck the front of the Station first, before the one at the back.

EQUIVALENCE OF MASS AND ENERGY
Now remeber Einstein's famous equation E = mc² ? I guess the equivalence of mass and energy speaks for itself here. All mass in the Universe possess an intrinsic energy even at rest. If this mass can be somehow made to vanish from the universe, an equivalent amount of energy must be released to replace the missing mass. For particle physicists such as our friends over in CERN, this is nothing new. So, let's take a brief little physics holiday into the sub-atomic world, where things just wink in and out of existence... From the Cosmic Engine module [I bravely assume?], one already knows that any particle in the universe has what is known as an antiparticle! When for example an electron meets up with its antiparticle the positron, the two of then will annihilate each other, producing both their total masses into energy [lot's of energy!] in the form of gamma rays. And of course if one can manage to scrap up enough energy ... ding!.... the opposite occurs and you have matter! And, that's what our pals in CERN do everyday...

LENGTH CONTRACTION
This is just one of the implications of relativity - the length of a moving object appears to contract in the direction of motion relative to a stationary observer. Now one may think "Whoa! That doesn't make sense, things don't get shorter just because they are moving!" But bear in mind that we are dealing with speeds approaching the speed of light here - the fastest Jetfighter today can easily be compared to a little microbe swimming slowly in a pond relative to the speed of light! [there goes that word again..] To explain this, consider this thought experiment. Anyway, let's say that someone dumped you in a carriage on speeding train [and I mean speeding...] So, using a light beam, and a clock, you manage to work out the length of the carriage. Einstein then decides to show up at the platform to prove his point, and somehow calculates the length of the carriage as the train passes by the platform.
 
 
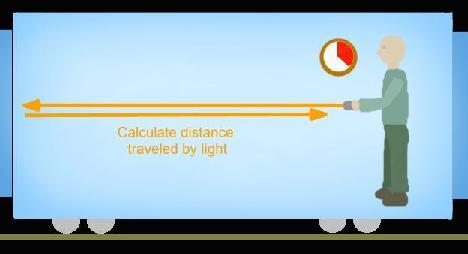
When the two results are compared, surprise, surprise... they are not the same! From Einstein's viewpoint as the train roars past, not only does the light move to meet the end of the carriage, the rear of the carriage is moving to meet the beam of light! So for him, the beam has traveled a shorter distance. But since light is a constant, when calculated, the length of the carriage becomes shorter ie. length contracts.

Now it's time for some math! I'm going to be lazy and just give you the magic formula for length contraction...
l = l_o x (1 - v²/c²)^1/2
Where" l_o " is the proper length of an object, ie. the length of the object measured in the frame where it is at rest (from your reference frame within the carriage in this case).

TIME DILATION
At this stage one may probably be thinking "Oh man, so length contracts...what happens to time?" So, let's do another thought experiment, a rather classical one at that... Consider the following situation, you are sitting in a train carriage which is travelling near the speed of light to some unknown destination (yes it is the train again - not very imaginative, but saves me time when making the graphics...). In front of you is a light hanging from the roof and there's a mirror on the floor which reflects the light back up. You have a large clock with which to time how long it takes for the light to reach the mirror and be reflected back to the top. Your good old buddy Einstein is standing outside, watching you and the train ride past. He too has a large clock, and is timing how long it takes for the light to travel down to the mirror and back.
 
 
As you can see in diagram 1, within your reference frame, the light only has to travel up and down. But in diagram 2, from Einstein's perspective, the light has to travel not only up and down but horizontally as well. Since the light has a longer distance to travel, more time is taken (remember that the speed of light is always constant!). Hence, the dilation of time.
 

Now for the mathematical part. The time interval between two events as seen by an observer (in this case, you) in the same reference frame where the events are taking place, is called proper time (t_o).The proper length (l_o) of an object is the length of the object measured in the frame where it is at rest. Let's simplify the above diagrams to the following two below. Diagram one is from your point of view in the carriage, and diagram 2 is from Einstein's perspective outside the train.

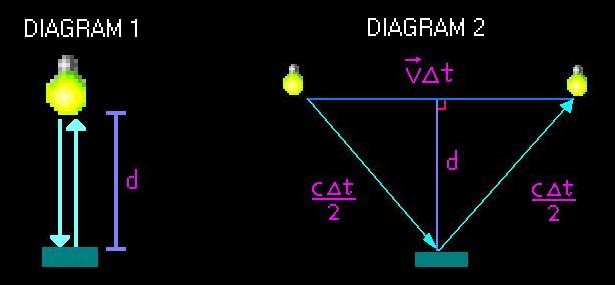
From diagram 1, t_o = 2d / c
From diagram 2 using Pythagoras' Theorem:
(c Δ t / 2)² = (v Δ t / 2)² + d ²
Solving for Δ t gives:
Δ t = 2d / (c² - v²)^1/2
Δ t = 2d/c x [1/ (1 - v²/c²)^1/2 ]
Since Δ t₀ = 2d/c, sub this into the equation:
Δ t = t_o / (1 - v²/c²)^1/2
And this is the formula you need to know for time dilation! (Pretty equations aren't they?)

Now just to stick to convention, we can take a look at the all famous twin paradox. Suppose we have 2 twins, Luke and Leia. Whilst Luke is stuck on Yavin, Leia boards a StarCruiser and travels near the speed of light to the planet Courscant, she doesn't get off but immediately orders the Captain to swing the ship around and head straight back to her brother who is waiting impatiently back on Yavin. Thanks to time dilation, Leia's biological clock would be ticking slower than Luke's, so when the two meet again, Leia would find that everyone else has aged more than she expected. But! Here's the paradox! That explanation was given only from Luke's reference frame! From Leia's perspective, she is stationary - it is her brother that is moving away from her, and so to her disappointment, it is he that is ageing slowly! So if both could somehow see each other, they would both think the other is ageing more slowly. Now who is older than who? The answer is quite simple really. Since Leia was forced to decelerate and turn around at Courscant, her frame of reference is no longer inertial - remember that word? So, her view of her brother ageing slowly is not valid in her case. Therefore, when they finally meet up on Yavin, she would be much younger than her brother.
 

But wait - there's more!!
Since length and time are relative, so too are momentum, mass and energy!! But before I go any further, let's look at the 'Gamma Factor'. Mathematically, relativistic effects are 'described' by a factor denoted by the Greek letter gamma g . This factor depends on the speed the object is traveling at. Now, looking at the formula for gamma, we have:
......
As you guys will eventually work out, the reason why we do not see the effects of relativity in everyday life is because this gamma factor is basically 1, but as we approach lightspeed, gamma tends towards infinity!
Now going back to momentum, mass and energy, since we are dealing with relativistic effects, we have to add in the gamma factor, giving us the equations below: (where m_o is rest mass)
p = g m_ov
m = g m_o
E = g m₀c²
So, as we approach lightspeed, the object's momentum and energy (in this case kinetic energy) increase at an astounding rate. But there's also some bad news... As you can see from the mass equation above, as we approach lightspeed, the mass of an object increases towards infinity. And thanks to Newton's F = ma, the more massive the object, the harder it is to accelerate it, hence we have to exert even larger forces on it, just to produce some puny little accelerations! So, for all you Sci-Fi fans out there [such as myself], sorry, but there goes lightspeed via 'conventional' means out the window... So much for those intergalactic space battles, what a bummer!

discuss the implications of time dilation and length contraction for space travel

The implications of time dilation and length contraction are not terribly useful to us at the moment - right now it seems quite unlikely that we'll ever reach speeds close to that of light. But what if we could? Well, the implications are basically, that less time is taken to travel from one point to another, as the distance becomes shorter, and time slows down. Hence, space travel would be much more...convenient, and not to mention that one will remain younger for a longer period of time. [But then again, even light speed may not be enough as discussed earlier...] Now, let's see what other implications you guys can come up with...

Students:

perform an investigation and gather first-hand or secondary data to model the Michelson-Morley experiment

Well, I'm afraid it's back to the science lab and out into the field for this dot-point!

perform an investigation to help distinguish between non-inertial and inertial frames of reference

Once again, to the labs guys! Just remember though that inertial reference frames are non-accelerating, and non-inertial frames are accelerating...

analyse and interpret some of Einstein’s thought experiments involving mirrors and trains and discuss the relationship between thought and reality

Hmm, methinks one can write an entire thesis on this dot-point! Some examples of Einstein's thought experiments have been given earlier, as for the relationship between thought and reality, maybe I'll come to that later in a more philosophical mood... Meanwhile I'll leave you guys to ponder over the philosophy behind what is considered as real and imaginary... ;P

analyse information to discuss the relationship between theory and the evidence supporting it, using Einstein’s predictions based on relativity that were made many years before evidence was available to support it

solve problems and analyse information using:

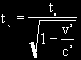
I'm afraid for this section you'll have to go away and do some mathematics homework...

gather, process, analyse information and use available evidence to discuss the relative energy costs associated with space travel

Time Dilation

Imagine that there is a car passing by you while standing on the sidewalk.  This car has a rather odd contraption: on top of the car is a light bulb attached right in the middle of the hood, and running from the car's two ends is a row of firecrackers.  At the instant the car passes by you, the light bulb turns on, sending light to the front and back of the car, which, when received by a device, detonates the firecrackers. 

We have already derived the many strange aspects of space.  Motion is relative.  The speed of light is absolute.  But what about time?  We know that motion inside the car will be viewed differently by the driver and you due to different reference frames.  But, in spite of this spatial disagreement, could there also be a temporal one?

Indeed there is! The driver, who is equidistant from both ends of the car (assuming that the car is designed in such that way) will measure that the light takes the same time to reach both ends of the car, and thus he will see the firecrackers detonate simultaneously.  You on the other hand, will not see this concurrence, as a consequence of light's constancy.

Since you are not moving with the car, the front part of the car, relative to the ground, is receding from the light.  Thus, its distance is increasing from the light beam and it therefore takes more time for the light to reach the forward end.  Conversely, the back of the car is moving towards the light and hence the distance between the two is decreasing.  Therefore, light takes a shorter time to reach the back end.  The observed effect is that the most rear firecrackers detonate before the ones in the front.

The crucial part about the constancy of light's speed is that it is not added with the velocity of the car.  Had we performed the same calculations carried out in the previous train scenario, then the added/subtracted velocities would have cancelled out with the receding/approaching ends of the car, and the simultainity of the exploding firecrackers would have been maintained (just like how the thrown ball on the train would still "work out symmetrically", and each person would receive the ball at the same time). 

[outlined in the above diagram is the reason why there is no agreement of simultaneity - simply because of the convergence and recession of the ends of the cars with the light beams; the incorrect version shows why if we still held classical physics with adding speeds to be true, there would in fact be the expected simultaneity, whereas in reality there is not one; the added velocities (either due to the converging rear end of the car or the light that moves in the forward direction of the car) cancel out with the velocities in the opposite direction (either due to the light moving in the opposite direction of the car or because the front end of the car is receding, respectively), as denoted by the crossing of the arrows]

Amazingly, not only are space and motion relative, but as we have just seen, time is also relative as well! This remarkable consequence may come as a bit of a surprise, since, in our day to day world, space and time seem like entirely separate entities.  Meter sticks measure distance.  Stop watches measure time.  There is no mixing of the two. 

But in actuality the two are quite related.  When one looks out into space, one looks back into time.  The light from which you see everything took time to cross the intervening distance between your eyes and the objects in sight.  For objects very near, this delay is hardly noticeable, as light a beam of light can circle the Earth seven times in a mere second.  However, objects that are considerably far outside the vicinity of our home planet will have a significantly longer delay.  Light from the sun, for instance, takes about 8 minutes to reach us here on Earth. The ball of fire in the sky is not how the sun is "now", but how it was 8 minutes ago, when the light that we see left the sun.  Other much more distant astronimical objects may be so far away that the light from them may take millions or even billions of years to cross the enormous void!  When the light from such objects left its surface, there were no humans around. 

So we can see how deeply space and time are interwoven.  We cannot look back into space, without looking back into time.  We have also seen previously how motion causes one to measure speeds differently.  Just now, we have also seen how motion distorts the simultaneity of two events.  But here's the truly shocking result - motion also causes time to run more slowly!  Hence, a moving clock would tick more slowly than one at rest! 

Up to now, all of our experiments and ideas have been purely conceptual and case by case.  Many (perhaps all) of the conclusions so far may seem beyond bizarre.  But in fact, numerous experiments have confirmed these predictions of  Einstein's relativity.  Sensitive atomic clocks in motion on airplanes have been shown to tick ever so slightly slower than the stationary clocks on Earth.  Subatomic particles accelerated to enormous speeds do indeed live longer than they would normally.   

Indeed, this "time dilation" effect is an actual property of nature.  Equally bizarre is the fact that moving objects additionally contract in the direction of motion (the Lorentz contraction)!  That is, if the object were moving in the west-east direction, then it would be contracted along that direction, and appear "thinner", and if it were moving in the down-up direction, then the object would look "squashed".  Furthermore, an object's mass also increases, by the same amount as the time dilation and length contraction, as it reaches the speed of light.  Thus, as an object continues to accelerate towards the speed of light, its mass increases without bound.  Consequently, more and more energy must be expended to continue to accelerate this moving body.  This is, mathematically, also where the cosmic speed limit comes in, for in order propel oneself faster than light, one must expand an infinite amount of energy. 

Keep in mind that these are all from the point of view from the "stationary" observer.  If you were traveling at high speeds, you yourself would feel nothing different.  Although your ten years may be fifty years for a standby observer, you still experience those ten years.  Similarly, though an observer may see you squeezed fivefold, your space and area still feels the same to you.  Hence, this time dilation is by no means a way to live forever.  The average life of a human may be around seventy or so years, and thus, even if you zip one million years into the future, you will still accumulate seventy years, eventually, in your "own time" frame. 

Now, proving how all this actually works and by what factor time is slowed will be substantially more complicated then what we have done so far, so if the reader is interested, please proceed to:

Light Clock

Otherwise, the said formula is:

T = 1/Ö(1 - (v/c )²),

T being the time dilation factor, and where v is the velocity of the object in question, and c is the speed of light.  Simply, we square the ratio of the speed of the moving object with that of light, subtract it from 1, take the square root of the difference, and finally reciprocate it.  This formula also gives the same factor for which length contracts and mass increases.  If one travels at 80% the speed of light, plugging this into the formula gives the factor 1.66.  Therefore, a clock 30 inches long will appear to be only 18 inches long, and to your hour, it would tick 36 minutes.  If one travels at 86.6% the speed of light, the calculated factor is 2, and thus lengths and times are halved, and mass is doubled, as seen by the stationary clock.  As speeds climb higher and higher, the ratio v/c approaches one and the denominator nears 0, making the entire ratio soar to infinity. 

Unfortunately, it is because we move at such slow speeds that we never see or experience these effects. 

The Twins Paradox

Given that things do age more slowly while in motion, suppose that we do indeed test this time dilation effect by holding one clock stationary on earth while sending another one fast into motion, out into space.  According to our previous conclusions, then the clock that is receding from the Earth ought to be the one that ticks the slowest.  However, if we remember that motion is relative, we also note that according to the clock that is receding, it appears as if it is the Earth and the clock that is moving away.  Therefore, according to that clock, then the clock that we perceive, here on Earth to be ticking regularly, ought to be slow.  But of course, both of them cannot be slower than each other! 

This absurdity is infamously known as The Twins Paradox.  But in fact, the contradiction above does not happen at all.  In fact we can resolve it: the only paradox left however, is that the two twins would have aged differently (which therefore agrees with the fact that a moving clock does indeed tick slower).  To explain, we must again open our minds to another thought experiment (adapted from . About Time)

Anne and Betty are two identical twins.  Betty is about to embark upon a journey to a star 8 light years away on a rocket traveling at 80% the speed of light (and from the above time dilation formula, the time dilation factor is 1.66). Anne will wait on Earth. The two are equipped with powerful telescopes to monitor each other on their long voyage.  They decide to leave in the year 2000.

Now realize here that Anne will see the trip take 20 years.  The star is 8 light years away and traveling at 80% speed of light, it will take 10 years to get there and another 10 to get back.  Betty, on the other hand will have that time reduce by 1.66, her time dilation factor, due to her speed of motion at 80% speed of light, and 20/1.66 = 12.  So Betty would only age 12 years and feel that the trip last 12 years, according to Einstein's relativity.

And now, they take off!  It would be appropriate to take acceleration into consideration but to keep the arithmetic simple, let's assume that for our purposes, that the acceleration is nearly instantaneous and that Betty can withstand such a colossal change in velocity. 

Now, after a while on the trip, what will Anne and Betty see?  At this point, the paradox takes place.  Anne, our competent comrade, expects to see Betty's clock run slow by a factor of 1.6 (36 minutes to the hour) and Betty, equally competent, will likewise see Anne's clock run just as slow.  To each of the twins, it will appear to be the other twin whose clock is running slow. In fact, however, the clocks register as even running slower than what our calculations tell us because of an additional effect: the Doppler effect . 

The Doppler effect is the compression of waves as the source of the waves approaches the receiver.  An example of this would be when you stand on the sidewalk and hear the change in pitch of a vehicle passing by.

(from Black Holes & Time Warps by Kip Thorne (c) 1994)

When, say, an ambulance truck rushes by you, the forward motion of the vehicle squeezes the waves in front of it, which decreases the wavelength and causes that higher pitch you hear.  Conversely, when the truck recedes from you, the sound waves become stretched out, the pitch drops until it can be heard no more.  It sounds something like:

Approaching                                                Receding

"...weeeeEEEEEEEEEEWWOOOOOOOOooooo....."

This is an auditory example of the Doppler shift, which causes a change in pitch.  However, pitch is to sound, what color is to light.  Thus, a Doppler shift for light waves causes the object to appear bluer, as blue light waves have a short wavelength - hence this effect is known as a blueshift.  Similarly, an object receding has its light waves stretched out behind of it - the effect known as a redshift, because red light has longest wavelength within the visible spectrum.   

Nonetheless, a car passing by, however, doesn't seem bluer and a car receding doesn't seem redder.  Once again, the speeds we are dealing with here are far too slow.  Since sound travels much much slower than light, the speed of a car constitutes a good fraction of such a speed, and thus, the effect is noticeable.  In order for this to occur for light, however, objects would need to travel at speeds vastly higher. 

But in our example with Anne and Betty, eighty percent the speed of light is much sufficient. When Betty speeds off, she will indeed appear redder, as she leaves her light waves stretched out behind her.  More importantly however, there will be a subsequent time delay because of this Doppler effect.  In effect, this time delay, due to the Doppler effect would occur anyways , without taking the separate, relativistic time dilation into consideration (which we did previously).

Recall our previous mixing of space and time, how we cannot look back into space without looking back into time.  As Betty's rocket, or any object for that matter, recedes from the observer, the space between the two will steadily increase.  Consequently, the time delay becomes progressively larger and larger as the object moves farther and farther away. Obviously, the rate at which the distance is growing, and hence the rate at which the time delay escalates, depends upon the speed of the object moving - the faster the object, the more pronounced the time delay.  For a moving car, it may move 30 or so meters further in one second, and thus the difference in time it takes for light to cross the increasing distance is unnoticeable.  However, if that car were allowed to travel for a few million years, out to a point where light would take days, months, or even a year to cross the steadily ever-increasing distance, the time delay would then become substantial.  But due to the fact that the car moves so slowly compared to light, however, the rate at which this effect happens is infinitesimal.

 
The Doppler effect will cause a fast moving object to have a longer time delay,
as it is farther away from the observer, causing the light to take a longer time to bridge the distance
(this diagram is not to scale)

However, Betty's enormous speed greatly exaggerates this effect.  In one hour, her rocket ship will be 48 light-minutes (eighty percent of one light hour) away from Earth.  Thus, it will take light 48 minutes to send the information on her clock back to Anne on Earth (and vica versa - Betty will see the events on Earth as 48 minutes "behind").  As Betty travels deeper and deeper into space, this delay, due to the Doppler effect becomes more and more severe.       

So, to finally answer our question, what will the two actually see on each other's clocks after one hour has lapsed?  Adding the Doppler effect with the time dilation effect, we find that the answer is 20 minutes.  Let me explain: 

Through our computation of the time dilation factor, we know that for every hour on Anne's clock that ticks, 36 minutes will have passed by on Betty's "slow" clock (and we also have established that up to now, both will see the same thing, so to Betty, this same slowdown effect will occur when she looks back at Anne's clock).  But we also now know of the additional time delay caused by the Doppler effect, namely, the rapidly increasing distance between Betty's rocket and the Earth.  After an hour, Betty and the Earth will be 48 light-minutes away.  Thus, the light that contains the information that 36 minutes that have ticked on Betty's rocket does not arrive to Anne until 48 minutes later.  When she receives the information, one hour plus these 48 minutes will have lapsed, for a total of 108 minutes.  To her, she sees Betty's clock at 36 minutes, and so it appears to be running at 1/3 the rate of hers.

Betty sees the exact same thing.  When Betty is 48 light minutes away from home, what she sees on Earth is what was 48 minutes "ago", Earth time.  We know that from the point of view of the Earth, it will have taken Betty one hour to travel 48 light minutes out into space.  Therefore, one hour minus 48 minutes is 12 minutes.  Thus, Betty, who sees her clock at 36 minutes, sees that it is Anne's clock that is the one running at 1/3 the rate of hers. 

This effect will continue on throughout the first half of the journey.  At any given time during the outward voyage, both Anne and Betty will see that is the other clock that is running at 1/3 the rate of their own.  In general, the formula to compute this combined slowdown factor [1] , F, is:

F = T/(1 + v/c)

So, thus far, neglecting acceleration, we see that the two observers experience the same symmetrical time slow down.  When Betty reaches the star, her clock will register as the year 2006, halfway from 2012, her set return date.  When she looks back at Earth, eight light years away, she sees what happens 8 years before the "current" Earth time, 2010 (halfway from 2020, the time on Earth when Betty is perceived to return).  Thus, Betty sees the clock at 2002, and as before, this seems as if the clock is running at 1/3 the rate of hers.

[Keep in mind these are what the twins are seeing.  Through the math we have done, these twins can certainly untangle the Doppler effect and find out the time dilation factor, and deduce how much slower the other clock is "really" ticking at, which is 1.66 times slower, instead of 3.]

Similarly, Anne will see Betty's clock run at 1/3 the rate of her own.  When Betty reaches the star, the image of her clock striking on the year 2006 will take another 8 years to propagate back to Earth.  Anne will receive this 8 years from 2010, in the year 2018.  Betty's clock will have seemed to only ticked for six years to Anne's eighteen. 

Now, for the return journey, the same symmetry occurs for both twins, but with one difference - the Doppler effect on an approaching object will now instead speed things up by a factor of 3.  This is because Betty is now rushing towards Earth at nearly the speed of light.  Images of Anne become successively less and less delayed as she nears the Earth, and eventually, as she comes within close proximity, she is swiftly moving into the incoming light rays, seeing a barrage of information come at her all at once.  The same occurs for Anne, as the rate at which incoming information from the rocket ship quickly rises. 

We have determined that Anne will witness Betty's arrival at the start in the year 2018.  Hence, as Betty will be arriving home in the year 2020, the entirety of the homeward bound voyage is seen to be compressed within the remaining two years of Anne.  Anne also sees that it is Betty's clock that registers as 2006 at the arrival of the star, but when she comes home, it is the year 2012 on her clock.  So to Anne, it appears as if six years have passed on Betty's clock to her mere two years - Betty's clock appears as if it were running three times faster.

In the same manner, Betty will see the same for Anne.  When she looked back on Earth at the star's arrival, Anne's clock registered as being the year 2002.  When she returns, she will be surprised to discover that it is the year 2020.  Thus, though her trip back takes her 6 years, she witnesses 18 years on Earth passing by - again, she observes the same tripled amount. 

[Remember this is what they visually see .  These twins could very well go through the math, just like we have, and remove the added Doppler effect, and find out the clocks are "really" running 1.66 times slower than their own.  In the case that the two clocks are approaching each other, the Doppler effect just so happens beats the time dilation effect, causing the clocks to appear tick faster instead of slower (in contrast to when they are receding, where the Doppler effect instead exaggerates the time lag).] 

So indeed the two twins return, with their expected discrepancies.  Anne has aged 20 years, and Betty, who has traveled at eighty percent the speed of light, ages only 12.  What we also just shown in the above analysis (hopefully you were able to keep up!) is that there is indeed no paradox about clocks being simultaneously behind and ahead of another clock.  The slowdown effect and speeded up events, a combination of both the time dilation and Doppler effect, fit together consistently.  Furthermore, the trip itself is not entirely symmetrical.  In order for Betty to leave and return, she must accelerate, move at her uniform speed, decelerate and then accelerate as she whips around the star, cruise back at her uniform speed again, and finally decelerate as makes it home.  These accelerations break the symmetry between what the two twins experience.  Relativity applies to uniform motion - accelerations are absolute .

[Also note that distances are also distorted with relativity.  Betty, who took 6 years to reach the star while travelling at 80 percent the speed of light will thus perceive the star to be only 6 x 0.8 = 4.8 light years away, whereas Anne measures it to be 8 light years away.  The distance to the start is shrunk by the same factor of 0.6.] 

What we have seen via the resolution of the twins paradox, however, is quite startling.  With time dilation and relative motion, there is in fact, no universal "now".  Both Anne and Betty (and all other observers in the universe), will each have their own time, their own "nows".  What they deem as simultaneous and what they experience to be the time interval between two events also obey the laws of relativity, despite how fixed and universal these measurements may intuitively seem to us.

Although many of our common, day to day assumptions have been shown to be relative, there are some things that simply stay constant from reference frame to reference frame.  The speed of light is absolute.  So are accelerations.  Another quantity that remains invariant is the spacetime separation between two events.  Let us return to our first example with the car and the detonating firecrackers. 

The above diagram is what is called a space-time diagram.  Imagine that all the space in the universe is somehow reduced down to one dimension, such that every point in space falls somewhere on that axis labeled space.  Then, given the time axis, each point along the time axis corresponds to some particular date in the universe.  Combining the two axis gives us a plane, in which every possible event (a location in space at a particular time) is mapped     (If we really wanted to have a complete space-time diagram, we would need four dimensions, three for space and one for time, but that would be impossible to draw.  So we have to use our imagination and scale the dimensions down). Each unique point corresponds to a unique event.  Moving in the left-right direction corresponds to moving through space and moving in the up-down direction is moving through time.  Thus, any point that lies directly horizontal of a point is simply another location at the same time.  Any point that lies directly above another point is the same location, only at a future time.   

A worldline is the line that an object traces out in space-time.  It can be thought of as the "history" of an object, since it gives information as to where it is, where it has been, and where it will be.  As an object moves, say, it will make a zigzag motion, as it will be moving simultaneously in the left-right direction (moving in space) and in the upward direction (moving forwards in time).  If, say, the object were at rest (in a particular reference frame of course), then it's worldline would simply be a vertical line (simply an upward motion in time).

Applying this to the diagrams above, let us look at how two different observers would map out the events of space-time on their axes.  We see that from the reference frame of the car (the diagram to the left), the two ends are not moving.  Thus, the two worldlines of the cars are simply vertical lines.  Sometime later, the detonation takes place simultaneously, as depicted by the horizontal line since this event takes place over the entire length of the car at one instant.  For the observer in the car, this is an event that merely spans space. 

But to the person standing on the ground (the diagram to the right), the two events are separated both spatially and temporally.  Due to how the constancy of light effects the detonation, as we have seen earlier, the rearmost firecrackers will detonate before the ones forward the front.  This is demonstrated by the sloping red line, as compared to the horizontal one.  Also, the worldlines of the ends of the cars are tilted, since a standby observer would see the car moving.  This consequently also effects the spatial separation of the detonation as viewed by the observer.

Yet, even though the two observers disagree both space-wise and time-wise how the two events differ, what they do agree upon is the spacetime separation between the two events.  This can be thought of as a line through spacetime connecting two events.  No matter how these two events may be viewed differently in terms of time or distance by two different observers, the spacetime separation remains the same. 

This is analogous to say, the radius of a circle.  No matter how we try to vary the horizontal and vertical components of the radius (the radius being the hypotenuse of the right triangle formed), the radius remains constant. 

To compute the radius, or the distance between any two points in a plane, we can simply use the Pythagorean Theorem: a² + b² = c² , where a and b are the variable legs (shown in orange) and c is the constant radius. 

However, due to the weird geometry of spacetime, the computation of the spacetime distance is a bit different.  Letting x represent space and t represent time, and c being the speed of light, then d, the spacetime distance is:

d² = x² - ( ct)²

Thus, to find the spacetime distance, we square the product of the speed of light with the time separation (converting it to units of space), subtract it from the square of the space separation, and then take the square root.  Having noted that the spacetime interval is invariant from reference frame to reference frame, we then have the following equality: 

x_c² - (ct_c)² = x_g² - (ct_g)²

Hence, although you and I may disagree upon what happens to the firecrackers, the above relationship still holds.  This equally applies to all events and all observers - that no matter how strong the disagreements over space and time may be, the same spacetime interval holds for all [2]. 

Nevertheless, the discovery of the constancy of light, that ether does not exist, and that there is no absolute state of rest has revolutionized our understanding of physics.  It has usurped Newton's clockwork model of the universe, a physics that treats space and time as universal, immutable quantities.  As Einstein has shown, these space and time are "malleable", changeable entities.

Relativity has also put a limit on what we can ultimately do.  With light being the cosmic speed limit, the idea of faster than light travel, of instant communication, of going off to a far away land at high speeds and then returning in the same epoch all become science fiction. 

However, there are still some areas yet to be explored.  The Special Theory of Relativity only takes into consideration uniform motion.  Moving linearly at a constant speed, one cannot determine for sure what is "really" moving, since different reference frames will yield different conclusions.  But with accelerations, a change in velocity has a definite outcome within the system accelerating (e.g. the force you feel when a car makes a swerve), making its effect "absolute".  In order to take into account these accelerations, we must turn to yet another theory: The General Theory of Relativity.     

[1] To derive the general formula for F, we simply take the ratio of the times observed by the observers at any particular instant.  In this scenario, computing the general formula from the stationary observer (Anne's point of view), we see that at any particular time of hers, t, Betty's clock would have ticked t/T, due to the time dilation effect.  However, there is a delay as to when this information comes back to Earth, due to the Doppler effect.  The distance between the two observers is simply the product of the velocity, v, and time, t, but since we want to know the light delay, we must also divide by c.  Thus, adding t with (v/c)t, we know what time it will be on Anne's clock, when Betty's clock registers at t/T.  Computing the ratios of these two times, we get:  

This last equation is the same equation that relativity predicts as the time dilation factor for an object moving with a velocity of v.

[2] We can actually prove that this works for one case from the Light Clock Demo (but it just so happens to work for all cases). 

We end up with the same time dilation equation once again.
 

Hiçbir yazı/ resim  izinsiz olarak kullanılamaz!!  Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla  siteden alıntı yapılabilir.

The Time Machine Project © 2005 Cetin BAL - GSM:+90  05366063183 -Turkiye/Denizli