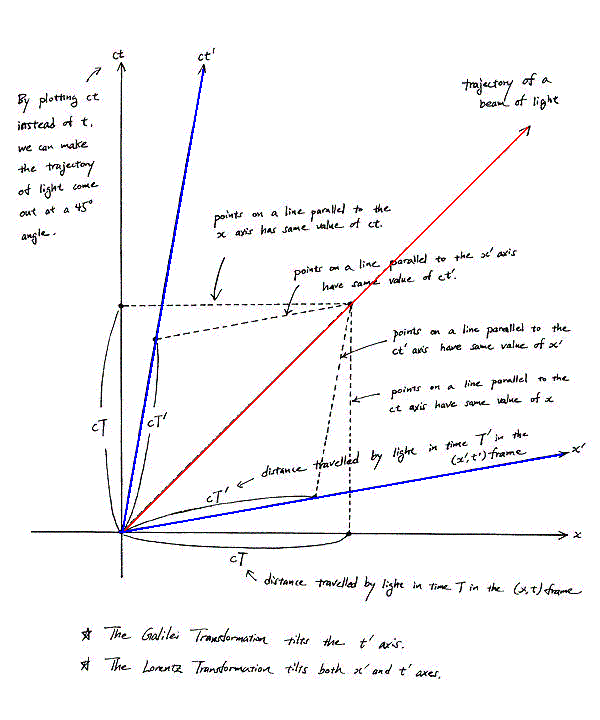
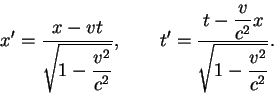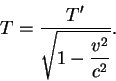Zaman Yolculuğunu Araştırma Merkezi © 2005 Cetin BAL - GSM:+90 05366063183 -Turkey/Denizli3. Eylemsiz Sistemlerde Fizik YasalarıEylemsiz sistemlerde fizik yasaları aynıdır. Daha açık söylemek gerekirse, birisi ötekine göre düzgün doğrusal hareket eden iki eylemsiz sistemin birisinde geçerli olan fizik kuralları diğerinde de aynen geçerlidir. Dolayısıyla, bir eylemsiz sistemin ötekine üstünlüğü yoktur. Bu özelik, fizik yasaları için istediğimiz eylemsiz konuşlanma sistemini seçebileceğimiz anlamına gelir. K ve K' iki eylemsiz konuşlanma sistemi olsun ve K' sistemi K ya göre sabit v hızıyla Ox doğrultusunda hareket etsin. Bir P noktasının (cisminin - şekildeki top) bu iki sisteme göre konaçları (koordinatları), sırasıyla, (x,t) ve (x',t') olsun. Bu konaçlar arasında
x' = x - vt , t' = t
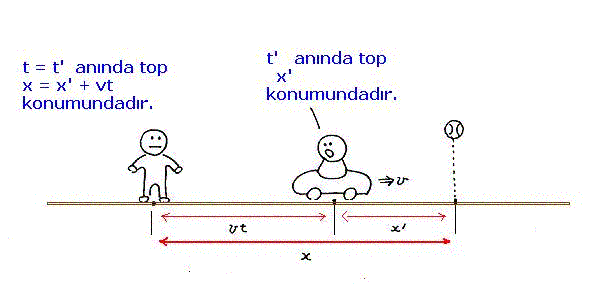
bağıntısı vardır. Burada, her iki sistemde zaman koordinatlarının (saatlerin) aynı olduğunu varsayıyoruz (t = t') K sistemi içindeki bir gözlemciye göre bir t anında topun yatay eksendeki konumu x = x' + vt dir. K' sistemi içindeki bir gözlemciye göre ise aynı t = t' anında topun yatay eksendeki konumu x' dür. Yukarıdaki bağıntıdan
x = x' + vt , t = t'
yazabiliriz. Galilei dönüşümü
denilen bu bağıntıları kullanarak, cismin bir eylemsiz sistemdeki
konumunu biliyorsak, öteki sistemdeki konumunu daima bulabiliriz. Yukarıda söylediğimiz kuralı, şöyle de ifade edebiliriz:
"Fizik kuralları Galilei dönüşümü altında
değişmezler."
Aşağıdaki şekiller, Galilei dönüşümünü daha iyi anlamamızı sağlayacaktır
4. Newton'un İkinci YasasıBir F kuvveti kütlesi m
olan bir cisme etki ederse cismin kazanacağı ivme
F kuvvetiyle doğru, m
kütlesiyle ters orantılıdır. Bu demektir ki
Newton'un İkinci Yasası eylemsiz konuşlanma sistemlerinde geçerlidir.
a ivme olmak
üzere, sözkonusu yasayı şu formülle ifade ederiz:
F = ma. Bu yasa, eylemsiz bir K sisteminde geçerli ise, başka eylemsiz bir K' sisteminde de geçerlidir. Böyle olduğunu göstermek kolaydır. Gerçekten, K ve K' sistemlerindeki hızları, sırasıyla u, u' ile ivmeleri a, a' ile gösterirsek, x' = x - vt , t' = t bağıntısından, yolun zamana göre türevini alarak, hızlar arasında u' = u - v bağıntısını buluruz. Benzer şekilde, hızın zamana göre türevini alarak, ivmeler arasında a' = a bağıntısını hemen çıkarabiliriz. 5. Eylemli (İvmeli) Sistemlerde Fizik KurallarıEylemli sistemlerde Newton'un ikinci hareket yasası
geçersizdir:
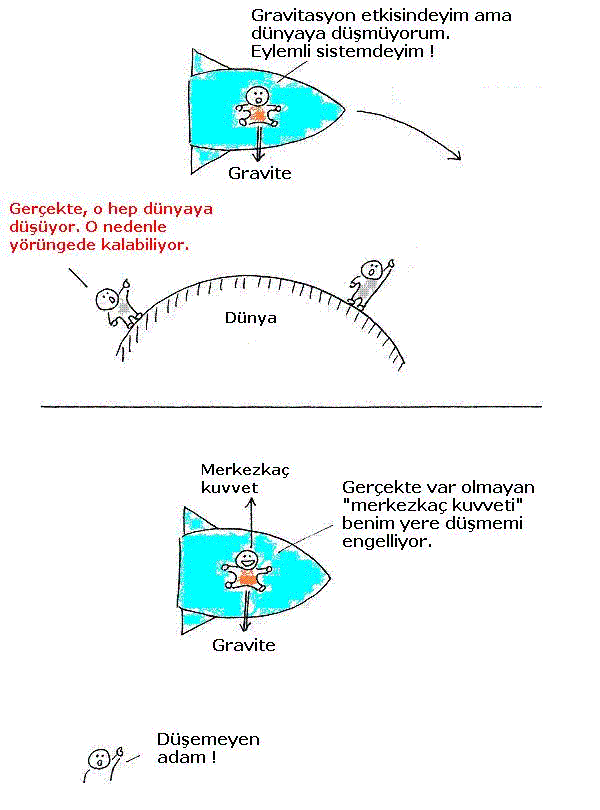
Fizik derslerinden anımsayacağınız gibi, (hayali) bir
merkezkaç kuvvet uygulayarak eylemli
sistemlerde de F = ma yasasını geçerli
kılabiliriz. Merkezkaç gibi hayali kuvvetlere
eylemsizlik kuvvetleri diyoruz. Eylemsizlik kuvvetleri, cisme
ivme kazandırmaya çalışan kuvvet(lere) karşı duran kuvvetlerdir.
6. Özel ve Genel Görelilik KuramlarıGörelilik Kuramı, hızı ışık hızına yaklaşan cisimlerin hareketini
inceler. Işığın hızı c=3×108m/sn
dir. Newton'un ikinci yasası, hızı ışık hızına yaklaşan cisimler
için geçerliğini yitirir. Görelilik Kuramı, Newton Mekaniğinin bu
eksikliğini giderir. Özel Görelilik Kuramı oldukça basit matematiksel formüllerle açıklanabilir. Genel Görelilik Kuramını açıklamak için farklı matematiksel yapılar kullanılabilir. Einsten, Riemann geometrisine ve tensör hesaba dayalı bir yöntem izlemiştir. Aradan gen yüzyıl boyunca, genel görelilik kuramını açıklamak için çok daha elverişli cebirsel yapılar ortaya konulmuştur. İki kuram arasındaki farkı ortaya koymak için, aşağıdaki tabloya baka
7. Biraz TarihNewton hareket yasaları 17.yüzyılda ortaya kondu. Newton Mekaniği diye adlandırılan bilim dalına esas olan Newton hareket yasaları, bilimde atılmış en büyük adımlardan biridir. 18. ve 19. yüzyıllarda Newton Mekaniği sayesinde muazzam bir teknoloji yaratıldı, gök cisimlerinin hareketleri belirlendi. Bu gün bile Newton Mekaniği yok sayılırsa, elimizde 20. yüzyıl teknolojisi yok olur. Maxwell
Newton hareket yasalarını belirleyen matematiksel
denklemler Galilei dönüşümü altında değişmiyordu (invariant). Ama,
Maxwell denklemlerinin Galilei dönüşümü altında değiştiği (non-invariant)
görüldü. Maxwell denklemi bir eylemsiz sistemde geçerli kabul edilse,
ışık hızını belirleyen denklemler başka bir eylemsizlik sistemine
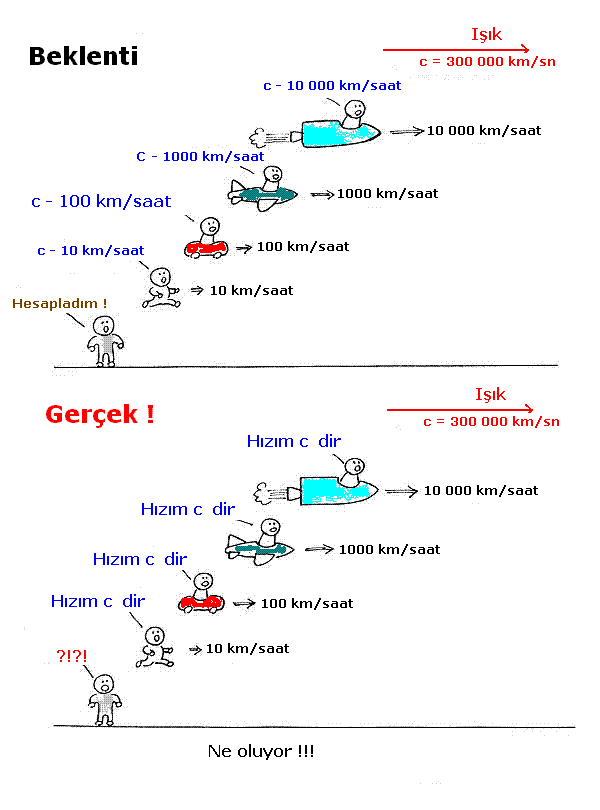
dönüştüğünde tamamen değişmektedirler. Bu güçlüğün çözümü için çeşitli görüşler ileri sürüldü. En geçerli görünen görüş ether kuramıydı. Ses dalgalarının yayılabilmesi için hava, su vb bir ortamın olması nasıl gerekiyorsa, ışık dalgalarının da boşlukta yayılabilmesi için bir ortama gereksinimi vardır. Bütün uzay boşluğunu doldurduğu varsayılan bu maddeye ether denildi. Maxwell denkleminin belirlediği ışık hızı ether'e göreli olarak belirleniyor olmalıydı. Eğer gözlemcinin gözlediği ışık hızı Maxwell denkleminin belirlediğinden farklı ise (ki bu çok küçük bir farktır), bunun nedeni, fizik kurallarının her eylemsiz sistemde aynı olmaması değil, gözlemcinin eylemsizlik konuşlanmasının ether'e göre hareket ediyor olmasıydı. Michelson-MorleyYüz yıl kadar önce Michelson & Morley adlı iki bilim adamı, uzay boşluğunun ether ile dolu olduğu varsayımını çürüttüler. Aslında, deneylere başlarken ether'in varlığına inanıyor ve onu kanıtlamak amacını güdüyorlardı. Beklentilerin aksine, boşlukta ether olmadığı, ışık hızının gözlemcinin hızına (onun bulunduğu eylemsiz sistemin hızına) bağlı olmadığı, her sistemden aynı hızla göründüğü kanıtlandı. Ortaya oldulça ilginç bir durum çıkmıştı. Maxwell denklemlerine göre ışık hızı bir eylemsiz sistemden ötekine değişiyordu. Ama Michelson & Morley deneyi, ışığın her eylemsiz sistemden aynı göründüğü sonucunu veriyordu. Şimdi problem şuna dönmüştü: Işığın hızı neden her eylemsiz sistemden aynı görünüyordu? Bunun yanıtı ancak, eşzamanlılık kavramımızın değişmesiyle verilebilirdi. Bunu 1905 yılında Einstein, Özel Görelilik Kuramı'nı ortaya atarak çözdü. 8. Lorentz DönüşümüÖzel Görelilik Kuramı özetle şunu söylüyor. Işığın hızının her eylemsiz sistemden aynı (sabit hız) görünmesinin nedenini anlamak için, bir sistemden ötekine geçerken kullandığımız dönüşümleri değiştirmeliyiz. Galilei dönüşümleri dediğimiz dönüşümler ışık hızı için yetersizdir. Onun yerine Lorentz Dönüşümleri denilen dönüşümler kullanılmalıdır:
Buradan görüldüğü gibi, bir frame ötekine göreli olarak sabit v
hızıyla gidiyorsa ve v< Bu söylediklerimizin sağlandığını matematiksel olarak kolayca gösterebiliriz. Gerçekten, Işık hızı'nın (x,t) and (x',t') frameleri içinde aynı olduğunu görmek için aşağıdaki usavurma yeterlidir. t'=t=0 anında x'=x=0 başlangıç noktasından bir ışık hüzmesi yola çıksın. Işığın hızı c olduğundan, t=T anında, sözkonusu ışık hüzmesi (x,t) frami içinde x=cT noktasına ulaşacaktır. Oysa, öteki frame içinde ışığın konumu olarak gözlenecektir. O halde, (x',t') frami içinde Işığın hızı olacaktır.
Aşağıdaki şekil Lorentz Dönüşümünü temsil etmektedir.
İki frame içinde ışık hızının aynı olduğunu
gösteren uzay-zaman çizeneği:
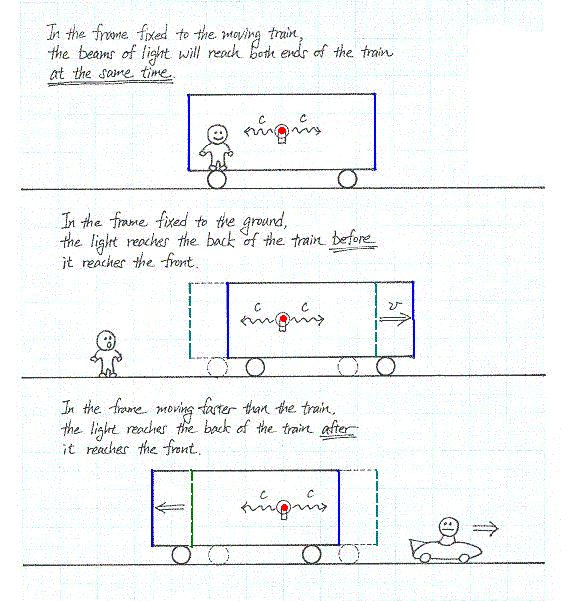
9. Eş ZamanlılıkLorentz Dönüşümü'nden sezinlenebileceği gibi, t=t' gibi basit bir bağıntı olmayacağına göre zaman göreli bir kavram halini almaktadır. Gerçekte bunun anlamı eşzamanlılık kavramının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olduğudur. Bu durum, ışık hızının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olmadığından çıkar. Hareket halindeki bir tren vagonunun tam ortasında bir lamba olsun. Lamba yandığında ışık hüzmesi hem trenin gidiş yönüne hem onun ters yönüne c=3×108m/sec hızıyla yayılacaktır. Vagonun içindeki bir gözlemci, ışığın vagonun önüne ve arkasına aynı anda (eş zamanlı) ulaştığını görecektir. Öte yandan, tren dışındaki bir gözlemci için durum farklıdır. Işığın hızı, gözlemcinin içinde bulunduğu eylemsiz sistememe bağlı olmaksızın, her gözlemciye göre aynıdır ve vagonun her iki yönüne doğru c hızıyla gider. Vagonun arkası kendisine doğru gelen ışığa yaklaşırken, vagonun önü kendisine doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha çabuk, vagonun önüne daha geç ulaşacaktır. Demek ki, bu iki olay, yerdeki gözlemci için eş zamanlı değildir. Görüldüğü gibi, tren içindeki gözlemciye eşzamanlı görünen iki olay tren dışındaki gözlemciye farklı zamanlarda olan iki olay olarak görünmektedir. Oyunu biraz daha eğlenceli kılmak için, trenden daha hızlı giden bir yarış arabası içindeki gözlemcinin olayları nasıl göreceğine bakalım. Gene, ışığın hızının, gözlemcinin içinde bulunduğu eylemsiz sistememe bağlı olmaksızın, her gözlemciye göre aynı olduğunu ve vagonun her iki yönüne doğru c hızıyla gittiğini anımsayalım. Yarış arabası trenden daha hızlı olduğu için, arabadaki gözlemciye göre tren ters yönde gitmektedir. Buna göre, vagonun önü kendisine doğru gelen ışığa yaklaşırken, vagonun arkası kendisine doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha geç, vagonun önüne daha erken ulaşacaktır. Demek ki, bu iki olay, arabadaki gözlemci için eşzamanlı değildir. Sonuç: Bir vagonda geçen iki olayın kronolojik sırası yerdeki, vagondaki ve trenden hızlı giden bir araçtaki üç gözlemci tarafından farklı görünmektedir. O halde, farklı eylemsiz sistemlerde eşzamanlılık olamaz.
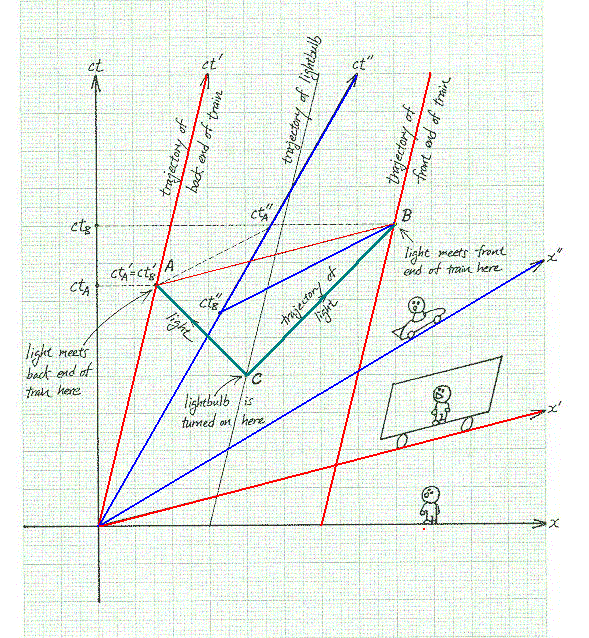
Tren ve Işık Problemi:
, yukarıda açıklanan eşzamanlılık kavramının farklı eylemsiz sistemler için varolamayacağı gerçeği, Işık hızının her gözlemciye göre aynı olmasının doğal bir sonucudur.
Yukarıda açıklanan üç ayrı sistemden ışığın
görünüşünün uzay-zaman çizeneği 10. Işıktan Daha Hızlı HareketEğer öncelik, eşzamanlılık ve sonralık kavramları gözlemciye göre değişiyorsa, bir olayın başka bir olayı yarattığı nedensellik kavramını nasıl açıklayacağımızı ciddi olarak düşünmeliyiz. Bunu biraz açıklamakta yarar vardır. Eğer bir A olayı
başka bir B olayının olmasının nedeni ise, A
olayı B olayından önce olmalıdır. Ama, bir gözlemci
A olayının B olayından önce olduğunu, başka bir
gözlemci ise A olayının B olayından sonra
olduğunu gözlüyorsa, nedensellik konusunda bir uyuşmazlık ortaya
çıkacaktır.
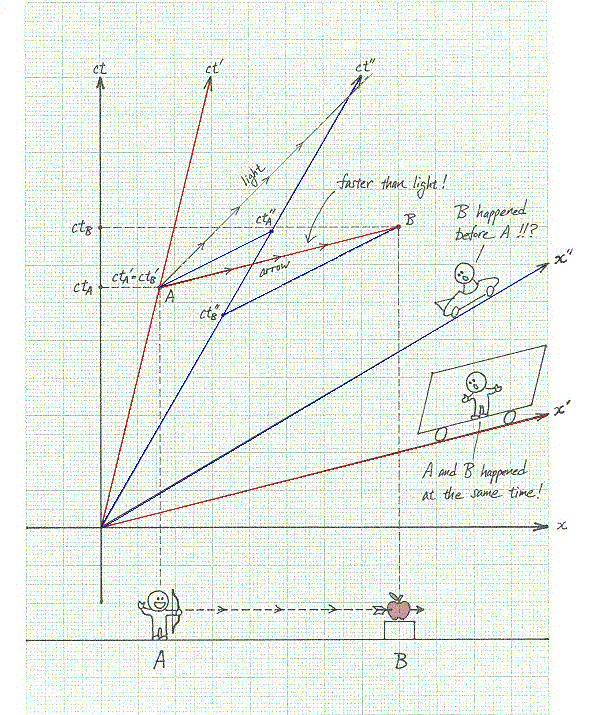
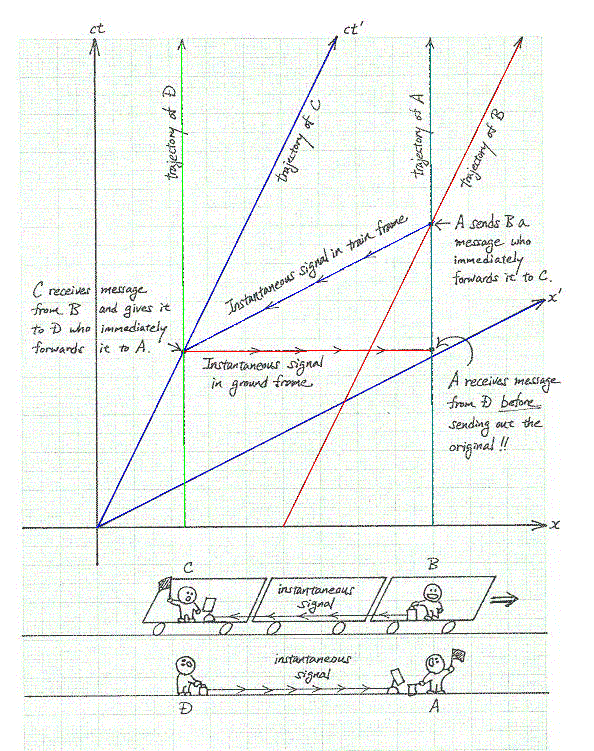
Ok ışıktan hızlı gitseydi ne olurdu? Let's consider another example. This thought experiment is discussed in Chapter 7 of the book "The Einstein Paradox and other Science Mysteries Solved by Sherlock Holmes" by Colin Bruce (Perseus Books, ISBN 0738200239). Assume that instantaneous communication were possible between remote points. In the spacetime diagram below, A and D are standing by the railroad tracks along which a speeding train passes by carrying B and C. Consider the following sequence of events:
It is clear from the spacetime diagram that A will receive the message from D before he has sent out the original!
What can happen if instantaneous
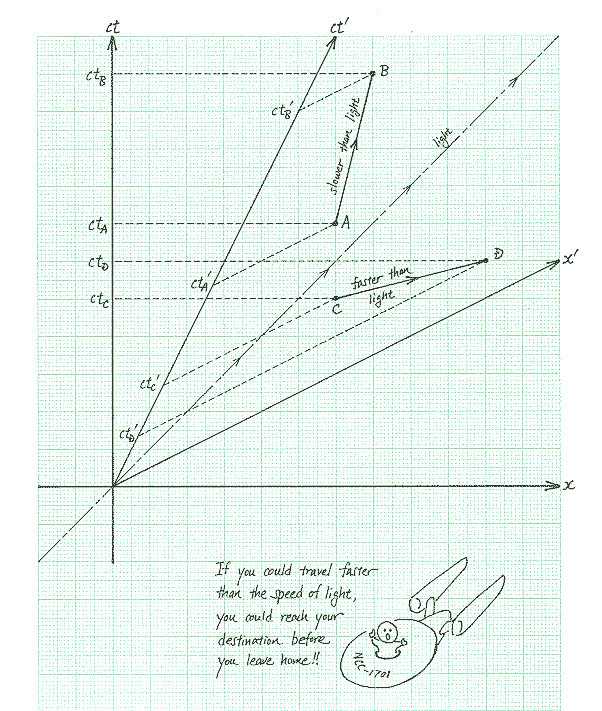
communication were possible As these examples show, contradictions can occur if objects or signals could travel faster than the speed of light. You could have arrows hitting their targets before they are shot or messages received before they are sent. However, if nothing could travel faster than the speed of light, we would not have this difficulty. This is because for objects or signals traveling at speeds slower than the speed of light from point A to point B, all observers will agree that A happened before B. Chronological order of timelike (AB) and
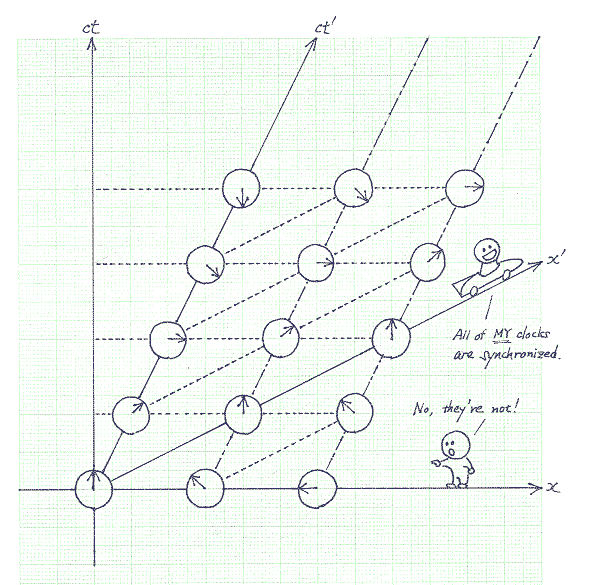
spacelike (CD) separated events in different frames So faster than light travel is impossible. This also means that Newton's second law must be modified since it says that you can accelerate anything to any speed you want. (Note that Newton's first law is still correct.) We won't be looking at HOW it has to be modified though, since it would be too mathematical. All you need to know is that the real theory says that you cannot accelerate things beyond the speed of light. (I'll add a section dealing with how Newton's second law must be modified later.) Some science fiction writers think that some new invention (like the warp drive, whatever that is) may let us accelerate to speeds faster than c. What you need to understand is that faster than light travel breaks causality so that it is inconceivable that some new invention is going to let us do it. Otherwise, we can have faster than light speed travel before we invent it! 11. Saatlerin Eşzamanlaştırılması (Synchronization)Eşzamanlılık kavramının göreli oluşu bazı sonuçlar doğuracaktır. Bu sonuçlardan birisi şudur: Bir frame içinde senkronize edilen saatler başka bir frame içinden senkronize edilmemiş görünür.
Yerdeki frame göre senkronize edilmiş saatler
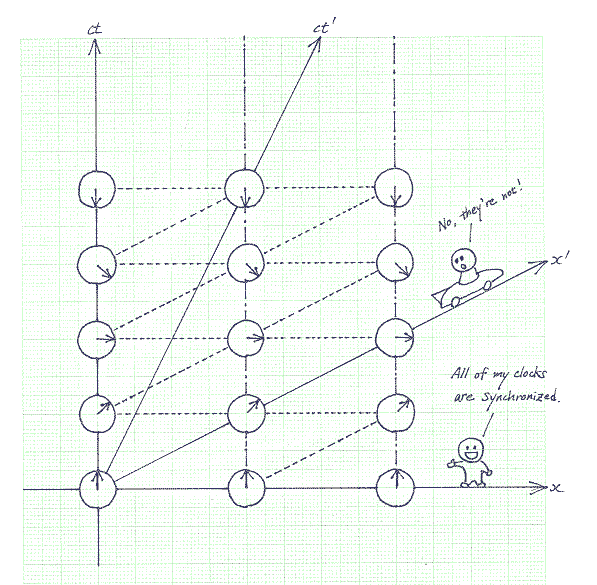
Yarış arabasına göre senkronize edilmiş saatler 12. Zaman Genişlemesi (Time Dilation)Eşzamanlılık kavramının göreliliğinin önemli
sonuçlarından birisi şudur: Farklı eylemsiz konuşlanma sistemlerinde
zamanın akış hızı farklıdır. Buna zaman
genişlemesi (time dilation) diyoruz.
Bu işi yaparken, parantez içindeki "aynı
anda" deyimini söylemeye bile gerek görmüyoruz. Çünkü o
yapacağımız mukayese için doğal olarak gereklidir. Oysa "aynı
anda" deyimi "eşzamanlılık"
deyimidir. Ama biliyoruz ki, farklı gözlemcilere göre "eşzamanlılık"
olamaz.
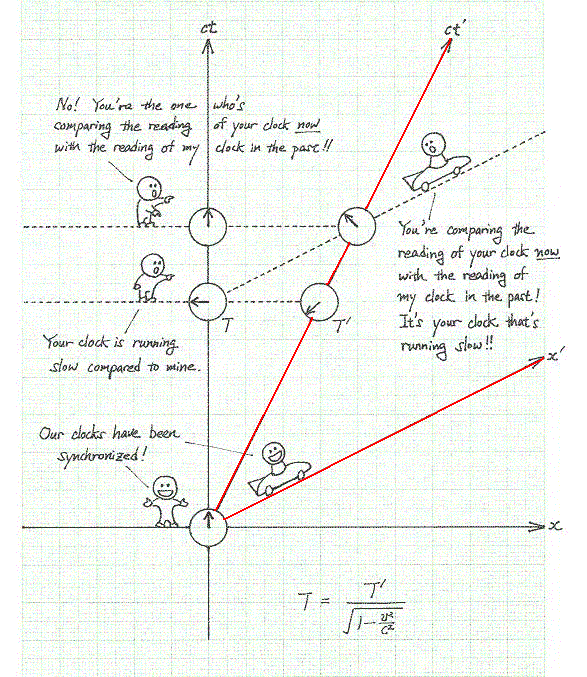
Zaman genişlemesini gösteren uzay-zaman çizeneği
bağıntısı vardır. Bu bağıntıdan hemen görüleceği gibi T > T' dür. Bu etkiye zaman genişlemesi (time dilation) diyoruz. 13. Lorentz DaralmasıEşzamansızlık kavramının sonuçlarından birisi de
uzunlukların gözlemciye bağımlı olarak
değişmesidir. Vagon içindeki gözlemci, vagonun ön ve arkası arasındaki uzunluğu,
kendi kon sistemine göre, vagonun ön ve arka duvarlarını eşzamanlı
olarak eksen üzerine izdüşürerek, vagonun uzunluğunu L' olarak ölçsün.
Yerdeki gözlemci de kendi kon sistemine göre, vagonun uzunluğunu L
olarak ölçsün. Trenin hızı v ise, Lorentz
dönüşümüne göre L ile L'
arasında
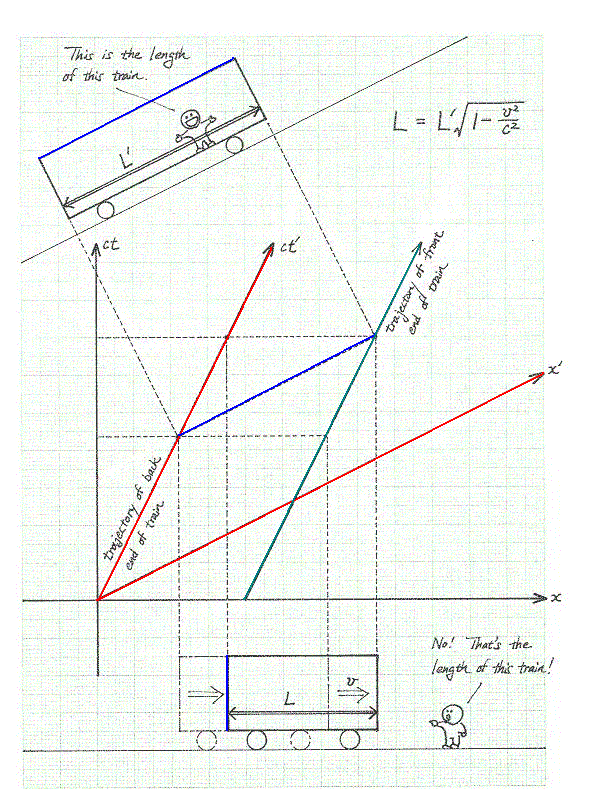
bağıntısı vardır. Buradan görüldüğü gibi, L > L'
dür. Bu demektir ki, yerdeki gözlemci hareketli treni daha kısa
görecektir. Bunun nedeni, farklı gözlemciler arasında
eşzamanlılık olamayışıdır. Bu etkiye
Lorentz Daralması diyoruz. Lorentz Daralması için uzay-zaman çizeneği Hareketsi iken cismin uzunluğuna onun doğal uzunluğu diyoruz. Bir
cismin doğal uzunluğu, hareket halindeki uzunluğundan daha büyüktür.
Başka bir deyişle, hareket eden cisimler (hareket yönünde) daha kısa
görünürler. Bu etkiye Lorentz Daralması (Lorentz
contraction) diyoruz. Lorentz Dönüşümü bu daralmanın
oranını vermektedir.
14. Eylemsiz Kon Sistemlerinin DenkliğiYerdeki bir gözlemciye göre (sabit eylemsiz kon sistemi), hareketli eylemsiz sistemdeki uzunlukların küçüldüğünü ve saatlerin yavaşladığını söyledik. Öte yandan, trendeki bir gözlemciye göre, trenin eylemsizlik kon dizgesi sabittir, yerdeki eylemsiz kon sistemi ise (trene göre ters yönde) hareket etmektedir. Bütün eylemsiz kon sistemleri denk olduğuna göre, trenden bakınca yerdeki uzunlukların küçüldüğünü ve saatlerin yavaşladığını gözlemlemeliyiz. Bu oluşumda bir çelişki yoktur. Farklı kon sistemlerinden
bakıldığında olayların farklı görünebileceğini göstermektedir. 15. İkizler Paradoksu (The Twin Paradox)Yirminci yaş gününde ikiz kardeşlerden birisi çok hızlı giden bir gemiyle uzay yolculuğuna çıksın. Seyahat, dünya zamanına göre yıllar (diyelim 40 yıl) sürsün. Dünyadaki konaç sistemine göre, hızlı uzay gemisinde zaman genişlemesi (yavaşlaması) olacağından, seyahat eden ikiz daha az yaşlanacaktır (diyelim 10 yıl). Geri döndüğünde, dünyadaki kardeşi 60 yaşında, kendisi ise 30 yaşında olacaktır. Öte yandan, hareket göreli olduğu için, uzay gemisindeki konuşlanma sistemine göre, dünya gemiden hızla (ters yönde) uzaklaşmaktadır. Aynı nedenle, bu kez, gemideki ikiz 60 yaşında, dünyadaki ikiz ise 30 yaşında olacaktır. Bu bir paradoks gibi görünmektedir. Çözüm için kendinizi deneyiniz. 16. SonuçlarÖzel Görelilik Kuramı ile ilgili olarak aklımızda kalması gerekli olanlar şunlardır:
17. Ünlü KişilerAşağıdaki adlar, bu dersin konusu ile ilgili önemli bulguları olan bilim adamlarından bazılarıdır.
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir. The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi / |
|
İçindekiler |
Önceki Sonraki |