Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey/Denizli
The (Alcubierre) Warp Drive
Spacetime
by: E. Halerewicz, Jr, düzenleme by: Cetin BAL
3-D plot modified on: 10/11/2001
May 25, 2001
produced and converted to HTML by Mathcad
Imagine you are in space ship who's position is given in Cartesian Coordinates by an arbitrary function xs (0,0). Now imagine that your space ship is coasting so that its future position is determined by an arbitrary function of time xs (t), this function yields the velocity of your space ship by the relation vs(t)=dx s (t)/dt. One of the "artifacts" of the Special Theory of Relativity (STR) is that nothing can travel Faster Than Light (FTL), however this restriction only applies to matter-energy and not space itself. During the "Big Bang" epoch the expanding universe would have appeared to exceed the speed of light as seen from two spatially separated observers, although locally the observers do not exceed the speed of light. This is the same principle that the Alcubierre Warp Drive is based on, since the General Theory of Relativity (GTR) is a symmetrical theory it makes sense to also include a contracting space (an ordinary gravitational field) along with an expansion (as the case with the Big Bang) to create an artificial velocity [this also acts to smooth out the spacetime in the center of the "warp drive" spacetime]. In the GTR the contraction of spacetime can bring two distant points to a common geodesic, thus greatly shorting the distance between two points (a similar effect happens when one compares a flat world projection to a globe). Therefore the Alcubierre Warp Drive can be imagined as special case geometry which brings a point in space to an observer as well as pushing an observer from their point of origin.
The purpose of the following work is to consider some arbitrary parameters in order to form numerical representation of the Warp Drive Spacetime. Thus the following does not describe every detail of the Alcubierre spacetime, but plots numerical sets in order to give graphical depictions of the warp drive (i.e. just enough information is inputted for Mathcad to understand the Alcubierre Warp Drive to graph the appearance of the spacetime theta function in three-dimensions) . In order to do so one will need to construct an arbitrary function f as to produce the contraction/expansion metric proposed by the Alcubierre Spacetime. One would then have to form a bubble around oneself, lets say that three spatial coordinates are given by:
With the ship's position
, the invariant lengths of this space is then given by:
One can now write the arbitrary function of the warp drive spacetime as a
function of the ship's positions rs
. Since this is a numerical presentation done with computer simulations I
will now define the parameters of the "top hat" function as defined in
Alcubierre's paper (Class Quant Grav
11 (1994) L73) as
for the radius of the function, and
for the energy-density:
When this function is plotted is seen quite clearly why the function chosen by Alcubierre is called the top hat function:
The Alcubierre top-hat function:
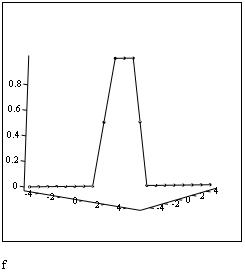
When the velocity of the warp drive is set to
then the Warp Drive Spacetime can be described by the metric:
[note: this does not have to strictly mean the velocity is given by one unit. When one defines G=c=1, the velocity given can be equal to that of light (with G being the gravitational constant and c the velocity of light). This is also the same parameter defined in Alcubierre's paper.]
Now for the really interesting part, what does the Warp Drive look like,
it can be given as a graph of q
as a function x and .
.
Alcubierre defined the velocity of the warp bubble to be
,
such that theta could be set to
q=vs(xs
/rs)(df/drs).
The following graph is suppose to be given with the following function z=q (x,r ), in reference to the work of Alcubierre. However, that would take much work for Mathcad to plot properly, so the standard bivariate function z=f(x,y) is used in its place, thus giving:
The Alcubeirre Warp Drive:
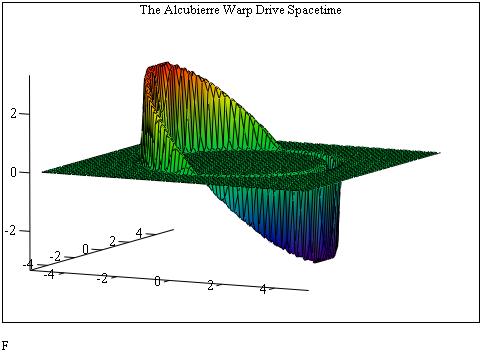
This figure however has one problem, the Minkowski space is not plotted properly (this is because Mathcad does not understand the concept of spacetime [to do so would require a lot of programming =( ]), all that is shown is an arbritary spatial displacement, but its good enough for all of us who think in three dimensions.
Reference:
M. Alcubierre Class Quant Grav 11 (1994) L73
Alıntı: http://members.tripod.com/da_theoretical1/alcmath/alcwarp.htm
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /
index /Roket bilimi /
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru