Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey / Denizli
General Relativity:
Note: The Feynman Lectures covers
most of the material from this lecture. I'm just adding a bit extra information
and a couple of comments...
Einstein's General Theory of Relativity can be summed up in two key concepts:
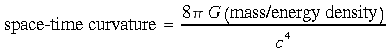
![]() .
.
General Relativity represents a new view of particle motion, different in character than Newton's Laws:
| old: | new: |
| given masses | given masses |
| figure out force field | figure out geometry of space-time |
| solve Newton's Laws | particles follow longest path (“proper time”) in curved space-time |
| figure out positions as function of time |
General Relativity is all about (non-Euclidean) geometry.
Aside - Geometry in Terms of "Intervals:"
-
One can actually describe different geometries in terms of “intervals:” the lengths of infinitesimal displacements in whatever space we're trying to describe. Space-time intervals ds are actually the fundamental quantities which one works with in General Relativity. Without going into any detail, I'll list the “intervals” corresponding to several types of interesting physics:
- Euclidean Geometry
-
ds2 = dx2 + dy2 + dz2
- this is just the familiar measure of distance in regular, classical space. It is the infiinitesimal version of the distance between two points: d2 = (x2-x1)2 + (y2-y1)2 + (z2-z1)2. Note that this quantity ds is invariant (doesn't change) under rotations. If we rotate our coordinate axes, though the components of vectors may change and though the coordinates of points may change, the distance between two points in space doesn't.
- Special Relativity (flat 4-dimensional space-time):
-
ds2 = c2dt2 - dx2 - dy2 - dz2
- this quantity is preserved under Lorentz transformations (see Ch. 15, Prob. 3). This is analagous to the invariance of the Euclidean interval ds under rotations (see above).
- General Relativity (gravitation/accelerating frames):
-
ds2 = g0 c2dt2 - g1 dx2 + g2 dy2 + g3 dz2
where g0, g1, g2, g3 are coefficients which may vary from point to point, depending on the distribution of mass/energy.
Aside: Why the Minus Sign?
-
In General Relativity, we say that the particle maximizes the proper time along its trajectory. Normally, the Principle of Least Action involves minimization. Or again, in Special Relativity, the space-time interval is ds2 = c2dt2 - dx2 - dy2 - dz2 whereas in Euclidean geometry, the interval of length is ds2 = dx2 + dy2 + dz2. Why is there this weird minus sign floating around in Relativity?
Well, the overall sign is just a matter of convention. We might as well choose ds2 = -c2dt2 + dx2 + dy2 + dz2 - the physics would still be the same. The real question is why time and space coordinates' signs differ in Relativity.
The real answer is - that's the way our universe is! When we go out and make actual measurements on our universe, we find that time-like dimensions and space-like ones behave differently - and the essence of that difference is encapsulated in the math in the differing sign.
I can try to motivate this a little more by just reminding you of the Lorentz transformations. Suppose the quantities u, x, dx, t, and dt are all positive. Then the Lorentz transformation between coordinates in two inertial frames moving with speed u with respect to one another are:
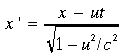
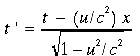 .
.Notice that the spatial and temporal coordinates have different signs! So this strange minus sign is there from the get-go in Relativity. Why? Well, that's just the sort of universe we live in...
Aside - Why the Differentials?
-
The space-time interval ds is an infinitesimal quantity - it's actually a differential. Why add calculus to the mix? Why not just measure regular ol' distances, of finite extent? Well, the problem is that, in General Relativity, space-time is curved! Remember trying to make distance and angular measurements on the surface of a sphere? We ran into trouble because our rulers were flat but “the world” was curved - a spot we got ourselves out of by only measuring distances and angles over a very small region, where the curvature was negligible (in much the same way that, over the small scale of our everyday lives, we don't notice that the Earth is curved!).
We understand orthogonal coordinate systems quite well, and we know how to reason and calculate with them.
On the other hand, warped, curved, coordinate systems are not so easy to work with! So, in General Relativity, what we do is focus our region in on a very small section of space-time (infinitesimally small!), where space-time is approximately flat. Then we use orthogonal coordinate systems in that small region. Problem solved!

Mathematically, what we do is approximate the actual, curved space time. We expand the coordinate axes in essentially a Taylor series (yet again!):
 .
.Recall, the first-order term is linear in dx - it's the equation of a straight line! So, if we don't let dx get too large, the actual, curved coordinates look essentially flat - just like regular ol' Cartesian coordinates...
The actual math is a little more messy - it involves what's known as differential geometry, which is a whole course in and of itself. But, nontheless, the idea is what I've just sketched out...
Experimental Proof for GR:
The book discusses several observations which support General Relativity. These are the “classic” experiments. However, I'd like to add my own two cents' worth...
Gravitational Radiation:
From classical electromagnetism, you know that an oscillating electric charge produces electromagnetic radiation (light!):
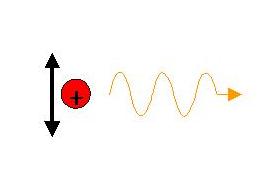
In the same way, the theory of General Relativity predicts that a time-varying distribution of mass should produce gravitational radiation - gravity waves. It would be very exciting to observe gravitational radiation. The problem is that gravity is so much weaker than electromagnetism - recall that even a tiny charge imbalance on, say, an electroscope or your socks when they come out of the dryer can counteract the force of gravity.

Nonetheless, there is some indirect proof of the existence of gravitational radiation. In 1974, Hulse and Taylor (Nobel, 1993) discovered a binary pulsar. A pulsar is a periodic stellar source of radio radiation - it is believed that a pulsar is a rotating neutron star, which channels charged particles out along magnetic field lines. As these particles move and accelerate in the magnetic field, they emit intense radiation - preferentially along the directions of the magnetic field lines. In a neutron star, these field lines are concentrated at the poles of the star - if the magnetic pole is off-axis (similar to the way the Earth's magnetic North pole does not lie on the “real” North pole), then as the star rotates, the magnetic field precesses about the rotational axis. From the point of view of observers on the Earth, the beam of radiation sweeps by us once every rotation - rather like the beam of light from a lighthouse (see Sec. 15.7 of the book).
In any case, a pulsar is a periodic source of detectable radiation. In the case of the binary pulsar, the usual “search-light” periodicity is modulated - the repitition rate of the observed beam first increases, then decreases. This is due to the Doppler effect as the pulsar orbits its companion star in the binary star system. What Hulse and Taylor noticed was that the period of this orbit was decreasing with time! This can be explained by the gravitational radiation which must be emitted by the system as the two objects orbit each other. As they radiate gravity waves, the energy of the system decreases. This means the radius of the orbit and its period decrease. When one calculates the expected change in period using General Relativity, the agreement is phenomenal!
So the binary pulsar provides indirect evidence for the existence of gravity waves. It would be satisfying, however, to directly observe gravitational radiation, similar to the way we observe electromagnetic radiation. As I mentioned above, this is difficult because gravity is so much weaker than electromagnetism. It is also difficult because the period of gravity waves is given by the oscillation frequency of the source, and for the astronomical sources which would radiate enough gravitational radiation for us to observe, the orbital periods are relatively long (on the order of Hertz to hundreds of Hertz). It is very difficult to eliminate extraneous noise at these frequencies (noise generically decreases with increasing frequencies - note to budding experimentalists: perform your measurements at the highest frequency you can!).
Nonetheless, there are gravitational wave observatories currently taking data or being commissioned. These include VIRGO (France/Italy), GEO 600. (Germany/Great Britain), TAMA 300 (Japan), ACIGA (Australia), and LIGO (US). By way of example, LIGO is a very large Michelson interferometer (what else!).
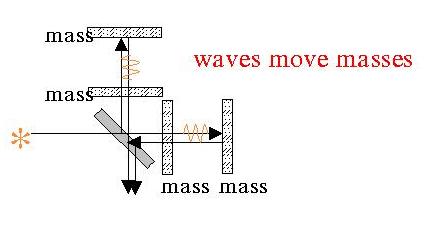

Each arm of the interferometer contains a resonant cavity. The mirrors of these cavities serve as reference masses - a passing gravity wave will warp space-time in the vicinity of the interferometer, shortening one arm and lengthening the other. The effect is not large, but LIGO should be able to detect it, nonetheless. To give you some idea of the sensitivity required, each of LIGO's arms is 4 km long, but the instrument can sense changes in arm length of on the order of the diameter of an atomic nucleus! LIGO is just beginning to take data...
Gravitational Lensing:
Warped space-time causes even light to deflect from what we would normally consider a geometric straight line. The deflection of starlight by the Sun, first observed during the 1919 solar eclipse, was the dramatic first experimental confirmation of the theory of General Relativity. In such effects, concentrations of mass serve as “lenses” to re-direct the path of light. If a star lies behind a massive object, then rays of light which normally would not reach our eyes can be re-directed towards us, allowing us to observe the normally obscured objetct:

Of course, the real situation can be much more complex - if the star isn't directly behind the lensing object, the image of the star can suffer various distortions. With the power of modern telescopes and observational techniques, gravitational lenses are routinely observed. See, for example, Pete Newbury's web site at UBC (click on “Examples.”). I pulled the following picture from the online archives of Hubble Space Telescope's pictures:

Black Holes:
The book discusses black holes in Sec. 15.8. Laplace, reasoning only using Newtonian gravity, posited the possible existence of an object whose escape velocity exceeded the speed of light. However, what we normally think of when we hear the phrase “black hole” is the offspring of General Relativity.
Einstein wrote down his differential equations for General Relativity, but he didn't find any solutions to the equations! The first person to do so was Karl Schwarzschild, in 1916. He worked out the solution and wrote it up while serving in the German army on the Russian Front! (Unfortunately for us all, he became ill whilst on the Front, and died soon thereafter...)
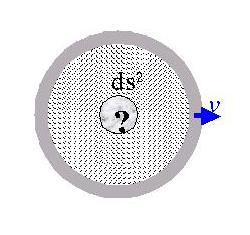
I'll write out his solution to the Einstein field equations just so that you can see what a result in General Relativity looks like (to remind you, the math - which involves differential geometry - can get pretty heinous pretty quickly). The solution gives the space-time interval in spherical-polar coordinates in the presence of a spherically symmetric, non-rotating mass distribution as:
 .
.
One can then use this quantity to calculate other
physical observables. For instance, if
![]() is
the time between two events as measured by someone a distance r from the
centre of the massive object, then an observer at a point P very far from the
massive object would measure a time interval of
is
the time between two events as measured by someone a distance r from the
centre of the massive object, then an observer at a point P very far from the
massive object would measure a time interval of

between the same two events.
Notice what happens to the space-time interval and
to
![]() as
as
,
known as the Schwarzchild radius. A divergence occurs! This divergence leads to the many bizarre effects of black holes. But note (as the book does on pg. 512) that this is a very “gentle” divergence. Nothing spectacular happens as an object passes the event horizon at rS. However, from the point of view of outside observers, the object appears frozen in time. From the point of view of the object, the rest of the universe blinks by in an instant!
If you haven't already, have a cruise through the event horizon at Andrew Hamilton's home page
You can see a catalogue of possible black holes at the Hubble Space Telescope home page.
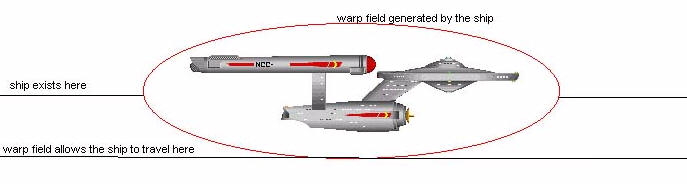
A “Teaser” - the “Alcubierre Warp Drive:”
So nothing can travel faster than the speed of light in a vacuum. This is a fundamental principle of modern physics, and it is correct. However, if one phrases it more accurately, “nothing can travel faster than the local speed of light in a vacuum.” Note the word local - what that means is that it is not inconsistent with the equations of General Relativity for an object at one point in space to move faster than the speed of light elsewhere, as long as it doesn't move faster than the speed of light where it is. Note that I said “not inconsistent!” Just because something is “allowed” by General Relativity, doesn't mean that it necessarily is possible, or even that it is consistent with the rest of physics!
Keeping that caveat in mind, however, let me share a cool theoretical result from 1994 with you - just to give you some idea of the fun you can have with GR if you're willing to wade through the differential geometry. In 1994, Miguel Alcubierre found the following solutions to the Einstein field equations:
![]()
where
![]() ,
,
![]() ,
,
and f(r) goes to zero for large r. Given these properties, ds becomes the usual space-time interval of Special Relativity (flat space-time) for large r.
This space-time interval describes a localized region of space-time which moves with velocity v. This velocity v may be arbitrarily large (i.e. v > c is allowed)! Also, time flows at the same rate inside the space-time “bubble” as it does outside, so that no relativistic time-dilation is experienced between observers inside/outside the bubble.
So this solution looks like a possible “warp drive!” However, it is unclear whether it is possible to actually create such a region of space-time. The space-time it describes has a very particular curvature, which requires a very particular distribution of mass/energy. Indeed, it has been proven that the only way to obtain the required curvature is if one can create regions of negative mass/energy density! While it is true that negative mass/energy can occur for short periods of time on very small length scales (this is a result from quantum field theory), it seems unlikely at present that one could find a way to realize such a beast on a macroscopic and non-transitory scale. The “Alcubierre warp drive” also raises the threat of strange causality paradoxes. But it's a tantalizing thought...
Next time: We start in on quantum mechanics!
Alıntı: http://physun.mcmaster.ca/~kingb/2C03_02/notes/Lecture_12/Lecture_12.html
Hiçbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.
The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru