Time Travel Research Center © 2005 Cetin BAL - GSM:+90 05366063183 - Turkey/Denizli
Alcubierre Warp Drive
Imagine the starship traveling from here to another star at some faster than c speed as in the first figure
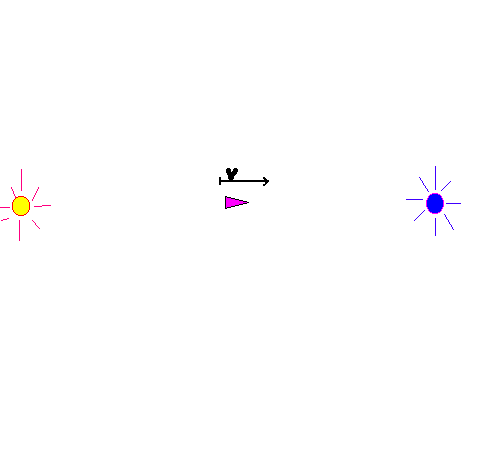
In a warp drive it does so by manipulating this remote frame coordinate speed of light.
Don't get caught up in the math for now, but for future reference-
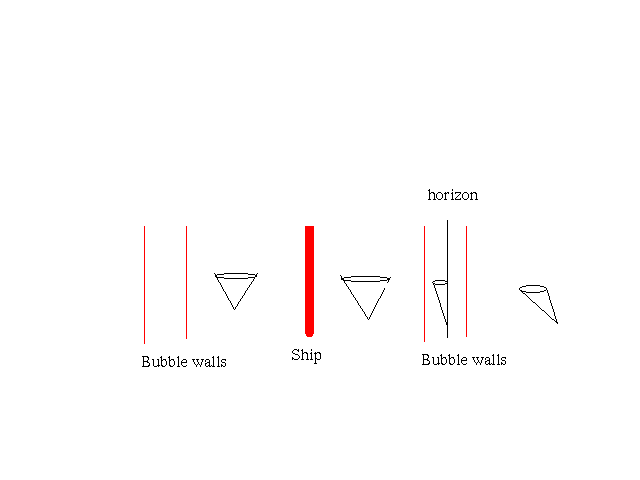
section 13.1 So consider the speed of photons traveling in the direction of the ship alone the path as in the next figure. Study it carefully.

Far from the ship, at points 1 and 5 the photons travel at c which is less than the speed of the ship according to this frame. Near the ship at point 3 the photons travel faster than the speed of the ship and here the ship speed is not limited to c, but to c' instead. This means that somewhere in between there is a surface on which points 2 and 4 lay at which the remote coordinate speed of light matches the speed of the ship. For a ship moving at constant speed, these points remain a constant distance in front of and behind the ship. The speed of information is limited to the coordinate speed of light. This means that information sent toward the ship behind point 2 will not enter the ship so long as it remains at this speed. It also means that information starting at the ship will not travel beyond point 4. This is not a matter of math, as you can visualize it as simple as the figures and no amount of math can change this fact.
For the Alcubierre warp drive, matter always extends beyond this event horizon. The concern this brings up is that one turned on, the ship can not send a signal to the matter in front of the horizon to dispel the matter and get the ship to drop back out of warp. So, consider the next figure.

The blue region is a matter region controlling the behavior of A near the ship making it go from 1 to a large number. The red region is another matter region controlling the behavior of b (ct)g(r ). The brown region is a matter region whose behavior is preprogrammed before flight based on the flight plan. It controls the behavior of A bringing it back down to 1. For a large enough A, the event horizon will be in the brown region. The brown region outside of the event horizon appears tachyonic in that this matter region moves with the ship at speeds greater than c even though its outside the event horizon where the coordinate speed of light is less than the speed of the ship. The ship is not causally connect to the brown matter region in the front outside of the event horizon, but with this arrangement of matter, if some emergency should occur and the ship needs to drop to sublight speed, it is causally connect to the red matter region which is responsible for the ship speed anyway. The front brown matter region outside the event horizon would tear away and fly off into space according to its preprogrammed behavior as though nothing had happened, but the ship can be stopped without any such difficulty.
Hopefully with this visualization you will see why there is always an event horizon no matter what math you do, but also why it needn't be a show stopper.
--------------------------------------------------------------------
here is a comment taken by a private email modified from Miguel Alcubierre sent to the authors of this page.the Horizon is a major trouble to the feasibility of a warp drive.his comments are more than valid.
--------------------------------------------------------------------
. The horizon is inevitable if you want to travel faster than light. If "forward" moving light rays moves forward close to the ship (as seen from the ship), and backward far ahead, then they obviously don't move somewhere in the middle. No way around it.
Form the metric, the horizon is where g00=0, which is just (in your notation):
g00 = a^2 - (v*g)^2
Now, far away we have flat space, so we MUST have a=1 (unless you want to modify the whole of spacetime which makes no sense). Since far away g=1 (ship frame), then:
g00 = 1 - v^2
If you travel faster than light the v>1 (natural units, c=1), so g00<0 (notice that if you use a warp drive to travel slower than light then v<1 and g00>0).
Close to the ship g=0 (ship frame again), and a^2>0 (regardless of the actual value of a in the ship, which we normally take to be 1, but need not be). So we have:
g00 > 0 at ship
g00 < 0 far in front.
Then g00 must be zero somewhere in between if you want to have a regular (continuous) spacetime. Voi'la, a horizon.
The horizon is only a big deal if you want the ship itself to generate the warp bubble. To travel faster than light the ship needs a bubble of exotic matter that extends beyond the place where it can reach with causal signals (beyond the horizon), so it can't create the bubble on its own (but presumably, someone could set it up from the outside,
-------------------------------------------------------------------------
the authors of this page (ZcPhysics-Zephram Cochrane Halgravity Loupwarp and RonaldHeld) are deeply grateful to Miguel Alcubierre for his assistance and advices
--------------------------------------------------------------------------
here is another comment from Miguel Alcubierre
--------------------------------------------------------------------------
Regardless of the exact form of the metric, if you have a bubble of more or less flat space travelling faster than light, then, seen from the point of view of the ship, light rays far in front the bubble, will always move towards the shift, even those moving "forward". On the other hand, a light ray sent forward by the ship, will move forward for a while (since space is flat there), until it enters the bubble walls. Because of continuity, this means that somewhere inside the bubble, the light ray must stop as seen from the ship, since we know that far ahead the light rays move backwards. The place where the light ray stops is the horizon. The ship can never reach beyond this point with any physical signal.
-------------------------------------------------------------------------
here is a figure drawn by Miguel Alcubierre himself
---------------------------------------------------------------------------
-------------------------------------------------------------------------
here is a comment from ZcPhysics-Zephram Cochrane
-------------------------------------------------------------------------
A must take that big drop somewhere outside of the event horizon which is also in that interval so that it contains the matter that manipulates the beta^2*f^2 peice of g00.
Therefor the matter that makes A dip back down to 1 is outside the horizon and is causally disconnect from the ship after it is has gone to warp. This is the part of the warp shell that you can not control. However, the matter that controls the beta^2*f^2 peice of g00 can be contained entirely within the event horizon. This means that you can control the speed even.
-------------------------------------------------------------------------
another comment from ZcPhysics-Zephram Cochrane
-------------------------------------------------------------------------
Another concern over the Alcubierre warp drive is that it once the ship goes superluminal, there may be a problem controlling the warp. At superluminal speeds, there are event horizons for this spacetime where g00 = 0, even in the case that we have transformed away the singularities there. These two horizons can be constructed as two half spheres enclosing the ship in a warp bubble. Information can not be sent from behind the ship outside the bubble to the inside. Also, information can not be sent from inside the ship to the region to outside, in front. For the warp drive, part of the matter region producing the warp, or the warp shell extends across the horizons. A signal sent from inside the ship can not reach the matter extending in front of the horizon that is in front of the ship. This piece of the warp shell can not then be turned off. This lead to the concern over the ability to control the warp at superluminal speeds. We can work around the problem as follows. The matter controlling the behavior of A(ct,xi ) can be arranged prior to the matter controlling the behavior of b(ct)g(r).
It is the behavior of b(ct)g(r) and not A(ct,xi ) that controls the speed of the ship. The horizon occurs where
A(ct,xi ) = b(ct)g(r).
The function g(r) is then manipulated so that it goes to 1 at a smaller distance from the ship then where
A(ct,xi ) = b(ct).
In other words, function A(ct,xi ) is larger than b(ct) for an interval extending beyond the place where g becomes 1. Now the portion of the matter shell that was formed to control the behavior of A(ct,xi ) that is in front of the horizon will not be accessible by a signal from the ship once superluminal speeds have been reached, but as far as controlling the speed of the ship goes, this does not matter. What matters is that the portion of the matter shell that controls the behavior of b(ct)g(r) is totally contained inside the horizons ensuring that the ship speed is controllable even after the ship has gone superluminal.
----------------------------------------------------------------
another comment from ZcPhysics-Zephram Cochrane
----------------------------------------------------------------
I'll try to give a clear description of what I meant. Consider the warp drive interval given according to the ship frame coordinates as ds^2 = [A^2 - (v(1 - f))^2]dt^2 -2vfdtdz - dz^2 - dy^2 - dx^2.
A is 1 at the location of the ship, becomes much large than v at rs = a and remains large until it drops back to 1 at a surface "somewhere outside" of rs = d.
This behavior of A would be preprogrammed into the matter responsible for it prior to the acceleration of the ship. The function f is 1 inside the interval 0 < rs < a but goes to 0 say at rs = b. If b is less than d, then the horizon will exist somewhere in the interval between b to d because the behavior of A is chosen so that g00 only goes to zero somewhere in that interval.
There will be the prearranged matter remaining outside the horizon associated with the preprogrammed behavior of the function A. However all of the matter associated with manipulation of v(t)*f and v(t)*(1 - f) will be contained in the interval from a to b. This region is causally connect to the ship.
Therefor if some sort of emergency occurs and the ship needs to drop out of warp to sublight speeds prior to where it was expected to when the behavior of A was preprogrammed, it could do so. The part of the matter in front of the horizon that is in front of the ship would tear away and continue on as it is causally disconnect from the rest of the ship, but the point is that the ship speed can still be controlled even after it has gone superluminal.
another comment from ZcPhysics-Zephram Cochrane
-----------------------------------------------------------------------------
To create the matter that "will be" outside the event horizon which only controls the external behavior of the lapse function the ship, yes the ship, can form a matter shell just fine whose behavior and velocity as a function of ship time is "preprogrammed" according to the flight "plan" ahead of the launch time. This external matter will be tachyonic no matter who makes it anyway because it will travel with the ship at superluminal speeds even though it is outside the event horizon once the event horizon is formed. The ship immediately afterward controls a different matter region inside of this to increase its own speed to faster than c at which point the event horizon forms. The ship can either go along with the flight plan or decrease its own speed and stop in an emergency from within without a need to communicate with the external tachyonic matter already formed and preprogrammed because that matter only controls the external behavior of the lapse function, not the speed of the ship. The tachyonic matter in front outside of the event horizon will tear away and continue along the preprogrammed flight plan if the ship does this, but we just don't care about that.
-----------------------------------------------------------------------------
a comment from Loupwarp
-----------------------------------------------------------------------------
we must outline that A have its behaviour engineered when the ship is subluminal and A do not depend in the ship SPEED.....then when the ship gest superluminal the ship will loose contact with A but since A is not function of the speed it does not change this behaviour......of course this is a theoretical model without giving a clue about the exotic nature of A.....this will be done in a future work
--- Ronald wrote:
I can see that, assuming you can go superluminal, that you can reduce speed within the causally connected region. I do not see what happens to the parts of the warp bubble that become causally disconnected, and how it affects future motion. with these answers, I will write more of Paper 2. without more explanation, It is my opinion that we are open to some external criticism.
Ronald
the answer from Loupwarp..although this was explained it is better to outline this for the external criticism....
the exotic matter responsible for the behaviour of A do not depend on the speed..so when you is subluminal ok...if you go to superluminal since the exotic matter do not depend on A you will be disconnected from parts of the Pfenning Warped Region but this does not affect the exotic matter responsible for A..since the exotic field do not change its behaviour because the exotic field is not function of the speed ..the part of vs*g(rs) is still connected to the astronaut so the astronaut can still control the speed....
Ronald wrote
I think it is important that Miguel agrees with what I(really the group) have written. If any of this is wrong, it should not be included. I still have not been convinced about the warp bubble stablity and maneuverablity. Assuming you have made warp speed, slowing down can be done. Speeding up or turning seems to have the same problem as slowing down, what happens to the acausal part of the warp bubble?
Ronald
answer from Loupwarp
from the photos from Ufokier and the postings from lifsspeed we can see that vs*g(rs) is connected to the astronaut and to the remote frame .....the astronaut "sees" until rs < R+1 and the remote frame "sees" until rs > R-1 if the astronaut changes the speed the remote frame will "see"......perhaps when the bubble slows down and according to Zephram Cochrane the part that is disconnected keeps flying away ......and when the bubble accelerates more exotic matter that was connected at subluminal speeds becames disconnected at superluminal speeds ..if we have a bubble with v > 1 lets say v=2 and we pass to v=3 we will have more disconnected matter and the matter at v=3 will collide with the matter at v=2 but this work is to show that while superluminally the vs*g(rs) is controllable by the astronaut and the ship can drop from warp and go back to subluminal velocities ....this is a work destinated to neutralize the arguments of Hitschcock .....not a study of warp dynamics... because warp dynamics would require other tensors available at http://www.geocities.com/einswarp different than G^00 and T^00 to study dvs/dt
----------------------------------------------------------------------------- skeleton of a possible second arXiv.org work
-----------------------------------------------------------------------------
authors
D.Waite(ZcPhysics-Zephram Cochrane) E.Halerewicz(Halgravity) F.Loup(Loupwarp) R.Held(Ronaldheld) M.Kuntzmann(Tecno Maniac 2001) M.Stabno(Ufokier) R.Sims(TvkWarp 5)
title
controlling the speed of superluminal warp drive starships in a modified Alcubierre warp drive spacetime
abstract
it is being shown while the horizons do not exist for warp drive starships moving at subluminal speeds the horizons starts to exist when the warp drive starship reaches the speed of light(when the ship goes luminal). part of the warped region becomes causally disconnected from the ship and remains disconnected when the ship achieves a faster than light(superluminal) speed.
however the control of the speed of the ship lies in the portion of the warped region that is still causally connected to the ship even when the ship is superluminal allowing the ship to slow down to subluminal speeds again or even to stop.
the part of the warped region that is causally disconnected from the ship MUST NOT depend in the ship velocity and its behaviour is not affected when the ship is subluminal,luminal or superluminal.
main text
one of the main obstacles posed by sceptic scientists against the warp driveis the appearance of the horizons when the ship is superluminal.
this is a problem to control the speed of the ship because if the bubble becames causally disconnected from the ship it would be a major problem because the ship cannot turn off the bubble so the ship cannot stop.
if the ship becames causally disconnected from the bubble then voyages to Messier-42 Orion nebula at 1500 light-years from Earth or Messier-1 at 6000 light years from Earth would be impossible because the ship being causally disconnected from the bubble the ship cannot turn off the bubble and cannot stop.
if the ship is causally disconnected from the bubble the ship must be turned out from outside and we dont know if there is "somebody out there" at Orion or Crab to turn off the warp bubble.
in this work we show that while part of the warped region becomes causally disconnected from the ship when the ship is luminal or superluminal the behaviour of that part do not depend on the ship speed and can be engineered while the ship is still subluminal.
also the control of the ship speed remains in the portion of the warped region that is still connected to the ship.
here comes the math the two dimensional ESAA metric written in Miguel Alcubierre formalism is:
ds^2 = -A^2 * dt^2 + [dx-vs*f(rs)*dt]^2
dx=dx'+vs*dt vs=dxs/dt
ds^2 = -A^2 * dt^2 + [dx'+vs*dt-vs*f(rs)*dt]^2
ds^2 = -A^2 * dt^2 + [dx'+vs*dt{1-f(rs)}]^2
ds^2 = -A^2 * dt^2 + [dx'+vs*g(rs)*dt]^2 g(rs)=1-f(rs)
ds^2 = -A^2 * dt^2 + dx'^2 + 2*vs*g(rs)*dx'*dt + {vs*g(rs)}^2 * dt^2
ds^2 = -A^2 * dt^2 + {vs*g(rs)}^2 * dt^2 + 2*vs*g(rs)*dx'*dt + dx'^2
ds^2 = A^2 * dt^2 - {vs*g(rs)}^2 * dt^2 - 2*vs*g(rs)*dx'*dt - dx'^2
ds^2 = [A^2 - {vs*g(rs)}^2]*dt^2 - 2*vs*g(rs)*dx'*dt - dx'^2
ESAA ship frame metric in two dimensions according to Zephram Cochrane Formalism...
the ESAA-Hitschcock ship frame metric can be written as:
ds^2 = -H(rs)*dT^2 + A^2(rs)*dx'^2/H(rs)
dT = [dt-{vs*g(rs)/H(rs)}*dx']
dT^2 = [dt-{vs*g(rs)/H(rs)}*dx']^2
dT^2 = dt^2 - 2*vs*g(rs)*dx'*dt/H(rs) + {vs*g(rs)/H(rs)}^2 * dx'^2
ds^2 = -H(rs)*{dt^2 - 2*vs*g(rs)*dx'*dt/H(rs) + {vs*g(rs)/H(rs)}^2 * dx'^2} + A^2(rs)*dx'^2/H(rs)
ds^2 = -H(rs)*dt^2 + 2*vs*g(rs)*dx'*dt - {{vs*g(rs)}^2/H(rs)} * dx'^2 + A^2*dx'^2/H(rs)
H(rs) = A^2 - {vs*g(rs)}^2 the ESAA-Hitschcock Horizon Function..
{vs*g(rs)}^2 = A^2 - H(rs)
ds^2 = -H(rs)*dt^2 + 2*vs*g(rs)*dx'*dt - {{A^2 - H(rs)}/H(rs)} * dx'^2 + A^2*dx'^2/H(rs)
ds^2 = -H(rs)*dt^2 + 2*vs*g(rs)*dx'*dt - A^2*dx'^2/H(rs) + H(rs)*dx'^2 /H(rs) + A^2*dx'^2 /H(rs)
ds^2 = -H(rs)*dt^2 + 2*vs*g(rs)*dx'*dt + H(rs)*dx'^2 /H(rs)
ds^2 = -H(rs)*dt^2 + 2*vs*g(rs)*dx'*dt + dx'^2
ds^2 = H(rs)*dt^2 - 2*vs*g(rs)*dx'*dt - dx'^2
H(rs) = A^2 - {vs*g(rs)}^2
ds^2 = [A^2 - {vs*g(rs)}^2]*dt^2 - 2*vs*g(rs)*dx'*dt - dx'^2
thus we have derived the ESAA ship frame metric written in Zephram Cochrane formalism...derived from an ESAA Hitschcock ship frame
----------------------------------------------------------------------
here comes the trick..the Pfenning Piecewise function is defined in function of A
-----------------------------------------------------------------------
ds^2 = H(rs)*dT^2 - A^2(rs)*dx'^2/H(rs)
H(rs) = A^2 - {vs*g(rs)}^2 the ESAA-Hitschcock Horizon Function..
defining now the value of A
in the Pfenning integration limits R-(delta/2) to R+(delta/2) being delta=2/@ and @=1 from Alcubierre tanh[@(rs+R)]-tanh[@(rs-R)]
the Pfenning limits would be the following: R-1 and R+1
A=1 rs < R-1
A=very large R-1 <= rs <= R+1
A=1 rs > R+1
-------------------------------------------------------------------------
IMPORTANT
---------------------------------------------------------------------------
A CANNOT be function of the speed...cannot change its behaviour in function of the speed
-------------------------------------------------------------------------
and now the values of the Pfenning Piecewise function f(rs)
f(rs) = 1 rs < R-1
f(rs) = 1-(1/A)*(rs-R) R-1 <= rs <= R+1
f(rs) = 0 rs > R+1
and now the ESAA ship frame Piecewise function g(rs)
g(rs) = 0 rs < R-1
g(rs) = (1/A)*(rs-R) R-1 <= rs <= R+1
g(rs) = 1 rs > R+1
the Pfenning Piecewise and ESAA Piecewise functions are defined in function of the term A. this will have some advantages that will be shown in the work-
we will study now the behaviour of the ESAA-Hitschcock Horizon function in three situations:
1-ship subluminal(v<1)
2-ship luminal(v=1)
3-ship superluminal(v>1)
------------------------------------------------------------------------
part 1------ship subluminal v < 1
------------------------------------------------------------------------
ds^2 = H(rs)*dT^2 - A^2(rs)*dx'^2/H(rs)
H(rs) = A^2 - {vs*g(rs)}^2 the ESAA-Hitschcock Horizon Function..
H(rs) = 1 since A=1 and g(rs) = 0 for rs < R-1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(vs/A)^2 rs = R-1 H(rs) > 0 causally connected to the ship
H(rs)=A^2 rs = R H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(vs/A)^2 rs = R+1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-{(vs/A)*(rs-R)}^2 R-1 < rs < R+1
H(rs) > 0 causally connected to the ship
since A is large from the above expressions it can be seen that the ESAA-Hitschcock Horizon function NEVER drops to zero
A is not function of the speed and A is included in the definition of the Piecewise functions that warrants for large A the ship will be ALWAYS connected to the region from rs=0(ship location) to rs=R+1(upper Pfenning limit).
H(rs)=1-vs^2 since A=1 and g(rs)=1 rs > R+1
H(rs) > 0 causally connected to the ship
in this region A must drop back from a large value at rs=R+1 to A=1 at rs > R+1 then part of the warped region is beyond R+1 since we need exotic matter to force the A drops back to 1.since A is not function of the speed if the ship changes the speed the behaviour of A will not be affected.
since H(rs) > 0 the ship is causally connected to this region and is subluminally that A must be engineered this way.
------------------------------------------------------------------------
part 2------ship luminal v = 1
------------------------------------------------------------------------
ds^2 = H(rs)*dT^2 - A^2(rs)*dx'^2/H(rs)
H(rs) = A^2 - {vs*g(rs)}^2 the ESAA-Hitschcock Horizon Function..
H(rs) = 1 since A=1 and g(rs) = 0 for rs < R-1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(vs/A)^2 rs = R-1 H(rs) > 0 causally connected to the ship
H(rs)=A^2 rs = R H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(vs/A)^2 rs = R+1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-{(vs/A)*(rs-R)}^2 R-1 < rs < R+1
H(rs)=(A^2)-(1/A)^2 rs = R-1 H(rs) > 0 causally connected to the ship
H(rs)=A^2 rs = R H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(1/A)^2 rs = R+1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-{(1/A)*(rs-R)}^2 R-1 < rs < R+1
H(rs) > 0 causally connected to the ship
since A is large from the above expressions it can be seen that the ESAA-Hitschcock Horizon function NEVER drops to zero
A is not function of the speed and A is included in the definition of the Piecewise functions that warrants for large A the ship will be ALWAYS connected to the region from rs=0(ship location) to rs=R+1(upper Pfenning limit).
H(rs)=0 since A=1 and g(rs)=1 and vs=1 rs > R+1
ds^2 = H(rs)*dT^2 - A^2(rs)*dx'^2/H(rs)
from the expression above a Horizon will appear.at luminal speeds the ship becomes causally disconnected from the region beyond R+1.
since A is large at rs=R+1 and must drop back to 1 when rs > R+1 we still need exotic matter beyond R+1 to drop the value of A back to 1 and this warped region is causally disconnected from the ship..the ship remains causal until rs=R+1 .
providing that A is not function of the speed then A is not affected when the Horizon appears in front of the ship when the ship gets luminal.the behaviour of A was engineered when the ship was subluminal.
and the part of of the speed control still lies in the region between R-1 to R+1 so the ship can change the speed and go back to subluminal if needed.
------------------------------------------------------------------------
part 3------ship superluminal v > 1
------------------------------------------------------------------------
ds^2 = H(rs)*dT^2 - A^2(rs)*dx'^2/H(rs)
H(rs) = A^2 - {vs*g(rs)}^2 the ESAA-Hitschcock Horizon Function..
H(rs) = 1 since A=1 and g(rs) = 0 for rs < R-1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(vs/A)^2 rs = R-1 H(rs) > 0 causally connected to the ship
H(rs)=A^2 rs = R H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-(vs/A)^2 rs = R+1 H(rs) > 0 causally connected to the ship
H(rs)=(A^2)-{(vs/A)*(rs-R)}^2 R-1 < rs < R+1
H(rs) > 0 causally connected to the ship
since A is large from the above expressions it can be seen that the ESAA-Hitschcock Horizon function NEVER drops to zero
A is not function of the speed and A is included in the definition of the Piecewise functions that warrants for large A the ship will be ALWAYS connected to the region from rs=0(ship location) to rs=R+1(upper Pfenning limit).
H(rs)<0 since A=1 and g(rs)=1 and vs>1 rs > R+1
ds^2 = H(rs)*dT^2 - A^2(rs)*dx'^2/H(rs)
from the expression above a Horizon will appear.at superluminal speeds the ship becomes causally disconnected from the region beyond R+1.
assuming a continuous spacetime(Miguel) H(rs) > 0 at rs = R+1 but H(rs) < 0 at rs > R+1...somewhere between H(rs)=0 anf then we have the Horizon.
since A is large at rs=R+1 and must drop back to 1 when rs > R+1 we still need exotic matter beyond R+1 to drop the value of A back to 1 and this warped region is causally disconnected from the ship..the ship remains causal until rs=R+1 .
providing that A is not function of the speed then A is not affected when the Horizon appears in front of the ship when the ship gets superluminal.the behaviour of A was engineered when the ship was subluminal.
and the part of of the speed control still lies in the region between R-1 to R+1 so the ship can change the speed and go back to subluminal if needed.
------------------------------------------------------------------------
consider now the following stress energy momentum tensor for a ship frame ESAA-warp metric
T^00 = -(vs^2/4)*(1/(8*pi))*[{dg(rs)/drs}^2]*[(sigma/rs)^2]*[(1/A)^4]
dg(rs)/drs=1/A and [{dg(rs)/drs}^2]=1/A^2
then T^00 = -(vs^2/4)*(1/(8*pi))*[(sigma/rs)^2]*[(1/A)^6]
this will low the negative energy densities even further
----------------------------------------------------------------------------------------------------
here is a comment from Techo Maniac 2001- another ESAA member
-----------------------------------------------------------------------------------------------------
Before you post the second work to arXiv.org, consider the following scenario:
A ship reaches luminal speed. The whole warp bubble is moving at light-speed, but some of it is now casually disconnected from the ship. The captain says "full speed ahead", and the ship accelerates. Since a part of the warp bubble is casually disconnected from the ship, it has no way of "knowing" that the ship has accelerated, and so it keeps moving at light-speed. But the rest of the bubble is moving faster!
The way I understand it, the two parts of the warp bubble will collide, and the warp bubble's shape may change as a result. Similarly, if the ship changes direction or drops to sub-luminal speed, I expect the disconnected part of the bubble to keep moving as as did before the change.
How does the bubble remain coherent in all these cicumstances, and if it doesn't - how does that affect the ship?
--------------------------------------------------------------------------------------------------------
this is a valuable question that could be launched by a arXiv.org scientist Tecno raised a important problem and due to Tecno our work will not be "caught in the middle"
--------------------------------------------------------------------------------------------------------
here comes the answer from Loupwarp
-------------------------------------------------------------------------------------------------------
the remote frame ESAA warp drive metric is given by:
ds^2 = -(A^2)*dt^2 + [dx-vs*f(rs)*dt]^2
A=1 rs < R-1
A=large value R-1 <= rs <= R+1
A=1 rs > R+1
f(rs) = 1 rs < R-1
f(rs) = 1-(1/A)*(rs-R) R-1 <= rs <= R+1
f(rs) = 0 rs > R+1
ds^2 = (A^2)*dt^2 - [dx-vs*f(rs)*dt]^2
ds^2 = (A^2)*dt^2 - [dx^2 - 2*vs*f(rs)*dx*dt + {vs*f(rs)}^2 * dt^2]
ds^2 = (A^2)*dt^2 - {vs*f(rs)}^2 * dt^2 + 2*vs*f(rs)*dx*dt - dx^2
ds^2 = [(A^2)-{vs*f(rs)}^2]*dt^2 + 2*vs*f(rs)*dx*dt - dx^2
g_00 = [(A^2)-{vs*f(rs)}^2]
we will examine the behaviour of g_00 with vs
rs < R-1
g_00 = 1-vs^2 if vs < 1 this is causally connected to the remote frame
vs = 1 this is disconnected from the remote frame
vs > 1 this is disconnected from the remote frame
because if vs < 1 g_00 > 0
vs = 0 g_00 = 0 Horizon appears
vs > 1 g_00 < 0 Horizon
R-1 <= rs <= R+1
g_00 = (A^2) - {vs[1-(1/A)*(rs-R)]}^2
providing a large A g_00 will be always g_00 > 0 and this region is
causally connected to the remote frame.....
rs > R+1
g_00 = 1 .....flat space seen by a remote frame observer...
when the ship is superluminal the Horizon lies at rs > R+1
for the ship frame ....this is the ship Horizon
the ship is causally connected from rs=0 ship location to
rs=R+1
when the ship is superluminal the Horizon lies at rs < R-1 for
a remote frame observer.....this is the remote frame Horizon..
the remote frame is causally connected from rs > R+1 at a
great distance and remains connected until rs=R-1
the ship frame cannot send signals to rs > R+1
the remote frame cannot send signals to rs < R-1
but the region between R-1 to R+1 remains connected to both observers...if the astronaut changes the speed the outer parts of the bubble will react although the astronaut cannot communicate with the outer parts of the bubble... then if the region between R-1 to R+1 is common to both observers
the bubble will not collapse
ds^2 = [A^2 - {vs*f(rs)}^2]*dt^2 + 2*vs*f(rs)*dx*dt - dx^2
ESAA remote frame
i will introduce here the I(rs) function
the I(rs) = [A^2 - {vs*f(rs)}^2] and is the equivalent of the ESAA Hitschcock Horizon function but suited to the remote frame.....
then in a remote frame observer
ds^2 = -I(rs)*dT^2 + [{A^2}/I(rs)]*dx^2
dT = [dt + ({vs*f(rs)}/I(rs))*dx]
dT^2 = dt^2 + {[2*vs*f(rs)*dx*dt]/I(rs)} + ({vs*f(rs)}/I(rs))^2 * dx^2
but {vs*f(rs)}^2=(A^2)-I(rs)
dT^2 = dt^2 + {[2*vs*f(rs)*dx*dt]/I(rs)} + (((A^2)-I(rs)) /I(rs)^2) * dx^2
ds^2 = -I(rs)*{dt^2 + {[2*vs*f(rs)*dx*dt]/I(rs)} + (((A^2)-I(rs)) /I(rs)^2) * dx^2} + ((A^2)/I(rs))*dx^2
ds^2 = -I(rs)*dt^2 - 2*vs*f(rs)*dx*dt - [({A^2}-I(rs))/I(rs)]*dx^2 + {(A^2)/I(rs)}*dx^2
ds^2 = -I(rs)*dt^2 - 2*vs*f(rs)*dx*dt - ({A^2}/I(rs))*dx^2 + [I(rs))/I(rs)]*dx^2 + {(A^2)/I(rs)}*dx^2
ds^2 = -I(rs)*dt^2 - 2*vs*f(rs)*dx*dt + [I(rs))/I(rs)]*dx^2
ds^2 = -I(rs)*dt^2 - 2*vs*f(rs)*dx*dt + dx^2
ds^2 = +I(rs)*dt^2 + 2*vs*f(rs)*dx*dt - dx^2
I(rs)=(A^2) - {vs*f(rs)}^2
ds^2 = [A^2) - {vs*f(rs)}^2]*dt^2 + 2*vs*f(rs)*dx*dt - dx^2
then we recovered the ESAA remote frame metric from a equivalent ESAA Hitschcock Horizon function for the remote frame
the I(rs) = [A^2 - {vs*f(rs)}^2] and is the equivalent of the ESAA Hitschcock Horizon function but suited to the remote frame.....
then in a remote frame observer
ds^2 = -I(rs)*dT^2 + [{A^2}/I(rs)]*dx^2
rs < R-1
this part of the warped region needed to make A drop back to 1
if vs < 1 I(rs) > 0 causally connected to ship and remote frame....
if vs = 1 I(rs) = 0 and the Horizon appears for the remote frame...this region while connected to the ship frame becames causally disconnected from the remote frame....
if vs > 1 I(rs) < 0 and assuming a continuous spacetime I(rs) < 0 at rs < R-1 bit between R-1 <= rs <= R+1 I(rs) > 0 then somewhere between rs=R-1 and rs < R-1 a Horizon appears..... causally disconnected from the remote frame while connected to the ship frame
R-1 <= rs <= R+1
I(rs)=(A^2) - {vs*f(rs)}^2
but f(rs)=1-(1/A)*(rs-R)
then
I(rs)=(A^2)-{vs*[1-(1/A)*(rs-R)]}
and providing a large A^2 >> {vs*f(rs)}^2 then I(rs) > o and this region will be causally connected to the remote frame...
the remote frame "sees" the Pfenning warped region(the part of the warped region responsible for the speed).the remote frame is causally connected to this region. if the astronaut changes the speed because the astronaut is causally connected to this region then the remote frame will "see" the changing speed.....
rs > R+1
I(rs)=1 this part of the warped region is always connected to the remote frame....this part of the warped region must make A drop back to 1 again....this is connected to the remote frame observer and is disconnected from the ship frame while luminal or superluminal....
a signal sent by the ship can go to rs=R+1
a signal sent by remote observer can go to rs=R-1
the region between R-1 <= rs <= R+1 is "seen" by both observers ship and remote frame...
the ship "sees" H(rs) = (A^2) - {vs*g(rs)}^2
the remote "sees" I(rs) = (A^2) - {vs*f(rs)}^2
the astronaut can change the ship speed because this region is connected to the ship
the remote frame "sees" the speed being changed because this region is connected to the remote frame....
so the outer part of the bubble "suffers" when the speed is changed although the astronaut cannot communicate with the outer parts of the bubble and the remote observer cannot communicate with the inner part of the bubble.....
the bubble remais stable-----this is the answer to Techni Maniac 2001
-------------------------------------------------------
-------------------------------------------------------
Conclusion...
in this work it was demonstrated how a A defined as a Pfenning-Piecewise like style function can solve the Horizons problem and can make the ship retains control of the speed and the bubble....it is assumed that A do not change its behaviour when the ship passes from subluminal to superluminal......
although we do not provide a source for the nature of A this will done in a future work...
if we use the original continuous expression for A the geometry of the ESAA warp drive would be the following.......
the calculations of the Cochrane-Halgravity obeys the following format
first i make
{{1+{tanh[@(rs-R)]^2}}/2}^(@R)
in the column labeled Cochrane-Halgravity Coefficient a
and the final form of a is given by Final Form of Coefficient a = 1/(Cochrane-Halgravity Coefficient a)
to produce the following expression
{{1+{tanh[@(rs-R)]^2}}/2}^(-@R)
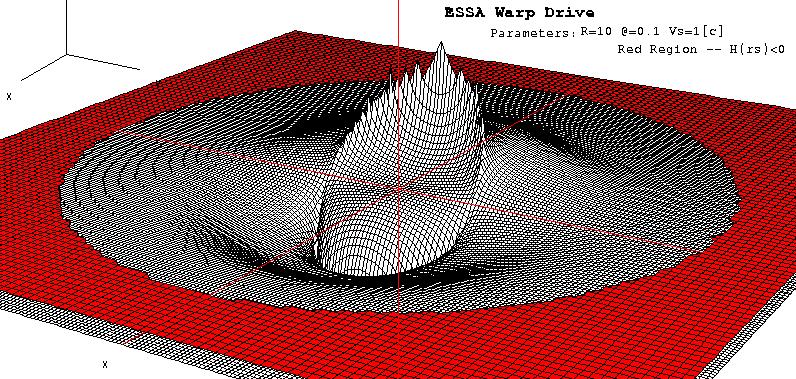
Ship Frame the Horizons are colored in red
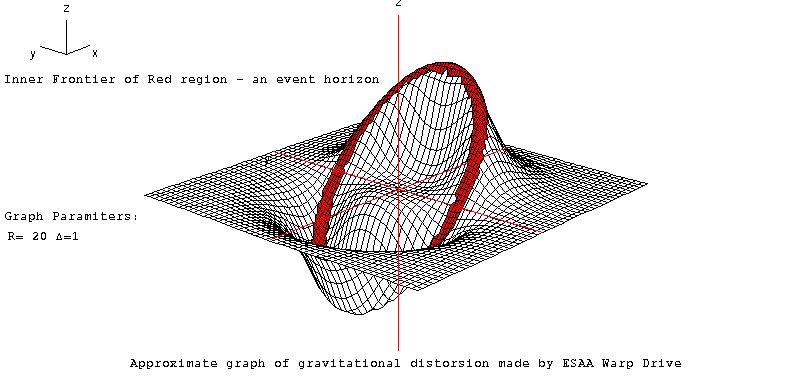
pictures generated by Ufokier and Halgravity using the program Derive version 4.02
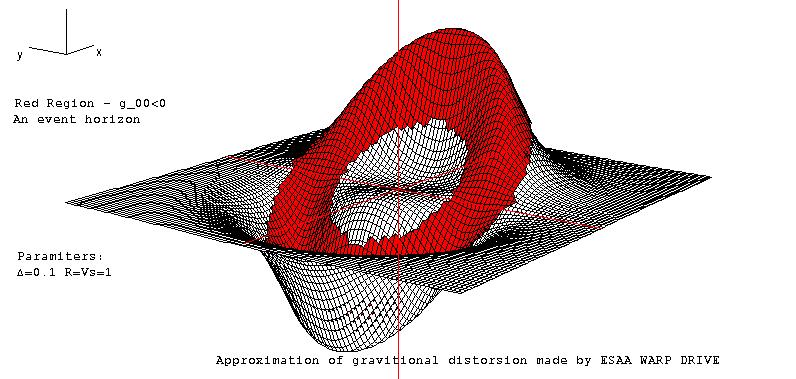
Ship Frame the Horizons are colored in red
Remote Frame Horizons are colored in blue

this one have in yellow the Pfenning Warped Region
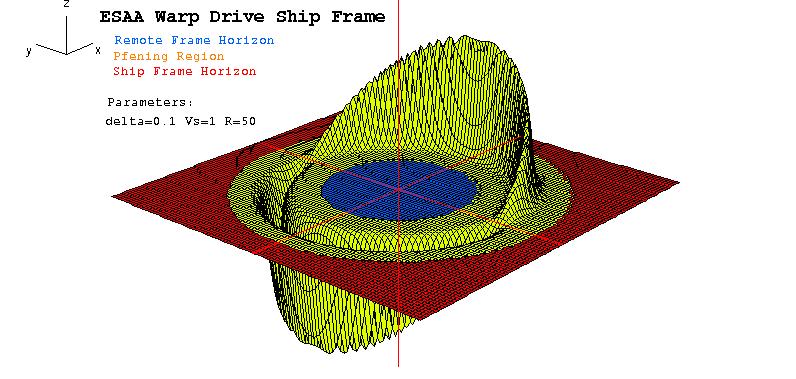
pictures generated by Ufokier and Halgravity using the program Derive version 4.02
another comment from Tecno Maniac 2001
As I remember it, the horizon problem was demonstrated along the following lines: From the ship's perspective, light that moves "forward" inside the bubble appears to move "forward", but light that moves "forward" outside the bubble appears to move "backward". So somewhere in the middle the light should appear to stop - that is where the horizon is.
However, there is no principal reason that the horizon should be somewhere *inside* the bubble's walls. Perhaps the gemotery of the bubble and/or other factors could somehow be adjusted so that the horizon is just on the outer edge of the bubble's walls, exactly where the bubble ends and normal space begins... If so, the whole bubble will be connected to the ship and so it can be both controlled and sustained (and of course created).
yes Halgravity....try A=[(1/2)*{1+tanh[@(rs-R)]^2}]^(-N)
AS DEPICTED IN LIFSSPEED
and not A=[(1/2)*{1+tanh[@(rs-R)]}] i forgot the tanh[@(rs-R)]^2
make R=50 @=1 and see A from 1 in the ship to 1 far from it while large in the
warped region
due to a N=100 Halgravity Parameter..
CONTRATULATIONS RONALD...
although i wrote
A=[(1/2)*{1+tanh[@(rs-R)]}]^(-N)
when i tried to wrote
A=[(1/2)*{1+tanh[@(rs-R)]^2}]^(-N)
you wrote
A=[(1/2)*{1+abs(tanh[@(rs-R)])}]^(-N)
which is the same....
A varies from 1 in the ship to 1 far from it while being large 10^30 in the
warped region....IN BOTH EXPRESSIONS
so we can make A drop back to 1 increasing the distance rs without a second
exotic field...
our results almost match
these two expressions gives almost the same result
A=[(1/2)*{1+tanh[@(rs-R)]^2}]^(-N)
A=[(1/2)*{1+abs(tanh[@(rs-R)])}]^(-N)
well Ronald....both simulations agree..we have the Horizons being pushed to
the outermost layers
of the Pfenning warped region and we have a continuous form for A being 1 in the
ship and 1 far from it while being large in the warped region
and A drops back to 1 outside Pfenning warped region being causally disconnected
from the ship and A is not function of the speed and we dont need exotic matter
to make A drop back to 1.
applying the H(rs)=(A^2)-{vs*g(rs)}^2 as in LoupwarpRonald2 or in Late Ronald
we will see Horizons in the outermost layers
of the Pfenning Warped Region...
lifsspeed updated
see Late Ronald,LateRonald2,Ufokier to Ufokier4,LoupwarpRonald and LoupwarpRonald2
I THINK WE ARE READY GUYS TO TELL A COUPLE OF THINGS TO HITSCHCOCK
Although we used the definition of "pre-programmed exotic matter" while the ship
is subluminal
and the nature of A do not change when the ship pass from subluminal to
superluminal the definition
of "pre-programmed" will be better explained below:
for a Pfenning Piecewise behaviour of A in the upper Pfenning limit R+delta/2
A still have a large value to keep this part causally connected to the ship
according to
ESAA-Hitschcock function H(rs)=(A^2)-{vs*g(rs)}^2 by making H(rs) > 0 even when
vs >1
(superluminal).
then we have the following values for A according to rs(already seen)
A=1 rs < R-(delta/2)
A=large value R-(delta/2) <= rs <= R+(delta/2)
A=1 rs > R+(delta/2)
providing that A is not function of the speed the ship will be disconnected
after rs > R+(delta/2)
but this does not affect the behaviour of A...Pfenning Piecewise is an
approximation used first by Pfenning
to simplify calculations and we are adopting Pfenning techniques here.
we know that the continuous form of the Top Hat is 1 in the ship and zero far
from it...
there exists a open interval ]1,0[ when the function f(rs) starts to decrease
from 1 to 0.
is in that region where the exotic matter resides...this the continuous
equivalent of the Pfenning warped region.
if we define A=[(1/2)*{1+tanh[@(rs-R)]^2}]^(-N) we will have a continuous
form of A
defined in function of the continuous Alcubierre Top Hat and A is function of rs,R,@
and N.
this expression can make A be 1 in the ship and far from it while being large in
the warped region...the region where f(rs)
starts to decrease from 1 to 0.
below there are some numerical simulations showing this behaviour..A drops
NATURALLY back to 1 after the
warped region EVEN IF THE SHIP IS DISCONNECTED due only to the distance rs..
and pushing the ESAA-Hitschcock Horizon to the outermost layers of the warped
region making the
speed controllable by the ship because the major part of the warped region is
connected to the ship so the ship can drop out of warp
Halgravity include from these links and the code is not necessary...anyone can code the expression
if someone uses
f(rs)={tanh[@(rs+R)]-tanh[@(rs-R)]}/{2*tanh(@*R)}
and A=[(1/2)*{1+tanh[@(rs-R)]^2}]^(-N)
with N=R*delta or R*@ arbitrarily and
g(rs)=1-f(rs) or even if we divide f(rs) by A to increase the pushing of the
Horizon to the outermost layers of the warped region in the ESAA-Hitschcock H(rs)=(A^2)-{vs*g(rs)}^2
in the following numerical simulations
everyone can see that rs can push the Horizon.
One of us argues that the solution is more mathematical than physical and this
point of view is correct.
However Miguel Alcubierre defined f(rs) mathematically leaving for a future work
the creation of a f(rs) physically.
This work was designed to conceive mathematically a better-behaved warp drive in
function of the Horizons and from the point of view of the numerical simulations
this approach is correct.
A ws designed in function of the Top Hat to correct the Horizons in ESAA warp
drive geometry.
the Authors of this work would like to express the most profound and sincere gratitude to Miguel Alcubierre for his time and patient(specially this one) during all the phases of development of this work.....
H
içbir yazı/ resim izinsiz olarak kullanılamaz!! Telif hakları uyarınca bu bir suçtur..! Tüm hakları Çetin BAL' a aittir. Kaynak gösterilmek şartıyla siteden alıntı yapılabilir.The Time Machine Project © 2005 Cetin BAL - GSM:+90 05366063183 -Turkiye/Denizli
Ana Sayfa /index /Roket bilimi /![]() E-Mail /CetinBAL/Quantum Teleportation-2
E-Mail /CetinBAL/Quantum Teleportation-2
Time Travel Technology /Ziyaretçi Defteri /UFO Technology/Duyuru