I have only recently come across Veljko Mircovic's work, and since I found it intriguing I have done a little work on the subject.

The things that stand out is that he comes across as a sincere man who appears to have stumbled across a phenomenon that traditional science is at a loss to explain. From his demonstrations one could easily come to the conclusion that Newtonian physics do not apply where his arrangement is concerned. That in itself is a dangerous road to travel as it stirs up emotions amongst physicists that, as irrelevant as they should be in science, are nevertheless a very real part of human inter-reaction. Right or wrong, people have a tendency to defend whatever they consider their turf to be.

So what does he do? Veljko Milkovic puts a pendulum on a balance beam with a counter weight on the other side to put the arm into equilibrium and then gets the pendulum to swing. The result is an oscillatory movement of the beam.

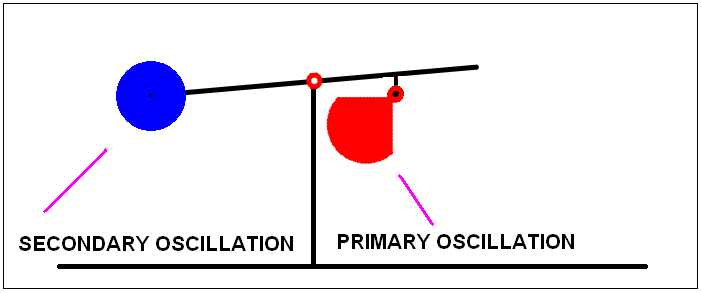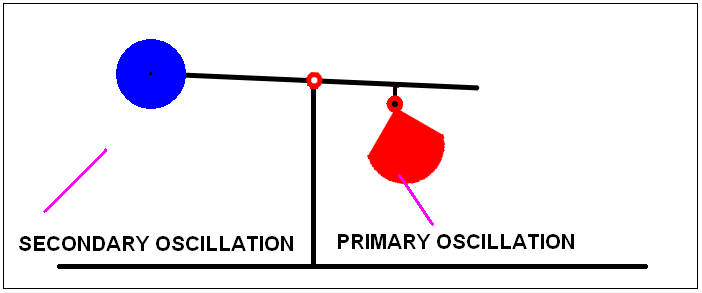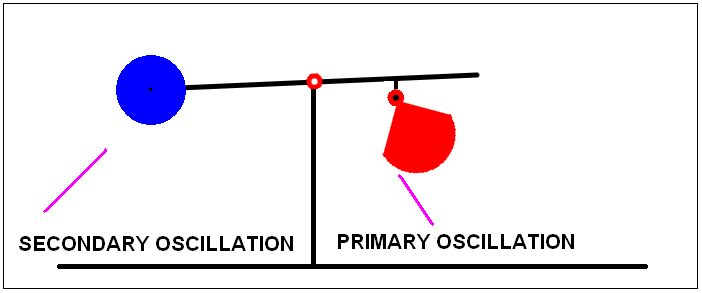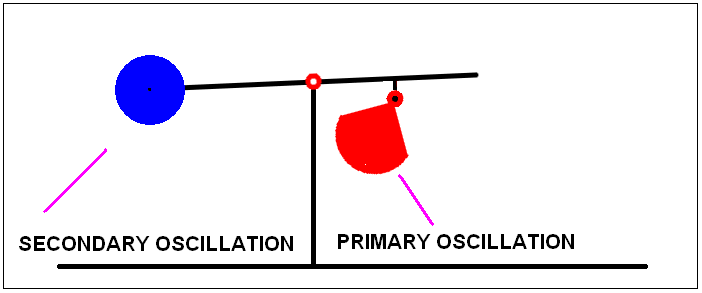
So far so good, that is what one would expect. He then claims that the mechanism does not work in reverse. He moves the balance beam from the opposite side up and down with the pendulum at a standstill and the pendulum does not swing. Case proved, Newton's third law is wrong. There is no equal and opposite reaction!

He even has a letter from Peter Lindemann D.Sc. to prove it. Lindemann goes as far as stating that something like Milkovic's discovery only comes around every three hundred years.

Sorry guys, but this is not a valid demonstration.

The demonstration is flawed because Milkovic does not truly reverse the process. If he were to agitate the beam at the natural frequency of the pendulum in even strokes he would soon find out that the pendulum would start to swing and gather momentum as he was feeding energy into it.

If the pendulum at all time was perfectly perpendicular and the fulcrum at all times at that axis the pendulum would only move up and down as there was no energy available to move it sideways. But such is not the case here.

There is horizontal movement, admittedly small, but it is there. That is why it takes a while before the pendulum can store enough energy to exhibit this. Inertia has yet to build up to show noticeable levels of movement.

Milkovic's demonstrations are far too short and uncontrolled to demonstrate this.

Let me explain:

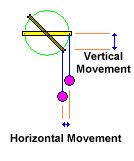
The pendulum's fulcrum at the end of the balance beam moves in an arc. As the balance beam goes up the fulcrum's position relative to the pendulum is displaced horizontally as well as vertically.. That means that the pendulum is no longer perpendicular to the earth's centre of gravity. That also means that it has to find a new position.

As the pendulum develops inertia when it is forced into the new position it swings past the natural point of equilibrium and will only return when the energy that has been fed to it is expended. But while it is doing that the balance beam is moving back putting the pendulum even more out of equilibrium, but now in the opposite direction.

So the pendulum swings back to repeat the process over and over again with increased amplitude as long as the introductory impulses are of the same frequency.

The only things that will stop the pendulum behaving in this manner is when the agitation stops or when the agitation is out of step with the natural frequency of the pendulum's oscillations in which case we have created forces that are out of phase with each other and therefore cancel each other out.

Consider the following:

You have a balance beam, but this time you have on each end a pendulum of exactly the same length. This is important since the pendulum's frequency in this case is solely dependent on its length. You now give one pendulum a push and it begins to oscillate. The balance beam behaves as before, going up and down at twice the frequency of the pendulum.

What do you think happens after a while?

This is one of the classical experiments in physics because the effects are so unsuspected. Say we have given the right pendulum a push. As it swings there is a noticeable diminishing of amplitude. The left pendulum now starts to pick up momentum, which increases with every loss of inertia on the other side. After a while the right pendulum will come to a standstill with the left one in full swing. Slowly the right pendulum will start to pick up momentum as the left one now starts losing energy. After a while, when the left pendulum's energy is spent the right one is in full swing again. The process keeps repeating itself until all energy is spent through friction, drag and heat. If there were no losses the process would carry on forever.

All this flies right into the face of what Milkovic and Lindemann are saying.

So where, if it is real, is the excess energy coming from? Certainly not from the assumed fact that both sides don't influence each other. Because they do!

There is more to this device than it's primitive construction would lead you to believe. From a purely mechanical evaluation of the device no one would go any further. Considering the totality of the forces in play however, there is doubt that such a slick evaluation is sufficient.

What is being left out of the equation by physicists and incidentally Milkovic and Lindemann alike is resonance. There is ample evidence that where resonance is concerned our friend Newton is not doing too well. This is natural, since he would not have known too much about it. Neither does conventional science for that matter. The study of resonance is mostly concerned with analogue electrical circuitry and acoustics, and even here investigation into the attending phenomena stopped far short of what there is to know. Engineering is mostly concerned with avoiding as much as possible oscillations that are anywhere near resonance because of their destructive character. Metal fatigue comes to mind here as a commonly encountered problem.

The chief obstacle with resonance in mechanical arrangements lies in its inherent characteristic to absorb energy from almost anywhere as long as the frequencies match.

A resonant body will accept energy at its own level of resonance and reject energy far removed from its own level of resonance. In the case of the Milcovic device the frequencies encountered are very low.

On the surface of the earth, the length of a pendulum (in metres) is approximately one quarter of the time period (in seconds) squared. Therefore the famous two second pendulum, as commonly employed in old fashioned grandfather clocks is 2*2/4 = 1 meter long. A time period of one second is equal to a pendulum length of 25 cm and so forth.

The above formula is only an approximation, since it assumes the force of gravity to be the same anywhere on earth. Such is not the case. The deviations are quite small however and for our purposes the above formula is quite sufficient.

So let us assume we have an effective pendulum length of 25 cm which completes its cycle in one second. This gives us a frequency of 1 Hertz. That is the fundamental frequency of the device. The secondary oscillation is double that, namely 2 Hertz. In terms of harmonics that is exactly one octave above the fundamental. But this is not where it stops. Further harmonic frequencies are generated in the process. We are now squarely in the realm of acoustics. The attendant frequencies that are generated are 3 times, four times, five times etc. that of the fundamental, commonly known as harmonics or overtones, if you want to use a musical term for the phenomenon. These harmonic frequencies are believed to extend into infinity, albeit with reduced amplitude as the frequency increases.

To put it into a nutshell, we have created a complex resonant field with our little device. That field exists in the device as a pressure wave that permeates the entire structure.

This is where it starts getting interesting. Remember the rule about resonant bodies:

A resonant body will accept energy at its own level of resonance and reject energy far removed from its own level of resonance.

What this means is that our device is capable of absorbing energy from any other resonant field that may be around in the environment on any of its harmonics.

Is that where any excess energy is coming from? Hard to tell. Very low frequencies are difficult to detect and even more difficult to quantify. We know that an earthquake can impart energy to a pendulum on the other side of the earth to the point where the energy can still be measured. It does this purely via resonance. So the effect is there.

Let me give another example:

You have built an AM transmitter with an output of one half a watt. Under ideal conditions this would cover easily a diameter of some 10 kilometres on level ground with a good aerial.

We now have a little guy who has just built himself an old fashioned crystal detector set, strung up an aerial and connected some old fashioned high impedance headphones.

What happens is our little fellow can hear, after tuning in to the broadcast, what is being said.

No big deal you say. Quite correct, this technology has been around for a long time. In fact so long that hardly anyone remembers how it worked.

Well, for one, a crystal detector as described does not have its own power source. All the energy necessary to drive the set is derived from whatever radiated energy the aerial can drag in.

But it very really transfers enough energy to two electromagnets to vibrate two diaphragms made of steel to vibrate the adjoining air to the point where it becomes possible to listen to the broadcasted sound, even after the carrier frequency has been stripped away.

So what, you say, its all simple stuff. We know all about radio broadcasting an such.

But do we?? What happens if we put two more detector circuits up?

Well nothing really they will hear the same stuff, if they are built properly.

Alright what about ten thousand or a million or so.

Same thing, as long as they are in range there is no reason why each one of these circuits would not perform the way the others do. And what about the transmitter?

What about the transmitter? There is no way any radio receiver can put a load onto a radio transmitter.

Are you trying to tell me than a single little transmitter with about half a watt output is capable of moving millions of membranes by millions of electromagnets without losing any energy?? And isn't the energy that is driving the magnets bigger than the one transmitted???

Well duuuuhhhhh, I don't know about that.

This is where science is stuck in its own debris. It has been known for a long time that traditional Newtonian concepts do not apply to resonant circuits of certain designs. No-one in the hallowed halls of academia is prepared to admit it though and you can get into a lot of trouble just pointing out the discrepancies to the wrong people as I have found out on a number of occasions.

Fact is that the behaviour of certain resonant circuits cannot be explained with Newtonian physics. There also appears to be a net gain of energy in those circuits which becomes more pronounced the closer we get to perfect harmony. Harmony with precisely what is anyone's guess.

What kind of resonant fields we could tune into with benefit with the right kind of circuitry is still open to speculation. The paradox here is that in spite of knowing it can be done science denies the possibilities. One must wonder why!

So where do we go from here? Is it possible to demonstrate overunity with a device that relies on secondary oscillations caused by a pendulum? Since we are possibly dealing with poorly understood phenomena or even completely unknown territory, the only way open to us to gain further knowledge is by way of experimentation.

The starting point is the assumption that there is a net gain of energy achievable by using the secondary oscillations of a pendulum in motion.

Traditional theory tells us that this is impossible, so we must prove that current theory is wrong, or that it is not applicable in relation to our device. This is a hard call, but let us not forget that according to the science of the day the flight of an aircraft heavier than air was considered impossible, in spite of the observable phenomenon of heavier than air flying machines in the form of birds. Or that scientists accused Thomas Alva Edison of ventriloquism when he demonstrated his phonograph. Never allow facts to contradict a good theory! :-)

In order to prove our theorem we must design an experiment where we have a measured input of energy to the pendulum and a measured output from the secondary oscillations. If the output exceeds the input we have proved what we set out to do.

So where do we start?

Since the pendulum is our source of power we must move it with a strictly controlled input of energy. Pushing it with a finger is certainly not the way to do this.

There are several ways to do it, the one I favour at the moment is to use two counter-rotating weights on a common axis as the pendulum bob. (This follows a suggestion by Mike Tempest from the U.K. who is working on a device that he calls the CENTOR that uses this principle. If Mike is agreeable I will publish his ideas on this website in the near future.) Though an unconventional way of going about it, it offers several advantages over more commonly used ways of imparting energy to a pendulum.

Take an electromagnet as the source of energy. Here we have an electromagnet pushing the pendulum at the correct moment by providing a magnetic field that is opposite in polarity to a magnet mounted on the pendulum.

Like this:

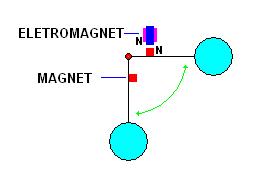
Not a bad way of moving a pendulum, besides, we can establish easily how much energy the electromagnet draws. Correct. But how much of that energy is actually used by the pendulum? That is far more difficult to establish. As the electromagnet pushes, the pendulum moves further and further away from the electromagnet. After all that is the idea behind the arrangement. As the pendulum moves away the effective push becomes more and more feeble even though the electromagnet still draws full power. Most of the power gets dissipated as the magnet moves out of the generated field. Also, as the permanent magnet approaches the electromagnet, it begins to inter-react with the iron core of the electromagnet before the electromagnet is energised. Too many unknown factors in this set-up to come up with accurate measurements.

By using counter-rotating weights we overcome many of the difficulties encountered here.

So how does it work? Let us look at the following arrangement. Here we have two counter-rotating weights around a common axis. The weights spin like this:

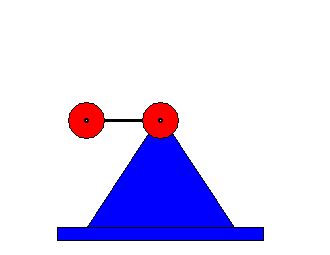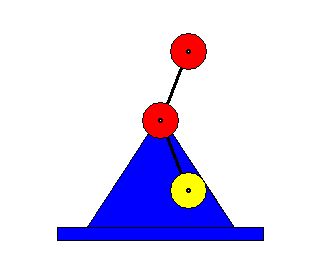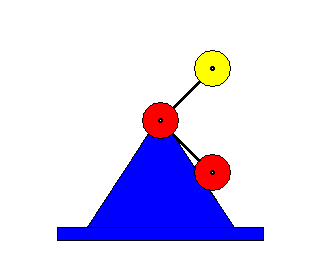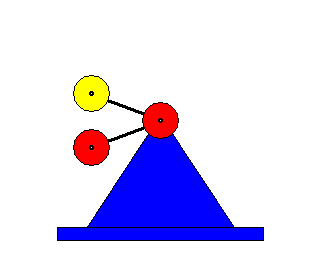
So, what happens here? As the weights spin we have a centrifugal force with its corresponding centripetal force developing along the horizontal axis in both directions. Since the weights are at all times opposite each other on the vertical plane the forces generated cancel each other out in the vertical. At the same time the centre of gravity between the counter-rotating weights shifts along the horizontal axis like this:

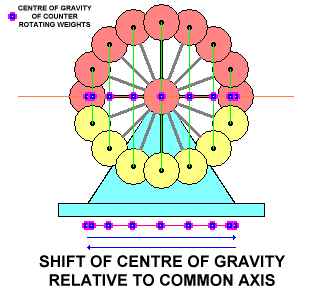
If we now, instead of mounting the device on a stand, suspend it on a lever from some sort of fulcrum we have a powered pendulum:

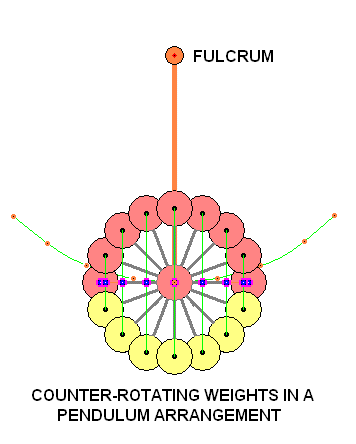
The advantages here are obvious. Instead of a relatively uncontrolled push we have a steady input of energy that causes the pendulum to move with no energy wasted. The displacement of the centre of gravity as well as the centrifugal forces that come into play all contribute to the harmonious motion of the pendulum, as long as the rate of rotation is matched perfectly to the natural frequency of the pendulum.

Each rotation of the weights causes a movement laterally back and forth. In other words if we spin a the weights at 60 rpm we get one cycle per second. Since one cycle per second is the equivalent of a pendulum length of 25 cm all we need to do is to suspend the centre of gravity, at rest, 25 cm from the fulcrum and we have the correct relationship without rogue frequencies being generated that would impede the mechanism.

The shift of the centre of gravity is the same as the energy supplied by a child on a swing by altering its body position in relation to the fulcrum in tune with the natural frequency of the swing. It generates a push, any kid knows that intuitively after playing on the swings for awhile. So how do we translate all that into a workable device?

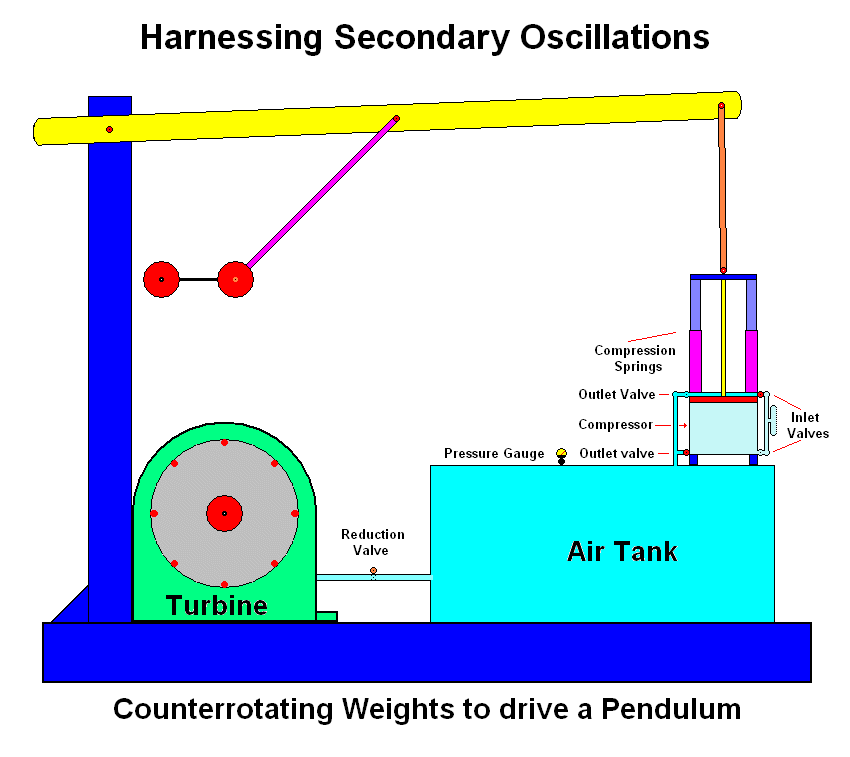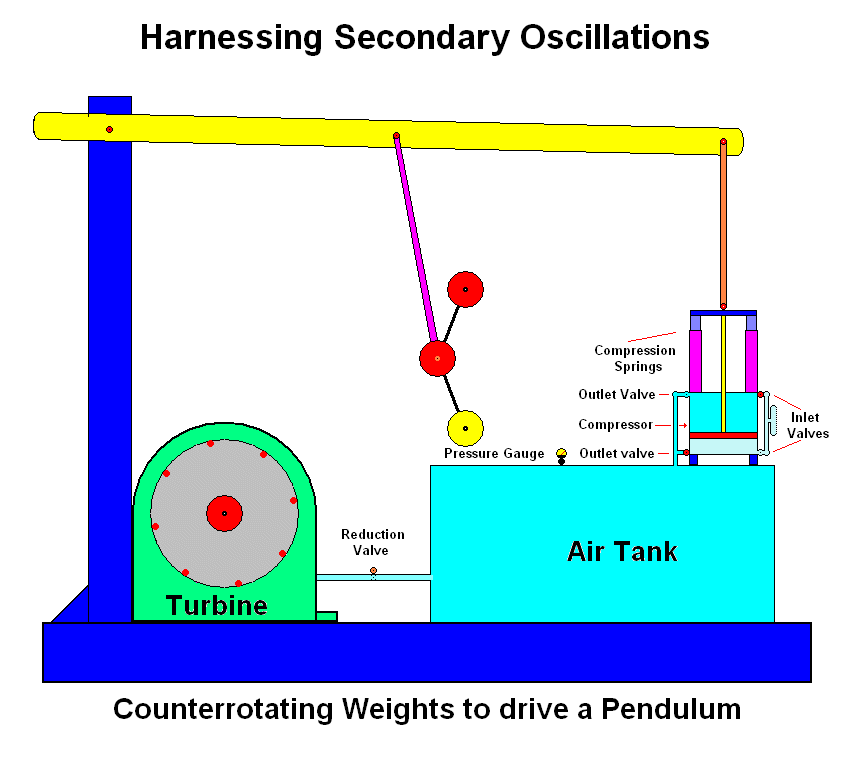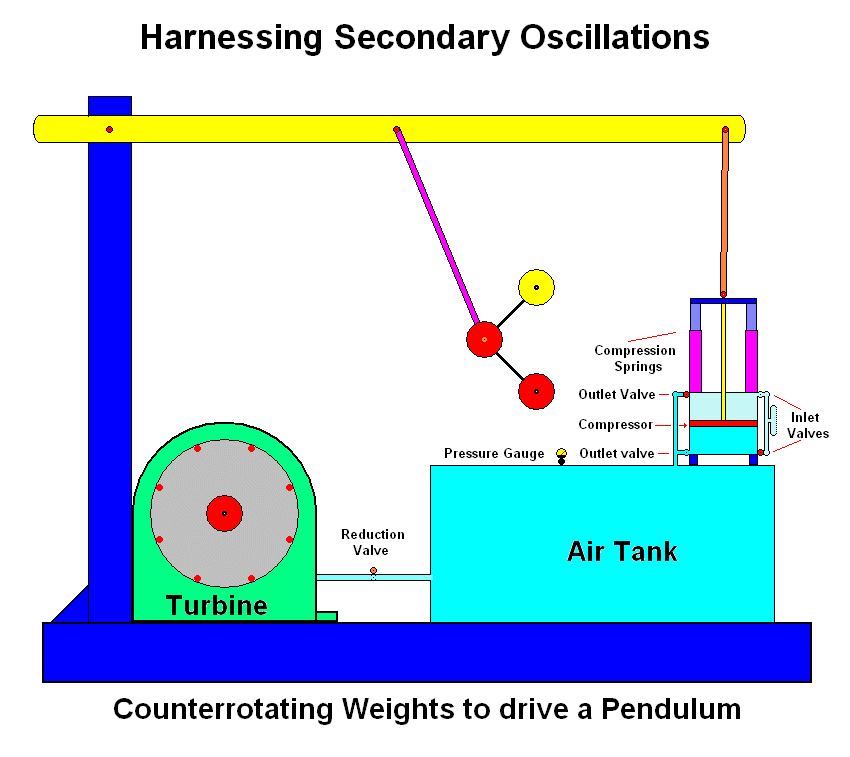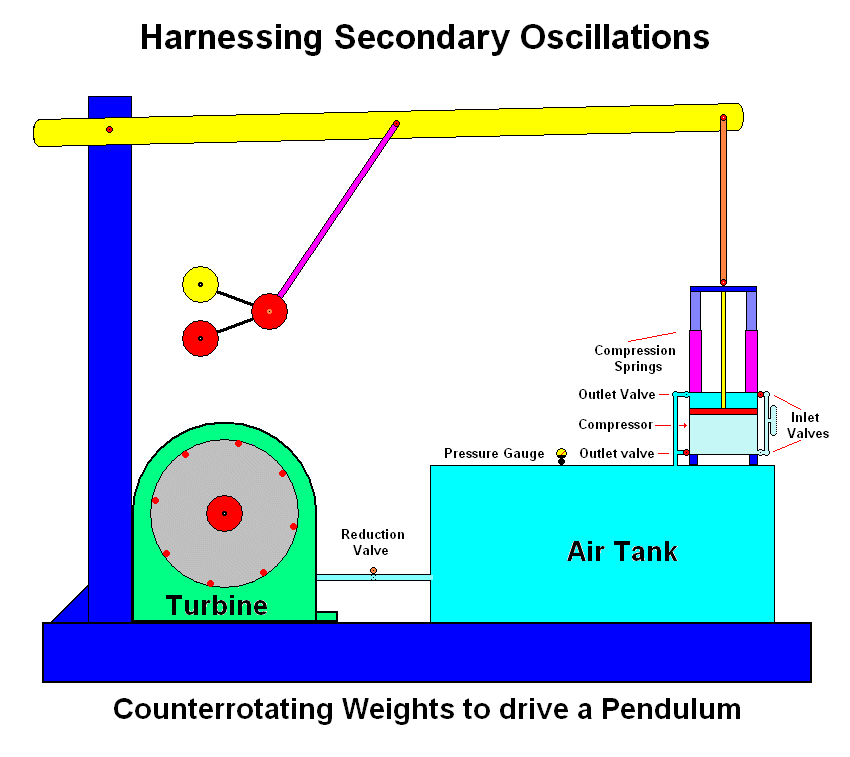
Below is a suggestion of how such a device might be built. The design relies as input on counter-rotating weights, as discussed. I have used a bi-directional compressor here as an output device. The reduction valve is simply there to smooth the output. To test the device all that would be necessary is to attach a flow meter instead of the turbine. That would give accurate results. Some hydraulic system based on the same concepts would probably be preferable. The design is a diagram and only intended to illustrate the inter-reaction of the different components. It is not to scale and should not be seen as a prototype for a working model. If such a device is capable of overunity I don't know. I haven't built it yet.

When I first started off as an engineer I received an advice from an old hand in the game that stayed with me all my life. He said: "Boy, if you have to make a mistake make it on paper, not on the job. It's cheaper."

He was, and still is, right of course. So, before we cut into steel let's have a closer look at it and let it stew for a while. Above all, let's look at alternative solutions before we commit ourselves. If it still looks good thereafter let's build the damn thing. It's early days yet.

So, here is the monster. Let me know what you think.